1 Introduction

The occurrence patterns of a considered word in a given written text can be interpreted as time series data along the text. Since analyses based on this dynamical interpretation provide abundant information compared to static pictures in which the written text is treated as an aggregation of statistically distributed words with certain probability distributions, methods of time series analysis have been adapted to written texts for various purposes including analysis of literary styles [1], investigations of word rhythms [2,3,4,5,6], and measurements of word importance [7, 8].

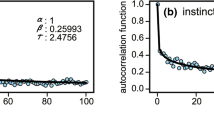
In a previous study [9], we investigated word occurrence patterns in written texts through analysis of autocorrelation function (ACF), which is known as one major method of time series analysis. The results of ACF analysis showed that frequent words which appear in written texts can be classified into two groups in terms of their ACFs. One group is the set of words that occur in a context-specific manner with memories that persist for, typically, several to several tens of sentences. The duration of the memories is thought to correspond to the length of sentences in which some notion or idea is described and therefore the considered word is important and indispensable for expressing that notion or idea. A word belonging to this group was called Type-I word. As seen in Fig. 1, the ACFs of Type-I words show a typical behavior of linear relaxation systems in which the ACF values gradually decreases from their initial value of one to the final constant values of almost zero. The words employed in the figure are typical Type-I words picked from ‘An Inquiry into the Nature and Causes of the Wealth of Nations’, which is an famous book in the field of political economy written by Adam Smith. The relaxation behavior of Type-I ACFs has been proved to be well described by stretched exponential functions [7,8,9]. The second group is the set of words that occur in a non-context-specific manner and therefore these words have occurrences that are governed by chance. Words belong to the second group were called Type-II words. ACFs of typical Type-II words, which are also taken from the book of Adam Smith, are shown in Fig. 2. As seen in the figure, ACFs of Type-II words abruptly decrease from their initial value of one at \(t=0\) to constant final values of almost zero at \(t>0\), indicating that ACFs of Type-II words can be well described by simple step-down functions. This behavior of ACFs means that stochastic processes generating Type-II words are completely memoryless. The most important difference between Type-I and Type-II words is, therefore, whether occurrence patterns of a considered word are accompanied by memories (Type-I words having long-range dynamic correlations/memories) or not (Type-II words having no dynamic correlations/memories).

Fig. 1
figure 1

Word occurrence signals \(X(t)\) (left column), which will be defined by Eq. (1) in the next section, and ACFs (right column) of the words “capital” ((a) and (b)), “price” ((c) and (d)), “revenue” ((e) and (f)), and “trade” ((g) and (h)), which are typical Type-I words picked from the Smith text. Occurrence of words in a context-specific and bursty manner, and long-range dynamic correlations are seen in the plots in the left and right columns, respectively. Red curves in the plots in the right column show best fitted results by use of the stretched exponential functions [7,8,9] optimized parameters of which are displayed in each of the plots

Full size image
Fig. 2
figure 2

Word occurrence signals \(X(t)\) (left column) and ACFs (right column) of the words “either” ((a) and (b)), “much” ((c) and (d)), “therefore” ((e) and (f)), and “though” ((g) and (h)), which are typical Type-II words picked from the Smith text. The words occur uniformly along texts (plots in the left column) and no types of correlations are seen (plots in the right column). Red lines in the plots of the right column show the step-down functions

Full size image

To classify a word as Type-I or Type-II without any ambiguity, we utilize the Bayesian information criterion (BIC) for model selection. Specifically, we evaluate two values of BICs one of which is a BIC for fitting a ACF of a considered word by using the stretched exponential function as a model function and the other of which is a BIC for fitting the ACF by using the step-down function. If the BIC of the fitting using the stretched exponential function is smaller than the BIC of the fitting using the step-down function, then we categorize the word as a Type-I word, otherwise we categorize the word as Type-II (For more detailed criteria for the classification, see [7]).

In the previous study [9], to investigate how memory works when Type-I words are emitted in texts, we have further performed simulations of generating texts by use of a pseudo‑text synthesis method. Although the simulations clarified that inheritance of words between subsequent paragraphs is key to generate dynamic correlations of Type-I words, the results of the previous study are still unsatisfactory in the following respects. First, structures of written texts were not taken into account in the simulations. This is a serious shortcoming because structured formats are their own characteristics of written texts and are considered to be one major origin of observed long-range dynamic correlations in written texts [8, 10,11,12]. To refine the previous model of generating Type-I words, it is therefore needed to incorporate hierarchical structures of written texts such as chapters, sections, subsections and paragraphs into a refined model of word generation. The second unsatisfactory point is that a stochastic process that governs the emissions of Type-I words has not been clarified. This is because the used simulation procedures in the previous study [9], which has certainly the ability of reproducing word occurrence patterns of Type-I words in real written texts, were too complicated to transform them into a stochastic model with suitable mathematical descriptions. To establish a stochastic model of generating Type-I words, therefore, we must extract substantial characteristics offering long-range memories from structures of written texts, and then construct a model based on those characteristics. The third point is that the stochastic process that governs the emissions of Type-II words was not clearly identified in the previous study. Although we have proposed that the Poisson point process is the first candidate of the stochastic process that yields Type-II words [7,8,9], it is still remains one candidate due to lack of verifications.

The purpose of this study is to establish stochastic models governing the occurrences of Type-I and Type-II words. To achieve this, we need more detailed information than that obtained by ACFs. In this study, we employ a waiting-time distribution (WTD) function to extract further information of the yielding processes of Type-I and Type-II words. To our knowledge, the WTDs have yet not been used for clarifying the stochastic processes of word occurrences. Therefore, the proposed stochastic models of yielding Type-I and Type-II words described in terms of WTDs are main contributions of this study. Furthermore, to verify our models of stochastic processes for Type-I and Type-II words, we will confirm that the results of classifying words into Type-I or Type-II using the proposed model functions of WTDs are asymptotically coincident with the results by using ACFs. This fact indicates that our models of WTDs capture the essential nature of the stochastic processes of yielding Type-I and Type-II words.

The rest of the paper is organized as follows. In the next section, in order to describe WTDs of word occurrences, the exponential, the q-exponential and the Weibull distributions are introduced with theoretical backgrounds. As will be illustrated later, stochastic processes having WTDs described by these three model functions are substantially memoryless, i.e., those stochastic processes do not show any type of dynamic correlations. Therefore, we can judge a stochastic process that yields a considered word as a memoryless one if the observed WTD for the word can be well described by one of the three model functions. After introducing the three model functions in Sect. 2, we present the results of curve fittings by use of these model functions in Sects. 3.1 and 3.2. The results show that WTDs of typical Type-II words are completely described by the q-exponential distribution but those of Type-I words cannot be fitted by any of the three model functions. Since all the model functions fail to fit observed WTDs of Type-I words, we develop a new stochastic model for WTDs of Type-I words in Sects. 3.3 and 3.4 based on the so-called Weiestrass random walk. It will be clarified that the model is consistent with the common hierarchical structure of written texts such as volumes, chapters, sections, subsections, paragraphs and sentences. It will be verified that the proposed model is very suitable to reproduce observed WTDs of Type-I words in Sect. 3.4. Section 3.5 presents a comparison of two classification criterions, both of which classify words into Type-I or Type-II but one criterion uses ACFs and the other uses WTDs. It will also be shown that both criterions become asymptotically coincident with each other as the number of occurrences of a considered word increases, indicating that both the proposed model for WTDs of Type-I words and the q-exponential distribution for WTDs of Type-II words are substantially valid. In the last section, we give our conclusions and discuss directions for our future research.

2 Methodology

In this section, we introduce three model functions of WTDs, which will be employed in Sects. 3.1 and 3.2 to fit observed WTDs for various Type-I and Type-II words.

2.1 Definitions of word occurrence signals and waiting time for word occurrences

First, we define a word occurrence signal of a considered word in a written text as

$$\begin{array}{l}X\left(t\right)=\left\{\begin{array}{c}1 \left(\mathrm{when~a~considered~word~occurs~at~the }~t\mathrm{th~sentence}\right)\\ 0 \left(\mathrm{when~a~considered~word~does~not~occur~at~the }~t\mathrm{th~sentence}\right)\end{array} . \right.\end{array}$$
(1)

We can adequately treat written texts as time series data with the \(X(t)\), because it has been proved that suitable ACF of word occurrences can be introduced by using that defined signals [7,8,9]. Note that, in Eq. (1), an ordinal number of sentences assigned from the first to the last sentences of a considered text plays a role of the time \(t\) along a considered text. Then a waiting time of the \(i\) th occurrence of a considered word can be defined as

$$\begin{array}{c}{t}_{wi}={t}_{i}-{t}_{i-1},\end{array}$$
(2)

where \({t}_{i}\) and \({t}_{i-1}\) are the times of the \(i\) th and \((i-1)\) th occurrences of a considered word. As usual time series data, distribution of \({t}_{wi}\), i.e., WTD of word occurrences, offers essential information of the stochastic process that yields a considered word in the text.

2.2 Model functions for WTDs of word occurrences

We consider three model functions to represent WTDs of word occurrences. The most fundamental one is the exponential distribution given by

$$\begin{array}{c}P\left({t}_{w}\right)={\lambda e}^{-\lambda {t}_{w}},\end{array}$$
(3)

where \(\lambda\) denotes the occurrence rate of the considered event, which corresponds to the average number of word occurrences per one sentence in our case. The exponential distribution, Eq. (3), is known as the WTD for the case in which occurrences of considered events are generated by an Poisson point process [13]. Since the Poisson point process is known as a completely memoryless process in which any two of non-overlapping time intervals do not exhibit any type of dynamic correlations [13], if the observed WTD for a considered word can be well described by Eq. (3), then we can conclude that the stochastic process that yields the word is memoryless.

The next model of WTDs is the q-exponential distribution defined by

$$\begin{array}{c}P\left({t}_{w}\right)=\left(2-q\right)\lambda {\left\{1+\lambda \left(q-1\right){t}_{w}\right\}}^{\frac{1}{1-q}},\end{array}$$
(4)

where \(q<2\) and \(\lambda >0\) are fitting parameters [14,15,16]. The q-exponential distribution, Eq. (4), is an extension of the exponential distribution, Eq. (3), in a sense that if we consider a limit \(q\to 1\), then Eq. (4) approaches to the limit given by Eq. (3). The q-exponential distribution can be derived from a superposition of the exponential distribution as follows. We consider a superposition of the exponential distribution with a weighting function \(f(\lambda )\);

$$\begin{array}{c}P\left({t}_{w}\right)={\int }_{0}^{\infty }f\left(\lambda \right)\lambda \mathrm{exp}\left(-\lambda {t}_{w}\right)d\lambda ,\end{array}$$
(5)

where \(\lambda\) is a rate parameter that characterizes the corresponding Poisson point process. Equation (5) is based on a super-statistical approach which is a major trend in the analysis of complex systems and has been used as a tool in physics, engineering, biology, and other fields [14,15,16]. If we assume that \(f\left(\lambda \right)\) is described by a Chi-square distribution, which is a reasonable assumption in the sense that their supports are limited to positive values, the WTD turns out to be the q-exponential distribution, Eq. (4) [17].

The third model function we employed for WTDs is the Weibull distribution given by [18]

$$\begin{array}{c}P\left({t}_{w}\right)=\alpha \beta {t}_{w}^{-\left(1-\beta \right)}\mathrm{exp}\left(-\alpha {t}_{w}^{\beta }\right).\end{array}$$
(6)

The Weibull distribution is another generalization of the exponential distribution, because substituting \(\beta =1\) and replacing \(\alpha\) with \(\lambda\) in Eq. (6) yields Eq. (3). The Weibull distribution has been widely used in areas including survival analysis, reliability engineering, electrical engineering, weather forecasting, and many more [19]. The Weibull distribution, Eq. (6), is known as the WTDs of the Weibull process which can be interpreted as one of inhomogeneous Poisson point processes. The inhomogeneous Poisson point process is a Poisson point process with a time-varying rate \(\lambda (t)\). The WTD of the inhomogeneous Poisson point process is then given by

$$\begin{array}{c}P\left({t}_{w}\right)=\lambda \left({t}_{w}\right)\mathrm{exp}\left\{-{\int }_{0}^{{t}_{w}}\lambda \left(\tau \right)d\tau \right\},\end{array}$$
(7)

which is apparently a generalization of the exponential distribution, Eq. (3). Using a time-varying rate function

$$\begin{array}{c}\lambda \left(t\right)=\alpha \beta {t}^{-\left(1-\beta \right)} \end{array}$$
(8)

and combining Eq. (8) with Eq. (7) gives the Weibull distribution, Eq. (6). This means that the Weibull process is an inhomogeneous Poisson point process having a time-varying rate given by Eq. (8). In the actual curve fitting procedures of WTDs for word occurrences, we used an alternative parameterization of the Weibull distribution which differs from Eq. (6). In the alternative parameterization, the WTD is expressed as [19]

$$\begin{array}{c}P\left({t}_{w}\right)=\frac{\beta }{\gamma }{\left(\frac{{t}_{w}}{\gamma }\right)}^{\beta -1}\mathrm{exp}\left\{-{\left(\frac{{t}_{w}}{\gamma }\right)}^{\beta }\right\}.\end{array}$$
(9)

Equation (9) is another expression of the Weibull distribution and it coincides with Eq. (6) when we define \(\alpha ={\gamma }^{-\beta }\). We use Eq. (9) instead of Eq. (6) because it is more popular for the purpose of expressing WTDs.

In short, we use three candidates to express the observed WTDs for word occurrences. The first is the exponential distribution given by Eq. (3), which is derived from the simplest Poisson point process. The second is the q-exponential distribution given by Eq. (4), which emerges from adopting a super-statistical approach to the Poisson point processes. The third is the Weibull distribution given by Eq. (9), the corresponding stochastic process of which is an inhomogeneous Poisson point process. As described above, the second and the third distributions are direct extensions of the exponential distribution, although the directions of the extensions are different. Note that the complete memoryless property of the original Poisson point process is inherited to processes having WTDs of the q-exponential distribution and to the processes having WTDs of the Weibull distribution. In the next section, we employ nonlinear curve fitting procedures to obtain best fitted curves of the observed WTDs using the three candidates.

3 Reuslts and discussion

3.1 Results of curve fittings for type-II words

Since the stochastic processes corresponding to the three model functions of WTDs described above are completely memoryless and thus do not have any dynamic correlations, we can expect that those three functions are suitable to describe WTDs of Type-II words but those are unsuitable to describe WTDs of Type-I words having dynamic correlations. We first consider WTDs of Type-II words. Figure 3 shows results of the nonlinear curve fitting to obtain best fitted curves of the observed WTDs for Type-II words with the three model functions. The words shown in the figure are the same as in Fig. 2. Optimized fitting parameters of the three curves in each plot are summarized in Table 1, which also shows the Bayesian information criterions (BICs) for the three candidates. The BIC is used as a criterion for model selection among the various models and the model with the lowest BIC is treated as the best [7]. As can be seen intuitively from Fig. 3, and also, can be clearly indicated by the values of the BICs, the q-exponential distribution gives the best fitted curves among the three candidates. In this study, we employed seven famous academic books to represent wide variety of written texts. Summary of the seven books employed are the same as listed in the Appendix of the previous study [9] with short names of Darwin, Einstein, Lavoisier, Freud, Smith, Kant and Plato. We performed nonlinear curve fitting procedures for all of the 359 Type-II words that appear more than or equal to 100 times in each of the seven books employed, and confirmed that the q-exponential distribution gives the best fitted curves among the three candidates without exceptions. This result means that the observed WTDs for Type-II words are best described by superpositions of exponential distributions. Consequently, the results tell us that the stochastic processes that govern generations of Type-II words are superpositions of Poisson point processes.

Fig. 3
figure 3

Plots of waiting time, \({t}_{w}\), versus proportion of \({t}_{w}\), \(P({t}_{w})\), for typical Type-II words. Linear scale plots are shown in the left column and log–log scale plots are shown in the right column. The results of non-linear curve fitting are shown as optimized fitted curves in the plots of the right column. Red, green, and blue curves show optimized fitted results using the q-exponential, the Weibull and the exponential distributions, respectively. Results for the words “either” ((a) and (b)), “much” ((c) and (d)), “therefore” ((e) and (f)), and “though” ((g) and (h)), which are typical Type-II words picked from the Smith text.

Full size image
Table 1 Optimized fitting parameters of best fitted curves shown in Fig. 3. The BICs corresponding to each fitting using the exponential, the q-exponential, and the Weibull distributions are also shown as BIC(exp), BIC(q-exp), and BIC(Weibull), respectively
Full size table

3.2 Results of curve fittings for Type-I words

Figure 4 shows WTDs of typical Type-I words which are the same as in Fig. 1. The two distinct characters of \(P({t}_{w})\) seen in the left column of the figure are as follows.

  • \(P({t}_{w})\) are more densely populated in a small \({t}_{w}\) region in the left column of Fig. 4 compared with Fig. 3. This result corresponds to the fact that Type-I words occur in a bursty and context-specific manner while Type-II words occur in a non-context-specific manner.

  • \(P\left({t}_{w}\right)\) of Type-I words for \({t}_{w}\) larger than 100 often does not decay to zero but takes positive finite values as seen in the left column of Fig. 4. However, the \(P\left({t}_{w}\right)\) of Type-II words for \({t}_{w}\) larger than 100 almost decays to zero as seen in the left column of Fig. 3. The duration of \(P\left({t}_{w}\right)\) for Type-I words is a reflection of the long-range dynamic correlation of Type-I words and the decay of \(P\left({t}_{w}\right)\) of Type-II words reflects their memoryless property.

Fig. 4
figure 4

Plots of waiting time, \({t}_{w}\), versus proportion of \({t}_{w}\), \(P({t}_{w})\), for typical Type-I words. Linear scale plots are shown in the left column and log–log scale plots are shown in the right column. In the right column, the results of non-linear curve fittings by using the q-exponential distributions are shown as green curves while red straight lines correspond to the best fitted hierarchical distribution, which will be described in subsection 3.4. Results are for the words “capital” ((a) and (b)), “price” ((c) and (d)), “revenue” ((e) and (f)), and “trade” ((g) and (h)), which are typical Type-I words picked from the Smith text

Full size image

As seen in the right column of Fig. 4, the fittings with q-exponential distributions are poor. We confirmed that both of the fittings using the exponential and the Weibull distributions are also failed to describe observed WTDs for Type-I words, although the fitted curves with these two model functions are omitted for clarity. The poor fitting results for Type-I words with the exponential, the q-exponential and the Weibull distributions mean that dynamic correlations of Type-I words inherently effect WTDs of Type-I words, and thus the WTDs of Type-I words are substantially different from those of Type-II words having no dynamic correlations. Therefore, the failures of fittings for Type-I words are reasonable because the employed three model functions represent WTDs of memoryless stochastic processes.

Another important finding in Fig. 4 is that plots of WTDs shown in the right column are well described by simple straight lines, which archive much better fittings than those by q-exponential distributions. The comparisons between fittings by use of the straight lines and those by use of the q-exponential functions will be described in Sect. 3.4, where it will be confirmed that fittings by use of the straight lines are more suitable in terms of BICs. A stochastic model which brings straight lines of WTDs in log–log plots is, therefore, preferable one for describing WTDs of Type-I words. In the following, we seek such a model through a simulation of generating Type-I word.

3.3 Simulation of generating type-I words in hierarchically structured texts

As mentioned before, the hierarchical structure embedded in written texts is considered as one major origin of dynamic correlations of Type-I words. Therefore, it is worthwhile to construct a stochastic model based on the hierarchical structure of texts and to check whether the model brings straight lines of WTDs in log–log plots or not. We tentatively construct a stochastic model which reflects the hierarchical structure of texts and simulate occurrence patterns of a Type-I word by using the model in the following manner.

We first assume that a considered text has 5 different levels of components, which are, for example, chapters, sections, subsections, paragraph and sentences. We further assume that there are 7 chapters in the text and each of the higher-level component consists of 7 lower-level components; that is, each of the 7 chapters consists of 7 sections, each section consists of 7 subsections, and so on. Consequently, the text has \({7}^{5}=\mathrm{16,807}\) sentences.

We then think a certain Type-I word and attempt to simulate occurrence patterns of the word in this text. To do this, we assume that the considered word is deeply related with some notion, i.e., the notion is not describable without the word. Basic idea of our model is that the notion has different affinities with individual components which exist at each of the different levels of the texts. To simulate those affinities, we simply identify certain portion of components at some level as relevant ones, which means that the relevant components have higher affinity to that notion than non-relevant components at the same level. We randomly choose 4 chapters as relevant chapters from the 7 chapters, randomly choose 4 sections as relevant sections from the 7 sections in the relevant 4 chapters, and randomly choose 4 subsections as relevant subsections from the 7 subsections in the relevant \({4}^{2}\) sections. This procedure of selecting 4 relevant components from 7 components in a relevant higher-level component continues until \({4}^{5}=\mathrm{1,024}\) relevant sentences are selected. Then, we tentatively set 6 values of occurring probability of the considered word, \(\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},{p}_{5},{p}_{6}\right)=\left(0.01, 0.02, 0.05, 0.1, 0.2, 0.9\right)\) each of which represents the following occurrence probabilities:

  • \({p}_{1}:\) Occurrence probability of the considered word in a sentence of irrelevant chapters.

  • \({p}_{2}:\) Occurrence probability of the considered word in a sentence of relevant chapters.

  • \({p}_{3}:\) Occurrence probability of the considered word in a sentence of relevant sections.

  • \({p}_{4}:\) Occurrence probability of the considered word in a sentence of relevant subsections.

  • \({p}_{5}:\) Occurrence probability of the considered word in a sentence of relevant paragraphs.

  • \({p}_{6}:\) Occurrence probability of the considered word in a sentence of relevant sentences.

Assigning one of the six probabilities, \({p}_{1}\sim {p}_{6}\), to each of the \(\mathrm{16,807}\) sentences results in Fig. 5(a).

Fig. 5
figure 5

Results of word occurrence simulation. (a) Simulated occurrence probability of a considered word in a text, which is constructed by a recursive algorithm. (b) Enlarged view of the dotted circle in (a). (c) Occurrence signal \(X(t)\) of the considered word in the text that is simulated by the probabilities shown in (a). (d) ACF calculated from \(X(t)\) shown in (c) and best fitted curve (red line) by use of the stretched exponential function of which optimized values of parameters are shown in the plot

Full size image

Given the probability function of Fig. 5(a), we can simulate word occurrences of the considered word in the text by using a simple Monte Carlo procedure. A realized occurrence/non-occurrence signal \(X\left(t\right)\) is illustrated in Fig. 5(c), which reveals the bursty and context-specific nature of word occurrences that is common in \(X\left(t\right)\) of real Type-I words (See the left column of Fig. 1). Figure 5(d) illustrates the calculated ACF from \(X(t)\) shown in Fig. 5(c), which shows typical ACF behavior of Type-I words, namely, a long-range dynamic correlation. Consequently, we can realize the ACF behavior of real Type-I words by using the recursive construction of a probability function \(P(t)\) described above in which the hierarchical structure of written texts is taken into account.

Figure 6 shows theWTD obtained from the simulated word occurrence \(X\left(t\right)\) shown in Fig. 5(c). The overall behavior of \(P({t}_{w})\) shown in Fig. 6 is very similar to Fig. 4; that is, it cannot be described by the q-exponential distribution but is more adequately presented by a linear function in the log–log plot. This result indicates that the simulated word occurrence \(X(t)\) has Type-I nature also in terms of WTDs.

Fig. 6
figure 6

Plots of waiting time, \({t}_{w}\), versus proportion of \({t}_{w}\), \(P\left({t}_{w}\right)\), for the simulated word occurrences in Fig. 5(c). (a) Linear scale plot and (b) log–log scale plot. The red straight line and the green curve show optimized fitted results by use of the hierarchical distribution (see Sect. 3.4) and the q-exponential distribution, respectively

Full size image

The difference between the simulation used in this study for generating Type-I words and that used in the previous study [9] is as follows. In the previous study, we introduced dynamic memory of word occurrences through word inheritance in which characteristic words of parent paragraphs are inherited to their subsequent paragraphs. In this study, the long-range dynamic memory is more naturally introduced through the affinity shared among components at various levels of hierarchical structure of texts.

3.4 Model of waiting time distributions for type-I words

What we have learned so far is that the recursive construction of a probability function \(P\left(t\right)\) based on the hierarchical structure of written texts is appropriate for reproducing WTDs of real Type-I words. Keep this result in mind, we try to construct a simple stochastic model which has an ability to offer the straight lines of WTDs in double-logarithmic plots.

An important inclusion in Fig. 5(c) is that the WTD is expected to have a hierarchical structure that consists of different levels of waiting times, such as waiting times between relevant sentences, those between relevant paragraphs, those between relevant subsections, those between relevant sections, and those between relevant chapters. Note that there is a distribution in each level of waiting times because the relevant components are selected in a random manner. To our knowledge, the simplest way to configure this kind of hierarchical WTDs is to utilize the so-called the Weiestrass random walk.

The Weierstrass random walk is an extension of the usual Brownian motion in which a Lévy-type jump-length distribution is incorporated and is used for modeling in physics, such as in nonlinear, fractal, chaotic, and turbulent systems [20,21,22], as well as for modeling in biology [23] and in finance [24]. The theory of the Weierstrass random walk suppose that the probability function of jump length \(l\) on a one-dimensional lattice with lattice spacing \(a\) is given by

$$\begin{array}{c}p\left(l\right)=\frac{M-1}{2M}\sum\limits_{j=0}^{\infty }\frac{1}{{M}^{j}}\left\{\delta \left(l-{b}^{j}a\right)+\delta \left(l+{b}^{j}a\right)\right\},\end{array}$$
(10)

where \(b>1\) and \(M>1\) are constants that characterize a considered Weiestrass random walk [22]. Equation (10) indicates that jumps of \(\pm a\) occur with probability \(C\), jumps of \(\pm ba\) with probability \(C/M\), jumps of \(\pm {b}^{2}a\) with probability \(C/{M}^{2}\), …, and jumps of \(\pm {b}^{j}a\) with probability \(C/{M}^{j}\) where \(C\) denotes the constant \((M-1)/(2M\)). An implication of Eq. (10) is that trajectories of the Weiestrass random walk form self-similar infinite hierarchies of visited sites, which becomes clearer when we consider 2 dimensional walks as seen in Fig. 7. In the figure, the lowest level clusters of visited sites consist of, on average, \(M\) jumps of length \(a,\) the second lowest level clusters consist of, on average, \(M\) such lowest level clusters separated by a distance \(ba\). This continues on at each level of hierarchy, resulting in a hierarchy of clusters within clusters. We modify Eq. (10) and then adopt the theory to express the WTD of Type-I words in the following manner.

Fig. 7
figure 7

Sample trajectory of a 2-dimensional Weiestrass random walk with 10,000 jumps. The trajectory was simulated using Eq. (10) with parameters \(a=1.0\), \(b=10.0\), and \(M=30.0.\) The directions of jumps were restricted to \(\pm x\) and \(\pm y\), and each direction was selected with equal probability

Full size image

Our model of WTD for Type-I words is based on the simple assumption that the waiting times defined by Eq. (2) are distributed according to a Lévy -like distribution defined by

$$\begin{array}{c}p\left({t}_{w}\right)=\frac{M-1}{M}\sum\limits_{j=0}^{\infty }\frac{\delta \left({t}_{w}-a{b}^{j}\right)}{{M}^{j}},\end{array}$$
(11)

Each of the terms of this sum give the \(j\) th level probability for the waiting time of \(a{b}^{j}\). The slight difference between Eqs. (10) and (11) emerges from the fact that waiting times \({t}_{w}\) are limited to take positive values in Eq. (11) while jump lengths \(l\) are allowed to take both positive and negative values in Eq. (10). A consequence of Eq. (11) is that the \(j\) th level waiting time \(a{b}^{j}\) occurs with a corresponding probability that is proportional to \(1/{M}^{j}\); that is, as the waiting time \({t}_{w}\) increases, the occurrence probability of that waiting time becomes smaller. Another consequence of Eq. (11) is that the occurrence times of a considered word along a timeline of a text, namely, \({t}_{1}, {t}_{2}, {t}_{3}, \dots\), (\({t}_{1}, {t}_{2}~ {\mathrm{and }~t}_{3}\) represent the times of the first, second, and third occurrences of a considered word), are expected to form a hierarchical cluster along the timeline as in the case of the two-dimensional Weiestrass random walks in which visited sites form hierarchical clusters as shown in Fig. 7. We think that this situation meets the key feature of WTD of Type-I words which have, as described before, a hierarchical structure consisting of different levels of waiting times.

From Eq. (11), we can write the waiting time and the corresponding occurrence probability of the considered word at level \(l\) as

$$\begin{array}{c}{t}_{w}=a{b}^{l}, {p}_{l}=\frac{{p}_{0}}{{M}^{l}},\end{array}$$
(12)

where \({p}_{0}=(M-1)/M\). Eliminating \(l\) from Eq. (12) gives

$$\begin{array}{c}\mathrm{log}{p}_{l}=-\left(\frac{\mathrm{log}M}{\mathrm{log}b }\right)\mathrm{log}{t}_{w}+\left(\frac{\mathrm{log}M}{\mathrm{log}b }\right)\mathrm{log}a+\mathrm{log}{p}_{0}\\ =-\alpha \mathrm{log}{t}_{w}+\beta \end{array}$$
(13)

where we define \(\alpha =\left(\frac{\mathrm{log}M}{\mathrm{log}b}\right)\) and \(\beta =\left(\frac{\mathrm{log}M}{\mathrm{log}b }\right)\mathrm{log}a+\mathrm{log}{p}_{0}\). Equation (13) indicates a linear relationship between \(\mathrm{log}{t}_{w}\) and \(\mathrm{log}{p}_{l}\). We call this relationship between \({p}_{l}\) and \({t}_{w}\) as "hierarchical distribution". This distribution is exactly what we see in Fig. 4 for WTDs of real Type-I words where linear functions give much better fits to the double-logarithmic plots of \({t}_{w}\) vs. \(P\left({t}_{w}\right)\) than those with the q-exponential distributions.

We attempt to fit the linear line given by Eq. (13) to the observed waiting time distributions of Type-I words in the double-logarithmic plots. The results are shown as red straight lines in Fig. 4. Note that we fix \(a=1\) in Eq. (13) because the value of \(a\) means the minimum value of waiting time, which is obviously one in our case of word occurrences. As mentioned before, the results of fittings using the q-exponential distribution are also shown as green lines in Fig. 4 for comparison. The optimized fitting parameters and corresponding BICs are shown in Table 2. Much smaller values of BIC(heir), which is the BIC for fittings using Eq. (13), compared with those of BIC(q-exp), which is the BIC for fittings using Eq. (4), indicate that the WTDs of Type-I words can be satisfactorily expressed by our model of hierarchical WTDs, Eq. (13). This result shows that the hierarchical distribution of WTD due to the hierarchical structure of written texts is a key to yield strong and long-range dynamic correlations of Type-I words. Hierarchical properties of written texts have also been reported [25] by using language frequency time series (LFTS) [26], although our methodology is different from that using LFTS.

Table 2 Optimized fitting parameters of best fitted lines/curves shown in Figs. 4, which are for the words “capital”, “price”, “revenue”, and “trade”
Full size table

3.5 Classification of words by ACFs and WTDs

We have been clarified that WTDs of Type-I words are well described by the proposed model of hierarchical WTDs (Eq. (13)), while those of Type-II words are well described by the q-exponential distribution (Eq. (4)). Therefore, in principle, we can judge the word type of a considered word by comparing the fitting result of WTDs by using Eq. (13) with the results by using Eq. (4). More specifically, if the fitting by using Eq. (13) gives a lower BIC value than that using Eq. (4), then we judge the considered word as Type-I otherwise we judge the word as Type-II. However, judging word type by comparing these two fittings has a weakness because Eq. (13) holds only in an approximate sense. The reasons why Eq. (13) is not strict are as follows. First, the parameters in Eq. (13), \(M\) and \(b\), cannot be constant throughout all levels of the hierarchy, but can vary among the hierarchical levels in real written texts. Moreover, the parameters can even be non-uniform within the same level in real texts. Next, the number of actual hierarchical levels is limited (probably not exceeding ten levels for almost all texts), although number of levels is unlimited in Eq. (13). The limitation of hierarchical levels in real texts lowers the quality of the fitting by using Eq. (13), particularly in the larger \({t}_{w}\) region where long range dynamic correlations play important roles.

In order to verify the validity of judging word type from fitting results of WTD by using Eqs. (4) and (13), we compare the results of the judging method with results using another method. The another method we use is classification of word type by use of the ACFs. This another method fits observed ACFs by using the stretched exponential function and it simultaneously fits observed ACFs by the step-down function, and then the corresponding two BICs are compared to determine the word type. A considered word is classified as Type-I if the BIC for the stretched exponential function is lower than that for the step-down function, otherwise the word is classified as Type-II [7]. The latter method using ACFs is expected to be more accurate than the method using WTDs, because it has been proven that fittings of Type-I ACFs by using the stretched exponential function give quite satisfactory results without any exceptions.

Table 3 gives a comparison of the classification results by using the two different judging methods. The classifications are performed on sets of frequent words that appear in the seven famous academic books. The results are shown at each of four different frequency levels of word occurrences. For example, Table 3(a) shows the results of frequent words that appear in 100 or more sentences in the corresponding book. The number of words that are classified as Type-I and of those classified as Type-II are listed in the table for each of the two methods. The heading “Concordance rate” in the last column of the table refers to the portion of words for which classification results by use of the two different methods coincide.

Table 3 Results of classifying word type for frequent words appearing in the 7 academic books. The classifications were made by using the two different types of curve fittings, namely, fitting to ACFs and to WTDs. Numbers of words that are classified into Type-I and Type-II are shown in the table for each of the two classification methods. Numbers of words for which the results of the two classification methods coincide are also shown as “number of concordances”. (a), (b), (c), and (d) are the results for words that appear in at least 100, 200, 300, and 400 sentences in each of the 7 books, respectively
Full size table

It is obviously seen in Table 3 and in Fig. 8 that the total concordance rate at a given frequency level (the bottom right cells of Table 3(a)–(d)) increases as the frequency level increases. This indicates that the results of classification using the two different methods asymptotically agree with each other when occurrences of words within a given text approach infinity. This result can be interpreted as follows. When the number of occurrences of a considered word increase, then the statistical quality of calculated \(P\left({t}_{w}\right)\) is also improved due to the increased sample size. This effect is more prominent in the larger \({t}_{w}\) region where there are insufficient samples. Therefore, as the occurrences of words in a text increase, the classification quality by use of WTDs is improved and it finally achieves almost compatible accuracy to the classification using ACFs under the condition that numbers of word occurrences are 400 or more. Although the classification of words using WTDs is not the best method as described above, the asymptotic coincidence seen in Fig. 8 suggests that the proposed model of the hierarchical WTDs (Eq. (13)) captures substantial stochastic structure of the occurrences of Type-I words.

Fig. 8
figure 8

Asymptotic change of concordance rates. The concordance rates are also shown in the bottom lines of Table 3(a)–(d) and are calculated as the total number of concordances divided by the number of all words under given conditions of occurrence times

Full size image

4 Conclusion

Words in written texts can be classified into two groups, namely, Type-I words and Type-II words. The former are words that show dynamic correlations in their occurrence patters, and the latter are words that do not show any dynamic correlations. In this study, we investigated the characteristics of these two types of words in terms of the distributions of waiting times. The waiting time distributions (WTDs) of Type-II words were proved to be well described by q-exponential distributions. This result indicates that the stochastic processes governing occurrences of Type-II words are superpositions of Poisson point processes with various occurrence rates. For Type-I words, we showed that the WTDs can be approximately reproduced by using a modified model of the Weiestrass random walk. We further checked the validity of the proposed model and showed that the description of WTDs by using the proposed model becomes satisfactory when the number of word occurrences in texts becomes larger than several hundreds. This result indicates that hierarchical distributions of waiting times, which reflect hierarchical structure of written texts, is a substantial property for yielding strong and long-range dynamic correlations of Type-I words.

The proposed model of WTDs for Type-I words needs some improvements. For example, we need to consider the distributions of parameters in the Weiestrass random walk model with some suitable probability distributions in order to describe word occurrences in real written texts. A study along this line that will attempt to improve on the expressive ability of the proposed model is left as future work.

Another possible direction of a future study is to establish a link between Type-I and Type-II words and their grammatical status. For example, we tentatively evaluate distributions of Type-I and Type-II words that appear in the seven employed books according to the parts of speech classification. For Type-I words that appear in at least 100 sentences, the top three categories are noun (76.7%), adjective (12.0%) and adverb (3.5%). On the other hand, for Type-II words at the same condition, the top three categories are noun (45.8%), adverb (19.6%) and adjective (14.4%). This result gives an impression that nouns are dominant in Type-I words while the proportion of nouns decreases and that of adverbs increases in Type-II words. It may be possible to contribute many language processing tasks by more detailed analysis of the link between Type-I and Type-II words and their grammatical functions.