Abstract
The main goal of this review is to provide a thorough scientific understanding of the interplay between stochastics and mechanics, by classifying what can be achieved by representing mechanical system parameters in terms of deterministic values (homogenization) versus random variables or random fields (stochastic upscaling). The latter is of special interest for novel Bayesian applications capable of successfully handling the phenomena of fracture in both the quasi-static and the dynamic evolution of heterogeneous solids where no scale separation is present, which we refer to as stochastic upscaling. We seek to quantify the sensitivity of these phenomena with respect to the size-effect (changes in characteristic system dimension) and to the scale-effect (changes in characteristic time evolution). The challenge is to provide an answer as to why a system that is big does not break under quasi-static loads in the same way as a small system, even when both are built of the same material, and further extend this to inelasticity and fracture under dynamic loads. We plan to illustrate the crucial role of fine-scale heterogeneities and to develop the ground-breaking concept of stochastic upscaling that can capture their influence on instability and dynamic fracture at the system macro-scale. The stochastic upscaling is the key to size and scale laws in the proposed multi-scale approach, which can reach beyond homogenization to properly account for epistemic uncertainties of system parameters and the stochastic nature of dynamical fracture.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Motivation and illustrations
The methodology proposed in this work develops novel concepts in irreversible thermodynamics of nonequilibirum processes (yet referred to as nonequilibrium statistical thermodynamics, see [12]), where neither space nor time scales are separated. This ground-breaking concept is here referred to as stochastic upscaling, providing a fruitful interaction of Mechanics (multi-scale approach) and Mathematics (uncertainty quantification). The stochastic upscaling truly applies across many scientific and engineering domains, where multiscale structure models are used to replace the testing procedure used to validate structure integrity or structure durability. The important challenge we deal within this paper is quantifying durability, life-time integrity, and safety against failure of massive composite structures under extreme loading conditions where real-size tests cannot be performed. The main applications come from the area of energy production, regarding dominant energy systems. Of special interest are (costly) massive structures (e.g. nuclear power plant) with irreplaceable components built of reinforced-concrete composites (e.g. nuclear reactor protection structure); see Fig. 1. The main difficulty pertains to characterizing a number of different failure modes that require the most detailed description and interaction across the scales. Here, we seek to significantly improve the currently dominant experimental approach, because the latter is either not applicable for the sheer size of the structure, or unable to exactly reproduce the extreme loads. We propose to use stochastic upscaling, where extensive small-scale (material) testing is supplemented with large-scale (structure) computations, which allows to explore the real fracture behavior of the system under various load scenarios in optimal design studies, and thus accelerate innovations in this domain.
Of special interest for the developments to follow are concrete composite materials (the dominant material in construction). However, the proposed methodology can also apply to carbon-fiber composites (the most advanced material in aerospace engineering), where the need for test replacements has already been recognized with the pyramid of tests [57] proposing multi-scale computations as complement or replacement of large-scale testing and leaving (extensive) testing only for small scales. Unfortunately, many homogenization-based approaches forget the need to address the role of probability, for the case when the scales are no longer separated. One such example is localized failure and fracture [30], where classical homogenization response remains insufficient for validation.
Another important reason for using a multi-scale approach is to predict crack spacing and opening in order to improve the durability of structures made of composite materials. For example, mixing cement-based composites with fiber reinforcements, one is able to compensate for the loss of durability of high-performance concrete with higher compressive strength. The latter occurs due to the use of a finer ground cement and increased C2S content, that results in a higher rate of hydration, which also produces higher peak temperatures due to cement drying, and more early-age cracks, or initial defects, thus reducing structure durability. Moreover, a high hydration rate also significantly reduces the subsequent self-healing capacity of micro-cracks typical of traditional concrete mixture, thus reducing high strength concrete durability, unless mixed with reinforcement fibers. Similarly, by adding to 3D woven carbon-fiber composites the corresponding reinforcement binders, we obtain a material with higher durability due to a much increased resistance to shear failure compared to traditional laminate composites.
From the standpoint of successfully constructing predictive fracture models, the composite materials of interest for the proposed multi-scale approach should share rather similar features with a two-phase meso-structure (aggregate vs. cement, or carbon vs. epoxy), a non-local dimension brought by long fiber reinforcement, and fabrication that is comparable to large-scale additive-manufacturing, where the complete structure is cast with the same material rather than an assembly of various components. The latter is the crucial hypothesis that can render the proposed stochastic approach feasible in terms of predicting probability-distribution-based estimates of material parameters valid for the whole structure (opposite to pre-fabricated structures characterized by a large difference between manufactured and on-site construction components).
1.2 Main research goals
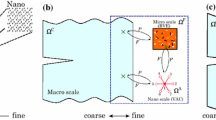
A new scientific challenge with respect to the state-of-the-art is to recast structure integrity and durability requirements for heterogeneous composites as a coupled stochastics-inelasticity problem at multiple scales. The heterogeneous composite materials with inelastic behavior leading to fracture can rather be considered as a dynamical system, where history dependent inelasticity at different scales will carry the information pertinent to durability or to material damage as the consequence of an applied loading program. The inelasticity at multiple scales implies using different spatial scales in order to reduce the uncertainty in providing the most appropriate representation of particular inelastic mechanisms typical of these heterogeneous composites, from initial defects to reinforcement slip (see Fig. 2). Given different sources of uncertainty at multiple scales concerned, it seems more appropriate to talk about inelasticity at multiple scales rather than multiscale inelasticity. This point-of-view is also in agreement with the role of probability, which is needed to retain the unresolved physics at smaller scales in terms of probabilistic noise at larger scales. This is done through stochastic upscaling (opposite to methods like relative entropy [83]). For the finest scales, due to composite material heterogeneities, one cannot predict the exact microstructure evolution with initial defects, unless assuming prior distributions of meso-scale fracture parameters at the aggregate–cement phase interface. Thus, one ought to find the solution to a multiphysics problem of coupled mechanics-chemistry of cement hydration by the National Institute of Standards and Technology (NIST) model (see Fig. 2), combined with cement-drying next to aggregates concrete composite resulting from shrinkage induced micro-cracks. Such results are then used to improve posterior probability distributions of meso-scale fracture parameters through Bayesian inference. This is an off-line probability computation performed as a pre-processing step were one can use many different microstructure simulations (or measurements) to construct predictive posterior distribution of meso-scale fracture parameters expressed as random fields (see Fig. 2). Subsequently, the uncertainty at the meso-scale will carry over to the macro-scale when computing the risk posed by concrete fracture to structure integrity. This ought to be performed as an on-line probability-finite-element computations that provides the variability of the structure response with uncertainty propagation starting from such meso-scale parameter probability distributions. Then, stochastic upscaling will be used again for scale-coarsening in order to produce a reduced model granting computational efficiency at the stage where the crack pattern in a particular finite element has stabilized. Finally, predicting crack spacing and opening, which plays the crucial role for structure durability, requires to deal with uncertainties in bond-slip distribution all along a particular reinforcement bar (see Fig. 2). Therefore, the proposed multiscale approach to quantify fracture integrity and durability of large structures built of concrete composites must be capable of spanning from fine scales defining initial defects, placed at microns (\(10^{-6} \text {m}\)), to structure scales that can reach over \(100\, \text {m}\) for large composite structures; see Fig. 2. Thus, the problem complexity is at least comparable to nano-mechanics (or classical domains of statistical mechanics), or even higher, due to microstructure complexities (16-phase representation of cement hydration product by the NIST model; see Fig. 2), that impose a more elaborate probability framework.
Ambitious objectives that go beyond the current state-of-the-art concern developments in a predictive multiscale approach where all scales are to be treated probabilistically, and not only capturing the average response on the larger scale by the classical homogenization approach. This is particularly important for concrete composites where the scales characterizing material heterogeneities are in general not well separated. Such is the case when testing reduced-size specimen with respect to microstructure heterogeneities, where significant variability occurs in the test results due to small-scale uncertainty. More important for these quasi-brittle composites is the fracture sensitivity to small-scale defects that trigger crack coalescence and accelerates structure failures. This is especially visible when more than one failure mode is active, where only fine-scale models representing material heterogeneities can provide sufficiently predictive results, and where classical homogenization fails. While there are already quite a few works on multiscale modeling of fracture, a multiscale two-way coupling for the probabilistic description presented herein is still lacking. Namely, all scales are considered as uncertain, and thus will be modeled with a stochastic description. This is done with a novel stochastic upscaling approach, where any coarse scale can retain the unresolved physics of the smaller scale in terms of the corresponding probability distribution properties to match a quantity-of-interest (e.g. strain energy or inelastic dissipation). The probability computations objective is twofold. First an off-line probability computation is performed in terms of pre-processing by Bayesian updates of (many) realizations for the particular composite material microstructure with initial (or aging-induced) defects to define meso-scale (e.g. phase interface) parameters as random fields. Second, an on-line probability computation to carry on with uncertainty propagation starting from such meso-scale to the structural scale, where computational efficiency with a mechanics-based model reduction is achieved by data compression with low-rank tensor approximations.
1.3 Novelty with respect to state-of-the-art
With the vast majority of recent works limited to the linear or mildly nonlinear case, a coupled nonlinear mechanics-probability formulation still remains an open problem. The high gain pertains to providing the predictive computational tools for accelerating experiments and offering a probability-supported explanation of the size effect (with different failure modes for different size structures built of same heterogeneous material), and to the scale effect (with different time-evolution regimes for different size of structure built of same heterogeneous material). The successful solution of the coupled probability–inelasticity problem at multiple scales is the key milestone in building the comprehensive tools for the monitoring of large composite structures, and for decision-making tools to quantify their fracture integrity and durability.
The main contribution going beyond the state-of-the-art is in seeking to connect such vastly different scales and their roles, from multiphysics driven microstructure evolution to non-local scales of long fiber reinforcement. This is a rather different point-of-view from the classical approach where each problem is typically studied independently, by a specialist of particular domain (i.e. cement hydration vs. concrete microstructure vs. concrete fracture vs. reinforcement design). More precisely, here we further discuss a number of novelties:
-
(i)
Thermodynamics-based theoretical formulation for fracture and inelasticity at multiple scales, which does not need any regularization, contrary to currently used models such as gradient plasticity [66], non-local damage models [63], or the phase-field approach [10]. The proposed theoretical formulation is firmly rooted in thermodynamics and energy based approximations that need no regularization of governing variational equations. It can represent correctly the additive split of total dissipation into volume and crack-surface components, the full set of fracture mechanisms at different scales, and their evolutions and interactions. It can also include the non-local representation of reinforcement slip.
-
(ii)
The proposed discrete approximation for each particular scale is the most suitable choice with: Voxel representation [5] of microstructure at micro-scale, Voronoi cells [38, 39] for meso-scale, embedded discontinuity finite element methods (ED-FEM) [40] for macro-cracks and extended finite element method (X-FEM) [3] for non-local slip or reinforcement. Namely, X-FEM is the most suitable global representation, which is precisely the case of non-local slips along a particular reinforcement bar. Similarly, ED-FEM combining volume dissipation in the fracture process zone and surface dissipation in the macro-crack is the best (element-wise) approximation of dissipated energy, as opposed to the best representation of a macro-crack as proposed with the earlier version of X-FEM [3] or phase field methods [10]. Finally, the choice of Voronoi cells, besides the most efficient mesh generation, can provide a representation of both elastic anisotropic response and the full set of failure modes for two-phase composites [45].
-
(iii)
The stochastic upscaling is an original approach that provides a scale-coarsening strategy, much different from previous ad-hoc choices (e.g. see [4]). The starting point in our discussion is the effect of initial defects at the meso-scale, with properties expressed as random fields. The probability distribution of such random fields can be obtained in off-line computations by using simulation tools for cement microstructure evolution [5]. The stochastic upscaling is capable of accounting for fine-scale initial defects, especially at the cement-aggregate interface as the weakest phase of concrete composites. From such a starting point we carry on with on-line computations, with two possible ways for stochastic upscaling to the macro-scale: (i) stochastic plasticity [31], where macro-scale material parameters are reduced to random variables in order to gain computational efficiency; (ii) probability-based interpretation of the size effect [35], where macro-scale material parameters have to represented by correlated random fields.
-
(iv)
The key point in uncertainty propagation is the computation of the probability distribution for coarse-scale models, which is carried out by Bayesian inference [62]. We discuss two possible methods to carry out the Bayesian inference based upon either the Markov Chain Monte Carlo (MCMC) or the Gauss Markov Kálmán Filter (GMKF) approach. With such an approach one can recover a reduced model that defines probability distributions of fracture parameters describing localized failure with both volume and surface dissipation. Such a mechanics-based model reduction is fundamentally different from the vast majority of recent works using statistical modes with either Proper Orthogonal Decomposition (POD) or Proper Generalized Decomposition (PGD) (e.g. see [8, 47, 68] or [7]). More importantly, we can thus recover any probability distribution of structure failure modes for advanced safety evaluation, contrary to previous works using pre-assigned probability distributions: log-normal for constructing fragility curves [85], uniform for constructing bounds [48], Weibull to account for weakest link failure [49], or ad-hoc combination of power law and Gaussian as two asymptotic values [2].
1.4 Paper outline
We have organized the paper as follows. In Sect. 2 we discuss the main ideas pertinent to the classical and numerical homogenization, which implies replacing elastic properties of heterogeneous composites by average values. We then take such simple setting of average elastic properties evaluation to introduce an alternative approach to homogenization based upon stochastics and to present two different methods Markov Chain Monte Carlo (MCMC) and Kalman Gauss Markov Filter (KGMF), given confirmation of superior efficiency of the latter. This is done in Sect. 3, which also presents the most complete developments of different tools for stochastics, since they apply in the same manner to either linear elastic behavior or to nonlinear fracture of heterogenous composites, although not with same outcome, as shown in Sect. 3.
The latter sections present the main thrust of the paper, with a number of recent (and original) results, most of which pertain to different mulitiscale modeling aspects of composite materials. In particular, in Sect. 4 we provide the reduced model of stochastic plasticity for localized failure and fracture of cement based composites. The proposed approach clearly illustrates the benefits of using Bayesian inference in order to replace computational intensive fine scale computations, whenever possible (typically, when the crack pattern has stabilized where we can use embedded discontinuity finite element discrete approximation) in terms of more efficient coarse scale model that can preserve the same results for quantities of interest (here chosen as either strain energy for elastic or plastic dissipation for inelastic response phase). We show how to define for such coarse scale reduced models not only their parameters, but also their probability distribution (i.e. defining the parameters of reduced model as random variables, with not necessarily simple Gaussian probability distribution).
In Sect. 5, we go a step further in modeling composite materials with fiber reinforcement and present the reduced model for reinforced concrete structures. The same stochastic tools are used, so we can focus on modeling issues, and illustrate that the proposed models are capable of capturing crack spacing and opening, along with corresponding variability of results.
Sections 6 and 7 present very important results for the final goal of our paper, which pertain to size and scale effects. Namely, the dominant failure modes are not the same for two structures (large vs. small) that are built of the same composite material, which is often referred to size effect. In Sect. 6, we provide the probability-based explanation of the size effect, with the main role played by sound modeling of reduced model parameters in terms of correlated random fields. Similar random fields parameter modeling also allows to illustrate that the dynamic response for two structures (large vs. small) built of the same composite material will not be the same. In Sect. 7, we present the probability-based explanation of this phenomena, which we refer to as scale effect. The practical benefit of capturing scale effect is illustrated in terms of classical Rayleigh damping by inelastic multiscale model.
For clarity, both ideas in Sects. 6 and 7 are illustrated in the simplest 1D setting. The same is done in Sect. 8 for stochastic solutions that go beyond Young measures, which represent the most general case with model parameters chosen as random fields. In Sect. 9, we state the paper conclusions.
2 Classical and numerical homogenization
Perhaps one of the most successful Reduced Order Models (ROM) was obtained by the classical homogenization approach, seeking to provide values for model parameter at a coarse (structure) scale in terms of an effective replacement of real properties on a fine (material) scale; see Fig. 3a. Thus, homogenization is intrinsically a multiscale method starting with corresponding microstructure observations.
Such a multiscale method was first successfully applied to estimate linear (elastic) behavior of heterogeneous composite materials, and produces the effective mechanical properties (e.g. effective elastic modulus). In mathematics, such an effective value may be reached by means of asymptotic analysis [52], and a solution to a cell problem of size T to define an effective modulus \({\bar{A}}(x)\) from the periodic variation of a real micro-scale modulus \(A^\varepsilon (x) = A (x, {x / \varepsilon })\), characterized by a scale separation parameter \(\varepsilon\), by introducing suitable parameterization at micro-scale with a new variable \(y = {x / \varepsilon }\). Furthermore, with the key assuming on scale separation, one may seek the solution \(u^{\varepsilon }\) in terms of asymptotic development in \(\varepsilon\) resulting with the asymptotic approach to homogenization summarized in (1):
where \({\bar{A}}(x)\) is the homogenized macro-scale modulus, and \(\chi\) is a T-periodic field provided as the solution to the cell-problem: \(-\nabla _y \cdot (\nabla _{y} \chi A^T) = \nabla _y \cdot A^T\) .
Classical homogenization in mechanics first requires to define a micro-scale representative volume element (RVE), where all microstructure details are visible (with their variations sufficiently well represented with variable y). At macro-scale, such RVE corresponds to a point x, with corresponding values of displacement \(u^M(x)\), strain \(\epsilon ^M(x)\) and stress field \(\sigma ^M(x)\); see Fig. 3b. The homogenization implies that one can match the (internal energy) results at two scales by averaging either stress or strains at micro-scale over RVE, as indicated in (2a). The main remaining question concerns the boundary conditions imposed on RVE in computing such homogenization. Here, one can define either an upper bound for the homogenized properties when imposing displacement boundary conditions on RVE, or a lower bound when imposing stress boundary conditions on RVE level [24]. Finally, we can impose the periodic boundary conditions on RVE leading to classical homogenization approach in mechanics, as summarized in (2) below:
where we denoted micro-scale displacement \(u^m(x)\), strain \(\epsilon ^m(x)\) and stress \(\sigma ^m(x)\), and \(F^M\) the corresponding macro-scale deformation gradient (see [37] for more details). Interestingly enough, both the asymptotic analysis in mathematics and the RVE approach in mechanics—when considering periodic boundary condition imposed on RVE scale and the energy norm in matching the two scales [24]—provide the same result for the linear elastic properties. Although these results in mathematics and mechanics were obtained at research centers at the same university in Paris, there was no apparent collaboration between the two groups (a practice that we seek to change with this review).
For a more general problem with lack of microstructure periodicity, one replaces classical homogenization with numerical homogenization combined with the weak form of the governing multiscale evolution equations [37]. The latter is proposed in [41], by considering the classical discrete approximation constructed with the finite element method resulting with:
where \(N^M_a(\cdot )\) and \(N^m_b(\cdot )\) are the shape functions corresponding to each scale in \({\mathcal {V}}^M\) and \({\mathcal {V}}^m\) respectively, \(d^M_a(t)\) and \(d^m_b(t)\) are the real time dependent nodal displacements, while \({w}^M_{a}\) and \({w}^m_{b}\) are the time-independent virtual displacement nodal values. An additional advantage of numerical homogenization is its straightforward extension to nonlinear problems, where, with no loss of generality, we assume that all the internal variables \(\xi ^{m}\) are defined only at the micro-scale. Thus, the state variables can be written as: displacements at the macro-scale \(d^M(t)\), displacements at the micro-scale \(d^m(t)\), and the internal variables governing the evolution of inelastic dissipation at the micro-scale \(\xi ^{m}(t)\), which can be obtained by a corresponding time-integration scheme used to compute their evolution in agreement with an applied loading program. This can be presented more formally in terms of:
Abstract numerical homogenization in \([t_n , t_{n+1}]\)
Given: \(d_n^M, d_n^{m,e}, \xi _n^{m,e} \ ; \ \forall e \in [1,n_{el}^M]\)
Find: \(d_{n+1}^M, d_{n+1}^{m,e}, \xi _{n+1}^{m,e}\)
Such that the (weak form of the) equilibrium equations discretized with (3) at the macro-scale and the micro-scale are satisfied:
where \({\mathbb {A}}\) symbolizes the FEM assembly operator, and e.g. \(\dots \biggr |_{d^{M,e}}\) in (5) means that the macro variables \(d^{M,e}\) are kept constant while solving (5) for \(d^{m,e}\) and \(\xi ^{m,e}\), and similarly for (4). The structure of the micro-macro equilibrium equation (5) and (4) is very much similar to those for the classical plasticity model [37], in the sense that the first part in (4) are global equations, which concern all the macro-scale elements and nodal values of \(d^M\), whereas the second part in (5) are local equations which concern the micro-scale values of \(d^m\) (and internal variables \(\xi ^m\)) computing the microstructure evolution within one particular macro-scale element at the time. Such analogy with classical plasticity allows us to directly exploit the operator split method in order to separate the global from the local equation solution process. In other words, for each one of the global iterations we carried out with (4), in general, several local iterations leading to converged solutions of (5) are performed. First, in each global iteration at the macro-scale, one solves the linearized form of the structure equilibrium equations with iteration over i
where the macro-scale stiffness matrix \(K^M\) and internal force vector \(f^{M,int}\) are obtained by the finite element assembly procedure taking into account the corresponding converged solution at the micro-scale [41]. In each i-iteration in the linearization (6) of (4), the local micro-scale linearizations (7) of (5) are iterated over j locally to convergence:
There is a fundamental difference between such a multiscale approach [41] versus numerical homogenization referred to as the finite element squared method (FE\(^2\)) [16],
Model FE\(^2\) for a three-point bending test, with a finite element mesh composed of Q4 isoparametric elements at macro-scale and another mesh of Q4 elements constructed at micro-scale: a FE\(^2\) method with micro-scale mesh constructed at each Gauss point of macro-scale element; b proposed method [41] with micro-scale mesh constructed for each macro-scale element—mesh-in-element (MIEL)
where one constructs the homogenized stress and elasticity tensor by using the results in (2) at each numerical Gauss quadrature point at the macro-scale, and then carries on with standard computations of the macro-scale element internal force and stiffness matrix by standard numerical integration; see Fig. 4.
The FE\(^2\) approach can face difficulties if used with a structured mesh. One illustrative example comes form [41], where a macro-scale finite element has a simple rectangular geometry, but with two-phase material properties and phase-interface placed inside the element. Fig. 5 provides a comparison between an exact microstructure representation for a coupled damage-plasticity model versus a structured mesh representation with a \(5 \times 5\) quadrature rule for a simple 4-node element suggested by [89]. Moreover, the standard FE\(^2\) approach fails in dealing with fracture mechanics problems, whereas the proposed numerical homogenization approach—mesh-in-element (MIEL)—remains capable of dealing with such a case, which is particularly important when the scales are no longer separated [77] and size effects come into play.
3 Stochastic homogenization
While the classical approaches to homogenization just described essentially assume a certain and deterministic micro-structure which varies on smaller scales amenable to possible (though costly) computational resolution, another approach is to start from the assumption that the micro-structure is uncertain, and possibly also has variations on scales finer than the numerical resolution. Such an uncertain micro-structure may be described with methods from probability theory and random fields, and these probabilistic methods also offer a way for the upscaling. Thus a short detour through the pertinent topics in stochastics is needed, especially as these methods will also be used in other circumstances than just elastic upscaling later.
3.1 Random fields for micro-structures
What is desired is, in this simplest case, to model the modulus A(x) in (1) resp. (2) as a random field (RF). Such a random field \(A(x,\omega )\) may be thought of at each fixed point of the domain \(x\in {\mathcal {V}} \subseteq {\mathbb {R}}^d\) as a random variable (RV) on a suitable probability space \(\left( \Omega , {\mathfrak {U}}, {\mathbb {P}}\right)\) (see e.g. [59]), where \(\Omega\) is the set of all elementary random events—the set of all possible realizations—and \({\mathfrak {U}}\) is the \(\sigma\)-algebra of measurable subsets \(S\subseteq \Omega\) to which a probability \({\mathbb {P}}(S)\) can be assigned. With such a RF, the probabilistic equivalent of (1) would be a stochastic partial differential equation (SPDE) (see e.g. [59]):
and the response \(u(x,\omega )\) is itself a random field.
The most basic characterization of such a RF is through its mean-value function or expectation \(\mu _A(x) = {\mathbb {E}}(A(x,\cdot )) = \int _\Omega A(x,\omega )\, {\mathbb {P}}(\mathop {}\!\mathrm {d}\omega )\), and its zero mean fluctuating part \(\tilde{A}(x,\omega ) = A(x,\omega ) - \mu _A(x)\), the part which is really random. A frequently employed representation of this fluctuating part is through a separated representation \(\tilde{A}(x,\omega ) = \sum _\ell \xi _\ell (\omega ) A_\ell (x)\), a linear combination of deterministic functions \(A_\ell (x)\) with random variables (RVs) \(\xi _\ell (\omega )\) as coefficients, and convergent limits of such expressions in appropriate topologies. The most useful topology on RFs is the one given by the inner product \(\left\langle \xi \mid \eta \right\rangle _{\Omega } {:=} {\mathbb {E}}(\xi (\cdot ) \eta (\cdot ))\) for two RVs \(\xi , \eta\), generating the Hilbert space of RVs with fine variance \(L_2(\Omega ,{\mathbb {P}})\), combined with the space \(L_2({\mathcal {V}})\) for spatial functions with the usual inner product \(\left\langle a \mid b \right\rangle _{{\mathcal {V}}} {:=} \int _{{\mathcal {V}}} a(x)b(x)\, \mathop {}\!\mathrm {d}x\). For RFs this gives the Hilbert space \(L_2(\Omega \times {\mathcal {V}}) = L_2(\Omega ) \otimes L_2({\mathcal {V}})\) with an inner product defined for elementary separated fields \(A(x,\omega ) = \xi (\omega ) a(x)\) and \(B(x,\omega ) = \eta (\omega ) b(x)\) by
and extended by linearity to all of \(L_2(\Omega \times {\mathcal {V}})\), so that the inner product of the fluctuating parts is the covariance \(\text {cov}(\xi ,\eta ) = \left\langle \tilde{\xi } \mid \tilde{\eta } \right\rangle _{\Omega }\); two RVs with \(\text {cov}(\xi ,\eta )=0\) have orthogonal fluctuating parts and are called uncorrelated.
One of the best known separated representations is the Karhunen–Loève expansion (KLE), which may be seen as a singular value decomposition (SVD) of the random field. It is usually computed using the covariance function \(C_A(x,z)= {\mathbb {E}}(\tilde{A}(x,\cdot )\otimes \tilde{A}(z,\cdot ))\)—the tensor product is there in case \(A(x,\omega )\) is vector valued—as the integral kernel of a self-adjoint positive definite Fredholm integral eigenvalue equation (see e.g. [59] for more details) to obtain \(L_2({\mathcal {V}})\) orthonormal eigenfunctions \(\varphi _\ell (x)\) with non-negative eigenvalues \(\lambda _\ell\), representing partial variances. The KLE—a concise spectral representation of the RF [59]—then reads
where \(\xi _\ell (\omega )\) are uncorrelated RVs of zero mean and unit variance (\(L_2(\Omega )\)-orthonormal), with the eigenvalues \(\lambda _\ell\) usually ordered in a descending order, so that a series truncated after N terms is the best N-term approximation in the \(L_2(\Omega \times {\mathcal {V}})\)-norm. In the end the RF is computationally represented by a (finite) set of RVs.
In case the field is Gaussian, i.e. the RVs \(A(x,\cdot )\) are Gaussian at each \(x\in {\mathcal {V}}\), so are the RVs \(\xi _\ell\) in (10), in which case they are then not only uncorrelated but independent. Material properties are usually non-Gaussian fields (e.g. log-normal), but a representation in independent RVs is very desirable in order to simplify integration of stochastic integrals. In such a case they may be expressed either directly as functions of Gaussian fields (see e.g. [59]) \(A(x,\omega ) = \Upsilon (x, \gamma (x,\omega ))\), where \(\Upsilon\) is a point-wise transformation, and \(\gamma (x,\omega )\) is a Gaussian random field represented as in (10), or the uncorrelated coefficient RVs \(\xi _\ell\) in (10) are non-Gaussian and may be expanded as functions of independent Gaussian RVs \(\varvec{\theta }(\omega )=(\theta _1(\omega ),\dots ,\theta _j(\omega ),\dots )\):
The multi-variate functions \(\Psi _{\varvec{\alpha }}\) are often chosen as a set of multi-variate Hermite-polynomials \(H_{\varvec{\alpha }}\) [90, 91], in which case in (11) one has Wiener’s well-known \(L_2(\Omega )\)-complete polynomial chaos expansion (PCE). In a computational setting, the expansion in (11) is naturally truncated to a finite number of terms. In the end, any RF or RV may be represented in appropriate topologies is such a way, the representation is given computationally via the tensor of coefficients \(\Xi ^{(\varvec{\alpha })}_\ell\).
3.2 Bayesian updating
How to obtain the probability distribution of these RFs resp. RVs on the macro scale will be shown in more detail in Sect. 4.1. One way to solve this task is provided by probability theory itself. It will be shown here in the simplest case of identification of macro scale elastic properties.
In Fig. 6 it is shown a realization of a highly heterogeneous random field for elastic properties, which we want to scale up to just one spatially constant homogenised value. To achieve this, one may use Bayesian methods (e.g. see [62]) by considering the macro-scale homogenized value as an uncertain quantity and modelling it as a random variable. To couple the two scales, one has to define quantities which have to be matched between the scales. Here, as elastic behavior describes mechanically reversible processes, similarly to (2), the stored strain energy was taken as quantity to be matched. This actually would allow the computational models on different scales to be totally different, as long as both support the notion of reversible stored energy \(y=\Phi _e\), which will be considered as the quantity to be observed. Denote the quantities to be identified by the symbol q, a RV with values in the space \({\mathcal {Q}}\), in our case \(q = (\kappa , G)\)—the bulk- and the shear-modulus; and these uncertain quantities are modelled as RVs with our current knowledge, the so-called prior distribution.
Bayes’s theorem is considered as the consistent way to update a probabilistic description when new data in the form of observations \(\varvec{\hat{y}}\) with values in the space \({\mathcal {Y}}\) (here the micro-scale stored energy \(\varvec{y}=\Phi _e\)) is available. Probably the best known version of Bayes’s theorem is the update of the probability density (pdf) of q, e.g. [6, 75, 87]. This formulation can be used when all considered quantities have a joint probability distribution [6, 73], which we shall assume from now on. In such case it is possible to state Bayes’s theorem for densities for the conditional density \(\pi _{(Q|Y)}(q|\varvec{y})\) of q given the observation \(\varvec{y}\):
where \(\pi _Y(\varvec{y}) = \int _{{\mathcal {Q}}} \pi _{(Q,Y)}(q,\varvec{y})\,\mathop {}\!\mathrm {d}q\)—the evidence—is the pdf of the RV \(\varvec{y}\) (the observation resp. measurement including all observational or measurement errors \(\epsilon\)), \(\pi _Q(q)\) is the prior pdf of q mentioned above, and \(\pi _{(Y|Q)}(\varvec{y}|q)\) is the likelihood of observing or measuring \(\varvec{y} {:=} Y(q,\epsilon )\) given q, where the function \(Y(q,\epsilon )\) predicts the measurement RV as a function of the RV q and some random observation errors \(\epsilon\). Typically the model resp. prediction of the observation will be a function of q through the solution \(u(x,\omega )\) of (8), i.e. \(\varvec{y}(q) = Y(q,\epsilon )=\hat{Y}(u(q),q,\epsilon )\). The joint density is factored into the likelihood and the prior: \(\pi _{(Q,Y)}(q,\varvec{y}) = \pi _{(Y|Q)}(\varvec{y}|q) \pi _Q(q)\), which is how the joint pdf is typically available. Given a specific observation resp. measurement \(\varvec{\hat{y}}\), the conditioned posterior pdf is then given simply by \(\pi _{(Q|Y)}(q|\varvec{\hat{y}})\).
The statements in (12) are formally correct both for the case where one wants to make a parameter update for just one realization or specimen of the meso-scale, and for the case where one seeks to update the parameters for a whole ensemble of meso-structures (an aleatoric uncertainty). The interpretation of the terms in (12) will be different in both cases. In the first case the likelihood \(\pi _{(Y|Q)}(\varvec{y}|q)\) in (12) contains only the epistemic uncertainty, whereas in the second case it contains also the aleatoric uncertainty. The first case, identification for just one realization \(\varpi \in \Omega\), is the usual and more familiar one. In a computational upscaling it would be possible to “observe” a whole random variable—a function of the aleatoric variable \(\omega \in \Omega\)—and use Bayes’s formula in such a way. In what follows later we use a simple scheme which can be applied also in experimental situations, where one can only observe samples of the aleatoric distribution, although more involved schemes are possible [79, 81]. The proposed scheme builds on employing the usual Bayesian methods for identifying parameters for a single specimen or realisation \(\varpi \in \Omega\), for more details see [31].
3.2.1 MCMC Bayesian updating of the measure
To evaluate (12), one may assume that the prior \(\pi _Q(q)\) is given. However, to evaluate the conditional pdf or likelihood \(\pi _{(Y|Q)}(\varvec{y}|q)\), for each given q one has to solve for the model response and evaluate the forecast measurement \(\varvec{y} {:=} Y(q,\epsilon )\). This computational expense is amplified when the evidence \(\pi _Y(\varvec{y})\) in (12) has to be evaluated, as it is often high-dimensional integral over \({\mathcal {Q}}\), requiring typically many evaluations of the likelihood.
Therefore most computational approaches to determine the conditioned posterior pdf \(\pi _{(Q|Y)}(q|\varvec{\hat{y}})\) employ variants which circumvent the direct approach just outlined, and use versions of the Markov-chain Monte Carlo (MCMC) method (see e.g. [22, 26, 56, 75] and the references therein), where at least the evidence \(\pi _Y(\varvec{y})\) does not have to be evaluated, as these algorithms can evaluate the Bayes-factor \({\pi _{(Y|Q)}(\varvec{y}|q)}/{\pi _{Y}(\varvec{y})}\) directly as a ratio of densities. One of the simplest and earliest versions of a MCMC algorithm is the Metropolis–Hastings algorithm [22, 26, 64], and looks as follows [75]: It constructs a Markov-chain that has a stationary distribution of states, which will be the posterior distribution one is seeking, and it may alternatively be viewed as a Monte Carlo search method for the maximum of the posterior. It will not be described in more detail, as it is well documented in the literature.
One can show (e.g. [22, 26, 56, 64]) that after the so-called burn-in, i.e. a number of steps which the Markov-chain needs to reach the stationary distribution, the relative frequency with which the states of the Markov chain are visited is equal to the conditioned posterior pdf \(\pi _{(Q|Y)}(q_\xi |\varvec{\hat{y}})\). The algorithm is a Monte Carlo (MC) method, or more precisely a MC method within a MC-method, meaning that it converges only slowly with the number of samples, so that there will always be a sampling error. In addition, successive Markov-chain samples are obviously not independent but highly correlated. This makes estimating any statistic other than the mean difficult.
3.2.2 Bayesian updates via filtering
Another possibility is to leave the base measure \({\mathbb {P}}\) resp. the pdf \(\pi _Q(q)\) unchanged, and to change the RV from the forecast \(q_f=q\) to an updated or assimilated RV \(q_a\). Such algorithms are often called filters, as the observation or measurement \(\varvec{\hat{y}}\) is filtered to update the forecast \(q_f\) to \(q_a\). This is often advantageous if one needs a RV to do further forecasts, as then the assimilated \(q_a\) becomes the new forecast. Here it is attempted to sketch one main idea behind the construction of such a filter. More detail can be found in [6, 60]. The idea is, given a forecast \(q_f\), to compute the forward problem \(\varvec{y}_f {:=} Y(q_f,\epsilon )\) and forecast the possible measurements or observations, then to compare this with the actual observation \(\varvec{\hat{y}}\), and to filter this noisy observation to obtain the assimilated RV \(q_a\), which should have as its distribution the conditioned posterior pdf \(\pi _{(Q|Y)}(q|\varvec{\hat{y}})\).
It is well known [6, 60, 73] that knowing the probability measure \({\mathbb {P}}\) resp. of the pdf \(\pi _Q(q)\) is equivalent to knowing the expected values of all reasonable functions \(\psi (q)\) of the RV q. Now given the posterior conditioned pdf \(\pi _{(Q|Y)}(q|\varvec{\hat{y}})\), one may compute other conditioned quantities, say the conditional expectation (CE) of a function \(\psi (q)\) of q as follows:
and this can be the start for a filter development [60].
The relation (13) between conditional density and expectation was turned around by Kolmogorov—who axiomatized probability—by taking conditional expectation as the primary object, and then defined conditional probabilities via conditional expectation, which is thus the mathematically more fundamental notion [60]. One way to make conditional expectation the primary object is to define it not just for one measurement \(\varvec{y}_f\), but for sub-\(\sigma\)-algebras \({\mathfrak {S}}\subseteq {\mathfrak {A}}\). The connection with a measurement \(\varvec{y}_f\) is to take \({\mathfrak {S}} = \sigma (\varvec{y}_f)\), the \(\sigma\)-algebra generated by \(\varvec{y}_f(\omega )\). This is the smallest sub-\(\sigma\)-algebra of \({\mathfrak {A}}\) which contains all the sets \(\varvec{y}_f^{-1}({\mathcal {A}})\subseteq \Omega\) for measurable subsets \({\mathcal {A}}\subseteq {\mathcal {Y}}\).
The conditional expectation is easiest to define [60] for RVs with finite variance, as in that case \({\mathcal {S}}_\infty {:=} L_2(\Omega ,{\mathfrak {S}})\)—the \(L_2\)-subspace of functions measurable w.r.t. the smaller \(\sigma\)-algebra \({\mathfrak {S}}\)—is a closed subspace of \({\mathcal {S}} {:=} L_2(\Omega ,{\mathfrak {A}})\), and the conditional expectation is simply defined as the orthogonal projection \({\mathbb {E}}(\psi (q)\mid {\mathfrak {S}}){:=}P_\infty \psi (q)\) of \(\psi (q)\in {\mathcal {S}}\) onto that subspace \({\mathcal {S}}_\infty\). The well know orthogonality relation for the orthogonal projection reads
This may be regarded as a Galerkin-orthogonality, immediately suggesting computational procedures based on (14).
To better characterize the subspace \({\mathcal {S}}_\infty\), one may observe that the Doob–Dynkin-lemma [6] assures us that this subspace is actually the space of all square integrable functions \(\chi (\varvec{y}_f)\) of \(\varvec{y}_f\). As obviously \(P_\infty \psi (q) \in {\mathcal {S}}_\infty\), there is a function \(\phi _\psi (\varvec{y}_f(q))\) such that
By taking in particular the function \(\psi (q)=q\), one obtains the CE of the assimilated RV as \({\mathbb {E}}(q \mid {\mathfrak {S}}) = \phi _q(\varvec{y}_f(q))\), and one may conclude that \(\phi _q\) is in some mean-square sense an inverse of \(\varvec{y}_f(q)=Y(q,\epsilon )\), this being a kind of justification for calling the whole update procedure an inverse problem.
This function \(\phi _q(\varvec{y}_f(q))=P_\infty q = {\mathbb {E}}(q\mid \varvec{y}_f)\) of \(\varvec{y}_f\) induces an orthogonal decomposition of
Such decomposition is used to build a first version of a filter to produce an assimilated RV \(q_a\) which has a correct conditional expectation. As the new information from the observation \(\varvec{\hat{y}}\) comes from the measurement map \(\varvec{y}_f\) one may define the CE-filter as
where the first component in (16) has been changed to the constant \(\phi _q(\varvec{\hat{y}}) = {\mathbb {E}}(q\mid \varvec{\hat{y}})\), and the orthogonal component \(q_f - \phi _q(\varvec{y}_f(q_f))\) has been left as it is. From the above observation on projections it is clear that in (17) the second summand on the right—the orthogonal component—has a vanishing conditional expectation, and thus \(q_a\) has the correct conditional expectation \({\mathbb {E}}(q_{a}\mid \varvec{\hat{y}}) = {\mathbb {E}}(q\mid \varvec{\hat{y}})\). We call \(q_{a}\) in (17) the analysis, assimilated, or posterior RV of the CE-filter, incorporating the new information at least in form of the correct conditional expectation, which is in many circumstances the most important part of the update.
The function \(\phi _q(\varvec{y}_f)\) may not be easy to compute, and usually has to be approximated. The simplest approximation one is by a linear map \(\phi _q(\varvec{y}_f) \approx K \varvec{y}_f\). As is well known, the linear orthogonal projector associated with (16) is the Kálmán-gain \(K\in {\mathscr {L}}({\mathcal {Y}}; {\mathcal {Q}})\), see [44, 54], which is given by:
with \(C_{\varvec{y}_f} {:=} {\mathbb {E}}(\tilde{\varvec{y}}_f(q_f)\otimes \tilde{\varvec{y}}_f(q_f))\) and \(C_{q_f,\varvec{y}_f} {:=} {\mathbb {E}}(\tilde{q_f}\otimes \tilde{\varvec{y}}_f(q_f))\). So one obtains [74] the so-called Gauss–Markov–Kálmán filter (GMKF) as an approximation of (17)
We have chosen such name for this filter [60, 61] due to the fact that it is a generalized version of the Gauss–Markov theorem [54], and gives as well a generalization of the well-known Kálmán filter (KF) [44]. In case \(C_{\varvec{y}_f}\) is not invertible or close to singularity, its inverse in (18) should be replaced by the Moore–Penrose pseudo-inverse. This update is in some ways very similar to the ‘Bayes linear’ approach, see [25]. If the mean is taken in (19), one obtains the familiar Kálmán filter (KF) formula [44, 54] for the update of the mean. But the filter (19) operates on the random variable and does not require a separate update for the covariance, in fact one may show [74] that (19) also contains the Kálmán update for the covariance and is thus a non-Gaussian generalization of the KF and of its more recent variants. It is well known [44] that for everything Gaussian and linear forward and observation models the linear update in (19) is in fact exact and not an approximation.
3.2.3 Stochastic computations
As one may recall, to predict the observation \(\varvec{y}\) resp. to evaluate the likelihood \(\pi _{(Y|Q)}(\varvec{y}|q)\) one needs to compute \(Y(q,\epsilon ) = \hat{Y}(u(q),q,\epsilon )\), and for that one needs the solution RF \(u(x,\omega )\) of (8). In a computational setting (8) must be discretized. For the spatial discretization any good method may be used, here mainly Galerkin methods using the finite element method (FEM) in particular are employed.
To discretize the stochastic part in (8), one may, similarly to (11), also use a truncated expansion for an approximate solution RF \(u_a(x,\omega )\) of (8):
Inserting this into (a FEM-discretized version of) (8), the deterministic coefficient functions \(u(x)^{(\varvec{\alpha })}\) may be determined (e.g. [59]) by a stochastic version of the weighted residual method: \(\forall \varvec{\beta }\)
where the weighting functions \(\hat{\Psi }_{\varvec{\beta }}(\varvec{\theta })\) can be chosen such as to give collocation, i.e. \(\hat{\Psi }_{\varvec{\beta }}(\varvec{\theta }) = \updelta (\varvec{\theta }-\varvec{\theta }_{\beta })\) for collocation points—samples—\(\varvec{\theta }_{\beta }\), or \(\hat{\Psi }_{\varvec{\beta }}(\varvec{\theta })=\Psi _{\varvec{\alpha }}(\varvec{\theta })\) for a stochastic Bubnov–Galerkin method [59]. The details of the computational procedure, although still actively researched, have been published in many places (e.g. [37] and references therein) and will not be explained any further here.
3.3 Stochastic elastic upscaling
The result of the Bayesian identification procedure for elastic properties as a RF on the micro-scale as in Fig. 6 may be gleaned from Fig. 7, see also [80, 81]. It shows how the bulk- and shear-modulus \(q = (\kappa , G)\) is identified with the GMKF over several load steps involving both shear and compression with the observation \(\varvec{y}=\Phi _e\) being the elastic stored energy.
The solid line is the median of the posterior distribution \(\pi _{(Q|Y)}(q|\varvec{y})\) in (12), whereas the broken lines denote the 5% and the 95% fractile of the posterior. It may be observed that the identification gives practically a deterministic result, the same that would have been achieved with the numerical homogenization procedure described in the previous section, as the linear elastic stored energy is a quadratic function of the imposed strains and can thus be represented perfectly on the coarse scale.
For a discrete fine resp. micro-scale model to be described in more detail later in Sect. 4—see also [31], we show in Fig. 8 that both procedures for Bayesian updates converge to the same posterior probability distribution of elastic parameters, either by MCMC or by a GMKF square root filter (see [31]). The two updates are practically on top of each other. The point marked with a cross on the x-axis is the value computed by a deterministic error minimization procedure (see [31]).
However, the CPU computation time for the GMKF update is orders of magnitude smaller than the one needed for the MCMC computations; see Table 1.
One may also observe a peculiarity of the Bayesian upscaling, in that it not only gives one value, but a whole distribution of values. This will be particularly important for next when updating inelastic properties governing fracture process.
3.4 Stochastic plastic upscaling
The next step in difficulty in these procedures is the upscaling of inelastic material behavior—see also [79,80,81], where more details may be found. Starting with a similar kind of model as the first example in the previous Sect. 3.3, we choose a coupled damage-plasticity model, presented in [58], that allows elasto-plastic behavior with hardening of the Drucker–Prager type, as well as damage in compression (crushing), as shown in the left of Fig. 9 in the pressure (p)—second invariant of the deviator (\(\sqrt{J_2}\))—plane.
On the right are shown the load paths that are used for the identification on the upscaled parameters. It may intuitively be clear, but is also borne out by the analysis, that identification of the parameters of some inelastic mechanism—say the Drucker–Prager parameter (cohesion) c or the failure stress \(\sigma _f\) in the left part of Fig. 9—is only possible if that mechanism is also activated in the experiment resp. meso-scale computation. Hence the load paths have to activate the mechanisms which are to be identified. As in Sect. 3.3, on the meso-scale the mechanical model is of the same kind as on the macro-scale, but whereas on the macro scale we are looking for spatially constant value, the parameters on the meso-scale are random fields, like shown for the elastic parameters in Fig. 6.
As observation resp. measurement for the inelastic mechanisms, the dissipation was used. This is again a fundamental thermodynamic property which any kind of model exhibiting irreversibility must contain, and mimics the used of stored energy for the elastic parameters previously.
In Fig. 10, as an example [80, 81], the results are shown for the updating of the failure stress \(\sigma _f\) and the Drucker–Prager cohesion (both seen on the left in Fig. 9). Although in both cases the final variance of the posterior is fairly small when compared with the prior—showing the success of the upscaling procedure, unlike for the elastic parameters, here the variance of the posterior will not shrink to zero, no matter how many observations and incremental updates are used. The reason is that the small-scale meso-model will go into the inelastic regime in some areas of the meso-scale domain but not in others, whereas the macro-model, as it has only one spatially constant parameter for the inelastic and irreversible behavior, can only start dissipating on the whole domain, or not at all.
The loss of spatial resolution through the upscaling is thus mapped into a larger posterior uncertainty of the parameters, meaning that in the ensemble of macro-models described by the posterior distribution of the inelastic parameters, some realizations will start dissipating with a certain probability, while other realizations will not. The loss of spatial resolution is thus expressed in such a probabilistic way.
The result of this non-negligible variance of the posterior distributions of the inelastic parameters on the macro-scale stored elastic energy as well as on the macro-scale plastic dissipation are shown in Fig. 11. Both half-figures show the meso-scale observation labeled as (fine), the distribution of the quantity (stored elastic resp. plastically dissipated energy) resulting from the macro-scale Bayesian prior distribution—median labeled (pr50) and the 5% (pr5) and 95% (pr95) quantiles—as well as the macro-scale Bayesian posterior distribution, with the median labeled (pf50) and the 5% (pf5) and 95% (pf95) quantiles. The macro-scale model is in this Bayesian way—given the prior—the best posterior to match the meso-scale stored energy and dissipation. The reduced variance from prior to posterior attests the success of the upscaling, but the posterior results will retain a residual variance due to the loss of spatial resolution being transformed into a probabilistic kind of background noise as described above.
4 Reduced model of stochastic plasticity for localized failure and fracture
In this work, which continues the development started in [27, 33] and more recent works in [31] or [30], we focus upon the uncertainty propagation across scales during different stages of the fracture process. More precisely, we propose the stochastic upscaling resulting with inelasticity at multiple scales, starting from the fine scale (meso-scale for concrete), where the failure mechanisms for heterogeneous composites and the variability of model parameters can be captured much better by a corresponding representation of different phases (aggregate vs. cement). The main goal is to provide the corresponding macro-scale reduced model of stochastic plasticity, which can significantly increase the computational efficiency by using a reduced model to make the analysis of complex structures feasible. The proposed approach can be considered as a part of a scale-coarsening strategy, much more sound than ad-hoc choices [4]. Such model reduction is used once the crack pattern at the meso-scale has stabilized, replacing subsequently the meso-scale, where the heterogeneity is modeled by random fields (RF), by a macro-scale generalized ED-FEM element where the parameters of the material model are random variables (RV), and thus spatially constant, as in Sect. 3.4. The stochastic variability of the parameters on the coarse or macro-scale reflects the aleatoric uncertainty of the fine meso-scale as it is visible on the macro scale, as well as the epistemic uncertainties of the modeling error involved by fixing a type of continuum mechanics model on the macro scale for the purpose of model reduction, the loss of spatial resolution, and any other epistemic errors involved in the upscaling and identification procedure.
4.1 Stochastic upscaling micro- to meso-scale
In our previous work [45], the material parameters on the meso-scale are considered as constant, the randomness was entirely due to a random geometrical arrangement of the aggregate; see Fig. 12. Here, we generalize this development to the case where the main source of uncertainty, fracture parameters of a coupled meso-scale-plasticity and probability model, can be considered as random fields (RF), as described in Sect. 3.1. We consider fracture stress components at the phase interface in modes I, II and III as the (vector) random field, which we denote ias \({\varvec{p}}(x,\omega )\) \(= (\sigma _u(x,\omega ), \sigma _v(x,\omega ),\sigma _w(x,\omega ))\). Thus, at a fixed point of the macro-element domain \(x\in {\mathcal {V}} \subseteq {\mathbb {R}}^d\), each component of \({\varvec{p}}(x,\omega )\) is a random variable (RV) on a suitable probability space.
How to obtain the probability distribution of these random fields? The usual approach would be via experimental measurements only. A very detailed microstructure observation can be made by using either Digital Image Correlation (DIC) measurements for 2D surface measurements or Digital Volume Correlations for 3D tomographic measurements and the latter are nowadays already well accepted as gold standard microstructure observation tools. However, in cement-base materials simple DIC or DVC observations are in general not enough, since one needs to account for complex phenomena in manufacturing such materials. In particular, processes of cement hydration and drying next to (dry) aggregate, resulting with so-called shrinkage cracks at the cement-aggregate interface, will require to represent phase interface fracture parameters as random fields. The complex geometry would make it very hard to quantify the probability distribution of phase interface fracture parameters, even with dedicated destructive or non-destructive measurements (e.g. [55]).
Thus, we argue that the most rigorous approach to provide probability distributions of meso-scale model parameters for fracture would be in terms of a computational procedure of stochastic upscaling from an even smaller scale; see Fig. 2. Namely, due to concrete meso-scale heterogeneities (aggregate vs. cement), one cannot predict the exact finer-scale (cement) microstructure evolution of initial defects influencing the meso-scale fracture parameters, unless assuming a prior geometry distribution at the meso-scale of the aggregate-cement phase interfaces. We can further find the solution to such a multi-physics problem of cement hydration, which involves probability-based simulations of chemical reactions by using the computational microstructures model in CEMHYD3D [5] (where the uncertainty stems from the chain of chemical reactions produced by the mixing of water with cement powder), combined with hydro-mechanics computations of cement-paste-drying next to aggregates [78] (where the uncertainty stems from the random distribution of the aggregate), all resulting in shrinkage induced micro-cracks and initial defects at the interface. Such computations can then be used to improve the distribution of meso-scale fracture parameters as a posterior probability through Bayesian inference, which is yet another example of a stochastic upscaling, which is, in principle, completely analogous to the one from meso- to macro-scale described here in more detail; hence, we further give only the model main ingredients and corresponding computational procedure (for more detail, see [31, 78]).
In short, for the microstructure at the finest scales in concrete, placed at level of microns (see Fig. 2—cement RVE), one can use a structured mesh of \(10^6\) voxels with each one occupying \(1 \mu ^3\) being filled with one of 16 different phases of product of hydration process of portland cement, such as made in CEMHYD3D code [5]. However, at the meso-scale (see Fig. 2—concrete RVE), the choice of microstructure representation with a structured mesh may no longer be optimal when seeking to capture the cement-aggregate interface. A very efficient representation of RVE-concrete meso-structure is proposed in our recent works (e.g. see [39] or [45]) in terms of Voronoi cells, with each cell represented as a convex polygon. The Voronoi polygon construction starts either by a random tessellation placing the cell centers for better representation of the scanner-type observation of heterogeneities. Each cell \(\tilde{{\mathcal {V}}}_i\) contains a set of points \(P_i ; i = (1,\dots ,n)\), which is closer to the center than to any other of the chosen points in \(\tilde{{\mathcal {V}}}_i = \{ P \, |\, \, d(P_i, P) \le d(P_i, P_j)\}\), where \(d(\cdot ,\cdot )\) denotes the usual distance in Euclidean space. Patched together, the collection of Voronoi cells will be covering by non-overlapping polygons an RVE-concrete or macro-scale element \(\tilde{{\mathcal {V}}} = \bigcup \tilde{{\mathcal {V}}}_i\); see Fig. 12. The connection among adjacent cells is ensured by cohesive links, placed along edges of tetrahedra in 3D or triangles in 2D, [38]. This is a Delaunay mesh [21], dual to the Voronoi cells representation. In keeping a fixed mesh for different realizations of the meso-structure with position of aggregate changing, results in three types of cohesive links: fully elastic and homogeneous if placed in aggregate, those that break and are homogeneous if placed in cement, and finally those representing interface properties placed partially in cement and partially in aggregate, see [38]. This kind of links require special treatment of the displacement representation in representing the fracture modes, by using ED-FEM with both strain and displacement discontinuities. Such choice is advantageous over X-FEM representation [38], with a clear physical interpretation of enhancement modes, with the former representing total deformation field for non-homogeneous link and the latter representing the fracture mode or crack opening. Thus, the deformation discontinuity computation belongs to the global phase of operator split solution procedure for fracture [37], while the displacement discontinuity belongs to the local phase for internal variable evolution computations [38].
a Voronoi cell representation of mesostructure of concrete RVE [31]; b voronoi ajdecant cells connected by cohesive links
More precisely, for any cohesive link built of heterogeneous material of this kind where each sub-domain can have different inelastic behavior, along with the possibility of localized failure at the interface with the softening behavior driving the stress to zero, we can define the corresponding plasticity constitutive model with different yield criteria in two sub-domains and
where \(\sigma _{y_{1}}\) and \(\sigma _{y_{2}}\) are, respectively, yield stress values in both sub-domains, whereas \(\overline{q}_{1}\) and \(\overline{q}_{2}\) are hardening variables, \(\sigma _{u}\) is the ultimate stress value where the localized failure is initiated, \(\overline{\overline{q}} (\overline{\overline{\xi }})\) is the softening variable which drives the current yield stress to zero, and t is the traction force at the interface. In the case of localized failure, the total strain ought to be split into a regular (smooth) part, containing both elastic and plastic strain \(\overline{\varepsilon }_i = \overline{\varepsilon }_i^e + \overline{\varepsilon }_i^p\), and an irregular part concentrated upon the discontinuity, which is written as
where \({\hat{G}}(x)\) and \({\tilde{G}}(x)\) are respectively the derivatives of the functions that limit the influence of the strain and displacement discontinuity to a given element domain, whereas \(\updelta _{\overline{x}}\) is the Dirac-\(\updelta\) function centered at the interface \({\bar{x}}\). The contribution of each cohesive link of this kind to the set of nonlinear equations to be solved can then be written as:
where
The solution of the global set of equations along with \(h^{e}_{1} = 0\) is done in the global phase, while the solution to \(h^{e}_{2} = 0\) is a part of the local phase [38]. We note in passing that the same kind of approximation for total strain and displacement fields can also be constructed by X-FEM (e.g. [43], but without a clear separation of global vs. local computation phase, and thus less robust computations.
In a computational setting the random field \(p(x,\omega )\) must be discretized. The choice used here is the truncated Karhunen–Loève expansion (KLE) in (10) as described in Sect. 3.1. We note in passing that the uncorrelated Gaussian RV \(\theta _i(\omega )\) are also independent and can be treated independently (just like Cartesian coordinates), which simplifies integration over stochastic domain. The random variables \(\varvec{\theta }(\omega )\) from the PCE (11) allow one to discretize any other field in terms of Hermite polynomials [59]; for example, by combining the FEM discretization (3) with the stochastic ansatz (20), the displacement vector can be approximated as
where the \(N_i(x)\) are finite element shape functions for cohesive links, \(\varvec{d}_{\varvec{\alpha }} = (\dots d_{\alpha ,i} \dots )^T\) is a vector of PCE coefficients for nodal displacement component i, and \(H_{\varvec{\alpha }}(\varvec{\theta }(\omega ))\) are the corresponding Hermite polynomials.
By approximating the nodal response by its PCE truncated representation \(u_i^m\) given in (26), and applying the Galerkin weighting residual procedure as described in Sect. 3.2.3, one arrives at:
where the colon ‘:’ denotes as usual the double contraction. Given the solution \(\varvec{d}\) to the stochastic Galerkin procedure, one may now easily define e.g. the expected value of the strain energy of this meso-scale model as:
One may note that the expansion and approximation of the parameter RF in (26) results in an analogous expansion and approximation of the random stiffness matrix [84]; thus, the stochastic version of Galerkin weighted residual procedure results in a number of copies of corresponding deterministic problem, with corresponding PCE truncated nodal parameters as unknowns. Finally, what is needed for macro-scale parameter identification is that both scales can perform the computation of the same Quantity-of-Interest (QoI), which is here chosen (in the spirit of homogenization) as the strain energy. One can carry on with identifying fracture parameters, in which case the QoI will be plastic dissipation. Somewhat more elaborate computations are needed to obtain the expected meso-scale model plastic dissipation and fracture parameters distribution; see [67] for details. Both of these QoI will be used to improve the posterior probability distribution of the total set of macro-scale reduced model parameters by using the Bayesian inference as described next.
4.2 Stochastic upscaling meso- to macro-scale
Subsequently, we assume that the meso-scale parameters are defined as random fields with their probabilistic description provided. Such a choice of meso-scale material parameters results wit quite realistic images for typical realizations of the fracture process at the meso-scale, as illustrated in Fig. 13. The main goal in this section is to explain in detail the Bayesian inference procedure for stochastic upscaling from the meso-scale to the macro-scale, which seeks to identify the probability distributions of material parameters at the macro-scale that is not necessarily Gaussian.
Meso-scale model computational results: a simple tension test: displacement contours or broken cohesive links [31]; b concrete as (statistically) isotropic material: tension test results in 3 orthogonal directions; c uniaxial compression force-displacement and failure mode with cohesive links failure; d biaxial compression (confirming compressive strength increase from uniaxial case) and failure mode
For such a macro-scale stochastic plasticity reduced model all the material parameters are chosen as random variables, with the model reduction performed for one particular macro-scale element in agreement with the computational procedure as explained in Sect. 2. Such a reduced element must include enhanced kinematics [31] that allows to provide a mesh-invariant response to softening phenomena typical of localized failure (or ductile fracture) in terms of an embedded-discontinuity finite element (ED-FEM) discrete approximation [30]. Moreover, such a macro-scale ED-FEM should implement a stochastic plasticity model capable of representing the full set of 3D failure modes [45]. We further briefly comment upon the role of each material parameter in characterizing the particular failure mode, and present the results of Bayesian inference leading to the identifcation of the corresponding probability distribution.
The simplest identification procedure concerns the elastic response of such a stochastic plasticity model, representing concrete response. The main important advantage of the Voronoi cell meso-structure representation with cohesive links placed along Delaunay tetrahedra over many other discrete models is in its ability to exactly represent homogeneous isotropic elastic behavior (see Fig. 13b), which can be characterized by Young’s modulus E and Poisson’s ratio \(\nu\). However, for the robustness of identification procedure, it is preferable to characterize isotropic response in terms of the bulk modulus K and the shear modulus G—the eigenvalues of the isotropic elasticity tensor—so that one can deal with only one parameter at the time; see Fig. 14a. Hence, the elastic response of the reduced model can be characterized by two independent RVs, bulk modulus \(K(\omega )\) and shear modulus \(G(\omega )\). In the computational setting, we rather consider a \(\log (\cdot )\)-transformation of each parameter—e.g. we consider and identify for example \(K_l(\omega ) {:=} \log (K(\omega )/K_0)\) instead of the bulk modulus \(K(\omega )\), where \(K_0\) is some reference value—in order to accommodate the constraint that \(K(\omega ) > 0\). The log-quantity \(K_l\) is a free variable without any constraint, and in the mechanical computation one uses the point-wise back-transformation, i.e. \(K(\omega ) = K_0 \exp (K_l(\omega ))\). We also follow such a procedure for the shear modulus with \(G(\omega ) = G_0 \exp (G_l(\omega ))\).
The QoI used to identify these two RVs is the strain energy, to be matched against its meso-scale computation given in (28). At the macro-scale, the strain energy computation involves in the most general case two volume integrals accounting for the elastic energy and hardening in the FPZ, and a surface integral accounting for softening mechanisms, which can be written as:
where the elastic strain energy density is given by
whereas \(\bar{\Xi }\) and \(\bar{\bar{\Xi }}\) are respectively hardening and softening potentials. The probability distribution of \(K(\omega )\) and \(G(\omega )\) is obtained by using Bayesian inference (see Sect. 3.2 or [62]), where only a few measurements in the beginning of loading program are sufficient in general for the linear elastic response.
Bayesian inference, based upon Bayes’s theorem [60] for computing conditional probabilities as described in Sect. 3.2, given new data on the quantity of interest Y from the computations in (28), improves the prior distribution (often given by an expert’s guess) of the desired parameter with the likelihood. Clearly, it follows from (12) that one can converge faster by choosing a better prior, which was confirmed in Fig. 14b. We also show in Fig. 14b that we can obtain a very narrow distribution for the concrete elastic parameters \(K(\omega )\) and \(G(\omega )\), which justifies the use of homogenization even when the scales are not fully separated. However, this no longer holds when we go towards inelastic behavior, and especially for localized failure, as shown next.
Contrary to (linear) elastic model parameters, the Bayesian inference of the model parameters governing plastic response and fracture that leads to coarse graining (i.e. the switching from meso-scale to macro-scale) should be performed once the crack pattern inside the corresponding macro-scale element has stabilized; see Fig. 15a. Moreover, the model reduction from meso-scale to macro-scale capable of describing the localized failure of concrete relies upon a stochastic plasticity model in terms of the theoretical formulation and an embedded discontinuity finite element method (ED-FEM) in terms of discrete approximation; see Fig. 15b. Clearly, the corresponding reduced macro-scale model with ED-FEM cannot match the crack pattern at micro-scale—see Fig. 15 for illustration—it only has to match the computed results at the meso-scale in terms of the total plastic dissipation as QoI for both the hardening phase in the FPZ and the softening phase in localized failure.
a Computed failure mode at meso-scale in simple tension test—illustrated with displacement contours and cohesive link failure; b reduced model at macro-scale with ED-FEM for tension failure mode with meso-scale (rough) surface replaced with a discontinuity (smooth) plane, not matching the crack but rather the fracture energy material parameter \(G_{f,t}\)
To compute such a QoI at the macro-scale in terms of total plastic dissipation, further denoted as \(Y_M(\omega )\), we must integrate in time the dissipation rate that is defined by the non-local form of the second principle of thermodynamics (e.g. see [37]) applied over the macro-scale element domain \(\tilde{{\mathcal {V}}}\) and crack surface \(\Gamma _s\); this can be written as:
where \({\bar{q}} = -{\mathop {}\!\mathrm {d}\bar{\Xi }\over \mathop {}\!\mathrm {d}\bar{\zeta }}\) and \(\bar{{\bar{q}}} = -{\mathop {}\!\mathrm {d}\bar{\bar{\Xi }} \over \mathop {}\!\mathrm {d}\bar{\bar{\zeta }}}\) are thermodynamic forces dual to strain-like hardening variables \(\bar{\zeta }\) and \(\bar{\bar{\zeta }}\) in (29) above. We note that in integrating the plastic dissipation we ought to solve a constrained evolution problem, enforcing the admissibility of the computed stress field with respect to multi-surface yield criteria; see Fig. 16 for illustration.
The proposed macro-scale plasticity model yield criteria jointly cover hardening and softening regimes and the full set of failure modes, by combining non-associated plasticity of Drucker–Prager type with hardening in (31) and St. Venant with softening in (32). For the hardening part we can write:
where \(\Vert {{\,\mathrm{dev}\,}}\varvec{\sigma }\Vert\) denotes the norm of the deviatoric stress tensor \({{\,\mathrm{dev}\,}}\varvec{\sigma }\), \(\tan (\varphi )\) characterizes the internal friction, \(\tan (\psi )\) characterizes internal dilatancy, \(\sigma _{y}\) denotes the uni-axial yield stress, and q is a thermodynamic force dual to hardening variable. For the softening part we can write:
where \(\varvec{t} = {\varvec{\sigma }} {\varvec{n}}\) is stress vector acting as crack driving force, \(\varvec{n}\) is unit vector of exterior normal, \(\varvec{m}\) is the corresponding failure mode, \(\sigma _u\) is a localized failure threshold, and \(\bar{\bar{q}}\) is the internal variable for softening that can be computed as:
with \(G_f\) as the corresponding value of the fracture energy. We note that contrary to the meso-scale model, where the compressive and the tension failure mechanisms are reproduced according to the same fracture mode of the cohesive links (see Fig. 13), the present macro-scale model has quite different amounts of fracture energy corresponding to failure in tension \(\textit{G}_{f,t}\) versus that in compression \(\textit{G}_{f,c}\), which can be written as
With such macro-scale stochastic plasticity reduced model, all the parameters governing the hardening behavior in the FPZ and the softening behavior in localized failure are chosen as random variables; the latter counts: yield stress, hardening parameter, angle of internal friction, angle of internal dilatancy, ultimate stress, and the fracture energies in tension and in compression, denoted respectively as
Again, we consider a \(\log (\cdot )\)-transformation of each parameter—i.e. we consider and identify for example \(\sigma _{y,l}(\omega ) {:=} \log (\sigma _y (\omega )/\sigma _{y,0})\) instead of the yield stress \(\sigma _y(\omega )\), where \(\sigma _{y,0}\) is some reference value—in order to accommodate the constraint that \(\sigma _y(\omega ) > 0\). The log-quantity \(\sigma _{y,l}\) is a free variable without any constraint, and in the mechanical computation one uses the point-wise back-transformation, e.g. \(\sigma _y(\omega ) = \sigma _{y,0} \exp (\sigma _{y,l}(\omega ))\).
In order to gain computational efficiency, Bayesian inference is further used to set up a computational procedure to replace subsequently the meso-scale computations with the corresponding stochastic macro-scale ED-FEM. Several loading programs are defined in Table 2 (indicating the computational savings in terms of CPU time), which allows to provide an extensive set of meso-scale computational results (i.e. measurements) that is sufficient to identify the probability distributions of all model parameters. Such a computational procedure is carried out in terms of an incremental analysis for each particular loading program that can improve a prior probability distribution (obtained by an expert choice or a guess) into a posterior for all the model parameters in (34) given the new observation results for Quantities-of-Interest defined as expected values of strain energy in (29) or plastic dissipation in (30) before this can be written as
Such an incremental procedure can be summarized in short as forecast-observe-assimilate algorithm that will produce the final probability distribution for each unknown parameter of the reduced model in (34) modeled as a random variable. The corresponding probability description has two constituents, the measurable function representing the random variable RV, and the measure. Markov chain Monte Carlo (MCMC) (e.g. see [22, 26]) updates the measure, whereas the GMKF filter (e.g. see [14, 44]) changes resp. updates of the measurable function. We formulated in Sect. 3 both methods as functional spectral approximations of stochastic problems, and introduced especially in combination with the second method a new procedure which does not need any sampling, hence works with the subsequent update in a deterministic manner. It also seems to be the fastest and more reliable when compared with other methods. We show by example that the spectral resp. polynomial chaos version of the GMKF also works for highly nonlinear non-smooth problems with non-Gaussian measures.
With such an approach one can recover a probabilistic reduced model on the macro-scale that defines the probability distributions of the fracture parameters describing localized failure with both volume and surface dissipation. See Figs. 17 and 18 for typical illustrative results on joint PDF showing strong coupling between model hardening parameters and a typical non-Gaussian PDF for softening parameters. Such a ‘mechanics-based’ model reduction is fundamentally different from the vast majority of recent works (e.g. see [8, 68] or [47] using statistical modes with either POD or PGD. Moreover, one can recover any probability distribution of structure failure modes for advanced safety evaluations, contrary to pre-defined distributions currently used: log-normal distribution to construct fragility curves [85], uniform to construct bounds [48], Weibull to account for weakest link failure [49], or ad-hoc combination of power law and Gaussian as two asymptotic values [2].
5 Stochastic upscaling in reinforced concrete: crack spacing and opening probability estimates
Modeling of reinforced concrete (RC) structures in order to ensure the optimal design with respect to structure integrity has a rather long tradition, which has been summarized in [28]. For such computations, one can use homogenized properties of the RC composite that are obtained by smearing the reinforcement within the concrete layers to provide the corresponding match of the total resistance. This approach aims for efficiency of computation without much concern for the accuracy of the behavior of each RC composite component, which can often be acceptable with respect to the main design goal of ensuring the structural integrity.
However, the current engineering design practice of RC structures no longer requires only the proof of structure integrity, but also the structure durability, either under long term, exploitation loading (such as ageing problems), or under short term, extreme loading (such as fire exposure). The answer to the question of RC structure durability requires a very detailed information on concrete crack patterns, with the results on crack spacing and opening or the bond slip, which none of the smeared RC models can provide. Thus, we have to provide a more detailed modeling approach for each of the RC composite two main ingredients that jointly determine crack spacing and opening: the cracks in concrete and the bond slip representation.
For the first one of these ingredients we have already presented in Sect. 4 a multi-scale model capable of representing concrete cracking, both in terms of micro-cracks in the fracture process zone (FPZ) and macro cracks, as well as the corresponding extension to a probability framework. Here, we carry on with the developments pertinent to bond-slip modeling, both in terms of its theoretical formulation, discrete approximation and its stochastic representation. The latter is developed by exploiting experimental results obtained in the testing procedure with tie-beams (see Fig. 19), without complete pull-out of steel reinforcement.
RC composite testing of crack spacing and opening: a experimental set-up of a tie-beam test; b experimental measurements of crack spacing and opening for a series of tie-beam specimens; c computational results for stress distribution along the bar in concrete, steel and bond; d computational results for plastic bond-slip along the bar
This kind of situation is more representative of the real behavior of a RC structure resulting with a particular crack spacing and opening as the most important computational result that pertains to the structure durability. The simple Drucker–Prager plasticity model for bond-slip, proposed in this work, is by far preferable to the complex one used in [11], since it has a reduced number of parameters with a clear physical meaning with respect to the essential features of bond-slip within the context of reinforced-concrete composite. The simple bond-slip model, similar to non-associative perfect plasticity sensitive to confining pressure, is shown to be quite sufficient for the problems of interest for this work, where the bond slip is never excessive, as opposed to the model proposed in [11] considering the complete pull-out of the steel reinforcement.
In terms of the discrete approximation, the approach proposed herein combines all the ingredients of the reinforced concrete composite into a single finite element model, which has practically the same outside appearance as the standard finite element model in terms of macro finite element, but provides inside detailed description of the strain field for each ingredient, concrete, steel or bond slip. The latter is achieved by the corresponding enhancements of the macro element strain field, where the ED-FEM is used to handle the macro-crack in concrete and the X-FEM method (e.g. see [3]) is used for representing the bond slip along a particular reinforcement bar. Thus, some elements are attributed to a combined ED-FEM and X-FEM interpolation, granting them capabilities of representing successive fracture mechanisms of cracks in concrete and subsequent bond-slip; see Fig. 20.
RC composite finite element model: a ED-FEM for concrete cracks (element-wise) representation and X-FEM for bond-slip (reinforcement bar) representation; b Combined representation and corresponding nodal displacements: \(d^c\) concrete, \(\alpha ^{bs}\) bond-slip, \(d^s = d^c + \alpha ^{bs}\) steel reinforcement
The weak form of the RC fracture problem can then be set by considering displacements in concrete \(d^c\) and bond-slip \(\alpha ^{bs}\) as state variables, and recover steel bar displacement as a dependent variable \(d^s = d^c + \alpha ^{bs}\). We can thus write the corresponding global residual for all ’concrete’ nodes as:
and requiring \({r}^{cs}=0\), where we simplified the notation with \(\alpha ^{bs} \equiv \alpha\). This global equation is accompanied by a non-local equilibrium equation which concerns redistribution of the slip with all nodes attached to a particular steel reinforcement:
The suitable form of the operator split procedure is then constructed in order to separate the main update procedure for the concrete displacement which also implies the corresponding steel displacement with the frozen value of bond slip, from the new slip computation. The latter is not equivalent to the local (Gauss quadrature point) plastic deformation, since it is computed from the corresponding slip equilibrium equations assembled from all bond slip contributions along the particular reinforcement bar.
For a time step from \(t_n\) to \(t_{n+1}\) one thus has:
—Given: \({ d}^c_n\), \({ \alpha }_n\), the internal variables at \(t_n\)
—Find: \({ d}^c_{n+1}\), \({ \alpha }_{n+1}\), the internal variables at \(t_{n+1}\)
—Iterate over i for concrete displacements \(d^c_{n+1}\),
—for each i and given \({ d}_{n+1}^{c,(i)}\),
—iterate over j for slip \(\alpha _{n+1}\), by solving
—set \(\alpha ^{(i)}_{n+1}\) to converged \(\alpha _{n+1}^{(j+1)}\);
—solve for new \({ d}_{n+1}^{c,(i+1)}\):
—at global convergence set
\(\alpha _{n+1} \leftarrow \alpha ^{(i+1)}_{n+1}\), \({ d}_{n+1} \leftarrow { d}_{n+1}^{c,(i+1)}\)
We note that the computation of the bond-slip parameters is carried out for the given nodal values of concrete displacements. Hence a smaller set of equations governing bond-slip is forced to converge for a given iterative value of concrete displacement. This could be interpreted as imposing the admissibility of the bond-slip forces in the sense of the given slip criterion, which is fully equivalent to imposing the admissibility of the stress field for each component of the reinforced concrete composite in the sense of the given damage criterion for concrete and the plasticity criterion for steel. It is important to note that such a computation is also carried out for each iterative sweep (either i or j) in order to provide the corresponding values of internal variables governing cracking of concrete or plastic yielding of steel. With these values in hand we can also obtain the corresponding form of the tangent moduli for concrete, steel and bond slip, which allows us to compute accordingly the tangent operators needed in (39) above. The key ingredient which allows this kind of operator split solution procedure, separating the bond slip computation from the reinforced concrete displacement (with the value of slip kept fixed), pertains to describing the bond slip with the relative degrees of freedom. This is in sharp contrast with the standard parametrization of interface discontinuities (e.g. see [43]), which (as noted in [38]) would not allow the use of the same operator split procedure. We shown in Fig. 21 the excellent predictive capability of the proposed model with respect to experimental results of EDF for a concrete mixture used for nuclear reactor shield structures [36]).
We next carry on with computing the probability estimates for crack spacing and opening, which requires the Bayesian inference identification procedure starting with the prior estimate of the model parameters distribution as shown in Table 3.
The corresponding parameters for concrete material are: bulk modulus K, shear modulus G, yield stress \(\bar{\sigma }_f\), hardening modulus \(K_h\), ultimate stress \(\bar{\bar{\sigma }}_f\), and fracture energy \(\bar{\bar{G}}_f\); while the remaining parameters are bond modulus \(K_{bs}\), and critical bond stress \(\tau _y\). The incremental Bayesian inference procedure, absorbing new data one step at the time, requires for better parameter estimates new data with measurements which contribute the most to quantifying crack spacing and opening; here, this happens at the final stage of the experiments, as shown in Fig. 22. Namely, such parameters can be updated only after the mechanisms of concrete cracking and bond-slip are active, which happens at the very end of each experiment.
6 Size effect: probability-based explanation
In this section we present a stochastic approach to model size effects in quasi-brittle failure, which implies that the large specimen does not fracture in the same manner as a small specimen, even though both are built of the same material. The most frequently found explanation of the size effect are either those based upon Weibull’s statistical theory of the weakest link [88], or the asymptotic fit between two extreme failure modes described by Continuum Damage Mechanics and Linear fracture Mechanics in [2]. Here, we offer a more sound probability-based explanation, where the key ingredients to use are correlated random fields in order to describe the material properties at the macro-scale. In other words, we still use a multi-scale computational approach and model order reduction to macro-scale, but rather than considering the corresponding macro-scale model parameters as deterministic (as in the homogenization described in Sect. 2), or random variables (as in the stochastic plasticity model described in Sect. 4), we consider the model order reduction to macro-scale properties to be random fields that can be characterized by a correlation length quantifying the distance to which the material parameter probability distribution would not change significantly (meaning they can be considered as statistically homogeneous). We show in the foregoing that such a stochastic framework in multi-scale analysis is especially suited for modeling the size effect encountered in quasi-brittle materials, such as soil, concrete, mortar etc. The intrinsic randomness of such heterogeneous geomaterials and in general large structure size impose a particular mechanical behavior at the structure failure characterized by hardening with a large fracture process zone (FPZ), followed by softening with localized failure. They are known as quasi-brittle materials which can be seen as a sub-category of softening materials (see [40] or [37]). We will further illustrate this in an 1D framework, where the simplest quasi-brittle material behavior can be described with four material parameters: the Young modulus E, the yield stress \(\sigma _{y}\) which induces micro-cracking in the FPZ, and the failure stress \(\sigma _{f}\) which induces macro-cracking after the sudden coalescence of the micro-cracks leading to a softening behavior (see Fig. 23a). The last parameter to define is the fracture energy \(G_f [\text {J\,m}^{-2}]\), which represents the amount of energy necessary to create and fully open a unit area of macro crack, reducing the stress to zero. We will show that the proposed multi-scale approach, where the macro-scale parameters are represented as random fields, can offer an intrinsic explanation of the size-effect, recovering the dominant failure modes for small (homogeneous) structures versus large (heterogeneous) structures, where small and large can be quantified with respect to the correlation length of the random field describing the macro-scale model parameters. Such a characterization is a sound alternative to an ambiguous structure size characterization (see Fig. 23b) that is supposed to define the roles between continuum damage mechanics (CDM) and linear fracture mechanic (LFM) in describing the type of fracture [2] .
Our goal is to present the possibility to model the size effect, taking place at the macro-scale, with the use of correlated random fields for the macro-scale model parameters. With some basic assumptions, such macroscopic random fields are defined by their marginal (point-wise) first and second moments as well as their covariance function. By assuming response isotropy, which is quite reasonable for concrete composites, this covariance function might be parameterized by using, for example, a unique scalar value: the correlation length \(L_c\). This length plays a key role in this context of size effects. Contrary to classical macroscopic models which are based on the RVE concept only, \(L_c\) actually defines a scale to which the whole structure size is compared. In that sense such correlated fields naturally incorporate size effects. Moreover, such a correlation length \(L_c\) might be compared against the so called ‘characteristic length’, which needs to be defined for non-local models of fracture (e.g. see [71]). Contrary to this characteristic length for which there is a lack of physical interpretation, the correlation length \(L_c\), as well as the marginal first and second order moments necessary to fully define the macroscopic properties random fields, might be retrieved from a two-scale analysis like the one presented in Sect. 4.2. Thus we draw here a complete macroscopic modeling methodology, starting from properties and uncertainties at the meso-scale (which appears to be the most pertinent one considering mechanical failure of cement based materials), to the macroscopic behavior.
In order to model the size effect with such a macro-scale model, the key idea is to consider its parameters (namely, limit of elasticity \(\sigma _y\) and the gap between fracture stress and yield stress \(e_f=\sigma _f-\sigma _y\)) as correlated random fields \(r(x,\omega )\) over one-dimensional geometric space \({\mathcal {D}}\). In simple 1D setting, each random field can be viewed either through its realizations \(r(x,\omega _i)\) or as a family of random variables \(r(x_i,\omega )\) assigned at each point \(x_i \in {\mathcal {D}}\). Similarly, one can appeal to the maximum entropy theory (e.g. see [82, 84]) to consider that these random fields \(\sigma _{y}\) and \(e_{f}\) would either have a lognormal distribution, or as further advocated herein be defined as non-linear transformations of Gaussian random fields \(\gamma _1\) and \(\gamma _2\):
where \(\gamma _1\) and \(\gamma _2\) are fully described by their expected values and their covariances:
In (41) above we indicated that the Gaussian random fields \(\gamma _1\) and \(\gamma _2\) are supposed to be weakly homogeneous with an exponential form of the covariance and the correlation length \(L_{c}\).
Solving for the response of such a stochastic system by Galerkin method essentially consists in computing some response statistics, e.g. its expected value. For that purpose, we employ here the classical Monte-Carlo method which requires to solve a number copies of deterministic problem, each of them being built with a particular realization of the random fields \(\sigma _{y}(x,\omega _i)\) and \(e_{f}(x,\omega _i)\) quantifying heterogeneities of the structure parameters along the bar length; see Fig. 24.
In order to provide these realizations, and decide which ones and how many to use, the correlated random fields \(\gamma _1\) and \(\gamma _2\) are generated from the Karhunen–Loève expansion (see [53]). For 1D domain \({\mathcal {D}}\), we can obtain the analytic solution (e.g. see [59]) to the Fredholm eigenvalue problem (42) for eigenvector basis \(\Phi _i(x)\) orthonormal in \(L_2({\mathcal {D}})\),
and further provide a closed form of Karhunen–Loève expansion, already mentioned in (10). For a more complex domain that cannot be reduced to a product of intervals, the solution of this eigenvalue problem is obtained by using the finite element method to discretize domain \({\mathcal {D}}\). For either case, we can further discretize the two Gaussian random fields \(\gamma _{i=1,2}\),
and consequently \(\sigma _{y}\) and \(e_{f}\) through relations (40).
We note that \(\xi _i(\omega )\) in (43) are univariate Gaussian random variables that are uncorrelated and thus independent, which ensures efficiency of stochastic integrals computations. Further computational efficiency is granted by truncating the infinite sum (43) to a finite number of terms. We refer to Fig. 25 for illustration of fast convergence of KLE representation by using a different number of eigenvectors, where the covariance is drawn as a space surface parameterized over two intervals each covering 1D space \({\mathcal {D}}\).
In a nut shell, one finally has to solve a number of copies of deterministic problem, corresponding to the truncated number of KLE modes leading to an acceptable approximation error. These computations are here performed using a modified version of the finite element code FEAP [92], integrated in within code-coupling framework [34].
We note that representing a realization (evaluation of the random field at a given point in the stochastic domain) of \(\gamma _1\) and \(\gamma _2\) via the truncated Karhunen–Loève expansion on each of these bars as described previously and using the relations (40) leads to perhaps the most efficient computational way of representing in each realization the fields \(\sigma _y(x,\omega _i)\) and \(e_f(x,\omega _i)\). The normalized fluctuating part of each realization of \(\sigma _y\) and \(e_f\) is shown in Fig. 26 for 3 bars of different length: small, which is equal to \(L_c\), medium, which is 10 times longer, and large, chosen as 100 times longer. It is worth to note that the larger the bar is with respect to the correlation length \(L_c\), the more fluctuating the random fields become. Thus, it is more likely that macroscopic properties will have low minimum values. In terms of strength, such lower minimum values obviously lead to a weaker behavior.
a Classification of three bars with respect to correlation length \(L_c\): short (1 \(L_c\)), medium (10 \(L_c\)) and large (100 \(L_c\)); b ultimate strength CDF; b probability-based explanation of size effect [35] illustrated with percentile of broken bars and d deterministic illustration of size effect [2]
Each of these independent realizations is used to perform Monte Carlo simulations with 10,000 samples for each case using the coFeap and the component template library (CTL) [34], with the overall results presented in Fig. 26. These computation results are obtained for all three bars in Fig. 26a with \(99\%\) confidence interval, where we checked that none of these error bars are overlapping. This allows us to conclude that the number of samples used for the Monte Carlo process is large enough to deliver sufficiently accurate results.
Figure 26b presents the cumulative density functions for the maximum strength of three bars, small, medium and large. It is worth to note that the smaller the bar is, the bigger is its ultimate stress: 3.68 MPa for the small bar, 3.3 MPa for the medium one and 2.87 MPa for the large bar. In other words, the strength of the structure is directly linked to its size. The larger is the structure compared to the correlation length, it is likely to be weaker with respect to its strength.
Moreover, we also show in Fig. 26c the percentile of bar that break for different bar length. Such diagram reproduces quite well the deterministic interpretation of size effect shown in Fig. 26d, where the participation of the fracture process zone (here the contribution of random field \(e_f\)) becomes a dominant factor for large bars, which is contrary to short bars, where the dominant contribution to complete failure pattern is the one coming from the random field \(\sigma _y\). Hence, this stochastic way of modeling quasi-brittle failure naturally reveals size effect. Clearly, the correlation length here plays a key role. Comparable to the characteristic length which appears in the non-local theory, it can be linked to the size of the fracture process zone (FPZ) where micro-cracking occurs. The more the size of the FPZ prevails on the global size of the structure (which is the case for a small bar), the more similar to continuum damage mechanics (CDM) the structure’s behavior is. In the opposite, if the FPZ size is negligible with respect to the size of the structure (which is the case for a large bar), its influence on the global behavior of the structure remains rather small. Thus a macro-crack occurs as dominant failure mode, which belongs to linear fracture mechanics (LFM) application domain. Modeling the behavior of quasi-brittle materials is an attempt to link these two limit behaviors (LFM and CDM). Figure 26 shows that one possible way is to consider correlated random fields to describe macroscopic quantities and and quantify the dominant failure mode by the correlation length \(L_c\).
7 Scale effect: damping model replacement for classical Rayleigh damping
For clarity, this crucial idea on how fine scale processes stochastically upscale to coarse scale in dynamics is further illustrated with a simple example problem of 1D beam multi-scale model (see Fig. 27). First, we discuss the size effect that can be illustrated by solving a direct problem of providing the estimates for damping in concrete, which can serve as a more comprehensive model replacing classical Rayleigh damping. Namely, when considering a macro-scale 1D beam with homogenized elastic behavior, eventual energy dissipation can be represented by classical Rayleigh damping. Such a damping effect is proportional to velocity with a damping matrix \(\varvec{C}\) as a linear combination of structure mass \(\varvec{M}\) and stiffness matrices \(\varvec{K}\) [9]; see (44). Next to model simplicity with only one model parameter, the so called damping ratio \(\xi\) (typically taken as 0.05 for concrete), the main advantage of Rayleigh damping is in matching the experimentally observed exponential decay of the vibration amplitude that can be quantified by the logarithmic decrement \(\delta\), which is proportional to the damping ratio; see (44). The main deficiency of Rayleigh damping is that the damping ratio \(\xi\) is a structural property, which pertains only to a particular structure size, characterized by its stiffness and mass matrices (e.g. see [9] or [32]).
How do we obtain the damping ratio for a different structure size without the need for new experiments? We follow recent work [29] to provide a multi-scale model of energy dissipation, which can deal with all progressive stages of dynamic fracture and also capture size effect. In particular, we will use a coupled plasticity-damage meso-scale beam model [37] to reproduce experimentally observed hysteresis loops.
For computational efficiency, we keep linear evolution equations of corresponding internal variables (plastic strain \({\epsilon }^{\mathrm {p}}\), damage compliance D, hardening variables for plasticity \({\xi }^{\mathrm {p}}\), or for damage \({\xi }^{\mathrm {d}}\)) and variables that handle softening phase, both for plasticity, \(\overline{\overline{u}}^{\mathrm {p}}\), and for damage, \(\overline{\overline{D}} {\mathrm {t}}\), in each particular fiber; see (45), which can match experimental hysteresis loops not only in terms of their shape, but rather in terms of the enclosed area representing the energy dissipated in each hysteresis loop; see Fig. 27.
The multi-scale approach combines these meso-scale evolution equations with a hybrid displacement–stress formulation for macro-scale state variables, and with their independent interpolation with an additive decomposition of internal variable contributions that simplifying tangent stiffness computations
with
The proposed approach results in a very efficient multi-scale computational model combining global and local equations, that is capable of capturing energy dissipation in each particular stage of the beam ductile failure, with a cost that is comparable to the solution of (44) with a standard time stepping scheme.
The final step is to consider the probability distribution of structure heterogeneities, as illustrated in Fig. 28a for the case of a plastic component with simple Gaussian distribution of the yield stress \(\sigma _y\). for each fiber. We note that such an assumption is equivalent to assuming a random field distribution of the beam structure macro-scale properties, given the beam bending problem with linear stress distribution. A larger beam structure size (with more likely concentration of initial and induced defects) results in stronger heterogeneities and thus a larger standard deviation \(\tau\). For such a large (heterogeneous) structure, we show in Fig. 28b the multi-scale model ability to recover exponential amplitude decay, as opposed to linear amplitude decay for a smaller (homogeneous) structure with almost constant yield stress everywhere; (linear amplitude decay is characteristic of frictional energy dissipation [42], which confirms the equivalence between plasticity and friction [37]). In conclusion, the multi-scale model of damping can represent the size effect through the crucial role of probability distribution of structure-scale heterogeneities.
Simple problem to illustrate stochastic upscaling in dynamical system: a Gaussian probability distribution of yield stress \(\sigma _y\) as random variable with \(\tau\) as standard deviation; b amplitude decay computed with the proposed multi-scale model, indicating transition from linear amplitude decay for homogeneous structure (bottom graph with \(\tau\) = 0.01) towards exponential amplitude decay for heterogeneous structure (top graph with \(\tau\) = 1.06), adapting energy dissipation to structure size, with more likely heterogeneities for larger structures
The scale effect in this model can be illustrated with the solution to an inverse problem by Bayesian inference: namely, we consider an inverse problem where one would like to provide a Reduced Order Model (ROM) at a macro-scale for a further increase in computational efficiency (since we target more demanding problems than this simple illustration of an 1D beam multi-scale model). In other words, from experimental measurements of energy at the macro-scale (see Fig. 27b), we would like to obtain the evolution equations of macro-scale internal variables that provide the best match to dissipated energy. We follow [46] by assuming these evolution equations to be linear stochastic differential equations, which will best describe the loss-of-information typical of model reduction. The Quantity of Interest (QoI) is still dissipated energy, and computed hysteresis loops will still resemble those in Fig. 27b, but they are now defined at the macro-scale. Contrary to current state-of-the-art approaches to Reduced Order Models (ROM), such as those already mentioned POD or PGD [47], all the internal variables remain active in constructing the best result of Bayesian inference computations [59], with their relative contribution handled by a Hidden Semi-Markov Model [51]. Consequently, the model can capture the scale effect with changes in the characteristic evolution rate of dynamic system. The main novelty of the proposed ROM is its ability to consider the problem of fracture and rupture, which so far has not been addressed. In a certain way, the proposed approach is dual to our recent work on reduced models of stochastic plasticity [31], in constructing stochastic process descriptions of evolution equations at the macro-scale rather than random field description of yield criteria at the macro-scale. We also note that a successful implementation of the ROM will require the judicious choice of embedded-discontinuity finite elements [30, 77] in order to accommodate softening phenomena in a multi-scale computational framework.
8 Stochastic solutions—beyond Young measures
A phenomenon which has been observed in the context of computations with brittle and quasi-brittle materials—or more generally softening materials for that matter—is that there are situations where slight changes in the mesh or computational algorithm lead to other solutions. The same is observed if physical parameters are slightly perturbed. This should not surprise too much, as for a softening material the incremental stored energy is not convex any more. Especially the perturbation of physical parameters may be connected to probabilistic descriptions, and then different solutions show different probabilities of occurrence. From this arose the idea [23] to describe all the possible solutions and their probabilities of occurrence with a random field, the probabilities resulting from the energy landscape of the problem. This—the randomly perturbed problem in the limit as the perturbation vanishes but the multiple solutions persist—may be viewed as a relaxatation of the original problem.
The concept of relaxation is quite common for non-convex problems. The approach [23] to be sketched here starts from the idea of parametrized measures, also known as Young measures and their generalizations, but will go beyond and extend these. Young measures have been used to mathematically describe oscillation and concentration effects in minimizing sequences [69, 70, 76], as well as damage evolution in materials [17], or more generally in rate-independent systems [65]. Such measure-valued solutions have recently also been considered for hyperbolic systems of conservation laws [18, 19, 50], in particular in connection with the occurrence of turbulence. Here the problem is reformulated with Young-measure-valued solutions, and then extended to an infinite system of Young correlation measures—a concept termed “statistical solution”. This defines a probability measure in some function spaces, and this solution concept apparently goes back at least to Foiaş, see [20] for a short account.
At least as powerful, and in our view easier to handle, is the new concept of “stochastic solution” [23], which uses generalized random fields. Here we will not go into mathematical details (they can be found in [23]), but be content to explain this with some examples.
The first example is a simple bar under tension with a varying product of cross-sectional area A and critical fracture energy \(G_f\), shown in Fig. 29a. Under sufficient tension, the bar will break at the points with a minimum of \(G_f A(x)\). In Fig. 29a, these are the points \(x=1\) and \(x=4\). If now that curve is perturbed with white noise, as shown in Fig. 29b, one can count in a histogram Fig. 29c how often the bar breaks at which position; the computation of this is extremely simple, one only has to find the minimum of \(G_f A(x)\). In Fig. 29d we show a kernel approximation of the probability density function resulting from the histogram in Fig. 29c). As one lets the perturbations in Fig. 29b vanish, the breakage probabilities settle down to \(p_1 = 1/3\) and \(p_4 = 2/3\). This is the stochastic solution in this simple case.
If the piecewise linear \(G_f A(x)\)-curve is changed to a piecewise quadratic as in Fig. 30a, this results in the breakage probability density function shown in Fig. 30b under perturbations. With vanishing perturbations the breakage probabilities again settle down to \(p_1 = 1/3\) and \(p_4 = 2/3\).
Combining a piecewise quadratic and piecewise linear \(G_f A(x)\)-curve as in Fig. 31a gives the breakage probability density function shown in Fig. 31b under perturbations. And with vanishing perturbations the breakage probabilities now settle down to \(p_1 = 1\) and \(p_4 = 0\). These simple examples with Young-measure-valued solution show that this concept can capture the probabilities of the different behaviors.
To show now an example which needs the generalization to stochastic solutions, we look at the so-called thermal shock problem from [15]. Here a plate with a certain thermal expansion coefficients is suddenly put in contact with a cold liquid, and the lower edged starts to contract and develop tensile stresses, which eventually lead to cracks, see Fig. 32.
Here \(\Updelta T_c\) is the critical initial temperature difference between plate and liquid where cracking starts. The computations were performed with a newly developed Quad6-element with embedded discontinuities, see [86] for details. The ultimate stress at the lower edge is slightly randomly perturbed, which then seeds a first crack at some random point. After this initial crack, the following crack development is more predictable and depends on the loading intensity, as seen in Fig. 32. The three columns are the different load intensities \(\Updelta T = 2 \Updelta T_c, 2 \Updelta T_c,\) and \(8 \Updelta T_c\). The stochastic solution can not only capture the random location of crack initiation, but more importantly with the concept of conditioning—which was used above for identification and upscaling—also the probable evolution of the cracks conditioned on the occurrence of the first crack. This conditional stochastic structure could not be described just with Young measures.
A final example, taken from [1], shows again this conditional stochastic structure, now in the context of crack branching. This is a single edge notched specimen, a benchmark test for crack branching. A plate with a short notch at the center is suddenly pulled apart, see Fig. 33, where only half the plate has to be computed due to symmetry considerations. Shown is the dynamic crack pattern evolving and the spontaneous crack branching in an unperturbed plate; details of the computation may be found in [86].
In Fig. 34 two computations of the same model are shown, but now the tensile stress has been randomly perturbed slightly (2% white noise). One may observe that the resulting crack pattern changes considerably, depending on the random realization. Again, the conditional stochastic structure inherent in describing these solutions with evolving random fields can be captured with the stochastic solution concept, and again these stochastic conditional dependencies could not be described just by Young measures.
9 Conclusions
The main thrust of this work was an overview on new developments for providing successful solutions to coupled problems of stochastics-inelasticity at multiple scales, as the key milestone in quantifying the fracture integrity and durability of reinforced concrete and concrete composites. The interplay between stochastics and inelasticity here has a crucial role in constructing the multiscale strategy in terms of stochastic upscaling, and a corresponding probability-based interpretation of size and scale effects, which quantify how the structure size is changing the dominant failure modes and dynamic response characteristics.
The main contributions that allow connecting vastly different scales for cement-based composites, spanning from multiphysics driven micro-structure evolution to non-local scales of long fiber reinforcement are numerous—the most important already is the attempt to connect the phenomena that constitute the successful solution ingredients; from cement hydration to concrete microstructure, and further on to concrete fracture and reinforcement design. A number of novelties had to be provided, as follows in this conclusion.
The sound theoretical formulation for fracture and inelasticity at multiple scales is deeply rooted in thermodynamics. We have constructed a multiscale formulation that needs no regularization, contrary to mainstream fracture models, such as gradient plasticity, non-local theory, or the phase-field approach. The proposed theoretical formulation can correctly represent the additive split of total dissipation into volume and crack-surface components, the full set of fracture mechanisms at different scales, their evolutions and interactions, and finally the non-local representation of reinforcement slip.
Another feature is the most suitable discrete approximation for each particular scale: Voxel representation of microstructure at the RVE-cement micro-scale, Voronoi cells at the RVE-concrete for the meso-scale combined with ED-FEM for macro-crack representation, and finally X-FEM for non-local slip or reinforcement. Such a set of choices covers practically all the current mainstream discrete approximations. The main novelty is that all of them are tied together within a proposed multiscale approach, finding their distinct place and the most efficient role.
The stochastic upscaling is the key contribution that allows to achieve computational efficiency by constructing the reduced order model for fracture in a very consistent manner, which is very much different from previous ad-hoc choices. The theoretical formulation of stochastic upscaling is presented in terms of a Bayesian inference procedure, and the computational procedure is illustrated on a number different scale transitions, from the finest to the coarsest scale considered in this problem.
Of special interest and value are the stochastic upscaling results that provide the most sound interpretation of the size and scale effects, and efficient computational procedures in terms of the Gauss Markov Kálmán Filter (GMKF) approach. With such an approach we can recover a reduced model that defines probability distributions of fracture parameters describing localized failure with both volume and surface dissipation, as well as the most general (non-Gaussian) probability distribution of structure failure modes for advanced safety and durability evaluation. We note that in a probability-based explanation of size and scale effects, as well as the proposed extension that goes beyond Young measures, the crucial role is played by random fields. These important concepts, illustrated for clarity in a simple 1D case, remain valid in a more general context.
Finally, it remains to once more point out that these advancements were only possible by finding the right interplay between stochastics, mechanics, thermodynamics, Bayesian upscaling, as well as the appropriate discrete approximation methods at each scale.
References
Armero F, Linder C (2009) Numerical simulation of dynamic fracture using finite elements with embedded discontinuities. Int J Fract 160:119–141
Bazant ZP (2004) Probability distribution of energetic-statistical size effect in quasi-brittle failure. Probab Eng Mech 19:307–319
Belytschko T, Black T (1999) Elastic crack growth in finite elements with minimal remeshing. Int J Numer Methods Eng 45:601–620
Belytschko T, Song JH (2010) Coarse-graining of multiscale crack propagation. Int J Numer Methods Eng 81:537–563
Bentz DP (2006) Quantitative comparison of real and CEMHYD3D model microstructures using correlation function. Cem Conc Res 36:259–263
Bobrowski A (2005) Functional analysis for probability and stochastic processes. Cambridge University Press, Cambridge
Boyard S, Lebris C, Lelievre T, Madey Y (2010) Reduced basis techniques for stochastic problems. Arch Comput Methods Eng 17:435–454
Chinesta F, Huerta A, Rozza G, Willcox K (2017) Model reduction methods. In: Stein E, de Borst R, Hughes TRJ (eds) Part 1. Solids and structures. Encyclopedia of computational mechanics, 2nd ed. Wiley. https://doi.org/10.1002/9781119176817.ecm2110
Clough RW, Penzien J (2006) Dynamics of structures. McGraw-Hill, London
Dittmann M, Aldakheel F, Schulte J, Wriggers P, Hesch C (2018) Variational phase-field formulation of non-linear ductile fracture. Comput Methods Appl Mech Eng 342:71–94
Dominguez N, Brancherie D, Davenne L, Ibrahimbegovic A (2005) Prediction of crack pattern distribution in reinforced concrete by coupling a strong discontinuity model of concrete cracking and a bond-slip of reinforcement model. Int J Eng Comput 22:558–581
Eu BC (1998) Nonequilibrium statistical thermodynamics: ensemble method. Springer, Berlin
Evensen G (2009) The ensemble Kalman filter for combined state and parameter estimation. IEEE Control Syst Mag 29:82–104
Evensen G (2007) Data assimilation. The ensemble Kalman filter. Springer, Berlin
Farrell P, Maurini C (2017) Linear and nonlinear solvers for variational phase-field models of brittle fracture. Int J Numer Methods Eng 109:648–667
Feyel F, Chaboche JL (2000) FE2 multiscale approach for modelling the elastoviscoplastic behaviour. Comput Methods Appl Mech Eng 183:309–330
Fiaschi A, Knees D, Stefanelli U (2012) Young-measure quasi-static damage evolution. Arch Rat Mech Anal 203:415–453. https://doi.org/10.1007/s00205-011-0474-3
Fjordholm US, Mishra S, Tadmor E (2016) On the computation of measure-valued solutions. Acta Numer 25:567–679
Fjordholm US, Lanthaler S, Mishra S (2017) Statistical solutions of hyperbolic conservation laws: foundations. Arch Rat Mech Anal 226(2):809–849
Foiaş C, Manley O, Rosa R, Temam R (2004) Navier–Stokes equations and turbulence. In: Encyclopedia of mathematics and its applications, vol 83. Cambridge University Press, Cambridge
Frey PJ, George PL (1999) Meshes in finite element applications. Hermes Science, Hamburg (in French)
Gamerman D, Lopes HF (2006) Markov chain Monte Carlo: stochastic simulation for Bayesian inference. Chapman and Hall, Boca Raton
Gerasimov T, Römer U, Vondřejc J, Matthies HG, De Lorenzis L (2020) Stochastic phase-field modeling of brittle fracture: computing multiple crack patterns and their probabilities. Comput Methods Appl Mech Eng 372:113353. https://doi.org/10.1016/j.cma.2020.113353
Germain P, Nguyen QS, Suquet P (1983) Continuum thermodynamics. ASME J Appl Mech 50:1010–1029
Goldstein M, Wooff D (2007) Bayes linear statistics, Wiley series in probability and statistics. Wiley, Chichester
Gilks RW, Richardson S, Spiegelhalter D (1995) Markov Chain Monte Carlo in Practice, Chapman & Hall, Boca Raton, FL
Hautefeuille M, Colliat JB, Ibrahimbegović A, Matthies HG, Villon P (2012) A multi-scale approach to model localized failure with softening. Comput Struct 94–95:83–95. https://doi.org/10.1016/j.compstruc.2011.11.007
Hofstetter G, Mang HA (1995) Computational mechanics of reinforced concrete structures. Vieweg, Braunschweig
Ibrahimbegovic A, Mejia Nava RA (2021) Heterogeneities and material scales providing physically-based damping to replace Rayleigh damping for any structure size. Coupl Syst Mech 10:201–216. https://doi.org/10.12989/csm.2021.10.3.201
Ibrahimbegovic A, Rukavina I, Suljevic S (2021) Multiscale model with embedded-discontinuity discrete approximation capable of representing full set of 3D failure modes for heterogeneous materials with no scale separation. J Multiscale Comput Eng. https://doi.org/10.1615/IntJMultCompEng.2021038378
Ibrahimbegovic A, Matthies HG, Karavelic E (2020) Reduced model of macro-scale stochastic plasticity identification by Bayesian inference: application to quasi-brittle failure of concrete. Comput Methods Appl Mech Eng 372:113428. https://doi.org/10.1016/j.cma.2020.113428
Ibrahimbegovic A, Ademovic N (2019) Nonlinear dynamics of structures under extreme transient loads. CRC Press, London
Ibrahimbegovic A, Matthies HG (2012) Probabilistic multiscale analysis of inelastic localized failure in solid mechanics. Comput Assist Methods Eng Sci 19:277–304
Ibrahimbegovic A, Niekamp R, Ch Kassiotis D, Markovic HM (2014) Code-coupling strategy for efficient development of computer software in multiscale and multiphysics nonlinear evolution problems in computational mechanics. Adv Eng Softw 72:8–17
Ibrahimbegovic A, Colliat JB, Hautefeuille M, Brancherie D, Melnyk S (2011) Probability based size effect representation for failure in civil engineering structures built of heterogeneous materials. In: Papadrakakis, M et al (eds) Computational methods in stochastic dynamics. Springer, pp 289–311 (2011)
Ibrahimbegovic A, Boulkertous A, Davenne L, Brancherie D (2010) Modelling of reinforced-concrete structures providing crack-spacing based on X-FEM, ED-FEM and novel operator split solution procedure. Int J Numer Methods Eng 83:452–481
Ibrahimbegovic A (2009) Nonlinear solid mechanics: theoretical formulations and finite element solution methods. Springer
Ibrahimbegovic A, Melnyk S (2007) Embedded discontinuity finite element method for modeling of localized failure in heterogeneous materials with structured mesh: an alternative to extended finite element method. Comput Mech 40:149–155
Ibrahimbegovic A, Delaplace A (2003) Microscale and mesoscale discrete models for dynamic fracture of structures built of brittle materials. Comput Struct 81:1255–1265
Ibrahimbegovic A, Brancherie D (2003) Combined hardening and softening constitutive model of plasticity: precursor to shear line failure. Comput Mech 31:88–100
Ibrahimbegovic A, Markovic D (2003) Strong coupling methods in multi-phase and multi-scale modeling of inelastic behavior of heterogeneous structures. Comput Methods Appl Mech Eng 192:3089–3107
Inman DJ (2001) Engineering vibrations. Prentice Hall, Prentice
Jirasek M, Belytschko T (2002) Vienna, pp 1–5
Kálmán RE (1960) A new approach to linear filtering and prediction problems, Transactions of the ASME — J. of Basic Engineering (Series D) 82, 35–45
Karavelic E, Nikolic M, Ibrahimbegovic A, Kurtovic A (2019) Formulation and numerical implementation. Concrete meso-scale model with full set of 3D failure modes with random distribution of aggregate and cement phase. Part I. Comput Methods Appl Mech Eng 344:1051–1072
Koutsourelakis PS, Bilionis E (2011) Scalable Bayesian reduced-order models for simulating high-dimensional dynamical systems. SIAM Multiscale Model Simul 9:449–485
Ladevèze P (2016) On reduced models in nonlinear solid mechanics. Eur J Mech A/Solids 60:227–237
Ladevèze P, Puel G, Romeuf T (2006) Lack of knowledge in structural model validation. Comput Methods Appl Mech Eng 197:4697–4710
Lamon J (2009) Ceramics reliability: statistical analysis of multiaxial failure using Weibull approach and the multiaxial elemental strength model. Compos Sci Tech 69:1607–1614
Lanthaler S, Mishra S (2015) Computation of measure-valued solutions for the incompressible Euler equations. Math Models Methods Appl Sci 25(11):2043–2088
Limnios N, Barbu V (2008) Semi-Markov chains and hidden semi-markov models. Toward applications. Their use in reliability and DNA analysis. Lecture Notes in Statistics 191. Springer
Lions JL (1980) Asymptotic calculus of variations. Academic Press, London
Loève M (1977) Probability theory. Springer, Berlin
Luenberger DG (1969) Optimization by vector space methods. Wiley, Chichester
Lura P, Couch J, Jensen OM, Weiss J (2009) Early-age acoustic emission measurements in hydrating cement paste: evidence for cavitation during solidification due to self-desiccation. Cem Concr Res 39:861–867
Madras N (2002) Lectures on Monte Carlo methods. American Mathematical Society, Providence, RI
Mahu M, Gaudin J, Grihon S, Leroux O (2013) Design optimization of composite structures AIRBUS challenge in MAXIMUS, Proc. Giens, pp 1–5
Markovic D, Ibrahimbegovic A (2006) Complementary energy based FE modelling of coupled elasto-plastic and damage behavior for continuum microstructure computations. Comput Methods Appl Mech Eng 195:5077–5093
Matthies HG (2007) Uncertainty quantification with stochastic finite elements. In Stein E, de Borst R, Hughes TJR (eds) Part 1. Fundamentals. Encyclopedia of computational mechanics, vol 1. Wiley (2007). https://doi.org/10.1002/0470091355.ecm071
Matthies HG, Zander E, Rosić BV, Litvinenko A, Pajonk O (2016) Inverse problems in a Bayesian setting. In: Ibrahimbegovic A (ed) Computational methods for solids and fluids—multiscale analysis, probability aspects, and model reduction, vol 41 of computational methods in applied sciences. Springer, Berlin, pp 245–286. https://doi.org/10.1007/978-3-319-27996-1
Matthies HG, Zander BV, Rosić A (2016) Parameter estimation via conditional expectation: a Bayesian inversion. Adv Model Simul Eng Sci 3:24. https://doi.org/10.1186/s40323-016-0075-7
Matthies HG (2017) Uncertainty quantification and bayesian inversion. In: Stein E, de Borst R, Hughes TRJ (eds) Part 1: Fundamentals. Encyclopedia of computational mechanics, 2nd edn. Wiley. https://doi.org/10.1002/9781119176817.ecm2071
Mazars J (1995) A description of micro and macro-scale damage of concrete structures. Eng Fract Mech 25:729–737
Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH Teller E (1953) Equation of state calculations by fast computing machines. J Chem Phys 21:1087–1092. https://doi.org/10.1063/1.1699114
Mielke A, Roubíček T (2015) Rate-independent systems: theory and application. Applied mathematical sciences. Springer, Berlin
Muhlhaus HB, Aifantis EC (1991) A variational principle for gradient plasticity. Int J Solids Struct 28:845–857
Nikolić M, Do XN, Ibrahimbegovic A, Nikolić Ž (2018) Crack propagation in dynamics by embedded strong discontinuity approach: enhanced solid versus discrete lattice model. Comput Methods Appl Mech Eng 340:480–499
Nouy A (2017) Low-rank tensor methods for model order reduction. In: Ghanem R, et al. (eds) Handbook of uncertainty quantification. Springer, pp 857–882
Pedregal P (1997) Parameterized measures and variational principles. Birkhäuser, Basel
Di Perna RJ, Majda AJ (1987) Oscillations and concentrations in weak solutions of the incompressible fluid equations. Commun Math Phys 108(4):667–689
Pijaudier-Cabot G, Bažant ZP (1987) Nonlocal damage theory. J Eng Mech 113:1512–1533
Ramtani S (1990) Contribution to the modeling of the multi-axial behavior of damaged concrete with description of the unilateral characteristics. PhD thesis (in French), Paris 6 University
Rao MM (2005) Conditional measures and applications. CRC Press, Boca Raton, FL
Rosić BV, Litvinenko A, Pajonk O, Matthies HG (2012) Sampling-free linear Bayesian update of polynomial chaos representations. J Comput Phys 231:5761–5787. https://doi.org/10.1016/j.jcp.2012.04.044
Rosić BV, Kučerová A, Sýkora J, Pajonk O, Litvinenko A, Matthies HG (2013) Parameter identification in a probabilistic setting. Eng Struct 50:179–196. https://doi.org/10.1016/j.engstruct.2012.12.029
Roubíček T (1997) Relaxation in optimization theory and variational calculus. Walter de Gruyter, Berlin
Rukavina I, Ibrahimbegovic A, Do XN, Markovic D (2019) ED-FEM multi-scale computation procedure for localized failure. Coupl Syst Mech 8:111–127. https://doi.org/10.12989/csm.2019.8.2.111
De Sa De C, Benkemoun N, Colliat JB, Benboudjema F (2009) Modélisation à l’échelle méso-scopique du comportement hydro-mécanique des matériaux à matrice cimentaire, Proceedings colloque du CSMA, Giens (2009)
Sarfaraz MS, Rosić BV, Matthies HG, Ibrahimbegovic A (2020) Bayesian stochastic multi-scale analysis via energy considerations. Adv Model Simul Eng Sci 7:50–68
Sarfaraz MS, Rosić BV, Matthies HG, Ibrahimbegovic A (2018) Stochastic upscaling via linear Bayesian updating. In: Sorić J, Wriggers P, Allix O (eds) Multiscale modeling of heterogeneous structures. Lecture notes in applied and computational mechanics, vol 86. Springer, pp 163–181. https://doi.org/10.1007/978-3-319-65463-8_9.
Sarfaraz MS, Rosić BV, Matthies HG, Ibrahimbegović A (2018) Stochastic upscaling via linear Bayesian updating. Coupl Syst Mech 7(2):211–232. https://doi.org/10.12989/csm.2018.7.2.211
Shannon CE (1948) A mathematical theory of communication. Bell Syst Tech J 27:379–423 and 623–659 (1948)
Shell MS (2008) The relative entropy is fundamental to multiscale and inverse thermodynamic problems. J Chem Phys 129(14):114108
Soize C (2001) Maximum entropy approach for modeling random uncertainties in transient elastodynamics. J Acoust Soc Am 109(5):1979–1996
Shinozuka M, Feng M, Lee J, Naganuma T (2000) Statistical analysis of fragility curves. J Eng Mech 126:1224–1231
Stanić A, Brank B, Ibrahimbegovic A, Matthies HG (2021) Crack propagation simulation without crack tracking algorithm: embedded discontinuity formulation with incompatible modes. Comput Methods Appl Mech Eng 386:114090. https://doi.org/10.1016/j.cma.2021.114090
Tarantola A (2005) Inverse problem theory and methods for model parameter estimation. SIAM, Philadelphia
Weibull W (1951) A statistical distribution function of wide applicability. J Appl Mech 293–297
Wriggers P, Zohdi TI (2001) Computational testing of new materials. In: Proceedings ECCM 2001, Crackow, Poland
Xiu D, Karniadakis GE (2002) The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J Sci Comput 24:619–644
Xiu D (2010) Numerical methods for stochastic computations: a spectral method approach. Princeton University Press, Princeton
Zienkiewicz OC, Taylor RL (2005) The finite element method, vol 1 and 2, 6th edn. Elsevier, Oxford
Acknowledgements
We acknowledge the funding sources that allowed our long-term collaboration: IUF Senior Member and Humboldt Research Award for AI, Gay-Lussac Humboldt Research Award for HGM, ANR-DFG international project SELF-TUM, ANR project MS3C, DFG projects PHAROS, SPP 1748, SPP 1886, GRK 2075, as well as Hauts-de-France and Niedersachsen grants to SD, RAMN, CUN, MSS, AS, and JV.
Funding
Funding was provided by Agence Nationale de la Recherche (Grant No. SELF-TUM).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
This work was supported by public agencies for funding scientific research: IUF and ANR in France, DFG in Germany, as well as Regional Governments of Hauts-de-France and Niedersachsen. Thus, none of the research results has any particular restriction on publication. The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ibrahimbegovic, A., Matthies, H.G., Dobrilla, S. et al. Synergy of stochastics and inelasticity at multiple scales: novel Bayesian applications in stochastic upscaling and fracture size and scale effects. SN Appl. Sci. 4, 191 (2022). https://doi.org/10.1007/s42452-022-04935-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-022-04935-y
Keywords
- Multiscale mechanics
- Bayesian inference
- Inelasticity and fracture
- Stochastic Upscaling
- Size and scale effects