1 Introduction

Reconstructing the 3D structure of a scene from a single RGB image has been receiving widespread attention owing to the comprehensive applications in the subject of image processing and computer vision. Precise depth information helps to understand the scene’s internal geometric structure better, which could significantly improve the performance on various existing vision tasks, such as autonomous driving, augmented reality, 3D reconstruction, semantic labeling, and pose estimation [1,2,3]. Traditional active depth generation methods typically use hardware devices, such as lasers and depth sensors, to simultaneously capture the RGB images and corresponding depth maps. Nevertheless, the disadvantages of low depth resolution, short distance perception, and high system cost seriously hinder the wide application of such methods [4]. In contrast, using computational schemes to infer depth from a single RGB image provides a reasonable and low-cost way to generate the depth map.

Last few years, many researchers have explored multiple algorithms for single image depth recovery. Traditional approaches mainly focus on the use of monocular depth cues [5, 6]. However, these approaches are not suitable for all actual scenarios. In parallel, some algorithms leverage geometric assumptions [7] and additional information [8, 9] to recover the depth information have been proposed. However, these methods cannot furnish detailed depth information, and additional clues are not available.

More recently, many researchers are focusing on machine learning methods to generate reasonable depth information. Recent learning-based depth prediction algorithms from a single RGB image can be classified into non-parametric learning algorithms and parametric learning algorithms. The first category casts depth recovery as a non-parametric learning process. Non-parametric approaches can transfer depth to a single input image by leveraging a wide-ranging RGBD dataset efficiently [10,11,12,13,14,15,16]. For an input image, similar candidate images are first retrieved from the RGB-D database by utilizing the k-nearest neighbors algorithm. Then, the dense pixel-pixel relationship between the test image and the candidate images is established. The corresponding depths of candidate images are warped and fused by leveraging an optimization algorithm for generating the final depth. Nevertheless, when the input image has a scene structure that is not similar to the training dataset, the non-parametric approaches cannot generate convincing depth maps.

Another category is the parametric learning method. As a groundbreaking work, Saxena et al. [17, 18] learned a Markov random field (MRF) for exploring the relationship between the color image and the depth information. In parallel, many scholars also proposed other parametric learning algorithms, for instance, conditional random field (CRF) [8] and structured forest [19]. Lately, deep learning-based depth prediction methods have emerged, which has influential feature learning ability and can recover accuracy scene depth information. Meanwhile, the leverage of convolutional neural networks (CNNs) has vastly enhanced the performance of depth prediction algorithms [20,21,22,23,24]. With a deeper architecture, the CNN-based methods can infer the global layout of scene reliability. Nevertheless, the reconstructed depth maps lack finer depth details after many times of convolution and max-pooling, and researchers demanded these details in many computer vision tasks.

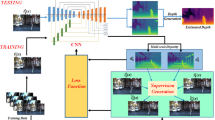
To fill the research gap mentioned above, we present an efficient framework for single image depth prediction based on modified fully convolutional residual network and gradient network in this study. The idea of this paper is to benefit from the capacity of CNN structure, but avoid the lack of depth details. Since gradient information is not very sensitive to the scene features of training data and can provide subtle details of the scene, we incorporate depth gradient information into the depth recovery process. In particular, first, an efficient deep network that combines the fully convolutional residual network (FCRN) [23] and U-net architectures [25] for recovering the global structure of a scene is proposed. Nonetheless, the depth details are imperfect, since the intermediate features are not integrated into the network. Since the depth gradients are very sparse, we designed a depth gradient generation network for capturing the local information of the depth map. In the end, an energy equation minimization scheme is proposed for integrating the complementary depth information and depth gradient information to infer a convincing depth map.

To sum up, the contribution of this paper is three-fold.

  • • We modified the classic network and loss function to generate the global 3D depth information of the scene.

  • • We designed a depth gradient acquisition scheme to generate the local details of the scene.

  • • Plausible depth map with better depth details can be recovered through our developed depth and depth gradients fusion strategy.

Sect. 2 describes the related works for single image depth prediction. Sect. 3 introduces the presented depth prediction algorithm. Sect. 4 summarizes all experimental results. Finally, Sect. 5 concludes this work.

2 Related work

Last few years, various methods have been exploiting how to infer depth from a single RGB image. Previous algorithms to depth prediction mainly focus on the use of monocular depth cues, for instance, defocus, saliency, atmospheric scattering, and occlusion [5, 6]. However, these kinds of methods are not suitable for all scenarios. In parallel, some schemes have been developed for estimating the depth map by utilizing geometric presumption [7]. These models can efficiently recover the global structure of a scene, but cannot obtain the desired result when the structure is complex. Meanwhile, depth prediction can be implemented by employing additional ancillary information, such as surface normal [8] and repetitive texture [9] if auxiliary cues are accessible. But, regrettably, such supplemental details are not always available in universal scenarios.

More recently, machine learning-based depth prediction methods have been receiving researchers’ great attention. We classified these  approaches into two groups: one is the non-parametric learning methods and the other is the parametric learning methods.

For non-parametric learning approaches, Konrad et al. [10] put forward the first pioneering work in this field. They used the histograms of oriented gradients (HOG) descriptor to select candidate images with the photo-metric content that best matched the test image. Later, the median operator was leveraged to fuse candidate depths to obtain the initial depth, which was enhanced by using efficient filtering. To enhance the quality of the depth map, Karsch et al. [11] deformed the corresponding depths of candidate images based on the pixel-pixel correspondence relationship. These deformed depths were integrated by solving nonlinear optimization issues for estimating the scene depth. To reduce the dependency on similar datasets, Chios et al. [12] designed an efficient non-parametric learning method, which is named the depth analogy method. They extracted the depth gradient and used the depth from the gradient algorithm for recovering the scene depth. Meanwhile, Herrera et al. [13] leveraged features based on Local Binary Patterns to retrieve candidate images. They recovered the final depth by integrating the depths of these candidate images adaptively. These methods could be impractical for large-scale databases as they carry out a time-consuming retrieve to select the matching candidates from the training dataset. To work out this difficulty, Herrera et al. [14] presented a graduated retrieve scheme based on a clustering algorithm. More recently, Mohaghegh et al. [15] combined the global and local features of the scene and devised a modified stacked generalization framework to learn depth values of image patches. Liu et al. [16] introduced an efficient monocular depth estimation strategy via an improved segmentation scheme and a consistency constraint. However, if the candidate images and the input image have different depth values in the regions with similar appearance, the problem of depth ambiguity will arise.

For parametric learning methods, this study tried to establish the mapping model between color images and depth values based on supervised learning. Lately, deep learning algorithm has been resoundingly applied in single image depth prediction. A depth recovery scheme was first introduced by Eigen et al. [20] via utilizing CNNs. They developed a two-scale architecture (a coarse-scale network and a fine-scale network) to obtain accurate depth information. Based on this study, a multi-task learning framework including depth estimation, semantic labeling, and surface normal was presented by Eigen et al. [21]. Moreover, a deep convolutional neural field framework was introduced by Liu et al. [22], they combined the strength of deep CNN and continuous CRF in a unified CNN framework. The residual network (Resnet) has effectively worked out the gradient vanishing issue when the network layer becomes deeper and deeper, and this network has also been used for single image depth prediction. For instance, Laina et al. [23] adopt a fully convolutional residual network (FCRN) as the encoder and four up-projection blocks as the decoder to perform up-sampling to generate a final depth map with higher resolution. An efficient convolutional neural field framework was introduced by Hars´anyi et al. [24], who combined the strength of the residual network and U-nets in a deep framework. As visual attention plays an essential role in vision tasks, Chen et al. [26] designed a supervised self-attention model and utilized it to adaptively learn the task-specific similarities between different pixels to model the continuous context information. Tu et al. [27] designed an efficient monocular depth estimation model (MDE) for precise depth sensing on edge devices. They employed a reinforcement learning algorithm and automatically prune redundant channels of MDE by finding a relatively optimal pruning policy. Song et al. [28] et al. proposed a simple but effective scheme by incorporating the Laplacian pyramid into the decoder architecture. Specifically, encoded features were fed into different streams for decoding depth residuals. Ye et al. [29] proposed DPNet for high-quality monocular depth estimation. They designed an efficient non-local spatial attention module and a spatial branch (SB) to preserve spatial information.

In this study, to enhance the quality of depth maps, an efficient single image depth prediction framework based on a modified fully convolutional residual network and gradient network is developed. An improved FCRN network-based depth estimation model is designed for reconstructing the overall depth structure. Then, we develop a gradient network-based depth gradient generation scheme to enhance the global depth map. As we combine gradient information outputs with the modified FCRN for enhancement, the final estimated depth contains both global information and local details.

3 Proposed algorithm

To fill the research gap noted above, a high-quality depth generation algorithm based on a modified fully convolutional residual network and gradient network is presented. The framework makes full use of the fully convolutional residual network, U-net architecture, and gradient information of the scene. An overview of our DPDE scheme is shown in Fig. 1. Input to the algorithm is an RGB image, its output is a corresponding depth map estimated by the algorithm. In particular, first, an improved framework that integrates FCRN and U-shaped architecture is introduced for predicting the depths. For single image depth prediction, the structure of FCRN has been proved to have powerful estimation ability, which was further boosted by combining it with a U-shaped architecture. Since gradient information can provide subtle details of the scene, depth gradient information is incorporated into the depth estimation process. Then, a depth gradients extraction scheme is designed for generating the depth gradients along with horizontal and vertical directions. Considering the sparseness of the depth gradients and gradient information is not very sensitive to the scene features of training data, a gradient network-based method is leveraged to perform the gradient generation process. Finally, a depth and depth gradient fusion scheme is designed to enhance the global depth map locally to produce a reasonable depth map with finer details via the optimization method.

Fig. 1
figure 1

Overview of our presented network architecture

Full size image

3.1 Network architecture

The proposed DPDE algorithm contains two different prediction frameworks. i.e., the deep learning-based depth prediction framework and transfer learning-based depth gradients prediction framework. This section describes the structure of a deep learning-based depth prediction network. Specifically, an improved depth prediction model which combines a fully convolutional residual network (FCRN) [23] and U-shaped architecture [25] is proposed.

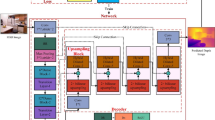
As the backbone of the entire depth prediction framework, a fully convolutional residual network (FCRN) was first introduced by Laina et.al [23]. The FCRN model in [23] comprises two components: encoding and decoding. Specifically, ResNet50 is utilized as the basic architecture of the encoding part, and several repeated up-projection modules constitute the decoding part. The structure of ResNet-50 [30] can make the FCRN network deeper and can avoid the problem of vanishing gradients. Therefore, FCRN has a large receptive field. In the training process, the entire convolutional network will generate billions of parameters and occupy dozens of GB of memory. To ease this situation, FCRN leverages the up-projection modules, which contain fewer parameters. The structure of FCRN has been proved to have a powerful estimation ability for recovering the scene depth, nonetheless, the local details of the depth maps are imperfect as the intermediate features are not integrated into the framework. Thus, FCRN was further modified by combining it with a U-shaped architecture.

Enlightened by the U-shape structure, we enhance the inter-connectivity of the model by bringing in lateral connections into the network flow rather than deepening the model by adding the network layers. These side-to-side links are established by connecting features of the same dimension between the Res-Block parts of the encoding and Up-Block parts of the decoding. Then, an additional 1 × 1 convolution is inserted after each depth concatenation to maintain the number of the up-projection modules’ input channels constant. Figure 2 demonstrates the detailed architecture of the modified network. Thanks to the lateral connections mentioned above, the network is capable to explore extra details in the previous features.

Fig. 2
figure 2

Structure diagram of the deep learning-based depth prediction method

Full size image

Horizontal and vertical gradients of the depth map contain information about meaningful depth differences in the local structure, which can be used to improve predicted depth maps for better details. Compared with the multi-scale deep network, the structure of the gradient network is relatively simple, which composes of 10 convolution layers with the 3 × 3 convolution kernel. Owing to the depth gradient containing s positive and negative values, we use ReLU for the first nine convolution layer and do not leverage it after the convolution of the last layer. Given a single input image, the horizontal depth gradient and vertical depth gradient of the image can be extracted through the gradient network. The following experiments will prove that our gradient network can obtain reasonable local depth gradients and can enhance the depth quality.

3.2 Loss function

The loss function used in the training process takes into account the difference between the ground truth depth map \(d^{gt}\) and the predicted depth \(d\). The definition of the loss function will affect the overall depth estimation performance.

For training our modified FCRN network, the loss \(L\) between \(d\) and \(d^{gt}\) is defined as the weighted sum of two-loss functions:

$$L\left( {d,d^{gt} } \right) = \lambda_{B} L_{B} \left( {d,d^{gt} } \right) + \lambda_{F} L_{FSIM} \left( {d,d^{gt} } \right)$$
(1)

The first loss term \(L_{B}\) is the reverse Huber loss [31], which was applied as the loss function during training by combining the regularly utilized \(\ell_{1}\) loss and \(\ell_{2}\) loss, which was first proposed by Laina et al. [23]. Through leveraging \(\ell_{2}\) loss, BerHu loss can give higher weight for pixels higher residuals. In parallel, owing to the utilize of \(\ell_{1}\) loss in the training process, the BerHu loss enables slighter residuals to have a greater impact on the gradients. For estimated depth maps \(d\) and the ground truth depth maps \(d^{gt}\), the BerHu loss \(L_{B} \left( {d,d^{gt} } \right)\) is defined as follows:

$$L_{B} \left( {d,d^{gt} } \right) = \left\{ {\begin{array}{*{20}c} {\left| {d - d^{gt} } \right|} & { \, \left| {d - d^{gt} } \right| \le {\text{c }}} \\ {\frac{{\left( {d - d^{gt} } \right)^{2} + c^{2} }}{2c}} & {\left| {d - d^{gt} } \right| > {\text{c}}} \\ \end{array} } \right.$$
(2)

where \(c = \frac{1}{5} \cdot \max_{i} \left| {d_{i} - d_{i}^{gt} } \right|\) \(i\) indicates the index of each pixel in each depth image \(d\). From Eq. (2) we can see that the BerHu loss is considered as the \(\ell_{1}\) norm when \(\left| {d - d^{gt} } \right| \in \left[ { - c,c} \right]\) and is equal to \(\ell_{2}\) when \(\left| {d - d^{gt} } \right| > c\). The form of BerHu loss is advantageous due to the continuity and differentiability at the switch point c.

The second term \(L_{FSIM}\) utilizes feature similarity, which is a commonly leveraged metric for the task of image reconstruction. Since the maximum and the minimum values of FSIM [32] are 1 and 0, respectively, the FSIM loss is defined as follows:

$$L_{FSIM} \left( {d,d^{gt} } \right) = \frac{{1 - FSIM(d,d^{gt} )}}{2}$$
(3)

For learning the gradient network to generate the horizontal and vertical depth gradients, we apply a new modified \(\ell_{1}\) loss term from the point of the logarithm. The pixel-level difference between the estimated depth gradients \({\mathbf{G}}\) and the ground truth depth gradients \(\nabla d^{gt}\) is defined as follows:

$$L_{g} = \ln \left( {\left\| {{\mathbf{G}}_{p}^{{}} - \nabla d_{p}^{gt} } \right\|_{1} + 1.0} \right)$$
(4)

where \({\mathbf{G}}_{p}\) represent the estimated depth gradients at a pixel \(p\).

By utilizing the deep learning-based depth estimation method, we can generate the global scene depth map. Nevertheless, the reconstructed depth maps lack finer depth details after many times of convolution and max-pooling. Based on our work, depth gradient can reflect the detailed information of the scene, thus a gradient network-based depth gradient estimation framework is proposed for extracting meaningful horizontal and vertical gradient information in the next section.

3.3 Depth and depth gradients fusion

As optimization strategies have been proved to be effective in improving the details of the output map [11]. A combination scheme based on the optimization method for fusing the depth and gradient information is proposed. The optimal depth can be estimated based on the following minimization:

$$\hat{d} = \arg \min \sum\limits_{p = 1}^{n} \phi \left( {d^{p} - d_{est}^{p} } \right){\kern 1pt} + \omega \sum\limits_{p = 1}^{n} {\left[ {\phi \left( {\nabla_{x} d^{p} - G_{x}^{p} } \right) + \phi \left( {\nabla_{y} d^{p} - G_{y}^{p} } \right)} \right]}$$
(5)

where \(d_{est}^{{}}\) is the predicted depth map based on multi-scale deep network, \(G_{x}^{{}}\) and \(G_{y}^{{}}\) are the recovered gradients in \(x\) and \(y\) directions. \(\nabla_{x}\) and \(\nabla_{y}\) are \(x\) \(y\) gradient operators on final depth \(d\). For designing the distance measure, \(\phi \left( x \right)\) is used as a replacement of the \(\ell_{1}\) norm:

$$\phi \left( x \right) = \sqrt {x^{2} + \varepsilon } ,\varepsilon = 10^{ - 4}$$
(6)

The final depth can be generated by leveraging iteratively re-weighted least squares (IRLS) for minimizing our loss function. IRLS is a better choice to solve unconstrained, nonlinear minimization issues. IRLS works by approximating the objective and solving the problem via minimizing the square residual; It is repeated until convergence.

4 Experimental results

4.1 Benchmark dataset

We conducted depth prediction experiments on indoor and outdoor datasets. Specifically, the proposed DPDE algorithm and other state-of-the-art algorithms are assessed on three RGBD datasets.

As an outdoor dataset, the Make3D dataset [18] is comprised of 534 color images and 534 ground truth depths. We utilize 400 images for training and 134 images for the test. For ensuring the consistency of comparison results, a bilinear interpolation algorithm is used to adjust all the images to the \(460 \times 345\) pixels.

As an indoor dataset, the NYUv2 dataset [33] is comprised of 1449 color images and 1449 ground truth depths. We utilize 795 images for training and 654 images for the test. For reducing the computational complexity, all images are rescaled to \(240 \times 320\) pixels via bilinear interpolation.

As an indoor testing dataset, the Middlebury stereo dataSet (MID) [34] is comprised of 35 pairs of color images and ground truth depths. Note that the disparity map is provided in the MID dataset. All original color images and disparity maps are rescaled to \(380 \times 430\) pixels. We used a simple division to convert the Middlebury disparity maps into the ground truth depth map and then compared it with the predicted Middlebury depths.

4.2 Implementation details

We perform all experiments on a PC platform with Intel Core i7-10,710 CPU 1.61 GHz and 16 GB RAM and Nvidia RTX2080 8 GPU. For the deep learning-based depth generation branch, we train the model on basis of the TensorFlow framework and initialize the network utilizing the ResNet-50 parameters pre-trained on ImageNet. Then the model weights are finetuned with its Berhu loss function for 30 epochs. In our study, a stochastic gradient descent optimizer is used, and the value of momentum is set to 0.9. The learning rate is initialized to 10–2 for all layers and halved after 10 epochs. In the last 10 epochs, it is reduced to 10–3. For transfer learning-based depth gradients generation branch. The parameters \(\lambda_{B}\) and \(\lambda_{F}\) were set to 1 and 1, respectively. For the depth gradients extraction branch, random initialization with Gaussian distributions was used for the gradient network. For the depth and gradients fusion branch, the parameter \(\omega\) is set to 10.

4.3 Performance evaluation

We performed the qualitative and quantitative evaluations in this section for evaluating the performance of the designed scheme.

4.3.1 Qualitative evaluation

For the outdoor scene, the qualitative evaluation between our DPDE method and other depth reconstruction methods is supplied: the Depth Transfer (DT) method [11], the Structured Forest (SF) method [19], the Deep Convolutional Neural Field (DCNF) algorithm [22] and the FCRN algorithm [23]. The qualitative evaluation results for test images in the Make3D dataset are provided in Fig. 3. It can be seen from the figure that all the methods used for comparison can estimate reasonable depth maps, but the depths predicted by the DT [11] method seem too smooth, as shown in the third column of Fig. 3. The depth values in the sky area of the depth map predicted by the SF [19] method are not accurate as in the fourth column in Fig. 4. On the whole, the performance of the DCNF [22] and FCRN [23] methods outperform that of the DT [11] and SF [19] methods, but the local details of the depth maps estimated by DCNF [22] and FCRN [23] methods are not very clear in some areas in the fifth column and the sixth column in Fig. 3. Due to the introduction of the gradient extraction process, depth, and gradient fusion scheme, our DPDE method can show the scene details better. The depth outputs predicted by our DPDE approach seem more convincing than other results from the point of the whole structure and local details, which can be confirmed in the last column in Fig. 3.

Fig. 3
figure 3

Experimental results on Make3D dataset a the input image b the ground truth c DT [11] d SF [19] e DCNF [22] f FCRN [23] and g the proposed method

Full size image
Fig. 4
figure 4

Experimental results on NYUv2 dataset. First row: the input image, second row: the ground truth, third row: DT [11], fourth row: DA [12], fifth row: DCNF [22], sixth row: FCRN [23] and last row: the proposed method

Full size image

For the indoor scene, our results are compared with other classic approaches [11, 12, 22, 23]. Figure 4 shows the depth evaluation results on the NYU dataset. From the figures, we can see that the structures of the predicted depths are most similar to the structures of the ground truth depths. On the whole, the performance of deep learning-based depth estimation methods [22, 23] is better than that of non-parametric learning-based methods [11, 12]. Deep learning-based methods can obtain reasonable depth maps, but some areas in the depth map estimated by DCNF [22] and FCRN [23] methods seem indistinct. Due to the introduction of a multi-scale feature extraction module, feature similarity-based loss term, and gradient network, the proposed method can obtain plausible depth outputs with better details, which can be verified in the last row in Fig. 4.

Figure 5 shows the test results on the MID dataset, which uses NYU as the training set. As demonstrated, the depth ordering of the depth maps predicted by our DPDE algorithm seems more reasonable. Compared with the proposed DPDE method, the depth outputs predicted by the methods [11, 12, 22, 23] cannot keep the depth boundaries sharp. On the whole, the results in NYUv2 are better than the MID as the images in the MID test set have a low depth distribution correlation with the images in the NYUv2 dataset.

Fig. 5
figure 5

Experimental results on MID dataset: First row: the input image, second row: the ground truth, third row: DT [11], fourth row: DA [12], fifth row: DCNF [22], sixth row: FCRN [23] and last row: the proposed method

Full size image

Furthermore, we provide the 3D reconstruction results in Fig. 6 and normalize the depth values to [0,255] for visualization. Aside from sharp depth discontinuities, the 3D reconstruction results from our method present realistic scenes compared to DCNF [22] and FCRN [23]. The effectiveness of the proposed DPDE algorithm can be confirmed by the reconstruction results. The reconstruction results from different views are shown in Fig. 7. The effectiveness of the presented DPDE algorithm can be proved by these visual results.

Fig. 6
figure 6

The 3D reconstruction results on the NYU v2 dataset: a the ground truth, b DCNF [22], c FCRN [23] and d the proposed method

Full size image
Fig. 7
figure 7

The 3D reconstruction results from different views: a the ground truth, b the proposed method (original view) and c the proposed method (alternative view)

Full size image

4.3.2 Quantitative evaluation

The similarity between the estimated depth maps \(d\) and the ground truth depths \(d_{{}}^{gt}\) can be measured by the following evaluation indicators:

Root mean squared error (RMS):\(\,\sqrt {\frac{1}{T}\sum\limits_{{i = 1}}^{T} {\left( {d_{i} - d_{i}^{{gt}} } \right)^{2} } }\).

Root mean squared error (RMS (log)):\(\,\sqrt {\frac{1}{T}\sum\limits_{i = 1}^{T} {\left( {Logd_{i} - Logd_{i}^{gt} } \right)^{2} } }\).

Mean relative error (REL): \(\,\frac{1}{T}\sum\limits_{i = 1}^{T} {\frac{{\left\| {d_{i} - d_{i}^{gt} } \right\|_{1} }}{{d_{i}^{gt} }}}\).

Mean log 10 error (log 10): \(\,\frac{1}{T}\sum\limits_{i = 1}^{T} {\left\| {{\text{log}}_{10} d_{i} - \log_{10} d_{i}^{gt} } \right\|_{1} }\).

Threshold: \(th\), i.e., the percentage of such that \(\delta = \max \left( {\frac{{d^{gt} }}{d},\frac{d}{{d^{gt} }}} \right) < th\).

The results of the presented DPDE method together with those of existing methods are shown in Table1. Our approach outperformed the algorithms presented in [4, 11, 14, 15] on all basic measures. It is observed that our proposed method obtains the best performance on Rel and RMS, while the method in [35] achieved the best RMS and log10 values. In addition, our method provided the second-best performance for log10. Compared with the case where gradient information is not used, the proposed DPDE method with gradient stream improves log10 and Rel values by 0.005 and 0.002.

Table 1 Comparison results on Make3D dataset
Full size table

The comparison results on the NYU dataset are shown in Table 2. It is evident that our DPDE method is slightly better for some cases compared with the FCRN [23] method. The performance of RMS, log10, Rel, δ < 1.25, δ < 1.252 and δ < 1.253 are improved by about 1.9%, 5.5%, 3%, 3%, 1.2% and 0.3% than FCRN [23], respectively. The RMS values of the presented algorithm with gradient stream increase by 0.638, 0.558,0.345,0.038, 0.007, 0.183, 0.478, 0.024, 0.259, 0.262, 0.011, 0.007,0.017 and 0.301 compared to the methods in [8, 11, 14,15,16, 20, 22, 23, 27, 35,36,37,38,39] and our DPDE method without gradient stream respectively. The proposed DPDE method attains best RMS and log10 values while the MS-CRF [35] method gets the lower scores for Rel and and log10 metrics. Our integration of local gradients enhances the performance on all metrics.

Table 2 Comparison results on NYUv2 dataset
Full size table

Table 3 shows the quantitative evaluation results on the MID dataset. To assist the evaluation, we chose three other indicators: structural similarity (SSIM) [41] and gradient similarity (GSM) [42], where a higher value indicates better performance for SSIM and GSM. As can be seen from the table, the method in [43] generates the best performance on RMS and Log10, while our DPDE method gets the lower Rel, SSIM, and GSM values. Thanks to the introduction of a U-shaped structure, the depth gradient extraction scheme, and the fusion strategy, our DPDE algorithm is superior to other methods for all metrics and reaches 0.684, 0.068, 0.206, 0.942, and 0.988 for RMS, log10, Rel, SSIM, GSM, and MGE metrics, respectively.

Table 3 Comparison results on MID dataset
Full size table

4.4 Ablation study

In this section, the larger and more challenging NYU v2 dataset is used to conduct our ablation study. The whole depth prediction processes are shown in the Fig. 8. Figure. 8a and b represent the input image and the ground truth epths respectively. Fig. 8c and d represent the FCRN and modified FCRN results respectively. Fig. 8e is the local depth gradient and Fig. 8f is the DPDE result. As shown in Fig. 8f, when integrating with each module in turn, the scene structures are clearer and more protected better. The final depths have a high similarity to the ground truth depths and have finer details. The reason is that the global depth map reflects the overall structure while the local depth gradient can represent the subtle details of a scene. A reasonable depth map with better details can be estimated via integrating the global and local information based on the optimization approach. Therefore, the means of extracting the depth gradient information and combining it with global depth is effective compared to only recovering the global depth.

Fig. 8
figure 8

Depth prediction results: a the input image b the ground truth c FCRN result d modified FCRN result e depth gradients and f) final result

Full size image

We divide the proposed network framework into three parts and verify the effectiveness of the proposed DPDE method by gradually adding it. The quantitative comparison results of the ablation experiment are shown in Table 4. It can be seen from the table that the FCRN alone can get a more reasonable depth map, but the RMS index is higher. After modifying the FCRN by adding the U-shaped structure, the overall performance of the network has been improved. When the depth gradient module is added, the depth quality is improved significantly. For example, RMS is increased from 0.569 to 0.562, and Rel is increased by 0.002. Therefore, a complete network framework can get better estimation results.

Table 4 Quantitative results of different variants of our method
Full size table

Table 5 shows the comparison of the number of parameters contained in different models. The parameter of the FCRN model is, and the parameter of the deep gradient network is, which is one of 76 of the FCRN model parameters. From the perspective of improving the performance, the addition of the deep gradient network is reasonable, which further verifies the effectiveness of the proposed DPDE method.

Table 5 Comparison of the number of parameters
Full size table

5 Conclusions

To reconstruct reasonable depth information from a single-color image, a novel detail preserving depth estimation (DPDE) approach that utilizes a fully convolutional residual network and gradient information was proposed. Practically, the global structure of a scene was recovered via learning the improved FCRN network. For preserving scene details, a gradient network-based depth gradient generation scheme is proposed to obtain the horizontal and vertical depth gradients. Then, an optimization scheme is proposed to integrate the local depth gradients and the global depth to generate a final depth map. Experimental results on indoor and outdoor datasets indicate that the presented depth prediction method can recover convincing depth information with better details and outperforms several classic approaches. In the future, we plan to utilize the semantic information and surface normal information of the scene to further improve the quality of the depth map.