1 Introduction

Pulp and paper-based industries manufacture products for a wide range of applications that includes printing papers, packaging, and personal hygiene [1]. In these industries, large volumes of water are utilised during the water-forming stage to prepare the pulp suspension. Consequently, a lot of energy is imparted to remove the excess moisture content from the final product [2, 3]. For that reason, the foam-forming technique, where air bubbles partly replace water, is considered a viable alternative. In addition, foam-forming enables manufacturing of new bulky structures and application of long man-made fibers of length greater than 3 mm [4,5,6,7,8].

To generate foam, industries adopt several unit operations including gas dispersion in mixing tanks, in-line air injection and membrane foaming. In case of mixing tanks, foam can be generated either in a batch mode or in dynamic mode. So far batch mixing with surface aeration has been carried out predominantly in laboratory [9, 10] and pilot-scale [6] foam-forming. Here water, surfactant and fibers are added in the mixing tank and rigorous mixing is carried out to generate a homogeneous fiber foam mixture with the desired foam quality in terms of air content, bubble size, and stability (half-life time). For actual industrial process, an ideal solution is a dynamic mixer combined with air injection. Here, the pulp suspension and surfactant is pumped into the mixing tank together with compressed air. As the term ‘dynamic’ indicates, there is a continuous inflow of pulp suspension—surfactant mixture and outflow of fiber-foam suspension. This approach can reduce the residence time inside the mixing tank significantly to a few tens of seconds instead of a few minutes typical of batch mixing [10]. This reduction in mixing time leads to cost savings in terms of power consumption. A detailed understanding of the foam generation in dynamic mixing is thus obligatory for developing energy-efficient foam-forming processes. The present work is focussed on understanding the effect of impeller geometry on foam generation by means of gas dispersion in a dynamic mixing tank.

Gas dispersion in mixing tanks is influenced by several design and operating parameters such as impeller design, tank geometry, impeller rotational speed, number of baffles, gas sparger design, and liquid and gas flow rates. In addition, these parameters govern the foam properties. Therefore, it is important to study the aforementioned items to improve the understanding of the foam-forming process. Over the past few decades, researchers have extensively investigated the mixing tanks with an objective to enhance the gas dispersion and reduce the power consumption. Most of the experimental work carried out in mixing tanks for gas dispersion has been listed by Prakash et al. [11] and the remaining studies are shown in Table 1.

Table 1 Recent experimental studies on gas dispersion in mixing tanks
Full size table

The majority of the gas dispersion studies carried out in the past are focussed on the two-phase gas–liquid batch mixing tanks, and most of the experiments were conducted using a Rushton turbine (RT) or a pitched blade turbine (PBT-45°). Fiber-foam generation involves a three-phase mixing, and the addition of fibers can change the mixing dynamics significantly from two-phase gas–liquid mixing. Limited data is available on fiber-foam batch mixing in the open literature. Al-Qararah et al. [9, 12] showed that bubble size can be affected by several parameters, such as rotational speed, surfactant dosage and type of surfactant. Moreover, with added wood fibers, they obtained a smaller bubble size than for aqueous foams. Al-Qararah et al. [13] studied the effect of different fiber types (natural and man-made) on the air content and bubble size distribution of the generated fiber foams. They observed that the mean bubble size become smaller for wood fibres than for viscose fibres even if the two types of fibres had similar geometric dimensions. Recently, we have investigated the effect of impeller type (RT and BT6), mixing speed and surfactant dosage on power consumption and foam properties of fiber-foam generation in a batch mixing tank [10]. The study revealed that the variation in impeller geometry for the tested radial impellers had a minimal influence on fiber-foam generation. Production of foams from viscous non-Newtonian fluids relevant to food industry using a dynamic rotor–stator assembly was investigated recently [21]. The impact of rotor speed, gas and liquid flow rate and surfactant dosage on bubble size distribution and foam stability was studied. Observations showed that the power consumption decreased when the gas to liquid flow rate was higher and the rotor speed dictated foam stability. Up to our knowledge, data on the dynamic fiber-foam generation is not available in the open literature.

The aim of the present study was to understand the influence of impeller type on dynamic aqueous foam and fiber foam generation in a mixing tank. To achieve the objective, dynamic foam-generation experiments were carried out in a 60 L mixing tank equipped with single or dual impellers. Three impeller geometries including two radial, one axial down-pumping impeller and four dual-impellers combinations were investigated. Compressed air, tap water and sodium dodecyl sulphate (SDS) solution were used as a gas phase, liquid phase and surfactant, respectively, to generate aqueous foams. Along with the abovementioned items, 1% mass consistency, softwood Kraft fiber was used to generate fiber foams. Foam density, bubble size and half-life time were measured to characterize the foam quality, whereas power consumption was measured to compare the impeller performance.

2 Experimental

2.1 Experimental set-up

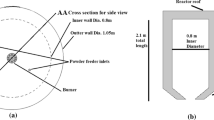
A schematic diagram of the experimental facility used in the present study is shown in Fig. 1. The flow facility included two mixing tanks and one storage tank. A 350 L conical-bottomed mixing tank (pulper) with three baffles placed at 120° from one another was used to disperse fiber suspension in tap water. The pulper was equipped with a radial impeller with profiled blades, bolted to the bottom of the tank and connected to a variable speed drive. In the experiments, both aqueous foams and fiber foams were investigated. For aqueous-foam studies, the pulper was filled with 350 L water whereas, in case of fiber-foam studies, a 350 L batch was prepared, i.e., final volume, 350 L = volume of fiber + volume of tap water. Dried bleached softwood Kraft pulp, a mixture of spruce and pine, from a Nordic pulp mill was used to prepare the fiber suspension. Schopper-Riegler number, oSR, denotes how fast or slow water drains through a fiber mat and is used to estimate how much the pulp fibers have been delaminated and fibrillated during refining (ISO 5267-1). For the used pulp oSR was 13; refining level was thus low and the fibers were mainly in their original form. The average (length weighted) fiber length was 2.2 mm. Desired mass of fiber sheets were torn into smaller pieces, soaked in water for 24 h, and then disintegrated in the pulper to prepare a homogeneous pulp suspension with a 1% consistency.

Fig. 1
figure 1

Schematic representation of the experimental facility. C1 = bottom impeller clearance; C2 = top impeller clearance; H = height of dynamic mixer; T = diameter of dynamic mixer; d = sparger diameter

Full size image

Once the fibers were well dispersed, the pulp suspension was pumped from the pulper into a foam generation tank along with sodium dodecyl sulphate (SDS, NaC12H25SO4) solution from a 40 L storage tank to achieve the foam generation. 600 ppm of SDS supplied by Sigma-Aldrich with a purity of 98.5%, 8.5 mM molar concentration and surface tension of 30 mN/m [22] was used in the present study. The dosage of SDS was determined from our previous experiments [10] carried out for batch mixing studies. The foam generation tank (Fig. 1) was an opaque 60 L flat-bottomed tank with three baffles mounted at 120° from one another. It had a continuous inflow of raw materials, namely pure water or pulp suspension, SDS and compressed air and a continuous outflow of product, say aqueous foam or fiber foam.

Conventionally, compressed air has been injected through a ring sparger in most industrial applications [23]. If the ring sparger diameter is large, most of the gas bubbles released from the sparger holes located on the ring circumference can bypass the impeller blades and reach the tank surface without being dispersed. Besides, the number of sparger holes is limited based on the diameter of the ring. Therefore, effectiveness of the ring sparger is not always high. In the present study, we employed a spider sparger [24], as shown in Fig. 1. The advantage of the spider design over a ring design is that it has a higher number of sparger openings, which lead to an effective gas dispersion.

Several single and dual impeller combinations were used in the experiments. For a single impeller type, the impeller was placed at a clearance of 0.13 m from the tank bottom. In case of dual impeller system, bottom and top impellers were placed at a clearance of 0.13 m and 0.45 m, respectively, from the tank bottom. Foam samples were collected from the foam generation tank through a sampling valve located at 0.29 m from the tank bottom (2nd valve from the bottom in Fig. 1) to measure bubble size, foam density and half-life time. Bubble size distribution was measured using Pixact online foam analyzer [25] and recorded to a Wedge data recording system. Pixact online foam analyzer uses optical microscopy and an advanced image analysis algorithm to provide real-time measurement data. Imaging of the foam is carried out continuously in a flow-through cuvette. The analyzer was installed in a short flow loop by the foam generation device. Surface-area weighted Sauter mean diameter \({D}_{32}={\sum }_{i=1}^{n}{n}_{i}{D}_{i}^{3}/{\sum }_{i=1}^{n}{n}_{i}{D}_{i}^{2}\) [26] was used as the average bubble size (here ni is the number of bubbles having the diameter of Di). Foam samples were collected in a 2 L container and weighed in gravimetric scale to estimate the foam density and half-life time. The half-life time of a foam is here defined as the time required by a foam to drain 50% of the weight of the initial conditioning liquid used in foam generation. Notice that in the literature half-life time has also been defined as the time when the foam has lost half of its initial volume. Half-life time typically increases with increasing air content and decreasing bubble size. Notice that during half-life time measurements, instead of observing a clear partition between pure water and pure foam layers, we observed three layers in a few cases: pure water layer, transition layer, and pure foam layer. In such cases, the borderline between the pure water layer and the pure foam layer was vague and accurate estimation of the half-life time was more difficult.

2.2 Details of the tested impellers

The three impeller geometries and seven impeller combinations that were used in this study are shown in Fig. 2. The top-entering impellers were mounted on a shaft connected to a 2.6 kW, 3-phase electric motor driven by ABB ACS850 frequency converter. Power Pm = 2πNT was obtained from the axial speed, N, and axial torque, T, measured by the converter. The measured values were recorded using ABB CP650 device. The net power applied to the fluid was calculated by subtracting the measured power consumption with air from the measured power consumption with fluid. We demonstrated the accuracy of the measurement setup in [10] with turbulent mixing of water.

Fig. 2
figure 2

Impeller combinations used in experiments. RT Rushton turbine, BT6 Bakker turbine, HSPBT high solidity pitched blade turbine (Blade dimensions (length and width) = \({l}_{b}\) and \({w}_{b}\) (10−2 m): RT—3 × 4; BT6—3 × 5; HSPBT—5 × 8)

Full size image

Figure 2a illustrates the conventional and most widely used Rushton turbine (RT) for gas dispersion in mixing tanks. RT is a radial impeller in which six flat blades are welded to a disc at 90 degree. The second radial impeller used was a Bakker turbine—BT6 (Fig. 2b) [27]. The difference between RT and BT6 is that the flat blades from RT are replaced with concave-shaped blades in BT6. In addition to the abovementioned radial impellers, an axial down-pumping high solidity pitched blade turbine—HSPBT [11] was used with blades mounted to impeller hub at a 45° pitch (Fig. 2c). The term solidity refers to the ratio of impeller blade area to total impeller area. If the solidity ratio is above 0.4, then the impeller is called as high solidity impeller. In the pitched blade impellers, an increase in blade angle leads to an increase in power consumption but results in improved dispersion of gas bubbles. Therefore, it is vital to use an optimised blade angle and 45° blade angle was chosen based on the observations from a previous study [11].

The flow pattern, power consumption and gas dispersion were influenced by the impeller geometries. For instance, for RT, gas bubbles accumulate in the low-pressure region behind the blades leading to cavity formation which controls the overall turbine hydrodynamics and dispersion characteristics [28]. Cavity formation can lead to a significant fall in power input as high as 50% compared to the ungassed value representing an inconvenience for power prediction [27, 28]. On the other hand, a similar drop in power curve is not observed for BT6. In BT6, the flat blades are replaced by concave-shaped blades which eliminates the low-pressure region behind the blades leading to reduced resistance from the fluid.

In many mixing processes, low power number is beneficial. It e.g. enables getting high shear rates at the impeller vicinity without high mixing power. However, in foam-forming, the performance of impellers cannot be solely assessed on the basis of power consumption. As reference [10] shows, similar foams can be obtained with similar mixing power while power numbers are very different. Moreover, foam-forming technology is used to manufacture various products that may require different properties from the foam.

Dual impeller combinations were also used in the present study. In dual impeller terminologies, the first and second term represents the bottom and top impeller, respectively. For example, in HSPBT-RT, HSPBT is the bottom impeller, and RT is the top impeller. In the first two dual impeller combinations, the axial impeller was placed at the bottom whereas, in the last two, the radial impeller was placed at the bottom. The distance between the two impellers was maintained at 0.3 m.

In addition to the impeller geometry, impeller swept area and impeller swept volume influence the gas dispersion. The impeller blade area and swept volume are calculated based on the area of rectangle and volume of cylinder formulae, respectively, as follows:

$$\text{blade area}= {n}_{b} *({l}_{b} * {w}_{b})$$
(1)
$$\text{swept volume}= \pi {R}^{2}{w}_{b}$$
(2)

Here, \({n}_{b}\), \({l}_{b}\), and \({w}_{b}\) denote number, length and width of blades, respectively. Using the blade dimensions (Fig. 2) in Eqs. (1) and (2), it is evident that HSPBT has 40% more swept volume than the radial impellers RT and BT6. Also, dual impellers have at least 40% more impeller swept volume in comparison to the rest.

2.3 Operating parameters

Generally, operating parameters such as impeller speed and gas flow rate are selected based on the gas flow regime and liquid flow regime for stirred tanks [31]. In an aerated mixing tank, at a high gas flow rate or low impeller speed, most of the gas bubbles released from sparger, reach the tank surface without getting in contact with the impeller blades. This regime is termed as flooding. With an increase in speed, the impeller starts to disperse the gas bubbles but not to a great extent. This particular operating area is represented as loading. With further increase in speed or reduction in gas flow rate, impeller starts shredding the gas bubbles effectively leading to a well-dispersed regime. Operating a gas–liquid mixing tank under the well-dispersed regime is preferred in most of the industrial operations, especially for foam generation.

Since we have carried out experiments in an opaque tank, it was difficult to identify the operating regimes visually. Therefore, two dimensionless numbers, namely, Froude number

$$\text{Fr}= \frac{nD{N}^{2}}{g}$$
(3)

and Flow number

$$\text{Fl}= \frac{Q}{nN{D}^{3}}$$
(4)

were used to characterise impeller speed and gas flow rate, respectively [29,30,31]. Here, Q is the gas flow rate, N is impeller speed, D is impeller diameter, n is number of impellers (here n = 1 or 2) and g is gravitational acceleration. Notice that the Froude number is proportional to the ratio of inertial force to gravitational force, and the Flow number is proportional to the ratio of gas flow rate to the impeller driven flow rate.

Colour markers in Fig. 3 show the Fr and Fl calculated from our experimental data. Several researchers have proposed a correlation between Fr and Fl to distinguish loading and well-dispersed regime; three examples; see Eqs. (5), (6) and (7) (Dickery et al. 1983 [32], Zlokarnik et al. 1967 [33], Rosseburg et al. 2018 [19]):

Fig. 3
figure 3

Operating regime for the different impeller combinations

Full size image
$$Fl=1.88 ({\text{Fr}}^{0.5})({T/D}^{-0.33})$$
(5)
$$Fl=1.94 ({\text{Fr}}^{0.75})$$
(6)
$$Fl=0.47 \text{Fr}$$
(7)

In Fig. 3, the black coloured markers represent the operating curve (transition to the well-dispersed regime) calculated using Eqs. (5), (6) and (7). Data points that lie above the operating curve indicate a loading regime, whereas that fall below show well-dispersed regime. It is evident from the graph that all our experiments are carried out in a well-dispersed regime, which should lead to rapid fiber-foam generation.

To achieve uniform mixing, it is recommended to operate a mixing system under a turbulent flow regime. This condition can be analysed by looking at the dependence of the (dimensionless) power number [19]

$$\text{Np}= \frac{P}{{\rho {N}^{3}D}^{5}}$$
(8)

where P is the power and ρ is fluid density, on the mixing Reynolds number [34]

$$\text{Re}= \frac{{\rho ND}^{2}}{\mu }$$
(9)

where µ is fluid viscosity. In Eqs. (8) and (9) ρ and µ are the density and the viscosity of the foam, respectively. As foams and fiber foams are shear thinning fluids, their viscosity depends on the applied shear rate. On the other hand, shear rate varies in different parts of the mixing tank. The mixing Reynolds number can be estimated for foams by substituting the viscosity of the foam at the characteristic mixing shear rate \({\gamma }_{ch}=13N\) to Eq. (9) [10].

Mixing is turbulent, when with a given power number, the mixing Reynolds number is higher than the transitional Reynolds number [35]

$${\text{Re}}_{\text{TT}}=6370 \left({\text{Np}}^{-0.33}\right).$$
(10)

In the present study, it was found by utilizing the foam viscosity data from [10] that mixing conditions were always turbulent; the Reynolds number, i.e., clearly exceeded the transitional Reynolds number ReTT at every trial point.

In foam forming, foam density ρf varies typically between 300 and 700 kg/m3 [6, 36]. The air content of foam, φ = (ρw—ρf)/ρw where ρw = 1000 kg/m3, varies thus between 35 to 70%. Based on this and the mixing regime analysis, the water/pulp suspension flow rate and gas flow rate was fixed as 1 L/s and 0.6 L/s respectively, giving nominally a 40% air content and a residence time of less than one minute. Besides the power input was varied between 0.75 to 2.25 kW to achieve always well-dispersed and turbulent flow conditions.

3 Results

3.1 Dynamic aqueous foam generation

Figure 4a shows the impeller rotational speed with a given power obtained for various impeller combinations for aqueous-foam generation. It is observed in Fig. 4a that HSPBT had the highest impeller speed at almost any given power input and RT and RT-HSPBT had usually the lowest RPMs.

Fig. 4
figure 4

a Impeller speed with applied power for different impeller combinations for aqueous foams. b Power number with applied mixing speed for different impeller combinations for aqueous foams

Full size image

Figure 4b shows the power numbers as a function of impeller speed. We observe in Fig. 4b that generally higher impeller speed corresponds to lower power number. As there are differences in foam density, there are, however, some exceptions to this rule. It is evident from Fig. 4b that for a single RT impeller the variation in power number with respect to power input is significant probably due to the cavity formation as explained in Sect. 2.2. The variation in power numbers for RT combinations, are also slightly higher as compared to other impellers. HSPBT and BT6 had the lowest power numbers with the average power numbers of 0.8 and 0.9, respectively. For BT6 we obtained similar power numbers in turbulent batch mixing of foams [10]. The low power number of HSPBT might be owing to its tangential flow pattern and absence of the disc which leads to reduced resistance from the fluid.

Figure 5a shows the variation in foam density as a function of power for different impeller combinations. As indicated by the black dotted line, single impellers created a dense foam (such foams are called bubbly liquids) in the range of 550 to 650 kg/m3, whereas dual impellers resulted in lower-density foams with 370 to 550 kg/m3. Moreover, foam density was lower if an axial impeller was placed at the bottom. The air content thus varied significantly even though the flow rates of the water and the compressed air to the mixing tank were fixed. There are two reasons for this, namely differences in self-aeration and escape rate of air from the tank due to large gas bubbles. Notice that for a given impeller, variation in foam density with respect to power input was minimal i.e., the change in foam density was limited to ± 40 kg/m3. Therefore, the present study indicates that in a dynamic mixing system, foam density is dictated by impeller type rather than power input.

Fig. 5
figure 5

a Foam density and b bubble size for aqueous foams

Full size image

Bubble size is a critical parameter to characterise the foam as smaller bubbles benefit foam forming in terms of increased half-life time and mass transfer area. Figure 5b shows the average bubble size for the different impellers. Two general trends were observed for RT and dual impellers: bubble size reduced with increasing power input from 750 to 1500 W and no significant change in bubble size above 1500 W. It was found that bubble breakage was intensive for single BT6 and HSPBT impellers and BT6-HSPBT dual impeller, where fine bubbles with diameter in the order of 30 to 40 µm were generated even at the minimum power input of 750 W. The reason for the finest bubble generation of BT6-HSPBT could be the placement of high shear BT6 impeller at the bottom near sparger and a tangential down-pumping HSPBT on top, which pumps back the rising gas bubbles towards the high shear impeller. Indeed, placing a radial impeller on top (HSPBT-RT or HSPBT-BT6), lead to significantly higher bubble size. In [10] fiber foam was generated with a combination of batch mixing and inline generation. There the relative standard deviation (RSTD) of bubble size varied between 0.3 and 0.7. In this study RSTD varied usually in the range of 0.4 and 1.0, but for pure foams it was in some cases significantly higher (see Supplementary material). The variation might be due to the low residence time of bubbles in dynamic mixing compared to batch mixing. Optimised process parameters such as gas and liquid flow rates can improve the bubble residence time resulting in minimal variation in RSTD.

Influence of impeller geometry and power input on the half-life time of aqueous foam is presented in Fig. 6. At low power inputs of 750 and 1000 W, air content was low and half-life time could not be measured for single impellers. As we see in Fig. 6, half-life time was similar for all impellers and increased by almost threefold from ~ 50 to ~ 150 s when the input power was increased from 750 to 2250 W. Overall, BT6-HSPBT generated the most stable aqueous foams compared to the rest of impeller combinations.

Fig. 6
figure 6

Half-life time of an aqueous foam as a function of power for different impeller combinations

Full size image

3.2 Dynamic fiber foam generation

In dynamic fiber foam experiments with dual impeller combinations, placement of radial impeller on top resulted in heavy vortex sloshing. This led to an unstable mixing behaviour throughout measurements. So we excluded HSPBT-RT and HSPBT-BT6 impellers from the fiber foam generation studies. RT-HSPBT impeller behaved similarly to BT6-HSPBT, but had slightly lower foam density, slightly bigger bubble size and slightly lower half-life time. RT-HSPBT has been omitted below from the analysis.

Influence of pulp fibers and impeller combinations on impeller speed is plotted as impeller speed against input power in Fig. 7a (the suffix ff in legends denotes fiber foam). It was found that at a low power input of 1000 and 1500 W impeller speed was slightly decreased with fibers due to the higher viscosity of the fiber foams. On the other hand, at high power input, impeller speed overcome the resistance from fiber particles due to strong shear thinning of fiber foams and therefore, variation in impeller speed with respect to fiber addition was negligible.

Fig. 7
figure 7

Effect of addition of fibers on a impeller speed, b foam density and c bubble size with different impeller types

Full size image

Impact of fibers and impellers on density of fiber foams is shown in Fig. 7b; the addition of fibers increased the foam density by 100–150 kg/m3. Fibers are likely to decrease self-aeration and increase the escape of air at the free foam surface due to higher bubble size. Similar to aqueous-foam results, BT6-HSPBT generated lower-density fiber foam in comparison with single impellers. While the impact of mixing power on foam density was minor for aqueous foams, the impact was more pronounced in making the fiber foams.

The average bubble size is shown for fiber foams in Fig. 7c, where solid lines and dotted lines in the plot represent bubble size data for aqueous foam and fiber foam, respectively. Notice that variation in bubble size with power input qualitatively followed the change of air content for fiber foam. It was observed that bubble size of fiber foams reduced by twofold with an increase in power input from 1000 to 2250 W. For example, the bubble diameter reduced from 90 to 42 µm for BT6-HSPBT impeller when the power was increased from 1000 to 2250 W.

The half-life time of fiber foams are shown together with aqueous foams as a function of mixing power in Fig. 8. Addition of fibers reduced the half-life time of the fiber foams by almost threefold due to larger bubble size and higher air content. Generally, fibers are known to slow down the drainage of foams [36, 37]. Fibres also slow down coarsening, i.e. increase in average bubble diameter due to gas diffusion [38, 39] Notice that, unlike aqueous foam, half-life time could be measured for RT impeller at a low power input of 1000 W.

Fig. 8
figure 8

Effect of addition of fibers and impeller type on half-life time

Full size image

Figure 9 shows the half life time as a function of average bubble diameter for both pure foams and fiber foams. Air content is shown in the figure with colours. We see from Fig. 9 that there is, as expected, an inverse relation between the half-life time and bubble size. We also see that half-life time generally increases with increasing air content. As air content is always rather high, available drainage theories cannot be used here [40,41,42]. However, the following simple formula for the half life time, which has only one free parameter,

$$ {\text{t}}_{{{1}/{2}}} = a\varphi D^{{ - {1}}} $$
(11)
Fig. 9
figure 9

Half-life time as a function of average bubble diameter for pure foam (spheres) and fiber foam (diamonds). Air content is shown with colours

Full size image

works reasonably well (R2 = 0.63). Here D is bubble diameter, φ is air content and a = 9000 is the fitting parameter.

The reason for the big difference in the bubble size and air content of pure foams and fiber foams is unclear. The higher viscosity of fiber foams might have changed the mixing flow pattern leading to gas bubbles bypassing the high shear region of impeller blades and escaping to the atmosphere. One should also notice that the residence time is rather low—less than one minute. Slight distortions in the mixing conditions could make the mixing time too short for sufficient mixing.

Table 2 shows a summary of bubble size, foam density and half life time for the different impellers both for aqueous foams and fiber foams. It tabulates the average values over the power range of 1500–2250 W, where no significant variation in foam properties were observed.

Table 2 Summary of the performance of the impeller for dynamic foam generation (average over the power range of 1500–2250 W)
Full size table

4 Conclusions

Dynamic generation of aqueous foams and fiber foams was investigated by carrying out experiments in 60 L lab scale mixing tank using seven impeller systems comprising of three impeller geometries. Specific conclusions made from the present study are listed below;

  • At a fixed power input, RT placed at the bottom (RT & RT-HSPBT) resulted in lower impeller speed with a given power input and the variation in power number with respect to power input was significant compared to other impellers.

  • The change in aqueous foam density for any given impeller was limited to ± 40 kg/m3 indicating foam density is dictated by impeller type rather than power input in a dynamic mixing system.

  • Single impellers generated bubbly liquids with foam densities in the range of 550 to 650 kg/m3 and dual impellers generated low-density aqueous foams in the range of 350 to 550 kg/m3. Besides, stable foam was produced by dual impellers at low power input compared to single impellers due to increase in impeller swept volume and blade contact area.

  • For RT and dual impellers, bubble size reduced with an increase in power input from 750 to 1500 W. Placement of high shear impeller at bottom and down-pumping axial impeller on top generated fine bubbles and dual impeller combinations with radial impeller on top resulted in larger bubbles.

  • For dynamic fiber foam generation, addition of fibers increased the foam density by ~ 100–150 kg/m3 and reduced the half-life time by almost threefold. Addition of fibers lead to larger bubble generation compared to aqueous foam.

  • The performance of impellers cannot be solely assessed on the basis of power consumption. Similar foams can be obtained with similar mixing power while power numbers are very different.

To date, foaming has been usually carried out in surface-aerated mixing tanks. However, for actual industrial processes, dynamic foam generation would likely be beneficial. This approach can reduce the residence time inside the mixing tank significantly which leads to cost savings both in terms of power consumption and equipment dimensions. In this study the used setup worked already rather well for pure foams. However, for fiber foams the setup needs to be improved; the foam density and bubble size were not low enough for many foam forming applications. Compared to batch mixing, dynamic foam generation is a more complicated process due to several extra process parameters and higher sensitivity to instabilities. In this paper, we focussed on understanding the effect of impeller geometry and power input on dynamic foam generation. In the future one should continue this study e.g. by studying how the suspension flow rate and gas flow rate effect on the mixing efficiency and obtained foam properties.