Sampling strategy for fuzzy numbers in the context of surrogate models

Abstract

The paper presents an investigation of the accuracy of surrogate models for systems with uncertainties, where the uncertain parameters are represented by fuzzy numbers. Since the underlying fuzzy arithmetic using $\alpha$-level optimisation requires a large number of system evaluations, the use of numerically expensive systems becomes prohibitive with a higher number of fuzzy parameters. However, this problem can be overcome by employing less expensive surrogate models, where the accuracy of the surrogate depends strongly on the choice of the sampling points. In order to find a sufficiently accurate surrogate model with as few as possible sampling points, the influence of various sampling strategies on the accuracy of the fuzzy evaluation is investigated. As well suited for fuzzy systems, the newly developed Fuzzy Oriented Sampling Shift method is presented and compared with established sampling strategies. For the surrogate models radial basis functions and a Kriging model are employed. As test cases, the Branin and the Camelback function with fuzzy parameters are used, which demonstrate the varying accuracy for different sampling strategies. A more application oriented example of a finite element simulation of a deep drawing process is given in the end.

1 Introduction

Today, computer-aided simulations play an important role in the design and control of manufacturing processes [1]. But while simulations are reproducible, real processes are subject to fluctuations for example due to varying operation conditions, batch variations etc. Therefore it is necessary to capture these uncertainties in a realistic virtual process model.

Uncertainties can be differentiated between epistemic and aleatoric ones [2]. Aleatoric uncertainties are stochastic deviations, which can be described by well established methods like Monte-Carlo simulations and shall not be discussed further here. In contrast, epistemic uncertainties are uncertainties that exist due to missing information and at least theoretically, they can be reduced by additional knowledge or additional effort. Since epistemic uncertainties can be minimised, for instance by better measurement methods, a description by convex fuzzy sets (e.g. fuzzy numbers) seems appropriate. The $\mu$-value of the fuzzy membership function can then be interpreted as a cost indicator, such that a higher $\mu$-value correlates to the higher costs associated with the corresponding reduction of the uncertainty.

A typical task in engineering is the evaluation of the robustness of a process with regard to parameter deviations (e.g. batch variations). A robust process will accept a broader variation of input parameters with only minimal influence on the output, such reducing the costs for accurately controlling the input parameters. Such an investigation is usually done by process simulation, where for mechanical engineering problems often finite element models with millions of degrees of freedom are employed. Since these models are numerically very expensive, their use in a fuzzy-framework becomes prohibitive.

Typical examples from the engineering field are expensive finite-element process simulations with computation times in the range of hours, as exemplified in [3] for a cold forging process with about 400,000 elements. In such a simulation many uncertain parameters can be defined, so that a dimension of 2–20 parameters seems to be common. The limiting factor here is the computation time, which allows a experimental design with a single-digit or maximum two-digit number of sampling points, independent of the dimension.

Therefore model order reduction methods or surrogate models are necessary to obtain results at acceptable costs. Model order reduction reduces the number of degrees of freedom by projection of the system onto a lower dimensional subspace. Surrogate models on the other hand just interpolate the input-output behaviour based on a (hopefully small) number of sampling points as a response surface, which can be queried at very low costs. While a reduced order model retains the underlying physics of the full model and can probably even be used for extrapolation, it requires access to the full model and the construction of an appropriate reduction at least for a nonlinear model is difficult. Here, a surrogate model has the advantage of just needing the evaluation of the system at some sampling points, which allows for example the use of commercial black-box FE-packages or the incorporation of sampling points from other sources like experimental data. However, this comes at the price that extrapolation outside of the sampling range is extremely dangerous.

A lot of applicable methods to construct such surrogate models exists, see e.g. [4,5,6,7,8]. Today, machine learning is predominantly used [9] and these tools (e.g. neural networks) show their great strength when big data is involved and there is enough data to learn from or to train with. However, the focus of the present study lies on sampling plans based on (very) small data, where the number of interpolation points has to be reduced as much as possible, because the complex systems allow only a one to low two-digit number of evaluations, regardless of the dimension.

This necessesitates the use of more traditional response surfaces methods like radial basis functions or Kriging models, which are discussed for instance in [10,11,12].

Investigations of sampling points strategies or sampling points optimization, such as those performed in [13,14,15], can keep the number of sampling points to a minimum. In these methods, the goal is to maintain global accuracy in the parameter space and to ensure that the parameter space is mapped as effectively as possible. In [15] for instance additional sampling points are generated depending on the surrogate model results. Differentiating from this, in the method presented here, the properties of the results are to be taken into account in the form of fuzzy uncertainties. Thus, the sampling plan is optimized for a parameter space described by fuzzy uncertainties, which is new for sampling plans.

The organisation of the paper is as follows: Sect.  2 recapitulates some basics of uncertainty analysis using fuzzy numbers. Section 3 introduces the relevant methods of surrogate modelling, which are used in the following. Section 4 shortly discusses two commonly used sampling strategies, full factorial design and Latin hypercube sampling, and presents the Fuzzy Oriented Sampling Shift (FOSS) in 4.3 as an optimized variant of the Latin hypercube sampling for fuzzy arithmetic applications. Section 5 compares the accuracy of two different surrogate models using different sampling designs when applied to two test functions. Section 6 applies the FOSS strategy to the finite element simulation of a deep drawing process with uncertain parameters. Section 7 finally summarizes the results.

2 Fuzzy numbers

Fuzzy sets were introduced by Zadeh [16] as an extension of the classical set. Each value of the set is assigned a membership value $\mu$, that defines its grade of membership in the set. For the membership function $\mu$, $\mu =1$ applies if a value is $x \in X$ and $\mu =0$, if $x \notin X$. In the classical set, $\mu \in [0;1]$, but for a fuzzy set instead, $\mu \in [0,1]$ is generally valid [17]. The classical set X is then a special case of the fuzzy set ${\tilde{X}}$.

Fig. 1

Fuzzy number ${\tilde{p}}_i$ with $\alpha$-cuts according to [18], (a) general (b) triangular

A fuzzy number ${\tilde{p}}_i$ is a special form of a fuzzy set, where the core, defined as

$$\begin{aligned} \text {core}({\tilde{p}}_i) = \{x \in {\tilde{X}} | \mu =1\} \;, \end{aligned}$$

(1)

is not an interval but a single value. A fuzzy number is a convex fuzzy set, because each interval $X^{(j)}$ with the membership function $\mu _{j}$ is a closed interval,

$$\begin{aligned} X^{(j)}=[a^{j},b^{j}] \;, \end{aligned}$$

(2)

as shown in Fig. 1. Moreover for all left-hand limits $a^{(j)}$ and all right-hand limits $b^{(j)}$:

$$\begin{aligned} a^{(j-1)} \le a^{(j)} \le a^{(j+1)} \text { and } b^{(j-1)} \ge b^{(j)} \ge b^{(j+1)}. \end{aligned}$$

(3)

These intervals are called $\alpha$-cuts, which define a crisp interval $X^{(j)}$ with a fixed membership function $\mu _j$, a left-hand limit $a^{(j)}$, and a right-hand limit $b^{(j)}$. A special type of often used fuzzy number is the triangular fuzzy number or linear fuzzy number, which is defined by a linear membership function. In the following the notation of [17] for triangular fuzzy numbers

$$\begin{aligned} {\tilde{p}} = \text {tfn}(\text {core}({\tilde{p}}),a(\mu =0),b(\mu =0)) \end{aligned}$$

(4)

is used.

The $\alpha$-cuts are commonly used for numerical calculations, because the fuzzy-arithmetic is thus reduced to interval-arithmetic [17]. This standard fuzzy arithmetic with decomposed fuzzy numbers, which will be employed also here, requires a huge number of system evaluations. Assuming a decomposition into $m+1$ $\alpha$-cuts, an addition of two fuzzy numbers for instance results already in $2*m+1$ arithmetic operations, since the limits $a^{(j)}_1$ and $a^{(j)}_2$, respectively $b^{(j)}_1$ and $b^{(j)}_2$, must be considered separately for each $\alpha$-cut $j = 0,\ldots ,m-1$, where at $j=m$ only a single operation for the core values is necessary. For functions in general, the minimum as well as the maximum result at an $\alpha$-cut, which represent the limits of the resulting fuzzy number, does not have to correspond to the operations on the limits $a^{(j)}_i$, respectively $b^{(j)}_i$. Thus, there exist two optimisation problems, which have to be solved for each $\alpha$-cuts m, leading to a very high number of function evaluations [17, 19]. Other approaches to fuzzy arithmetic instead of $\alpha$-level decomposition are also possible, see for example [20], but do not significantly reduce the number of necessary function evaluations. So the use of an inexpensive surrogate model is mandatory for most applications involving engineering systems but the simplest.

3 Surrogate models

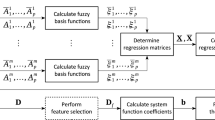
As mentioned above, uncertainty analysis using fuzzy numbers requires many system evaluations. If the evaluation of the underlying system $f({\mathbf {x}})$ is expensive, only a few such evaluations can be done in a reasonable time or at reasonable costs. For this reason the full system has to be replaced by a cheaper surrogate model ${\hat{f}}({\mathbf {x}})$, where the surrogate model is regarded as an approximation of the full system,

$$\begin{aligned} {\hat{f}}({\mathbf {x}})\approx f({\mathbf {x}}) \;. \end{aligned}$$

(5)

To construct such a surrogate model, the system $f({\mathbf {x}})$ is evaluated at n sampling points

$$\begin{aligned} {\mathbf {X}}=[{\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_n]^T \;, \end{aligned}$$

(6)

where each vector ${\mathbf {x}}_i=\{x_1,x_2,\ldots ,x_k\}^T,\;1\le i \le n$ consists of k entries, corresponding to k input parameters of the system.

For the surrogate model ${\hat{f}}({\mathbf {x}}_i)$ different approaches exist, see for example [21]. In the following examples a surrogate based on radial basis functions (RBF) [5] and a Kriging based surrogate called Design Analysis of Computer Experiments (DACE) [22] are employed. Both the RBF and the DACE are interpolating approaches, whereby the relationship

$$\begin{aligned} {\hat{f}}({\mathbf {x}}_i)=f({\mathbf {x}}_i) \end{aligned}$$

(7)

applies at the sampling points ${\mathbf {x}}_i$. Other approaches like regressions could also be used. However, it should be pointed out that neural networks are deliberately not applied here, since the training of a neural networks requires a larger amount of data and the focus is here on “small data” and not on “big data”.

3.1 Radial basis functions

The ansatz for the surrogate based on radial basis functions is given by

$$\begin{aligned} {\hat{f}}({\mathbf {x}})=\sum _{i=1}^{n} \rho _i \psi (\Vert {\mathbf {x}}-\mathbf {x_i} \Vert ) \;, \end{aligned}$$

(8)

where $\mathbf {x_i}$ is the ith sampling point from (6) [5]. The parameters $\rho _i$ represent weighting factors, which have a linear influence on the basis functions. The basis functions $\psi (r)$, which are evaluated at the Euclidean distances r between the sampling points ${\mathbf {x}}_i$ and the input vector ${\mathbf {x}}$, can map different approach functions [21]. Out of a large number of possibilities to chose the basis functions, only one function is selected, a simple cubic trial function

$$\begin{aligned} \psi (r)= r^3 \;, \end{aligned}$$

(9)

which has the advantage that no further parameters are introduced which would have to be optimised.

3.2 DACE functions

The other surrogate model used here is the DACE model. It is an interpolation model, which based on the Kriging model developed by Krige [7] and is applied via the Matlab toolbox from [22, 23]. As shown in [23], it combines a random process $z(\mathbf x )$ (also called stochastic process) and a regression model $\varvec{\phi }({\mathbf {x}})$ with the regression parameters $\varvec{\beta }$ and results in

$$\begin{aligned} {\hat{f}}({\mathbf {x}})= \varvec{\beta ^T \phi } ({\mathbf {x}})+ z({\mathbf {x}}) = \sum _{j=1}^{m} \beta _{j} \phi _{j}({\mathbf {x}}) + z({\mathbf {x}}) \;. \end{aligned}$$

(10)

The regression model describes a deterministic response surface and the random process describes the deviation of the function value to this surface. The regression model $\varvec{\beta ^T \phi } ({\mathbf {x}})$ is constructed as a linear combination of m selected functions $\phi _{j}$. For the linear model used here, $m=k+1$ (k corresponds to the number of input parameters) results in a first order polynomial with the components

$$\begin{aligned} \phi _{1}({\mathbf {x}}) =1,~ \phi _{2}({\mathbf {x}})=x_{1},~\ldots ,~ \phi _{m}({\mathbf {x}})=x_{k} \;. \end{aligned}$$

(11)

For the random process, it is assumed that the deviation of the sampling points from the constant response surface results in an average of 0 and that a covariance between $z({\mathbf {x}})$ and $z(\mathbf {x_i})$ in the form

$$\begin{aligned} E[z({\mathbf {x}})z(\mathbf {x_i})]=\sigma ^2 R(\varvec{\theta },\mathbf {x_i},{\mathbf {x}}) \end{aligned}$$

(12)

exists, where $\sigma ^2$ is the process variance and R the correlation model. For an exponential correlation, the approach results in

$$\begin{aligned} R(\varvec{\theta },\mathbf {x_i},{\mathbf {x}}) = \prod _{j=1}^{k} R_{j}(\theta _j,x_{i,j}-x_j) = \prod _{j=1}^{k} \exp (-\theta _j\vert x_{i,j} - x_j \vert ^p) \;, \end{aligned}$$

(13)

whereby the norm can be selected by the parameter p and thus allows further variations of the model. It is limited here to the Euclidean norm ($p=2$).

The equations of the surrogate models (8)–(13) apply to the cases ${\hat{f}}({\mathbf {x}}) \in {\mathbb {R}}$. An extension ${\mathbb {R}} \rightarrow {\mathbb {R}}^q$ is possible without any problems. For further details see [10, 23].

4 Sampling plans

For the approximation using surrogate models, the sampling points required in (6) can be generated by different sampling strategies also called design of experiments. Depending on the structure of such a design of experiments, the number of sampling points is not freely selectable. However, a useful comparison of the sampling strategies can only be made if the number of sampling points is identical. Therefore, only designs are considered in which the number of sampling points is identical. These are the full-factorial design (FFD), the Latin hypercube sampling (LHS) and the here newly introduced fuzzy oriented sampling shift (FOSS).

4.1 Full-factorial design

The simple and well known full-factorial design is a popular method to build a design of experiments. The range of each parameter $x_j,\; 1\le j \le k$ is sampled by $n_{\text {s},j}$ points and the sampling points ${\mathbf {x}}_i$ are obtained by using all combinations forming a regular k-dimensional grid as shown in Fig. 2 (left) for the case $k=2$ and $n_{\text {s},1} = n_{\text {s},2} = 3$. If all parameters are sampled using the same number of points $n_{\text {s},j} = n_{\text {s}}$, the total number of sampling points $n_{\text {FFD}}$ is given by

$$\begin{aligned} n_{\text {FFD}}={n_{\text {s}}}^{k} \;. \end{aligned}$$

(14)

In a fuzzy framework, the samples of a fuzzy parameter ${\tilde{p}}_i$ should contain at least the minimum and the maximum of ${\tilde{p}}_i$ at $\mu =0$. Further points in between increase both the accuracy, but the full-factorial design quickly becomes large and expensive due to its exponential dependence on the number of parameters.

Fig. 2

Examples for full-factorial design (left) and Latin hypercube sampling (right)

4.2 Latin hypercube sampling

In contrast to the FFD, Latin hypercube sampling (LHS) [24] is a random sampling strategy. The parameter space ${\mathbb {R}}^k$ for n sampling points is divided for each input parameter k into n equal non-overlapping intervals. A sampling point is then randomly generated in each interval and dimension with uniform stochastic distribution, see the example in Fig. 2. Its advantages as compared to other random sampling strategies are discussed in [24] and the LHS has become one of the most popular methods for the design of experiments. Since the number of sampling points n in a LHS desing is freely selectable, LHS designs can be easily compared to FFD by choosing equal numbers of sampling points.

4.3 Fuzzy oriented sampling shift (FOSS)

The accuracy of surrogate models can be distinguished in global and local accuracy and a lot of investigations deal with adding sampling points to improve either global or local accuracy, for instance [25, 26]. However, keeping the number of sampling points fixed, the placement of the sampling points determines the global and local accuracy, where these two goals are competing, since an improvement of global and local accuracy cannot be achieved simultaneously. Both FFD and LHS are designed to maximise global accuracy by distributing the sampling points more or less evenly over the whole parameter space, but this is not always optimal.

As already stated in the introduction, fuzzy numbers describe reducible epistemic uncertainties. However, the uncertainty reduction comes usually with an increase in costs or effort. The $\mu$-value of membership can then be interpreted as a cost indicator for the uncertainty reduction [27]. It seems natural that the accuracy should increase in the high cost regime, i.e. at high $\mu$-values, while some accuracy could be sacrified in the low cost regime, i.e. at low $\mu$-values. The sampling points of the surrogate model should therefore be arranged in such a way that the local accuracy of the results increases when the input value approaches the core value, while the global accuracy in the entire parameter space is maintained as far as possible.

The global error increases if the design space for the sampling points is significantly smaller than the possible parameter space and thus many evaluations represent an extrapolation and not an interpolation [28]. Therefore, enough sampling points should lie near the edges of the parameter space in order to cover the entire parameter space. However, the majority of the sampling points are to be generated near the core value in order to achieve a higher accuracy in higher $\alpha$-cuts.

Based on this rationale, the Fuzzy Oriented Sampling Shift (FOSS) is presented here as an extension of the LHS. The idea is to shift the uniformly distributed sampling points generated by a LHS. To achieve the desired balance of local and global accuracy as discussed above, points lying at the edge of the design space are not or only slightly shifted in the direction of the core value, while points lying further inward are shifted more strongly towards the core value. This is achieved by using a standardised weighting. The procedure is explained below:

• 1. First $n-1$ sampling points $\mathbf{x }_i$ are generated by LHS. The parameter space is taken as the maximum uncertainty range at $\mu =0$. The set of sampling points is then collected into a matrix as defined in (6) and can be represented as

  $$\begin{aligned} {\mathbf {X}}= \begin{bmatrix} {\mathbf {x}}_1^T \\ {\mathbf {x}}_2^T \\ \vdots \\ {\mathbf {x}}_{n-1}^T \end{bmatrix} = \begin{bmatrix} x_{1,1} &{} x_{1,2} &{} \cdots &{} x_{1,k} \\ x_{2,1} &{} x_{2,2} &{} \cdots &{} x_{2,k} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ x_{n-1,1} &{} x_{n-1,2} &{} \cdots &{} x_{n-1,k} \end{bmatrix} \end{aligned}$$

  (15)

  The ith column vector of ${\mathbf {X}}$ denoted as ${\mathbf {p}}_i$

  $$\begin{aligned} {\mathbf {p}}_i = \begin{bmatrix} x_{1,i} \\ x_{2,i} \\ \vdots \\ x_{n-1,i} \end{bmatrix} \end{aligned}$$

  (16)

  spans the sampled uncertainty range of the fuzzy parameter ${\tilde{p}}_i$ at $\mu =0$, such that $p_{i,j} \in [a_i(\mu = 0),b_i(\mu =0)]$ for $a_i,b_i$ from (4).

• 2. Denoting the distances of the sample values in ${\mathbf {p}}_i$ from the respective core value as

  $$\begin{aligned} d_{i,j} = p_{i,j}-\text {core}({\tilde{p}}_i) = x_{j,i}-\text {core}({\tilde{p}}_i), \end{aligned}$$

  (17)

  which can be written more compact as

  $$\begin{aligned} {\mathbf {d}}_i = {\mathbf {p}}_i-\mathbf {\mathbb {1}} \text {core}({\tilde{p}}_i) \text {, with}~ \mathbf {\mathbb {1}}:=\begin{bmatrix} 1 \\ \vdots \\ 1 \end{bmatrix} \end{aligned}$$

  (18)

  and the maximum norm as

  $$\begin{aligned} \Vert {\mathbf {d}}_i\Vert _{max} =\text { max}(\vert p_{i,1}-\text {core}({\tilde{p}}_i) \vert ,\ldots , \vert p_{i,n-1}-\text {core}({\tilde{p}}_i) \vert ) \;. \end{aligned}$$

  (19)

  We introduce a normalised signed shift by

  $$\begin{aligned} {\mathbf {g}}_i = \text {sgn}({\mathbf {d}}_i) \left( \frac{|{\mathbf {d}}_i|}{\Vert {\mathbf {d}}_i \Vert _{\text {max}}} \right) ^{n_{\text {wFOSS}}} \;, \end{aligned}$$

  (20)

  where elementwise operation is presumed as follow:

  $$\begin{aligned} & g_{i,j} = \text {sgn} (p_{i,j}-\text {core}({\tilde{p}}_i)) \cdot \\ & \left( \frac{\vert p_{i,j}-\text {core}({\tilde{p}}_i) \vert }{\text {max}(\vert p_{i,1}-\text {core}({\tilde{p}}_i) \vert ,\ldots ,\vert p_{i,n-1}-\text {core}({\tilde{p}}_i) \vert )} \right) ^{n_{\text {wFOSS}}}. \end{aligned}$$

  (21)

  This shift is then used to obtain the new FOSS sampling values as

  $$\begin{aligned} {\mathbf {p}}_{i,\text {FOSS}} =\mathbf {\mathbb {1}}\cdot \text {core}({\tilde{p}}_i) + \Vert {\mathbf {d}}_i \Vert _{\text {max}} \,{\mathbf {g}}_i\;, \end{aligned}$$

  (22)

  where a power $n_{\text {wFOSS}}>1$ moves the sampling values closer to the core value, while a power $n_{\text {wFOSS}}<1$ moves them towards the edges.

  This scheme is shown in Fig. 3 for a $n_{\text {wFOSS}}>1$ The asteriks correspond to the sampling plan according to the LHS method for $n-1$ points. The dotted lines show the shifted sampling points obtained by (22).

• 3. To complete the FOSS method for a n-point sampling strategy, the n-th point is set to the core value of each input parameter by

  $$\begin{aligned} {\mathbf {x}}_{n}^{\text {T}} = \begin{bmatrix} x_{n,1}&x_{n,2}&\cdots&x_{n,k} \end{bmatrix} = \begin{bmatrix} \text {core}({\tilde{p}}_1)&\text {core}({\tilde{p}}_2)&\cdots&\text {core}({\tilde{p}}_k) \end{bmatrix}. \end{aligned}$$

  (23)

Fig. 3

Scheme of the FOSS method based on a LHS for $n-1$ points, whereby the asterisks belong to the LHS method and the crosses to the FOSS method. The cross in the center is the additional core value in contrast to the LHS method

Figure 3 shows the shift effects of the FOSS method compared to the LHS. The points located close to the edge of the parameter space hardly shift towards the center. Centrally located points are shifted more towards the center. The points staying close to the edge should avoid extrapolation as far as possible, while the points shifted more towards the center should increase the local accuracy exactly there. The uniform distribution of the LHS transitions into a $\alpha$-cut optimization depending on the exponent $n_{\text {wFOSS}}$ from (20), which allows to better represent the fuzzy uncertainties.

The implementation in the programming code is mostly possible by simple matrix operations. For this purpose, the code implemented in Matlab is shown in Fig. 4.

Fig. 4

Coding of the FOSS method in the environment of MATLAB

5 Application to test problems

By means of two test problems the advantages and disadvantages of the three presented sampling methods shall be shown.

Fig. 5

Branin function(left) and Camelback function(right) in the given limits as testfunctions

As a first test problem, a fuzzy Branin function (Fig. 5 left)

$$\begin{aligned} f({\tilde{x}}_1,{\tilde{x}}_2)=\left( {\tilde{x}}_2-\frac{5.1}{4\pi ^2}{\tilde{x}}_1^2+\frac{5}{\pi }{\tilde{x}}_1-6\right) ^2+10\left( 1-\frac{1}{8\pi }\right) \cos ({\tilde{x}}_1)+10 \end{aligned}$$

(24)

with ${\tilde{x}}_1=\text {tfn}(2.5,-5,10)$ and ${\tilde{x}}_2=\text {tfn}(7.5,0,15)$ is used. The second test problem is a fuzzy Camelback function (Fig. 5 right)

$$\begin{aligned} f({\tilde{x}}_1,{\tilde{x}}_2)=\left( 4-2.1{\tilde{x}}_1^2+\frac{{\tilde{x}}_1^4}{3}\right) {\tilde{x}}_1^2+{\tilde{x}}_1{\tilde{x}}_2+(-4+4{\tilde{x}}_2^2){\tilde{x}}_2^2 \end{aligned}$$

(25)

with ${\tilde{x}}_1=\text {tfn}(0,-2,2)$ and ${\tilde{x}}_2=\text {tfn}(0,-1,1)$. For each function, 100 sampling plans for the LHS and FOSS are used for analysis.

The root mean squared error

$$\begin{aligned} RMSE = \sqrt{\frac{\sum \nolimits _{l=1}^s ({\hat{f}}_j-f_j)^2}{s}} \end{aligned}$$

(26)

is used to compare the accuracy of the surrogate models to the full models. If the evaluation points are distributed globally, this is also a global error measure. In the case of the discretised fuzzy number being used, the RMSE is calculated for each $\alpha$-cut. A uniform grid of $s=10 \times 10$ is placed on each $\alpha$-cut, which has the boundaries of the $\alpha$-cuts as vertices. Since the RMSE is an absolute error measure, the true range of values of the respective function must be taken into account, when comparing results.

5.1 Dependency of the FOSS method on $n_{\text {wFOSS}}$

First, the functions (24) and (25) are used to investigate the FOSS strategy. The influence of the power $n_{\text {wFOSS}}$ introduced in (20) on the accuracy is examined for the DACE and the RBF surrogates with 4, 9, and 16 sampling points, respectively. A distinction is made between the global accuracy, which refers to the full parameter space at $\mu =0$, and the $\alpha$-cut accuracy, which includes the reduction of the parameter space with increasing $\mu$-values.

The main focus is on qualitative comparison. Since the RMSE is an absolute error measure, the error values must be seen in relation to the function value range, which is for the Branin function (24) in ${\mathbb {W}} \approx [0;220]$ and for the Camelback function (25) in ${\mathbb {W}} \approx [-1;6]$.

5.1.1 Global accuracy

Figures 6 and 7 show for different numbers of sampling points, the global error for $n_{\text {wFOSS}} \in [0.2,4]$ for the Branin function.

The 5 lines are given by the “Five-number summaries”, which are calculated from 100 different sampling designs and consist of the minimum value, the lower quartile, the median value, the upper quartile and the maximum value. In the Figs. 6 and 7 the maximum RMSE values at four sampling points (left) are so high that they are not visible in the displayed area. The curves behave similarly to the median curves. However, they reach approximately the 6-fold values. Considering the curves of the 3rd quartile, it becomes obvious that such high values are extreme outliers. The more sampling points are used, the smaller is the scatter in the values.

As expected, the global accuracy increases with an increasing number of sampling points and also the variance between the sampling designs reduces with the number of sampling points.

Fig. 6

Branin function: Curves of the RMSE of 100 FOSS sampling plans as a function of the FOSS exponent $n_{\text {wFOSS}}$ for the DACE model with 4 (left), 9 (center), and 16 (right) sampling points

Fig. 7

Branin function: Curves of the RMSE of 100 FOSS sampling plans as a function of the FOSS exponent $n_{\text {wFOSS}}$ for the RBF model with 4 (left), 9 (center), and 16 (right) sampling points

Fig. 8

Camelback function: Curves of the RMSE of 100 FOSS sampling plans as a function of the FOSS exponent $n_{\text {wFOSS}}$ for the DACE model with 4 (left), 9 (center), and 16 (right) sampling points

Fig. 9

Camelback function: Curves of the RMSE of 100 FOSS sampling plans as a function of the FOSS exponent $n_{\text {wFOSS}}$ for the RBF model with 4 (left), 9 (center), and 16 (right) sampling points

The figures show that higher values of $n_{\text {wFOSS}}$ have a negative effect on the global accuracy. The minimum of the RMSE lies in a range $0.2< n_{\text {wFOSS}} < 1$. Obviously, a slight shift towards the edges is beneficial here. This effect increases with an increasing number of sampling points. But $\min \limits _{\text {sampling points} \rightarrow \infty }(n_{\text {wFOSS}}) \rightarrow 0$ does not hold, since a too small power finally overweighs the edge area and the global error increases again.

Figures 8 and 9 show the equivalent results for the Camelback function. Beside the different value range, there are hardly any qualitative differences to the Branin function, so the statements made above are also valid here. Also for the Camelback function the best global accuracy is achieved with $0.2<n_{wFOSS}<1$. However, as discussed in the introduction, for fuzzy systems the global accuracy may not be the optimal criterion, but an increasing accuracy for higher $\mu$-values can be desirable at the expense of global accuracy, which was the rationale for developing the FOSS method.

5.1.2 $\alpha$-Cut accuracy

Fig. 10

Branin function: Average RMSE over the $\alpha$-cuts of the result space for the DACE model with 100 underlying FOSS sampling plans with 4 (left), 9 (center), and 16 (right) sampling points

Fig. 11

Branin function: Average RMSE over the $\alpha$-cuts of the result space for the RBF model with 100 underlying FOSS sampling plans with 4 (left), 9 (center), and 16 (right) sampling points

As in the previous section, the RBF and the DACE model with 100 sampling designs are used for the approximation of the Branin function and the Camelback function. Figures 10 and 11 show the average RMSE over the 100 sampling designs evaluated at different $\alpha$-cuts for varying $n_{\text {wFOSS}}$.

Fig. 12

Camelback function: Average RMSE over the $\alpha$-cuts of the result space for the DACE model with 100 underlying FOSS sampling plans with 4 (left), 9 (center), and 16 (right) sampling points

Fig. 13

Camelback function: Average RMSE over the $\alpha$-cuts of the result space for the RBF model with 100 underlying FOSS sampling plans with 4 (left), 9 (center), and 16 (right) sampling points

For the designs with 9 and even more pronounced with 16 sampling points the desired effect of the FOSS can be seen. A shift towards the core value ($n_{\text {wFOSS}} > 1$) increases—as intended—the accuracy for higher $\mu$-values, while sacrificing accuracy at lower $\mu$-values. A shift towards the edges ($n_{\text {wFOSS}} < 1$) has the inverse effect. The choice of the surrogate model, RBF or DACE, has no influence.

With only 4 sampling points, this observation cannot be made. The reason is that with such a low number of sampling points, the influence of each individual sampling point is very high and bad designs have a significant influence, which overlay the effect of the FOSS. Obviously, results based on such a small number of sampling points have to be treated with caution.

As Figs. 12 and 13 show, the results for the Camelback function are similar.

5.2 Comparison of different sampling strategies

The accuracy of surrogates obtained from a FOSS design (with $n_\text {wFOSS}=2$) is assessed by comparison to LHS and FFD designs with the same number of points, as discussed in Sect. 4. The discussion is presented separately for the RBF and the DACE surrogate.

5.2.1 Comparison for RBF

Table 1 Average RMSE for a RBF surrogate based on FFD, LHS and FOSS with 4, 9 and 16 sampling points(SP)

Table 1 shows the global RMSE for RBF surrogates of the two test problems using FFD, LHS and FOSS designs. For the stochastic LHS and FOSS designs the RMSE is obtained as the average over 100 sampling plans and the variance is also given. Again, one has to bear in mind that the absolute values of the two test functions vary significantly, such that only a qualitative comparison between the two test function can be made.

As expected, the table clearly shows that the error decreases with an increasing number of sampling points. An exception is the RMSE of the Camelback function with 9 sampling points and FFD. Here the form of the function plays a decisive role, since the chart can be represented in simplified form as a “U” and with 9 FFD sampling points this shape is well matched. The variance also decreases with an increasing number of sampling points. But, as can be seen for the Branin function, it can assume very high values despite the averaging over 100 sampling plans.

Overall, the FFD performs significantly better with an increasing number of sampling points. This is also due to the functions themselves. Since the largest values of the functions are located in the border area and the border is strongly weighted in an FFD (4SP $\rightarrow$ 100%, 9SP $\rightarrow$ 89%, 16SP $\rightarrow$ 75%), this method performs better. The FOSS loses global accuracy compared to the LHS, due to the shift.

However, the picture changes if the error is evaluated at different $\alpha$-cuts. In the following only the Branin function is used to show the advantages and disadvantages of the FOSS method over the other two sampling strategies. The results for the Camelback function are again comparable and are not shown.

Fig. 14

Branin function: average RMSE on $\alpha$-cuts for a RBF surrogate with 4 (left), 9 (center), and 16 (right) sampling points

Figure 14 shows again the average RMSE over 100 LHS and FOSS designs compared to a FFD result, but now for $\alpha$-cuts of the fuzzy result. It should be kept in mind that the range of values is also restricted by the limits of the $\alpha$-cuts. Thus, a lower RMSE in a higher $\alpha$-cut does not necessarily mean a better accuracy, if at the same time the function value range is significantly smaller.

If the three sampling strategies are analysed separately, large differences become apparent. The FFD with only four vertex points has a slightly increasing RMSE over all $\alpha$-cuts as the membership function value increases. With nine sampling points, one of them describes the core value of the input variables and the error decreases in the higher $\alpha$-cuts as the interval approaches this core value. However, this only applies if the fuzzy numbers are symmetric. With 16 interpolation points, the center is no longer part of the sampling design. Instead, the sampling points are located near the limit values of the input parameter of the $\alpha$-cuts $\mu = 0$ respectively $\mu = 0.6$. This is shown by lower RMSE in these $\alpha$-cuts. The FFD cannot achieve the accuracy of the other two methods in higher $\alpha$-cuts, if there is no sampling point at the core value. For the evaluation with four sampling points, even the lowest $\alpha$-cuts give worse results.

The LHS method shows a strong increase of the RMSE at 4 sampling points for lower membership functions. The behavior is similar at nine as well as at 16 sampling points. The error in the higher $\alpha$-cuts are approximately the same, here the method does not ensure that sampling points are close to the core value at $\mu = 1$. Obviously, it is a disadvantage if there is no sampling point at the core value. However, the error is highest at $\mu =0$, because these are mainly extrapolations and have a much lower accuracy than interpolations [28]. This effect is also seen with 16 sampling points, although the LHS coves the parameter space uniformly.

The FOSS method has the lowest error in the higher $\alpha$-cuts. However, as the $\mu$ decreases, this error increases much more than the other two sampling strategies.

Fig. 15

Branin function: maximum RMSE on $\alpha$-cuts for a RBF surrogate with 4 (left), 9 (center), and 16 (right) sampling points

Figure 15 shows the maximum RMSE out of the 100 sampling designs instead of the average error. Here, the LHS method shows an extreme increase of the RMSE at 4 sampling points for lower membership functions. This is due to a very unfavorable sampling plan. Considering all three graphs in Fig. 15, it can be noted that only the FOSS method keeps the error low in the higher $\alpha$-cuts, which is mostly due to the fact that the core value is explicitly set as a sampling point.

5.2.2 Results for DACE

In the following section the analysis is repeated for a DACE surrogate instead of the RBF surrogate. For the DACE a linear regression model and an exponential correlation model are used, see Sect. 3.

Table 2 Average RMSE for a DACE surrogate based on FFD, LHS and FOSS with 4, 9 and 16 sampling points (SP)

Table 2 shows again the average RMSE and the variance based on 100 stochastic sampling plans for the LHS and FOSS compared to a FFD plan with equal number of sampling points. The mean values and the variances show the same behavior as for the RBF. However, the DACE converges more slowly than the RBF when the sampling points are increased and the results for all sampling strategies are worse than the respective RBF results. In this case, the RBF approach is obviously the better choice.

Fig. 16

Branin function: average RMSE on $\alpha$-cuts for a DACE surrogate with 4 (left), 9 (center), and 16 (right) sampling points

Fig. 17

Branin function: maximum RMSE on $\alpha$-cuts for a DACE surrogate with 4 (left), 9 (center), and 16 (right) sampling points

The avarage and maximum $\alpha$-cut RMSE in Figs. 16 and 17 behave also similar to the RBF model. Only the high error values for the FOSS method at four sampling points is to be emphasised. But such negative outliers could also be found for the RBF surrogate with LHS. Nevertheless, although the RMSE here is many times higher in the lower $\alpha$-cuts, it is still lower in the higher $\alpha$-cuts. The shift ensures that the higher $\alpha$-cuts are more accurate despite very large errors in the overall model.

6 Mechanical example: plastic deformation with unloading

The application of the FOSS method to an engineering problem is demonstrated by an example taken from the Abaqus tutorial “Simple plastic deformation with unloading” of Simuleon [29]. It shows the plastic deformation of a simple beam, which can be seen also as a simple deep drawing process with springback. The process is simulated using the Abaqus FEA software [30].

6.1 Model system

Figure 18 shows the simulation setup of the deformation process. The punch presses centrally on the beam, while the beam sits on both ends on the drawing matrix. All three parts are modelled using an isotropic elastic material model for steel. Young’s modulus is set at $E=2.1 \times 10^{5}\ \mathrm{N}\,\mathrm{mm}^{-2}$ and the Poisson ratio at $\nu =0.3$. The initial yield stress of the beam is set to $\sigma _{y,0} = 300\ \mathrm{N}\ \mathrm{mm}^{-2}$ with isotropic hardening such that a yield stress of $\sigma _{y,0.05}=310\ \mathrm{N}\ \mathrm{mm}^{-2}$ is reached at an equivalent plastic strain of $\varepsilon ^{p}_{\text {eqv}} = 0.05$. The beam, with dimensions $100\ \mathrm{mm} \times {10}\ \mathrm{mm} \times {10}\ \mathrm{mm}$, is meshed with 2 mm edge length hexahedrons, and the two remaining parts with 3 mm edge length hexahedrons. This results in a total of 1836 nodes and 1250 linear hexahedral elements of type C3D8R. The punch is given a displacement of $u_{\text {P}} = {35}\,\mathrm{mm}$ in the negative y-direction using displacement edge constraints. After loading, the punch is returned to its original position. Due to symmetry, only one half is calculated in the simulation and the right-hand edge is fixed in the z-direction, as shown in Fig. 18.

Fig. 18

Deep drawing process in Abaqus

However, the focus is not on the exact representation of a deep drawing process, but on an uncertainty analysis by means of parameter variation. In order to ensure some complexity, four parameters are considered as uncertain,

• 1. the friction coefficient $\mu = 0.1 \pm 0.05$,

• 2. the displacement boundary condition of the punch $u_{\text {P}}=35 \pm 0.01 \text {mm}$,

• 3. the initial yield stress $\sigma _{y,0} = 300 \pm 2 \frac{\text {N}}{\text {mm}^2}$,

• 4. and the yield stress at 0.05 plastic strain $\sigma _{y,0.05} = 310 \pm 2\frac{\text {N}}{\text {mm}^2}$.

The four uncertain parameters are modelled as triangular fuzzy numbers as described in Sect. 2. As result variable the maximum deformation of the beam in y-direction after relief of the punch is chosen.

Two DACE models using 16 sampling points each are constructed, one based on a LHS and the other based on the FOSS (with $n_\text {wFOSS}=2)$.

6.2 Evaluation of the maximum displacement

The resulting fuzzy output for the two surrogate models are shown in Fig. 19. For a nonlinear problem with triangular inputs, the output fuzzy numbers are not necessarily triangular again. This can be observed also here, where the effect is stronger for the FOSS based surrogate.

Fig. 19

Maximum fuzzy displacement for DACE models with LHS and FOSS method

To evaluate the error, the RMSE is calculated for a single $\alpha$-cut at $\mu =0.8$. For this purpose, the full model is evaluated at 256 points from a FFD over the corresponding parameter range. The resulting RMSE is 0.0059 for the FOSS and 0.01 for the LHS design. To see the influence of the stochastic placement of the sampling points in the LHS and FOSS, the evaluations are repeated with two other sampling plans, resulting in a RMSE of 0.006 for the FOSS and 0.0069 for the LHS. Even if just two evaluations per sampling strategy are too few for a quantitative comparsion, both simulations show a superior behavior of the FOSS.

At this $\alpha$-cut, the displacement deviations due to parameter uncertainty are about 0.07 mm and the error due to the surrogate modelling is in the range 0.005–0.01 mm. With a total displacement of about 35.1 mm the modelling error does correspond to about 0.01–0.03%, which is definitely a very good result for a surrogate model. However, when considering the relation between parameter uncertainty and modelling error, the sampling strategy makes a significant difference. The FOSS method gives a deviation of

$$\begin{aligned} \frac{0.005}{0.07}\times 100 =7\%, \end{aligned}$$

(27)

while the LHS method gives

$$\begin{aligned} \frac{0.01}{0.07}\times 100 = 14\%. \end{aligned}$$

(28)

Especially in higher $\alpha$-cuts, where the parameter uncertainty is smaller, the modelling error dominates.

7 Conclusion

Surrogate models are necessary when many evaluations of an expensive full model are required. However, the accuracy of a surrogate model depends stronly on the number and placement of the underlying sampling points, i.e. the so called design of experiments. Typical applications are optimization problems or systems with uncertain parameters. For example, the description of epistemic uncertainties using fuzzy numbers necessitates many system evaluations either to solve the corresponding $\alpha$-cut optimizations or to provide enough evaluations for pure sampling based approaches. While most common design of experiments try to achieve an equal accuracy over the whole parameter space, this may not be suitable in a fuzzy context. Here the interpretation of fuzzy numbers makes a higher accuracy close to the core values desirable. This is adressed here by introducing the Fuzzy Oriented Sampling Shift (FOSS), which is a Latin hypercube based design of experiments modified for use in a fuzzy arithmetical context. The FOSS method is optimized to achieve higher accuracy at higher $\alpha$-cuts, while maintaining sufficient accuracy over the whole parameter space. This ability is demonstrated for two test functions. A superior performance compared to standard Latin hypercube and full factorial designs with equal number of sampling points is achieved for higher $\alpha$-cuts as intended, albeit at the price of some accuracy loss in the lower $\alpha$-cuts. Similar results are obtained for an application example, where LHS and FOSS designs give similar results, but the FOSS performs better at higher $\alpha$-cuts.

The FOSS method is therefore recommended when there is an uncertain, expensive system which cannot be described statistically and nonetheless a higher weighting with decreasing uncertainty is to be achieved. The uncertainty was described here by means of fuzzy numbers. The extension to general fuzzy quantities (e.g. fuzzy intervals) can be part of further research work. Another aspect is a more detailed investigation of the influence of the used surrogate model, which was limited here to two models. The focus should remain on small data, otherwise the advantages of the FOSS method are lost.