1 Introduction

Study on the seismic ground motions and damage investigations in the presence of subsurface openings such as transportation tunnels and pipelines has been highlighted among the most important topics of geotechnical earthquake engineering [80]. This issue is more significant for shallow lined tunnels because of their stiffer materials compared to the surrounding medium as well as their proximity effect on the ground surface. These features can change the initial properties of incident waves to create the amplification/de-amplification on different zones of the surface. In this regard, utilizing appropriate approaches for modeling the problems of wave scattering to evaluate the effective factors such as site conditions, type of seismic waves, the heterogeneities, the geometry, and the number of features will be inevitable. Therefore, researchers have proposed various approaches for seismic analysis of subsurface tunnels, which can be divided into analytical, semi-analytical, experimental and numerical methods [70]. The pioneering studies by analytical and semi-analytical approaches on subsurface tunnels date back to the late 1970s where the studies of Lee [33] and Lee and Trifunac [34] can be addressed. After that, Datta and Shah [11] studied the scattering of SH waves by embedded cavities. The dynamic response of twin circular tunnels subjected to incident SH waves was investigated by Balendra et al. [5]. In the following years, Shi et al. [69] studied the propagation of SH waves in the presence of a lined cavity embedded in an anisotropic media. Liang et al. [36] obtained a series solution for surface motion amplification due to underground twin tunnels. Hasheminejad and Kazemirad [22] and Jiang et al. [25] were able to present the seismic response of lined cylindrical cavity in a poroelastic medium. In this period, the effect of underground cavities on earthquake ground surface motion under SH-waves’ propagation was investigated by Smerzini et al. [71]. Moreover, Yi et al. [89] analytically solved the scattering of plane SH waves in the presence of a circular lined tunnel with an imperfectly bonded interface. Fu et al. [16] presented an analytical solution for deforming twin-parallel tunnels in an elastic half-plane. Gao et al. [18] and Faik Kara [17] analyzed the scattering of SH waves by a horseshoe- and cylindrical-shaped cavities, respectively. Later, Wang et al. [82] obtained analytical solutions of stresses and displacements for deeply buried twin tunnels in a viscoelastic rock. Recently, He et al. [23] analytically modeled the vibration prediction of two parallel tunnels buried in a full space. Although the analytical and semi-analytical methods have high accuracy for benchmark purposes, their lack of flexibility in modeling and analysis of arbitrary and sophisticated shaped models with different boundary conditions has forced the researchers to use alternative approaches like numerical methods.

In recent decades, increasing the power of computers besides the development of numerical approaches has made researchers eager to use them for analysis of wave propagation problems as well as predicting the real responses of topographic features more than ever [40]. In this way, one can never claim that the obtained results are completely exact; rather, the main purpose is to move toward accurate responses. Based on the formulation, the numerical methods can be usually divided into two general categories known as the domain and boundary methods. The common domain methods are including the finite element method (FEM) and finite difference method (FDM). These methods require discretization of the whole body including internal parts of the model and its boundaries. A review of technical literature shows that Karakus et al. [32], Yamamoto et al. [88], Mirhabibi and Soroush [41], Zhang et al. [90], Das et al. [14], and Tsinidis [79] were among the researchers who studied the twin tunnel problems by FEM. In the use of FDM can name the studies of Chakeri et al. [9], Do et al. [15], Jamshasb et al. [26], Narayan et al. [44], and Ziaei and Ahangari [91] as well. Some other researchers like [2,3,4, 82], Zeng et al. [92], Song et al. [72,73,74] and Song and Rodriguez-Dono [75] presented specific numerical approaches such as the convergence–confinement method (CCM) for tunnels’ excavation in rock masses. Although the simplicity of domain methods makes them favorable for seismic analysis of finite media, the models are intricate because of discretizing the whole body and closing the boundaries at a considerable distance from the desired zone.

The boundary methods have overcome the shortcomings of domain methods. In boundary approaches, which are mostly known today as the boundary element method (BEM), due to the concentration of discretization only around the boundary of the desired features, the satisfaction of wave radiation conditions at infinity is achieved automatically. Moreover, the volume of input data/memory seizure and analysis time are remarkably reduced. On the other hand, because of the large contribution of analytical processes in solving various problems, the high accuracy of the obtained results is guaranteed. Therefore, the BEM provides a better manner for modeling infinite/semi-infinite problems [46]. In this regard, Beskos [8] and Stamos and Beskos [68] were able to present a complete review of the BEM and its applications in modeling of underground structures, respectively. The BEM can be formulated in two general categories including full-plane (FP-BEM) and half-plane (HP-BEM) that each one developed in the transformed (frequency and Laplace) and time domains as well [12]. Among the pioneering researches based on FP-BEM, the studies of Crouch and Starfield [10], Yang and Sterling [85], and Xiao and Carter [84] can be addressed. The effective parameters on the underground tunnel stability were evaluated by Panji et al. [45]. Wu et al. [81] exhibited the stress distribution in subsurface structures. In another study, Panji et al. [48] analyzed the stability of shallow tunnels subjected to eccentric loads. Manolis and Beskos [39], 35], Kattis et al. [31], and Liu and Liu [37] presented their researches in the transformed domain. In the time domain, studies of Takemia and Fujiwara [78] and Kamalian et al. [30] can be addressed as well. In the application of FP-BEM, in addition to truncate the model from a full space, it is required to discretize all the boundaries of the problem including the interfaces, smooth ground surface and enclosing boundaries. This leads to the approximate satisfaction of stress-free conditions on the surface and reduces the accuracy of its results in some cases [1].

In the HP-BEM approach, the discretization of smooth ground surface and definition of fictitious elements for enclosing the boundaries are ignored and the stress-free boundary condition of the surface is satisfied in an exact process. Despite difficult implementation and creating large equations in the HP-BEM compared to the FP-BEM, the mentioned advantages help to make the simple models. The HP-BEM was statically developed by Telles and Brebbia [77] for stress analysis of plane problems and completed by Ye and Sawada [86] who studied the numerical properties of two-dimensional elastostatic problems. In the following years, Panji et al. [49] and Panji and Ansari [50] used static HP-BEM for analyzing the shallow tunnels and pressure pipes embedded in layered soils, respectively. This method was established for analyzing the dynamic problems in the transformed and time domains as well. In the frequency domain, Benites et al. [7] and Yomogida et al. [87] investigated anti-plane/plane strain elastic wave scattering for a system of multiple cavities. Rus and Gallego [67] presented a boundary integral equation (BIE) for sensitivity analysis of inclusion and cavity features in the harmonic elastodynamic medium. Parvanova et al. [47] studied the seismic response of lined tunnels with surface topography. Liu et al. [38] were able to obtain the seismic response of twin lined tunnels subjected to P/SV waves. Utilizing time-domain BEM, Hirai [19] presented the transient response of SH-wave scattering in a half-space. Then, Kamalian et al. [28] obtained the 2D site response of topographic structures. A direct time-domain boundary integral method for a viscoelastic plane with circular holes was suggested by Huang et al. [21]. The transient analysis of wave propagation problems was investigated by Panji et al. [46]. Recently, Panji and Ansari [51] studied the SH-wave scattering by the lined tunnels located in an elastic half-plane. Next, 52, 53 analyzed the seismic behavior of twin and multiple subsurface cavities and obtained the amplification patterns on the surface. The scattering of plane P and SV waves by twin lined tunnels with imperfect interfaces embedded in an elastic half-space was discovered by Huang et al. [24]. In the most recent studies of Panji & Ansari [55], Panji & Habibivand [54], Panji et al. [58, 59, 60] and Panji and Mojtabazadeh-Hasanlouei [56, 57, 59, 60, 61], they investigated the SH-wave dispersion by various topographic features. In another study, Mojtabazadeh-Hasanouei et al. [42] studied the seismic response of multiple subsurface inclusions as well. Recently, Mojtabazadeh-Hasanouei et al. [43] presented a review on SH-wave propagation for orthotropic topographic features.

The reviews showed that the twin tunnels are frequently used as Metros, underground transportation tunnels, mining tunnels, and pipelines for water and petroleum conveyance [29]. On the other hand, as far as the authors know, a general seismic investigation was not done in the literature on the geometrical effects of twin lined tunnels embedded in an elastic half-plane. In the present study, a new and fast approach based on a direct half-plane time-domain boundary element method (HP TD-BEM) was applied to analyze the seismic ground response in the presence of twin circular-, elliptical-, horseshoe-, square-, and rectangular-shaped lined tunnels subjected to the propagation of incident SH waves. For this purpose, by using an appropriate sub-structuring process, the models are prepared in two separate parts including a twin-pitted half-plane and a system of twin liners that are assembled on each other. The proposed method is implemented in the general DASBEMFootnote 1 algorithm [46]. As a numerical scheme by considering some intended parameters, the synthetic seismograms beside two- and three-dimensional amplification patterns of the surface are presented. Moreover, the wave propagation below the surface is illustrated by wave scattering snapshots in different significant times.

2 Problem statement

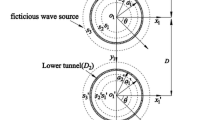
As depicted in Fig. 1, a system of twin lined tunnels is embedded in a linear elastic homogeneous isotropic half-plane subjected to the incident out-of-plane SH waves of the Ricker type [65]. The function of Ricker wavelet is defined as Eq. (1):

$$f\left( t \right) = \left[ {1 - 2\left( {\pi f_{p} \left( {t - t_{0} } \right)} \right)^{2} } \right]e^{{ - \left( {\pi f_{p} \left( {t - t_{0} } \right)} \right)^{2} }} ,$$
(1)

in which \(f_{p}\) is the predominant frequency of the wave and the time-shifting is \(t_{0}\). By conducting the model in half-plane and satisfying the stress-free boundary conditions on the ground surface (G. S.), free-field displacement (\(u^{ff}\)) can be obtained as follows [66]:

$$u^{ff} \left( {x,y,t} \right) = \alpha_{max} \cdot \left( { \begin{array}{*{20}c} {\left[ {1 - 2\left( {\frac{{\pi f_{p} }}{{{\text{c}}_{1} }}\alpha^{inc.} } \right)^{2} } \right]e^{{ - \left( {\frac{{\pi f_{p} }}{{c_{1} }} \alpha^{inc.} } \right)^{2} }} H\left( {t - \frac{{r^{inc.} }}{{c_{1} }}} \right) + } \\ {\left[ {1 - 2\left( {\frac{{\pi f_{p} }}{{c_{1} }}\alpha^{ref.} } \right)^{2} } \right]e^{{ - \left( {\frac{{\pi f_{p} }}{{c_{1} }} \alpha^{ref.} } \right)^{2} }} H\left( {t - \frac{{r^{ref.} }}{{c_{1} }}} \right)} \\ \end{array} } \right) ,$$
(2)

where \(\alpha^{inc.}\), \(\alpha^{ref.}\), \(r^{inc.}\), and \(r^{ref.}\) are obtained from Eqs. (3) and (4):

$$\alpha^{inc.} = c\left( {t - t_{0} } \right) + r^{inc.} ,\quad r^{inc.} = - {\text{sin}}\left( \theta \right) \cdot x + {\text{cos}}\left( \theta \right) \cdot y ,$$
(3)
$$\alpha^{ref.} = c\left( {t - t_{0} } \right) + r^{ref.} ,\quad r^{ref.} = - {\text{sin}}\left( \theta \right) \cdot x - {\text{cos}}\left( \theta \right) \cdot y ,$$
(4)
Fig. 1
figure 1

The schematic HP-BEM model for the twin lined tunnels with different geometries subjected to the incident SH waves

Full size image

In Fig. 1, \(\Omega\) is the domain and \(\Gamma\) is the boundary of the body, which are defined separately for the pitted domain and the closed filled liners. b is the radius of tunnels, \(c\) is the wave velocity of the half-plane and \(\theta\) is the angle of the incident waves. To initiate the formulation procedure, the equation of motion for the anti-plane strain model should be utilized as Eq. (5):

$$\frac{{\partial^{2} u_{j} \left( {x,y,t} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} u_{j} \left( {x,y,t} \right)}}{{\partial y^{2} }} + b_{j} \left( {x,y,t} \right) = \frac{1}{{c_{j}^{2} }}\frac{{\partial^{2} u_{j} \left( {x,y,t} \right)}}{{\partial t^{2} }} , \quad j = 1, 2, 3$$
(5)

In this equation, \(u_{j}\)(x, y, t) is out-of-plane displacement and \(b_{j}\)(x, y, t) is out-of-plane body force for the \(j\)th domain at the point (x, y) for the current time of t. The shear-wave velocity for the \(j\)th medium is defined by \(c_{j}\) and determined by \(\sqrt {\mu_{j} /\rho_{j} }\), where \(\mu_{j}\) is the shear modulus and \(\rho_{j}\) is the mass density for the mentioned domain. Based on the boundary conditions illustrated in Eq. (6), solving Eq. (5) results in a 2D anti-plane semi-infinite medium.

$$\left. {\frac{{\partial u_{1} \left( {x,y,t} \right)}}{\partial n} } \right|_{y = 0} = 0 ,$$
(6)

The half-space Green’s functions can be achieved by simultaneously taking the singular solution into account for Eqs. (5) and (6) [46].

3 HP time-domain BEM

To concentrate the meshes exclusively around the boundary of tunnels, the wave source image technique should be used to satisfy the stress-free boundary conditions on the ground surface. This procedure significantly simplifies the model and helps to decrease the volume of input data and time of analysis [46].

3.1 BIE

In the first step, the weighted residual integral without considering the boundary condition of Eq. (6) should be applied in Eq. (5). Using boundary methods for eliminating the volumetric integral defined on the domain, ignoring the body forces and contributions of the initial conditions, the direct BIE in the time domain can be achieved as Eq. (7) [6]:

$$c\left( \xi \right)u\left( {\xi ,t} \right) = \mathop \smallint \limits_{{\Gamma_{1} \cup \Gamma_{2} \cup \Gamma_{3} }}^{ } \left\{ {\mathop \smallint \limits_{0}^{t} \left[ {u^{*} \left( {x,t;\xi ,\tau } \right) \cdot q_{j} \left( {x,t} \right) - q^{*} \left( {x,t;\xi ,\tau } \right) \cdot u_{j} \left( {x,t} \right)} \right]d\tau } \right\}d\Gamma \left( x \right) + u_{1}^{ff} \left( {\xi ,t} \right) , j = 1, 2, 3$$
(7)

In the above equation, the half-space displacement and traction Green’s functions of the time domain are shown by \(u^{*}\) and \(q^{*}\), respectively. Also, \(u_{j}\) and \(q_{j}\) are the displacement and traction fields on the boundary; x and ξ are the coordinates of source and receiver, respectively. The Riemann-convolution integrals are shown by \(u^{*} \cdot q_{j}\), \(q^{*} \cdot u_{j}\) and \(u_{1}^{ff}\) is the free-field displacement of the surface. The angle of boundary refraction (geometry coefficient) is defined by \(c\left( \xi \right)\) [13, 20, 27].

4 Numerical implementation

To obtain field variables, the discretization of geometric boundary of the body as well as time axis should be carried out before solving Eq. (7). Therefore, there is no approximation in Eq. (7) before discretizing on the boundaries of the twin-pitted medium and closed filled liners. An analytical process and a numerical procedure are applied in Eq. (7) to obtain its matrix form for temporal and spatial integration, respectively. The details of these processes can be found in Panji and Ansari [51, 55].

5 Applications

The above formulation was implemented in the DASBEM algorithm. Some verification examples were solved, which can be found in the study of Panji and Ansari [51, 55]. Thus, in the present work this part was ignored. The mentioned program is developed for the seismic analysis of 2D underground arbitrary-shaped structures such as twin lined tunnels embedded in an elastic half-plane. To study the behavior of twin underground lined tunnels subjected to the seismic SH waves numerically, some key parameters including the shape of tunnels, angle of incident waves (\(\theta\)), the depth ratio (DR) and the space ratio (SR) of the tunnels are considered. The shapes of circular, elliptical, horseshoe, square and rectangular are considered for the tunnels, respectively. In the following sections, the normalized displacement amplitude (NDA) is the ratio of the Fourier amplitude of the total ground surface motion obtained by BEM to the Fourier amplitude of the incident motion. The flexibility ratio (\(F\)) is the relative stiffness ratio of tunnels’ lining to the surrounding soils and determined as \((F = \rho_{l} c_{l} /\rho_{m} c_{m} )\), where \(\rho_{l}\) and \(c_{l}\) are the mass density and shear-wave velocity of linings; \(\rho_{m}\) and \(c_{m}\) are the mentioned parameters for surrounding soils, respectively. The dimensionless frequency (\(\eta\)) is defined as (\(\eta = \omega b/\pi c\)), where \(\omega\) is the angular frequency of the wave, b is the radius of tunnel, and the shear-wave velocity of the domain is shown by c. The ratio of the surface response amplitude to free-field motion is known as the amplification. Due to the comparative nature of this research, the angles \(({\theta )}\) of 0° and 90° are considered for incident waves. The linings are made of concrete, and the flexibility ratio (\(F\)) is equal to 10 [55]. First, to illustrate the propagation and diffraction of the incident waves on the ground surface, the responses of time domain are presented in 3D and 2D modes (Sect. 5.1). To complete the results, the wave propagation below the ground surface is exhibited by some wave scattering snapshots at different significant times (Sect. 5.2). Then, the general pattern of amplification and displacements of the ground surface are demonstrated by 3D and 2D frequency-domain results (Sect. 5.3). In the last part, some linear graphs were fitted to estimate the maximum responses in different cases for engineering applications (Sect. 6). The numerical procedure is implemented in the MATLAB programming software.

5.1 Time-domain responses

Figure 2 shows the general pattern of responses in the time domain to present the scattering of the SH waves in the presence of twin lined tunnels with different shapes. The values of DR and SR are considered equal to 2.5 and 4.0 for all shapes of tunnels, respectively. By colliding the seismic waves to the lining of each tunnel, because of their extreme hard material compared to the surrounding medium (\(F\) = 10), their boundaries act like mirror and trap the waves between the top boundary of tunnels and ground surface. Therefore, the fluctuations of the responses and the duration of convergence time are increased. For the circular-, horseshoe- and square-shaped tunnels, the amplitudes in central point of the surface are higher than the elliptical- and rectangular-shaped tunnels. Therefore, the large space occupied by the tunnels intensifies the volume of trapped waves to create a high-risk zone between the tunnels. In the following, Figs. 3 and 4 show the 2D time-domain responses for incident angles \((\theta )\) of 0° and 90°, respectively. The results are presented based on three stations marked by 1 to 3 on the ground surface. The stations 1 and 3 are located on the center line of tunnels and station 2 is placed at the central point of the surface between the tunnels. When the incident wave is applied vertically (Fig. 3a), the maximum amplitudes of square- and rectangular-shaped tunnels are recorded equal to 1.3 and 1.7, respectively, which are higher than the other models. In these specific cases, the smooth surfaces of tunnels sections increase the effect of wave trapping between the top boundary of tunnels and ground surface. This effect is weak when the tunnels have rotary cross sections like circular-, elliptical- and horseshoe-shaped models. As can be seen in Fig. 3b, the obtained amplitudes are increased to 2.6 for the second station. Therefore, the middle area between the tunnels is considered as a critical point for surface structures when the incident waves are radiated vertically. In Fig. 4, the horizontal scattering of incident waves increases the maximum amplitudes to 2.8. Therefore, when the incident waves are horizontally propagated, the tunnels directly reflect the waves toward the surface. In this case, the effect of trapped waves is weak, but the severe collision of the reflected waves to the surface creates higher amplitudes.

Fig. 2
figure 2

Synthetic seismograms of the ground surface and the procedure of the SH waves’ dispersion with time, for the model of twin a circular-, b elliptical-, c horseshoe-, d square- and e rectangular-shaped lined tunnels subjected to vertical incident waves

Full size image
Fig. 3
figure 3

The amplitude of propagated waves on the surface versus time, for the model of twin lined tunnels with different geometries in a centerline of the tunnels and b central point subjected to the vertical incident SH waves

Full size image
Fig. 4
figure 4

The amplitude of propagated waves on the surface versus time, for the model of twin lined tunnels with different geometries in a centerline of the first tunnel, b central point, c centerline of the second tunnel subjected to the horizontal incident SH waves

Full size image

5.2 Snapshots

Presenting the wave scattering snapshots is the best way to see the seismic waves’ propagation below the surface in significant times. Therefore, Figs. 5, 6, 7, 8 and 9 are presented to show the diffraction of vertical SH waves in the presence of twin lined tunnels with different shapes. In order for preparation of the snapshots, 14,028 and 10,201 internal points are considered for the domain and each of tunnels, respectively. The surface range is assumed between − 5b and 5b and the depth range of 0 ~ − 5b is considered as well. comparison of the responses in different shapes of tunnels, the snapshots are presented for six specific times including the seconds of 3, 3.5, 4, 5, 5.5 and 6, respectively. The results clearly show the effect of tunnels geometry on waves scattering to form the trapped waves between the boundary of tunnels and ground surface.

Fig. 5
figure 5

Wave propagation snapshots and the procedure of the SH waves’ dispersion below the ground surface, for the model of twin circular-shaped lined tunnels subjected to vertical incident waves

Full size image
Fig. 6
figure 6

Wave propagation snapshots and the procedure of the SH waves’ dispersion below the ground surface, for the model of twin elliptical-shaped lined tunnels subjected to vertical incident waves

Full size image
Fig. 7
figure 7

Wave propagation snapshots and the procedure of the SH waves’ dispersion below the ground surface, for the model of twin horseshoe-shaped lined tunnels subjected to vertical incident waves

Full size image
Fig. 8
figure 8

Wave propagation snapshots and the procedure of the SH waves’ dispersion below the ground surface, for the model of twin square-shaped lined tunnels subjected to vertical incident waves

Full size image
Fig. 9
figure 9

Wave propagation snapshots and the procedure of the SH waves’ dispersion below the ground surface, for the model of twin rectangular-shaped lined tunnels subjected to vertical incident waves

Full size image

5.3 Frequency-domain responses

Illustrating the frequency-domain responses is the best way to show the general pattern of ground surface displacements in the presence of twin subsurface lined tunnels with different shapes subjected to seismic waves and Fig. 10 is presented for this purpose. The surface range of − 10b–10b and the dimensionless frequencies (\(\eta\)) of 0.25–5 are considered, respectively. When the vertical incident waves are applied to the models, the responses are symmetric. The collision of the incident waves to the boundary of lined tunnels separates the direct waves to reflected and refracted phases of waves. A portion of the reflected waves leaves the medium, and another portion deviates from its initial paths to reach the surface. The main volume of the refracted waves is trapped between the tunnels and ground surface where they experience the intermittent reflections. This effect can significantly increase the amplifications between the tunnels. On the other hand, the lowest amplifications are obtained in the location of tunnels where a small volume of waves can enter. This phenomenon is called shadow zone [76], which is because of the stiffer material of linings to the surrounding soils, which creates a safe zone above the tunnels by blocking the passage of the waves. Comparing the responses shows that the maximum amplifications are occurred for the horseshoe- and square-shaped tunnels with the values more than 2.5 in central zone. The horseshoe-shaped tunnels create the large safe zones above the tunnels. On the other hand, when the elliptical- and rectangular-shaped tunnels are considered, the maximum amplifications are distributed in the central and peripheral areas with the lower value of 2.2, which exactly shows the effect of tunnels geometry on the surface displacements. In the following, the 2D frequency-domain responses are presented in Figs. 11 and 12 for the dimensionless frequencies of 0.5, 1 and 3 under vertical and horizontal incident waves. As can be seen in Fig. 11, the fluctuation of the results is increased at higher frequencies and the maximum NDA is recorded in the presence of horseshoe-shaped tunnels with the value of 4.6 at \(\eta\) equal to 3 for the central point of ground surface. By applying the horizontal incident waves (Fig. 12), the NDA values are increased for different dimensionless frequencies when compare to Fig. 11. Based on the results (Fig. 12), the maximum displacement on the ground surface is obtained for square-shaped tunnels with the value of 5.4 at \(\eta\) equal to 3 in the position of first tunnel. Therefore, when the seismic waves are propagated vertically, the safe zones are located above the tunnels. But, by applying horizontal waves, the upper areas of the tunnels have the highest seismic risk for surface structures. To complete the responses, Figs. 13 and 14 are presented to show the amplifications versus different dimensionless frequencies at three surface stations. The responses are illustrated for \(\eta\) between 0.1  and  3. In Fig. 13a, the maximum amplification of 1.7 in \(\eta\) of 1.37 is recorded above the location of tunnels and related to the rectangular-shaped model. For the central point of the surface (Fig. 13b), this value is increased to 2.28 in \(\eta\) of 3. Also, in horizontal radiation of incident waves, the maximum amplification is occurred in stations 1 (Fig. 14a) and 2 (Fig. 14b), which is related to the square- and horseshoe-shaped tunnels with the value of 2.5 in the \(\eta\) of 3 and 0.9, respectively. Given that a lower volume of waves has reached the third station (Fig. 14c), the maximum value is decreased to 2.3 in \(\eta\) of 2.4 for circular tunnels.

Fig. 10
figure 10

The 3D amplification of the ground surface versus different dimensionless frequencies for the model of twin a circular-, b elliptical-, c horseshoe-, d square- and e rectangular-shaped lined tunnels subjected to vertical incident SH waves

Full size image
Fig. 11
figure 11

The normalized displacement amplitude of the ground surface versus \(x/b\), for the model of twin lined tunnels with different geometries and dimensionless frequency of a \(\eta = 0.5\), b \(\eta = 1.5\) and c \(\eta = 3.0\) subjected to the vertical incident SH waves

Full size image
Fig. 12
figure 12

The normalized displacement amplitude of the ground surface versus \(x/b\), for the model of twin lined tunnels with different geometries and dimensionless frequency of a \(\eta = 0.5\), b \(\eta = 1.5\) and c \(\eta = 3.0\) subjected to the horizontal incident SH waves

Full size image
Fig. 13
figure 13

The amplification of the ground surface versus different dimensionless frequencies, for the model of twin lined tunnels with different geometries in a centerline of the tunnels, b central point subjected to the vertical incident SH waves

Full size image
Fig. 14
figure 14

The amplification of the ground surface versus different dimensionless frequencies, for the model of twin lined tunnels with different geometries in a centerline of the first tunnel, b central point, c centerline of the second tunnel subjected to the horizontal incident SH waves

Full size image

6 Conclusion

The geometrical effect of shallow twin lined tunnels was discovered by a direct half-plane time-domain BEM approach. The tunnels were embedded in a 2D linear elastic half-space subjected to vertical/horizontal incident SH waves. To establish the models, only the interfaces and internal boundaries of the lined tunnels were required to be discretized. A computer program was encoded based on the proposed method [51, 55]. Then, by considering some intended parameters such as depth and space ratio of the tunnels and the angle of incident waves, a parametric study was evaluated to present the seismic ground motion in the presence of the twin lined circular-, elliptical-, horseshoe-, square- and rectangular-shaped tunnels, respectively. First, the 3D synthetic seismograms of the surface were illustrated for different models. To complete the results, the 2D responses of time-domain were demonstrated for specific stations on the surface. To show the wave propagation below the surface, some snapshots were presented at significant times. Finally, by converting the time-domain responses to frequency-domain, the displacements of the ground surface and amplification patterns were depicted as well. Some key results obtained from the parametric study are summarized as follows:

  1. 1.

    The HP time-domain BEM was able to prepare the simple models for time-history step-by-step seismic analysis of the ground surface in the presence of arbitrarily shaped twin subsurface lined tunnels.

  2. 2.

    Comparing the seismic responses of twin unlined underground cavities [52] with the present results showed that the role of lined tunnels was stronger on the seismic isolation to create the safe area on the ground surface.

  3. 3.

    When the incident wave was applied vertically/horizontally, the maximum amplitudes of 2.6 and 2.8 were recorded on the ground surface, respectively.

  4. 4.

    The maximum amplification occurred for the horseshoe- and square-shaped tunnels with values more than 2.5 in the central zone.

  5. 5.

    By applying the vertical incident waves, the maximum NDA was recorded in the presence of horseshoe-shaped tunnels with a value of 4.6 in the central point of the ground surface.

  6. 6.

    In horizontally propagating waves, the maximum displacement was obtained for square-shaped tunnels with the value of 5.4 on the location of the first tunnel.