Abstract
The finite elements method allied with the computerized axial tomography (CT) is a mathematical modeling technique that allows constructing computational models for bone specimens from CT data. The objective of this work was to compare the experimental biomechanical behavior by three-point bending tests of porcine femur specimens with different types of computational models generated through the finite elements’ method and a multiple density materials assignation scheme. Using five femur specimens, 25 scenarios were created with differing quantities of materials. This latter was applied to computational models and in bone specimens subjected to failure. Among the three main highlights found, first, the results evidenced high precision in predicting experimental reaction force versus displacement in the models with larger number of assigned materials, with maximal results being an R2 of 0.99 and a minimum root-mean-square error of 3.29%. Secondly, measured and computed elastic stiffness values follow same trend with regard to specimen mass, and the latter underestimates stiffness values a 6% in average. Third and final highlight, this model can precisely and non-invasively assess bone tissue mechanical resistance based on subject-specific CT data, particularly if specimen deformation values at fracture are considered as part of the assessment procedure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Bone tissue is formed by tissue components with varying mechanical properties. This results in complex bone geometry as cortical and trabecular tissues have different mechanical traits and are distributed heterogeneously. As such, the creation of computational models that facilitate accurate assessments of osseous behavior first depends on developing a non-invasive technique able to analyze the geometry and the spatial distribution of tissues, as well as respective mechanical properties.
Currently available non-invasive clinical methods for estimating osseous resistance in a specific bone include bone densitometry (i.e., dual-energy X-ray absorptiometry) and peripheral quantitative computed tomography. However, these techniques are limited to information on regional and geometric density and do not consider factors such as three-dimensional structure, materials distribution within a structure, mechanical properties, or load condition [1].
The finite elements method (FEM) based on computerized axial tomography (CT) involves applying mathematical techniques to create a bone tissue model that incorporates information related to three-dimensional architecture and the distribution of osseous density, as provided via a CT scan of the bone under study [2, 3]. Greater precision predicting structural behavior occurs as this mesh becomes more refined, as well as by increasing the quantity of materials in the model.
Several bone models using the FEM already exist [4,5,6]. These models could potentially serve to non-invasively evaluate a bone through the application of distinct mechanical force tests. Furthermore, these models can reveal compression, tension, fatigue, and fracture zones, as well as the respective force limits needed. Importantly, these models can be subject specific; in other words, they can be characterized for each specimen under investigation [7, 8]. Complementary to what was previously published, predictive models of the highest precision are required, which would be capable of non-invasively and individually assess mechanical properties of bone in patients with pathological bone structure.
The use of a multiple materials FEM scheme [6, 11] renders an enhancement of the FEM technique as it can realistically include the distribution of the mechanical properties of the subject-specific bone specimen. When loads and boundary conditions are well determined spatially and do not change significantly over time, deformations are bounded and materials properties are homogeneous; then, the FEM scheme in general will render results, from which output practical decisions could be made. In recent years, there has been a common tendency to include non-linear behavior of materials as part of the FEM scheme. This in order to achieve a higher fidelity of the expected mechanical behavior of the material modelled system. On one hand, non-linear FEM schemes are computationally costly [9, 10] in terms of implementation and of the CPU time required to solve the simulation, as commonly an iteration procedure is needed to achieve convergence. While on the other hands, it means to include additional unknown parameters (depending upon the constitutive model used) or an adjustment procedure to represent the non-linear behavior of the involved materials. The latter is otherwise difficult to find or fit even from phenomenological data [10]. In despite of this fact, whenever a linear model is used, overestimation of the onset of damage stress is a known resulting feature of this simplification. However, the clinical praxis may overcome this overestimation by considering the experience of the specialist, who then can from the linear model prediction, correct the diagnosis using, for example, the data associated with the deformation values occurring at the onset of fracture, plus of course his or her expert knowledge. The tradeoff between this a posteriori correction and the additional costs of a more sophisticated non-linear model implementation is yet a matter of assessment and discussion. However, linear model implementation would be more feasible to transfer initially into the clinical realm in the early stages of a computational-assisted diagnosis initiative.
Regarding clinical application, the subject-specific prediction of mechanical bone properties is a highly valuable tool as this technique allows to precisely replicate morphology and structure, as shown in recent studies (Ramezanzadehkoldeh and Skallerud [12], Bahia [13] and Väänänen [14]). Particularly, if one considers this FEM analysis to enter the clinical daily praxis, where more concern is centered toward estimating critical loads at which fracture could occur rather than precisely knowing the load level at which transition to damage occurs. For ex vivo mechanical force tests in small animals, the femur is commonly used because of its size, length-to-width ratio, and consistent cross-sectional shape along the entire length [15]. Other studies have shown that the three-point bending test is a relevant biomechanical test that can provide information about the structural and material properties of the bone [15,16,17].
The objective of this study was to carry out subject-specific simulations for the effects of three-point bend tests in porcine femur models. The models were developed using the finite element method and individual CT scan data. Distinct quantities of materials in the models were also analyzed. In parallel, the biomechanical properties of osseous tissue were characterized for the assessed animal model, and a comparison was made between computer-simulated fractures and real-life ex vivo biomechanical testing.
2 Materials and methods
2.1 Selection of bone specimens
Five femur specimens from 3-month-old Landrace pigs were used for analyses. Macroscopic examination and X-rays were utilized to rule out any bone abnormalities in the specimens. This study was approved by the Animal Welfare Ethics Committee, School of Medicine, Pontificia Universidad Católica de Chile, and it complies with the requirements regarding the allowed number of tested specimens.
2.2 Mechanical study of bone specimens
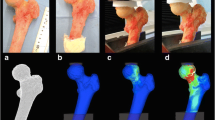
Mechanical tests were performed using an INSTRON Model 4206 Universal Testing Machine (Instron, Canton, MA, the USA). The machine was adapted to perform the three-point bend test on specimens. The epiphyses of the femurs were supported by resin molds with the exact shape of the bone to restrict any movement. For each specimen, vertical force was applied to the midpoint of the diaphysis at 0.5 mm/min, with registries every second until bone failure (Fig. 1). The exact location of bone failure and the failure pattern were recorded for later comparison with the finite elements model. These coincide with forces suffered in trauma-induced fractures.
2.3 Boundary conditions
Molds from the epiphyses of each femur (distal and proximal sides) were resin casted and used to rigidly hold the femur horizontally in place inside the testing machine. This prevented sliding of the bone epiphyses during the test as the middle point of the diaphysis was pressed down by the punch rod. Therefore, boundary conditions implemented in the model consisted in fixing these femur lateral regions in two nodes at each side. These nodes were arbitrarily selected within the neighborhood of the distal and proximal epiphyses, restricting their motion along the x-, y- and z-directions, nonetheless allowing for numerical convergence of the numerical solution to result. The midpoint of the diaphysis was calculated as the semi-length between each pair of nodes.
2.4 Numerical modeling
Numerical models were created through the following steps sequence (Fig. 2a), which ranged from radiological assessments to model creation through the FEM:
-
1.
Acquiring CT Information: A helical CT scan was conducted using a GE LightSpeed Ultra CT Scanner (GE Medical Systems, Chicago, IL, the USA) with a 0.625-mm slice separation. The information was digitized and converted into Digital Imaging and Communication in Medicine (DICOM) files.
-
2.
Image Segmentation: This process was completed using the InVesalius v1.0 software (Renato Archer Information Technology Center, Campinas, Brazil). After geometric segmenting, the model was exported using the native stereolithography CAD format (i.e., STL). The number of triangles generated from the tessellation process on each of the 5 femurs specimens, ranged from 116,040 units for femur 4 up to 124,200 units for femur 3.
-
3.
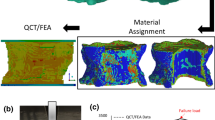
Finite Elements Mesh Generation: This step was carried out with the ANSYS ICEM CFD v11.0 software (ANSYS Inc., Canonsburg, PA, the USA) [19]. The study mesh contained 34,000 nodes and 26,000 elements that varied depending on the geometric characteristics of each specimen as shown in Fig. 3.
-
4.
Assigning Material Properties: The DICOM files were imported into the Data Manager v1.3.1.217 software (B3C BioComputing Competence Center, Bologna, Italy), and using the Visualization Toolkit v5.2 (Kitware Inc., Clifton Park, NY, the USA), a grayscale volume was obtained. The finite element mesh was then combined with grayscale volume information using the BoneMat v3.0 software (Instituto Ortopedico Rizzoli, Bologna, Italy) [6], resulting in the assignment of specific mechanical properties to the models.
-
5.
Gray Calibration Values: This process was used to establish density values from CT grayscale volume values, as already reported by several other authors. [2, 5, 20]. A linear regression curve was then constructed that correlated each scalar value with a corresponding tissue density. This process was confirmed by calculating the total bone mass and comparing it against the mass of the FEM mesh. The equation relating density and CT numbers is linear and can be written according to Taddei et al. [6], as follows:
$$\overline{\rho }_{n} = \alpha + \beta \cdot CT_{n}$$(1)where \(\overline{\rho }_{n}\) is the uniform density assigned to the n element of the mesh, CTn is the uniform CT number, and α and β are the calibration coefficients provided by the user. An iterative process was used to calculate the minimum and maximum bone densities from the CT scan of each specimen (see Fig. 2b).
-
6.
Relations of Density and Elasticity: The mechanical properties of each defined material were estimated based on density values in the form of power laws, as proposed in other studies [2, 3, 21]. For this, techniques proposed in the literature were applied [22,23,24]. A distinction was made between the properties of the trabecular and cortical bones to create a robust model. The correlation between apparent density (grams/cm3) to cortical and trabecular tissue elastic modulus (MPa) is shown in Eqs. 2 and 3, respectively. The latter study did not provide a correlation linking Poisson ratio with apparent density; however, an average value for Poisson ratio equal to 0.3 was then adopted.
$$E^{c} = 2065.\rho_{{{\text{app}}}}^{3.09}$$(2)$$E^{t} = 1904.\rho_{{{\text{app}}}}^{1.64}$$(3)Quantity of Materials in the Generated Models: Five models with increasing quantities of materials were created for each specimen. The reference model (r) was created with two materials, while the following models (a thru d) were created with 20, 40, 75, and 140 material types, respectively, where each material was defined as having a specific tissue density. The material distribution is illustrated in Figure 4. The difference in the number of materials to be incorporated into each model is carried out by defining a given spacing between consecutive elastic modulus values. Results from the reference model were compared with regard to results obtained from the models that incorporate variable material properties.
Table 1 illustrates the number of materials of each model assigned at Specimen 5, both at the cortical (c) and trabecular regions (t), and the value range of the mass density and elastic modulus.
-
7.
Finite Elements Analysis: This analysis was performed using the ANSYS v11.0 software (ANSYS Inc.), using tetrahedrons with ten nodes for each element [2, 20, 21, 25]. Approximately 20,000 elements considering approximately 35 different material groups were chosen for the calibration procedure. Three to four iterations were conducted to reach a total mass value closed enough to the experimentally measured value for each bone. In all cases, values with less than 1% of difference were achieved. Once the iterative process was finished, the density value that made it possible to calculate a total bone mass closer to the obtained in the experimental results was chosen. Regarding the mesh sensitivity analysis, significant differences across the parameters under study (longitudinal component of elements stress and longitudinal component of nodal stress) were not observed. The measured differences in no case exceed 6%. The mesh was chosen for sensitivity analysis then consisted of 34,000 nodes and 26,000 elements. These amounts varied depending on the geometric characteristics of each bone´s anatomical features.
2.5 Mechanical study of computational models
Force values applied to real specimens were used as boundary conditions in the generated computational models. The latter was run under a load equivalent to 1500 N in the femoral diaphysis (midpoint) as schematically indicated in Fig. 5.
Moreover, Table 2 indicates the exact node location and value of the applied vertical deformation (i.e., boundary condition) for each of the five femur models, as well as the corresponding value of the application point.
The similarities between reaction and tension forces were compared through linear regression of the force values measured from each of the five specimen models as presented in the following graph (Fig. 6). From this correlation, one can obtain the coefficients of linear regression, the intercept, and curves by using the method proposed in Helgason et al. [2] and prior studies [18, 25]. These results show how the linear model can be used to predict the onset of damage in the bone. Fracture locations in the models were inferred through the von Mises yield criterion according to Keyak et al. [26].
Specimen fracture was evaluated considering the surface area containing elements whose stress values exceeded the strength of the bone tissue. Thus, it was necessary to choose a criterion to assess the computed stresses. According to the literature, there are several fracture criteria that can be considered for bone material: the von Mises stress, maximum principal stress and maximum principal strain. However, none of these criteria has been used to evaluate juvenile porcine femur fracture. The approach adopted in this study was the von Mises stress criteria, which has proven to be useful for studying other long bones (e.g., tibiae) that are anatomically similar to the femur (Keyak et al. 1994). On the other hands, this criterion yields values which fall in between other relationships such as the one of Schileo et al. 2008 (maximum principal strain) and Keyak et al. 1994 (maximum principal stress), so its use would avoid over- or underestimation. In summary, to evaluate bone fracture at local levels, stresses were calculated according to the von Mises criterion and their values compared to the estimate given by the relationship proposed by Keyak et al. (1994):
where sigma_lim is the maximum stress (MPa) value the bone can withstand before fracture and corresponds to the mineral density tissue value (g/cm3). Mineral density is calculated from the apparent density according to the ratio as suggested by Schileo et al. (2007). Table 3 shows maximum stress values calculated from the average density of each specimen model.
2.6 Statistical analysis
We performed statistical analysis using Microsoft Excel (Microsoft 2017. Microsoft Excel version 15.39) and Stata 13 (StataCorp. 2013. Stata Statistical Software: Release 13). Data distribution assessed using the Shapiro–Wilk test. Descriptive statistics were used to report specimen data and results. Correlations between the experimental model and the finite elements model were determined using Wilcoxon signed-rank test for paired data and Bland–Altman analysis. Linear regression analysis of the experimental model was also conducted, the results of which were compared with the FEM. Statistical significance was set at p value < 0.05.
3 Results
Basic specimen measurements are summarized in Table 4. The median length of specimens was 130 mm (128–135 mm). The median diaphysis diameter was 19 mm (18–20 mm), and the median total mass was 94.78 g (91.9–106.8 g).
The median reaction force at fracture, measured experimentally, that occurred in the specimens was 1005 N (968–1857 N). Maximum displacement ranged between 2.62 and 4 mm, with the median being 3 mm (Fig. 7). The sigmoidal shape of the five curves is due to several factors, namely an initial sliding and accommodation of the bone epiphysis within the molded fixture at the initiation of the bending test. This is followed by a decreasing increment behavior of the ultimate force at the end of the test due to the non-linear elastic response of the bone material. The middle regions show clearly a linear behavior as expected from elasticity theory at low elongations, with quasi-parallel slopes. Elastic stiffness obtained as the slope in the linear zone account to m1 = 714 N/mm (Femur 5), m2 = 600 N/mm (femurs 1 and 3), m3 = 576 N/mm (femurs 2 and 4). Femur 5 has the largest mass (106.8 g) thus highest stiffness, while Femur 2 has the lowest mass (91.9 g) and lowest stiffness. It can be also observed that fractures occur just prior to peak forces in all specimens, suggesting that the material has not yielded before break and that it has rather followed a non-linear elastic behavior, particularly at the last stage of deformation.
On the other hands, from the computational models, the median maximum reaction force prior to fracturing was 1177 N (904–2087 N). When comparing maximum force, models a (20 materials) and b (40 materials) significantly differed from the experimental values obtained (p = 0.043 and p = 0.044, respectively); while models c (75 materials) and d (140 materials) were not significantly different than the specimen values (p = 0.078 and p = 0.225, respectively). Although reaction force versus displacement showed a tendency of linear behavior (Fig. 8), the median displacement was also 3 mm (2.60–4 mm). It can be noticed the similarity of the simulated reaction force magnitude to that from the experimental model; however, a stronger linear tendency is observable. The linearity of the latter five curves is expected as the implemented FEM model is based on a linear elastic model. In this case elastic stiffness obtained as the slope in the linear zone accounts to m1 = 667 N/mm (Femur 5), m2 = 633 N/mm (Femur 3), m3 = 546 N/mm (femurs 1, 2 and 4). Here again, femur 5 has the highest stiffness value, while femur 2 has the and lowest value. However, it is worth noticing that predicted stiffness values slightly fall within a range of 5–7% lower values than real stiffness values.
Moreover, from Figs. 7 and 8, the % error associated with the underestimation of the specimen deformation at fracture is less than the % error associated with the overestimation of the force at fracture. In the case of Femur 5, the % error for the maximum force accounts to (2076–1848 N)/1848 N = 12.4% versus the % error for the deformation at fracture which comes to (4.04–3.68)/4.04 = 8.9%. In the case of Femur 4, the former % error is 24.7%, while the latter is 20.6%. For Femur 3, 19.3% and 19.3%, respectively. In case of femur 2, both percentage errors are almost zero, and in the case of Femur 1, % error corresponds to 5% and 2.3%, respectively. In summary, the average % error of the ultimate force accounts to 12.3%, while the average % error for the underestimation of the specimen deformation at fracture only equals 10.3%. Suggesting the latter measured estimates a 16% closer the onset of fracture under a deformation observation.
Finally, linear regression of the mechanical behavior of real specimens versus the computational models revealed that the model with the greatest quantity of materials (model d) provided more precise results. Specifically, an R2 and R2adj ≥ 0.97 and a root-mean-square error range of 3.29–5.29% were observed (Fig. 9 and Table 5). However, use of less materials also allows acceptable simulation precision of the experimental model.
Furthermore, visual inspection of the locations where damage accumulation has occurred in the five specimens (i.e., signaling fracture onset) can be obtained from Fig. 10. Comparison between the experimental specimens and the ones obtained from the computational models coincides significantly and closely resembles fractures in the bone specimens.
Finally, Bland–Altman analysis comparing real specimen deformation to model deformation showed low bias across all five specimens (Fig. 11). Bias did not change significantly secondary to increase in deformation averages, with a median bias of 0.67% (0.01 mm), with a range from 0.35–0.89%. This analysis illustrates a high degree of correlation between the experimental measurements and the finite elements model (d) regarding specimen deformation values.
4 Discussion
As the number of materials increased, the spacing between the values of continuous elastic modules decreased, and clusters with lower density values were created. Due to this, a progressive decrease was observed in the maximum reaction force value. Figure 12 shows the results of the maximum reaction force value calculated computationally for each specimen, using an increasing number of materials. The sharp decline recorded in the first points of the curve is associated with a notable difference between the reference model (homogeneous 2 materials model) and the simplest model that incorporates spatially variable material properties (model-a incorporating 20 materials). On the other hands, the computations involving models having spatially variable material properties show percentage variations near to 15% when comparing the simplest (model-a) with the most detailed model (model-d) that incorporates ca. 140 materials. The more precise models tested approximated a final reaction force very close to that found in the experimental models. In other words, by incorporating a high number of material types, certain elements of the finite mesh were given isotropic properties (i.e., independent of spatial direction). Values were assigned depending on bone density where the element was located. Therefore, an anisotropic problem, where properties depend on spatial orientation, would be approximated as the sum of distinct, discrete and spatially minute isotropic problems distributed over the space. The three-point bend test was chosen because of its simplicity and capacity to provide information about the structural and material properties of the bone [15,16,17,18].
Various other bone models using the FEM have been reported as shown in Table 6. Huiskes and Chao [27] provide a good review on the first research studies conducted in this area. Other references to initial models combined with the use of CT scans are given by Huang et al. [28] and Seitz and Rüegsegger [29], among others. Current models can predict forces of stress with high precision through this combined technique (R2 > 0.9, root-mean-square error < 10%) [21, 29]. Worth noting, the method presented in our research achieves the highest precision, and the applied mesh morphing has been used with a high degree of predictive precision in recent clinical applications [19, 30, 31]. Nonetheless, once a mathematical model is obtained, according to Choi, the finite element method can be implemented to solve the model; however, it is difficult for numerical simulations to consider every mechanical condition arising in real applications [32].
Despite the reduced quantity of specimens used in the present study, the fact that various scenarios were assessed for each specimen (25 in total) increased the amount of obtained information. Furthermore, the uniformity of results supports the validity of the employed method; especially considering the use of the von Mises criterion for determining fracture location. After the original article describing the technique [26], many articles compared the use of strain base methods (principal strain) and stress-based criteria (principal stress, von Mises) [33, 34]. Although Schileo et al. [5] proposed the use of a strain criteria after the analysis of three cadaveric femurs, it continues to be a lack of consensus on the preferred criteria [35]. Furthermore, our current study supports the use of stress-based von Mises with a high correlation between the location of the specimen fracture and the predicted computational model.
Finally, from the recent study of Fung et al. [36], Schileo et al. [37] and others [38, 39], subject-specific prediction of mechanical bone properties is a useful tool, particularly in clinical applications, allowing morphology and structure replication. The potential applications of non-invasive prediction include predicting fracture risk in pathological bone, managing rehabilitation in complex skeletal reconstructions, and evaluating bone consolidation and the incorporation of bone grafts, among other applications. Furthermore, the herewith presented model evidences the possibility of obtaining high precision with a manageable (i.e., not so high) materials quantity, thus providing the advantage of decreasing data processing times without sacrificing model predictive precision. Particularly, when specimen deformation measurements at fracture are considered, as the % error is less compared to the force estimation % error. These latter could mean advancements in applicability in clinical contexts, where increasing age of the population is leading to increased patients in risk of pathological bone fractures that could benefit from a predictive model to guide prophylactic bone fixation surgery.
5 Conclusions
The present study compared the experimental biomechanical behavior of porcine femur specimens with distinct types of computational models generated through the finite elements’ method based on computed axial tomography under a multiple density materials scheme.
One advantage of this method is the ability to use an increasing number of materials, (i.e., from 2 to ca. 140), thus, to explore the compromise between the overestimation of the ultimate stress from a single isotropic linear material model and the more accurate yet intricate and computationally costly non-linear elastic model.
Main highlight result obtained, in first place, shows a high precision prediction for measured reaction force versus displacement between the experimental three-point bending tests and simulations (i.e., R2 of 0.99 and a minimum root-mean-square error of 3.29% in the model with greatest definition). Second highlight result indicates that elastic stiffness, both measured and computed, follows the trend, higher the mass—higher the stiffness; however, stiffness predictions are in average a 6% below real stiffness values. As third highlight, the model can precisely and non-invasively assess bone tissue resistance based on subject-specific CT data, particularly if specimen deformation values at fracture are taking into consideration.
The present study represents a contribution to the development of biomechanical bone behavior assessment based on computed axial tomography and the finite elements method.
References
Crawford RP, Cann CE, Keaveny TM (2003) Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone 33:744–750
Helgason B, Taddei F, Pálsson H, Schileo E, Cristofolini L, Viceconti M, Brynjólfsson S (2008) A modified method for assigning material properties to FE models of bones. Med Eng Phys 30:444–453
Keyak JH, Kaneko TS, Tehranzadeh J, Skinner HB (2005) Predicting proximal femoral strength using structural engineering models. Clin Orthop Relat Res 219–228
Cristofolini L, Juszczyk M, Martelli S, Taddei F, Viceconti M (2007) In vitro replication of spontaneous fractures of the proximal human femur. J Biomech 40:2837–2845
Schileo E, Taddei F, Cristofolini L, Viceconti M (2008) Subject-specific finite element models implementing a maximum principal strain criterion are able to estimate failure risk and fracture location on human femurs tested in vitro. J Biomech 41:356–367
Taddei F, Schileo E, Helgason B, Cristofolini L, Viceconti M (2007) The material mapping strategy influences the accuracy of CT-based finite element models of bones: an evaluation against experimental measurements. Med Eng Phys 29:973–979
Viceconti M, Davinelli M, Taddei F, Cappello A (2004) Automatic generation of accurate subject-specific bone finite element models to be used in clinical studies. J Biomech 37:1597–1605
Viceconti M, Olsen S, Nolte L-P, Burton K (2005) Extracting clinically relevant data from finite element simulations. Clin Biomech 20:451–454
Imai K, Ohnishi I, Bessho M, Nakamura K (2006) Nonlinear finite element model predicts vertebral bone strength and fracture site. Spine 31
Macneil JA, Boyd SK (2008) Bone strength at the distal radius can be estimated from high-resolution peripheral quantitative computed tomography and the finite element method. Bone 42
Alister F, Ramos-Grez JA, Vargas AP (2012) Generation of mineral density distribution maps from subject-specific models of mandibles—a preliminary study. Int J Med Robot Comput Assist Surg 8(3):311–318
Ramezanzadehkolde M, Skallerud BH (2017) MicroCT-based finite element models as a tool for virtual testing of cortical bone. Med Eng Phys 46:12–20
Bahia MT, Hecke MB, Mercuri EGF (2019) Image-based anatomical reconstruction and pharmaco-mediated bone remodeling model applied to a femur with subtrochanteric fracture: a subject-specific finite element study. Med Eng Phys 69:58–71
Väänänen SP, Grassi L, Venäläinena MS, Matikka H, Zheng Y, Jurvelin JS, Isaksson H (2019) Automated segmentation of cortical and trabecular bone to generate finite element models for femoral bone mechanics. Med Eng Phys 70:19–28
Sharir A, Barak MM, Shahar R (2008) Whole bone mechanics and mechanical testing. Vet J 177
Goodyear SR, Aspden RM (2012) Mechanical properties of bone ex vivo. Method Mol Biol 816
Kourtis LC, Carter DR, Beaupre GS (2014) Improving the estimate of the effective elastic modulus derived from three-point bending tests of long bones. Ann Biomed Eng 42, 2 edn
Turner CH, Burr DB (1993) Basic biomechanical measurements of bone: a tutorial. Bone 14
Falcinelli C, Schileo E, Balistreri L, Baruffaldi F, Bordini B, Viceconti M, Albisinni U, Ceccarelli F, Milandri L, Toni A, Taddei F (2014) Multiple loading conditions analysis can improve the association between finite element bone strength estimates and proximal femur fractures: a preliminary study in elderly women. Bone 67:71–80
Keyak JH, Rossi SA, Jones KA, Les CM, Skinner HB (2001) Prediction of fracture location in the proximal femur using finite element models. Med Eng Phys 23:657–664
Schileo E, Taddei F, Malandrino A, Cristofolini L, Viceconti M (2007) Subject-specific finite element models can accurately predict strain levels in long bones. J Biomech 40:2982–2989
Carter DR, Hayes WC (1997) The compressive behavior of bone as a two-phase porous structure. J Bone Joint Surg 59:954–962
Morgan EF, Bayraktar HH, Keaveny TM (2003) Trabecular bone modulus–density relationships depend on anatomic site. J Biomech 36:897–904
Wirtz DC, Schiffers N, Pandorf T, Radermacher K, Weichert D, Forst R (2000) Critical evaluation of known bone material properties to realize anisotropic FE-simulation of the proximal femur. J Biomech 33:1325–1330
Taddei F, Cristofolini L, Martelli S, Gill HS, Viceconti M (2006) Subject-specific finite element models of long bones: an in vitro evaluation of the overall accuracy. J Biomech 39:2457–2467
Keyak JH, Lee IY, Skinner HB (1994) Correlations between orthogonal mechanical properties and density of trabecular bone: use of different densitometric measures. J Biomed Mater Res 28:1329–1336
Huiskes R, Chao EYSA (1983) survey of finite element analysis in orthopedic biomechanics: the first decade. J Biomech 16:385–409
Huang HK, Suarez F, Toridis TG, Khonozeimeh K, Ovenshire L (1980) Utilization of computerized tomographic scans as input to finite element analysis. In: International conference procedings: finite element in biomechanics, vol 2
Seitz P, Ruegsegger P (1983) Fast contour detection algorithm for high precision quantitative CT. IEEE Trans Med Imaging 2:136–141
Maquer G, Bürki A, Nuss K, Zysset PK, Tannast M (2016) Head-neck osteoplasty has minor effect on the strength of an ovine cam-FAI model: in vitro and finite element analyses. Clin Orthop Relat Res 474:2633–2640
Qasim M, Farinella G, Zhang J, Li X, Yang L, Eastell R, Viceconti M (2016) Patient-specific finite element estimated femur strength as a predictor of the risk of hip fracture: the effect of methodological determinants. Osteoporos Int 27:2815–2822
Choi DK (2016) Mechanical Characterization of Biological Tissues: Experimental Methods Based on Mathematical Modeling. Biomed Eng Lett 6:181–195
Ota T, Yamamoto I, Morita R (1999) Fracture simulation of the femoral bone using the finite-element method: how a fracture initiates and proceeds. J Bone Miner Metab 17
Gómez-Benito MJ, García-Aznar JM, Doblaré M (2005) Finite element prediction of proximal femoral fracture patterns under different loads. J Biomech Eng 127
Keyak JH, Rossi SA (2000) Prediction of femoral fracture load using finite element models: an examination of stress- and strain-based failure theories. J Biomech 33
Fung A, Loundagin LL, Edwards WB (2017) Experimental validation of finite element predicted bone strain in the human metatarsal. J Biomech 60
Schileo E, Balistreri L, Grassi L, Cristofolini L, Taddei F (2014) To what extent can linear finite element models of human femora predict failure under stance and fall loading configurations? J Biomech 47
Christen D, Zwahlen A, Müller R (2014) Reproducibility for linear and nonlinear micro-finite element simulations with density derived material properties of the human radius. J Mech Behav Biomed Mater 29
Eberle S, Göttlinger M, Augat P (2013) An investigation to determine if a single validated density-elasticity relationship can be used for subject specific finite element analyses of human long bones. Med Eng Phys 35
Op Den Buijs J, Dragomir-Daescu D (2011) Validated finite element models of the proximal femur using two-dimensional projected geometry and bone density. Comput Method Program Biomed 104
Enns-Bray WS, Owoc JS, Nishiyama KK, Boyd SK (2014) Mapping anisotropy of the proximal femur for enhanced image based finite element analysis. J Biomech 47
Nishiyama KK, Gilchrist S, Guy P, Cripton P, Boyd SK (2013) Proximal femur bone strength estimated by a computationally fast finite element analysis in a sideways fall configuration. J Biomech 46
Luisier B, Dall Ara E, Pahr DH (2014) Orthotropic HR-pQCT-based FE models improve strength predictions for stance but not for side-way fall loading compared to isotropic QCT-based FE models of human femurs. J Mech Behav Biomed Mater 32
Dall´Ara E, Pahr D, Varga P, Kainberger F, Zysset P (2012) QCT-based finite element models predict human vertebral strength in vitro significantly better than simulated DEXA. Osteoporos Int 23
Koivumäki JEM, Thevenot J, Pulkkinen P, Kuhn V, Link TM, Eckstein F, Jämsä T (2012) CT-based finite element models can be used to estimate experimentally measured failure loads in the proximal femur. Bone 50:824–829
Anez-Bustillos L, Derikx LC, Verdonschot N, Calderon N, Zurakowski D, Snyder BD, Nazarian A, Tanck E (2014) Finite element analysis and CT-based structural rigidity analysis to assess failure load in bones with simulated lytic defects. Bone 58
Mirzaei M, Keshavarzian M, Alavi F, Amiri P, Samiezadeh S (2015) QCT-based failure analysis of proximal femurs under various loading orientations. Med Biol Eng Comput 53
Hambli R, Allaoui S (2013) A robust 3D finite element simulation of human proximal femur progressive fracture under stance load with experimental validation. Ann Biomed Eng 41
Acknowledgements
Work presented in this manuscript was supported by the Pontificia Universidad Católica Medicine School and the Mechanical and Metallurgical Engineering Department from the same institution. The authors would also like to acknowledge FONDEF Project D06I1026 for its collaboration in the accomplishment of this research work. We would also like to acknowledge University of Notre Dame, Aerospace and Mechanical Engineering Department, for granting a Melchor Visiting Scholarship to the corresponding author, time during which part of this manuscript was prepared.
Funding
None.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Each author certifies that he or she has no commercial associations (e.g., consultancies, stock ownership, equity interest, patent/licensing arrangements, etc.) that might pose a conflict of interest in connection with the submitted article.
Ethical approval
This study was approved by the Animal Welfare Ethics Committee, School of Medicine, Pontificia Universidad Católica de Chile.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Irarrázaval, S., Ramos-Grez, J.A., Pérez, L.I. et al. Finite element modeling of multiple density materials of bone specimens for biomechanical behavior evaluation. SN Appl. Sci. 3, 776 (2021). https://doi.org/10.1007/s42452-021-04760-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-021-04760-9