1 Introduction

The progressing land use and cover (LU-LC) change induced by human beings is among the major factors responsible for water level changes of lakes as its change consequences changes in lake water balance components at a varying space and time dimensions [1, 2]. Ethiopia is a developing country where LU-LC change is intensified at a faster rate because of the fact that charcoal and firewood are the common sources of energy besides food and housing demands of the growing population [3,4,5,6]. Hence, in Ethiopia, the LU-LC change was mainly manifested by the conversion of forest land to agriculture and/or urbanization which influenced the hydrologic processes and consequently caused considerable water level fluctuations of lakes [7,8,9]. Hayk Lake basin, which is found in the northeastern Ethiopia has entertained the pronounced LU-LC changes of increased farmlands/settlement and shrublands; a decreased bush lands, grasslands, forestlands, and lake surface area during 1957–2007 [5]. However, the significance of the LU-LC change on the decrease in water surface area of Hayk Lake was the pending question that required attention and therefore, it became objective of this study.

The LU-LC change strongly influences the creation, progress, and concentration of surface runoff during hydrological transformation within the lake basin [10]. However, the relationship between LU-LC change and surface runoff is naturally complex as it also relies on other physical characteristics of a basin, such as the size, topography, and types of soils [11, 12]. Such kinds of hydrological problems with multitude relationships can be resolved through the use of hydrologic models like the Hydrologic Engineering Centre-Hydrologic Modeling System (HEC-HMS) model with the integration of remote sensing and geographical information system [12, 13]. The HEC-HMS model is a powerful, widely applicable tool that is capable of solving wide ranges of hydrologic problems and also it is flexible, i.e., different combinations of model sets are possible for the loss, transform, routing, and baseflow separation methods based on the nature of the study [14]. Among the many alternative models under loss method package of the HEC-HMS, the soil conservation service- curve number (SCS-CN) loss method is the most relevant method to estimate the infiltration loss during the computation and modeling of surface runoff for small basins and local spatial scale studies [10]; even for those characterized by diverse LU-LC, soil, and physical conditions [15,16,17]. This is because of its simplicity and its capacity to offer results as good as those of complex models [18].

At various levels of space and time in Ethiopia, attempts have been made to calibrate and apply HEC-HMS simulate runoff for different purposes [19,20,21] and they showed that the HEC-HMS model works well to simulate runoff in every climate zone in the country. However, rainfall-runoff modelling for the LU-LC impact assessment using the HEC-HMS model for the Hayk Lake basin has not yet been conducted. Thus, this study used remote sensing, geographic information system (GIS), and HEC-HMS in combination with HEC-GeoHMS and Arc-Hydro for rainfall-runoff modeling of Hayk Lake basin by adopting the SCS-CN method to assess the impact of LU-LC change on surface runoff between 1989 and 2015 to alleviate the declining water level problem of Hayk Lake in the endorheic lake basin. This provides a science-based understanding to set up a sound water management program for Hayk Lake which is jeopardized with the consistent water level reduction in the lake basin.

2 Materials and methods

2.1 Study area

The Hayk Lake basin is located in the northeastern part of Ethiopia, extending from 39.68°E to 39.81°E, 11.24°N to 11.39°N. Its total area is 85926.8 × 103 m2, of which 21,567.6 × 103 m2 is a lake. The Hayk Lake basin is naturally endorheic, where there is no water outflowing from it. Hayk Lake is a sink in the lake basin. Seventeen ephemeral streams in the upper catchment transport surface runoff and discharge it into the Hayk Lake (sink of the lake basin) through their individual outlets. Total surface runoff in the Hayk Lake was then obtained from the lake water level reading of a gauge on the southwest shore of the lake (Fig. 1). This gauge was used to run hydrological models in the lake basin to simulate total surface runoff at Hayk Lake. Simulation of this challenging lake basin hydrology may be the novelty of the study.

Fig. 1
figure 1

Map showing location and subbasins of Hayk Lake basin. (The subbasins and their associated stream networks for each outlet point were delineated in batch following terrain preprocessing of the DEM using Arc Hydro)

Full size image

The sub-humid tropical climate with bimodal rainfall pattern (the long rainfall season from June to September and the short rainfall season, which lasts from March to May) characterizes the lake basin. The basin has 5 dry months from October to February. It received an average annual precipitation of 1.19 m, with an average annual temperature of 17.58 °C. The basin is also characterized by uneven topography with an elevation ranging from 1878 to 2817 m asl.

2.2 Data used

The datasets required to carry out this study were daily hydro climate (precipitation, temperature and water level) and Landsat images for the years 1989, 2000, and 2015; soil data, and Digital Elevation Model (DEM) data. The years 1989, 2000, and 2015 were chosen because of the lack of pre-1989 lake water level data and the adequacy of the time gap to perform LU-LC change analysis.

Only the Hayk Meteorological Station (11.31˚N, 39.68˚E; 1984 m asl) (Fig. 1) was a source of daily climate data. It was chosen for 3 reasons. Its proximity to Hayk Lake provides measured data that are almost the same as the actual data received by the lake and surroundings. It contains sufficient historic climate data for this study and an adequate density of meteorological stations (85.93 square kilometer per station) to adequately represent the Hayk Lake basin as per the WMO recommendation: 300–1000 square kilometer per station in mountainous regions of temperate, Mediterranean and tropical zones [22].

The Hayk Lake water level (LWL) time series for the years 1989, 2000 and 2015 was collected from the gauge situated on the southwest shore of Hayk Lake (Fig. 1). The daily LWL data were used to estimate surface runoff for calibrating and validating the HEC-HMS model. In the absence of inflow of natural water sources (such as springs) to the lake and any nonnatural diversion of water into the lake and/or out of the lake, the surface runoff is calculated from the water balance equation of endorheic or terminal lakes as shown in Eq. (1) [23].

$$\Delta H\, = \,P + Q - PET$$
(1)

where ΔH is the change in lake water level; P is precipitation on the lake; Q is surface runoff; PET is the lake evapotranspiration or potential evapotranspiration.

The Landsat image Multispectral Scanner (MSS) acquired on 21 November 1989, Thematic Mapper (TM) image on 28 January 2000, and Enhanced Thematic Mapper Plus (ETM +) on 29 January 2015 were obtained from the archiving system of Earth Explorer (http://earthexplorer.usgs.gov/) to generate the LU-LC map. The Hayk Lake basin was entirely covered by a single image of Landsat that did not display any spatial asymmetry with the basin meteorological station.

The soil data for the Hayk Lake basin were extracted from the FAO soil shapefile of the Amhara region (a region where the study area is located). It was used to obtain the Hydrologic Soil Group (HSG) data that assisted in the curve number calculations.

The Shuttle Radar Topography Mission (SRTM) Digital Elevation Model (DEM) with a spatial resolution of 20 m was used to delineate subbasins and stream networks in the basin and to extract their physical features.

The tools employed for the analysis were ArcGIS 10.1 to determine the topographic features from DEM, LU-LC maps from Landsat images, and HSGs from soil data; Arc Hydro 1.0 beta 2 to delineate subbasins and their associated streams in batch following preprocessing the DEM; HEC-GeoHMS 10.1 to estimate the model parameters (CN, lag time, and initial abstraction) from physical properties of subbasins and streams, LU-LC maps, and soil data; and HEC-HMS 4.0 to calibrate and validate model parameters using initial model parameters, daily precipitation, and daily surface runoff. The calibrated HEC-HMS model was then used to simulate surface runoff and quantify the impact of the LU-LC change on the magnitude of surface runoff.

2.3 Methods of data analysis

The research methodology is summarized according to the conceptual framework presented in Fig. 2.

Fig. 2
figure 2

Conceptual framework of the research methodology

Full size image

2.3.1 Classifying landsat images of Hayk Lake basin

The LU-LC maps of the lake basin were produced from Landsat images using ArcGIS 10.1 software. The maximum likelihood supervised classifier classified the images [24]. The LU-LC classes were categorized into five types, including water body (lake), shrubland, plantation, cultivation, and grassland. The accuracy of the classification was evaluated using the overall accuracy (OA) and kappa coefficient derived from the error matrix [25, 26]. Overall accuracy is the ratio of the total number of correctly classified pixels to the total number of sample data, while the KAPPA coefficient is computed from Eq. (2) [26].

$$\mathop K\limits^{ \wedge } \,\, = \,\,\,\,\,{{\left( {N\sum\limits_{i = 1}^{r} {x_{ii} } \, - \,\sum\limits_{i = 1}^{r} {\left( {x_{i + } \,.\,\,x_{ + i} } \right)} } \right)} \mathord{\left/ {\vphantom {{\left( {N\sum\limits_{i = 1}^{r} {x_{ii} } \, - \,\sum\limits_{i = 1}^{r} {\left( {x_{i + } \,.\,\,x_{ + i} } \right)} } \right)} {\left( {N^{2} \, - \,\sum\limits_{i = 1}^{r} {\left( {x_{i + } .\,\,x_{ + i} } \right)} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {N^{2} \, - \,\sum\limits_{i = 1}^{r} {\left( {x_{i + } .\,\,x_{ + i} } \right)} } \right)}}$$
(2)

where r is number of rows and columns in error matrix; N is total number of observations (pixels); xii is the number of observations in row i and column i; xi+ is marginal total of row i, and x+i is marginal total of column i. [27] indicated that the minimum level of interpretation accuracy should be at least 85%.

2.3.2 Estimating model parameters of the lake basin

The physical characteristics of subbasins (basin slope, longest flow path, basin centroid, centroid elevation, and centroidal longest flow path) and streams (river length, upstream and downstream elevations, and river slope) were extracted from terrain data using HEC-GeoHMS. HEC-GeoHMS used these data with LU-LC and soil data to generate the model parameters (CN, lag time, and initial abstraction) in each subbasin of the lake basin. The model parameters of the lake basin, daily precipitation, and daily observed surface runoff were used to calibrate and validate the HEC-HMS model. The calibrated HEC-HMS model was used to simulate surface runoff and quantitatively assess the impact of LU-LC on surface runoff.

2.3.3 Runoff simulation using HEC-HMS modeling tool

The four model components of HEC-HMS known as basin models, meteorologic models, control specifications, and input data should be first created properly to execute simulation and interpret results of simulation [13]. The subbasin hydrologic element of the basin model was used for runoff simulation. The meteorologic model links the daily precipitation input time series (in this case, time series of years 1989, 2000, and 2015) to the subbasin hydrologic element. The control specification model controls the start and end dates of the simulation and the time interval of the simulation. The simulation time interval must be less than 29% of lag time for a satisfactory definition of the ordinates on the rising limb of the SCS Unit Hydrograph (SCS UH) [28]. A simulation time interval of 15 min was therefore set for this study.

Methods to assess the impact of LU-LC on the magnitude of surface runoff in 1989, 2000, and 2015 in the endorheic lake basin were the loss method and the transformation method. The SCS-CN loss model defines the rainfall-runoff relationship based on Eq. (3) to determine the infiltration loss of the lake basin.

$$Q={\left(P-{I}_{a}\right)}^{2}/\left(P-{I}_{a}+S\right)$$
(3)

where Q is precipitation excess in mm; P is total rainfall in mm; S is potential maximum soil moisture retention in mm and Ia is initial abstraction of rainfall in mm. Taking Ia = 0.2S and substituting in Eq. (3), it gives:

$$Q={\left(P-0.2S\right)}^{2}/\left(P+0.8S\right),P\ge 0.2S$$
(4)
$$S\,\, = \,\,\,\left( {{{24500} \mathord{\left/ {\vphantom {{24500} {CN}}} \right. \kern-\nulldelimiterspace} {CN}}} \right)\,\, - \,254$$
(5)

CN is a dimensionless parameter that is dependent on the LU-LC class, HSGs, and the antecedent soil moisture condition (AMC). The AMC is the wetness condition of the soil based on total precipitation 5 days antecedent to the storm [29]. In practice, CN values range from 100 for water bodies to about 30 for permeable soils with high infiltration rates [30]. The weighted average CN (CNw) value of the basin can be calculated using Eq. (6).

$$CN_{w} \,\,{{ = \,\,\,\left( {\sum\limits_{i = 1}^{n} {CN_{i} \,A_{i} } } \right)} \mathord{\left/ {\vphantom {{ = \,\,\,\left( {\sum\limits_{i = 1}^{n} {CN_{i} \,A_{i} } } \right)} A}} \right. \kern-\nulldelimiterspace} A}$$
(6)

where i is an index of the basin subdivisions of uniform LU-LC and soil type; CNi is the CN for subdivision i; and Ai is the basin area of subdivision i.

The SCS UH then transforms the precipitation excess to produce direct runoff hydrograph in which the hydrograph is scaled by the parameter called lag time to produce unit hydrograph. A negligible baseflow is assumed in the absence of net ground flow data around the lake [31]. The basin lag time (Tlag) of each subbasin in the lake basin is highly related to the characteristics of the main stream (length, slope, and roughness) as shown in Eq. (7) [32].

$$T_{lag} \,\, = \,\,0.0057\,\left( {\frac{100}{{CN}}\,\, - \,\,9} \right)^{0.7} \,\frac{{L^{0.8} }}{\sqrt S }$$
(7)

where L denotes the longest stream flow path in kilometers and S is the average basin slope in m/m. On the other hand, in a basin with a more or less uniform runoff distribution, lag time can be related to time of concentration (Tc) as follows:

$$T_{lag} \, = \,\,0.6T_{c}$$
(8)

2.3.4 Sensitivity analysis

The sensitivity of the model parameters (SCS CN, initial abstraction, and lag time) on the runoff volume, peak discharge, and time to peak runoff characteristics were analyzed using HEC-HMS. The initial parameter values were used as base values for the evaluation and one parameter at a time was analyzed between ± 20% ranges at 5% intervals while the other parameters were held constant. The ± 20% range was chosen because the estimated initial CN values were 80 and greater, which can reach a maximum of 100. The absolute average sensitivity index is a value used to rank parameters based on their sensitivity status, from the most to the least sensitivity to model output. It is calculated on the basis of the sensitivity index [33] by:

$$R_{p} \,\, = \,\,\frac{1}{n}\,\left( {\sum\limits_{i = 1}^{n} {\left| {S_{i} } \right|} } \right)$$
(9)
$$S_{i} \,\, = \,\,\,\,\left( {{{I_{avg} } \mathord{\left/ {\vphantom {{I_{avg} } {I_{2} \, - \,I_{1} }}} \right. \kern-\nulldelimiterspace} {I_{2} \, - \,I_{1} }}} \right)\,\,\,\left( {{{O_{2} \, - \,O} \mathord{\left/ {\vphantom {{O_{2} \, - \,O} {O_{avg} }}} \right. \kern-\nulldelimiterspace} {O_{avg} }}} \right)$$
(10)

where Si is the sensitivity index; O1 is the model output value corresponding the smallest input value (I1); O2 is the model output value corresponding the largest input value (I2); Iavg is the average of I1 and I2; Oavg is the average value of O1 and O2. In this study, the I1 and I2 values are ± 20% for a given parameter.

2.3.5 HEC-HMS calibration and validation

The daily precipitation and observed surface runoff from 01 January to 31 August of the years 1989, 2000, and 2015 were used to calibrate a model and the values from 01 September to 31 December of the same years were used for validating a model. The univariate gradient search algorithm and the peak weighted root mean square error (PWRMSE) objective function were used to optimize the model parameters. The objective function PWRMSE is expressed [13] as:

$$PWRMSE\,\, = \,\,\sqrt {\frac{{\sum\nolimits_{t = 1}^{N} {\left( {Q_{0} \,\left( t \right)\, - \,Q_{S} \,\left( t \right)} \right)^{2} \,\frac{{Q_{0} \,\left( t \right)\, + \,Q_{a} }}{{2Q_{a} }}} }}{N}}$$
(11)
$$Q_{a} \, = \,\frac{1}{N}\,\sum\limits_{t = 1}^{N} {Q_{0} \,\left( t \right)}$$
(12)

where Qo (t) and Qs (t) are respectively the observed and simulated flows at time t, and Qa is the average observed flow [34]. Using a weighting factor, the PWRMSE measure gives a greater overall weight to error near the peak discharge. It implicitly measures the comparison of peak values, volumes, and peak times of the two hydrographs [13].

The performance of the model was assessed by visual hydrograph comparison and use of the goodness of fit measures. The known goodness of fits in HEC-HMS tool version 4.0 are mean absolute error (MAE), root mean square error (RMSE), and Nash Sutcliffe efficiency (NSE).

$$MAE\,\, = \,\,\frac{1}{N}\,\,\sum\limits_{i = 1}^{N} {\left| {O_{i} \, - \,S_{i} } \right|}$$
(13)
$$RMSE\,\, = \,\,\sqrt {\frac{1}{N}\,\,\sum\limits_{i = 1}^{N} {\left( {O_{i} \, - \,S_{i} } \right)^{2} } }$$
(14)

NSE evaluates the overall model performance [35] and it is defined based on Eq. (15).

$$NSE\,\, = \,\,1 - \,\,\,\left( {{{\sum\limits_{i = 1}^{N} {\left( {O_{i} \, - \,S_{i} } \right)^{2} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{N} {\left( {O_{i} \, - \,S_{i} } \right)^{2} } } {\sum\limits_{i = 1}^{N} {\left( {O_{i} \, - \,\overline{O} } \right)^{2} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{i = 1}^{N} {\left( {O_{i} \, - \,\overline{O} } \right)^{2} } }}} \right)\,$$
(15)

The performance ratings of NSE recommended by [36] are very good for 0.75 < NSE ≤ 1.0; good for values 0.65 < NSE ≤ 0.75; satisfactory for 0.50 < NSE ≤ 0.65 and unsatisfactory for NSE ≤ 0.50.

2.3.6 Contribution of land use and cover change to surface runoff generation

The HEC-HMS used the historical scenario simulation method to separate the contribution of LU-LC change from the combined LU-LC and climate change effects on surface runoff generated in the lake basin [37]. Precipitation variation is the prominent and the only climate factor to significantly affect runoff and all other elements of water balance [38]. Therefore, 12 scenarios were developed by combining different LU-LC and precipitation data to separate the contribution rate of LU-LC change from climate change as shown in Table 1.

Table 1 Scenarios used for quantitative impact analysis
Full size table

The scenarios created were used to determine the rate of impact of LU-LC change (L) and climate change (C) on the generation of surface runoff in the Hayk Lake basin as shown below.

  1. (i)

    Calculating the contribution rate between 1989 and 2000 based on the 1989 reference period

    $$L_{1989 - 2000} \,\,\left( \% \right)\,\, = \,\,\left( {{{\left( {Q_{3} \, - \,Q_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {Q_{3} \, - \,Q_{1} } \right)} {\,\left( {Q_{4} \, - \,Q_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\,\left( {Q_{4} \, - \,Q_{1} } \right)}}} \right)\,x\,100\%$$
    (16)
    $$C_{1989 - 2000} \,\,\left( \% \right)\,\, = \,\,\,\left( {{{\left( {Q_{2} \, - \,Q_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {Q_{2} \, - \,Q_{1} } \right)} {\,\left( {Q_{4} \, - \,Q_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\,\left( {Q_{4} \, - \,Q_{1} } \right)}}} \right)\,x\,100\%$$
    (17)
  2. (ii)

    Calculating the contribution rate between 2000 and 2015 based on the 2000 reference period

    $$L_{2000 - 2015} \,\,\,\left( \% \right)\,\, = \,\,\left( {{{\left( {Q_{7} \, - \,Q_{5} } \right)} \mathord{\left/ {\vphantom {{\left( {Q_{7} \, - \,Q_{5} } \right)} {\,\left( {Q_{8} \, - \,Q_{5} } \right)}}} \right. \kern-\nulldelimiterspace} {\,\left( {Q_{8} \, - \,Q_{5} } \right)}}} \right)\,x\,100\%$$
    (18)
    $$C_{2000 - 2015} \,\,\left( \% \right)\,\,\, = \,\,\left( {{{\left( {Q_{6} \, - \,Q_{5} } \right)} \mathord{\left/ {\vphantom {{\left( {Q_{6} \, - \,Q_{5} } \right)} {\,\left( {Q_{8} \, - \,Q_{5} } \right)}}} \right. \kern-\nulldelimiterspace} {\,\left( {Q_{8} \, - \,Q_{5} } \right)}}} \right)\,\,x\,100\% \,$$
    (19)
  3. (iii)

    Calculating the contribution rate over the study period based on the 1989 reference period

    $$L_{1989 - 2015} \,\,\left( \% \right)\,\, = \,\,\left( {{{\left( {Q_{11} \, - \,Q_{9} } \right)} \mathord{\left/ {\vphantom {{\left( {Q_{11} \, - \,Q_{9} } \right)} {\,\left( {Q_{12} \, - \,Q_{9} } \right)}}} \right. \kern-\nulldelimiterspace} {\,\left( {Q_{12} \, - \,Q_{9} } \right)}}} \right)\,x\,100\%$$
    (20)
    $$C_{1989 - 2015} \,\,\left( \% \right)\,\,\, = \,\,\left( {{{\left( {Q_{10} \, - \,Q_{9} } \right)} \mathord{\left/ {\vphantom {{\left( {Q_{10} \, - \,Q_{9} } \right)} {\,\left( {Q_{12} \, - \,Q_{9} } \right)}}} \right. \kern-\nulldelimiterspace} {\,\left( {Q_{12} \, - \,Q_{9} } \right)}}} \right)\,\,x\,100\% \,$$
    (21)

3 Results

3.1 The land use and cover mapping and change analysis

Five LU-LC classes (water body, shrubland, plantation, cultivation and grassland) were produced using Landsat images for the years 1989, 2000, and 2015. To assess the accuracy of the classification, 170 observations were used, covering 20, 30, 30, 50, and 40 points of the lake, shrubland, plantation, cultivation, and grassland respectively. The ground truth data were collected with reference to the previous topographic map (scale 1: 50,000), regional LU-LC maps and Google Earth. Most importantly, the good knowledge of the researchers in the study area ensured that historical data were easily obtained for each year 1989, 2000 and 2015. The error matrix was used to determine the overall and kappa accuracies (Tables 2, 3, 4). It has been identified that out of the 170 points collected, 157 in 1989, 160 in 2000 and 163 in 2015 were classified correctly showing an overall accuracy of 92%, 93% and 96%; and a Kappa coefficient of 0.90, 0.93, and 0.95 respectively for the 3 years. This indicates a high degree of agreement between the classified LU-LC and the ground truth data. Accordingly, the LU-LC maps produced were correct and adequate for further analysis.

Table 2 Classification accuracy (1989)
Full size table
Table 3 Classification accuracy (2000)
Full size table
Table 4 Classification accuracy (2015)
Full size table

The spatial coverage and change patterns of the LU-LC types are shown in Tables 5 and 6 and Fig. 3. During 1989–2000, there was a reduction in shrublands from 13,318.7 to 4210.4 × 103 m2 (68.39%), plantation from 21,266.9 to 11,875.1 × 103 m2 (44.16%), grassland from 14,092.0 to 9503.5 × 103 m2 (32.56%), and lake water from 21,859.8 to 21,619.2 × 103 m2 (1.10%). Conversely, cultivation land increased from 15,389.5 to 38,718.6 × 103 m2 (151.59%). Between 2000 and 2015, cultivation land decreased by 5.5%, plantation by 20.91% and lake water by 0.24%. However, shrubland and grasslands increased to 59.8% and 22.6% respectively over 15 years, from 2000 to 2015. Over the 1989–2015 period, shrublands decreased by 49.48%, plantation by 55.84%, grassland by 17.32% and lake water by 1.34%. In contrast, the cultivation land was increased by 137.74%.

Table 5 Spatial coverage of land use and cover classes of Hayk Lake basin
Full size table
Table 6 Change pattern in land use and cover classes of Hayk Lake basin
Full size table
Fig. 3
figure 3

LU-LC map of Hayk Lake basin for years (a) 1989 (b) 2000 (c) 2015

Full size image

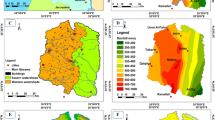
3.2 Soil data of Hayk Lake basin

Soil texture classes of the lake basin are shown in Fig. 4. They were grouped into HSG B and HSG D according to infiltration rate criteria (Fig. 5). HSG B soils have moderate runoff potential, while HSG D soils have high runoff potential due to low infiltration rates. The textural classes of loam, silty loam, and sandy loam are predominantly found in the northeastern and southeastern parts of the basin. These soils were grouped under GHG B, which represents 9.57% coverage. Most parts of the lake basin are dominated by HSG D (90.43%) which are attributes of clay, clayey loam and heavy clay soils.

Fig. 4
figure 4

Soil texture classes in Hayk Lake basin

Full size image
Fig. 5
figure 5

HSG classes of Hayk Lake basin

Full size image

3.3 Model parameters of Hayk Lake basin

HEC-GeoHMS was employed to generate the model parameters (CN for AMC II, lag time, and initial abstraction) of each of the 17 subbasins pre delineated in batch in the Hayk Lake basin using hydro DEM (filled DEM), merged features of LU-LC and soil data, and CNLookUp table input datasets (Table 7).

Table 7 Model parameters of Hayk Lake basin (1989, 2000, and 2015)
Full size table

The weighted CN (AMC II), the lag time, and the initial abstraction values representing the entire lake basin were the initial input model parameters for HEC-HMS modeling (Table 8).

Table 8 The initial model parameters of Hayk Lake basin
Full size table

3.4 HEC-HMS modeling

3.4.1 Sensitivity analysis

The runoff model output for the Hayk Lake basin was less sensitive to the initial abstraction loss parameter during all simulation periods (Table 9). On the contrary, SCS CN and lag time, in their order of listing, have a very significant impact on runoff volume and peak discharge in the Hayk Lake basin.

Table 9 Parameter sensitivity analysis and parameter sensitivity ranking
Full size table

3.4.2 Calibration and validation of model parameters

The results of the calibration and validation of the model parameters (SCS CN, initial abstraction, and lag time) for the years 1989, 2000, and 2015 are shown in Table 10 and Figs. 6 and 7. Calibration and validation results confirmed the adequacy of the HEC-HMS model for rainfall-runoff simulation in the Hayk Lake basin. This result agrees with the findings of [19,20,21] that ensured the applicability of the HEC-HMS model at various spatiotemporal scales in Ethiopia for various purposes such as water availability assessment and flow forecasting.

Table 10 Model performance measurements during runoff simulation
Full size table
Fig. 6
figure 6

Calibration of HEC-HMS model (01 Jan to 31 Aug) (a) 1989 (b) 2000 (c) 2015

Full size image
Fig. 7
figure 7

Validation of HEC-HMS model (01 Sep to 31 Dec) (a) 1989 (b) 2000 (c) 2015

Full size image

3.4.3 Evaluating the level of impact of land use and cover change on surface runoff

To determine the combined and isolated contributions of the LU-LC and climate change on runoff, along with LU-LC data, it is important to analyze trends of climate change indicators briefly to find out if the climate change signal is revealed within the study area. At the same time, the monotonic trend direction and magnitude of change of the observed surface runoff for the same period was analyzed. Therefore, trend analysis of the mean annual precipitation, temperature and observed surface runoff time series at the local level in the Hayk Lake basin during the study period 1989–2015 was performed by the nonparametric methods of Mann–Kendall and Sen to test the trend and the magnitude of the trend respectively. A Mann–Kendall test for trend and Sen's slope estimates (MAKESENS) Excel model was used for the analysis. The details of these theories are presented in [39].

The result of the statistical calculation of trends is presented in Table 11. The Z test statistic values for each parameter indicated a statistically significant downward trend in precipitation and surface runoff at the 0.1 level of significance and a statistically significant upward trend in temperature at the 0.05 level of significance. The precipitation and surface runoff decreased at a rate of approximately 69 mm and 54 mm per decade. On the contrary, the mean temperature has warmed at a rate of 0.28 °C per decade. Similar findings were reported by the Federal Democratic Republic of Ethiopia [40] in its Climate Resilient Green Economy National Adaptation Plan document.

Table 11 Trend statistics of mean precipitation and temperature in Hayk Lake basin
Full size table

Then, the individual rates of impacts of LU-LC and climate change on the generation of surface runoff in the Hayk Lake basin for the period 1989–2015 were calculated based on Table 12 using Eqs. (16–21) and the analysis result is shown in Table 13. As shown in Table 13, during the period 1989–2000, there was an increase in the total surface runoff of 0.54 m resulted from the combined effects of LU-LC and climate changes. The isolated contribution of each of the LU-LC or climate changes indicated only 1.6% of the increase (8.6 × 10–3 m) was due to human effects (change in LU-LC), whereas 98.4% of the increase (0.53 m) was caused by climate change. Between 2000 and 2015, simulated surface runoff was decreased by 0.57 m. The 0.23% decrease was attributable to the LU-LC change, while 99.77% of the decrease in surface runoff was attributable to climate change. Over the three decades (1989–2015), there was an average decrease in simulated surface runoff of 3.63 × 10–2 m. The LU-LC change increased it by 7.33 × 10–3 m, representing 20.18% of the total surface runoff change. In contrast, climate change decreased surface runoff to 4.37 × 10–2 m, or 120.18% of the total change.

Table 12 Simulated annual surface runoff in different scenarios
Full size table
Table 13 Impact proportions on surface runoff (1989–2015)
Full size table

4 Discussion

The combined and isolated impacts of LU-LC and climate change on surface runoff between 1989 and 2015 were quantified after the detection and simulation of LU-LC change and climate trend analyzes were carried out. The trend analysis of the two key indicators of climate change (precipitation and temperature) demonstrated that the climate in the Hayk Lake basin has warmed and become slightly drier over the time frame studied. This meant that the change in runoff in the lake basin was directly linked to changes in LU-LC and climate change. Therefore, the combined and isolated impacts of LU-LC and climate change on surface runoff for the periods 1989–2000, 2000–2015 and 1989–2015 were quantified through scenario simulations using the HEC-HMS model.

During the period 1989–2000, the major LU-LC changes were a change in cultivation land that changed positively (151.59%), while other LU-LC types changed negatively with the highest negative change in shrubland (68.39%). These changes increased surface runoff by 8.6 × 10–3 m, representing 1.6% of the overall surface runoff change (0.54 m). Between 2000 and 2015, the major LU-LC changes were an increase in shrubland (59.8%) and grasslands (22.6%) with the expense of a decrease in cultivation (5.5%), plantation (20.91%), and lake water (0.24%). This LU-LC change reduced surface runoff by 1.33 × 10–3 m, representing 0.23% of the total surface runoff change (0.57 m) from 2000 to 2015. Over the study period (1989–2015), the cultivation land use was expanded by 137.74% with the expense of a decrease in other LU-LC types. This change increased the surface runoff by7.33 × 10–3 m, representing 20.18% of the total surface runoff change (3.63 × 10–3 m). Conversely, climate change alone reduced it by 120.18%.

The change in the magnitude of surface runoff depends upon the characteristics of the LU-LC to affect infiltration and evapotranspiration processes. LU-LC increases surface runoff by decreasing infiltration and evapotranspiration [7,8,9]. The expansion of cultivation disturbs the soil structure and reduces surface roughness, eventually increasing surface runoff by decreasing infiltration and evapotranspiration processes. Decrease in plantation decreases the canopy cover causing reduced interception, loss of permeability (due to exposure of soil particles to raindrop impacts), and decreased surface roughness that reduces interception, infiltration, and evapotranspiration to increase surface runoff.

The possible reason for the expansion of cultivation land at the cost of reduction on plantation, shrubland, and grasslands may be the increasing population growth and its associated increase in demand for new cultivation land and settlement in the lake basin. Similarly, [3,4,5,6] indicated the increment of cultivation land at the expense of other LU-LC types is the common trend of LU-LC changes in Ethiopia to satisfy the demand for more agricultural lands and settlements of the growing population in the country.

5 Conclusion

The study analyzed the LU-LC change pattern and its impact on the magnitude of surface runoff generated in the endorheic Hayk Lake basin for the period 1989–2015. It has also identified warmed and slightly drier climate change signals dominating the Hayk Lake basin to affect the runoff in the lake basin. The LU-LC change alone was found to increase surface runoff by 20.18% and climate change decreased it by 120.18%. The increase in the magnitude of surface runoff was related to the conversion of shrubland, plantation, and grasslands to cultivation land, whereas the decreased surface runoff amount was related to the decreased precipitation. The combined impact of LU-LC and climate change has caused Hayk Lake's water level to continue to fall. Therefore, this hydrological disturbance of Hayk Lake requires immediate and appropriate water management of Hayk Lake to ensure that the water resource of Hayk Lake in the endorheic Lake basin is sustainable.