1 Introduction

Liquefaction in soil due to an earthquake is one of the important phenomena and causes severe damages to structures and lifelines. During an earthquake, the pore water pressure increases in loose saturated granular soils (and clayey soils in special conditions), and then, the soil tends to reduce its volume to confine the stress. Finally, shear strength in the soil is about equal to zero, and liquefaction happens in this state. This phenomenon occurs in conditions such as extended ground settlements, sand boiling, and water seepage on the ground. Several factors, such as earthquake magnitude and duration, void ratio, relative density, fines content, and plasticity index can affect the occurrence of liquefaction [42]. Liquefaction resistance of soils can be evaluated using laboratory tests, such as cyclic simple shear test, cyclic triaxial tests, and cyclic torsional test or field tests (e.g., standard penetration test, SPT) [24], cone penetration test (CPT) [39], and shear wave velocity (Vs) [1, 2]. Artificial neural networks (ANNs) or synthetic neural networks or, simply, neural networks, are new computational systems and methods for machine learning, knowledge demonstration, and ultimately applied knowledge acquisition to maximize the outputs of complex systems. The idea behind these networks is partly inspired by the way the biological nervous system works to process information for learning and creating knowledge. A key element of this idea is to create new structures in the information processing system. It consists of a large number of highly interconnected processing elements, called neurons, which work together to solve a problem and transmit information through synapses (electromagnetic communications). If one cell is damaged in these networks, the rest of the cells can compensate for their absence and contribute to its regeneration. These networks are capable of learning. By burning the touch nerve cells, for example, the cells learn not to move toward the hot object, and with this algorithm, the system learns to correct its error. The learning process is adaptive in these systems. For example, it can happen via using the weight of the synapses that is altered to produce a correct response when new inputs are generated. The main aim of this paper is to utilize some intelligent techniques in overcoming the mentioned issues in dealing with liquefaction. This paper proposes a novel prediction approach based on an ANN to adequately predict the liquefaction potential for a specific range of soil properties. Since ANN is a fairly respected tool for response prediction, utilizing this intelligent method is a challenging act that is addressed in this paper. For this purpose, a whole set of 100 soil data is collected to calculate the liquefaction potential using empirical approaches in Tabriz, Iran. Then, the results of the empirical approaches are utilized for data training in an ANN, which is considered as an option to predict the liquefaction. The archived configuration of the ANN is utilized for predicting the liquefaction of 10 other data sets for validation purposes. It should be noted that the liquefaction prediction in Tabriz city is conducted for the first time in this study, and therefore, the results of this paper should be utilized for future applications in different fields. Many studies have been conducted to develop empirical prediction approaches for the liquefaction phenomenon.

A majority of these studies have been conducted in the most important areas of the world [7, 15, 19, 24, 30, 36, 37, 45]. Recently, the utilization of neural networks has increased for liquefaction prediction due to the development of computer systems. Some of the previous studies are briefly indicated here. Xue and Liu [49] proposed two optimization techniques, namely genetic algorithm (GA) and particle swarm optimization (PSO), to improve the efficiency of a backpropagation (BP) neural network model in predicting the liquefaction susceptibility of soils. The study concluded that the proposed PSO–BP model improves the classification accuracy and is a feasible way to predict soil liquefaction. Xue et al. [50] presented the hybrid probabilistic neural network (PNN) and particle swarm optimization (PSO) techniques to predict soil liquefaction. The PSO algorithm is employed in selecting the optimal smoothing parameter of the PNN to improve the forecasting accuracy. The study concluded that the proposed PSO–PNN model could be used as a reliable approach for predicting soil liquefaction. Zhang and Goh [51] assessed the liquefaction of soils based on the capacity energy concept and backpropagation neural networks. They presented the model accuracy, model interpretability, and procedures to perform a parameter with relative importance for the prediction process. Asvar et al. [3] discussed blast-induced liquefaction for estimating the residual pore pressure ratio through a multilayer perceptron neural network, in which an error (RMS) of 0.105 was calculated for the network. Next, the neuro-fuzzy network, ANFIS, was used for modeling. Different ANFIS models were created using grid partitioning (GP), subtractive clustering (SCM), and fuzzy C-means clustering (FCM). The results revealed that the SPT was the most effective factor in determining the blast-induced liquefaction. Kurnaz and Kaya [31] presented a novel ensemble group method of a data handling model, called EGMDH, based on a classification for predicting the liquefaction potential of soils. The database used in this study consisted of 212 CPT-based field records from eight major earthquakes. The results indicated that the proposed EGMDH model achieved more successful results in predicting the liquefaction potential of soils than the other classifier models via improving the performance prediction of the GMDH model.

Some other works have been done in recent years. Hwang et al. [23] evaluated the soil liquefaction potential regarding an update of the HBF method focusing on research and practice in Taiwan. Njock et al. [35] presented the evaluation of soil liquefaction using the AI technology incorporating a coupled ENN/t-SNE model. Das et al. [16] proposed multi-objective feature selection (MOFS) algorithms for the prediction of liquefaction susceptibility of soil based on in situ test methods. Mele and Flora [32] predicted the liquefaction resistance of unsaturated sands and achieved outstanding results. Shahri and Moud [44] analyzed the liquefaction potential using a hybrid multi-objective intelligence model. The novelty of this paper can be considered from two specific perspectives. The first is that the liquefaction has not been considered in Tabriz city as the case study of this paper, and the second is the application of ANN in the liquefaction prediction. Since the empirical equations are not sufficient for parameter determination of physical phenomena, it is necessary to utilize artificial intelligence. Therefore, this paper aims to use these actions in predicting one of the most difficult physical problems on the earth.

2 General conditions and geology in the study area

The city of Tabriz is one of the largest cities in Iran in the Azerbaijan region, with a population of more than 2,500,000 people. This city is surrounded by the Eynali mountain range in the east–west and not-so-high consolidated alluvial deposits and conglomerates in the south. The general slope of the plain is toward the west, and as a result, the direction of the general drainage of the surface and underground water is also westward. The surface of the plain is generally covered by alluvial deposits. The average height of the city of Tabriz is 1340 m above sea level (Fig. 1). With respect to stratigraphy, Azerbaijan has a long period of expansion, and there are also extensive Cambrian outcrops in the surroundings of the Tabriz plain. However, the stones and the alluvium in the area of Tabriz do not date back to such a time period, with their formation components being related to the Cenozoic and Quaternary periods. The Cainozoic component in the Tabriz plain started from the Miocene Age and lasted up to the Quaternary era (Table 1). The alluvial of the fourth period including, soft to hard conglomerates, is located on this sediment [30].

Fig. 1
figure 1

The scope of the study area

Full size image
Table 1 Geological sequences and formations of Tabriz city [20]
Full size table

Also, the city of Tabriz is located in the west of the Alborz zone and follows the governing tectonic regimes. The formation of the Tabriz plain sediment in it and the formation of tectonic structures, which often emerge as fractures or faults, follow this system. The Tabriz plain is surrounded by the mountains of Eynali in the north and by the volcanic altitudes of Sahand and its pyroclastic sediments in the south. The reverse function of the North Tabriz Fault with the slope to the north caused the collapse of its southern part. As a result, the southern plains were created parallel to the northern part fractures with normal displacement, resulting in a gardenlike collapse of the east–west continuation. The current formation on which Tabriz is located is the result of such a collapse. As a result of this collapse, the rest of the Miocene and pyroclastic sediment of the east and the south of the city are observable in lower height balances. Furthermore, the erosive function due to the entrance of the big rivers caused the deposit of alluvial material with high thickness in the plain. Particle reduction is expected due to the headwaters of the river from the south and the east of the Tabriz plain and its elongation in an east–west state by moving toward the west. The area is tectonically active according to the fault system activity and the earthquakes that occurred in the region and observation of fractures in younger sediments. Iran is located in the Alpine–Himalayan belt as one of the world’s most important seismic belts. Azerbaijan province is also located in this belt and experienced destructive earthquakes in the past. There are many large and small faults in the region that may cause destructive tremors [20]. The level of the groundwater can be considered as one of the main factors in the assessment of the liquefaction potential of the soils. The results of the study showed that there were not many changes in the groundwater level after being static, and a higher level of the groundwater was observed in spring. The balance of the groundwater decreased from the east to the west, showing that the water flow was from the east to the west, corresponding to the slope of the Tabriz plain. Groundwater depth variations in the city of Tabriz are shown in Fig. 2.

Fig. 2
figure 2

Variations of the water table in depth below the ground level in the study area

Full size image

Once more, the peak ground acceleration (PGA) of the study area should be assessed to analyze the boreholes and identify the liquefaction potential of soil layers. The length of the Tabriz north fault from Bostan abad to Sofian cities is at least 90 km, but it seems to continue toward the southeast and the northwest (Fig. 2). Therefore, the PGA in the study area and soil layers were assessed according to the stochastic finite-fault modeling to analyze the site response.

2.1 Stochastic finite-fault modeling

Motazedian and Atkinson [34] proposed a method to simulate earthquake seismogram using the stochastic finite-fault method relying on dynamic corner frequency. In their method, more accurate results are obtained because high frequencies are generated using the Boore random method, and at the same time, it has the ability to generate short frequencies using the analytical method and simulate their combination. In this method, the fault is divided into smaller parts (N), called sub-faults, and each part is assumed as a point-source. The rupture starts from a given point (seismic focus), and when it reaches any part, that part releases its energy. The main earthquake related to all faults is obtained by adding small events from each sub-fault at the site and based on their time delay. The explanation of this process is shown in Fig. 3.

Fig. 3
figure 3

Finite-fault model for dividing the fault plane into N sub-faults [34]

Full size image

EXSIM is an open-source stochastic finite-source simulation algorithm, which is written in FORTRAN and generates the time series of the ground motion for the earthquakes. In the finite-fault modeling of the ground motion, a large fault is categorized into N sub-faults where each sub-fault is considered as a small point-source. The ground motion contributed to each sub-fault can be calculated by the stochastic point-source method and then summed at the observation point with a proper time delay in order to obtain the ground motion from the entire fault. The time series from the sub-sources are modeled using the point-source stochastic model developed by Boore [9, 10] and popularized by the Stochastic-Method Simulation computer code [10, 11]. Furthermore, the ground motion from each sub-source is treated as the random Gaussian noise of a specified duration by having an underlying spectrum as given by the point-source model [13] for shear radiation. This basic idea was implemented in many studies (e.g., [4, 8, 12, 25,26,27, 34, 41]). Motazedian and Atkinson [34] introduced the new variety of this method based on the dynamic corner frequency. Their implementation had a significant advantage over previous algorithms such that it made the simulation results relatively insensitive to the sub-source size and thus eliminated the need for the multiple triggering of the sub-events [6]. Boore [12] further improved the algorithm with modifications to the sub-event normalization procedures that eliminated the remaining dependency on sub-source size and improved the treatment of low-frequency amplitudes. In this model, the corner frequency is a function of time, and the rupture history controls the frequency content of the simulated time series of each sub-fault. Moreover, the rupture begins with a high corner frequency and progresses to lower corner frequencies as the ruptured area grows. Additionally, limiting the number of active sub-faults in the calculation of dynamic corner frequency can control the amplitude of lower frequencies. In the revised EXSIM algorithm, Boore [12] properly normalized and delayed sub-source contributions, which are summed in the time domain as:

$$ A\left( t \right) = \mathop \sum \limits_{{i = 1}}^{N} H_{i} \times Y_{i} \left( {t - \Delta t_{i} - T_{i} } \right) $$
(1)
$$ H_{i} = \frac{{M_{0} }}{{M_{{0_{i} }} }}\sqrt {\frac{{\mathop \sum \nolimits_{j} \left( {\frac{{f_{0}^{2} f_{i} }}{{f_{0}^{2} + f_{j}^{2} }}} \right)^{2} }}{{N\mathop \sum \nolimits_{j} \left( {\frac{{f_{{0_{i} }}^{2} f_{i} }}{{f_{{0_{i} }}^{2} + f_{j}^{2} }}} \right)^{2} }}} $$
(2)

where A(t) is the total seismic signal at the site, which incorporates the delays between the sub-sources. In addition, Hi denotes a normalization factor for ith sub-source that aims to conserve high-frequency amplitudes. Furthermore, Yi (t), N, and Δti indicate the signal of the ith sub-source (the inverse Fourier transform of the sub-source spectrum), the total number of sub-sources, and the delay time of the sub-source, respectively. Additionally, Ti and M0 are a fraction of the rise time and the total seismic moment, respectively. Finally, M0i displays the seismic moment of ith sub-source, which is internally calculated by the EXSIM based on the sub-source size [5, 6]. The final version of the EXSIM, named “EXSIM12” by Atkinson and Assatourain [5], was used in the present research.

2.2 Site response analysis

Various evidence was reported regarding the site effect and nonlinear behavior of the local soil in previous earthquakes. The soil type and thus the dynamic characteristics of the soil profile (e.g., attenuation and shear modulus, moisture content, the number of layers, and their thickness) were all mentioned as factors that affect the nonlinear behavior of the soil [17, 18]. Many researchers investigated the effects of different parameters on seismic magnification. For example, Hashash et al. [21, 22] and Rodriguez-Mark et al. [40] highlighted soil thickness as one of the most significant parameters for the seismic response. Pitilakiz et al. [38] also considered very high effects of different variables on seismic bedrock, including the soil type, soil classification and thickness, the dominant period of the local soil, and the average velocity of shear wave in the alluvial layer. It is noteworthy that the DEEPSOIL software, which is applied for site response analysis, was used for seismic magnification in the current study. DEEPSOIL is a unified one-dimensional program that is utilized for the dynamic analysis of the site response in linear, equivalent-linear, and nonlinear approaches. Moreover, this software provides the user with the required outputs by accelerograms and applying site conditions. The linear approach was utilized in this research as well. In this method, a conversion function with dynamic and force properties was determined based on one of the dynamic properties of the bedrock. This approach, which is based on the principle of force summation, is a very simple method based on complex number calculation. The bedrock motion, which is considered as accelerograms, can be converted to the Fourier series that can be further changed into the Fourier series of the ground motion of the used conversion function. Thus, the conversion function easily determines the resonance or damping of the bedrock motion when it arrives at the surface. After selecting the appropriate parameters for modeling in the study area, the simulation was conducted on the seismic bedrock surface based on the mentioned parameters. Figure 4 depicts the points of the simulation of strong ground motion. The PGA is estimated from the answer summing to obtain the results of the accelerogram and plot them based on acceleration and distance. Figure 5 shows a map of the chirp lines for the simulated maximum horizontal acceleration.

Fig. 4
figure 4

The points of artificially produced accelerograms

Full size image
Fig. 5
figure 5

The simulated horizontal maximum acceleration map in the study area

Full size image

As depicted above, the peak horizontal acceleration produced by the northern fault of Tabriz reaches 0.80 g in the northern part of the city while the peak acceleration in the southern part decreases to 0.40 g. Furthermore, the massive losses and destructions are estimated in Tabriz because of the direct rupture hazard in the city, the fault in the urban area on Tabriz, and the effects of near-field fault in due time of the earthquake. There is a high potential for a landslide because of the marl-clay deposits in settlements such as Baghmisheh, Roshdieh, Eram, and Valiamr, at the northern part of Tabriz and near-field fault. Given that Tabriz Airport is located in the near-field fault, earthquakes can cause serious destructions, which could lead to the disruption of assistance at the time of a possible earthquake. After obtaining the seismic zonation of the target area, downhole data from different points of the urban area of Tabriz were gathered to assess the effect of soil stratification on the earthquake specification in terms of peak acceleration and frequency content. As shown in Fig. 6, data from all points of the target area are used to have good distribution. The DEEPSOIL software was used to determine the peak ground acceleration at the surface and to imply the amplification of the soil stratification effect. Accordingly, by having the seism frequency in different points of the area, the gathered geotechnical characteristics (e.g., the soil layer thickness, specific gravity, the shear wave velocity of the soil layer, and attenuation in different layers) were utilized as the input variables for the software. Finally, the magnitude and effect of seismic frequency traveling from soil layers were determined in different samples. After collecting and presenting the results within the target area, seismic zonation after reflection of the effect on the ground surface using the Arc map software is depicted in Fig. 7.

Fig. 6
figure 6

Distribution of collected data for seismic amplification

Full size image
Fig. 7
figure 7

The seismic zonation of Tabriz surface after amplification

Full size image

2.3 Liquefaction potential in the study area

Liquefaction occurs when vibrations or water pressure within the soil mass causes the particles to lose contact with each other. As a result, the soil behaves like a liquid fluid, is unable to withstand weight, and can flow on very gentle slopes. These conditions are usually temporary and often occur as a result of earthquakes in saturated bays of water or non-consolidated soils. Some of the important liquefaction effects were discovered in terms of the effects of the Kobe earthquakes in Japan (1995), Chi-Chi in Taiwan (1999), Bhoj in India (2001), and Fukushima in Japan (2011), which indicate these contents. Many structures that lie on the bed of saturated and loose soils are vulnerable to liquefaction. Soil liquefaction is one of the most complex phenomena to evaluate in geotechnical earthquake engineering. Many methods have been studied and evaluated over the years to evaluate the potential of liquefaction, the most common of which can be categorized into three sections, as schematically displayed in Fig. 8:

  • Experimental or laboratory methods (intermittent stress, intermittent strain, and energy methods)

  • Numerical methods (neural network, etc.)

Fig. 8
figure 8

The most common evaluation methods of liquefaction

Full size image

The intermittent stress method is the most common technique for evaluating liquefaction, which was presented by Seed and Idriss [42]. This method is mainly experimental and is based on laboratory and field observations. Seed et al. [43] proposed a method for estimating the liquefaction potential of grain soils based on standard penetration test (SPT) data. The scientist also presented an experimental version of Seed et al.’s [43] method to evaluate the liquefaction potential of silty sand and sandy soils by refining their previous method based on (N1)60, the SPT blow count normalized to an overburden pressure of approximately 100 kPa (1 ton/sq ft) and a hammer energy ratio or hammer efficiency of 60%, which affects the parameters of drilling rods, and ambient pressure provided another relationship. Cetin et al. [14] presented a new correlation based on SPT data to evaluate the possibility of soil liquefaction. These correlations eliminated several sources of deviation from the past and resulted in a significant reduction in uncertainty and overall dispersion. In this method, therefore, the overall uncertainty is further reduced compared to the one in previous methods. Sonmez [47] also provided additional factor-based (F.S) constraints for SPT and CPT data-based research. Sonmez and Gokceoglu [48] investigated and modified the structure of the liquefaction potential index (LPI) equation that was first classified by Iwasaki et al. [28, 29]. Since then, the liquefaction potential index has been studied by many researchers in different regions. Idriss and Boulanger [24] provided a comprehensive stress-based method to estimate the liquefaction potential via publishing a set of their research results. In this method, the value of cyclic stress ratio (CSR) is first estimated to express the rate of the severity of the earthquake load in an MW = 7.5, which is evaluated using Eq. (3):

$$ {\text{CSR}} = 0.65 \times \frac{{a_{{\max }} }}{g} \times \frac{{\sigma _{V} }}{{\sigma _{V}^{'} }} \times r_{d} $$
(3)

where amax is the peak ground acceleration, g is the acceleration of gravity, σv is total stress in the depth in the question, σ΄v is effective stress in the same depth, and rd is the shear stress reduction factor that accounts for the dynamic response of the soil profile, which is estimated using Eqs. 4, 5, and 6 based on two parameters of depth (Z) and earthquake magnitude (MW).

$$ r_{d} = \exp \left[ {\alpha \left( Z \right) + \beta \left( Z \right)*M} \right] $$
(4)
$$ \alpha \left( Z \right) = - 1.012 - 1.126*\sin \left( {\frac{Z}{{11.73}} + 5.133} \right) $$
(5)
$$ \beta \left( Z \right) = 0.106 - 0.118*\sin \left( {\frac{Z}{{11.28}} + 5.142} \right) $$
(6)

Second, a simplified and modified method proposed by Seed et al. [43] is used to determine the cyclic resistance ratio (CRR) of the soils. In this step, the results obtained from the standard penetration test are modified based on Eq. (7) proposed by Skempton [46] from Eq. (7). The values of parameters can be observed in Table 2.

$$ \left( {N_{1} } \right)_{{60}} = N_{{{\text{SPT}}}} \cdot C_{N} \cdot C_{E} \cdot C_{B} \cdot C_{R} \cdot C_{S} $$
(7)

where NSPT is the number of standard penetration resistance test, CN, CE, CS, CB, and CR are the coefficients of the overburden stress, the hammer energy, the sampling method, the borehole diameter, and the rod length, respectively, and (N1)60 is the modified number of the SPT. After that, the value of CN is obtained from Eq. 8 as proposed by Idriss and Boulanger [24].

$$ C_{N} = \left( {\frac{{P_{a} }}{{\sigma _{V}^{'} }}} \right)^{m} ~ \le 1.7 $$
(8)
$$ m = 0.784 - 0.0768\sqrt {\left( {N_{1} } \right)_{{60{\text{CS}}}} } $$

where Pa = 100 kPa is the atmospheric pressure, σ΄V is the effective stress at the depth in question, and (N1)60 modified the number of the SPT. An equivalent for the number of the SPT is determined in clean sand ((N1)60CS) after its modification. According to the method of Idriss and Boulanger [24], the CRR is then assessed by the application of the following equations:

$$ \left( {N_{1} } \right)_{{60{\text{CS}}}} = \left( {N_{1} } \right)_{{60}} + \Delta \left( {N_{1} } \right)_{{60}} $$
(9)

where \(\Delta {\left({N}_{1}\right)}_{60}\) is a function of the percentage of fine grains in the soil (FC) as follows:

$$ \Delta \left( {N_{1} } \right)_{{60}} = \exp \left( {1.63 + \frac{{9.7}}{{{\text{FC}} + 0.01}} - \left( {\frac{{15.7}}{{{\text{FC}} + 0.01}}} \right)^{2} } \right) $$
(10)
$$ {\text{CRR}}_{{M = 7.5}} = \exp \left( {\left( {\frac{{\left( {N_{1} } \right)_{{60{\text{CS}}}} }}{{14.1}}} \right) + \left( {\frac{{\left( {N_{1} } \right)_{{60{\text{CS}}}} }}{{126}}} \right)^{2} - \left( {\frac{{\left( {N_{1} } \right)_{{60{\text{CS}}}} }}{{23.6}}} \right)^{3} - \left( {\frac{{\left( {N_{1} } \right)_{{60{\text{CS}}}} }}{{25.4}}} \right)^{4} - 2.8} \right) $$
(11)

where FC is fines content in the soil layer. In the calculation of the CRR, if the amount of effective vertical stress at the depth in question is more than 100 kPa, the CRR value is modified by the following equation:

$$ {\text{CRR}}_{J} = {\text{CRR}}_{{M = 7.5,\sigma _{V}^{'} = 1}} \times {\text{MSF}} \times K_{\sigma } ~~~~ $$
(12)
$$ K_{\sigma } = \left[ {1 - C_{\sigma } \times L_{n} \left( {\frac{{\sigma _{V}^{'} }}{{P_{a} }}} \right)} \right]~~ \le 1.1 $$
(13)
$$ C_{\sigma } = \left[ {\frac{1}{{18.9 - 2.55\sqrt {\left( {N_{1} } \right)_{{60{\text{CS}}}} } }}} \right]~ \le 0.3 $$
(14)

where MSF (magnitude scale factor) is earthquake magnitude scale factor that is calculated based on Andrus and Stoke (1997) using Eq. 15.

$$ {\text{MSF}} = \left[ {6.9\exp \left( {\frac{{ - Mw}}{4}} \right) - 0.058} \right]~~ \le ~~1.8~~ $$
(15)
Table 2 Values of the correction coefficients of Eq. 5 [46]
Full size table

Kσ is the overburden correction factor, σ΄V is the effective vertical stress, and f is an exponent that is a function of site conditions, including relative density, stress history, aging, and the over-consolidation ratio. At last, the safety factor (Fs) against liquefaction in soil layers is calculated using Eq. (16):

$$ F_{{\text{S}}} = \frac{{{\text{CRR}}_{j} }}{{{\text{CSR}}}} $$
(16)

2.4 Liquefaction potential index (LPI)

Researchers presented several methods for the assessment of the rate of liquefaction and the level of occurrence. One of the common methods was proposed by Iwasaki et al. [28, 29] presented in the following equations:

$$ {\text{LPI}} = \mathop \smallint \limits_{0}^{{20}} W\left( Z \right) \times F\left( Z \right).{\text{d}}z $$
(17)
$$ F\left( Z \right) = 1 - F_{{\text{S}}} \quad {\text{For }}F{\text{s }} < {\text{ }}1 $$
(17a)
$$ F\left( Z \right) = 0\quad {\text{For }}F{\text{s }} \ge {\text{ }}1 $$
(17b)
$$ W\left( Z \right) = 10 - 0.5Z\quad {\text{For }}Z{\text{ }} < {\text{ }}20{\text{ }}m $$
(17c)
$$ W\left( Z \right) = 0\quad {\text{For }}Z{\text{ }} > {\text{ }}20{\text{ }}m $$
(17d)

where Z is the depth of midpoint in the layer of interest. The liquefaction intensity is stated between zero and 100. The liquefaction risk can be obtained using Table 3 based on the LPI value.

Table 3 Liquefaction risk analysis based on the liquefaction potential index [28, 29]
Full size table

For example, Fig. 9 shows the location of boreholes and soil layers based on the geological and groundwater data obtained from boreholes of the western part of tunnel route line 2 of the metro in Tabriz city. Geologically, this part of the tunnel comprises sedimentary rocks consisting of marls, claystone, siltstone, and sandstone, which are underlain by surface alluvium with a thickness of 5–15 m. In this part, the water table varies between 6 and 30 m, and the consistency of the alluvium is classified as hard and very hard [33].

Fig. 9
figure 9

Geotechnical section of the western part of tunnel route line 2 of the metro in Tabriz city [33]

Full size image

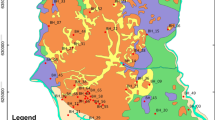
With the evaluation of 260 boreholes in the study area, the zoning map of the liquefaction potential index can be presented based on the method of Iwasaki et al. [29] according to Fig. 10. According to the results, the highest risk of liquefaction is limited to the southeastern regions of Tabriz. Also, a number of points with low liquefaction risk are observed in the soil stratifications in the northeastern regions of Tabriz due to the type of materials and groundwater level.

Fig. 10
figure 10

Zoning map of liquefaction potential Index (LPI) in the study area based on Iwasaki et al. [29]

Full size image

According to Fig. 11a–e, the highest risk of liquefaction is observed in the lower soil stratifications on the I–J axis. Also, according to Fig. 13 diagrams, risk index in the soil stratifications in the eastern part of Tabriz is the lowest. However, according to the liquefaction zoning curve, it can be seen that northeast of Tabriz has a minimum liquefaction risk.

Fig. 11
figure 11

Location of five axes in study area for evaluation of LPI in soil layers. Based on Iwasaki et al. [29] and variation of LPI in soil stratifications, a A–B axes, b C–D axes, c E–F axes, d G–H axes, e I–J axes

Full size image

2.5 Data collection

To estimate the soil liquefaction potential in different parts of the earth, there is a need for a scientific and numerical description of the resistance of different layers of the soil. Usually, laboratory and field methods are the best tools in this case. Although the laboratory results are usually better than the field ones, they usually use field results due to a wide range of factors. One of the methods widely used by researchers is the SPT. This test is one of the oldest and most extensive field geotechnical tests used to estimate the resistance of soil layers, which is considered an effective parameter in many other areas of geotechnics. Despite the disadvantages assigned to this test, the SPT test has three important advantages:

  • The test provides an example of the soil in which the experiment was performed and thus determines the overall classification of the soil. Many penetration tests have a cone tip and do not have this capability. In these cases, soil classification can be derived solely on the basis of the correlation between the results of the experiment or through the results of boreholes and adjacent pits.

  • The SPT is a fast and inexpensive test that is usually performed in a borehole drilled for other purposes, and thus, it does not impose any additional cost on the design.

  • Almost all the test equipment is the same as used for drilling, and the proprietary equipment of this test is limited. However, other tests typically use extensive proprietary equipment.

In this study, the proposed equation by Idriss and Boulanger [24], which is a stress-based method, was used to estimate the liquefaction potential. This method requires the geotechnical description of the subsurface layers, such as the amount of resistance, the groundwater level, the percentage of fines content, the type of soil, and the thickness of the layers. Therefore, to describe the potential of liquefaction at a regional level, valid data were collected from exploratory boreholes. The scope of the study is displayed in Fig. 1. For this purpose, 260 out of 446 boreholes containing complete and descriptive data were selected here. The position of these boreholes with the curves of PGA values is presented in Fig. 12. The calculation of the liquefaction potential in soil layers revealed that there were 63 boreholes with liquefaction risks. The summarized data in Table 4 show that H represents the maximum depth of the soil levels, SPT shows the SPT value, (N1)60CS is the modified penetration number equivalent to clean sand, FC stands for fines content percentage in soil, TC is the depth of the soil layer, A is the ground acceleration of the soil, and W.L represents the maximum water level in meter. The results indicate that there is a likelihood of liquefaction in 100 boreholes in the area. These data are utilized to train an ANN to numerically predict the liquefaction potential.

Fig. 12
figure 12

The positions of the boreholes with curves of PGA values in the study area

Full size image
Table 4 Characteristics of the boreholes
Full size table

3 Artificial neural network

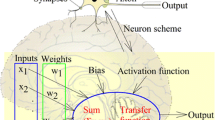
An ANN is an idea for processing information, which is inspired by the biological nervous system and processes information similar to the brain. A key element of this idea is the new structure of the information processing system, consisting of a large number of highly interconnected processing elements called neurons that work together to solve a problem. Similar to humans, ANNs learn by example, and a neural network is set up to perform specific tasks, such as identifying patterns and categorizing information, during a learning process. In biological systems, learning is accompanied by adjustments in the synaptic connections between the nerves. This method is also used in neural networks. ANNs transfer the knowledge or rule behind the data to the network structure by processing experimental data, which is called learning. The ability to learn is essentially the most important feature of an intelligent system. A system capable of learning is more flexible, easier to program, and can be better responsive to new problems and equations. The neural network structure of humans has long been sought to understand the bio-physiology of the brain. In fact, it has always been interesting for humans to be intelligent, capable of generalization, creativity, flexibility, and parallel processing in the brain and use these capabilities in machines very well. Algorithmic methods are not suitable for the implementation of these properties in machines, and thus, the methods must be devised based on the same biological models. In other words, the neural network is a data processing system that originates from the human brain and leaves the data processing to large multiple processors that operate in a networked and parallel way to solve a problem. Using programming knowledge in these networks, a data structure is designed that can act as a neuron called a node. In this structure, the network is trained through creating a network between these nodes and applying a training algorithm inside. In this memory or neural network, the nodes have two active (on) and inactive (off) states, and each edge (synapse or linkage between nodes) has a weight. Positive-weight edges stimulate or activate the next inactive node, and negative-weight edges inactivate or inhibit the next connected node (if active). The general configuration of neurons is depicted in Fig. 13.

Fig. 13
figure 13

The general configuration of neurons

Full size image

3.1 ANN configurations

As it is known from the literature, a usual kind of neural network includes tens, hundreds, thousands, or even millions of artificial neurons in a single group of layers, which are interconnected with the rest of the layers that are famous as input units. The considered units are configured to receive various forms of information from the outside world that the network seeks to be trained, recognize, and do processes. Some of the other parts, called output units, are on the opposite part of the network and identify the network reaction to the information achieved. Among the input and output units, there are secret units that come together from the majority of the artificial brains. These neural networks are completely joined, meaning that each hidden and output unit is attached to layer units on each side. The connection of these units is satisfied by a number called weight. Weights are almost positive (if one unit triggers another unit) or even negative (if one unit suppresses or inhibits another unit). The higher the weight is, the greater the effect of one unit on another would be. This is known to the way in which real brain cells stimulate each other in tiny fissures, called synapses. Various kinds of ANNs have been proposed, each of which has a specific application. One of the most basic available neural models is the multilayer perceptron (MLP) model that simulates the transient function of the human knowledge and brain. Most of the network behavior in these types of neural networks have been taken into account in the human brain and its signal propagation and hence are sometimes referred to as feedforward networks. Every neuron in the human brain processes the input after receiving it (from one neuronal or non-neuronal cell) and sends the result to another (neuronal or non-neuronal) cell. This kind of behavior continues until reaching a definite result, which may eventually lead to a decision, process, thought, or move. The general configuration of an MLP is depicted in Fig. 14. As with the MLP neural network paradigm, there is another kind of neural network in which processor units are process-focused in a particular location. This focus is modeled through radial basis functions (RBFs). Regarding the overall structure, RBF neural networks are not much different from MLP networks and are merely the type of processing that neurons perform on their inputs. Meanwhile, RBF networks often have a faster learning and preparation process. Since the neurons focus on a specific functional range, they are easier to adjust. The general configuration of an RBF is depicted in Fig. 15. In MLP and RBF neural networks, the focus is often on enhancing the neural network structure, which can minimize the estimation error and error rate of the neural network. In a particular type of neural network, called a support vector machine (SVM), however, the focus is solely on reducing the operational risk associated with malfunction. The structure of an SVM network has many similarities to the MLP neural network, and the main difference lies in the way of learning. The general configuration of an SVM is depicted in Fig. 16. The self-organizing map (SOM) is a specific type of neural network that is quite similar to those studied in terms of functionality, structure, and application. The basic idea of self-organizing mapping is inspired by the functional division of the cerebral cortex, and its main application is to solve a problem known as “unmanaged learning.” In fact, the main function of a SOM is to find similarities and clusters among a vast array of data at its disposal. This is similar to what the human brain does and has classified (or better to say clustered) a bunch of sensory and motor inputs to the brain. The general configuration of a SOM is depicted in Fig. 17.

Fig. 14
figure 14

The general configuration of an MLP

Full size image
Fig. 15
figure 15

The general configuration of an RBF

Full size image
Fig. 16
figure 16

The general configuration of a SVM

Full size image
Fig. 17
figure 17

The general configuration of a SOM (schematic view)

Full size image

3.2 ANN for the liquefaction prediction

In this paper, an MLP ANN is configured to predict liquefaction. In this regard, four sets of different MLP ANNs with different characteristics are configured to establish a better prediction model for LPI. The specific characteristics of these models are presented in Table 5. An important difference between these ANN models is the number of neurons in the hidden layer, where a total set of 5–20 neurons is utilized for this purpose. The configuration of the ANN1 for predicting liquefaction is presented in Fig. 18.

Table 5 The specific characteristics of different ANN models
Full size table
Fig. 18
figure 18

The configuration of the ANN1 for liquefaction prediction

Full size image

3.3 Results of the ANN analysis

The numerical results of the ANN training process are presented in this section. The liquefaction prediction process is estimated through different ANN models to select an effective ANN model. Based on the presented information in the previous sections in terms of the experimental liquefaction results and the specific characteristics of the ANN models, the training process of the ANNs is conducted based on the use of the Levenberg–Marquardt backpropagation MLP for training the ANNs. In this process, the training, validation, and test ratios are selected as 70%, 15%, and 15% of the total data, respectively. The ANN training results are presented in Table 6. Based on the provided details for the ANN models, the performance and convergence history of the training process for this network are presented in Figs. 19 and 20, respectively, while the error histogram of this network is depicted in Fig. 21.

Table 6 The specific characteristics of ANN models
Full size table
Fig. 19
figure 19

The performance of the ANN models for liquefaction prediction, a Model No.1 (ANN 1), b Model No.2 (ANN 2), c Model No.3 (ANN 3), d Model No.4 (ANN 4)

Full size image
Fig. 20
figure 20

The convergence history of the ANN models for liquefaction prediction, a Model No.1 (ANN 1), b Model No.2 (ANN 2), c Model No.3 (ANN 3), d Model No.4 (ANN 4)

Full size image
Fig. 21
figure 21

The error histogram history of the ANN models for liquefaction prediction, a Model No.1 (ANN 1), b Model No.2 (ANN 2), c Model No.3 (ANN 3), d Model No.4 (ANN 4)

Full size image

Based on the provided details of the training process for the liquefaction in the ANN models, the training regressions are presented in Figs. 22, 23, 24 and 25. The regression for the training, validation, and test phases, as well as the overall regression of the network are presented in these figures. Based on the trained neural network for predicting liquefaction through ANN models, the overall performance of this network is examined via the provided input data to evaluate the exactness of the network. The performance evaluations of the ANN1 based on the predicted and experimental data are presented in Figs. 26, 27, 28, and 29. Based on the results in Table 6 and illustrations, it is evident that ANN4 has a better performance in predicting LPI, which could be considered as the best ANN for practical applications. To evaluate the overall performance of the ANN4 through different training processes, one of the input data is selected to verify the ANN4, for which the BH-3 is utilized with an LPI value of 17. The training process for ANN4 is repeated 10 times, and the LPI in each of them is predicted through the trained networks. As Fig. 30 clearly shows, the ANN4 is capable of predicting LPI values via maximum errors of lower than 10% in most cases.

Fig. 22
figure 22

The training regression of the Model No.1 (ANN 1) for liquefaction prediction

Full size image
Fig. 23
figure 23

The training regression of the Model No.2 (ANN 2) for liquefaction prediction

Full size image
Fig. 24
figure 24

The training regression of Model No.3 (ANN 3) for liquefaction prediction

Full size image
Fig. 25
figure 25

The training regression of Model No.4 (ANN 4) for liquefaction prediction

Full size image
Fig. 26
figure 26

The performance evaluation of the Model No.1 (ANN 1) based on the predicted and experimental data

Full size image
Fig. 27
figure 27

The performance evaluation of Model No.2 (ANN 2) based on the predicted and experimental data

Full size image
Fig. 28
figure 28

The performance evaluation of Model No.3 (ANN 3) based on the predicted and experimental data

Full size image
Fig. 29
figure 29

The performance evaluation of Model No.4 (ANN 3) based on the predicted and experimental data

Full size image
Fig. 30
figure 30

The performance evaluation of the Model No. 4 (ANN 4) with different configurations

Full size image

In the regressions, the inputs are the H as the maximum depth of the soil levels, SPT as the SPT value, (N1)60CS as the modified penetration number equivalent to clean sand, FC as the fines content percentage in soil, TC as the depth of the soil layer, A as the ground acceleration of the soil, and W.L as the maximum water level in meter while the output is the liquefaction of the soil.

In the next step, an additional verification procedure is conducted for the best ANN model of the previous section to demonstrate the overall capability of the trained ANN model in dealing with some unknown borehole data from Tabriz city. It should be noted that these data have not been utilized for the training process of the ANN models in the previous section. The characteristics of these soil data are presented in Table 7. The process is verified using the configuration of the ANN4, which has a better regression (R) value of 0.97073. The results of the ANN4 for each of the additional boreholes (Table 7) are provided in Table 8 accordingly. It should be noted that the ANN4 is capable of predicting the LPI with an acceptable error rate of less than 5 in all of the cases.

Table 7 Characteristics of the additional boreholes
Full size table
Table 8 Results of the ANN4 for the additional boreholes
Full size table

4 Conclusions

Many empirical approaches have been proposed to predict the liquefaction potential, each of which has its own advantages and disadvantages. Soil liquefaction is a phenomenon in which saturated soil completely loses its strength and hardness and behaves like a liquid due to the severe stress it entails. This stress can be caused by earthquakes or sudden changes in soil stress conditions. In this paper, a novel prediction approach based on an ANN is proposed to adequately predict the liquefaction potential of a specific range of soil properties. To this end, a whole set of 100 soil data is collected to calculate the liquefaction potential using empirical approaches in Tabriz city, Iran. Then, the results of the empirical approaches are utilized for data training in an ANN, which is considered as an option for predicting liquefaction. The achieved configuration of the neural network is utilized to predict the liquefaction of 10 other data sets for validation purposes. The obtained results proved that the well-trained ANN is capable of predicting the liquefaction potential by an error value of less than 5%, which represents the reliability of the proposed approach. It should be noted that the present study is the first attempt to comprehensively predict liquefaction in the Tabriz metropolis. Hence, the results of this paper could be utilized for future applications in different fields.

In this research, the finite-fault method by EXSIM 14 program and its reflection from the bedrock to the ground surface by Deepsoil v6.1 software were used by performing seismic calculations to determine the maximum vibrational acceleration (PGA). By processing the data in the GIS environment, a liquefaction zoning map was also conceived for this city. Moreover, a process was presented for predicting liquefaction capability using data training in the ANN and its control. Therefore, since comprehensive studies have not been conducted on the possibility of liquefaction in this area, the innovation of this research is evident. It should also be noted that the results of this research can be utilized as a prediction method before the excavations, which reduces the overall costs of the earth investigations.