1 Introduction

We can enhance the efficiency of heat exchangers in two ways: active and passive techniques [1]. Using Helical tubes is an inactive technique to increase the heat transfer coefficient. Twisting the tube may allow to improve heat transfer rate without increasing the surface area of the heat exchanger. Using helical tubes could cause secondary flows, on the one hand, and turbulent flows, on the other. Also, they can disturb the boundary layers and increase the heat transfer rate.

Nowadays, it is more common to use nanofluid in heat transfer investigation because of their superiority in heat transfer than the base fluids. The conventional cooling fluids thermal property outcomes at significant obstacle in the creation of progressive cooling techniques are frustrating. The nanofluid utilization gently indicates an increasingly remarkable obligation in progressive cooling techniques. Choi [2] defined nanofluids as fluids with suspended nanoparticles. Saidur et al. [3] studied different applications and challenges of nanofluids in thermal engineering. Several studies were carried out to investigate the thermal properties of nanofluids, focused on density, viscosity, thermal conductivity, and specific heat [4, 5].

Moreover, a number of studied were conducted on nanofluid convective heat transfer increment. Pourmahmoud et al. [6] accomplished a numerical investigation on modeling of mixed convection heat transfer in two-dimensional double lid-driven cavity filled with Al2O3-H2O nanofluid. The results indicated that rising the heat transfer is generated by considering the nanoparticle size effects and interfacial-layer thickness. Ghafouri et al. [7] conducted another study on the convective heat transfer in a square enclosure using Al2O3-H2O nanofluid as a cooling fluid. The results indicated an expected increase in heat transfer rate regarding nanoparticle size and bulk temperature. Faridi et al. [8] studied the effects of heat transfer and characteristics of flow in pipes fitted with dimpled helical centers using Al2O3, TiO2, and CuO-H2O nanofluid as cooling fluids. where, the importance of turbulent and secondary flows were considered.

Rogger and Mayhew [9] investigated heat transfer and pressure drop in helical coils. They offered relations for Nusselt number, friction factor, coil pitch and Pr for turbulent flow. Kalb and Seader [10] conducted an experimental test to explore the heat transfer coefficient for viscous flows in curved circular tubes. Jones et al. [39] applied different coil diameters to examine how efficiency and turbulence can be improved without a mixer. By considering Jones et al.’s geometry, Archarya et al. [11] studied the effects of geometry on coil heat transfer and offered two relations for Nusselt number in terms of coil pitch, Re and Pr.

No comprehensive numerical study was conducted until 1995 due to the lack of cheap and fast processors. Yang et al. [12] simulated the coils and studied the effects of Pr and coil pitch. The constant heat flux and constant temperature were applied as boundary conditions. Heris et al. [13] studied the convective heat transfer of Al2O3 and CuO water nanofluids in a simple circular pipe. They indicated a decline in the heat transfer coefficient and Péclet number by increasing the nanofluid friction factor. Akbarnia et al. [14] carried out a numerical study on the convective heat transfer of the nanofluid in horizontal curved tubes and reported that the friction factor has no direct effect on friction. Jayakumar et al. [15] conducted both experimental and CFD simulations of heat transfer rate in helical coil heat exchangers to obtain the Nusselt number and convective heat transfer of internal walls. Hashemi et al. [16] studied the pressure drop and heat transfer rate of CuO-base oil nanofluid in a horizontal helical-coil tube with constant heat flux. They indicated that heat transfer is affected more by using a coiled tube rather than nanofluids. Jamshidi et al. [17] investigated the effects of coil diameter and pitch on heat transfer of nanofluid flow in helical coils. Akbaridoust et al. [18] performed both experimental and numerical investigations on heat transfer in helical-coil tubes. They indicated a reduction in heat transfer rate and pressure drop by increasing the coil pitch ratio (with Re in the range of 0–1000).

In another investigation, the different functional covalent groups effect on the thermophysical properties of carbon nanotube-base fluid was experimentally studied. The improvement of nanofluid heat transfer characteristic is depend on enhancement of fraction of nanomaterial, Peclet number or Reynolds number. Although, nanomaterial fraction or Reynolds number increment for a specific material increase the pumping power. However, this penalty is small. Power consumption and heat transfer rate for water were less than nanofluids in all cases [19]. The experimental results of specific heat capacity, viscosity and thermal conductivity of Nitrogen doped graphene nanofluids in a double pipe heat exchanger were investigated by Goodarzi et al. [20]. Convective heat transfer coefficient has an enhacement of 15.86% in comparison with water by adopting 0.06 wt.% nanoparticle in the base fluid. The heat transfer coefficient was increased 16.2% by average. By adopting a horizontal rib-microchannel, Akbari et al. [21], investigated the Al2O3 nanofluids laminar forced convection heat transfer. They considered volume fraction of 0 to 4% and Re = 10 &100. Outcomes showed that the convective heat transfer in a microchannel can be improved by using turbulators or ribs. Although, a bigger friction factor can caused by using high ribs in compare than the ribs with constant height. The results indicate that average Nusselt number, friction coefficient and heat transfer rate raised up by the ribs heights enhancement.

Bahmani et al. [22] investigated the Al2O3-water nsnofluid turbulent flow and heat transfer by adopting the double pipes as heat exchanger. They showed that the convection heat transfer coefficient and Nusselt number will be rise up by Reynolds number or nanoparticles volume fraction enhancement. Also, the wall and the fluid outlet temperature was increased because of nanoparticles volume fraction enhancement. Onyiriuka et al. [23] by using a circular tube studied the nanofluids internal forced convective flow heat transfer coefficients. It was indicated that the deviation of discrete phase model from single-phase homogeneous model was 2%, where, the local heat transfer coefficients was closely predicted by variable properties of discrete phase model, for turbulent flow regime. Tian et al. [24] numerically investigated heat transfer and fluid flow in a heat exchanger with spiral double pipe. They studied the effect of nanoparticle volume fraction, type of nanoparticle and fluid temperature on heat transfer coefficient. The results indicated that SiO2-water and Al2O3-water are the best selection for adopting Reynolds range (10,551 to 17,220 and 17,220 to 31,910, respectively). Sarafraz et al. [25] accomplished an experimental investigation for a heat exchanger equipped fitted with rectangular micro passages by using liquid metal mixture. Temperature and pressure drop profile measured. It was indicated that the plausible thermal response happened at temperatures > 200 °C for Ga-In-Sn eutectic.

Bahmani et al. [26] by using a double tube heat exchanger investigated the forced convection by adopting the nanofluids. The hot fluid which flows in the inner tube was Al2O3-water nanofluid and distilled water was the cold fluid. Re = 100–1500 was adopted for nanofluid and the volume fraction equal to 2.5–10%, while Re = 500 for distilled water. It was identified that the Reynolds number and nanoparticles volume fraction increment can raised the heat transfer rate, where the average Nusselt number is better with variable characteristics and constant thermophysical characteristics is better for thermal efficiency. Jiang et al.[27] experimentally investigated the thermal conductivity of Al2O3-water nanofluid in different volume fraction and temperatures. It was found that enhancement of nanofluid thermal conductivity has a direct relation to nanoparticles concentration and temperature increasing. Also, by developing the fuzzy lookup table method a new prediction approach to estimate the mixture thermal conductivity.

Sarafraz et al. [28] experimentally investigated graphene nano-platelets, with water-ethylene glycol as base fluid, convective heat transfer. The coolant fluid was used in a micro channel, where the system pressure drop values and heat transfer coefficient was studied. The outcomes indicated that the working fluid thermal conductivity can improved with using graphene nano-platelets by 32.1%. Also, the coefficient of heat transfer increased by enhancement of heat flux, which indicated the superiority of using nano suspension in high heat flux thermal applications. In another investigation by using a double pipe heat exchanger the heat transfer characteristics of nanofluids were considered. The nanoparticle diameter considered by 100 nm. Also, it was indicated that the average heat transfer coefficient trend with some specific amount Reynolds numbers [29]. Li et al. [30] using a micro-channel heat sink to experimentally investigated the convective heat transfer of carbon-acetone nanofluid. The friction factor, thermo-hydraulic performance, pressure drop value and coefficient of heat transfer were studied. It was indicated that the heat transfer coefficient value can be increase by 73% with using carbon-acetone nanofluid as coolant. It was found that the micro-scale phenomena such as thermophoresis and Brownian motion lead to the heat transfer promotion.

Adio et al. [31] considered entropy generation and thermo-hydraulic effects in a microchannel heat sink with rib turbulators, where the Al2O3‐water nanofluid used as a coolant. It was also found, to improve the system functioning, the rib edges can help to reduce the pressure drop. Sheikh et al. [32] numerically investigated nine types of buffel heat exchangers. The distances between the baffles, thickness, angle and their heights were considered. The best results happened by highest generated power, when the angle and thickness of the baffles at the inlet of the heat exchanger were adopted.

Recently researchers have been fascinated to study heat transfer following modifications in cooling techniques. These studies have been mainly focused on modifying the flow structure by changing heat transfer area, raising heat transfer surfaces, generating turbulent mixing. They have even considered making thinner boundary layers and enhance the heat transfer efficiency of the working fluid by modifying thermophysical properties, such as discovering better thermal conductivities [29,30,31].

The mentioned literature review demonstrates that using different coil structures can considerably change the heat transfer rate in the helical tube heat exchangers. However, the effects of nanoparticles volume fraction on laminar and turbulent heat transfer inside the helical tubes are not studied. In the present study, the effect of geometric parameters on thermal performance enhancement and pressure drop in helical tube heat exchanger filled with Alumina–water nanofluid flows are investigated by solving governing equations of continuity, momentum, energy and turbulent kinetic energy using the CFD method. For this purpose, coil geometric properties, volume fraction, thermal conductivity, and the diameter of nanoparticles were considered. By separating the geometry investigation from thermo-physical properties investigation this manuscript represented into two main parts. In the first part the results of investigating the nanoparticle diameter (5, 15 and 35 nm) and volume fraction in the range of 1–4% are discussed. In addition, in the next part by considering different parameters like coils diameter (400 and 200 mm), tube diameter (12.7 and 25.4 mm) and coils pitch (54 and 108) the effects of curvature ratio and coils pitch on thermal performance and pressure drop are also discussed by using numerical simulations.

2 Model description and numerical method

2.1 Model description

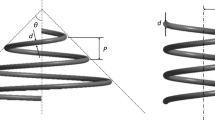
For modeling the coils, several major parameters were used, including coil diameter, tube diameter, and coil pitch. The number of coil rings was ineffective due to using non-dimensional parameters like Nusselt number and friction coefficient. Thus, in the same coil pitch, coil diameter and tube diameter (which detailed in the Table 1), two rings coils were adopted to save time in calculations (Table 2).

Table 1 Geometrical dimensions of adopted coils (2 rings and 5 rings coils)
Full size table
Table 2 Comparing the difference of Pressure drop and local nusselt between two rings and five rings coils
Full size table

In this study, four different helical coils were made to operate as cooling passages. To organize the results, there were divided into two groups: (1) determining nanofluid properties and (2) determining the effects of geometry. Table 3 demonstrate coil diameter (D), coil pitch (H), tube diameter (d) and \(\frac{d}{D}\), as well as details of all cases in this research. The case in which φ = 0% indicates that water has been used as the base fluid.

Table 3 Dimension details of sixteen investigated cases
Full size table

The Reynolds number is used depending on inlet velocity and the hydraulic diameter, ranging from 2000 to 40,000. The inlet velocity was calculated using the Reynolds number at tube inlet. Furthermore, the atmospheric pressure was determined by the pressure outlet boundary condition. As a frequently-adopted heat flux thermal boundary condition [33], a constant heat flux, i.e., 3 × 104 W.m−2 with the nonslip condition was used on the walls.

2.2 Numerical method

The present study has used steady incompressible flows without weighing the effect of gravity. The flow is considered both laminar and turbulant. The sst k − ω model used for turbulent modeling. Nanofluid properties are loaded in the software both as UDF function and polynomial function. The properties of pure water are loaded in the software as polynomial functions. Modeling is solved in steady state and based on pressure. The three-dimensional steady Navier–Stokes equations were determined using the finite volume method (FVM, based on the computational fluid dynamics (CFD) commercial software ANSYS Fluent 19.2). Continuity, momentom, and energy equations were adopted to evaluate the convergence of calculations, and the scale of convergence was defined to be 1 × 10−6. Moreover, the velocity, the wall temperature, and the temperature of the specified point were taken to study the convergence. The flow in the developed state was analyzed and an entrance length was added to the beginning of the geometry to ensure that the flow was developed. A schematic view of the studied geometry is given in Fig. 1. Also, graphical steps of solution is presented in Fig. 2.

Fig. 1
figure 1

schematic view of the studied geometry

Full size image
Fig. 2
figure 2

Method of Numerical Section Flow chart

Full size image

The momentum, energy, and mass conservation equations are given below:

$$\frac{{\partial \rho U_{i} }}{{\partial X_{i} }} = 0$$
(1)
$$\frac{{\partial \rho U_{i} U_{j} }}{{\partial X_{i} }} = \rho g_{i} + F_{i} - \frac{{\partial P}}{{\partial X_{i} }} + \frac{\partial }{{\partial X_{i} }}\left( {2\mu S_{{ij}} } \right)$$
(2)
$$\frac{{\partial \rho U_{i} E_{0} }}{{\partial X_{i} }} = \rho \mu _{i} F_{i} - \frac{{\partial q_{i} }}{{\partial X_{i} }} + \frac{\partial }{{\partial X_{i} }}\left( {U_{i} T_{{ij}} } \right)$$
(3)

2.3 Thermal properties of nanofluids

In this research, Al2O3-water nanofluids were chosen to function as the cooling fluid. Different nanofluid volume fractions φ (1 to 4%) were adopted to examine the effects of volume fractions of nano particle. Moreover, a varied range of nanoparticle diameters dp (5 nm, 15 nm, 35 nm) were adopted due to dp effects. The single-phase model was considered due to heat transfer and nanofluid flow. Several recently-published studies have shown that the single-phase model is extraordinarily beneficial and is in the spotlight. Accordingly, it has been selected in this study, along with no-slip condition as another condition. The following section will describe the thermophysical properties. The nanofluid density and specific heat capacity equations [34, 35] can be determined as follows:

$$\rho _{{nf}} = \left( {1 - \varphi } \right)\rho _{f} + \varphi \rho _{p}$$
(4)
$$\left( {\rho C_{p} } \right)_{{nf}} = \left( {1 - \varphi } \right)\left( {\rho C_{p} } \right)_{f} + \varphi \left( {\rho C_{p} } \right)_{p}$$
(5)

The nanofluid volume fraction is determined by φ. ρ represents density and C represenrs the specific heat capacity. The p, f, and nf subscripts indicate nanoparticle, base fluid, and nanofluid used in this paper, respectively. The dynamic viscosity of the nanofluid [36] is shown below:

$$\mu _{{nf}} = \mu _{w} \left( {1 + \frac{\emptyset }{{100}}} \right)^{{11.3}} \left( {1 + \frac{{T_{{nf}} }}{{70}}} \right)^{{ - 0.038}} \left( {1 + \frac{{d_{p} }}{{170}}} \right)^{{ - 0.061}}$$
(6)

µ is the dynamic viscosity. Concerning the effective thermal conductivity, the correlation by Azmi et al. [36] has been used in this study to define the thermal conductivity of nanofluids after testing different related equations to compare the experimental data with other models. The diameter of nanoparticles dp, thermal diffusivity \(\alpha\), volume fraction φ, temperature T, and Brownian motion were appropriated into observation. The engaged, effective thermal conductivity can be determined by:

$$k_{{nf}} = k_{{water}} 0.8938\left( {1 + \frac{\emptyset }{{100}}} \right)^{{1.37}} \left( {1 + \frac{{T_{{nf}} }}{{70}}} \right)^{{0.2777}} \left( {1 + \frac{{d_{p} }}{{150}}} \right)^{{ - 0.0336}} \left( {\frac{{\alpha _{p} }}{{\alpha _{{water}} }}} \right)^{{0.01737}}$$
(7)

Also, the temperature-dependent thermal conductivity kwater and the dynamic viscosity of the base fluid µwater [36], employed in this research, can be determined by:

$$k_{{water}} = 0.56112 + 0.00193 \times T_{{water}} - 2.60152749e - 6 \times \left( {T_{{water}} } \right)^{2} - 6.08803e - 8 \times \left( {T_{{water}} } \right)^{3}$$
(8)
$$\mu _{{water}} = 0.00169 - 4.25263e - 5 \times T_{{water}} + 4.9255e - 7 \times \left( {T_{{water}} } \right)^{2} - 2.09935e - 9 \times \left( {T_{{water}} } \right)^{3}$$
(9)

2.4 Non-dimensional parameters definition

The Reynolds number is introduced as follows:

$$Re = \frac{{\rho U_{{in}} D_{h} }}{\mu }$$
(10)

In the inlet section, Uin shows the average velocity; ρ and µ are the density of the cooling fluid and the dynamic viscosity, respectively. Dh is the hydraulic diameter (tube diameter) can be determined by:

$$D_{h} = D$$
(11)

The heat transfer efficiency (convective heat transfer coefficient) can be determined by Eq. (12). Also, q stands for heat flux.

$$h = \frac{q}{{\Delta T}}$$
(12)

∆T is the average temperature difference, defined as follows:

$$\Delta T = T_{w} - T_{f}$$
(13)

Tw indicates the average wall temperature, and Tf is the temperature of fluid bulk. The average Nusselt number, which was used in the validation method and grid independence evaluation is defined by Eq. (14), where k is determined the thermal conductivity of cooling fluid.

$$Nu = \frac{{hD_{h} }}{k}$$
(14)

Also, Fanning friction factor f is utilized to investigate the resistance characteristics, where the ∆P is the pressure drop between the inlet and outlet by the x-direction.

$$f = - \frac{{2\left( {\frac{{\Delta P}}{L}} \right)D_{h} }}{{\rho U_{{in}}^{2} }}$$
(15)

PEC as the general heat transfer performance evaluation criteria determined in this research to investigate the heat transfer changes and the friction coefficient is also determined by

$$PEC = \frac{{Nu/Nu_{0} }}{{\left( {f/f_{0} } \right)^{{\frac{1}{3}}} }}$$
(16)

2.5 Validation method

Selecting the turbulence model is the major parameter to affect the results. Therefore, choosing fine and standard turbulence is very important for numerical investigations. One of the standard turbulence models is SST k-ω, in which it has a particular preference for flow characteristic and heat transfer prediction in helical tubes.

Due to Tang et al. [37] research, the SST-Kω is the best model for helical tubes than the other weighed models with correlations. To assure from the precision of the computations, by utilizing the SST k-ω as a turbulence model, the validation method is achieved. Ito experimental correlation [38] for f and the Guo et al. empirical correlation [33] for Nu are utilized to investigate the procedure by applying a simple tube. Figure 3(a, b) indicate that the present Nu values has good agreement by Guo et al. with a avarage error of 16.4%, and values of f following the diagram from Ito [38] with a average error of 15.2%. The coil with 2 rings, which the Coil diameter is 200 mm, the tube diameter is 25.4 mm and the coils pitch is 54 is considered for the validation model.

Fig. 3
figure 3

Method validation results. a the Nusselt number versus Reynolds number for comparison between present work and Guo et al. [33]. b the Friction factor versus Reynolds number for comparison between present work and Ito [38]

Full size image

In turbulent flow because of calculations accuracy enhancement and wall functions, all tetrahedral and hexahedral mesh is made very fine. For turbulent flow, a perfect way to evaluate the manner of the flow near the walls is using y + . The generated mesh was build and calculate to consider the perfect range of y + , where the value of y + is less than 1, and it is in the adequate range due to the turbulent model. Figure 4 shows the differences for Nu in comparison with the Mesh No.4 and the Mesh No.3, which is less than 1% (Table 4). So, the mesh No.3 is acceptable to offer the exact numerical outcomes.

Fig. 4
figure 4

Grid independence study at Re = 40,000, a Nusselt number versus Grid number. b y + versus Grid number

Full size image
Table 4 Grid independence study
Full size table

For grid study to make sure we have a reliable model for turbulent flow we rise up the velocity above the studied value. The adopted Reynolds for this case is Re = 40,000.

3 Results and discussions

3.1 First group; nanofluid investigation

3.1.1 Pressure and temperature contours

It is found that the flow structures are entirely the same at a different range of Re. Thus, Re = 10,000 took as a case, to determine the distributions of wall temperature and drop pressure on limit contours in Fig. 5, to have an evaluation image of the flow structure, the helical tube, and the tube wall. Because of considering the atmosphere outlet pressure as a boundary condition, the outlet pressure became zero in Fig. 5.

Fig. 5
figure 5

Pressure [pa] distribution contour

Full size image

Figure 6 indicates that despite having constant heat flux 30,000, the wall has a lower temperature because of secondary flows and more vortexes. The flow has a higher speed in this area, and as a result, there is no time for convection.

Fig. 6
figure 6

Wall temperature [k] distribution contour

Full size image

3.1.2 Nanofluid effects on heat transfer

In Fig. 7(a), the different volume fraction of cooling fluids compares with each other. As it indicated, rinsing the Reynolds number in every case, make the Nu rise up. Also, by volume fraction enhancement, the Nu amount rises again. Figure 7(b) shows the effect of different volume fractions against the Nu. It indicates that by volume fraction enhancement at a specific Reynolds, the Nu rises. For example, the Nu of base fluid where Re = 40,000 is 345, this amount for φ = 1 and φ = 4 is 376 and 480, respectively. It means that the ratio of the changes of Nu for φ = 4 versus base fluid is 1.39.

Fig. 7
figure 7

Nanofluid effects on Nusselt number. a The Nusselt number versus Reynolds for comparison between the base fluid and different Friction factors (φ). b The Nusselt number versus Volume Fraction for comparison between the all adopted Reynolds. c The Nusselt number versus nanoparticle diameter for comparison between the base fluid and different Friction factors (φ)

Full size image

Figure 7(c) indicates that the Nu number declines by increment of nanoparticles diameter. By reduction of nanoparticle diameter, the mixture of base fluid and nanoparticles is an approach to the best level, so the Nu rises. Also, in the same diameter, by increasing the volume fraction, the Nu increases too.

3.1.3 Nanofluid effects on friction factor

The numerical results of the friction factor calculation for different volume fractions shown in Fig. 8. By rising the Re, friction factor declines. This reduction for lower Reynolds is more considerable than the higher amounts of Re. By increasing the Reynolds number, the flow rate and the flow velocity increase as well. According to Eq. (15), the reduction of friction factor by increasing the Re is predictable. Also, in the same Re by rising the volume fraction, the friction factor increases too, and this issue happens because of nanoparticles amounts enhancement on base fluid, which could cause a pressure drop and raise the friction factor as a result.

Fig. 8
figure 8

Friction factor versus Reynolds number by different volume fractions of cooling fluid

Full size image

Figure 9(a) shows the friction factor against the volume fraction for different Reynolds. The friction factor rises due to the volume fraction enhancement. Also, the gradients of lower Reynolds lines are higher than the higher Reynolds. Figure 9(b) also indicates that the friction factor decline by nanoparticle diameter enhancement. Furthermore, for the same diameter, the friction factor of higher volume fractions is greater than lower volume fractions. This situation could cause by raising the nanoparticle amount in the base fluid, so the enhancement of the friction factor is predictable.

Fig. 9
figure 9

Friction Analysis. a the Volume Fraction versus f for comparison between the all adopted Reynolds. b the dp versus f for comparison between the base fluid and different amounts of φ

Full size image

3.1.4 Nanofluid effects on PEC

As discussed, the result of using helical tubes with nanofluid is heat transfer enhancement and pressure drop enhancement. The pressure drop enhancement is not desirable and could cause many problems by using them in industrial equipment. So, for investigating the best performance and considering the heat transfer enhancement besides the pressure drop, PEC as the performance evaluation criteria is determined, Eq. (16).

Figure 10 (a) indicates that the PEC goes up first, and when it reaches the Re = 4000 falls for other higher Reynolds. This change of trend is mainly due to change of flow regime from laminar to turbulent. Also, Fig. 10(b) shows the superiority of the same Re as the previous one. It indicates that the PEC rise by volume fraction enhancement.

Fig. 10
figure 10

PEC Analysis. a Reynolds number versus PEC for comparison between the base fluid and different amounts of φ. b Volume Fraction versus PEC for comparison between the adopted Reynolds. c dp versus PEC for comparison between the different amounts of φ. d T (k) versus PEC for comparison between the different amounts of φ

Full size image

As determined from Fig. 10(c), due to dp enhancement, the PEC goes down as well. The last part of Fig. 10 goes to describing the inlet temperature effect on PEC. Figure 10(d) shows that the increment of inlet temperature makes the PEC rise, and its best evaluation happens on Tin = 315 k.

3.2 Second group; geometry investigation

The significant parameters to helical tubes designing are coil pitch and curvature ratio. For this investigation, four different helical tubes were designed with different geometrical properties, which are demonstrated in Table 5.

Table 5 Geometry description for different curvature ratio and coils pitch
Full size table

3.2.1 Coils pitch effects on heat transfer and friction factor

Coil No.1 and No.2 have the same tube diameter and coil diameter. These two coils are considering in this part, due to their coils pitch difference.

Figure 11(a) indicates that increasing in Coils pitch causes an improvement on friction factor. Also, friction reduction is much more sensitive for lower Reynolds, although it goes down gradually in higher Reynolds. This reduction could cause by changing the flow from laminar to turbulent. Coil no 1, which has less Coils pitch, has more friction factor than the other one. The results have excellent matching with Ito’s results.

Fig. 11
figure 11

Coils pitch investigation. a indicates the Reynolds number versus f comparison between the Coil No.1 and No.2 with Ito [38]. b indicates the Reynolds number versus Nusselt number comparison between the Coil No.1 and No.2 with Guo et al. [33]

Full size image

In Fig. 11(b), where the Nu compared against the different Re for coil numbers 1 and 2, it indicates that the heat transfer rate in helical tubes has a direct relation with Coils pitch. Coil No.1 has better performance in most of the Reynolds than the other coil. This superiority had happened because of the eccentricity of the flow in helical tubes, which could cause strong secondary flows and raise the heat transfer coefficient.

3.2.2 Curvature ratio effects on heat transfer and friction factor

In this section, the curvature ratio effect on heat transfer and friction factor discuss. Coils No.3 and No. 4 are considered because of their curvature ratio differences. curvature ratio reduction makes vortex flow where the fiction factor rises. Also, this forces speed up the velocity of flow and make the development length shorter. Although the velocity and pressure of the flow near exterior surfaces are higher than the velocity and pressure of the interior surfaces because of the eccentricity.

Coil No. 3 has a higher curvature ratio than the other one, so its pressure drop is lower. So, the friction factor in coil No. 4 is higher than No.3 Fig. 12(a). Also, higher curvature ratio makes turbulent flow and helps secondary flows to rise, so the heat transfer coefficient increase too Fig. 12(b).

Fig. 12
figure 12

Coils pitch investigation. a Reynolds number versus f for comparison between the Coil No.3 and No.4 with Ito [38]. b Reynolds number versus Nusselt number for comparison between the Coil No.3 and No.4 with Guo et al. [33]

Full size image

4 Conclusion

This research numerically investigates the geometrical effects of helical tubes and nanofluid flow on heat transfer and friction factor. Helical tubes, due to their less space than direct pipes and their excellent efficiency on heat transfer and pressure drop, have essential rules in industries. Al2O3-water nanofluids are used to investigate the nanofluid effects on heat transfer and flow characteristics. Some proper and trustworthy results are indicated in follow.

In all cases, φ increment makes the Nu and drop the pressure to rise because of nanofluids higher heat transfer coefficient than the base fluid, where the Nu of nanofluid 4% was near 440, with 45% increase in Nu than the base fluid in the same Re. The reduction of nanoparticle diameter causes an enhancement of heat transfer and friction factor and the best results happen in dp = 5 nm and φ = 4%,where the it was ~ 40.64% more efficient than base fluid.This amount for φ = 3%, φ = 2% and φ = 1% is 31.80%, 18.02% and 8.83%, respectively. Reynolds increment makes heat transfer increases too, and as the result of flow velocity enhancement and the secondary flows increase. Rising the inlet temperature makes an enhancement on heat transfer, where the best PEC of investigated temperatures happen in 315 K in all cases.

Geometrical properties affect the heat transfer and friction factor too. Increasing the coil pitch and curvature ratio, due to eccentricity reinforcement and secondary flows, enhance heat transfer and friction factor even though the effect of curvature ration is more than coil pitch.

Also, in PEC investigation, it could be mention that the significant amount of PEC happens when Re = 4000, and that because of transferring the fluid manner from laminar to turbulent. The best PEC occurs with a temperature of 315 k in this research.

Due to the widespread use of spiral pipes in the industry, the analysis of other aspects of the research could be useful in improving the use of these converters. The following can be proposed as suggestions for continuing the work:

  • Using other sections of helical tubes such as oval, square, triangular

  • Use of deviated helical tubes and compare it with ordinary helical tubes.

  • Using a spiral tube with a rough inner surface and comparing it with a normal tube and investigating the effect of roughness.

  • Use of various forms of nanofluids such as spherical, tubular and so on.

  • Modeling of two-phase flow (solid nanoparticles suspended in a base fluid).