1 Introduction

The formation of photoinduced gratings was first demonstrated by Hill et al. [1, 2] and these gratings written were referred to as Hill gratings. A decade later, the side-writing interferometric technique [3] has drawn the interest of several researchers and led to the development of different grating structures using suitable fabrication techniques ([4] and references therein). The term fiber Bragg grating (FBG) was adopted from the concept of Bragg’s condition applied to the periodical structures inscribed inside the core of the optical fiber. FBGs have plenty of applications in various fields, the prominent being in communications (wavelength division multiplexing (WDM), dispersion compensation, filters, wavelength converters, etc.) and sensing (strain, temperature, displacement, vibration, humidity, etc.) [5, 6].

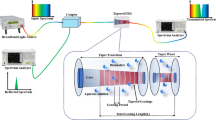
FBG consists of a periodic modulation of refractive index along a definite length of the core of a single-mode optical fiber (shown in Fig. 1), which is typically created using internal and external writing techniques [4]. If an optical signal is launched from one end of the fiber, a small portion of it is reflected by each grating plane (by Fresnel effect) and the remaining is transmitted without any loss. The reflected light signals combine coherently to one significant reflection (at Bragg’s condition) at a particular wavelength termed as Bragg wavelength. A typical layout of a uniform FBG with input and output signal is shown in Fig. 1. The Bragg wavelength is represented as

$$\lambda_{B} = 2n_{{{\text{eff}}}} \Lambda$$
(1)

where Λ is the grating period and \(n_{{{\text{eff}}}}\) is the effective refractive index of the fiber core. Equation 1 signifies that any change in \(n_{{{\text{eff}}}}\) and Λ results in the shift of reflected Bragg wavelength.

Fig. 1
figure 1

Refractive index profile and spectral response of an FBG

Full size image

Further, many grating structures can be visualized [7] by varying the refractive index or grating period along the fiber axis as needed for desired applications. In the case of a uniform FBG, the grating period and the index modulation are constant over the length and the grating planes are normal to the fiber axis. When light is propagated through a uniform FBG, total reflection occurs at Bragg wavelength and few sidelobes exist in the reflection spectrum, which is undesirable. Hence, the apodized FBGs (gradual reduction in the amplitude of the refractive index to zero towards the end of the grating) [8], which help to suppress sidelobes’ intensity while still maintaining reflectivity (of the main or primary peak) and narrow bandwidth, are often preferred. However, the challenge lies in properly identifying the optimal grating parameters like period, length, index modulation, and apodization function to obtain an ideal spectral response for some specific applications.

As known, maximum reflectivity, minimum bandwidth and minimum or no sidelobes are essential for some practical applications in communication and sensing. However, the use of expensive and delicate manufacturing systems has to be avoided until one has a clear estimate of the optimized design parameters to achieve the aforesaid spectral characteristics. In the context, before actually inscribing the grating in the fiber it is always reasonable to know the optimal parameters by studying the spectral characteristics. For this, simulation studies can be employed comfortably, which allow the user to vary FBG parameters and thereby provide a rapid and accurate outcome for optimizing the design parameters. Due to the tremendous potential of FBGs, the present work is focused on the design and optimization of grating parameters for uniform and apodized (Gaussian, hyperbolic tangent, apod1, sine, and raised sine) FBGs. Although some stand-alone reports are available on uniform [9,10,11,12,13] and apodized FBGs [14,15,16,17,18,19], but they are focused on one or two profiles (mostly Gaussian) or at only few specific grating lengths or index modulation values. Hence it is felt pertinent to undertake a comprehensive study to understand as to which apodized profile is ideal for sensing applications and what are the optimal grating parameters. The present article improves upon the earlier work by addressing the above-mentioned issues. To this end, the simulation studies of spectral characteristics viz., reflectivity, bandwidth (FWHM), and intensity of first sidelobe of uniform and apodized FBGs were undertaken by varying the grating lengths (1 to 10 mm) and index modulation (0.0002 to 0.0020) over a wide range and thereafter optimal design parameters are identified. The results are discussed in the following sections.

2 Theory and model of FBG profiles

2.1 Coupled mode theory

The coupled-mode theory (CMT) is a mathematical tool to obtain quantitative information about the spectral dependence of fiber gratings ([5, 6, 8] and references therein). It is the most widely accepted and employed method to accurately model and understand the optical properties of gratings. In CMT, a linear combination of the modes (of unperturbed or uncoupled structures) is used as a testing solution to Maxwell’s equations for complicated perturbed or coupled structures. The derived coupled-mode equations are then solved analytically or numerically. In the case of an FBG, the periodic variation of the effective refractive index is given as:

$$\delta n_{{{\text{eff}}}} (z) = \vec{\delta }n_{{{\text{eff}}}} (z)\left\{ {1 + \nu \cos \left[ {\frac{2\pi }{{ \wedge_{0} }}z + \phi (z)} \right]} \right\}$$
(2)

where \(\vec{\delta }n_{{{\text{eff}}}} (z)\) is the dc index change spatially averaged over a grating period, ν is the fringe visibility of the index change, ΛO is the grating pitch, and ϕ(z) denotes the grating chirp. It is assumed that the single-mode optical fiber (for Bragg reflection grating) is weakly guiding and no energy is coupled to radiation modes. Hence, a single-mode FBG has the following relations:

$$\vec{\sigma } = \delta + \sigma - \frac{1}{2}\frac{{{\text{d}}\phi }}{{{\text{d}}z}}$$
$$k = \frac{\pi }{\lambda }\nu \vec{\delta }n_{{{\text{eff}}}} (z)$$
$$\sigma = \frac{2\pi }{\lambda }\vec{\delta }n_{{{\text{eff}}}} (z)$$
$$\delta = 2\pi n_{{{\text{eff}}}} \left( {\frac{1}{\lambda } - \frac{1}{{\lambda_{B} }}} \right).$$
(3)

The parameter \(\vec{\sigma }\) is a dc self-coupling coefficient, k is an ac coupling coefficient, σ is a dc (period-averaged) coupling coefficient, and δ is a detuning coefficient. For unchirped FBG, the parameter \(\frac{1}{2}\frac{{{\text{d}}\phi }}{{{\text{d}}z}} = 0\). By specifying the appropriate boundary conditions, the reflectivity can be described as

$$r(\lambda ) = \frac{{k^{2} \sinh^{2} \left( {\gamma_{B} L} \right)}}{{\vec{\sigma }^{2}\sinh^{2} \left( {\gamma_{B} L} \right) + \gamma_{B}^{2} \cosh^{2} \left( {\gamma_{B} L} \right)}}$$
(4)

where \(r(\lambda )\) is the amplitude reflectance and \(\gamma_{B} = \sqrt {k^{2} - \vec{\sigma }^{2} }\) if \(k^{2} > \vec{\sigma }^{2}\) or \(\gamma_{B} = i\sqrt {\vec{\sigma }^{2} - k^{2} }\) if \(k^{2} < \vec{\sigma }^{2}\).

The coupled-mode equations can be solved by applying the transfer matrix method (TMM), where the advantage lies in its flexibility to apply for both uniform and non-uniform gratings [6, 12]. In this method, a grating of length L is divided into N short uniform sections (which decides the accuracy of TMM) where each section is represented by a 2 × 2 matrix. A global matrix representing the FBG results from multiplying all the individual matrices. Using simulation studies, the spectral characteristics of an FBG can be analyzed through coupled-mode equations via TMM for solving matrices.

2.2 Apodization profiles

From Eq. 2, \(\vec{\delta }n_{{{\text{eff}}}} (z)\) can have different apodization profiles defined by

$$\vec{\delta }n_{{{\text{eff}}}} (z) = \vec{\delta }n_{{{\text{eff}}}} f(z)$$
(5)

where f(z) is the apodization profile described as follows:

  1. (i)

    Uniform \(f(z) = 1\)

  2. (ii)

    Gaussian apodization \(f(z) = \exp \left\{ { - 4\log (2)\left[ {\frac{{\left( {z - \frac{L}{2}} \right)}}{s \cdot L}} \right]^{2} } \right\}\)

  3. (iii)

    Hyperbolic Tangent apodization \(f(z) = \tanh \left( {s \cdot \frac{z}{L}} \right) \cdot \tanh \left[ {s \cdot \left( {1 - \frac{z}{L}} \right)} \right] + 1 - \tanh^{2} \left( \frac{s}{2} \right)\)

  4. (iv)

    Apod1 apodization \(f(z) = \tanh \left( {s \cdot \frac{z}{L}} \right) \cdot \left( {\tanh \left( {s \cdot \left( {1 - \frac{z}{L}} \right)} \right)} \right)\)

  5. (v)

    Sine apodization \(f(z) = {\text{Sin}} \left( {\frac{\pi \cdot z}{L}} \right)\)

  6. (vi)

    Raised Sine apodization

    $$f(z) = {\text{Sin}} \left( {\frac{\pi \cdot z}{L}} \right)$$
    (6)

where z is the direction of signal propagation along the length of FBG, L is the grating length, and s is the taper parameter.

2.3 Conditions for simulation

Computer simulation is a vital tool in fiber optic research as it evades the use of expensive manufacturing processes until the design is optimized or improved [7, 18, 20]. The simulation allows adjustments to design parameters like shape, length, apodization, index modulation, etc. for a Bragg grating needed for the analysis. The input parameters considered for the present simulation studies are core diameter-6 µm, cladding diameter-40 µm, central wavelength-1.55 µm, grating period-0.5338 µm, grating length-1 to 10 mm, and grating index modulation-0.0002 to 0.0020, as they are the most suitable values for the FBGs to be considered for practical applications. Further, keeping in view of the possible optimum range for grating length and index modulation, the present values were considered.

3 Results and discussion

3.1 Spectral response as a function of the grating length

The grating length plays a significant role in the spectral response of FBGs; hence the reflectivity, bandwidth, and strength of sidelobes are assessed for the uniform and apodized gratings by varying the grating length from 1 to 10 mm with an interval of 0.5 mm in each case. The index modulation is kept constant at 0.0017. From the data obtained through simulation studies, graphs are plotted between reflectivity and wavelength at each grating length for all the profiles under study. The following are the salient features one can observe from the graphs and table:

  1. i.

    As grating length increases, the reflectivity (of main peak) increases in an exponential manner for all the grating profiles under consideration (Fig. 2). The results obtained for uniform and Gaussian apodized FBGs are in conformity with earlier reports, which were presented only at few grating lengths [8, 13, 16]. The trend of continuous increase in reflectivity with grating length up to 5 mm for almost all the profiles and thereafter reaching and maintaining 100% reflectivity even with increase in grating length leads to saturation [10, 11].

  2. ii.

    Optimal grating length is one of the important requirements for a compact FBG sensor. The reflectivity reaches almost 100% at much lower grating lengths (3.5 mm) for uniform and hyperbolic tangent profiles as compared with the other profiles under study. However, Gaussian and raised sine profiles offer poor reflectivity at very low grating lengths. The order in which reflectivity reaches a maximum at a shorter grating length is as follows:

    $${\text{Uniform}} < {\text{hyperbolic}}\;{\text{tangent}} < {\text{sine}} < {\text{apod}}1 < {\text{Gaussian}} < {\text{raised}}\;{\text{sine}}{.}$$
  3. iii.

    A closer look at Fig. 3 reveals that as grating length increases, bandwidth decreases linearly for all the grating profiles under study [9]. However, for a grating length of 7 mm and beyond (nearly for the same grating length in case of reflectivity), the bandwidth attains saturation i.e. remains constant even with increase in grating length. The saturation in reflectivity is accompanied by decrease in bandwidth and then becoming constant. Further, within these profiles, at a constant grating length, the increasing order of bandwidth is as follows:

    $${\text{sine}} < {\text{apod}}1 < {\text{hyperbolic}}\;{\text{tangent}} < {\text{uniform}} < {\text{raised}}\;{\text{sine}} < {\text{Gaussian}}{.}$$
  4. iv.

    Suppression of sidelobes is one of the main objectives of apodization, which helps to minimize power loss, eliminate crosstalk, and also for wavelength division multiplexing [10, 16]. Hence an apodization with minimum or no sidelobes is always preferred. Figures 4 and 5 depict the typical reflection spectrum of all the grating profiles under study at a grating length of 1 and 2.5 mm, respectively. It is observed that as the grating length increases, the strength of the sidelobes also increases. The uniform and hyperbolic tangent profiles offer multiple sidelobes when compared to other profiles. Further, the strength of the first sidelobe is tabulated in Table 1, which indicates that of the grating profiles under study; uniform and hyperbolic tangent profiles offer maximum sidelobe strength whereas for the others, it is almost negligible. The increasing order of the sidelobe strength is as follows:

    $${\text{Gaussian}} < {\text{sine}} < {\text{raised}}\;{\text{sine}} < {\text{apod}}1 < {\text{hyperbolic}}\;{\text{tangent}} < {\text{uniform}}.$$
  5. v.

    Sine, Gaussian, apod1, and raised sine profiles are the order of preference based on both the lower strength for sidelobes and optimized reflectivity/bandwidth. Further, the ideal grating length for the FBG sensor can be 5 mm based on the comprehensive understanding from the above analysis.

Fig. 2
figure 2

Reflectivity versus grating length for different grating profiles

Full size image
Fig. 3
figure 3

Bandwidth versus grating length for different grating profiles

Full size image
Fig. 4
figure 4

Reflection spectrum at a grating length of 1 mm (uniform, Gaussian, hyperbolic tangent, apod1, sine, and raised sine)

Full size image
Fig. 5
figure 5

Reflection spectrum at a grating length of 2.5 mm (uniform, Gaussian, hyperbolic tangent, apod1, sine, and raised sine)

Full size image
Table 1 First sidelobe strength at different grating lengths for various grating profiles
Full size table

3.2 Spectral response as a function of the index modulation

Index modulation is another important grating parameter that shows an influence on the spectral response of uniform and apodized gratings. To study the influence of this parameter, the index modulation is varied from 0.0002 to 0.0020 with an increment of 0.0002 in each case, keeping the grating length constant at 7 mm. Graphs are plotted between reflectivity and wavelength at each modulation depth for all the profiles based on the simulated results. The following are the observations are made based on the results:

  1. i.

    The reflectivity increases exponentially with an increase in index modulation and the same trend is followed for all the profiles [9, 11], as shown in Fig. 6. It can be observed that the reflectivity reaches a maximum value (100%) at an index modulation of 0.0008 for all the profiles and thereafter, attains a saturation value i.e. no further increase in reflectivity even with increase in index modulation. This trend is identical to the variation with the grating length discussed in the previous section.

  2. ii.

    The reflectivity reaches almost 100% at a lower modulation of 0.0008 for uniform, hyperbolic tangent, and apod1 profiles when compared to the other profiles under study. The same profiles had also shown maximum reflectivity at lower grating lengths. However, sine and raised sine profiles offer poor reflectivity at very low index modulation. The order in which reflectivity reaches a maximum at lower index modulations is as follows:

    $${\text{Uniform}} < {\text{hyperbolic}}\;{\text{tangent}} < {\text{apod}}1 < {\text{Gaussian}} < {\text{raised}}\;{\text{sine}} < {\text{sine}}.$$
  3. iii.

    Figure 7 indicates that as index modulation increases, bandwidth also increases [9] for all the grating profiles. However, for the modulation of 0.0013 and beyond, the bandwidth remains constant based on the standard relation connecting the grating parameters [21]. Further, at a constant modulation, the increasing order of bandwidth is as follows:

    $${\text{Raised}}\;{\text{sine}} < {\text{sine}} < {\text{apod}}1 < {\text{Gaussian}} < {\text{uniform}} < {\text{hyperbolic}}\;{\text{tangent}}.$$
  4. iv.

    Figures 8 and 9 show the typical reflection spectrum for all the grating profiles at a modulation of 0.0002 and 0.0008, respectively. It is observed that as the index modulation increases, the strength of the sidelobes also increases. Even in this case, the uniform and hyperbolic tangent profiles offer multiple sidelobes, which are the most undesirable profiles for communication and sensing applications. The strength of the first sidelobe is listed in Table 2, which shows that uniform, hyperbolic tangent, and apod1 grating profiles offer maximum sidelobe strength whereas, for the others, it is almost negligible. The increasing order of the sidelobe strength is as follows; the order is almost similar to that followed for grating length:

    $${\text{Gaussian}} < {\text{raised}}\;{\text{sine}} < {\text{sine}} < {\text{apod}}1 < {\text{hyperbolic}}\;{\text{tangent}} < {\text{uniform}}.$$
  5. v.

    From the above observations, one can infer that raised sine, Gaussian, sine, and apod1 profiles can be the order of preference based on the lower strength for sidelobes and optimized reflectivity/bandwidth. The ideal modulation depth for an FBG must be 0.0008 to obtain an optimal spectral response.

Fig. 6
figure 6

Reflectivity versus index modulation for different grating profiles

Full size image
Fig. 7
figure 7

Bandwidth versus index modulation for different grating profiles

Full size image
Fig. 8
figure 8

Reflection spectrum at an index modulation of 0.0002 (uniform, Gaussian, hyperbolic tangent, apod1, sine, and raised sine)

Full size image
Fig. 9
figure 9

Reflection spectrum at an index modulation of 0.0008 (uniform, Gaussian, hyperbolic tangent, apod1, sine, and raised sine)

Full size image
Table 2 First sidelobe strength at different index modulations for various grating profiles
Full size table

4 Conclusions

A comprehensive investigation of the spectral characteristics of uniform and apodized (Gaussian, hyperbolic tangent, apod1, sine, and raised sine) FBGs is taken up by varying the grating parameters viz. grating length (1 to 10 mm with an increment of 0.5 mm) and index modulation (0.0002 to 0.0020 with an increment of 0.0002). The significant inferences are as follows:

  1. i.

    The reflectivity of the main peak and the intensity of sidelobes increase with grating length and index modulation.

  2. ii.

    The bandwidth decreases with grating length, whereas it increases with index modulation for all the grating profiles. The grating with a longer length and small index change has the narrow bandwidth, which points to the need for finding optimal grating parameters.

  3. iii.

    The ideal grating length and index modulation are found to be 5 mm and 0.0008 respectively to obtain maximum reflectivity and minimum sidelobes, as desired for an FBG to be used as a sensor.

  4. iv.

    Sine, Gaussian, and raised sine profiles are the best suitable apodization profiles among those considered in the present work.