1 Introduction

Breast cancer is the leading cause of cancer deaths in women. It is originated from breast tissues specifically from the lobules that help in delivering milk through ducts. To detect breast cancer, mammography that spots abnormalities like masses and calcifications [1] is used. Based on the structure of the abnormality, radiologists categorize the mammogram either as malignant or benign. Benign tumors are generally oval or round. On the other hand, malignant tumors are partially round in shape having spiked or irregular boundaries. In general terms, cancerous or malignant tumors refer to the uncontrolled or abnormal growth of breast tissues while breast hematose, cysts, and Fibroadenomas are considered non-cancerous or benign tumors [1].

There are higher chances of developing breast cancer in women with dense breasts. Breast density can be of four types comprising least dense with less than 10% density, 10–24% density, 25 to 49% density, and denser with 50% or higher density [2]. During the screening, each mammogram is scrutinized by two radiologists independently who either concur or approach a third radiologist to arbitrate in a process called double reading [3]. Double reading improves early detection and recall rate but it requires more resources [4]. For a second opinion, computer-aided diagnosis offers succor to radiologists [5].

Although the use of Convolutional Neural Network (CNN) and later deep neural networks become more popular with the development of Alexnet in 2012, the number of works related to applications of deep learning in the field of medical image processing exploded in 2016 [6]. Modified Alexnet was proposed in [7] for classifying breast masses of the DDSM (Digital Database for Screening Mammography) dataset. In [8] CNN is used for three-class classification (normal, malignant, benign) after dividing the images from the mini-MIAS (Mammographic Image Analysis Society) dataset into patches followed by feature-wise data augmentation.

Deep ensemble transfer learning and Neural Network classifier are proposed in [9] for automatic feature extraction followed by classification of mammograms from the DDSM dataset into malignant and benign classes. CNN is employed in [10] to categorize mammograms into malignant and benign mammograms. Before classification, mammograms from the mini-MIAS dataset are preprocessed and augmented to 2576 mammograms (322 × 4 × 2). In this maximum accuracy achieved on Matlab is 84.02% in 45 min while 87.98% accuracy is achieved in 6 h using TensorFlow. In [11], a convolution-based modified adaptive k-means (MAKM) segmentation algorithm is used to extract the tumor from a mammogram of the mini-MIAS database. In [12], a CNN-based pretrained model called VGG-19 is used to extract features from both mini-MIAS and DDSM datasets. These features are classified using k-nearest neighbors (KNN) classifier into normal and abnormal classes with the highest accuracy of 98.75% and 98.90% on mini-MIAS and DDSM datasets respectively.

The mini-MIAS dataset is categorized into normal, benign, and malignant using transfer learning on a pretrained inception v3 network in [13]. A fine-tuned CNN, wavelet transform, and modified AlexNet are used in [14] for classifying mammogram images into heterogeneously dense and scattered density classes. Data enhancement, normalization, and breast density classification are done in [15] using the SE (squeeze and excitation) mechanism with a Convolutional Neural Network. In this context, we note that most of the researchers prefer to work on publicly available mini-MIAS [16] and INbreast datasets [17] that suffer from class imbalance problems.

To reduce the computation and complexity of a computer-aided diagnosis system, a fuzzy Gaussian mixture model-based algorithm is proposed in [18]. It categorizes the DDSM dataset into malignant and benign images. The feature extraction by fast finite shearlet transform, feature selection by t-test, and classification of mammograms from the mini-MIAS database into abnormal and normal and further categorization of abnormal mammograms into malignant and benign are done using SVM (Support vector machine) in [19]. A spatial gray level co-occurrence matrix (SGLCM), Fourier power spectrum (FPS), statistical feature matrix (SFM), Law’s texture energy measures (TEM), fractal features, gray level difference statistics (GLDS), and first-order statistics (FoS) are employed in [20] to classify mammograms into dense and fatty tissues using the KNN classifier on the mini-MIAS database. The computer-aided diagnosis system is proposed in [21] for the categorization of mammograms into fatty, dense, and glandular by removing artifacts, background, and pectoral muscle and applying a decision tree. Non-subsampled contourlet transform and gray level co-occurrence matrix are used in [22] for extracting texture features from the mini-MIAS database. These extracted features are categorized into normal and abnormal mammograms using SVM and KNN classifiers.

A block-based discrete wavelet packet transform (BDWPT) is used in [23] to extract energy, Renyi, Shannon, and Tsallis entropies based features from the datasets of mini- MIAS, DDSM, and Breast Cancer Digital Repository (BCDR) followed by reduction of dimensions using principal component analysis (PCA). These reduced features are then classified into normal and abnormal classes by employing an optimized wrapper-based kernel extreme learning machine (KELM) and a weighted chaotic salp swarm algorithm (WC-SSA).

1.1 Motivation

The above methods are not geared to deal with the representation of certainty associated with tissues in a mammogram to a class so we are motivated to use the possibilistic entropy function. The widely sought-after deep learning networks used for feature extraction and classification of mammograms suffer from the requirement for a large number of annotated datasets, heavy computational time, susceptibility to inter and intraobserver variations, dependence on filter responses from a large training data, and overfitting problem. The fuzzy classifiers favored in case of less number of features are prone to the problem of improper choice of a membership function. Also, the feature selection techniques used by the fuzzy classifiers to reduce the number of features increase the computational complexity. Buoyed by the success of Information set features for the classification of mammograms in our recent work [24], we are motivated to investigate the Intuitionistic fuzzy sets in the backdrop of Information sets for deriving probability-based fuzzy Hanman transform and probability-based pervasive membership function with a view of improving the fuzzy modeling aimed at the improved classification of digital mammograms.

The work proposed in [24] deals with the basic information set features (i.e. sigmoid, energy, and effective information) based on possibilistic entropy function which are fed to the hesitancy-based Hanman transform classifier to performs two-class and three-class classification of mammograms from the mini-MIAS dataset. Whereas the work presented in this manuscript gives the formulation of the five higher-level information set features involving probability-based fuzzy Hanman transform and pervasive membership function which are fed to Hanman transform classifier to perform an additional six class and seven class classification along with the two-class and three-class classification of mammograms from the same mini-MIAS database as well as mammograms from DDSM database.

Because of using the higher-level features, the classification performance of the proposed work is coming better as compared to our recently published work.

2 Methodology

The proposed work deals with the formulation of probabilistic hesitancy entropy features and a Hanman transform classifier for the categorization of mammograms into multi classes. The proposed work is implemented on the publicly available DDSM [25] and mini-MIAS datasets [16]. The ground truth information for these datasets is provided by a team of expert radiologists.

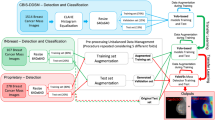
For categorization first, the mammogram images are pre-processed to remove the images with no tumor or more than one tumor. The proposed hesitancy entropy-based and pervasive membership function-based features are extracted from the pre-processed mammograms and then the proposed Hanman transform classifier is applied to the extracted features to categorize the images into multi classes (i.e. two, three, six, and seven). Precision, F-score, accuracy, specificity, and sensitivity are used for evaluating the performance of the proposed approach. The results of the proposed algorithm are validated by the team of expert radiologists which makes it clinically significant. Figure 1 shows the methodology involved in the present work.

Fig. 1
figure 1

The methodology of the proposed approach

Full size image

The organization of the remaining paper is as trails. Section 2 discusses the methodology of the proposed work whereas Sect. 3 provides a brief discussion of Intuitionistic fuzzy sets followed by the derivation of hesitancy entropy functions in Sect. 4. A brief description of Information sets followed by the proposition pervasive information concept and feature extraction is detailed in Sect. 5 and the development of the proposed Hanman transform classifier is relegated to Sect. 6. The experimental results and discussions are given in Sect. 7. Finally, conclusions are provided in Sect. 8.

3 The preliminaries of intuitionistic fuzzy sets and information sets

Mammograms are associated with uncertainty in intensity called fuzziness or vagueness that affects the decision of radiologists. Fuzzy sets are widely used for dealing with vagueness in mammograms. But the success of a fuzzy set depends on the correct choice of a membership function which is not always possible. In this regard, Intuitionistic fuzzy sets come to our rescue by coping with the incorrect choice of a membership function.

Before going to the Intuitionistic fuzzy set, let us recapitulate the evolution of fuzzy sets from type-I to type-II first. A type-I fuzzy set comprises pairs as it elements with each element constituting an attribute value “\(a\)” at pixel location (x, y) as coordinates in the context of an image and its membership function value \({\upmu }_{\mathrm{a}}\), defined as:

$$I_{type I} = \left\{ {a,\mu_{a} |a \in A\} } \right.$$
(1)

Then the type II fuzzy set is defined to have two membership functions, viz., upper \(\mu_{a} \left( u \right)\) and lower \(\mu_{a} \left( l \right),\) as:

$$I_{type II} = \left\{ {a,\mu_{a} \left( u \right),\mu_{a} \left( l \right)|a \in A\} } \right.$$
(2)

They satisfy the condition

$$\mu_{a} \left( l \right) < \mu_{a} < \mu_{a} \left( u \right), \mu_{a} \in \left( {0, 1} \right)$$
(3)

3.1 Intuitionistic fuzzy sets

The Intuitionistic fuzzy set [26] extends the concept of a fuzzy set by including the non-membership function and hesitancy as additional components. Let \({\text{A}} = \left\{ {a_{1} ,a_{2} , \ldots .a_{n} \} } \right.\) be a set of attribute values then an Intuitionist fuzzy set \(I_{int}\) in which each element is a 4-tuple is defined as:

$$I_{int} = \left\{ {(a,\mu_{a} } \right., v_{a} ,\pi_{a} |aA) \} ;A \to \left[ {0,1} \right]$$
(4)

where the functions denoted by \(\pi_{a} ,v_{a} and \mu_{a}\) are the values of hesitancy function, non-membership function, and membership function respectively of an attribute “\(a\)” of A. The components of the Intuitionistic fuzzy set satisfy the following condition:

$$\mu_{a} + v_{a} + \pi_{a} = 1$$
(5)

This means the hesitancy function \(\pi_{a} = 1 - \mu_{a} - v_{a}\) must lie in the range given by

$$0 \le \pi_{a} \le 1\quad \forall a \in A$$
(6)

3.2 Information sets

The concept of the Information set is proposed in [27]. It extends the scope of a fuzzy set by providing certainty or uncertainty of the attribute values of the fuzzy set since it only gives the degree of association of each attribute value. By fitting the distribution of attribute values termed as information values in a fuzzy set with a membership, these are transformed into information values constituting an Information set with the help of an information-theoretic entropy function called as Hanman–Anirban entropy function [28] given in (44) of Appendix-A. It gives the derivation of the formula for the Information set and employs a fuzzifier [29] in the membership function.

3.3 Definition of the information set

The set of information values which are the products of the membership function values and information source values is called the Information set and the sum of these information values provides the information or the certainty linked with the information source values to a concept represented by the fuzzy set.

We will present the Hanman transform resulting from the adaptive Hanman–Anirban entropy function whose properties are given in [30] and [31]. It is similar to (44) except that its parameters are variables. The adaptive form is given by

$$H_{I} \left( k \right) = \mathop \sum \limits_{x = 1}^{n} \mathop \sum \limits_{y = 1}^{n} I_{a} e^{{ - \left[ {a\left( . \right)I_{a}^{3} + b\left( . \right)I_{a}^{2} + c\left( . \right)I_{a} + d\left( . \right)} \right]}}$$
(7)

Substituting \(a\left( . \right) = b\left( . \right) = d\left( . \right) = 0 and c\left( . \right) = \mu_{a}\), we get the Hanman transform, given by:

$$H_{I} \left( k \right) = \mathop \sum \limits_{x = 1}^{n} \mathop \sum \limits_{y = 1}^{n} I_{a} e^{{ - \mu_{a} I_{a} }}$$
(8)

This is a higher form of the Information set as it provides the new information (l.h.s.) based on the old information (r.h.s.). So it can be used as an evaluator, classifier, and learner. The properties of Hanman transform are elaborated in [32].

As can be noticed from above, the Intuitionist fuzzy set has a role for the non-membership function unlike in a fuzzy set such that changing both non-membership function and membership function, the value of hesitancy function can be varied to keep the deficiency in the fuzzy model within the tolerable limits. As the non-membership function is difficult to choose, we consider the complement of the membership function as a close substitute of the non-membership function to extend the concept of the Information set to encompass the Intuitionistic fuzzy set because complementary membership has a role in the Information set. This is achieved through the Hanman–Anirban fuzzy entropy function as we shall see shortly.

4 Derivation of hesitancy entropy functions

As our objective is to develop the hesitancy entropy function from the Hanman–Anirban fuzzy entropy function, let us recapitulate the hesitancy function \(\pi_{a}\) from (5) as:

$$\pi_{a} = 1 - \mu_{a} - v_{a}$$
(9)

We will propose an approach for the modification of hesitancy function values. In this approach, we use hesitancy degree as the power which has been used in the literature for taking care of the inaccurate fuzzy modeling.

4.1 An approach for the modification of hesitancy function

Assuming the hesitancy degree as ‘k’, the above hesitancy function can be expressed as:

$$h_{a} = k. \pi_{a} = 1 - (\mu_{a} )^{k} - (v_{a} )^{k}$$
(10)

By varying hesitancy degree, the corresponding change in hesitancy is:

$$h_{e} = k. \pi_{a} - \pi_{a} = \mu_{a} - (\mu_{a} )^{k} + v_{a} - (v_{a} )^{k}$$
(11)

This can be written as:

$$h_{e} = \mu_{a} \left( {1 - (\mu_{a} )^{k - 1} } \right) + v_{a} \left( {1 - (v_{a} )^{k - 1} } \right)$$
(12)

Realizing that the terms in the parentheses are the approximations of the exponential gain this function leads to:

$$h_{e} = \mu_{a} e^{{ - (\mu_{a} )^{k - 1} }} + v_{a} e^{{ - (v_{a} )^{k - 1} }}$$
(13)

where \(k > 1\) for \(k - 1\) to be positive. We will now show that the two terms in the r.h.s. of (13) are the fuzzy entropy values.

Proof

Consider the generalized non-normalized possibilistic Hanman–Anirban entropy function which provides the uncertainty in an attribute expressed as [32]

$$H_{I} \left( k \right) = \mathop \sum \limits_{x = 1}^{n} \mathop \sum \limits_{y = 1}^{n} I_{a} e^{{ - \left[ {aI_{a}^{3} + bI_{a}^{2} + cI_{a} + d} \right]^{\gamma } }}$$
(14)

where \({\text{I}}_{{\text{a}}}\) is the grey level/attribute at the location (x, y).On fuzzification using \({\upmu }_{{\text{a}}}\) of \({\text{ I}}_{{\text{a}}}\), Eq. (14) becomes the generalized Hanman–Anirban fuzzy entropy function shown by

$$H_{F} \left( \gamma \right) = \mathop \sum \limits_{x = 1}^{n} \mathop \sum \limits_{y = 1}^{n} \{ \mu_{a} e^{{ - \left[ {a\mu_{a}^{3} + b\mu_{a}^{2} + c\mu_{a} + d} \right]^{\gamma } + }} \overline{\mu }_{a} e^{{ - \left[ {a\overline{\mu }_{a}^{3} + b\overline{\mu }_{a}^{2} + c\overline{\mu }_{a} + d} \right]^{\gamma } }} \}$$
(15)

where \(\overline{ \mu }_{a} = 1 - \mu_{a}\), i.e. the complement of \(\mu_{a}\).

With the substitution of parameters as a = b = d = 0 and c = 1, (15) is simplified to:

$$H_{F} \left( \gamma \right) = \mathop \sum \limits_{x = 1}^{n} \mathop \sum \limits_{y = 1}^{n} \{ \mu_{a} e^{{ - \left( {\mu_{a} } \right)^{\gamma } + }} \overline{\mu }_{a} e^{{ - \left( {\overline{\mu }_{a} } \right)^{\gamma } }} \}$$
(16)

If \(\overline{\mu }_{a}\) is replaced with \(v_{a}\) and \({\gamma }\) with k-1 the generalized Hanman–Anirban fuzzy entropy function (16) takes the form of the hesitancy entropy function from (13) as given by:

$$H_{Fh} \left( \gamma \right) = \mathop \sum \limits_{x = 1}^{n} \mathop \sum \limits_{y = 1}^{n} \{ \mu_{a} e^{{ - \left( {\mu_{a} } \right)^{k - 1} + }} v_{a} e^{{ - \left( {v_{a} } \right)^{k - 1} }} \}$$
(17)

We have thus proved a relation between the generalized Hanman–Anirban fuzzy entropy function (16) and the hesitancy entropy function (17) and this relation will be used in extending the Information set to the Pervasive Information set later thereby increasing the potential of the Information set. To derive the higher form of (16) the generalized adaptive form of the Hanman–Anirban fuzzy entropy function having its parameters a, b, c, d is expressed as:

$$H_{\mu } = \sum \limits_{x = 1}^{n} \sum \limits_{y = 1}^{n} \left\{\mu_{a} e^{{ - \left[ {a(.)\mu_{a}^{3} + b(.)\mu_{a}^{2} + c(.)\mu_{a} + d(.)} \right]^{\gamma } }} + \overline{\mu }_{a} e^{{ - \left[ {a(.)\overline{\mu }_{a_{a}}^{3} + b(.)\overline{\mu }_{a_{a}}^{2} + c(.)\overline{\mu }_{a_{a}} + d(. )} \right]^{\gamma } }} \right\}$$
(18)

With a(.) = b(.) = d(.) = 0 as above but \(c\left( . \right) = I_{a}\) in (18) we get the following fuzzy Hanman transform as per Eq. (8):

$$H_{FT} \left( \gamma \right) = \mathop \sum \limits_{x = 1}^{n} \mathop \sum \limits_{y = 1}^{n} \{ \mu_{a} e^{{ - \left( {I_{a} \mu_{a} } \right)^{\gamma } }} + \overline{\mu }_{a} e^{{ - \left( {I_{a} \overline{ \mu }_{a} } \right)^{\gamma } }} \}$$
(19)

It is easy to obtain the corresponding hesitancy fuzzy Hanman transform from (19) by replacing \(\overline{ \mu }_{a}\) with \(v_{a}\) and \({\gamma }\) with k-1. Though finding \(v_{a}\) and k-1 is difficult, an estimate of \(v_{a}\) is given in [32]. In this work, we will be using the complementary membership function as a substitute for \(v_{a}\) and the probability as the substitute for the hesitancy degree k − 1.

To take account of the probabilities of \({\text{ I}}_{{\text{a}}}\)’s in (19), we go in for the histogram representation of an image by replacing 2-Dimensional grey level, \({\text{I}}_{{\text{a}}}\) with 1-Dimensional grey level denoted by \({ }g\).

4.2 The generalized adaptive Hanman–Anirban fuzzy entropy function in the histogram representation

A histogram is a plot of (g vs. p) where \(g\) is represented as an integer and \(p\) is the frequency of its occurrence or probability. Let \(\mu_{g}\) be the membership function selected to represent the degree of association of grey levels \(g\) of a digital mammogram. First of all the histogram representation of (17) is obtained by replacing \(\mu_{a }\) with \(\mu_{g}\),\(\overline{ \mu }_{a}\) with \(\overline{ \mu }_{g}\) and \({\upgamma }\) with \(p\).

$$H_{Fp} = \mathop \sum \limits_{g = 1}^{n} \{ \mu_{g} e^{{ - \left( {\mu_{g} } \right)^{{p_{g} }} }} + \overline{ \mu }_{g} e^{{ - \left( {\overline{ \mu }_{g} } \right)^{{p_{g} }} }} \}$$
(20)

Next, the histogram representation of the fuzzy Hanman transform is obtained by replacing \(I_{a}\) with g, \(\mu_{a}\) with \(\mu_{g}\),\(\overline{ \mu }_{a}\) with \(\overline{ \mu }_{g}\) and \({\upgamma }\) with ‘\(p\)’ in (19):

$$H_{Fpp} = \mathop \sum \limits_{g = 1}^{n} \{ \mu_{g} e^{{ - \left( {g\mu_{g} } \right)^{p} }} + \overline{ \mu }_{g} e^{{ - \left( { g\overline{ \mu }_{g} } \right)^{p} }} \}$$
(21)

where we have taken \(p_{g}\) as the hesitancy degree in the form of power. We can get another form of fuzzy Hanman transform from (19) in the histogram representation by replacing \(I_{a}\) with \({ }p_{g}\), \(\mu_{a}\) with \(\mu_{g}\),\(\overline{{{{ \upmu }}}}_{{\text{a}}}\) with \(\overline{ \mu }_{g}\) and \(\gamma\) with 1:

$$H_{Fps} = \mathop \sum \limits_{g = 1}^{n} \{ \mu_{g} e^{{ - p_{g} \mu_{g} }} + \overline{ \mu }_{g} e^{{ - p_{g} \overline{ \mu }_{g} }} \}$$
(22)

where \(p_{g}\) acts as a scale. It may be noted that the histogram representation of the above two fuzzy Hanman transforms to make them probability-based fuzzy Hanman transforms. The difference between (21) and (22) is that in (21) \(p\) acts as the hesitancy degree and modifies both certainty information value \(g\mu_{g}\) and the uncertainty value \(g\overline{ \mu }_{g}\) and in (22), \(^{\prime}p^{\prime}\) acts as the scale and modifies only \(\mu_{g}\) and \(\overline{\mu }_{g}\). These are higher-level entropy functions accounting for possibilistic, probabilistic, and intuitionistic certainties and uncertainties. Multiplying the hesitancy entropy function value \((\mu_{a} e^{{ - \left( {\mu_{a} } \right)^{k - 1} }} + v_{a} e^{{ - \left( {v_{a} } \right)^{k - 1} }} ){ }\) from (17) with \(I_{a}\) bestows us a higher form of Pervasive Information set which is a sum of the corrected certainty (internal) information \(I_{a} \mu_{a} e^{{ - \left( {\mu_{a} } \right)^{k - 1} }}\) and the uncertainty (external) information \(I_{a} v_{a} e^{{ - \left( {v_{a} } \right)^{k - 1} }}\). The corrections account for the deficiencies in the respective fuzzy model through the corresponding exponential gain function.

5 A brief description of pervasive information sets

The above derivations and relations evolve into Pervasive Information sets having wider scope than that of the Information sets. Recall the certain information value \(I_{a} \mu_{a}\) in (47) which tells how much \(I_{a}\) belongs to the concept (normal or abnormal) represented by the membership function (MF) value \(\mu_{a}\). The Hanman–Anirban has helped us in finding the certainty information from the distribution of the values of \(I_{a}\) by fitting MF. Thus a fuzzy set comprising (\(I_{a} , \mu_{a}\)) as pairs is converted into the Information set \(\left\{ {I_{a} \mu_{a} } \right\}.\) Consider \(I_{a} - I_{a} \mu_{a}\) = \(I_{a} \overline{\mu }_{a}\) which contain uncertain (external) information. In the case of the Intuitionistic fuzzy set, the complementary membership function is a special case of non-membership function \(v_{a}\). The sum of certain and uncertain information is \(I_{a} \mu_{a} + I_{a} v_{a}\) and, residual information is \(I_{a} - \left( {I_{a} \mu_{a} + I_{a} v_{a} } \right) = I_{a} \left( {1 - \mu_{a} - v_{a} } \right) = I_{a} \pi_{a}\). By resorting to better modeling, the residual information becomes \(I_{a} \left[ {1 - (\mu_{a} )^{k} - (v_{a} )^{k} } \right] = I_{a} h_{a}\). At this juncture, let us define the pervasive membership function that translates to the Pervasive Information set.

5.1 Formulation of hesitancy based pervasive membership function

It is defined as the sum of the modified non-membership and the membership functions. The modification is accomplished by the hesitancy degree as either a power or a scale.

$$M_{a}^{k} = (\mu_{a} )^{k} + (v_{a} )^{k}$$
(23)

In the case of histogram representation, \(a\) is replaced with \(g\), and \(k\) is replaced with \(p\). So (23) becomes:

$$M_{g}^{p} = (\mu_{g} )^{{p_{g} }} + (v_{g} )^{{p_{g} }}$$
(24)

It can be noted that while relating the Hanman–Anirban fuzzy entropy function with the hesitancy entropy function, \(k - 1 = {\text{p}}_{{\text{g}}}\), instead of keeping the hesitancy degree k as a power, let us consider it as a scale then (23) can be rewritten as:

$$M_{a\gamma } = \gamma \mu_{a} + \gamma v_{a}$$
(25)

In the histogram representation the above equation turns about to be:

$$M_{gp} = p_{g} \mu_{g} + p_{g} v_{g}$$
(26)

Note that (24) and (26) are termed as probability-based pervasive membership functions with probability as a power and a scale respectively.

5.2 Formulation of probability-based pervasive information set

As coined in [32], this consists of information values as the products of pervasive membership function values and the information source values. The pervasive membership is the combination of modified membership and non-membership which not only represents the certainty/uncertainty in the information source value but also takes care of the inaccurate choice of the membership functions. The modification of these two membership functions is accomplished by the hesitancy degree and their combination becomes the pervasive membership function. As we have taken probability as hesitancy degree both as a power and a scale, this becomes a probability-based pervasive membership function. The corresponding information sets are \(\{ g.M_{g }^{p} \}\) and \(\{ gM_{gp} \}\) denoted by \(\{ H_{g}^{p} \}\) and \(\{ H_{gp} \}\) from the grey levels in a window. As it is difficult to estimate the non-membership function we take it as either the Sugeno complement or Yager complement of the membership function.

5.3 Feature extraction

We have derived the probability-based fuzzy Hanman transforms and also the probability-based pervasive membership function from the mammograms using the histogram representation of grey levels as the information source values ranging from 0 to 255 in a window of the chosen size and probabilities as the hesitancy degrees. We also choose the Gaussian membership function for the grey levels. In this context, probability-based fuzzy Hanman transform helps us derive feature \({ }Fe1{ }\) with the probability \(p\) as the hesitancy degree in the form of power.

$$Fe1 = \mathop \sum \limits_{g = 1}^{n} \mu_{g} e^{{ - \left( {g\mu_{g} } \right)^{{p_{g} }} }} + \overline{ \mu }_{g} e^{{ - \left( { g\overline{ \mu }_{g} } \right)^{{p_{g} }} }}$$
(27)

Replacing \(\overline{ \mu }_{g}\) with \(v_{g}\), and \(g\) with \(\overline{g} = 1 - g\) results in another probability-based fuzzy Hanman transform as feature \(Fe2\)

$$Fe2 = \mathop \sum \limits_{g = 1}^{n} \mu_{g} e^{{ - \left( {g\mu_{g} } \right)^{{p_{g} }} }} + v_{g} e^{{ - \left( {\overline{g}v_{g} } \right)^{{p_{g} }} }}$$
(28)

The third feature \(Fe3\) is also the probability-based fuzzy Hanman transform but with \(p\) as a scale factor

$$Fe3 = \mathop \sum \limits_{g = 1}^{n} \mu_{g} e^{{ - p_{g} \mu_{g} }} + v_{g} e^{{ - p_{g} v_{g} }}$$
(29)

As mentioned above, we make use of either Yager complement \(\left( {1 - \mu_{g}^{s} } \right)^{1/s}\) or Sugeno complement, \(\left( {1 - {\upmu }_{{\text{g}}} } \right)/(1 + {{{\text{s}}\upmu }}_{{\text{g}}} )\), where s is a scale parameter to get \({\text{v}}_{{\text{g}}}\). By varying the value of s, \({\upmu }_{{\text{g}}}\) can have different distributions for the non-membership function. In this work, the Sugeno complement is opted with s = 0.5 to get suitable values of the non-membership function.

The fourth and fifth features comprise the probability-based pervasive information, given by:

$$Fe4 = \mathop \sum \limits_{g = 1}^{n} gM_{g}^{k} = \mathop \sum \limits_{g = 1}^{n} g.\{ \mu_{g}^{{p_{g} }} + v_{g}^{{p_{g} }} \}$$
(30)
$$Fe5 = \mathop \sum \limits_{g = 1}^{n} g.M_{gk} = \mathop \sum \limits_{g = 1}^{n} g.p_{g} \left\{ {\mu_{g} + v_{g} } \right\}$$
(31)

The above feature types are formed from: (i) information source values (grey /complement grey levels here), (ii) probabilities (frequencies of occurrence of grey levels) considered as hesitancy degrees, (iii) membership functions chosen to characterize the grey levels, and iv) non-membership /complement membership functions that account for the deficiencies in the fuzzy modeling. It may be noticed Fe3 does not use the information source values. We call \(\left\{ {Fei} \right\}, i = 1,2,.,5\) as the probability-based pervasive information set features and these are more powerful than fuzzy sets that involve only membership functions, information sets that involve both information source values and membership functions, intuitionistic fuzzy sets that involve non-membership functions, membership functions, and hesitancy degrees and pervasive information sets that involve information source values, membership functions, and non-membership functions. We will now present an algorithm for the classification of the mammograms using Hanman transform as a classifier from the feature vectors of the training set of mammograms and the test feature vector of an unknown mammogram.

6 Development of Hanman transform classifier

The development of the proposed Hanman transform is concerned with utilizing both the training feature vectors and a test feature vector of an unknown mammogram at a time to determine which class it belongs to. This approach is useful for a small number of samples of a patient. The error vectors between the training feature vector and the testing feature vector contain the residual information that reflects the variations in mammograms due to the onset of breast cancer. Then taking two error vectors at a time, we apply the t-norm to extract all possible normed-error vectors for each class. The normed-error vector with the minimum high-level entropy value obtained using Hanman transform is treated as the representative of that class. This normed error vector acts as a support vector in SVM. The infimum from these values gives the class of the unknown mammogram. The algorithm for the classifier is described as under.

6.1 Algorithm for the Hanman transform classifier

Step 1: Split the features \(F_{ij}\) denoting the jth features of ith samples into training set {\(F_{tr} \left( {i,j} \right)\)} and testing set {\(F_{te} (j\)}. Here i = 1,2,…..M; j = 1,2,……N; M represents the training set samples and N symbolizes the number of features.

Step 2: Compute absolute errors of ith and kth training samples and one randomly selected test samples using

$$e_{ij} = \left| {F_{tr} \left( {i,j} \right) - F_{te} \left( j \right)} \right|$$
(32)
$$e_{kj} = \left| {F_{tr} \left( {k,j} \right) - F_{te} \left( j \right)} \right|$$
(33)

Before going to Step 3, let us define adaptive Hanman–Anirban conditional entropy function as

$$H(A_{ij} |B_{j} ) = \mathop \sum \limits_{i = 1}^{n} P_{i/j} e^{{ - \left[ {c\left( . \right)P_{i/j} + d\left( . \right)} \right]}}$$
(34)

where \(P_{i/j}\) denotes the conditional probability between \(A_{ij}\) and \(B_{j}\) and c(.) and d(.) are considered as the variables. Similar to the conditional probability we coin the conditional possibility as \(cPoss\left( {F_{tr} \left( {i,j} \right)|F_{te} \left( j \right)} \right)\) where \(F_{tr} \left( {i,j} \right)\) is the jth feature of ith training sample and \(F_{te} \left( j \right)\) is the jth feature of the test sample. As we don’t know the relation between these two samples, the possible way is to take their difference. Accordingly, the conditional possibility is defined as:

$$cPoss\left( {F_{tr} \left( {i,j} \right)|F_{te} \left( j \right)} \right) = F_{tr} \left( {i,j} \right) - F_{te} \left( j \right) = e_{ij}$$
(35)

Using the above, the possibilistic version of the conditional Hanman–Anirban entropy function can be written as the entropy of the error vector denoted by \(H\left( {E_{i} } \right)\) in the following:

$$H\left( {E_{i} } \right) = \mathop \sum \limits_{j = 1}^{n} e_{ij} e^{{ - \left[ {ce_{ij} + d} \right]}}$$
(36)

Step 3: Use Yager t-norm to generate the t-normed error vectors between the ith and kth error vectors for the jth feature samples from:

$$E_{ik} \left( j \right) = ty\left( {e_{ij} ,e_{kj} } \right), i \ne k; i,k = 1, \ldots , ns, j = 1, \ldots ,nf$$
(37)

where \(ty = \max \left[ {1 - \left[ {\left( {1 - e_{ij} } \right)^{q} + \left( {1 - e_{kj} } \right)^{q} } \right]^{\frac{1}{q}} ,0} \right]\); \(ns\) denotes the number of samples and \({ }nf\) denotes the number of features and we set \(q = 22.\) All possible combinations of the error vectors taking two (ith and kth vectors) at a time are considered to generate the t-normed error vectors such as ikth normed error vector.

Step 4: Substitute and d(.) = 0 in Eq. (37) to get the expression for the Hanman transform given by:

$$H\left( {E_{ik} \left( j \right)} \right) = \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{n} E_{ik} \left( j \right)e^{{ - \left[ {M_{ik} \left( j \right)E_{ik} \left( j \right)} \right]}}$$
(38)

Step 5: Repeat Steps 1–4 for all the-t-normed errors of each class to find the t-normed vector with the least Hanman transform value using (38). Repeat this all for classes.

Step 6: Find the infimum of the Hanman transform values in Step 5 which gives the class of the unknown mammogram.

7 Results and discussions

To classify mammograms using five types of proposed features, the Hanman transform classifier is applied to a publicly available mini-MIAS database [16]. This database comprises 61 benign, 53 malignant, and 208 normal mammograms. Each mammogram used for implementation is the 8-bit grey level image having size 1024 × 1024 pixels. As we are considering the window size of 63 × 63 so mammogram images are cropped in such a way to make them exactly divisible by 63. From each window or subimage, a single feature is extracted. So in total 256 features are extracted from one mammogram which is equal to the number of windows. The ground truth of this dataset is validated by a team of expert radiologists. Figure 2 displays the sample images of normal, malignant, and benign mammograms.

Fig. 2
figure 2

a Normal mammogram image (considered from a mini-MIAS database, mdb259) with dense background tissue noticeable as a white region b Benign Mammogram (mdb152) having architecture distortion on fatty background tissue pointed by black arrow c Malignant Mammogram (mdb178) having spiculated mass pointed by the black arrow on the fatty glandular background tissue [16]

Full size image

First, mammograms are classified into abnormal and normal classes. Out of 322 mammograms, features of 276 mammograms are extracted for categorizing mammograms into abnormal and normal mammograms. Then dataset is split into a testing set of 92 mammograms and a training set of 184 mammograms. Secondly, mammograms are classified based on the severity of abnormality into malignant and benign mammograms. Now for this classification, we have considered 114 abnormal mammograms comprising 53 malignant and 61 benign. These are divided into 38 and 76 for testing and training correspondingly. Table 1 provides the classification accuracy obtained with five types of features. From Table 1, it can be concluded that the Hanman transform classifier works well on three types of features (i.e. Fe2, Fe3, and Fe5) giving 98.91% accuracy while the Fe1 feature gives 97.82% and the Fe4 feature gives 100% accuracy. But for the further categorization of abnormal images into malignant and benign classes, Fe2, Fe4, and Fe5 features achieve 100% accuracy while the other two features achieve 97.36% accuracy. To evaluate the efficiency of the proposed results, F-score, sensitivity, accuracy, precision, and specificity are considered. Accuracy provides the ratio of correctly labeled cases to a whole set of cases. Sensitivity gives the ratio of positive labels (TP) which are detected correctly to those who are tested positive whereas specificity provides the ratio of negative labels (TN) which are detected correctly to those who are healthy in reality.

Table 1 Accuracy of the Hanman transform classifier ( in percentage) for two-class classification
Full size table

Precision computes the number of positive-class predictions that belong to the positive class. Recall calculates the number of positive class predictions made out of all positive examples in the dataset. F-Measure gives a single score constituting both recall and precision. For computing these performance measures, the following formulas are used [33].

$$Precision = \frac{{True \;Positive\; \left( {TP} \right)}}{{True\; positive\; \left( {TP} \right) + False \;positive\; \left( {FP} \right)}}$$
(39)
$$Sensitivity\; \left( {Recall} \right) = \frac{{True\; Positive \left( {TP} \right)}}{{False \;Negative \left( {FN} \right) + true \;Positive \;\left( {TP} \right)}}$$
(40)
$$Specificity = \frac{{True \;negative \;\left( {TN} \right)}}{{False \;positive\; \left( {FP} \right) + True \;negative\; \left( {TN} \right)}}$$
(41)
$$F\_score = \frac{2*Precision*Recall}{{Precision + Recall}}$$
(42)
$$Accuracy = \frac{{True\; Negative\; \left( {TN} \right) + true \;positive\; \left( {TP} \right)}}{{True \;Negative \;\left( {TN} \right) + true \;positive \; \left( {TP} \right) + false \;negative\; \left( {FN} \right) + false \;positive\; \left( {FP} \right)}}$$
(43)

Classification accuracy achieved with the proposed method is compared with that of feed-forward backpropagation network (BPN) and SVM classifier in Table 2. Feed-forward BPN applied to texture and energy features gives an accuracy of 93.90% in [34] whereas the SVM classifier applied on shape and texture features gives an accuracy of 83.87% in [35]. Hanman transform classifier when applied on Fe4 features gives 100% accuracy. This accuracy is quite higher compared to the accuracies obtained using state of art techniques on the mini-MIAS database.

Table 2 Comparison of classification accuracy (Normal vs Abnormal)
Full size table

Table 3 shows the classification accuracy achieved in categorizing mammograms into malignant and benign classes obtained with some features and classifiers in the literature. From the table, it can be observed that the accuracy of 94.57% is achieved by applying Fisher’s Linear discriminant analysis on the neighborhood structure similarity and linear binary pattern (LBP) based features [36]. CNN features and parasitic metric learning-based features give 96.7% accuracy [37]. The Neural Network classifier gives an accuracy of 95.2% on texture features [38] whereas the accuracy of 96.7% is achieved with a simple logistic classifier on the statistics texture features [39]. The Hanman transform classifier provides 100% accuracy on Fe2, Fe4, and Fe5 features on the database under consideration.

Table 3 Comparison of classification accuracy (Benign vs Malignant) in percentage
Full size table

Next, we have used the above five types of features for 3-class classification comprising normal, benign, and malignant classes using the Hanman transform classifier. To carry out this, we have used 176 mammograms in which 44 mammograms are used for testing whereas the remaining 132 mammograms are utilized for training. Classification accuracies achieved by this classifier on five feature types, i.e. Fe1, Fe2, Fe3, Fe4, and Fe5 are shown in Table 4. In 3-class classification, Fe1and Fe3 feature types work well with the highest accuracy of 97.72% while Fe2, Fe4, and Fe5 features yield 100% accuracy.

Table 4 Three -class classification accuracy of the proposed classifier (in percentage)
Full size table

On comparing the results obtained with the proposed features using the Hanman classifier with those of Multiscale All-Convolutional Neural Networks (MA-CNN) [40] in Table 5, it is found that the performance of MA-CNN providing specificity = 96%, F-score = 0.97, Sensitivity = 96%, and accuracy = 96.47% is inferior to that of Fe4 feature giving specificity = 100, sensitivity = 100%, F-score = 1 and accuracy = 100% on the mini-MIAS database.

Table 5 Classification results (normal/ benign/malignant) in percentage
Full size table

The mammograms from the mini-MIAS database contain 112 dense glandular, 103 fatty glandular, and 107 fatty mammograms. Mammograms are further classified based on the character of background tissue into these three subclasses. Out of 320 mammograms, 240 mammograms are set aside for training and the remaining 80 for testing. The performance of the Hanman transform classifier applied on the proposed five types of features is given in Table 4 and the comparison with the performance of the literature features in Table 6. From Table 4, it is clear that the Hanman transform classifier performs well on three features (Fe2, Fe3, Fe4) giving 98.75% as the highest accuracy whereas providing 97.5% accuracy on Fe1 and Fe5 features. Table 6 shows the comparison of proposed classification results with those of the other states of the art techniques.

Table 6 Classification accuracy (fatty/ fatty glandular/ dense glandular) in percentage
Full size table

From Table 6, it can be seen that the KNN classifier categorized the Gray level co-occurrence matrix (GLCM) features with an accuracy of 82.5% [41] whereas the SVM classifier provides 85.5% accuracy on uniform directional pattern-based features [42]. The two-layer feed-forward network provides 97.66% accuracy on statistical features [43] whereas the Artificial Neural network (ANN) provides an accuracy of 97.5%, the specificity of 98.75%, and the sensitivity of 97.5133% on features including gray level difference matrix (GLDM), linear binary pattern( LBP), grey level run length matrix (GLRLM), trace transform, Gabor wavelet, histogram, and gray level co-occurrence matrix(GLCM) [44]. Compared to some of the state-of-the-art techniques applied on the mini-MIAS database, the Hanman transform classifier applied on Fe4 features provides accuracy (Acc.) of 98.75%, a specificity of 99.22%, and sensitivity of 98.72% respectively.

The mini-MIAS dataset can also be categorized based on the type of abnormality present. The dataset has 208 normal (NORM), 25 calcifications (CALC), 22 well-defined/circumscribed mass (CIRC), 14 ill-defined mass (MISC), 15 asymmetry (ASYM), 19 architecture distortion (ARCH), and 19 spiculated masses (SPIC). For dividing mammograms based on the class of abnormality present into these seven classes, features of 104 mammograms are extracted. For training 91 mammograms are used while for testing 13 mammograms are utilized. Leaving normal mammograms aside, they can be classified into six classes.

For this, 78 mammograms are used for training while the remaining 13 mammograms are considered for testing. Table 7 shows the classification accuracy achieved for six-class and seven-class classification. From Table 7, it can be noticed that the Hanman transform classifier gives 92.30% classification accuracy with Fe2, Fe3, Fe4, and Fe5 features while it provides 84.61% classification accuracy with Fe1 features in the case of seven-class classification. For six-class classification, 100% classification accuracy is achieved with Fe2, Fe4, and Fe5 features while 92.30% classification accuracy with Fe1 and Fe3 features.

Table 7 Multi-class Classification accuracy in percentage (i.e. seven-class and six-class classification)
Full size table

Table 8 provides the comparison of classification accuracy for multi-class classification. It can be seen that MM-ANFIS (memetic meta-heuristic adaptive neuro-based fuzzy inference system) classifier applied to the features from 2D wavelet transform, Zernike moments and GLCM descriptors provide 82% classification accuracy for the six-class classification and 82.56% for the seven-class classification [45]. On the other hand, the combination of Fe4 features and Hanman transform classifier provides 100% classification accuracy for the six-class classification and 92.30% accuracy for the seven-class classification which is higher than that achieved with the approaches compared.

Table 8 Comparison of classification accuracy for multi-class classification
Full size table

7.1 Statistical significance

A statistical test called Analysis of variance (ANOVA) is done on the proposed five feature types extracted from the mini-MIAS database. For this test, the confidence interval is set at 5% and two hypotheses are considered. First is the null hypothesis in which the average values or mean of all five types of features must be equal and second is the alternative hypothesis in the average value or mean of at least one feature type is different from those of other feature types. Table 9 provides the terms and measures required for the statistical analysis by ANOVA. In Table 9,\({\text{ MS}}_{{\text{W}}}\) is the variance within each feature type and \({\text{MS}}_{{\text{B}}}\) is the variance between the feature types. F is the ratio of \({\text{MS}}_{{\text{B}}}\) to \({\text{ MS}}_{{\text{W}}} .{ }\) p-value and F_crit are obtained using the ANOVA test. Table 10 shows the values of the terms and measures used in Table 9. Here \({\text{df}}_{{\text{N}}} = {\text{Number of samples }} - 1\) i.e. 5–1 = 4 and \({\text{df}}_{{{\rm D}}}\) = Sum of sample sizes –Number of samples = 322 × 5–5 = 1605.

Table 9 The measures/terms required for the analysis of variance
Full size table
Table 10 Computation of terms/measures for the statistical analysis using Analysis of variance
Full size table

As per Table 10, F is found to be 119.253 which is much greater than the value 2.377 of F_crit. Also, p-value (3.78E−89) is less than the confidence level of 5% (i.e. 0.05). The measures F, F_crit, and p indicate that the proposed features are statistically significant. These features are also significant statistically in the classification performance with a p value < 0.05.

7.2 Implementation results on digital database for screening mammography dataset

For further evaluating the robustness of the proposed work, we have implemented the proposed work on the DDSM dataset [25]. It consists of both mediolateral oblique (MLO) and craniocaudal (CC) views of mammograms with ground truth provided by expert radiologists. The images of the DDSM dataset are resized to 1024 × 1024 pixels along with the quantization of grayscale intensity to 8 bits as per the mammogram images of the mini-MIAS dataset. We have considered 900 mammograms from this dataset comprising 405 normal and 495 abnormal for the categorization of mammograms into abnormal and normal classes and the training to testing ratio is 2:1. The abnormal samples comprising 495 mammograms include 247 benign and 248 malignant mammograms. These abnormal mammograms are further categorized into benign and malignant mammograms. Table 11 displays the classification accuracy attained for the two-class classifications. From Table 11, it can be noted that the Hanman transform classifier gives 98.66% accuracy on Fe1, 99.67% accuracy on Fe4, 100% accuracy on Fe5, 99.33% accuracy on Fe2, and Fe3 respectively in categorizing the mammograms into normal and abnormal mammograms. But for the further categorization of the abnormal mammograms into malignant and benign classes, Fe4, and Fe5 features achieve 100% accuracy while Fe1, Fe2, and Fe3 features achieve 98.18%, 99.39%, 98.79% classification accuracy respectively. Table 12 provides the comparison of two-class classification accuracy on the DDSM dataset.

Table 11 Accuracies of the Hanman transform classifier (in percentage) for the two-class classification
Full size table
Table 12 Assessment of classification accuracy for two-class classifications
Full size table

From Table 12, it can be concluded that 98.90% accuracy is obtained using the VGG-19 pretrained CNN model for feature extraction, PCA for dimensionality reduction, and KNN for categorization of mammograms taken from the DDSM dataset into abnormal and normal mammograms [12]. On the other hand classification of Fe5 features using the Hanman transform, classifier achieves 100% classification accuracy for the same classification on the DDSM dataset which is higher compared to other state of art techniques. Fine-tuning ResNet achieves 93.15% accuracy in classifying mammograms of the DDSM dataset into malignant and benign mammograms [46]. On the other hand, the Hanman transform classifier gives 100% classification accuracy for the categorization of abnormal mammograms into malignant and benign mammograms on the same dataset.

For three-class classification, 1000 mammograms are considered in which 337 are normal, 333 are malignant and 330 are benign. The training to test ratio is taken as 3:1. Table 13 shows the classification accuracies achieved for the three-class classifications on the DDSM dataset. From Table 13, it can be concluded that the Hanman transform classifier gives 100% classification accuracy on Fe4 while it provides 98.4%, 99.2%, 98.8%, and 99.6% classification accuracy on Fe1, Fe2, Fe3, and Fe5 features respectively.

Table 13 Three-class classification accuracies with Hanman transform classifier (in percentage)
Full size table

Table 14 provides the comparison of the accuracy for three class classifications. From Table 14, it can be concluded that the Convolutional Neural Network with the reduced number of parameters and layers provides 96.47% accuracy in categorizing mammograms from the DDSM dataset into normal, benign, and malignant [47]. Compared to this, the Hanman transform classifier applied on Fe4 features provides 100% classification accuracy.

Table 14 Comparison of accuracy for three class classifications (Normal/Benign/Malignant)
Full size table

7.3 Comparison with deep learning architectures

We have applied some Convolutional Neural Network-based pretrained network architectures such as ResNet-18 [48], AlexNet [49], GoogLeNet [50], and VGG-16 [51] on mammograms from the mini-MIAS database. The features extracted from these architectures are reduced with the principal component analysis [52] and used for the multi-class (two-class, three-class, six-class, and seven-class) classification using the Hanman transform classifier. The training to testing ratio is the same as that used for the proposed technique. As shown in Table 15, ResNet-18 [48] provides the highest accuracy of 98.91% for the classification of mammograms into normal and abnormal with the reduced feature vector of length 342 whereas the accuracies of 97.82%, 96.73%, and 95.65% are achieved with AlexNet [49], VGG-16 [51] and GoogLeNet [50] with the reduced feature vectors of 1365, 342, and 682 lengths respectively. In comparison to these lengths, the feature vector of each of the five feature types has a length of 256 accompanied by better performance. The computational complexity is limited to finding a single feature from a window as against enormous computations involved in deep learning network architectures.

Table 15 Accuracies achieved with the Hanman transform classifier (in percentage) for the multi-class classifications
Full size table

Similarly in classification of abnormal mammograms into benign and malignant AlexNet [49] and VGG-16 [51] achieves 94.73% accuracy whereas 92.10% and 97.36% accuracy is achieved with GoogLeNet [50] and ResNet-18 [48] respectively. In three class classification of mammograms into fatty, dense glandular and fatty glandular AlexNet [49] and ResNet-18 [48] achieves 98.75% accuracy whereas VGG-16 [51] and GoogLeNet [50] achieves 97.5% and 96.25% accuracy respectively. In classification of mammograms into normal, malignant and benign VGG-16 [51] and ResNet-18 [48] achieves 97.72% accuracy whereas 95.45% and 93.18% accuracy is achieved with AlexNet [49] and GoogLeNet [50] respectively.

Now coming to six-class and seven-class classifications AlexNet [49] achieves 84.61% accuracy whereas ResNet-18 [48] achieves 92.30% accuracy. The accuracies of VGG-16 [51] and GoogLeNet [50] for six-class are 84.61% and 76.92% and for seven-class are: 76.92% and 92.30% respectively. From these results, we notice that the performance of CNN-based architectures degrades beyond three-class classification. Surprisingly for seven-class classification the maximum accuracy obtained by the proposed five feature types is the same, i.e. 92.30% as that of features from CNN architectures, viz., GoogLeNet [50] and ResNet [48]. This implies that the features don’t have sufficient information to give us 100% accuracy. Thus we conclude that the five feature types mostly outperform the features from CNN architectures compared for multi-class classifications of mammograms.

Thus, the work presented in this paper provides three major contributions: The formulation of hesitancy entropy function, fuzzy Hanman transform and hesitancy based fuzzy Hanman transform; Devising five new feature types based on these concepts to represent probabilistic, possibilistic, and intuitionistic certainties and uncertainties; and the classification of mammograms using these features and the proposed classifier. The purpose of the proposed approach is to eradicate the problems of the existing classical models as well as the deep learning networks used for the classification of mammograms.

The novelty of the work lies in devising the concept of pervasive membership function for the proposition of new features which have an immense practical relevance, especially in medical diagnosis. Consider the case in which a doctor diagnoses the patient. The diagnosis of the patient by the family doctor is the information accrued from the membership function and considering an opinion of an expert doctor is the information accrued from the non-membership function in external diagnosis. Both doctors may give conflicting or the same opinions on the disease. Thus both membership and non-membership functions play their respective roles in providing complete information. Moreover, we have improvised the pervasive membership function by taking the probability as the hesitancy degree. The proposition of the pervasive membership function and its improvisation using probability are well thought out concepts used in the formulation of the probability-based pervasive information set features that have also proved their mettle in the proposed classification approach for mammograms.

8 Conclusions

The proposition of hesitancy entropy function, probability-based fuzzy Hanman transform, and probability-based pervasive information are the hallmarks of the research work presented in this paper. The hesitancy entropy function results from the change in hesitancy function values due to a change in hesitancy degree and it becomes the generalized Hanman–Anirban fuzzy entropy function when the non-membership function of the Intuitionistic fuzzy set is taken as the complement of the membership function of the fuzzy/information set. The generalized adaptive Hanman–Anirban fuzzy entropy function helps derive fuzzy Hanman transform. The pervasive information set is the outcome of extending the information set to encompass the Intuitionistic fuzzy set. Three feature types are derived from the probability-based fuzzy Hanman transform using probability as the hesitancy degree in the form of power and a scale factor and the rest two feature types are derived from the probability-based pervasive information using probability as a power and a scale. Each feature of each feature type is extracted using the histogram and membership function of grey levels in a window. The five feature types are powerful as they possess the embedded information from information source values, non-membership and membership function values, and probabilities. These feature types have opened up a new direction for use in image processing applications and will be useful for recommender systems, social networks, and sentiment analysis.

The Hanman transform classifier is developed for the categorization of mammograms into two-class (abnormal and normal, benign and malignant), three-class (malignant, normal, benign), three-subclass (fatty, fatty glandular, and dense glandular), six-class (CIRC/MISC/SPIC/ASYM/CALC/ARCH), and seven-class (CIRC/MISC/SPIC/ASYM/CALC/ARCH/NORM) using the five feature types. The performance of the Hanman transform classifier on these feature types outperforms that of some of the state-of-the-art methods and the results are clinically validated by the team of expert radiologists.

The results of the proposed features and classifier are demonstrated on two small datasets (mini-MIAS and DDSM) and also compared with the results of some deep learning network architectures. It is found that the performance of five feature types competes with that of deep learning features with less number of features and less computational time. The contribution of the paper includes the derivation of the hesitancy entropy function, formulation of five feature types due to the probability-based fuzzy Hanman transform and the probability-based pervasive information, and the design of the Hanman transform classifier. Our future endeavor is to work on a large database of mammograms to see the effectiveness of our features and classifier.