1 Article Highlights

  • A temperature based maximum power point tracking algorithm is proposed.

  • Thermal imaging is used to measure the temperature of the photovoltaic module.

  • The proposed algorithm results in fast tracking of MPP and provides a stable PV output.

2 Introduction

In recent years solar photovoltaic energy harvesting has been increased exponentially. It has been possible due to the abundance of solar irradiance, ease of installation, and green nature of solar energy [1]. Despite the tremendous growth in solar PV installations, the efficiency of solar PV modules is less. To extract the maximum available power, it is necessary to continuously track the operating voltage without interruptions and fluctuations in output power [2]. To achieve this, a large number of MPPT algorithms have been available in the literature [3, 4].

A comparative study on MPPT methods has been provided by Subudhi et al. [5], Esaram et al. [6]. All these algorithms have variations in terms of speed, efficiency, accuracy, and quality of power output. Among these techniques, P&O is widely used and many modified versions of P&O are available. In P&O MPPT, the output voltage of the PV module is observed and the voltage is perturbed till the maximum power point is achieved. Alik et al. (2015) provided a detailed review of MPPT algorithms [7]. They presented an improved version of P&O with a checking algorithm and provided a simulation of boost convertor in SIMULINK. Hynuh et al. presented a P&O algorithm that overcomes the drawbacks of conventional P&O by determining the short circuit current before each perturb step [8]. Chaieb et. al provided a method to track MPPT based on simplified accelerated particle swarm optimization (SAPSO) which is a combination of particle swarm optimization and Hill climbing (HC) [9]. Two important parameters which affect the efficiency of any MPPT algorithm are convergence time to reach MPP and oscillations in output power. Haque et al. [10] proposed P&O by selecting an MPPT zone and setting the initial value to Vmpp = K*Voc. Value of K is taken at STC (1000, 25 °C) which may vary at ambient conditions and can increase dV. Satish et al. [11], Liu el. al [12] proposed adaptive P&O MPPT with variable perturbation size. Yan et. al [13] designed a P&O based on irradiance data classification. Jian et. al [14, 15] purposed a variable perturbation frequency method to improve the controller speed.

The major drawback of conventional P&O MPPT schemes discussed in the above references is that they maintain their accuracy and speed only in stable environmental conditions. Frequent deviation from MPP happens due to change in ambient conditions [16,17,18]. Temperature is an important factor that strongly affects the output power of the PV module. Dincer et al. did analysis of critical factors which affects the efficiency of solar PV cell including temperature [19]. Coskun et. al provided a sensitivity analysis of implicit correlations that affects the module temperature [20]. Conventional P&O may take more time to settle output power if the initial set point is not chosen correctly and the difference voltage is large. Besides, there is always a challenge of choosing the correct step size in conventional P&O, and in adaptive step size MPPT, computational load is more.

Although temperature-based MPPT techniques have already been suggested in literature but most of them suggested to take STC (25 °C) to model the PV voltage which avoids the actual temperature of the PV module, and since it is well established that PV output significantly changes with temperature, these methods result in more convergence time and more fluctuations. Coelho et al. [21] provided a temperature measurement-based MPPT method but the temperature measurement was done with the help of a thermometer. Vicente et al. [22] used a low-cost sensor to measure the temperature of the PV module. Some authors have suggested using STC (25 °C) but this may produce erroneous results as the varying environmental conditions may cause a change in the actual temperature of the PV module [23, 24]. The flow graph of the proposed technique is given in Fig. 3.

In this paper, a thermography-based modified P&O is purposed which overcome the drawbacks of conventional and variable step size P&O. Rest of the paper is organized as follows. In Sect. 2, need of temperature based MPPT scheme is justified. Proposed algorithm is given in Sect. 3. Simulation and experimental results of the proposed algorithm and convention P&O MPPT are compared in Sect. 4. Conclusion is discussed in Sect. 5.

3 Need of temperature based MPPT

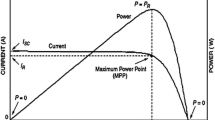
PV Module operating temperature is the most important parameter which needs to be determined to know the reliability and efficiency of the module output. Modules are rated at STC and the actual output varies to a great extent with temperature. In general, module efficiency decreases with an increase in module operating temperature as given in [25] and by Eq. (1) and Fig. 1.

$${\upeta }_{{\text{c}}} = { \upeta }_{{{\text{Tref}}}} { }\left[ {1 - {{ \upbeta }}_{{{\text{ref}}}} { }\left( {{\text{ T}}_{{\text{c}}} - {\text{ T}}_{{{\text{ref}}}} } \right)} \right]$$
(1)
Fig. 1
figure 1

PV module characteristics with temperature

Full size image

\({\upeta }_{{{\text{Tref}}}} { }\) is the module efficiency at \({\text{T}}_{{{\text{ref}}}}\) which is taken as STC (25 °C). \({\text{T}}_{{\text{c}}}\) is the cell operating temperature. \({\upeta }_{{\text{c}}}\) is the efficiency at cell operating temperature. \({\upbeta }_{{{\text{ref}}}}\) is the temperature coefficient at \({\text{T}}_{{{\text{ref}}}}\).

PV Cell operating temperature of the PV module is also varied by incident solar radiation and ambient temperature as given by a well-known expression (Eq. 2) for Tc by (Kou et al.) [26].

$${\text{T}}_{{\text{c}}} = {\text{ T}}_{{\text{a}}} + { }\left( {\frac{{{\text{G}}_{{\text{T}}} }}{{{\text{G}}_{{{\text{NOCT}}}} }}} \right)\left( {\frac{{{\text{U}}_{{{\text{L}},{\text{NOCT}}}} }}{{{\text{U}}_{{\text{L}}} }}} \right)\left( {{\text{T}}_{{{\text{C}},{\text{ NOCT}}}} - {\text{ T}}_{{\text{a}}} } \right)\left[ {1 - \frac{{{\upeta }_{{\text{c}}} }}{{{{\uptau \upalpha }}}}} \right]$$
(2)

where \({\text{G}}_{{\text{T}}}\) is the incident solar radiation and \({\text{G}}_{{{\text{NOCT}}}}\) is solar radiation at NOCT condition. \({\text{T}}_{{\text{c}}}\) is the cell operating temperature, \({\text{T}}_{{{\text{C}},{\text{ NOCT}}}}\) is the cell temperature at NOCT, \({\text{T}}_{{\text{a}}}\) is ambient temperature, \({\upalpha }\) is the cell absorption and \({\uptau }\) is the cell cover transmittance and \({\text{U}}_{{\text{L}}}\) is the heat loss coefficient.

In the P&O method, convergence time is high because the actual temperature of the PV module is not taken into consideration while calculating the value of the reference signal. In conventional methods, the startup value of MPP is taken at NOCT (800 W/m2, 45 ± 3 °C) while the actual temperature of the PV module is often different. This increases the value of change in the voltage \(\left( {\Delta {\text{V}}} \right)\) and hence in turn increases the convergence time.

At steady-state conditions, there is always a challenge to reduce the fluctuations in output power with a variable load. Fluctuations can be reduced by controlling the MPPT algorithm by the actual temperature of the PV module. The control signal \(\left( {\Delta {\text{V}}} \right)\) has a reduced value when it is calculated using temperature-based empirical model given in Eqs. (13) and (14).

The duty cycle of the buck DC–DC converter changes according to the MPPT algorithm to bring back the system at the optimum point in case it deviates from the MPP due to variable load [7]. The DC–DC converter is controlled by the MPPT system as shown in Fig. 2.

Fig. 2
figure 2

Solar power system components block diagram

Full size image

The output voltage of PV module is the input voltage of Boost converter i.e. \({\text{V}}_{{{\text{PV}}}} = {\text{V}}_{{{\text{in}}}} { }\) and \({\text{ V}}_{{\text{o}}} = {\text{d* V}}_{{{\text{in}}}} = {\text{d*V}}_{{{\text{PV}}}} { }\); Hence in order to \({\text{V}}_{{\text{o}}}\) and \({\text{V}}_{{{\text{PV}}}}\) equal, the duty cycle has to vary in accordance with MPPT algorithm.

$${\text{d}}\left( {{\text{t}} + 1} \right) = {\text{d}}\left( {\text{t}} \right) + { }\tau {\text{ d}}\left( {\text{t}} \right)$$
(3)

where ‘d’ is the duty cycle at time ‘t’ and ‘t + 1’.

Value of ‘\(\tau\)’ in Eq. (3) is to be decided based on the magnitude of difference signal \(\left( {\Delta {\text{V}}} \right)\) as given in Eq. (15).

4 Proposed MPPT technique

In this work, a thermography based MPPT technique has been proposed to overcome the slow speed and transient problem in conventional MPPT methods. The flow graph of the proposed technique is given in Fig. 3. Temperature is measured using a Fluke TiS45 thermal image. Existing methods of PV module temperature measurement e.g. RTD sensor, thermistors have some limitations as given below.

  1. A.

    Use of a temperature sensor takes a certain time to record the temperature and it is not possible to synchronize the thermometer with the rest of the system hardware used to track MPP as other parts of the system are too fast.

  2. B.

    Sensor measures the temperature of a particular location where it is mounted on the panel. It does not provide the average thermal condition of the module.

Fig. 3
figure 3

Flow graph of thermography based MPPT technique

Full size image

To overcome these issues an IR imaging-based temperature measurement method is used to determine the instantaneous temperature of the PV module and used in the empirical temperature model of PV modules to determine the maximum power.

4.1 Temperature modeling of solar module

Numerous empirical relations have been established in literature to find the maximum power point with temperature. Benmessaoud et al. [27] established a generic analytic model to find out the peak power parameters as given by Eqs. (4) and (5). They have taken reference temperature 25 °C to calculate maximum power.

$${\text{V}}_{{{\text{MPP}}}} = \frac{{{\text{K T}}_{{\text{n}}} }}{{\text{q}}}{\text{ ln}}\left( {\frac{{{\text{I}}_{{\text{L}}} - {\text{I}}_{{{\text{MPP}}}} }}{{{\text{I}}_{{\text{o}}} }} + 1} \right) - {\text{ I}}_{{\text{MPP }}} {\text{R}}_{{\text{S}}}$$
(4)
$${\text{I}}_{{{\text{MPP}}}} = {\text{G }}\left( {{\text{ I}}_{{{\text{MPP}},{\text{ ref }}}} - {{ \upmu }}\left( {{\text{T}}_{{\text{C}}} - {\text{ T}}_{{{\text{ref}}}} } \right){ }} \right)$$
(5)

where \({\text{V}}_{{{\text{MPP}}}}\) and \({\text{I}}_{{\text{MPP }}}\) are voltage and current at the maximum power point. \({\upmu }\) is the current coefficient for temperature. \({\text{I}}_{{\text{o}}}\) is the reverse saturation current. \({\text{I}}_{{\text{L}}}\) is the load current. \({\text{R}}_{{\text{S}}}\) is the series resistance connected in Fig. 4. G is the solar radiance.\({\text{ I}}_{{{\text{MPP}},{\text{ ref }}}}\) is the current at MPP when the temperature is taken as the reference temperature.

Fig. 4
figure 4

Single diode model of PV cell

Full size image

Since the drawbacks of using NOCT have been discussed above in the paper, we have used an empirical relation that works on any ambient temperature value as suggested by Moradi et.al. [4] and derived below. A single diode model of a PV cell can be represented as shown in Fig. 4.

Model consists of a current source in parallel to a diode. In a PV module, numerous cells are connected either in series or parallel or a combination of both. Cell equations representing voltage and current characteristics can be derived by applying Kirchhoff's law in above circuit. Ignoring parallel resistance, the output current can be represented as given by Eq. 6.

$${\text{I}} = {\text{I}}_{{{\text{ph}}}} - {\text{ I}}_{{\text{D}}}$$
(6)

\({\text{I}}_{{\text{D}}}\) is given by Shockley diode equation as follows (\({\text{I}}_{{\text{o}}} { }\) represents the reverse saturation current):

$${\text{I}}_{{\text{D}}} = {\text{ I}}_{{\text{o}}} [\exp \left\{ {\frac{{{\text{q}}\left( {{\text{ V}} + {\text{IR}}_{{\text{s}}} } \right)}}{{{\text{AkT}}}}} \right\} - 1]$$
(7)

\({\text{I}}_{{{\text{ph}}}}\), Photocurrent can be calculated as given by equation below:

$${\text{I}}_{{{\text{ph}}}} = { }\frac{{\text{G}}}{{{\text{G}}_{{{\text{ref}}}} }}{ }\left( {{\text{ I}}_{{{\text{ph}},{\text{ ref}}}} + {\text{K}}_{{\text{i}}} \left( {{\text{ T}} - {\text{ T}}_{{{\text{ref}}}} } \right)} \right)$$
(8)

\({\text{I}}_{{\text{o}}}\), reverse saturation current can be found as follows

$${\text{I}}_{{\text{o}}} = {\text{ I}}_{{{\text{o}},{\text{ref}}}} \left( {\frac{{\text{T}}}{{{\text{T}}_{{{\text{ref}}}} }}} \right)^{3} [\exp \left\{ {\frac{{{\text{qE}}_{{\text{g}}} }}{{{\text{AkT}}}}{ }\left( {{ }\frac{1}{{{\text{T}}_{{{\text{ref}}}} }} - { }\frac{1}{{\text{T}}}} \right)} \right\}$$
(9)

\({\text{I}}_{{{\text{ph}},{\text{ ref}}}}\) is the PV current at reference temperature i.e. 25 °C and at radiation level 1000 W/m2. \({\text{K}}_{{\text{i}}}\) is the temperature coefficient of short circuit current. \({\text{I}}_{{{\text{o}},{\text{ref}}}}\) is the reverse saturation current at reference temperature.

Reverse saturation current at reference temperature can be found at from the equation given below;

$${\text{I}}_{{{\text{o}},{\text{ref}}}} = { }\frac{{{\text{I}}_{{{\text{sc}},{\text{ ref}}}} }}{{\exp \left( {\frac{{{\text{V}}_{{{\text{oc}},{\text{ ref}}}} }}{{{\text{aV}}_{{\text{t}}} }}} \right)}}$$
(10)

The accuracy of the model depends upon the appropriate selection of parameter ‘A’ which depends upon the material of the module (Carrero et al. [28]). Short circuit current and open-circuit voltage can be derived from Eqs. 5 and 6 are given below;

$${\text{I}}_{{{\text{sc}}}} = { }\frac{{\text{G}}}{{{\text{G}}_{{{\text{ref}}}} }}{ }\left( {{\text{ I}}_{{{\text{sc}},{\text{ ref}}}} + {\text{K}}_{{\text{i}}} \left( {{\text{ T}} - {\text{ T}}_{{{\text{ref}}}} } \right)} \right)$$
(11)
$${\text{V}}_{{{\text{oc}}}} = {\text{ V}}_{{{\text{oc}},{\text{ref}}}} + {\text{ K}}_{{\text{v}}} \left( {{\text{ T}} - {\text{ T}}_{{{\text{ref}}}} } \right){ }$$
(12)
$${\text{V}}_{{{\text{MPP}}}} = {\text{ K}}_{1} {\text{V}}_{{{\text{oc}}}} = {\text{K}}_{1} {\text{V}}_{{{\text{oc}},{\text{ref}}}} + {\text{ K}}_{1} {\text{K}}_{{\text{v}}} \left( {{\text{ T}} - {\text{ T}}_{{{\text{ref}}}} } \right)$$
(13)
$${\text{I}}_{{{\text{MPP}}}} = {\text{K}}_{2} { }\left( {{\text{I}}_{{{\text{sc}},{\text{ ref}}}} + {\text{ K}}_{{\text{i}}} \left( {{\text{ T}} - {\text{ T}}_{{{\text{ref}}}} } \right)} \right)$$
(14)

\({\text{K}}_{1}\) ratio of voltage at maximum power to open-circuit voltage; \({\text{K}}_{2}\) ratio of current at maximum power to short circuit current.

Approximate values of MPP calculated from the above equation are used to arrive at a more accurate value of MPP. A difference signal \(\left( {\Delta {\text{V}}} \right)\) was calculated by taking the difference between \({\text{V}}_{{\text{MPP }}}\) and actual PV voltage \({\text{V}}_{{{\text{PV}}}}\). Further tracking to the exact value of MPP is done by the conventional P&O method. The main purpose of using the temperature model to find MPP was to minimize this difference signal as given in Eq. (15), so that actual MPP can be reached in minimum time.

$$\Delta {\text{V}} = {\text{V}}_{{{\text{MPP}}}} - {\text{V}}_{{{\text{PV}}}}$$
(15)

Less will be the value of difference signal, shorter will be the time required to reach the actual MPP and lesser will be the computational load because less number of iterations will be required to stabilize the signal as compared to the conventional P&O method.

4.2 Infrared imaging

In thermal imaging, IR radiation emitted by an object is detected by an IR detector lens fitted in a thermal imager. The color intensity of the IR image represents the temperature distribution pattern of the surface of the object. IR images can be further processed to extract the required information for monitoring purposes. IR images can also be used to monitor the health of the PV module along with temperature measurement. In this work, IR images taken with the help of an IR camera as shown in Fig. 5 were directly fed into the Labview environment to have the temperature profile of the PV module.

Fig. 5
figure 5

Infrared image of a PV module

Full size image

The average temperature of any object using an IR image having N number of pixels can be calculated by using Eq. 16, where \({\text{T}}_{{\text{i}}}\) is the temperature of ith pixel calculated by color intensity converted to the corresponding temperature. Hence IR camera takes into account even a small part of the module while calculating the temperature. This increases the accuracy of this method as compared to other temperature-based methods.

$${\text{ T }} = { }\frac{1}{{\text{N}}}{ }\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{N}}} {\text{T}}_{{\text{i}}}$$
(16)

The use of thermal imager has numerous advantages over conventional temperature measurement based MPPT and other variable step size MPPT techniques.

  1. A.

    Thermal imager overcomes the drawback of conventional P&O for not accommodating changing ambient conditions.

  2. B.

    It provides the average temperature of the whole module instead of some selected locations as in the case of sensor-based temperature measurement method.

  3. C.

    Along with temperature measurement, a thermal imager can also be used to monitor any thermal anomaly that appeared in the PV module due to any overheating or physical damage.

  4. D.

    It provides a more accurate estimation of MPP which in turn reduces the convergence time to actual MPP.

  5. E.

    Thermal imager is a non-invasive device.

5 Implementation and results

For verification of the proposed MPPT algorithm, first, a SIMULINK model was developed and results were analyzed. A hardware implementation is also done with the help of a thermal imager and supporting software and hardware circuit as shown in Fig. 13.

5.1 Simulation

In this section, the proposed method was simulated in MATLAB/SIMULINK and the outcomes were compared to the conventional P&O method. SIMULINK model is shown in Fig. 6.

Fig. 6
figure 6

SIMULINK Model of proposed system

Full size image

For Simulation purpose, a 60.53Watt module from the NREL system advisor model was used with open-circuit voltage as 21.1 V and VMPP as 17.0458 V. A variable temperature profile was chosen and various parameters were analyzed for both methods (convention P&O and Temperature based P&O). Temperature was varied at four different time instances and output power and voltage results were analyzed at those instances.

This paper focuses on two aspects of a maximum power point tracker. First, how fast a tracker reaches the maximum power point when ambient conditions changes and how stable is the output when the PV power system is running in its normal conditions. We have analyzed output power characteristics at the startup phase and the instants when there is a temperature change. Figure 7a, b gives the change in power output with a change in temperature for conventional P&O and thermography based P&O method. Change in temperature with time is given in Fig. 8.

Fig. 7
figure 7

a Output power with conventional P&O method. b Output power (thermography MPPT)

Full size image
Fig. 8
figure 8

Change in temperature profile

Full size image

In Fig. 9a, b, the power curve is expanded at the startup of PV system to determine the time to reach and stabilize the signal. In the thermography-based MPPT system, it comes out to be 0.220 s and in the case of conventional P&O, it comes out to be 0.45 s.

Fig. 9
figure 9

a Power signal expanded at startup (Conventional MPPT). b Power signal expanded at startup (thermography MPPT)

Full size image

In Fig. 10a, b, Output at time t = 1.5 s is taken when temperature changes from 30 to 32 °C when the system is already in running condition. In the case of conventional P&O method, it takes 39 ms time to reach the reach maximum power and stabilize. In the case of thermography based system, it takes only 5 ms and takes only 5 pulses to stabilize. This shows how fast the MPPT tracker works with the proposed technique.

Fig. 10
figure 10

a Power signal at t = 1.5 s (Conventional MPPT). b Power signal at t = 1.5 s (thermography MPPT)

Full size image

In Fig. 11a, b, the Gate signal is analyzed between the duration for which power signal is taken in Fig. 10a, b i.e. t = 1.5 s to t = 1.539 s for conventional P&O and t = 1.5 s to t = 1.505 s for the proposed technique. For the same component values, duty cycle comes out to be 53.51% in case of the proposed method and 64.60% in case of the conventional method.

Fig. 11
figure 11

a Gate pulse (conventional MPPT). b Gate pulse (thermography MPPT

Full size image

Important parameters are given in Table 1 for both the algorithms for comparison that shows a considerable improvement in the case of thermography based MPPT tracker. In Fig. 12a, b, the Output voltage signal is shown as temperature change at various instants of time. The output voltage is thermography based MPPT settles quickly as compared to conventional MPPT. Table 1 compares different parameters for the proposed as well as convention p&O method.

Table 1 Simulation results summary
Full size table
Fig. 12
figure 12

a Output voltage (conventional MPPT). b. Output voltage (thermography MPPT)

Full size image

5.2 Experimental setup

PV module built by VikramSolar (Model: Eldora40, module specification given in Table 2) is used for experimental purpose. An experimental setup was developed on the rooftop of university building as shown in Fig. 13.

Table 2 Specifications of PV module used
Full size table
Fig. 13
figure 13

Experimental setup at rooftop

Full size image

Thermal imager built by Fluke was used to take real-time IR images of the PV module. Thermal imager output was given to the Labview vision module to process the IR image and to obtain the average temperature of the PV module in real-time. IR camera was set to take images in automatic mode Labview vision module reads the images instantly from camera memory. The maximum frequency of thermal imager is 9 Hz and we can further set the frequency as per our need.

MPPT controller algorithm (both, conventional as well as thermography based) was implemented with the help of a microcontroller (PIC-16F887) along with the supporting hardware and DC-DC Coverter (Table 3).

Table 3 Parameters of buck DC–DC converter
Full size table

Plots were recorded using a data logger using Ecosense software. Temperature is obtained from IR images by converting color intensity value to temperature [29, 30]. The approximate value of \({\text{V}}_{{\text{mpp }}}\) was calculated using this temperature value which was further used to calculate the difference voltage signal \(\left( {\Delta {\text{V}}} \right)\).

Results have been analyzed for the constant load as well as variable load. Variable load at buck convertor output was taken for steady-state analysis and the constant load was taken for startup condition.

Figure 14a, b show the graphs for startup conditions for the constant load. For the conventional P&O MPPT method, the time to reach MPP is 2.18 s while in the case of the thermography-based P&O technique, it takes 0.68 s to reach MPP. Less time taken in thermography based MPPT is the direct result of decreased difference signal due to more accurate approximation of MPP using the temperature of the module through a thermal camera.

Figure 15a, b show steady-state conditions with perturbation in the duty cycle. When a 5% duty cycle perturbation is applied, Power varies in both cases (conventional as well as thermography based) but in the case of thermography based method, output power stabilizes within 0.33 s but for conventional technique, fluctuations remain for a long time.

For power-voltage curves in Fig. 16a, b, the load was varied at buck convertor output several instances. For conventional MPPT, Power goes back to previous levels with load variation (as shown in in Fig. 16a, power level down to point A, B and C) and it take much time to come back to the same power level as before load variation. But for the proposed temperature based MPPT method, Power drops and maintains the same level instantly. In thermography-based techniques, when load is varied, Camera instantly takes IR image and feeds it to the system to calculate MPP and the power level is maintained within milliseconds. IR cameras can be programmed to take images at fixed time intervals as per our requirements. Conventional MPPT will affect the working of Buck converter due to its more recovery time as the duty cycle of the buck converter is too small as compared to the recovery time of the module.

6 Cost of the proposed system

It is obvious from the results that standard technique (P&O) supported by further hardware and software gives better results, but this performance improvement can slightly increase the cost of the system due to additional hardware (IR Camera). Nowadays IR imagers have become a household technology. From the automobile industry to security and surveillance, Condition monitoring of machines and products to the food industry, it has a wide range of applications. With such a large number of applications, competition in the production industry has increased the number of players in the industry and the consequence is a drastic decrease in the price of IR Cameras.

Moreover, if IR camera is properly mounted, a single camera can cover several modules as shown in Fig. 17. This reduces the cost of the overall system, e.g. If a single camera costs 200$ and if it covers 20 modules, then per module cost would be 10$. This cost can be recovered through a more energy-efficient system.

Fig. 17
figure 14

IR camera mounted on multiple modules

Full size image

7 Conclusion

In this paper, temperature-based P&O MPPT techniques is proposed and implemented on a specifically designed MPPT controller hardware. Results of the proposed technique are compared to the conventional adaptive size P&O MPPT method (Table 4). The method is tested for both, constant load as well as variable load. It is found that the thermography-based method is fast and resulted in fewer transients in the output voltage and power. This technique can also be used for preventive fault monitoring of the PV power system by keeping an eye on the maximum temperature of the PV module. The proposed method is designed to give stable and more power in case of changing ambient environmental conditions. Scope to improve the accuracy of this method depends on the chosen empirical model of PV module to calculate the peak parameters i.e. \({\text{V}}_{{{\text{mpp}}}}\) and \({\text{I}}_{{{\text{mpp}}}}\).

Table 4 Hardware results of conventional and thermography based MPPT methods
Full size table

Future prospects of the proposed methods can be in the form of implementing this method on a plant level. This is quite possible because a single IR camera can cover a large number of PV modules at a single time if mounted properly. The slight increase in cost can be easily compensated by a more efficient and stable power generation system.