Performance of rainfall–runoff models in reproducing hydrological extremes: a case of the River Malaba sub-catchment

Abstract

Daily River Malaba flows recorded from 1999 to 2016 were modelled using seven lumped conceptual rainfall–runoff models including AWBM, SACRAMENTO, TANK, IHACRES, SIMHYD, SMAR and HMSV. Optimal parameters of each model were obtained using an automatic calibration strategy. Mismatches between observed and modelled flows were assessed using a total of nine “goodness-of-fit” metrics. Capacity of the models to reproduce historical hydrological extremes was assessed through comparison of amplitude–duration–frequency (ADF) relationships or curves constructed based on observed and modelled flow quantiles. Generally, most of the hydrological models performed better for high than low flows. ADF curves of both high and low flows for various return periods from 5 to 100 years were well reproduced by AWBM, SAC, TANK and HMSV. ADF curves for high and low flows were poorly reproduced by SIMHYD and SMAR, respectively. Overall, AWBM performed slightly better than other models if both high and low flows are to be considered simultaneously. The deviations of these models were larger for high than low return periods. It was found that the choice of a “goodness-of-fit” metric affects how model performance can be judged. Results from this study also show that when focusing on hydrological extremes, uncertainty due to the choice of a particular model should be taken into consideration. Insights from this study provide relevant information for planning of risk-based water resources applications.

1 Introduction

Heavy rainfall events have increasingly been experienced in various regions, while other areas of the world receive light or no rains as reported by the Intergovernmental Panel on Climate Change IPCC [1]. This results in floods, landslide, drought, hurricanes, hence, causing distressing damages and losses to public life and property. The study area of the present work (River Malaba sub-catchment) is not exceptional to these extreme weather events. River Malaba sub-catchment in Eastern Uganda has fertile soils which support agriculture and livestock grazing. In addition, River Malaba provides for other economic activities including fishing and fish farming. The River Malaba sub-catchment within the Mpologoma catchment has been affected by rainfall-induced landslides in the highland districts of Manafwa and Bududa. Within the same area, annually, disastrous floods have been experienced in the low-lying districts of Butaleja and Manafwa [2, 3]. These disasters could be linked to impacts of human factors on the sub-catchment hydrology. Besides, the study area hydrometeorology could be influenced by climate variability. Consequently, the possibility of Uganda “Vision 2040” targets has been compromised as noted by the Ministry of Water and Environment, MWE [3, 4]. Some of the dramatic events include (1) the floods of December 2019 with at least 4 death and over 2,000 people displaced [5]; (2) the October 2018 severe floods and landslides in Bududa, displacing 858 people, 51 death and a total of 12,000 people affected [6]; (3) the severe landslides of March 2010 killed over 400 people, displacing 5,000 people in Bududa district [7], and over 33,000 households affected in Butaleja [8]. These events tend to be punctuated by long dry spells, for instance, after the floods and landslide in 2014, there was a long dry spell [9]. In May 2012, flooding resulted in bursting of River Malaba banks affecting over 200 families in Malaba town council and Osukuru sub-county, Tororo district. These events destroyed acres of food crops and resulted in at least 4 death [10]. Furthermore, the report by Reliefweb [11] categorised the Elgon sub-region (where the study area is located) as one of the most affected areas by the 2007 floods that resulted in destruction of several infrastructure, particularly roads, bridges and buildings, killed human beings, and wrecked crops. This event affected almost the entire Uganda.

To facilitate predictive planning and operation of risk-based water resources management within the study area, where rain-fed agriculture and livestock grazing are major economic activities, there is need to perform hydrodynamic modelling. Hydrodynamic modelling of weather events such as floods, necessitates understanding the hydrological processes with focus on the extremes. Hydrological modelling can be performed using either lumped conceptual, semi-distributed or distributed models. Distributed models consider the spatial distribution of rainfall, evapotranspiration and watershed characteristics at a resolution normally selected by the modeller to reflect the spatio-temporal variability of runoff. Some of the distributed (physically based) hydrological models include the Gridded Surface Subsurface Hydrologic Analysis (GSSHA) [12], Systeme Hydrologique Europeen, “SHE” [13], European hydrological system model (MIKE-SHE) [14], modular modelling system (MMS) [15]. Some models are not physically based but rather semi-distributed, e.g. Soil and Water Assessment Tool (SWAT) [16] which is operated on hydrological response unit (HRU) and necessitates parameter calibration. Whereas the physically based (distributed) models have better computational capacity and are robust, with well-implemented numerical methods, their application particularly, in rainfall–runoff simulations is still inadequate. Huge amount of data inputs may undesirably result in a more complex model which may lead to high prediction uncertainty especially if a model has large number of parameters [17].

On the other hand, lumped conceptual models are based on average spatial characteristics of the system, whose basis is to simulate flow at the outlet of the catchment [18, 19]. Examples of lumped conceptual models include the Australian water balance model (AWBM) [20], Sacramento (SAC) [21], TANK [22], Identification of Unit Hydrographs and Component Flows from Rainfall, Evaporation and Stream-flow data (IHACRES) [23, 24], SIMHYD [25], soil moisture accounting and routing (SMAR) [26], hydrological model focusing on sub-flows’ variation (HMSV) [27], Pitman model [28], hydrological engineering centre-hydrological modelling system (HEC-HMS) model [29], hydrologiska byråns vattenbalansavdelning (HBV) model [30]. The high capacity to simulate runoff with easy to use methods, and the minimum data requirement, has made the lumped conceptual models prevalent to distributed models for rainfall–runoff modelling. Lumped conceptual models have widely been applied [31]. Rainfall–runoff modelling can be done based on event-based or continuous approach. Recently, there is a transition from event-based continuous hydrological modelling. For instance, Grimaldi et al. [32] applied the Continuous Simulation Model for Small Ungauged Basins (COSMO4SUB) to ungauged catchment and the results were comparable with the event-based approach. Similarly, several studies have reported superior performance of Artificial Neural Network (ANN) models [31, 33, 34]

Within Uganda (where the study area is located), several studies [35,36,37] have applied lumped conceptual hydrological models. However, it was noticeable that most studies applied a single hydrological model except for Onyutha et al. [36] that compared the performance of seven lumped conceptual models in the simulation of daily River Kafu flows. However, this study was conducted in western Uganda and not in the eastern part of Uganda (where the study area is located). Furthermore, most of these studies applied either one or very few (maximum of 3) “goodness-of-fit” measures. The selection and application of a particular model and “goodness-of-fit” measure from the several can result in a huge bias while concluding on the worthiness of the obtained model results [38]. This could be attributed to the varying structures and parameters amongst different model [39]. In addition, a particular “goodness-of-fit” measure may not provide information on some analyses components such as model residuals, making them inadequate in assessing model performance [38, 40].

Reliable hydrological modelling results are vital for decision makers to avoid profligate expenditures resulting from wrongly informed predictive planning. Prior to conducting this research article, studies conducted to evaluate several lumped conceptual models’ performance based on multiple “goodness-of-fit” statistics to simulate hydrological extremes in River Malaba sub-catchment were lacking. Therefore, to address the above research gap, this study evaluated the performance of seven rainfall–runoff models in simulating hydrological extremes of River Malaba sub-catchment while assessing model performance using nine “goodness-of-fit” metrics.

2 Study area, data and models

2.1 The study area

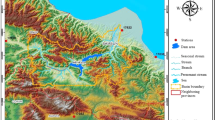
The River Malaba sub-catchment (Fig. 1) has a drainage area of approximately 3500 km². The sub-catchment is part of the Mpologoma catchment under the Kyoga Water Management Zone (KWMZ), stretching between latitudes 0° 19′ N and 1° 07′ N and longitudes 33° 37′ E and 34° 37′ E. The sub-catchment drainage area is transboundary, shared between Uganda (about 69% or 2395 km²) and Kenya (around 31% or 1100 km²). River Malaba sub-catchment is comprised of River Malaba, formed by two tributaries of Lwakhakha and Makalisi which are later joined by the Lumbaka/Kibimba tributary.

Fig. 1

Location of River Malaba sub-catchment. The background map is the Digital Elevation Model (DEM) acquired via http://srtm.csi.cgiar.org/ (accessed: 08 February, 2021)

The basin has a flow outlet at Budumba with latitude = 0° 49′ N and longitude = 33° 47′ N. The River Malaba sub-catchment extends from Mount Elgon at about 4320 m above sea level traversing through the districts of Bududa, Manafwa, Tororo, Butaleja, and discharging into River Mpologoma at the shores of Lake Kyoga at about 1000 m above sea level. The core land use in the sub-catchment is rain-fed subsistence agriculture employing approximately 85% of the population. Practically, the region beyond the Mount Elgon forested area consists of agricultural and grassland, fallow land and isolated woodlots. Land use changes in the sub-catchment ecosystem have adversely changed the river Malaba hydrological flow regimes [41]. The major soils types in the sub-catchment are Petric Plinthosols and Gleysols. The other types include Lixic ferralsols, Acric ferrasls and Nitisols [42, 43]. The rainfall over the study area occurs in two seasons with the first and more intense from March to May (MAM), while the second and highly variable occurs between October and December (OND). The basin receives an average annual rainfall of about 1375 mm, though the districts of Bududa and Manafwa receive slightly higher rains (on average 1800 mm per annum). The basin climate is partly affected by the existence of large water bodies (such as Lake Victoria and Lake Kyoga) and the mountain Elgon slope breezes that tend to affect the afternoon convection [44]. It is clear that the altitude is higher in the highlands of Mount Elgon. The sub-catchment wettest and driest periods occur from March to April and June to October, respectively, with an average temperature range of 15.8 to 30.6 °C [45].

2.2 Data

2.2.1 Rainfall and potential evapotranspiration data

As noted in the previous study by Mubialiwo et al. [46], the study area has poor distribution of meteorological stations, with the existing ones having few data available in the recent years in addition to uncertain and questionable quality [47, 48]. Therefore, the daily precipitation, minimum (T_min) and maximum (T_max) temperature data in a gridded (0.25° × 0.25°) form of the Princeton Global Forcing (PGF) [49] were obtained from http://hydrology.princeton.edu/data/pgf/v3/0.25deg/ (accessed: 07 February 2021). The PGF data was previously applied by Zhang et al. [50] to evaluate performance of four models in streamflow simulation. Like any other reanalysis datasets, PGF has a few shortcomings including bias and random errors which are attributed to numerous factors such as sampling rate, inadequate spreading of sensors and uncertainties in the rainfall retrieval algorithms [51,52,53]. Furthermore, the study by Mubialiwo et al. [46] revealed that the PGF data overestimated and/or underestimated the oscillation highs and lows from observed rainfall over the Mpologoma catchment (where the study area is located). This evidenced existence of bias in the PGF data. Therefore, prior to the use of PGF data, it was thought vital to perform bias correction [53], using observed rainfall data from the six stations in and around the study area (Table 1). For each station, the annual rainfall statistical metrics (coefficient of variation (C_v), skewness (C_s), actual excess kurtosis (C_k) and annual mean rainfall (AMR)) were determined. From Table 1, the values of C_v varied from 0.12 to 0.28, which represent a modest variability on a year to year basis. Under ideal situation, the values of C_s and C_k are expected to be equal to zero for a normal distribution. However, from Table 1, data at the 6 stations are, on average, somewhat positively skewed (Cs = 0.54) and platykurtic (C_k = −0.04). The highest values of C_k and C_s were obtained at Sukulu VTRO, while Butaleja prison exhibited the smallest values. The AMR varied between 1020.79 and 1640.66 mm. The highest AMR was observed at Dabani catholic while Butaleja prison exhibited the lowest value AMR value.

Table 1 Rainfall station, their coordinates, data record period and statistical metrics

With the exception of station 4 (Tororo), the remaining stations have data ending in the 1980s. This is attributed to the non-functionality of weather stations subsequent to the civil war that started in 1981, resulting in the breakdown of many measuring stations across Uganda according to the Japan International Cooperation Agency [54].

The missing values in the observed rainfall data were in-filled using the Inverse Distance Weighted (IDW) interpolation [55], a technique previously applied by Mubialiwo et al. [46]. The bias correction was done using the simple multiplicative bias correction method [56]. This method was adopted because of the poor distribution of the rain gauge networks within the study area. The study by Tian et al. [57] compared the two common error models (additive and multiplicative) and recommended the use of multiplicative bias correlation method for bias removal. The monthly bias correction factor $B_{{{\text{cf}}}}$ was used to adjust the daily PGF precipitation data. The $B_{{{\text{cf}}}}$ was obtained as follows:

$$B_{{{\text{cf}}}} = \frac{{P_{{{\text{obs}},i}} }}{{P_{{{\text{PGF}},i}} }}$$

(1)

where $P_{{{\text{obs}},i}}$ and $P_{{{\text{PGF}},i}}$ are station-based and PGF-based rainfall data at monthly time scale, respectively.

One bias factor was calculated for each month in a year and applied to daily data. The study by Saber and Yilmaz [58] applied a similar approach with monthly bias factors used to correct hourly data.

The daily bias corrected PGF rainfall was computed as follows:

$$P_{{{\text{PGF}}\_{\text{after}}\left( {x,y} \right),T_{i} }} = B_{{{\text{cf}}}} \times P_{{{\text{PGF}}\_{\text{before}}\left( {x,y} \right),T_{i} }}$$

(2)

where $P_{{{\text{PGF}}\_{\text{before}}\left( {x,y} \right),T_{i} }}$ and $P_{{{\text{PGF}}\_{\text{after}}\left( {x,y} \right),T_{i} }}$ are the PGF products for day $T_{i}$ at grid $(x,y)$ before and after bias removal, respectively.

Monthly bias factors were computed considering the station(s) that is(are) located in a particular grid cell or the closest station(s). It is noticeable from Table 1 that only the Tororo station had data of corresponding period to the PGF-based rainfall.

The computed bias factor at Tororo station did not exhibit noticeable variability for the period before and after 1983. Therefore, since all stations were from the same region, they were presumed that they exhibit minimal variation in the bias factors. Consequently, the available periods of station-based data (Table 1) were used to compute monthly bias correction factors, and applied to daily PGF data from 1999 to 2016. This approach was previously used by Piani et al. [59] on statistical bias correction for daily precipitation in regional climate models over Europe. In the study [59], bias correction factors were calculated using data from 1961 to 1970 and applied to data of a different period (from 1991 to 2000).

In the current study, the catchment-wide rainfall averages were obtained using the Thiessen polygon [60] (Fig. 1) constructed from the 14 grid points. It is noticeable that 5 grid points fall inside the study area while an additional nine are situated outside but very close (on average less than 10 km from the sub-catchment boundary). All the 14 grids were used in obtaining the average rainfall over the sub-catchment. The sub-catchment daily rainfall time series are shown in Fig. 2a.

Fig. 2

Time series of a daily rainfall, b daily PET and c daily observed flow used in rainfall–runoff modelling

The sub-catchment $PET$ (mm/day) (Fig. 2b) was computed using the Hargreaves formula [61, 62] (Eq. 3). The method requires mainly minimum and maximum temperatures as the key inputs. The Hargreaves method, was recently applied by Mubialiwo et al. [46] in Mpologoma catchment and Onyutha et al. [63] in KWMZ, where the study area is located.

$${\text{PET}} = 0.0023\left( {T_{{{\text{mean}}}} + 17.8} \right)\left( {T_{\max } - T_{\min } } \right)^{0.5} {\text{Ra}}$$

(3)

where $R_{a}$ measures the incoming extra-terrestrial radiation (in W/m²), estimated based on the location’s latitude and the calendar day of the year, $T_{{{\text{mean}}}}$ in °C is the mean temperature.

2.2.2 Observed flow data

Average daily River Malaba flow series measured at Budumba gauge station (with station ID 82,217, latitude = 0º49′N and longitude = 33° 47′ E) (Fig. 1) from 1999 to 2016 was obtained from the Uganda Ministry of Water and Environment (MWE). The data was checked for quality assurance using visual inspection and statistical methods to ensure only satisfactory and quality data is used in the research. Only eighteen (18) years of recent flow data (from 1999 to 2016) for River Malaba were used (Fig. 2c). Their selection was linked to the anticipated studies of flood analysis in the study area (requiring recent information) that will be based on output from this study. Nevertheless, the eighteen years of data were considered very sufficient because longer calibration data series do not certainly yield better model performance [64]. The study by Li et al. [64] revealed that only eight years of data are adequate to get a stable approximation of model performance. Since rainfall–runoff modelling required the same period of rainfall, PET and flow data, the period from 1999 to 2016 is considered here. This is because PGF-based data currently ends in 2016.

Similar to the observed rainfall data, statistical metrics in the PGF-based rainfall, PET and observed flow were computed as shown in Table 2. Rainfall, PET and observed flow were negatively skewed (negative C_s values) and platykurtic (negative C_k values) compared with the normal distribution, for which it is anticipated that C_s = 0 and C_k = 0. However, their C_v values indicated that there is slight variation on a year to year basis. The average annual rainfall was 1125.25 mm with mean annual PET of 5.57 mm and annual mean flow of 10,436.15 m³/s.

Table 2 Statistical metrics in PGF rainfall, PET and observed flow

3 Methodology

3.1 Rainfall-runoff modelling

This study used seven lumped conceptual rainfall–runoff models. Of the seven models, the six are internationally well-known including the Australian Water Balance Model AWBM [20], SACRAMENTO [21], TANK [22], Identification of Unit Hydrographs and Component Flows from Rainfall, Evaporation and Stream (IHACRES) flow data [23, 24], SIMHYD [25], and Soil Moisture Accounting and Routing SMAR [26]. These six models were obtained from the “eWater Toolkit” of the Cooperative Research Centre for Catchment Hydrology in Australia via http://www.toolkit.net.au/ (accessed: 08 February 2021). The seventh model or Hydrological Model focusing on Sub-flows Variation HMSV [27] was accessed freely via https://sites.google.com/site/conyutha/tools-to-download (accessed: 10 February 2021). These models were selected because they (1) are freely available online and (2) were found to be robust for rainfall–runoff modelling under various climatic conditions as demonstrated in several recent studies [27, 36, 65,66,67,68,69].

Here is a brief mention of each model’s parameters. Detailed description of the models and their parameters including sensitivity analyses are included in the Supplementary Material (Sub-Sect. M1.1–M1.7, Table M1 and Figs. M9–M11). AWBM has 8 parameters, but three of them (Baseflow index, baseflow recession constant, surface flow recession constant) are considered the major ones. SAC model has 17 parameters, with three designed for direct runoff simulation, other 3 for water capacity in upper zone, 2 for percolation into lower zones, while the remaining 9 are designed for water capacity in the lower zone. TANK model has 18 parameters categorised under 7 classes. The model has 3 major parameters (i.e. water levels in the tanks, height of outlets at tanks and runoff coefficients. IHACRES model has 11 parameters. SIMHYD model has 9 parameters, with 4 sensitive ones (i.e. infiltration coefficient and shape, interflow coefficient, and base flow coefficient). SMAR model has five water balance parameters and 4 routing parameters. HMSV has total of 10 parameters. Four parameters are for baseflow, 2 for interflow and 4 for overland flow simulation. A combination of the 10 parameters is used to calibrate the full model to simulate the total runoff. Higher values of recession constants imply delayed contributions of different components to the total runoff. Higher values of initial soil moisture storage indicate faster contribution of runoff from the catchment.

Modelling was done using meteorological data (rainfall and potential evapotranspiration) as described in Sect. 2.2.1. Prior to inputting the data into the models, it was converted into formats required by each of the seven rainfall–runoff models. The Initial model parameters for each model as provided in Podger [70] (for AWBM, TANK, SAC, SIMHYD and SMAR), Croke et al. [23] (for IHACRES), and Onyutha [27] (for HMSV) were set and the model ran to generate outputs. Sensitivity analysis on the model parameters was done prior to calibration. This was done to establish the contribution of a particular parameter variation to model output in order to identify which parameters have a great or less impact on the model response. This study adopted the use of local sensitivity analysis (LSA) method because it is simple, fast and can yield results similar to the global sensitivity analysis (GSA) [71]. The LSA method focuses of the impact on model output caused by a single parameter while other parameters are fixed. The corresponding Nash–Sutcliffe efficiency (NSE) [72] values were obtained and NSE curves plotted for each parameter.

The model parameters were calibrated using the observed river flow data (sub-Sect. 2.2.2) from 01/01/1999 to 31/12/2009, until there was a reasonable match between the simulated and observed flow. Model calibration can be based on manual or automatic strategy. With manual calibration, there is a trial and error adjustment of parameters based on the modellers’ visual inspection of simulated and observed values, making it is very difficult to yield hydrologically sound results, and the process is tedious, time-consuming, especially for models with many parameters [73]. When comparing models, manual calibration also yields subjective results. Thus, in this study, calibration was done using the automatic calibration strategy with model parameters automatically adjusted following systematic search algorithms based on the set objective function. In the rainfall–runoff models’ frameworks, Nash–Sutcliffe efficiency (NSE) [72] was used as the optimisation objective function, while the models’ performance was further assessed based on other eight “goodness-of-fit “metrics as described shortly next. Five models (AWBM, SACRAMENTO, TANK, SIMHYD and SMAR) were calibrated based on shuffled complex algorithm (SCE) [74]. The calibration of IHACRES followed the approach described by Croke et al. [23]. Similarly, the HMSV was automatically calibrated based on the Generalised Likelihood Uncertainty Estimation (GLUE) developed by Beven and Binley [75]. HMSV framework allows a “step-wise” calibration strategy, first by calibrating parameters based on each of the sub-flows (baseflow, interflow and overland flow). The full model run is then performed combining parameters from the sub-flow models. This approach allows modelling of quick flows focusing on high flows while baseflow considers variation of the low flows. The models were validated using the observed river flow data for a record outside the calibration period (from 01/01/2010 to 31/12/2016). During validation, the same parameters and corresponding values used for calibration were maintained.

The models performance were evaluated based on nine widely used statistical indicators, including, Nash–Sutcliffe efficiency (NSE) [72], model average bias (MAB) (%), Ratio of Root Mean squared error to the maximum event (RRM), relative efficiency (R_e) [76], index of agreement (I_a) [77], coefficient of determination (R) [78], mean absolute error (MAE), coefficient of model accuracy (CMA) [38] and Kling–Gupta efficiency (KGE) [79] as shown in Eqs. (4) to (12). For all the seven model, NSE was used as the optimisation objective function for calibration. Consider $Q_{{{\text{obs}}}} ,Q_{{{\text{sim}}}} ,\overline{Q}_{{{\text{obs}}}} ,{\text{and }}\overline{Q}_{{{\text{sim}}}}$ as the observed, modelled, mean of observed and mean modelled flows, respectively. Furthermore, take $Q_{{{\text{max}}}} ,\sigma_{{{\text{obs}}}} ,\sigma_{{{\text{sim}}}}$ and $n$, to denote the maximum observed flows, standard deviation in observed, standard deviation in modelled flows and sample size, respectively. Lastly, consider $r$ as the rank-based Spearman correlation coefficient between $Q_{{{\text{obs}}}} \,{\text{and}}\,Q_{{{\text{sim}}}}$. The various “goodness-of-fit” metrics were computed using:

$${\text{NSE}} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left( {Q_{{{\text{sim}},i}} - Q_{{{\text{obs}},i}} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {Q_{{{\text{obs}},i}} - \overline{Q}_{{{\text{obs}}}} } \right)^{2} } }}$$

(4)

$${\text{MAB}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\frac{{Q_{{{\text{sim}},i}} - Q_{{{\text{obs}},i}} }}{{Q_{{{\text{obs}},i}} }} \times 100} \right)}$$

(5)

$${\text{RRM}} = \frac{1}{{Q_{\max } }}\left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {Q_{{{\text{sim}},i}} - Q_{{{\text{obs}},i}} } \right)^{2} } } \right)^{0.5}$$

(6)

$$R_{{\text{e}}} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left| {Q_{{{\text{sim}},i}} - Q_{{{\text{obs}},i}} } \right|^{{f_{p} }} } }}{{\sum\nolimits_{i = 1}^{n} {\left| {Q_{{{\text{obs}},i}} - \overline{Q}_{{{\text{obs}}}} } \right|^{{f_{p} }} } }}$$

(7)

$$I_{{\text{a}}} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left| {Q_{{{\text{obs}},i}} - Q_{{{\text{sim}},i}} } \right|^{{f_{p} }} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {\left| {Q_{{{\text{sim}},i}} - \overline{Q}_{{{\text{obs}}}} } \right| + \left| {Q_{{{\text{obs}},i}} - \overline{Q}_{{{\text{obs}}}} } \right|} \right)^{{f_{p} }} } }}$$

(8)

$$R = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {Q_{{{\text{obs}},i}} - \overline{Q}_{{{\text{obs}}}} } \right)\left( {Q_{{{\text{sim}},i}} - \overline{Q}_{{{\text{sim}}}} } \right)} }}{{\sqrt {\sum\limits_{i = 1}^{n} {\left( {Q_{{{\text{obs}},i}} - \overline{Q}_{{{\text{obs}}}} } \right)^{2} \times } } \sqrt {\sum\limits_{i = 1}^{n} {\left( {Q_{{{\text{sim}},i}} - \overline{Q}_{{{\text{sim}}}} } \right)^{2} } } }}$$

(9)

$${\text{MAE}} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {Q_{{{\text{obs}},i}} - Q_{{{\text{sim}},i}} } \right)} }}{n}$$

(10)

$${\text{CMA}} = \left| r \right| \times \frac{{\min \left( {\overline{Q}_{{{\text{sim}}}}^{2} ,\overline{Q}_{{{\text{obs}}}}^{2} } \right)}}{{\max \left( {\overline{Q}_{{{\text{sim}}}}^{2} ,\overline{Q}_{{{\text{obs}}}}^{2} } \right)}} \times \frac{{\sum\nolimits_{i = 1}^{n} {\min \left( {\left( {Q_{{{\text{obs}},i}} - 3\overline{Q}_{{{\text{obs}}}} } \right)^{2} ,\left( {Q_{{{\text{sim}},i}} - 3\overline{Q}_{{{\text{obs}}}} } \right)^{2} } \right)} }}{{\sum\nolimits_{i = 1}^{n} {\max \left( {\left( {Q_{{{\text{obs}},i}} - 3\overline{Q}_{{{\text{obs}}}} } \right)^{2} ,\left( {Q_{{{\text{sim,}}i}} - 3\overline{Q}_{{{\text{obs}}}} } \right)^{2} } \right)} }}$$

(11)

$${\text{KGE}} = 1 - \sqrt {\left( {r - 1} \right)^{2} + \left( {\frac{{\sigma_{{{\text{sim}}}} }}{{\sigma_{{{\text{obs}}}} }} - 1} \right)^{2} + \left( {\frac{{\overline{Q}_{{{\text{sim}}}} }}{{\overline{Q}_{{{\text{obs}}}} }} - 1} \right)^{2} }$$

(12)

where f_p is the power factor.

NSE demonstrates how fit the simulation mimics the observation, and it varies between –∞ and 1.0, with the value of 1.0 denoting a perfect match. A value greater than 0.5 for NSE is considered acceptable [80]. MAB and MAE denote the bias and mean error magnitude between modelled and observed values. The value of MAB and MAE equal to 0 signifies an unbiased model [81]. RRM was considered in this study instead of the root mean squared error because it is unitless and has a small value, making it suitable to compare with MAB. The values of R_e and I_a range between 0 and 1. A value of 1 designates perfect match between simulated and observed, while 0 implies total divergence. I_a is known for its insensitivity to systematic model overestimation and underestimations [77]. In this study, the values of f_p = 1 were used to balance between high flows and low flows [76, 81]. However, the value of f_p can be greater than 1 if the model evaluation is focused on high flows. R quantifies how much the observed dispersion is explained by the simulation. R ranges between 0 and 1. A value of 1 means perfect prediction of the modelled dispersion to the observed, and 0 indicates no correlation. This indicator has a weakness, as it only measures the dispersion, hence it is not recommended to be used solely [76]. The values of CMA range from 0 to 1 with CMA equal to 1 signifying a perfect model, while CMA equal to 0 indicates that the model simulations do not match the observations [38]. Similar to NSE, a value of KGE equal to one denotes a perfect agreement between observations and simulation [82].

3.1.1 Comparison of the model performance based on the “nine goodness-of-fit” measures

For the three periods of calibration (01/01/1999 to 31/12/2009), validation (01/01/2010 to 31/12/2016), and entire data period (01/01/1999 to 31/12/2016), models were ranked from 1 to 7 denoting the best and worst performance, respectively. Ranking was initially done based on individual “goodness-of-fit” statistic. For instance, a model with the highest (lowest) KGE was allocated rank 1 (7), indicating best (worst) model. This was done for all the nine metrics. The summation of ranks for the three periods (calibration, validation and entire period) were obtained for the nine metrics (NSE, MAB, MAE, RRM, R_e, I_a, R, CMA, and KGE). The model with the smallest (largest) sum of ranks for each individual metric was considered the best (worst).

3.2 Amplitude–duration frequency analyses

To facilitate planning, design and operation of various water management projects against weather events (such as floods, drought) and/or to reduce human and economic losses, there is need to understand the hydrological extremes and their frequency at selected temporal scales [83, 84]. This can be through extreme value analysis on the hydrological time series for different aggregation levels, which generates Amplitude–Duration–Frequency (ADF) relationships. ADF for discharge and rainfall are called Flow–Duration Frequency (FDF) and Intensity–Duration Frequency (IDF), respectively. In this study, only the FDF are developed for both observed and modelled flow for each of the seven hydrological models. Aggregation simply converts fine resolution data into coarser time units, e.g. from daily to monthly, which hydrologically implies representing a delayed response of a watershed [85]. Here, aggregated hydrological time series were obtained by use of n-day moving window. Aggregation levels are selected with the consideration of appropriate water resources management aspects such as floods and drought in agriculture and domestic water supply. The considered aggregation levels ranged from 1 day to 3 months (1, 3, 5, 7, 10, 30, 60, 90 days) for high flows and 1 day to 1 year (1, 10, 30, 90, 150, 180, 240, 365 days) for low flows. The adopted aggregation levels were applied and/or recommended in previous studies [81, 86, 87].

While analyses of high flows were based on aggregation of original flow series $(X)$, for low flows, the original flows were transformed as $\left( {{1 \mathord{\left/ {\vphantom {1 X}} \right. \kern-\nulldelimiterspace} X}} \right)$. The transformed flow series now follows exponential or Generalised Pareto Distribution (GDP) [88] as an alternative of the Weibull or Fréchet distribution. Besides, the transformation makes it possible to perform extreme value analyses on both high and low flows following the same approach. Taking $x_{{\text{t}}} ,\beta \,{\text{and}}\,\lambda$ as the threshold, scale and shape parameters, respectively, and considering ${1 \mathord{\left/ {\vphantom {1 X}} \right. \kern-\nulldelimiterspace} X}$ as $H$, calibration of the exponential extreme value distribution, above the defined threshold $h_{{\text{t}}}$, follows the following expressions as clearly described by Onyutha [85].

$$G\left( h \right) = P\left\{ {H \le h\left| {H \ge h_{t} } \right.} \right\} = 1 - \exp \left\{ { - \frac{{\left( {h - h_{t} } \right)}}{\beta }} \right\} \, .$$

(13)

Assuming $x_{{\text{t}}} = {1 \mathord{\left/ {\vphantom {1 {h_{{\text{t}}} }}} \right. \kern-\nulldelimiterspace} {h_{{\text{t}}} }}$, Eq. (13) becomes:

$$\begin{gathered} G\left( h \right) = P\left\{ {X \le x\left| {X \ge x_{{\text{t}}} } \right.} \right\} = P\left\{ {H \le h\left| {H \ge h_{{\text{t}}} } \right.} \right\} \hfill \\ G\left( h \right) = 1 - P\left\{ {H \le h\left| {H \ge h_{{\text{t}}} } \right.} \right\} \, \hfill \\ \end{gathered}$$

(14)

$$\begin{gathered} G\left( h \right) = \exp \left( { - \frac{{h - h_{{\text{t}}} }}{\beta }} \right){\text{ = exp}}\left( { - \frac{{x_{{\text{t}}} - x}}{{x_{{\text{t}}} x\beta }}} \right) \, \hfill \\ G\left( h \right) = P\left\{ {X \le x\left| {X \le x_{{\text{t}}} } \right.} \right\}{\text{ = exp}}\left( { - \frac{{x_{{\text{t}}} - x}}{{x_{{\text{t}}} x\beta }}} \right). \, \hfill \\ \end{gathered}$$

(15)

Considering the values lower than $x_{{\text{t}}}$, Eq. (15) matches the Fréchet distribution $G\left( x \right) = \exp \left( { - {{x^{ - \kappa } } \mathord{\left/ {\vphantom {{x^{ - \kappa } } \beta }} \right. \kern-\nulldelimiterspace} \beta }} \right)\,{\text{where}}\,\,\kappa = 1$.

The subsequent step after aggregation of the time series was the extraction of independent hydrological extreme events. This was done for each aggregation level, for both high and low flows. Two main approaches exist for extracting extreme hydrological events and these include the Peak-Over-Threshold (POT) and the Annual Maxima Method (AMM) techniques [89, 90]. While the AMM is simple and generates extreme events that have high independence, the number of events can be few particularly for the short data record length as they generate only one event per year. On the other hand, the POT technique generates a satisfactory number of extreme events above the set threshold [91]. Nevertheless, closely successive flood peaks could actually be a one flood, because the damage results from the highest and the related peaks may only have indirect contribution effects [90]. In this study, both the AMM and POT approaches were used. The AMM-generated independent events were used to compare the model performance in reproducing annual maxima and minima flows, while the POT-generated independent events were used for frequency analysis of hydrological extremes (in construction of FDF curves).

Several tools for extracting POT values exist including the WETSPRO: Water Engineering Time Series Processing tool [92], and Frequency Analyses considering Non-Stationarity (FAN-Stat) [93]. The study by Mubialiwo et al. [46] revealed the presence of trends and shifts in the rainfall and potential evapotranspiration over the study area. Since the same meteorological datasets (rainfall and potential evapotranspiration) were used in this study as inputs in the hydrological models, the generated flows were presumed to exhibit non-stationarity. Therefore, the FAN-Stat tool that considers non-stationarity was adopted to obtain the independent POT value. The FAN-Stat tool was downloaded freely online via https://sites.google.com/site/conyutha/tools-to-download (accessed: 10 February 2021). Using the extracted POT events, the extreme value distribution (EVD) was fitted to the independent extreme high and low flow events. According to Segers [94], in extreme value theory, a conditional probability distribution of independent extreme events follows a Generalised Pareto Distribution (GPD), if only values above an appropriately high threshold $x_{t}$ are used such that:

$$G\left( x \right) = 1 - \exp \left\{ { - \frac{{\left( {x - x_{t} } \right)}}{\beta }} \right\}\,{\text{for}}\,\lambda = 0$$

(16)

and

$$G\left( x \right) = 1 - \left\{ {1 + \lambda \frac{{\left( {x - x_{t} } \right)}}{\beta }} \right\}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} \lambda }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\lambda $}}}} \,{\text{for}}\,\lambda \ne 0$$

(17)

for values of $\,\lambda = 0$, the generated shape of the distribution tail is “normal” but when $\,\lambda > 0\,\,{\text{or}}\,\,\lambda < 0$, the tail is heavy or light, respectively. For normal tail $\,\left( {\lambda = 0} \right)$, the GPD matches the exponential distribution.

Following the above concept, the distribution tail analysis in River Malaba sub-catchment is done for the high and low extreme river flow events. The weighted linear regression method recently applied by Baig et al. [95] was used to determine the EVD parameters. To compute the EVD parameters in Eq. (16), exponential quantile plot with $- \ln \left[ {1 - G\left( x \right)} \right]$ in the abscissa and $x$ in the ordinate is adopted. The distribution assumes a straight line with a slope equal to $\beta$ that can be computed using Eq. (18) by implementing the weighting factors suggested in Hill [96].

$$\beta_{{\text{t}}} = \frac{1}{t - 1}\left[ {\sum\limits_{i = 1}^{t - 1} {\left( {x_{{\text{t}}} } \right)} } \right] - x_{{\text{t}}}$$

(18)

where $t$ denotes the number of POT events above the selected threshold $x_{t}$.

On the other hand, for parameters of a GPD as in Eq. (17), the plot with $- \ln \left[ {1 - G\left( x \right)} \right]$ in the abscissa and $x$ in the ordinate is used. The GPD appears as a line and the slope approximated to $\lambda$.The slope value of $\beta$ in the GPD expression (Eq. 17) can be computed using Eq. (19), and the shape parameter $\lambda$ can be estimated by the least square weighted linear regression assuming the weights suggested in Hill [96] as shown in Eq. (20).

$$\beta_{{\text{t}}} = \lambda_{{\text{t}}} \times x_{{\text{t}}}$$

(19)

$$\lambda_{t} = \frac{1}{t - 1}\left[ {\sum\limits_{i = 1}^{t - 1} {\ln \left( {x_{i} } \right)} } \right] - \ln \left( {x_{t} } \right).$$

(20)

The finest value of $x_{{\text{t}}}$ is selected from the exponential Q–Q plot at the point with minimum mean squared error (MSE). The MSE of the respective weighted linear regressions in EVD and GPD can be obtained from Eqs. (21, 22), respectively.

$${\text{MSE}}_{{\text{t}}} = \frac{1}{t - 1}\left[ {\sum\limits_{i = 1}^{t - 1} {\left( { - \ln \left( \frac{i}{t} \right)} \right)^{ - 1} .\left( {x_{i} - x_{{\text{t}}} - \beta_{{\text{t}}} \ln \left( \frac{t}{i} \right)} \right)^{2} } } \right]$$

(21)

$${\text{MSE}}_{t} = \frac{1}{t - 1}\left[ {\sum\limits_{i = 1}^{t - 1} {\left( { - \ln \left( \frac{i}{t} \right)} \right)^{ - 1} .\left( {\ln \left( {\frac{{x_{i} }}{{x_{t} }}} \right) - \lambda_{t} \ln \left( \frac{t}{i} \right)} \right)^{2} } } \right].$$

(22)

After calibration of the distribution and establishing the parameters, flow quantiles were computed. By taking $n$ to be the data record length in years (in this case 18 years) and $r$ as the rank of the generated POT extreme events (with 1 allocated to the highest POT values), the theoretical return period $T$ based on the calibrated distribution was computed (Eq. 23). Similarly, the empirical return period (Eq. 24) was determined.

$$T({\text{years}}) = \left( \frac{n}{t} \right)\frac{1}{{1 - G\left( {X_{T} } \right)}} = \frac{n}{{t \times \exp \left( { - \frac{{\left( {x - x_{{\text{t}}} } \right)}}{\beta }} \right)}}$$

(23)

$$T({\text{years}}) = \left( \frac{n}{r} \right)$$

(24)

where $X_{{\text{T}}}$ is the flow value corresponding to $T$ obtained from Eq. (24). $t$ was previously defined as the rank of the threshold values. $\left[ {1 - G\left( x \right)} \right]$ is the fitted EVD.

To carry out an extrapolation of the flow quantiles, Eqs. (25) and (26) can be used for exponential distribution and generalise Pareto Distribution, respectively.

$$X_{{\text{T}}} = x_{{\text{t}}} + \beta \left\{ {\ln \left( T \right)} \right\} - \ln \left( \frac{n}{t} \right)\,{\text{for}}\,\lambda = 0$$

(25)

$$X_{{\text{T}}} = \exp \left( {\ln \left( {x_{{\text{t}}} } \right) + \lambda \left\{ {\ln \left( T \right) - \ln \left( \frac{n}{t} \right)} \right\}} \right)\,{\text{for}}\,\lambda \ne 0.$$

(26)

The flow quantiles were extrapolated to a particular return period (e.g. 25, 50, 100 years) for various purposes of water resources engineering applications such as determining the return period of an historical flow event. It is worth noting that in this study, extrapolation of quantiles is based on data of 18 years (1999 to 2016). However, the study by Schulz K, Bernhardt M [97] discovered that extrapolations of quantiles for higher return periods (say 100 years) based on series of short-term can bring about large uncertainties. To minimise the possible uncertainties resulting from a small sample size, extrapolation of quantiles should not be for a return period greater than three times the record length (in years) of the data being used for analysis [87]. Using the calibrated distribution parameters, the FDF relationships comprising of the accumulated values of flow for all the aggregation levels at three return periods (25, 50 and 100 years) were developed for both high and low flows. Lastly, the average model biases in replicating the observed high and low-flow quantiles at different aggregation levels were computed based on Eq. (5).

4 Results and discussion

4.1 Model performance for the calibration, validation and entire data period

Figure 3 shows the graphical comparison of observed and simulated river flow time series from the seven rainfall–runoff models. The set of parameters used to attain results in Fig. 3 are included in Supplementary Material M2 (see Table M1). It is noticeable from Table M1 that optimised parameters were all with in the allowable ranges for each model. There is noticeable underestimation of the peaks especially by TANK, IHACRES, SMAR and HMSV (Fig. 3c–d, f–g). There was an underestimation of low flows by IHACRES, SIMHYD and SMAR (Fig. 3d–f).

Fig. 3

Observed discharge and simulated flows using a AWBM, b SAC, c TANK, d IHACRES, e SIMHYD, f SMAR, g HMSV

It is worth noting that calibration of a model based on total catchment water balance allocates more value to the high flows than low flows [81]. Nonetheless, generally all the models well reproduced the pattern in the observed flow.

Figure 4 shows ranking of the model performance based on NSE (Fig. 4a) and KGE (Fig. 4b) “goodness-of-fit” statistics. Additional information of model ranking (based on the remaining seven metrics (MAB, RRM, Re, Ia, R, MAE, CMA)) can be obtained in Supplementary Material M2 Fig. M8a–g. Generally, AWBM had the smallest rank (1) hence, exhibiting the best performance (Fig. 4a,b and Supplementary Material Fig. M8a–f)). However, when based on CMA (Supplementary Material M2 Fig. M8g, AWBM ranked third after SAC and Tank. In several past studies [36, 81], AWBM exhibited superlative performances. On the other hand, SMAR exhibited unsatisfactory performance with NSE of 0.46, 0.28 and 0.44 for calibration, validation and entire period, respectively (Fig. 4 and Table 3). All models had NSE values above 0.50 (except SMAR).

Fig. 4

Model performance in terms on ranking based on a Nash–Sutcliffe Efficiency (NSE), b Kling–Gupta efficiency (KGE). Ranks 1 and 7 denote best and worst performing model, respectively

Table 3 Statistical performance evaluation of the models

The nine “goodness-of-fit” measures used for the calibration, validation and entire periods of the seven models are shown in Table 3. All models (except SMAR) exhibited laudable performance in simulating flows in the catchment. The values of NSE varied between 0.46 to 0.83, 0.28 to 0.81 and 0.44 to 0.84 for calibration, validation and entire period, respectively. The best performance was obtained with the entire period, followed by the calibration period. Statistically, the best model performance would be shown by MAB of 0%. However, in this study, the MAB values varied amongst the models with some exhibiting negative, while others showed positive. This discrepancy in the MAB value amongst the models could be attributed to the varying model structures used to convert rainfall into runoff. The values of RRM ranged between 0.048–0.085 and 0.069–0.133, for calibration and validation, respectively. Of the seven models, AWBM had the smallest value, while SMAR exhibited the largest values of RRM (Table 3). Based on R_e and I_a, the best performance of a model would be indicated by a value of 1. Nevertheless, highest R_e and I_a values of 0.595 and 0.798, respectively, were obtained by the AWBM. The lowest R_e and I_a values of 0.242 and 0.635, respectively, were realised by the SMAR. This further attests the unsatisfactory performance of SMAR. The values of R ranged between 0.712–0.917 and 0.552–0.901, respectively, for calibration and validation periods. This indicates that for all the models, the modelled dispersion to the observed was generally well predicted. The MAE values did not vary much amongst the models, except for SIMHYD and SMAR that slightly varied from other models. The values were within the ranges of 5.0–9.6 m³s⁻¹ and 6.6–14.2 m³s⁻¹, respectively, for the calibration and validation periods.

By using the CMA, the best model performance would be shown by the value of 1. In this study, SAC had the highest value (0.791) followed by HMSV (0.725) for the calibration period (Table 3). Considering the validation period, SAC still had the highest value (0.807) followed by TANK (0.745). For both calibration and validation period, SMAR had the smallest values of 0.466 and 0.293, respectively. Considering the KGE metric, AWBM performed best followed by SAC and TANK while SMAR performed last for all the periods. Generally, it can be concluded that the SMAR model performed worst, while AWBM performed finest based on the nine considered statistical indicators. However, in some studies, e.g. Onyutha et al. [36], SMAR generally performed better than SAC and TANK models. This could be attributed to the varying spatial resolution of catchments such as the size, climate, geology, landscape and hydrological data [70, 81]. In some cases, the lumped conceptual models have been found to perform better than physically based models. For instance in the study by Jaiswal et al. [98], for calibration, AWBM and TANK yield NSE values of 0.76 and 0.84, respectively, while SWAT had NSE of 0.75. However, in other areas, some rainfall–runoff models can exhibit unsatisfactory performances. For instance, the study by Pérez-Sánchez et al. [68], that compared six hydrological balance models (Témez, ABCD, GR2M, AWBM, GUO-5p and Thornthwaite-Mather) in several basins within Spain, AWBM model did not perform well.

Figure 5 shows the performance of models based on compiled values of ranking from all the nine “goodness-of-fit” measures constrained to the catchment total water balance. This followed a procedure described in Sect. 3.1.1. Production of Fig. 5 considered the performance of models during calibration, validation and entire period (Table 3). It is noticeable from Fig. 5 that AWBM performed best followed by SAC, while SMAR performance last. It should be noted that performance of these models can vary based on the catchment of application. For instance, while TANK was amongst the best 3 models in this study, the study by Onyutha et al. [36], that compared the performance of several lumped conceptual models in the simulation of daily River Kafu flows, TANK did not perform better. In the same study [36], SMAR generally performed well.

Fig. 5

Assessment of model performance based on compiled values of ranking from all the nine “goodness-of-fit” considering the overall water balance. The best performing model is ranked 1 while the worst takes rank 7

4.2 Comparison of model performance in simulating annual maxima and annual minima flow events

Figures 6 and 7, respectively, show the performance of models to simulate annual maxima and minima flow events in each year. For a superlative model, all the observed and simulated scatter points would be plotted along the 45° line.

Fig. 6

Model performance assessment based on comparison of observed and simulated annual maxima flows in each year for a AWBM, b SAC, c TANK, d IHACRES, e SIMHYD, f SMAR, g HMSV, Sim. stands for simulated, while Obs. means observed

Fig. 7

Model performance assessment based on comparison of observed and simulated annual minima flows in each year for a AWBM, b SAC, c TANK, d IHACRES, e SIMHYD, f SMAR, g HMSV; Sim. stands for simulated, while Obs. means observed

It is observed that all the hydrological models simulated high flows (Fig. 6), better than low flows (Fig. 7). AWBM model performed better in simulating annual maxima flow events (Fig. 6a), followed by SACRAMENTO (Fig. 6b), while IHACRES performed last (Fig. 6d). The annual maxima observed flow events beyond 100 ms⁻¹ were slighted underestimated by HMSV and TANK models (Fig. 6c,g). It is evident that the annual minima flow events in each year were largely overestimated by AWBM, SMAR and HMSV (Fig. 7a,f and g). However, SAC, IHACRES, SIMHYD models underestimated the low flow events (Fig. 7b,d,e). It is only TANK model exhibited a somewhat realistic balanced over- and underestimation with scatter points falling on both sides of the 45° line (Fig. 7c). Generally, HMSV model exhibited the best performance (Fig. 7g), while the SMAR performed last (Fig. 7f) in simulating annual minima.

The performance of hydrological models based on compiled values of ranking from all the nine “goodness-of-fit” measures considering the annual maxima and minima flows in each year is shown in Figs. 8 and 9. Like in Fig. 5, Figs. 8 and 9 are obtained based on the procedure explained in Sect. 3.1.1. Similar to the observations in Table 3 and Figs. 3, 4 and 5, AWBM model performed better than other models in simulating the annual maxima series, except when based on the MAB statistical indicator (Fig. 8). Similarly, SAC model performed second best. While Fig. 5 shows that SIMHYD and SMAR performed last, these two models exhibited commendable performance in simulating annual maxima flows. Instead, IHACRES, TANK and HMSV portrayed the worst performances. By considering the annual minima series, largely HMSV had the best performance, followed by AWBM and TANK (Fig. 9). Similar to the observations in Fig. 5, SMAR, SIMHYD and IHACRES performed last in simulating annual minima flow events (Fig. 9).

Fig. 8

Assessment of model performance based on compiled values of ranking from all the nine “goodness-of-fit” considering the annual maxima flows. The best performing model is ranked 1 while the worst takes rank 7

Fig. 9

Assessment of model performance based on compiled values of ranking from all the nine “goodness-of-fit” considering the annual minima flows. The best performing model is ranked 1 while the worst takes rank 7

4.3 Amplitude–duration frequency analyses

In this study, the extreme value distribution tail analysis at all aggregation levels showed a normal tail for the exponential quantile–quantile (Q–Q) plot for both high and low flow events. For instance, results of the calibrated exponential distribution obtained at 1-day aggregation level for high and low flows are shown in Figs. 10 and 11, respectively. In the same figures, empirical and extrapolated quantiles are shown. In all cases, linearity behaviour in the quantiles was realised towards the tail of the distributions. While the exponential plot was adopted to obtain the linear behaviour of the quantiles, log-transformation was applied to the return period T on the x-axis. Towards the tail of the distribution, the mismatch between the empirical and modelled quantiles gest systematically larger than those for small return periods. This tends to result from the influence of flooding on flow measurement stemming from the bias in rating curve extrapolation or the difference between the river discharge and the catchment rainfall–runoff discharge [87]. Censoring out outliers prevents underestimation of flow which could result from assuming a light instead of normal tail. Assuming a light tail may result in underestimation of design quantiles for sizing water infrastructures such as bridges. In the Supplementary Material M3 Figs. M12 to M17, exponential Q–Q plots obtained at different aggregation levels for both high (5, 30 and 90 days) and low flows (30, 180 and 365 days) are provided.

Fig. 10

Comparison of exponential quantile–quantile plot for the high flow POT events considering 1-day aggregation level. The markers represent the empirical, solid lines signify theoretical (calibrated distribution), while dashed lines represent extrapolated quantiles

Fig. 11

Comparison of exponential quantile–quantile plot for the low flow POT events considering 1-day aggregation level. The markers represent the empirical, solid lines signify theoretical (calibrated distribution), while dashed lines represent extrapolated quantiles

Considering the high flows (Fig. 10), the frequency curve for SIMHYD and SMAR showed substantial deviations from the observed curve for the estimated flows especially at higher return periods, while AWBM, SAC, TANK, IHACRES and HMSV frequency curves did not display substantial deviations. From Fig. 10, the return period for an average 1-day flood of 150 m³s⁻¹ is 24 years based on the observed flow curve, while the same event has a return period of 17 years for an evaluation based on AWBM model. However, when considering the HMSV model, the same event will have a return period of 30 years, while for the SIMHYD model, the return period is 10 years.

It is noticeable that for low flows (Fig. 11), the actual quantiles were attained after back transformation of the (1/X). In view of the low flows (Fig. 11), SMAR, SIMHYD and IHACRES flow curves exhibited large deviations from the observed quantile even at return periods less than 1 year. The AWBM, SAC, TANK and HMSV flow curves have close agreement with the observed quantiles throughout all the return periods (despite slight deviations on the extrapolated quantiles). The extrapolated quantiles for high flows can be relevant for vigilant flood analysis which can guide the planning and designing of risk-based water engineering structures such as bridges and slipways. Similarly, the extrapolated quantiles for low flows can be relevant for cautious drought analysis which is key in water resources management aspects such as determining irrigation water for agriculture and domestic water supply.

The ADF relationships considering all the aggregation levels are shown in Figs. 12 and 13 for high and low flows, respectively. These were generated from the quantiles projected based on the EVD. For high flows, it is shown that SMAR (Fig. 12f) overestimated the high-flow quantiles for the aggregation level of one day. However, for aggregation levels higher than 3 days, SMAR underestimated the high-flow quantiles, except at 60 and 90 days. For all aggregation levels, SIMHYD (Fig. 12e) overestimated the high-flow quantiles particularly for the return periods of 25 and 100 years. For all aggregation levels, considering the AWBM, SAC, TANK, HMSV (Fig. 12a–c, g), the observed and simulated high-flow quantiles were generally in close agreement. The underestimation of high-flow quantiles at higher aggregation levels by SMAR could be attributed to the model inadequacy in capturing higher quantiles in the extreme value distribution tail. Similarly, the overestimation or underestimation of flow quantiles at one-day aggregation level could be linked to the high noise in flow time series at low aggregation levels, resulting in uncertainties in calibration of the extreme value distribution.

Fig. 12

The FDF plots for high extreme observed and simulated flows obtained at different aggregation levels (1–90 days) for a AWBM, b SAC, c TANK, d IHACRES, e SIMHYD, f SMAR, g HMSV obtained at 25-, 50- and 100-year return periods. In the legend, dashed lines denote simulated flow, while the markers signify observed flow

Fig. 13

The FDF plots for low extreme observed and simulated flows obtained at different aggregation levels (1–365 days) for a AWBM, b SAC, c TANK, d IHACRES, e SIMHYD, f SMAR, g HMSV obtained at 25-, 50- and 100-year return periods. In the legend, dashed lines denote simulated flow, while the markers signify observed flow

Considering the low flows, IHACRES, SIMHYD and SMAR (Fig. 13d–f) underestimated the low-flow quantiles. However, for AWBM, SAC, TANK, HMSV (Fig. 13a–c, d), the quantiles from the observed and simulated low flows were comparable, except at aggregation level of one day with noticeable overestimation.

The model biases in reproducing high and low quantiles at different aggregation levels are shown in Tables 4 and 5, reactively. From Table 4, SIMHYD exhibited positive biases at all aggregation level indicating an over estimation of high-flow quantiles. Except for the one-day aggregation level, SMAR showed an underestimation of high-flow quantiles. For low flows (Table 5), IHACRES, SIMHYD and SMAR showed large negative biases at all aggregation levels signifying an underestimation of low-flow quantiles. HMSV showed positive biases throughout (except for 150 days aggregation level), and on average it exhibited the smallest biases compared to other models.

Table 4 Model biases (%) in simulating high-flow quantiles

Table 5 Model biases (%) in simulating low-flow quantiles

4.4 Explanation of the differences in performance of the various models

As earlier noted, all the seven rainfall–runoff models (AWBM, SAC, TANK, IHACRES, SIMHYD, SMAR and HMSV) simulated the high flows better than the low flows. The study Staudinger et al. [99], that assessed the impact of model structure on low flow simulation, established that most rainfall–runoff models poorly reproduce low flows because their structures are largely designed to mimic high flows. Li et al. [100] also stressed that the structure of a model may influence its performance. However, in this study, the variability in model performance could not evidently be attributed to the differences in model structures. This is because various models performed either better under the consideration of total water balance and/or extreme hydrological conditions. Generally, four models (AWBM, SAC, TANK and HMSV) performed well regarding simulating flows in the catchment. Considering the total water balance, AWBM had the highest NSE values of 0.828 and 0.808 for calibration and validation periods, respectively. In addition, AWBM had the lowest MAB value of 0.186% for the entire period (1999–2016). Equally, AWBM performed better than other models in simulating the annual maxima flows. However, the model came second after HMSV in simulating the annual minima flows.

Model performance in simulating flows could as well be associated with model parameters [101]. For instance, the influence of low flows in most squared residual-based objective functions is low. Models’ parameters exhibited varying sensitivity. In supplementary material M2 Figs. M9–M11, a sample of parameter sensitivity analyses for AWBM, SACRAMENTO, SMAR can be found. AWBM was highly sensitive to higher values (close to 1.0) of base flow recession constant and also relatively sensitive to surface flow recession constant, storage capacity of third store and fraction of catchment area for the first store. However, fraction of catchment area for the second store and storage capacity of second store were almost insensitive parameters with minimal variation in the NSE values (supplementary material Fig. M9). The baseflow index, baseflow and surface runoff recession constant parameters in AWBM could justify the laudable performance of the model in reproducing both high and low flows. Previous studies [36, 81, 102] revealed good performance of AWBM. However, in some cases, the AWBM may not yield better results. For instance, in the study by Pérez-Sánchez et al. [68], that compared six hydrological models including the AWBM, revealed poor performance of the AWBM. Conclusively, it can be stated that the AWBM structure is tailored towards better capturing high flows than low flows.

Similarly, the SACRAMENTO model with a set of seventeen parameters had the second-best performance in simulating flows during calibration and validation and mimicking of the annual maxima flows. Some of the SACRAMENTO parameters exhibited high sensitivity only at small values (e.g. additional fraction of pervious area, exponential percolation rate) while other had high sensitivity at higher values (e.g. fraction of base flow which is groundwater flow, lower zone free water primary maximum). Other parameters were almost insensitive (e.g. upper zone Free water maximum, fraction of water unavailable for transpiration) (supplementary material Fig. M10).

The performance of SIMHYD model with nine parameters was not adequately better for both low and high flow simulation. The study by Li et al. [100], that compared three hydrological models (HBV, SIMHYD and XAJ), revealed lower efficiency of the SIMHYD model. While SMAR model generally had well-identified parameters, three parameters (unit hydrograph linear routing, unit hydrograph linear routing component, infiltration rate) exhibited low sensitivity (supplementary material Fig. M11). This might have resulted in the lower performance of the model. In some studies (e.g. Bashar [103]), SMAR model yielded sufficiently better results. The performance of a model may not be associated with the number of parameters it has [104]. This is because, SACRAMENTO model that could be regarded as being over-parameterised with 17 parameters, performed better than other models with relatively fewer parameters, e.g. SIMHYD (9 parameters), IHACRES (11 parameters), SMAR (9 parameters) and HMSV (10 parameters). Besides, AWBM model with the smallest number of parameters (eight), performed best overall. Although the calibration of HMSV was based on the “step-wise” (sub-flow variation) strategy (calibration baseflow, interflow and overland flows separately), the model did not perform well in simulating annual maxima, despite it performing best in simulating annual minima flows. The commendable performance of HMSV model in simulating low flows could be attributed to the base flow parameter and baseflow recession constant. The credible ranking of HMSV in reproducing annual maxima flow could also be linked to the overland and interflow parameters in the model.

Interestingly, the performance of a model may as well be attributed to the selected “goodness-of-fit” measures [38, 81]. For instance, it is noticeable that for annual minima flows, HMSV generally performed better than TANK model. However, when based on the MAB “goodness-of-fit” metric, TANK model displayed better performance than HMSV. Similarly, for annual maxima flows, AWBM performed far better than other models. However, when based on the MAB, SAC and SMAR models performed better than AWBM. Besides, under the consideration of total water balance, using the CMA and KGE statistical indicators, SAC and TANK model performed better than the AWBM, despite AWBM displaying overall superlative performance. Hence, to strongly conclude on the efficacy of a particular rainfall–runoff model, it is vital to assess its performance using various “goodness-of-fit” statistics as implemented in this study.

5 Conclusion

Previous studies conducted to evaluate several conceptual rainfall–runoff models (AWBM, SACRAMENTO, TANK, IHACRES, SIMHYD, SMAR and HMSV) performances based on multiple “goodness-of-fit” metrics in simulating hydrological extremes in River Malaba sub-catchment are lacking. This study analysed seven lumped conceptual rainfall–runoff models based on nine “goodness-of-fit” measures in simulating hydrological extreme of River Malaba sub-catchment. Because of the poor distribution of meteorological stations, with the existing ones having few data available in the recent years, in addition to the uncertain and questionable quality, this study was based on PGF meteorological dataset recorded from 1999 to 2016. Bias correction in the PGF data was performed using the simple multiplicative bias correction method. Daily River Malaba observed flow time series at Budumba station were used in model calibration and validation. Considering the total water balance, largely the models (except SMAR) well reproduced the observed flow pattern. All the models (except AWBM, TANK and HMSV), largely underestimated the base flow. Generally, AWBM performed better than other models with NSE of 0.83 for calibration, while SMAR performed last with NSE of 0.46.

The seven rainfall–runoff models simulated the high flows better than the low flows. This could be attributed to the structure of most rainfall–runoff models tailored at reproducing high flows better than the low flows. By designing hydrological model structures flexible in capturing both high and flow flows could avert the situation. The AWBM model performed better than other models in simulating annual maxima flow events. The annual minima flow events in each year were largely overestimated by AWBM, SMAR and HMSV, but underestimated by the SAC, IHACRES, SIMHYD models. Largely HMSV ranked number one, followed by the AWBM and TANK in simulating annual minima flow events. SMAR, SIMHYD and IHACRES did not exhibit satisfactory performance in simulating annual minima flows.

Flow–Duration Frequency (FDF) analyses yielded a normal tail of the exponential Q–Q plot at the selected aggregation levels for both low and high flows. The frequency curves for SIMHYD and SMAR showed large deviations from the observed curve especially at higher return periods, while AWBM, SAC, TANK, IHACRES and HMSV frequency curves did not display substantial deviations. For the same flood event, different models yielded varying return periods. For instance, the return period for an average 1-day flow of 150 m³s⁻¹ is 24 years based on the observed flow curve, while the same event has a return period of 17 years for an evaluation based on AWBM model. However, using the HMSV model, the same event will have a return period of 30 years, while for the SIMHYD model, the return period is 10 years. The discrepancy in mimicking the observed frequency curves by different models demonstrates how implicit determination of the return period for a particular flow event can vary depending on the considered hydrological model. For the low flows, SMAR, SIMHYD and IHACRES flow curves exhibited large deviations from the observed curve even at return periods less than 1 year. The AWBM, SAC, TANK and HMSV flow curves had close agreement with the observed curves throughout all the return periods.

The simulated high-flow quantiles from AWBM, SAC, TANK, HMSV and the observed were generally in close agreement. However, SMAR and SIMHYD underestimated and overestimated high-flow quantiles, respectively. IHACRES, SIMHYD and SMAR underestimated the low-flow quantiles. With AWBM, SAC, TANK, HMSV, the quantiles from the observed and simulated low flows were comparable. All models exhibited varying biases (positive and/or negative) in reproducing the extreme flow quantiles. The differences in biases designate the influence of model selection for hydrological extreme analysis. The biases could be attributed to errors in model inputs (in this case, rainfall and PET) or in the observed flows used for model calibration and validation. Errors in observed flow could be due to flooding influence or due to wrong extrapolation made by the rating curve [105]. Flooding influence results in down bending of the rating curve to lower water levels hence leading to underestimation for higher flows. Besides, the errors in estimating the EVD parameters especially the slope parameter $\beta$ might have contributed to the biases. However, in spite of accurate estimation of parameters, an extrapolation outside the calibration and validation periods of a distribution can be very erroneous.

By simultaneously considering the overall assessment of high and low flows, AWBM slightly performed better than other models in simulating hydrological extreme in River Malaba sub-catchment, while SMAR ranked last. A few limitations to this study and recommendations for future research studies are worth stating. The study adopted the computation of bias correction factors for PGF data without distinguishing between seasons but rather monthly values were used. It is likely that omitting seasonal difference in the analysis might yield biased results due to blind temporal relationship. To even out the possible uncertainties in the computed bias factors, it is recommended that future research studies consider seasons and temporal changes. Besides, the uncertainties in the use of uncalibrated empirical Hargreaves method for PET estimation should be quantified in future research. Future research studies may also evaluate the hydrological models’ performance without bias correction of PGF data. The study by Mubialiwo et al. [46] revealed the presence of trends and shifts in the rainfall and potential evapotranspiration over the study area. Since the same meteorological datasets (rainfall and potential evapotranspiration) were used in this study as the inputs in the hydrological models, the generated flow is presumed to contain trends and sub-trends, which could indicate possible surge of flooding events and/or severity of hydrological droughts. However, this was not analysed in this study and is recommended for investigation in the future research studies. Furthermore, the impact of human factors (e.g. land use) and climate variability on water resources in the River Malaba sub-catchment should be investigated by future research.

Even with the above-mentioned limitations (which may be addressed by the suggested future research studies), this study provides relevant information for planning of risk-based water resources applications. The flow data from the best hydrological model (AWBM) can be used for many applications in water resources management. For instance, the FDF relationships can be used to construct rainfall–runoff design hydrographs as inputs in the hydrodynamic flood model to simulate discharge at different locations along the river. The simulated discharge can then be applied in the design of flood protection systems and calculation of flood maps for different return periods in the study area. Besides, FDF relationships can be adopted to estimate the return periods of historical flow events. Worth noting is that for the same catchment, even models of the same family (e.g. the “e-Water Toolkit” RRLs) can produce varying results and their performance can differ based on the selected “goodness-of-fit” measures. Therefore, it is necessary to compare results from various models prior to selection of a particular model to support decision regarding water resources management application, e.g. simulating flows that can support floods or drought analysis.