1 Introduction

The offshore wind power industry is an emerging and exponentially growing sector expected to be the main source of energy in a near future, where Europe is currently the leader of this initiative due to the wind energy potential in shallow waters that is available in the North Sea [2]. The increase in the implementation of this type of energy calls to a necessity for a cyclical monitoring and inspection to ensure the safety and efficiency of the wind farm facilities.

The current Operations and Maintenance (O&M) methodologies used on offshore wind farms (e.g. inspection tasks) are highly human dependent, long, challenging, dangerous and greatly conditioned by environmental constraints, mainly in Winter time. Currently, it uses Remotely Operated Vehicles (ROVs) and divers for the underwater components, and rope access and tele-operated Unmanned Aerial Vehicles (UAVs) for the dry parts. Therefore, the application of autonomous vehicles would be beneficial for monitoring and inspection creating cost-effective O&M strategies ensuring repeatability and less risk for human life [3]. For instance, the introduction of bathymetry and 3D reconstructions of the dry components can aid and enhance the retrieved information in several inspection processes, such as scour protection integrity and transition piece defects inspections [4]. As well, with the usage of autonomous vehicles the process can be automated and more standardized. Moreover, current initiatives such as the European project ATLANTIS [5] will provide powerful tools towards the research for O&M tasks.

Nevertheless, the different domains of the marine environment, emersed and immersed domains, inflicts distinct constraints on the sensor availability and performances for autonomous vehicles. This leads to the usage of different vehicles for each task. Nowadays marine robotics research usually focus in the work on a single domain for specific tasks using ROVs and Autonomous Underwater Vehicles (AUVs) for the immersed region and Autonomous Surface Vehicles (ASVs) for the emersed domain in structure reconstruction or immersed for bathymetric data.

In this context, the research presented in this work, extended from [1], proposes the use of a single ASV equipped with navigation sensors (GPS and IMU) and perception sensors (3D Lidar and a Multibeam echosounder sonar, MBES) to perform real-time survey tasks for both emersed and immersed regions simultaneously. Therefore, it allows the creation of a complete 3D representation of the scenario that can be used for visual inspection or, even, to enhance the information provided to obstacle avoidance and autonomous docking techniques.

For the multi-domain mapping methodology, an architecture is proposed that evaluates the vehicle odometry using the navigation sensors to provide a reference towards an initial guess of the system state. Moreover, several filtering and data modality modification methodologies are proposed to reduce the impact of the heterogeneous data provided by the perception sensors. Also, an outlier filter, registration and organization methods will enhance the data alignment and create the reconstruction. As so, this architecture is expected to provide a guideline to improve scene understanding for O&M and proposing an adaptable infrastructure to different distance measurement sensors, e.g. the MARESye [6].

Therefore, the major contributions of this paper include:

  • ASV localization methodology using typically available sensors without requiring external features;

  • Generation of 3D maps for the immersed region using a multibeam echosounder. Thus, it tackles challenges to data fusion related to low update rate, noisy and non-correlated measurements due to the limited field-of-view.

  • Creation of 3D maps for the emersed region using sparse point clouds obtained with a low-resolution Lidar;

  • Development of a generic multi-domain mapping architecture for ASVs to reconstruct the scenario using heterogeneous sensors, with range data acquisition capabilities, operating in both the emersed and immersed regions.

The paper presents a revision of related work in Sect. 2. In Sect. 3 is described the application scenario. The architecture for multi-domain mapping is described in Sect. 4 and, subsequently, all the processes considered to create a full representation, namely the GPS-IMU fusion, data filtering and modality transformation, and the data registration method. The results of the proposed method are presented in Sect. 5 and, at last, a brief conclusion appears in Sect. 6.

2 Related work

Marine robotics presents a vast number of possible applications, such as exploratory missions, oceanography, and inspection and maintenance tasks. For all possible use cases the scenario reconstruction becomes an advantage to better describe the surroundings improving the situational awareness used for multiple purposes, such as:

  • Increase safety, e.g. provide data for obstacle avoidance methodologies [7,8,9];

  • Enhance autonomous deploy/recover procedures, for instance docking of ASVs [10];

  • Create 3D representations for visual inspection, such as the inspection of transition pieces of offshore wind turbines or the scour protection integrity [4].

Nevertheless, contrary to aerial or ground robots, where normally the environment is bounded to a single domain, marine robotics is composed by two distinct domains, namely the emersed and immersed regions divided by the water surface. Both domains have different sensor requirements and constraints for mapping technologies. Typical approaches tackles issues on a single domain, using Remotely Operated Vehicles (ROVs) [11], Autonomous Underwater Vehicles [12] or hybrid ROV/AUV solutions [13] on the immersed regions and ASVs [14, 15] on the emersed domain.

To the best of our knowledge approaches for merging both emersed and immersed maps to recreate the full scenario is still a research line with small work dissemination being depicted in the works of Papadopoulos et al. (2014) [16], where the trajectory generated by the emersed sensor is used to register the underwater sonar sensor, and of Leedekerken et al. (2014) [17], where a set of 2D laser scanners and an imaging sonar are combined with a high-accuracy localization unit that fuses GPS-IMU and DVL presenting a SLAM base solution. This two approaches either rely on feature-based localization or in high-cost sensors such as DVL, and do not provide a modular architecture where other perception sensors can be included for the representation. Thus, the multi-domain mapping architecture here presented offers a tool that can reconstruct and fuse the representations from the sensor data through a modality transformation to point cloud. Moreover, it uses typical navigation sensors available on ASV platforms that on open scenarios are capable of estimating the vehicle pose, independently of having distinctive environmental features in the vicinity.

When considering single domains approaches, several methods have been explored, as depicted in Table 1 with the summary of the related work, where E, I and E&I are Emersed, Immersed and Emersed & Immersed, respectively.

Table 1 Summary of the related work approaches
Full size table

3 Problem description

Marine scenarios, such as offshore wind farms, present two very distinct domains, Fig. 1, namely:

  • Emersed Aerial scenario where a higher sensor variety can be used (e.g. GPS and 3D Lidar). The vehicles operating at this environment are disturbed by the tidal waves and wind flowing in this locations. This domain in offshore wind farms is composed by the dry parts of the turbine foundations (fixed or floating) and the turbine itself;

  • Immersed Underwater scenario with several constraints on the available sensors, with higher noise and reduced field-of-view (e.g. Multibeam echosounder, imaging sonar, camera and lighting). In this GPS deprived environment localization presents as difficult task requiring equipment such as Doppler Velocity Log (DVL) and Long baseline acoustic positioning systems (LBL). This domain in offshore wind farms is composed by the wet parts of the turbine foundations (fixed or floating), cable arrays, flotation systems and scour protections.

Fig. 1
figure 1

Different domains of the marine environment

Full size image

Typical inspection tasks of offshore wind farms are done manually or using ROVs. Moreover, current research lines for inspection operations assume the use of distinct vehicles for each domain. In this work, it is proposed to explore the possibility of using a single vehicle to survey both domains creating an unique and complete 3D reconstruction of the visited neighborhood.

Thus, for this work an Autonomous Surface Vehicle (ASV), the INESC TECs’ SENSE vehicle depicted in Fig. 2, composed with a sensor payload capable of operating in both domains was considered. In Table 2 the list of the SENSE sensor payload and respective location frame is provided.

Fig. 2
figure 2

INESC TECs’ SENSE vehicle and payload

Full size image
Table 2 Sensors available in the SENSE and respective frames in Fig. 2b
Full size table

The vehicle is equipped with two distinct navigation sensors, namely: GPS, to acquire an absolute position with high precision capable of providing the latitude and longitude coordinates with a low frequency; and IMU, a dead-reckoning sensor inferring the acceleration, angular velocity and attitude of the vessel at a high frequency. Despite having a RTK solution (Swift Navigation Piksi Multi GPS) providing a high precision localization, the structures (e.g. wind turbines and foundations) will decrease the performance or even deprive the system of this feature, thus it will not be considered as an input (only used for ground-truth when available). Also, the vehicle have distinct perception sensors, namely a stereo camera and a 3D Lidar for the emersed domain, and a Multibeam Echosounder (MBES) for the immersed domain.

Since currently multi-domain datasets or access to a real offshore wind farm environment are not available, this work was developed and tested using a realistic 3D simulator, Gazebo [22]. Distinct offshore wind farms scenarios were recreated using the sensor and dynamic plugins for the emersed areas from the Virtual RobotX [23] and for the immersed region from the UUV Simulator [24]. In the simulation, all the available sensors were modeled to depict, as much as possible, the data type, frequency, resolution, accuracy, error and noise from the real sensor using the specifications in the manufacturers datasheets, as well as the integration of widely used Gazebo sensor plugins, such as the Velodyne VLP-16 plugin.Footnote 1 In Fig. 3 an example of a scenario is presented. In this instance, the SENSE starts in a dock near to the inspection site and to several wind turbines with respective jacket foundations placed at the seafloor, simulating the Burbo Bank Extension offshore wind farm [25]. A randomized seafloor heightmap was also considered for the environment.

Fig. 3
figure 3

Example of the Burbo Bank Extension offshore wind farm scenario

Full size image

For validation, a sample from a dataset acquired on the Marina de Leça harbor with the SENSE was used. The scenario presents several fixed structures (e.g. docks, ramps, walls and a bridge) and dynamic objects, namely vessels. The environment is depicted in Fig. 4.

Fig. 4
figure 4

Marina de Leça harbor scenario

Full size image

4 Architecture for multi-domain mapping

On offshore wind farms, the availability of accurate GPS, RTK and IMU measurements allows a precise localization that contribute to a good representation of the scenario. Nevertheless, the available sensors can produce noisy, imprecise and spurious measurements and the environment dynamics (tidal ripples, currents and wind) can account to the deformation of the representation, producing several effects, such as motion-induced distortion on the sensor measures, outlier data and low vehicle stability. Moreover, the presence of tall structures can generate GPS or RTK deprivation situations. Also, each domain sensor presents disparate information and with distinct modalities which requires distinct preprocessing approaches.

Fig. 5
figure 5

Proposed architecture for the multi-domain mapping

Full size image

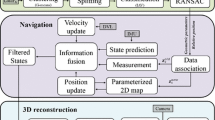
As so, a ROS (Robot Operating System) based pipeline to perform a robust data association for each domain was proposed, Fig. 5, by estimating the odometry of the ASV through a sensor fusion approach, namely of GPS and IMU. Furthermore, the observations of each domain are acquired, filtered and reconstructed. Then, the point clouds are registered to create a complete map, taking the odometry as the initial seed. Thus, an estimation of the error relative to the current pose of the ASV for the aerial and underwater domains (\(e_l\) and \(e_m\), respectively) is acquired and the RMSE fitness of the alignment for each domain (\(c_l\) and \(c_m\)) provides a measure of the data misalignment, which can be used for instance to perform point cloud based odometry.

4.1 GPS and IMU odometry

From the available sensors, absolute position measures are acquired from the GPS (latitude, longitude and altitude) and the vehicle acceleration, angular velocity and attitude from the IMU. From the GPS, the position evolution could be acquired by integrating the displacement between measures. Nevertheless, to establish a geographic location on a map it is required a map projection to convert geodetic coordinates to plane coordinates, by projecting the datum ellipsoidal coordinates and height onto a flat surface. As such, the first step at each iteration is to project the GPS data to the Universal Transverse Mercator (UTM) using the transformation defined in the USGS Bulletin 1532 [26]. This projection will allow to estimate the initial position the evolution throughout time along side with the IMU angular data to obtain the odometry.

To better understand the odometry estimation process, consider a 2D problem example where the vehicle will begin somewhere within the UTM zone at position \((x_{UTM}, y_{UTM})\) converted from the GPS coordinates with the initial orientation at some angle \(\theta\) in relation to the UTM frame X-axis. Such is depicted in Fig. 6, where the vehicle is in \((x_{UTM}, y_{UTM}, \theta )\) on earth, while the odometry (\(x_w,y_w\)) and the robot (\(x_r,y_r\)) frames are coincident at the initial state.

Fig. 6
figure 6

Initial state frames for a 2D example

Full size image

The odometry frame origin point (\(O_w,O_w\)) location will be initialized with the position associated with the initial GPS coordinates acquired in the UTM frame. As for the attitude, it is initialized using initial angular information retrieved from the IMU. From there on, all GPS coordinates in UTM space will be integrated and associated to the respective IMU angular variation estimation.

Nevertheless, the different acquisition rate from both sensors provide a challenge due to out-of-sequence data. To tackle this issue, the fusion of both sensors is handled using an Extended Kalman Filter (EKF) described as a non-linear system, Eq. 1, where \(x_k\) is the robot’s system state (i.e., 3D pose) at time k, f is a nonlinear state transition function, and \(w_{k-1}\) is the process noise, which is assumed to be normally distributed [27]. x is comprised by the 3D position, 3D orientation (Euler angles) and their respective velocities.

$$\begin{aligned} {\hat{x}}_k = f(x_{k-1})+w_{k-1} \end{aligned}$$
(1)

The measures are on the form of Eq. 2 where \(z_k\) is the measurement at time k, h is a nonlinear sensor model that maps the state into measurement space, and \(v_k\) is the normally distributed measurement noise.

$$\begin{aligned} z_k = h(x_{k})+v_k \end{aligned}$$
(2)

During the prediction step the current state estimate and error covariance are projected forward in time using the standard 3D kinematic model derived from Newtonian mechanics used in [28].

The EKF will allow to predict the ASV poses throughout time when no sensor measure exists using the defined motion model and correct them as soon as new data arrives. As so, the input measurements used towards the sensor fusion are the IMU attitude (roll, pitch and yaw) and angular velocity data, and the positional information of an odometry inferred from the GPS and IMU initial state.

4.2 Emersed data filtering

The use of a Lidar sensor on the emersed region provides a vast 3D information near offshore infrastructures and other vessels. Nevertheless, the sparseness of the data and the waves presents a potentially ambiguous set that can produce erroneous estimations of the current point cloud deviation in relation to the estimated map.

One major challenge is the observation of some outlier data on the water level that can represent a considerable portion of the perceived data in a sparse environment, such as offshore wind farms where the structures are hundreds of meters away from each other. This outliers presents itself as spurious information, since no static, distinctive and reliable feature can be inferred, as depicted in Fig. 7.

Fig. 7
figure 7

Ground plane observations in simulation. Yellow points are the point cloud

Full size image

To remove this spurious ground plane, a passthrough filter was applied that clears all measures with an altitude below a \(z_{min}\) or above \(z_{max}\), considering that the Z-axis in the sensor frame and the world frame are parallel. This parallelism is ensured by the estimation of the static homogeneous transformation matrix between the Lidar frame and the robot base frame (\(T^v_r\)) and, posteriorly, the evaluation of the homogeneous transformation matrix describing the ASV position in the world (\(T^r_w\)), considering only the rotational component, Eq. 3, where \(R^r_w\) is a 3x3 rotation matrix of the robot in relation to the world.

$$\begin{aligned} T_w^r=\begin{bmatrix} R^r_{w} &{} \begin{matrix} 0\\ 0\\ 0 \end{matrix}\\ \begin{matrix} 0 &{} 0 &{} 0 \end{matrix}&1 \end{bmatrix} \end{aligned}$$
(3)

Both homogeneous transformations will then be applied to each point in the point cloud to ensure the alignment of the data to filter, Eq. 4, where \(p'_i\) is the projection of the point \(p_i\) in the world.

$$\begin{aligned} p'_i = T_w^r T^v_r p_i \end{aligned}$$
(4)

At last, the passtrough filter is applied to each \(p'_i\) point creating a filtered point cloud to be projected back to the sensor frame using the inverse homogeneous transformations, Eq. 5.

$$\begin{aligned} p_i = (T^v_r)^{-1} (T_w^r)^{-1} p'_i \end{aligned}$$
(5)

Besides the outlier data on the water level, this filter can be used to remove long range measures that due to the sparseness can introduce low feature data that is less accurate and more susceptible to motion estimation errors. To do such, during the passthrough filter stage the X and Y axis can be limited as well by removing all points \(p'_i\) that are below a minimum or above a maximum thresholds for each axis.

4.3 Modality transformation for immersed sensor data

The mapping of the underwater environment is achieve with the sweep of the multibeam echosounder (MBES) through the scenario to be inspected. This sensor provides data in polar coordinates (Fig. 8a), with a range measure for each beam placed at different angles. Thus, it is created a two-dimensional scan with the depth information along a line perpendicular to the heading direction of the vessel, as depicted in Fig. 8b, where the red to magenta color indicates the depth variation from higher to lower, respectively. The sensor modality and position on the ASV will generate multiple situations where the observations are not correlated between consecutive frames.

Fig. 8
figure 8

Multibeam Echosounder scan. Rainbow-color line represents a scale variation, where the red to magenta color goes from higher to lower scales, respectively

Full size image

With the assumptions that the odometry error is negligible for a small displacement, a 3D representation with several scans can provide overlap areas between different samples. Thus, a 3D sliding window will provide a correlation area to estimate alignment errors between a previous map and the current observations. To build the sliding window each MBES scan (\(S_i\)) is associated to the corresponding odometry pose and added to a circular buffer. Once the number of scans (N) required for the window are inserted, all scans in the buffer are concatenated, creating a sliding window (\(SW_i\)). Moreover, to ensure an overlapping region, a number of the latest scans will be kept from one SW to the next, filling the free space with new observations, as depicted in Fig. 9, where the red area is the scans to be forgotten and the green area the one to hold in memory.

Fig. 9
figure 9

Sliding window iterations. Scans to forget in red and to keep in green

Full size image

Furthermore, before inserting a scan to the buffer it is verified if the vehicle is in motion using the current odometry estimation, i.e. evaluates if the 2D displacement (XY-Plane) relative to the previous measure (\(\varDelta p\)) and the variation in heading (\(\varDelta \theta\)) are superior to some predetermined thresholds, \(d_m\) and \(\theta _m\) respectively. If the required motion is detected the measure (S) is accepted. To create an uniform data modality for all available sensors, a polar to Cartesian space transformation is applied on the MBES scan. Further a homogeneous transformation matrix from the MBES to the world frame (\(T^m_w\)) is estimated and introduced to the window buffer. Fig. 10 illustrates the step-by-step method for the sliding window creation.

Fig. 10
figure 10

Sliding window creation approach

Full size image

4.4 Multi-domain map representation

To minimize the impact of the odometry deviations and the sensor imperfections, the source observations (filtered emersed point cloud and the 3D sliding window) must be aligned with the current map estimation. As such, a registration approach that removes outliers, registers and organizes an input point cloud was developed. Since all the data perceived was reshaped to have the same modality, the registration methodology can be applied equally to both emersed and immersed scenarios.

As depicted in Fig. 11, initially the input point cloud is preprocessed to remove spurious and noisy observations, reducing the propagation of errors in the reconstructed map through the registration process. Thus, a Statistical Outlier Removal (SOR) filter performs the statistical analysis of the neighborhood of each point in the dataset, computing the average distance to the k nearest neighbors of each point [29]. Posteriorly, the mean ( \({\overline{d}}\) ) and standard deviation ( \(\sigma _d\) ) of all these distances are computed in order to determine a distance threshold \(t_d\) equal to Eq. 6, where \(m_\sigma\) is a standard deviation multiplier. The points will then be classified as inlier or outlier according to their average neighbor distance. When a distance is above the threshold \(t_d\) the point is considered an outlier and as such it will be trimmed.

$$\begin{aligned} t_d = {\overline{d}} + \sigma _d * m_\sigma \end{aligned}$$
(6)

After the outlier filter process of the input point cloud, the registration method is applied to optimize the alignment in relation to the template given by the concatenation of the previous registered point clouds. The first point cloud (It=1) is directly inserted to the map, while the posterior ones are aligned and concatenated to it. As so, for the registration process is used a non-linear variation of the Iterative Closest Point (ICP). It is based on the work by Fitzgibbon [30] using the Levenberg-Marquardt optimization algorithm to minimize the registration error (LM-ICP). The LM-ICP achieves the registration by matching each point in the input cloud to the closest point in the template. Afterwards, it estimates the rotation and translation using the Levenberg-Marquardt algorithm which will align each source point to its best match found in the previous step. This rotation and translation are applied to the source points and iteratively repeats the process until a minimum fitness is achieved or the number of iterations surpasses a maximum value.

Fig. 11
figure 11

Point cloud registration approach

Full size image

The iterative concatenation of points to the map leads to a quick growth in the memory consumption, as well as in the execution time between processing cycles. This leads to the increase of the computational complexity for the algorithm. With this in mind, after the alignment of the filtered input point cloud, an organization method is applied to speed up the concatenation process using an octree division to perform a spatial partition. This method creates cubic boxes that surrounds all the points defining a tree structure. At each level of this structure, a subdivision occurs denominated as a voxel. The voxels are subdivided consecutively up to a predefined minimum size l, while it contains points from the data. Furthermore, each tree node has eight connected child nodes. When no child node can be found, the tree extremities (leaf nodes) are defined [31].

This organization reduces the registration process complexity by allowing a more efficient neighborhood search, since all points are grouped in small neighborhoods by their distance. As an extra simplification to decrease the effect of small observation errors, all voxels are compressed to be represented by their centroid reducing also the impact in the computational complexity.

This registration method provides a visually accurate representation of the scenario for each sensor passing through this step. This allows the emersed and immersed representation to be fused using the available common information, the GPS-IMU odometry, while compensating the noisy data from the sensors.

5 Results

5.1 Experimental setup

To test and validate the multi-domain mapping methodology a realistic 3D environment in Gazebo of a offshore wind farm with realistic structures and scale was created. The environment takes into account both emersed and immersed scenarios to be inspected using with a model of the SENSE, shown in Fig. 2b, including all the onboard sensors, namely the GPS, IMU, Lidar and MBES. All sensors are affected by Gaussian noise, parametrized according to the specifications of each sensor datasheet.

To ease visualization, the tests were conducted using the compact scenarios, such as the one depicted in Fig. 12. All tests were performed on a MSI GS40 6QE-095PT laptop with the CPU Intel Core i7-6700HQ @ 2.6 GHz - 3.5 GHz and 16GB DDR4 RAM.

Fig. 12
figure 12

Implementation and validation offshore wind farm scenario

Full size image
Fig. 13
figure 13

Inspection trajectory. The orange points depicts the trajectory and the green one the dock

Full size image

One sample mission for the GPS/IMU fusion and the multi-domain map evaluation uses the inspection trajectory depicted in Fig. 13. The experiment considered zero wind velocity and the tidal was formed by the composition of three ripples with the configuration presented in Table 3. The ripple components are asynchronous, where at some points in time the maximum peak is given by the sum of the amplitude of all components. This trajectory performs the following steps:

  1. 1.

    ASV starts berthed on a dock (green point).

  2. 2.

    SENSE passes between the two closest wind turbines with an almost linear motion towards the furthest wind turbine.

  3. 3.

    In the furthest wind turbine performs a close range inspection contouring the jacket foundation.

  4. 4.

    The vehicle moves outside the wind farm passes through a wind turbine and docks at the starting pose.

Table 3 Ripple configuration for simulation
Full size table

During the execution of the trajectory no positional control was added and, thereby, drift in the XY-Plane was observed due to the tidal ripples, which impacts also the altitude of the ASV.

5.2 GPS and IMU odometry

On the inspection trajectory, the GPS/IMU fusion results were evaluated against a perfect odometry estimation acquired with the Gazebo simulator. In Fig. 14 the XY trajectory and Z-axis variation through time on the previously presented example are illustrated.

Fig. 14
figure 14

Odometry results during the sample trajectory execution. The orange, blue and green dots are the ground truth, GPS-IMU fusion and starting pose, respectively

Full size image

As depicted in Fig. 14a, a small error was observed during the route execution, where the orange line is the ground truth and the blue is the GPS-IMU fusion. In Fig. 14b it is visible a small variation between the ground truth and estimation which are mainly more prominent during movements with angular component. Using the metric proposed by Zhang and Scaramuzza in [32], the odometry estimation in this XYZ trajectory presents an average RMSE error of 0.04 m with a standard deviation of 0.01, with a traveled distance of 750 m. One explanation for the error is the low acquisition rate of the GPS sensor (5 Hz) relying most of the time in the predictions acquired by the Newtonian mechanics model, which does not account for the lateral movement due to the tidal ripples. Moreover, the estimated altitude also displays similar errors, Fig. 14c, since it relies in the altitude measure of the GPS which is typically the less accurate.

The odometry was tested using different configurations for tidal ripples and wind as shown in Table 4 by performing a 250 m route along the centre of the scenario depicted in Fig. 12. The increase of the tidal ripples provides the major impact on the accuracy of the system, where higher amplitudes causes bigger RMSE and standard deviations. This is due to the environment dynamics that drifts from the EKF prediction model. Moreover, the introduction of wind (Scenarios D, E and F) does not present a large impact on the accuracy, showing a small increase on the standard deviation. Thus, even with harsher conditions the odometry provides an accurate estimation of the vehicle motion throughout time.

Table 4 Odometry results with distinct ripple and wind configurations
Full size table

At last, it is possible to conclude that a good odometry estimation can be achieve by using an EKF to fuse positional information of the GPS with the attitude and angular velocities measurements provided by the IMU.

5.3 Emersed data filtering

With an accurate odometry and if the sensors data were perfect the map reconstruction could be performed through a simple concatenation procedure. However, the deviations during the odometry process and the sensors imperfections requires a filtering and alignment process.

On simulation the emersed data ground plane must be filtered to remove this spurious information. The application of this filter on the tested scenarios denoted that the ground plane filtering approach for the emersed sensors was capable of discard the sea level data without loss of the structural measurements, as depicted in Fig. 15.

Fig. 15
figure 15

Ground plane filter. Yellow points are the point cloud

Full size image

Note that this ground plane filter presents a naive approach designed mainly for the simulation trials. On real marine environment the presence of the sea surface points on the Lidar data is negligible, observing almost no points on the water surface due to the material reflective properties. Such was seen during a trial on Marina de Leça harbor, Fig. 16, prior to the simulation scenario development.

Fig. 16
figure 16

Data recovered on Marina de Leça harbor

Full size image

The lack of reflections is caused by the sensor wave length which is 905 nm, as such it can only penetrate 1 cm of the water surface providing no reflections. This difference is derived from the ocean material reflectivity on the simulator.

5.4 Modality transformation for immersed sensor data

With the sliding window (SW) creation for the MBES, the data modality was changed to a 3D point cloud, creating an overlapped area defined by the number of scans to concatenate and the ones to keep.

Fig. 17
figure 17

Sonar sliding window with size N consecutive iterations, maintaining K scans for overlap

Full size image

Three examples are depicted in Fig. 17 considering two consecutive iterations for distinct configurations. In Figs. 17a and 17b only one scan is forgotten between consecutive SW presenting a high similarity between them, while almost no new information is added. When keeping an overlapping area of 50% of the scan size a balance is obtained between new and old scans during consecutive SW, Figs. 17c and 17d . The increase in the data to be forgotten will impact the correlation between consecutive SW that will become smaller. This may impact during the data registration process since in extreme situations non-correlated data can be either misaligned or ignored. Figs. 17e and 17f illustrates the case where only 25% of the scans are kept between iterations.

Furthermore, the definition of the size and data to hold will limit the SW creation rate, since it will influence the quantity of MBES observations required to complete the sliding window and, consequently, the amount of time to wait.

At last, another effect to account for is the size of the overlapping area, which will increase the probability of causing data incest with the number of scans to be kept in memory, since the data may be held for several consecutive sliding windows.

5.5 Multi-domain map representation

With the odometry estimations and the data preprocessing (filtering and modality transformation) the multi-domain map representation can be created through the registration of the current observations with the previously aligned and concatenated data.

Using the world configuration presented in Fig. 12, this approach produces visually accurate representations of the surroundings for each domain presenting smooth transitions in both domains, as it can be seen in Fig. 18. Where for the immersed layer, Fig. 18b, the mapping presents denser results in areas perpendicular to the ASV heading, due to the sensor field of view (FoV) limitations.

Fig. 18
figure 18

Map reconstruction for each domain

Full size image

Moreover, the concatenation of the 3D maps for both emersed and immersed regions presented accurate results. As depicted in Fig. 19, the common structures in both layers (fixed foundations) are aligned concentrically and with a visible variation in the size up to the seabed. Nevertheless, due to limitations in the sensors FoV there are areas with incomplete data on the transition pieces of the wind turbines fixed foundation.

Fig. 19
figure 19

Maps of both emersed and immersed domains merged

Full size image

For evaluating the multi-domain map accuracy, the root mean square error was calculated from the 3D representation and the ground-truth point cloud from the Gazebo world. This fitness score is a function of the distance of each point in the map to the closest point in the ground-truth. Since the wind shows a low impact on the odometry accuracy, tests with no wind and with two distinct ripple configurations were performed for two worlds. The first world is composed by a single wind turbine as depicted in Fig. 20, where the trajectory illustrated in Fig. 21 is performed, while the second world represents the scenario depicted in Fig. 12 with a trajectory similar to Fig. 13.

Fig. 20
figure 20

Single turbine offshore scenario

Full size image
Fig. 21
figure 21

Inspection trajectory. The orange points depicts the trajectory

Full size image

In Table 5 the evaluation results are summarized. As it can be seen, the increase of the ripple size induces a higher error on the map reconstruction, mainly due to the odometry deviation. Nevertheless, through the LM-ICP registration the error was reduced when compared to the odometry deviation, since this method performs a correction to the data alignment. Moreover, higher populated scenarios, such as world 2, present larger errors due to the increase in trajectory length and to the sum of the data noise. Nevertheless, the application of the SOR filter reduces the outliers. Also, the octree representation, using only the voxel centroids, performs an average of a small neighborhood, thus reducing the sensor noise impact.

Table 5 Multi-domain map RMSE score with distinct ripple configurations
Full size table

At last, the proposed methodology was able to perform in real time requiring an average of 300 ms per iteration to reconstruct the scenario thanks to the organization step that optimized the neighborhood search process, which presents one of the highest computational complexity on the LM-ICP.

5.6 Test on a real scenario

A partial patch of a non-public dataset from INESC TEC was used to validate the multi-domain mapping architecture. The dataset is ROS-compliant and all sensor data collected from the scenario is stored in bag files. The acquisition was carried out at the biggest port for yachting on the North of Portugal, namely the Marina de Leça harbor, depicted in Fig. 22. This dataset was acquired on a partially cloudy day, Fig. 22b, with slow wind speeds (4 km/h North) and good illumination circumstances.

Fig. 22
figure 22

Marina de Leça harbor - 240 mooring places with entry and yacht basins depth of 4m and 2-3.5m, respectively

Full size image

This dataset was obtained on a mission performed during the field tests of the SENSE vehicle at the harbor with the sensor payload placed as shown in Fig. 2b. The sensor configurations used were:

  • Xsens MTi-30 IMU, 200Hz;

  • Swift Navigation Piksi Multi GPS, RTK at 10Hz and GPS at 8Hz;

  • Velodyne VLP-16, 10Hz with a range of 100 m and field of view of 330\(^\circ\) horizontal and 30\(^\circ\) vertical, due to a support structure behind the sensor;

  • Mynt Eye D, 20 fps with 1280x720 resolution;

  • Imagenex “Delta T” 837B, 12Hz with 120 beams and constrained to 5 m depth readings.

The sensor payload extrinsic calibration and synchronization was represented using ROS available tools for transform and timestamping data. The GPS, IMU, Velodyne and the Mynt Eye were calibrate and synchronized following the same procedures as in a previous work by Gaspar et al [33] for acquiring a dataset on an urban scenario. As for the MBES (Imagenex) a manual measurement was performed in relation to the base link.

Therefore, the proposed methodology for multi-domain map was applied to the patch provided. As depicted in Fig. 23, when comparing the position estimates from the GPS/IMU odometry (green line) with the RTK estimation (red line) similar curves are acquired, where the RMSE error between them is approximately 0.07m with a standard deviation of 0.04. Thus, the odometry provides a good accuracy even in proximity to metallic structures and with ripples caused by larger vehicle crossings.

Fig. 23
figure 23

Odometry estimation for the dataset patch. In red is the RTK measure and in green the GPS/IMU odometry

Full size image

Thus, the map obtained through the proposed architecture is depicted in Fig. 24. Since no ground-truth was provided for the 3D scenario, no metric can be estimated. Nevertheless, through visual analysis it is distinguishable several moored vessels, as well as the pillars, ramps and walls from the real test area. Moreover, from the underwater map a depth from 1.9-3.0m was observed which is consistent with the depth measures provided at the harbor web page.Footnote 2, where at the yacht basin has 2-3.5m depth. Nevertheless, some spurious data can be observed on the multi-domain representations, where the surface noisy elements (blue box) are caused by dynamic objects (vessels) that currently are not filtered, and underwater noise is observed on the MBES from false reflection readings, mainly around 1m from the sensor (red box).

Fig. 24
figure 24

Multi-domain map of the Marina de Leça harbor yacht basin. The red box highlights an example of the underwater outlier readings, blue and purple points. The blue box shows an example of the surface spurious data caused by dynamic objects

Full size image

6 Conclusion

This paper proposes an architecture for multi-domain inspection of offshore wind farms infrastructures using heterogeneous sensors, namely a 3D Lidar and a MBES, to create a 3D reconstruction of the scenario. The method is capable of reconstructing both emersed and immersed domains into a single coherent representation. An accurate odometry was acquired through the fusion of the navigation sensors, GPS and IMU, providing a valuable reference to the creation of the MBES sensor sliding window, the Lidar ground plane filtering and the initialization of the LM-ICP registration.

Moreover, through the emersed data ground plane filtering, the less representative information was discarded reducing possible bias in the alignment process. Furthermore, the modality transformation of the MBES 2D scan to a 3D point cloud, using a sliding window methodology, provides an overlap section for the immersed map creation. Nevertheless, the overlap can lead to double counting issues, which demands a careful selection of the number of scans to hold.

Throughout the experiments, the architecture showed promising results towards multi-domain mapping. The odometry process was capable of providing the ASV poses with a positional error of at most 0.049 m on simulation and 0.07 m on real data. Moreover, the mapping methodology provided a visually accurate and real-time representation of the scenario, requiring an average of 300 ms to reconstruct the environment. In simulation, an error of at most 0.042 m was obtained, which provides a good accuracy of the representation. As well, from preliminary tests performed on a real operation visually accurate representations were acquired.

Therefore, several improvements were proposed in this paper to increase offshore wind farms 3D representation completeness in distinct domains capable of enhancing real-time visualization of inspection tasks.