1 Introduction

An electromagnetic actuator that consists of the aggregation of adjusted magnets along with the spanwise arranged layout of electrodes with alternation mounting on a flat surface is indicated as a Riga plate. This actuator is responsible for the generation of exponentially decreasing Lorentz force within the BL. This device has been employed in the reduction of pressure drag and friction with the aid of the prevention of the separation in the boundary layer (BL) and to abate the generation of turbulence criteria [1]. Magnetohydrodynamics (MHD) flows with the Riga surface exert a workable role in miscellaneous engineering actions like in MHD generators, flow meters, and thermal nuclear reactors, etc. The flows with the consideration of the Riga plate have comprehensive usages in chemical engineering, civil engineering, mechanical engineering, etc. Riga plate can be efficiently used in biomedical sciences with nanoparticles based fluid flow.

The flow concerning Newtonian fluid under the influence of the Riga plate generates the “Grinberg term” that produces the electromagnetic parameter naming as the modified Hartmann number [2]. For aiding flow, this parameter possesses positive values, and opposing flow possesses negative values [3]. Micro-electromagnetic systems are growing faster with rapidly renewed applications of flow mechanisms concerning the Riga plate. Biomechanically, for developing smart lubrication, the flow concerning the Riga plate is significant.

Electrically conducting fluids in MHD flows have captivated many investigators for their medley applications in engineering assignments, see Refs. [4,5,6,7,8,9,10,11,12]. But unfortunately, a large electrical conductivity is not often contained by all the available fluids. Taking this deficiency into consideration, the Riga plate was foremost introduced by Gailitis and Lielausic [13] as a flow monitoring device to produce parallel Lorentz force to the wall. The decision by their investigation concluded that the electromagnetic forces can govern the fluid with electric conduction to compensate for the lack of momentum in the BL. The study incorporating the inspection of the fluctuating non-Newtonian flow nature of a Maxwell fluid with changeable suction velocity was performed by Wang and Hayat [14]. They have noted a negative BL flow criteria with the large amplitude of oscillation of the free stream flow, albeit the nature of the external flow is always forward-flowing. Deswita et al. [15] established similarity solutions for BL laminar flow with regard to a horizontal plate of permeable nature. The consideration of Riga plate to quest Blasius and Sakiadis flow was researched by Pantokratoras [16]. Two wielded flows with the shifting Lorentz points in the positive and negative direction along the Riga plate have been inspected by Magyari and Pantokratoras [17]. Vadher et al. [18] took an endeavor to observe the MHD squeeze films through a conducting lubricant bounded by two conical porous surfaces. Abbas et al. [19] established numerical reckoning of the entropy generation process on nanoparticle flow aiding a horizontally placed Riga plate. They examined the functioning of the profile of entropy as an escalating case for all the possible combinations of parameters. The effect of buoyancy by shooting procedure on nanofluid flow with the involvement of the Riga plate adopting convective heating was developed by Ahmad et al. [20]. Thermal radiation effect on MHD nanofluid flow dealing with no-slip setting past a Riga plate was depicted by Bhatti et al. [21]. Hayat et al. [22] inquired about the nanofluidic BL flow over the Riga plate of varying thickness by addressing the workable convective boundary conditions. Among many geometries of flow regarding the Riga plate, the flow wielding the inner zone of two Riga plates has created a remark for the number of applications. Paying heed to this context, The study on the observation of carbon–water nanofluidic squeezed flow between Riga plates by involving the radiation effects was presented by Ahmed et al. [23]. In the same year, Hayat et al. [24] observed the impact of the Riga plate involving in the EMHD flow of radiating and squeezing nature by addressing chemical reaction and convective conditions. Further, Hayat et al. [25] conducted a numerical study on EMHD squeezing flow with the rotation of carbon–water-kerosene oil nanofluid past through two Riga plates which are stretchable. Iqbal et al. [26] reckoned the statistics of numerical elucidation on the transport of nanofluid concerning gyrotactic microorganisms drowned in water through the Riga plate with varying thickness and bio-convection. Under the involvement of Nield convective boundary conditions and flow activation energy, a research was executed by Khan et al. [27] on the flow analysis of thixotropic nano liquid over the Riga surface by aiming a biotechnological model. Iqbal et al. [28] considered the Keller box scheme to investigate the dissipative and radiating effects on nanofluidic flow nature flowing through Riga surface under the property of erratic thickness. They reported an interesting fact that the transportation of heat flux rate is physically inverse to the mass flux rate for the radiational effect. An analytical approach on the third-grade flow of nanofluids adopting the condition of zero mass flux for the nanoparticles past a Riga plate by employing the Cattaneo-Christov model was performed by Naseem et al. [29]. Rasool and Zhang [30] considered the HAM scheme to count the influences of convective boundary settings along with a chemical reaction on the Powell-Eyring type nanofluidic flow concerning Riga plate. Daniel et al. [31] considered the flow of nanofluid with reaction phenomena and electric field impacts under the employment of a nonlinear surface.

Overall, it is understood that thermal radiation is a key factor in analyzing different flow geometries for recent decades. This fact motivates the present study to deal with a radiating flow for the operational and fascinating Riga plate. Shafiq et al. [32] imposed a homotopy analytical technique to explore the Marangoni BL flow with radiation of carbon nanotubes along a Riga plate. Krishnamurthy et al. [33] worked out the chemical reaction effect of BL slip flow of radiating nanoparticle fluid along a stretching sheet of nonlinear type.

Prasannakumara et al. [34] accomplished the reckoning of the MHD flow problem emphasizing the dusty fluid containing double phase with the aid of convective boundary conditions and quadratic temperature at the surface. The phase velocity for particle was pointed lesser than the phase velocity for fluid simultaneously, the phase temperature for the dust was prescribed lesser than the phase temperature of the fluid. Shamshuddin et al. [35] paid their attention to analyze the Squeezing MHD flow by characterizing joule heating phenomena along with the heat flux structure of the Cattaneo-Christov type. The targetted purpose was the systematic improvement of the biomechanical smart lubrication. Furthermore, Heat flux of non-Fourier type has been characterized by Shamshuddin and Satya Narayana [36] with the relaxation of thermal behavior in the squeezing MHD flow. To mathematically inspect the squeeze films that are affected by magnetic force, the extensively used methodologies are mainly MHD viscous type. Nasir et al. [37] explored the numerical findings on the flow along a Riga plate of stretching/shrinking nature, where they considered dual solutions for the plate types. By their substantial inquiry, the upper branch of the solution was mentioned as a stable type while the lower branch wasn’t. Ramesh et al. [38] researched Maxwell nanofluidic flow under MHD phenomena by the incorporation of heat source/sink. Due to the involvement of nano liquid, they observed an increment in velocity for the Maxwell parameter which denies the regular tendency of pull downing velocity by Maxwell parameter (without nano liquid).

The EMHD flow of conducting fluid for the permeable Riga surface is worthy of dealing with wall suction or injection, some investigations are [39,40,41,42]. Substantial studies on the magnetohydrodynamic flow of rotating fluid and/or system rotation along with the preparation and applications of radiative heat flux have been executed by [43,44,45,46,47].

All the researches that have been surveyed above, clearly reflect that the flow maintaining device (Riga plate) is capturing the interests of researchers rapidly to quest the different causation of flow nature. However, to the best of the authors’ knowing, no endeavor has yet been created to deal with the investigation of explicit FDM solution on the unsteadiness nature of viscous and incompressible flow induced by the vertical Riga plate of infinite length by considering the MHD phenomena with system rotation, thermal radiation, and suction. Mostly, the research endeavors that have been so far mentioned are constructed to deal with the flow that occurred by an external free stream or plate’s motion however, the motivation of the present article is to observe the flow induced by the flow controlling device (Riga Plate) itself. Hence, to enhance the weighing of the literature in the authors’ sense, a numerical and mathematical model is proposed here to understand the above-mentioned flow phenomena. The set of prevailing equations have been discretized to solve numerically. The numerical procedure for the current study is an explicit FDM (Eva et al. [48]). Outlining structures are; Sect. 2 explains the considered model with the mathematical representation. Section 3 presents the expressions for Nusselt number and shear stress. The numerical approach and its stability criteria are discussed in Sect. 4 and Sect. 5 respectively. Section 6 discusses the results in five subsections- Mesh Sensitivity, Time Sensitivity, Validation Test (Comparison), Effects of Affined Parameters, and Overall Qualitative Comparison. The salient marks of the results have been portrayed graphically and depicted in words.

2 Model establishment and analysis

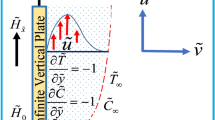
An unsteady viscous, incompressible, and radiating fluid flow in a rotating system along a vertical Riga plate of infinite length has been considered under the action of Lorentz force due to the MHD phenomena. The repercussion of suction velocity is also considered by the action of the permeable Riga plate [39]. The Riga plate is assumed as an infinitely long surface that is erected at \(y = 0\) and holding the \(x\)-axis in the vertical position as configured in Fig. 1. Wielding of the fluid occurs through the vertical plate under the influence of Lorentz force that is generated by the flow monitoring device itself, and the Grinberg term is taken place into the mathematical scheme. The uniform magnetic field vector and the intensity of the electric field are organized in a parallel direction to the alignment. Assume, the plate surface temperature is \(T_{w}\), while the external temperature of the BL region is \(T_{\infty }\); to be more exact, \(T_{w} > T_{\infty }\). Ineffective edge-effects can be deemed for the Riga plate and the imposed electric as well as magnetic fields that have elements particularly in \(y\) and \(z\) directions. As per the consideration of uniform suction, \(\frac{\partial u}{{\partial x}} = 0\), and the continuity equation \(\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0\) generates \(\frac{\partial v}{{\partial y}} = 0\), which is taken as \(v = \,\, - V_{0}\) (constant), see Refs. [49, 50].

Fig. 1
figure 1

The physical model and coordinates of the schematic problem

Full size image

Under the explications of the above-narrated assumptions, the prevailing BL equations (see, [12, 21]) related to the rotating frame by the operation of BL approximations are noted as:

Continuity equation

$$v = \,{\text{constant}} = - V_{0}$$
(1)

Momentum equations

$$\frac{\partial u}{{\partial t}} - V_{0} \frac{\partial u}{{\partial y}} = \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\pi }{8\rho }J_{0} M_{0} \exp \left( { - \frac{\pi }{a}y} \right) + 2\Omega w$$
(2)
$$\frac{\partial w}{{\partial t}} - V_{0} \frac{\partial w}{{\partial y}} = \upsilon \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{\pi }{8\rho }J_{0} M_{0} \exp \left( { - \frac{\pi }{a}y} \right) - 2\Omega u$$
(3)

Energy equation:

$$\left\{ \begin{gathered} \frac{\partial T}{{\partial t}} - V_{0} \frac{\partial T}{{\partial y}} = \frac{\kappa }{{\rho c_{p} }}\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \frac{\mu }{{\rho c_{p} }}\left[ {\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \right] \hfill \\ \, + \frac{1}{{\rho c_{p} }}\frac{{16\sigma^{*} }}{{3k^{*} }}T_{\infty }^{3} \frac{{\partial^{2} T}}{{\partial y^{2} }} \hfill \\ \end{gathered} \right\}$$
(4)

The boundary settings for the prevailing system of equations are:

$$\,\left\{ {\left. \begin{gathered} t > 0,\,\,\,u = 0,w = 0,T = T_{w} \,\,\,\,{\text{at}}\,\,y{ = 0} \hfill \\ \, \,\,\,\,\,\,\,\,\,\,\,\,\,\,u \to 0,w \to 0,T \to T_{\infty } \,\,\,\,{\text{at}}\,\,y \to \infty \hfill \\ \end{gathered} \right\}} \right.$$
(5)

where the density of the fluid is \(\rho \left( {kg/m^{3} } \right)\), the thermal conductivity is \(\kappa \left( {W/mK} \right)\), the specific heat at the constant pressure is \(c_{p} \left( {J/Kkg} \right)\), the dynamic viscosity is \(\mu \left( {kg/ms} \right)\), the electrodes current density is \(J_{0} \,\left( {A/m^{2} } \right)\), the magnetization of the adjusted magnets is \(M_{0} \left( T \right)\), and the uniform width of the magnets and electrodes is \(a\left( m \right)\).

Notably, The radiative heat flux \(Q_{r}\) is defined as depicted in Chauhan and Khemchandani [51] by the Rosseland approximation in the form \(Q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\left( {\frac{{\partial T^{4} }}{\partial y}} \right)\), where, mean absorption coefficient (\(k^{*}\)), and Stefan-Boltzmann constant (\(\sigma^{*}\)). The Taylor series expansion with a familiar supposition for \(T^{4}\) in terms of \(T_{\infty }\) implies \(T^{4} \cong 4T_{\infty }^{3} - 3T_{\infty }^{4}\) as conducted in Hassan et al. [52], which leads, \(Q_{r} = - \frac{{16\sigma^{*} }}{{3k^{*} }}T_{\infty }^{3} \frac{\partial T}{{\partial y}}\).

To get the benefit of explicit FDM in manipulating the Eqs. 1–4 under the boundary conditions 5, it is essential to ensure a dimensionless conversion of the equations. The following quantities in the dimensionless form are employed for the implementation of the non-dimensionalization process:

$$\left\{ \begin{gathered} X = \frac{x}{l},Y = \frac{y}{L},U = \frac{u}{{U_{0} }},W = \frac{w}{{U_{0} }},\tau = \frac{{tU_{0} }}{l}, \hfill \\ \theta = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}{;}\,\,\,\,\,{\text{where, }}l = \frac{{U_{0} L^{2} }}{\upsilon },L = \frac{a}{\pi }\,\,\,\,\, \hfill \\ \end{gathered} \right\}$$
(6)

The derived dimensionless system of non-linear PDEs can be expressed as follows:

$$\frac{\partial U}{{\partial \tau }} - S\frac{\partial U}{{\partial Y}} = \frac{{\partial^{2} U}}{{\partial Y^{2} }} + Ze^{ - Y} + 2RW$$
(7)
$$\frac{\partial W}{{\partial \tau }} - S\frac{\partial W}{{\partial Y}} = \frac{{\partial^{2} W}}{{\partial Y^{2} }} + Ze^{ - Y} - 2RU$$
(8)
$$\frac{\partial \theta }{{\partial \tau }} - S\frac{\partial \theta }{{\partial Y}} = \frac{1}{{P_{r} }}\frac{{\partial^{2} \theta }}{{\partial Y^{2} }} + E_{c} \left[ {\left( {\frac{\partial U}{{\partial Y}}} \right)^{2} + \left( {\frac{\partial W}{{\partial Y}}} \right)^{2} } \right] + \frac{4}{3}R_{d} \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}$$
(9)

The dimensionless boundary conditions are noted as:

$$\,\left\{ \begin{gathered} \tau > 0,\,\,\,U = 0,W = 0,\theta = 1\,\,\,\,\,\,\,\,\,\,\,{\text{at}}\,\,Y{ = 0} \hfill \\ \, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,U \to 0,W \to 0,\theta \to 0\,\,\,\,\,\,\,\,{\text{at}}\,\,Y \to \infty \hfill \\ \end{gathered} \right\}$$
(10)

The dimensionless equations disclose several dimensionless parameters with their respective physical meaning. The dimensionless parameters have alluded to below:

\(R = \frac{{\Omega L^{2} }}{\upsilon }\)(rotational parameter), \(P_{r} = \frac{{\upsilon \rho c_{p} }}{\kappa }\) (Prandtl number), \(E_{c} = \frac{{\mu lU_{0} }}{{\rho c_{p} L^{2} \left( {T_{w} - T_{\infty } } \right)}}\) (Eckert number), \(R_{d} = \frac{{4\sigma^{*} T_{\infty }^{3} }}{{k^{*} \rho c_{p} }}\) (radiation parameter), \(S = \frac{{V_{0} L}}{\upsilon }\) (suction parameter), and \(Z = \frac{{J_{0} M_{0} a^{2} }}{{8\pi \rho U_{0} \upsilon }}\) (modified Hartmann number); see Refs. [1,2,3].

3 Quantities of engineering curiosity

The entities which have effective importance in miscellaneous Engineering purposes are stated here. The shear stress phenomena feature the landmarks of the fluid layer vicinity to the plate. The Nusselt number stands for the counting of heat transfer by the convection process. The primary velocity (\(X\)-direction), secondary velocity (\(Z\)-direction), and temperature profile respectively yield the primary shear stress (\(X\)-direction) as \(\tau_{LX} = \mu \left( {\frac{\partial U}{{\partial Y}}} \right)_{Y = 0}\), secondary shear stress (\(Z\)-direction) as \(\tau_{LZ} = \mu \left( {\frac{\partial W}{{\partial Y}}} \right)_{Y = 0}\), and Nusselt number as \(Nu_{L} = - \mu \left( {\frac{\partial \theta }{{\partial Y}}} \right)_{Y = 0}\).

4 Numerical computation technique

The discretization of the system of coupled non-dimensional PDEs (Eqs. 7–9) has been accomplished in both time and space by the explicit FDM [7, 48]. Time-dependent iterative computations are reckoned to find the values of the set of finite difference equations that are gained by the use of MATLAB simulations. In that context, the furcation of the BL region is implemented to construct the grid of lines perpendicular to \(Y\)-axis, as shown in Fig. 2.

Fig. 2
figure 2

FDM grids

Full size image

Here the maximum width of the BL is arbitrarily deliberated as \(Y_{\max } \left( { = 2} \right)\) i.e. \(Y\) ranges from 0 to 2. Numerical iterations for the discretized equations are conducted with a grid number \(n = 60\). The choice of taking \(n = 60\) is based on the mesh sensitivity experiment (Sect. 6.1). Based on the grid number, the mesh size in Y-direction is taken as \(\Delta Y = 0.033\,\left( {0 \le x \le 60} \right)\)(constant); regarding the infinitesimal time-step, \(\Delta \tau = 0.0001\).

The territory within the BL has been placed with a finite number of a set of points. The FDM schemes are constructed by using backward difference style for single-order derivatives and central difference style for higher-order derivatives. Time-domain effects on flow equations are reckoned such that the former time values are imported to calculate the subsequent time values.

5 Analysis of stability and convergence criteria

Without addressing the criteria for stability and convergence on the constructed finite difference schemes, the study will become imperfect. For the constant grid space and time difference, the stability analysis (Reza-E-Rabbi et al. [11]) has been conducted, and the final consequence is given below:

$$\frac{2\Delta \tau }{{P_{r} \left( {\Delta Y} \right)^{2} }} + \frac{4}{3}R_{d} \frac{2\Delta \tau }{{\left( {\Delta Y} \right)^{2} }} - S\frac{\Delta \tau }{{\Delta Y}} \le 1$$
(15)

Applying \(\Delta Y = 0.033,\,\,\Delta \tau = 0.0001\), and the initial conditions, the inequality 15 produces the converging restrictions on pertinent quantities as \(P_{r} \ge 0.19,\,\)\(R_{d} \ge 0.1,\,\,\)\(S \ge 1,\) \(E_{c} = 0.01\,\,\) and \(0 < R \le 0.1\). These converging ranges are used to obtain the parameters effect with the steady-state value of time as well as with suitable mesh size on the flow model equations.

6 Results and discussions

Exploration of BL incompressible and electrically conducting flow wielding through an infinite Riga plate in a rotating system under the action of MHD phenomena with suction and thermal radiation have been instituted numerically. This study has been constructed to deal with some Newtonian fluid, for which the BL flow nature reflects the flow criteria through the vertical flow monitoring device (Riga plate). Normalization of the governing equations has been accomplished under the suitable boundary layer approximations. For the purpose of investigating the mechanical characteristics of the constructed mathematical structure, the steady-state behavior of pertinent physical parameters on dimensionless primary velocity \(\left( U \right),\) secondary velocity \(\left( W \right)\), and the temperature \(\left( \theta \right)\) is analyzed. At first, the sensitivity test on meshes has been demonstrated to attain the perfect grid number for the execution of numerical performance. Then, to acquire the sloution in steady-state, the sensitivity test on time has been performed. Thereafter, the effects of some pertinent parameters like as, modified Hartmann number \(\left( Z \right),\) suction parameter \(\left( S \right),\) and rotational parameter \(\left( R \right)\) on both the velocities and energy field, simultaneously on both the shear stresses and Nusselt number are graphically demonstrated with descriptions. To make this study concise, the impacts of the rest of the parameters like radiation parameter \(\left( {R_{d} } \right),\) Eckert number \(\left( {E_{c} } \right),\) and Prandtl number \(\left( {P_{r} } \right)\) have not been included. At last, the present results have been compared in tabular form with published results.

6.1 Mesh sensitivity

To justify the compatible number of grid lines i.e. the value of \(n,\) the computational procedure is continued for triplicate individual values of grids and the values are \(n = 60,\) \(n = 70\,\) and \(n{ = 80}\,\) which are sketched in Figs. 3, 4, and 5 for primary velocity, secondary velocity, and temperature field. The calculation is performed with the assumption of \(Z = 3.00,\) \(R = 0.01,\) \(R_{d} = \,2.00,\) \(E_{c} = 0.01,\) \(P_{r} = \,7.00\) and \(S = 1.00\). A situation of mesh independence is observed among these curves. According to this situation, \(n = 60\) is chosen as the perfect grid space line. In further numerical computations, the results of both the velocities and temperature field along with both the shear stresses and Nusselt number have been carried out for \(n = 60\).

Fig. 3
figure 3

Sensitivity test for mesh on primary velocity

Full size image
Fig. 4
figure 4

Sensitivity test for mesh on secondary velocity

Full size image
Fig. 5
figure 5

Sensitivity test for mesh on temperature profile

Full size image

6.2 Time sensitivity

In order to acquire the steady-state solutions, the computational procedure is conducted for six individual non-dimensional time step such as \(\tau =\) 0.50, 1.00, 1.50, 2.00, 2.50, and 3.00, where \(Z = 3.00,\)\(R = 0.01,\)\(R_{d} = \,2.00,\)\(E_{c} = 0.01,\) \(P_{r} = \,7.00\), and \(S = 1.00\). It is noticed from Figs. 6,7, and 8 that the resulting computations for \(U,\,\,W\,\,{\text{and}}\,\,\theta\) show a tiny change after \(\tau =\) 1.50 also show an ineffective change after \(\tau = 2.00\). Upon observing the situation, the time value \(\tau = 2.00\) is taken as the steady-state time value for all the profiles. Moreover, the temperature field is found to gain steady-state prior to the primary and secondary velocity profiles.

Fig. 6
figure 6

Sensitivity test for time on primary velocity

Full size image
Fig. 7
figure 7

Sensitivity test for time on secondary velocity

Full size image
Fig. 8
figure 8

Sensitivity test for time on temperature profile

Full size image

6.3 Validation test (comparison)

The current section is discussed to analyze the prescribed results of the present study with the numerical results of Islam et al. [12]. The qualitative and quantitative similarity, as well as dissimilarity, is portrayed in Fig. 9(a,b). The prescription of both the results show an excellent appearance in the qualitative sense. In a quantitative sense the results are not identical, since the present study concerns with the action of suction velocity while the study of Islam et al. [12] doesn’t. Furthermore, all the possible sensitivity analyses have been tested and reported rigorously, which emphasize the exactness of the presented numerical performance.

Fig. 9
figure 9

Comparison of the effect of \(\left( Z \right)\) on primary velocity between a (present study) and b (reprinted from Islam et al. [12], with the permission of AIP Publishing)

Full size image

6.4 Effects of affined parameters

To clarify the physical outlines of this paper, the impacts of three parameters namely modified Hartmann number \(\left( Z \right)\), rotational parameter \(\left( R \right),\) and suction parameter \(\left( S \right)\) on both the velocity profiles \(\left( {U,W} \right)\)(primary and secondary), and temperature field \(\left( \theta \right)\) along with both the local shear stresses \(\left( {\tau_{LX} ,\tau_{LZ} } \right)\)(primary and secondary), and local Nusselt number \(\left( {Nu_{L} } \right)\) are demonstrated and described in words by adopting the Prandtl number \(\left( {P_{r} = 7.00} \right)\), radiation parameter \(\left( {R_{d} = 2.00} \right)\) and Eckert number \(\left( {E_{c} = 0.01} \right)\) (see Figs. 10(a–f)–12(a–f)).

Fig. 10
figure 10

Effect of \(\left( Z \right)\) on a \(U\); b \(\tau_{LX}\); c \(W\); d \(\tau_{LZ}\); e \(\theta\); and f \(Nu_{L}\); where \(R_{d} = \,2.00,\)\(E_{c} = 0.01,\)\(P_{r} = \,7.00,\) \(S = 1.00\), and \(R = 0.01\) at time \(\tau = 2.00\) (steady-state)

Full size image

The impacts of Modified Hartmann number on primary velocity profile, local primary shear stress, secondary velocity profile, local secondary shear stress, temperature, and local Nusselt number are sketched in Fig. 10(a–f), where, \(R_{d} = \,2.00,\)\(R = 0.01,\)\(E_{c} = 0.01,\)\(P_{r} = \,7.00\), and \(S = 1.00\) at time \(\tau =\) 2.00. Taking aim on Fig. 10(a,b,c,d), it is reckoned that the primary velocity, primary shear stress, secondary velocity, and secondary shear stress substantially rise while the increasing estimations of the modified Hartmann number \(\left( Z \right)\) are adopted. The inner physics supports this acceleration of velocities with the uprising of modified Hartmann number \(\left( Z \right)\) because positive assumptions of \(\left( Z \right)\) notifies favoring flow criteria. The physical understanding behind this fact is that comparatively stronger estimations of \(\left( Z \right)\) causes strengthen in the electric field which results in the acceleration of velocities. With the uplift of the magnetic field, a simultaneous uplifting happens in the electromagnetic field and consequently, the generation of Lorentz force produces extra surface tension that later specifies the flow acceleration. Temperature distribution critically rises by the increment of the modified Hartmann number \(\left( Z \right)\) while the local Nusselt number reduces slowly (see Fig. 10(e,f)).

Again, the influences of the rotational parameter on primary velocity profile, local primary shear stress, secondary velocity profile, local secondary shear stress, temperature, and local Nusselt number are demonstrated in Fig. 11(a–f), where \(Z = 2.00,\)\(R_{d} = \,2.00,\)\(E_{c} = 0.01,\)\(P_{r} = \,7.00\) and \(S = 1.00\) at time \(\tau =\) 2.00. Figure 11(a,b), pointing out the enhancing phenomena of the primary velocity and the local primary shear stress while the rising values of the rotational parameter \(\left( R \right)\) take place. Opposite occurrence is marked on the secondary velocity and the local secondary shear stress for the rotational parameter \(\left( R \right)\) in Fig. 11-c and d. These facts imply that the causation of heighten in primary velocity occurs due to the motility of rotation while secondary velocity obstructs this happening. Actually, in primary velocity, enhancement in the rotational parameter \(\left( R \right)\) indicates enhancing Coriolis force that results in the development of rotational velocity. Due to this boosting in rotational velocity, the kinetic energy of the fluid rises that outcomes in the expected elevation in primary velocity. Furthermore, the temperature field reduces slowly with the enhancement of the rotational parameter \(\left( R \right)\) while the local Nusselt number rises a bit by the enhancement of the rotational parameter \(\left( R \right)\) (see Fig. 11-e and f).

Fig. 11
figure 11

Effect of \(\left( R \right)\) on a \(U\); b \(\tau_{LX}\); c \(W\); d \(\tau_{LZ}\); e \(\theta\); and f \(Nu_{L}\); where \(Z = 2.00,\)\(R_{d} = \,2.00,\)\(E_{c} = 0.01,\) \(P_{r} = \,7.00\), and \(S = 1.00\) at time \(\tau = 2.00\) ( steady-state)

Full size image

Furthermore, the impacts of the suction parameter on primary velocity profile, local primary shear stress, secondary velocity profile, local secondary shear stress, temperature, and local Nusselt number are presented in Fig. 12(a–f), where \(Z = \,2.00,\)\(R_{d} = \,2.00,\)\(E_{c} = 0.01,\)\(P_{r} = \,7.00\) and \(R = 0.01\) at time \(\tau = 2.00\). From Fig. 12(a,c,e), it is noticed that the primary velocity, secondary velocity, and temperature field reduce with the enhancement of the suction parameter \(\left( S \right)\). While wall suction increases, the velocity of the flow experiences retardation on it that comes to an outcome of narrowing the momentum boundary layer. Suction specifies fluid transportation to a higher pressure regime from a lower pressure regime. The hike in the suction parameter ensures the increasing transportation of fluid to the regime of higher pressure. The fluid movement in the direction of the permeable wall (Riga plate) cuts down its volume and later diminishes the flow velocity. The decrement in velocity affects the fluid temperature and pulls it down. On contrary, From Fig. 12(b,d,f), it is perceived interestingly that, the local primary shear stress, local secondary shear stress, and local Nusselt number rise with the increment of the suction parameter \(\left( S \right)\).

Fig. 12
figure 12

Effect of \(\left( S \right)\) on (a) \(U\); (b) \(\tau_{LX}\); (c) \(W\); (d) \(\tau_{LZ}\); (e) \(\theta\); and (f) \(Nu_{L}\); where \(Z = 2.00,\)\(R_{d} = \,2.00,\)\(E_{c} = 0.01,\) \(P_{r} = \,7.00\), and \(R = 0.01\) at time \(\tau = 2.00\) (steady-state)

Full size image

6.5 Overall qualitative comparison

To claim the validity of the present findings, a qualitative comparison with published studies have been presented in Table 1. This study involves a new investigation on MHD fluid flow towards a radiating Riga plate with rotational impact while Bhatti et al. [21] investigated the irrotational EMHD nanofluid flow by considering the thermal radiation impacts on a Riga plate; Abbas et al. [19] reckoned the generation of entropy due to the nanofluidic flow through a Riga plate of horizontal orientation, and Wakif et al. [42] examined EMHD flow that subjected to suction for permeable and moving Riga plate. To make this comparison section as brief as possible, the effect of the suction parameter \(\left( S \right)\) is analyzed only.

Table 1 Comparison
Full size table

7 Conclusions

In this study, the EMHD rotational and unsteady fluid flow through an infinitely long permeable Riga plate with thermal radiation has been investigated by employing explicit FDM. The only responsible wiellding force for the flow is the body force that is generated by the electromagnetic actuator. The presented flow model is being subjugated by uniform suction, thermal radiation with the system rotation. The transition of the nature of the flow from the state of unsteadiness to the state of the complete steady-state has been gained for the velocities (primary and secondary) in a smooth swift-moving way (see Figs. 6 and 7) while for the temperature it is as fast as instant (see Fig. 8). The converging ranges for the numerical solutions are \(P_{r} \ge 0.19,\,\)\(R_{d} \ge 0.1,\,\,\) \(S \ge 1,\) \(E_{c} = 0.01\,\,\) and \(0 < R \le 0.1\). On the basis of the results and discussions, some salient observations are stated below:

  1. 1.

    The fastest steady-state is gained by the temperature distribution among all the profiles. All the profiles have reached steady-state within \(\tau = 2.00\).

  2. 2.

    Converging solutions occur for the relevant restrictions as, \(P_{r} \ge 0.19,\,\)\(R_{d} \ge 0.1,\,\,\) \(S \ge 1,\) \(E_{c} = 0.01\,\,\) and \(0 < R \le 0.1\).

  3. 3.

    The increasing value of \(\left( Z \right)\) and \(\left( R \right)\) both cause an increment in primary velocity while local primary shear stress slowly increases. Also, the reason for the reduction of the primary velocity is \(\left( S \right)\) but local primary shear stress shows uplifting nature.

  4. 4.

    Enhancement in the secondary velocity and a slow rise in the local secondary shear stress have been marked whilst the estimations of \(\left( Z \right)\) rises there out both of them show a decreasing effect for the enhancement of \(\left( R \right)\). Moreover, the secondary velocity falls for the enhancement of \(\left( S \right)\) while the local secondary shear stress rises.

  5. 5.

    The temperature profile boosts up with the increment of \(\left( Z \right)\) whilst reduces with the enhancement of both the \(\left( R \right)\) and \(\left( S \right)\).

  6. 6.

    The local Nusselt number reduces for the rise of \(\left( Z \right)\) while rises with the increment of \(\left( R \right)\) and \(\left( S \right)\) both.

The future direction of this research is to the possible analysis of the EMHD flow of rotating fluid through the inclined Riga plate with the incorporation of a non-uniform heat source.