Heat transfer and entropy generation analysis in a horizontal channel filled with a permeable medium in the presence of aligned magnetic field and temperature gradient heat source

Abstract

The current investigation is concerned with heat transfer and entropy generation analysis in a horizontal channel brimming with porous medium in the existence of aligned magnetic field, viscous and joules dissipation and temperature gradient heat source. The boundary conditions are treated as constant values for velocity and temperature at lower and upper walls. An explicit solution of governing equations has been attained in closed system. The repercussions of pertinent parameters on the fluid velocity, temperature, entropy generation and Bejan number are conferred and scrutinized through graphs in detail. Additionally the expressions for shear stress and the rate of heat transfer coefficients at the channel walls are derived and results obtained are physically interpreted through tables. From the conquered results, it is addressed that Brinkman number Br enhances boundary layer thickness. Entropy generation increases with intensifying values of $M$, aligned angle ϕ, temperature gradient heat source parameter Q, characteristic temperature ration $\omega$ and permeability parameter K. The shear stress is same at both the lower and upper walls.

1 Introduction

Magnetohydrodynamics is a main branch of fluid dynamics. It is concerned with the interaction of electrically conducting fluids and electromagnetic fluids. When a conducting fluid transports through a magnetic field, an electric field, ergo current may be induced and, in turn the current combine with the magnetic field to generate a body force. Magnetohydrodynamics interactions transpire both in environment and in man-made appliances. Magnetohydrodynamics flow ensues in the earth, ionosphere, sun, stars and atmosphere. In the research laboratory bounteous innovative devices have been invented which exploit the magnetohydrodynamics interaction precisely such as propulsion units and power generators or which implicate fluid-electromagnetic field connections, like electron beam dynamics, travelling wave tunnels, electrical exonerations and abounding others.

The investigation of heat relocation and fluid flow in a penetrable channel have secured perceptible responsiveness throughout the last many decades owed to their applicability in an extensive assortment of biological and engineering like water, geophysical science irrigation and cesspit issues and also in captivation and percolation method in chemical engineering. Temperature gradients are imperative in the meteorological sciences like climatology, meteorology and allied fields. The solar light captivation proximate the planetary surfaces will proliferation the temperature gradient. The temperature gradient may amendment significantly in time, as an outcome of diurnal or seasonal warming and cooling. For illustration in the day the temperature at ground stratum could also be frost while its radiator up in the air, since the day moves over to night time the temperature valor drip briskly while at another regions on the land sojourn cooler or warmer at an commensurate ascent. This will ensue on the west coast of the United States occasionally.

It is discerned that everywhere the irreversible processes in that time equilibrium is wrecked. The disparity within reversible and irreversible process was first imported in thermodynamics by the theory of entropy. Entropy generation denigration analysis are valuable for clinching the optimal thermic methods in industrial and scientific arenas like voltaic refrigerating, warmth exchangers, geothermal structures. The generation of entropy is exactly combined by thermodynamic irreversibility. In scheming thermal system, the focus on energy usage and the entropy generation has evolve into one of the prime intents. Bejan [1] reported the potent method of reckoning entropy generation through temperature and fluid stream in heat transfer. Denigration of entropy generation is a technique for both designing and reinforcing of power structures that is given by Bejan [2]. In prior investigations associated to the natural transmission, merely the first rule of thermodynamics was applied. Though, the mode of entropy generation blends almost substantial parameters of heat deportation, thermo dynamics & fluid dynamics. Principles and operations of entropy generation are given by Rosen [3], Narusawa [4]. Ko and Cheng [5] reported the impacts of heat transmission and entropy generation in a wavy conduit through numerical techniques. Mojtaba Aghajani Delavar and Mehdi Hedayatpour [6] investigated entropy generation by utilizing Boltzmann model in a conduit with heat producing chunk porosity. Makinde and Samuel Eigunjobi [7] applied thermo dynamics laws to analyze entropy in a duct. Tirivanhu Chinyoka and Makinde [8] explored the result of entropy generation rate and Navier slip on convective cooling flow in a permeable channel. Sanatan Dasa and Rabindra Nath Jana [9] examined in a horizontal conduit the Naver slip property on entropy generation of viscous stream by means of stable pressure gradient. Anthony Rotimi Hassan, Jacob Abiodun Gbadeyan [10] portrayed the brunt of inner warmth generation on entropy in an exothermic MHD flow by aid of Arrhenius kinetics. In this article the solutions of governing Partial differential equations are procured by adopting perturbation technique. Hatami et al. [11] studied instinctive convection heat relocation of nano-fluids in a rounded wavy-cavity by finite element technique. Sukumar and Varma [12] explored the prominence of entropy generation and viscid dissipation with temperature dependent heat source on magnetohydrodynamic generalized horizontal channel with absorbent base. Suvanjan Bhattacharyya et al. [13] analyzed the entropy as well as the enhancement of heat transmission in a wavy channel where constant temperature walls using water (H₂O) as a fluid. Rashidi et al. [14] analyzed the Brownian motion of flowing non-Newtonian (third grade) with magnetic arena. To solve the non-dimensional entropy equations authors applied method of optimal homotopy analysis (OHA). Baag et al. [15] conferred the impact of entropy generation through second law of thermo dynamics to Walters B liquid over stretching surface in the manifestation of both Darcy and Joule dissipation. To solve the equations of boundary layer authors exploited analytical method Kummer’s function. Abiodun and Thomas [16] examined the impacts of irreversibility ratio as well as entropy cohort on steady viscid fluid flow in a vertical absorbent conduit. Wenhui Tanga et al. [17] presented geometry with dual sinusoidal wavy walls of different phase aberrations for natural convection heat transfer. Saman Rashidi et al. [18, 19] presented the applications of magnetohydrodynamics in heat transfer and nano fluids. Srinivasacharya and Hima Bindu [20] presented entropy generation and Bejan number of micro rotation polar flow fluid in a concentric annulus by means of the external cylinder with fixed velocity. In this investigation utilized quasi linearization technique to solve the equations. Sudhakar and Balamurugan [21] investigated the repercussions of (Navier) slip and entropy generation between steep parallel plates with drag/inoculation. Balamurugan et al. [22] explored the reputation of entropy generation in stable Couette flow confined by a permeable bed in the manifestation of aligned magnetic arena, viscous dissipation, thermal radiation and joules dissipation. Lalrinpuia Tlau and Surender Ontela [23] explored the impact of entropy generation for Cu-water (nanofluid) flow in a conduit with Navier slip. PK Reddy and R Murthy [24] studied entropy generation with Bejan number in a rectangular channel with drag walls and perpetual temperature and torridity flux. Rahila Naz et al. [25] examined entropy generation in Williamson nanofluid with gyrotactic microorganisms along with a cylinder with engrossment of tending angle, Brownian motion and viscous dissipation effects.

In all the above cited articles, it is discerned that the authors are not considered temperature gradient heat source which is practically significant and boundary conditions $u^{*} = - u_{0}$ on the lower boundary and $\,u^{*} = u_{0}$ on the upper boundary. Therefore, this paper is apprehensive with the impacts of entropy generation as well as temperature gradient heat source on steady Couette flow with both plates lower and upper move with a uniform velocity by the means of aligned magnetic field, thermal emission, viscous dissipation and joules dissipation. An explicit solution of governing equations has been attained in closed system. The repercussions of the physical parameters on the fluid velocity, temperature, entropy generation and Bejan number are accomplished graphically and discussed in detail. Also the shear stress and heat transfer rate at the channel surfaces are derived and discussed their behavior through tables.

2 Mathematical formulation

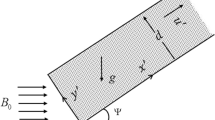
Contemplate the viscous incompressible fluid confined by two endless horizontal parallel plates alienated by a width H. The lower and higher plates move with a uniform velocity in the direction of fluid flow. A constant aligned magnetic arena of forte B at an angle ϕ is applied in the transverse direction of fluid flow. A Cartesian coordinate system is selected with $x$-axis on the lower moving plate and the y-axis at right angles to the plates (Fig. 1). It is assumed that.

• The channel is long enough in the x-direction so that complete physical variables are freelance of x (except pressure).

• The flow is totally developed hydro dynamically and thermally.

• Pressure and buoyancy forces as well as induced magnetic and electric fields are neglected.

• The temperatures of the lower and upper plates are $T_{1}$ and $T_{2}$ respectively, where $T_{2} > T_{1}$.

• Viscous dissipation, joules dissipation and temperature gradient heat source possessions are taken into account.

• In the equation of energy the radiative heat flux is meant to adapt Rosseland approximation.

Fig. 1

Scheme diagram of the flow model

The main momentum equation and energy equation for a steady stream of viscous incompressible fluid are conferred based on the previous studies [12].

$$\mu \frac{{\partial^{2} u^{*} }}{{\partial y^{{*^{2} }} }} - \sigma B_{{}}^{2} \sin^{2} \phi \;u^{*} - \frac{\mu }{{K^{*} }}u^{*} = 0$$

(1)

$$k\frac{{\partial^{2} T^{*} }}{{\partial y^{{*^{2} }} }} + \mu \,\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}} \right)^{2} + \sigma \,B^{2} \sin^{2} \phi \,u^{{*^{2} }} - \frac{{\partial q_{r}^{*} }}{{\partial y^{*} }} + Q^{*} \frac{\partial }{{\partial y^{*} }}(T^{*} - T_{1} ) = 0$$

(2)

The boundary conditions are considered as constant values for velocity and temperature for lower and upper walls, thus

$$\begin{aligned} y^{*} = 0: & \quad u^{*} = - u_{0} ,\quad T^{*} = T\quad {\text{On the lower boundary}} \\ y^{*} = H: & \;\,u^{*} = u_{0} ,\quad \;T^{*} = T_{2} \quad {\text{On the upper boundary}} \\ \end{aligned}$$

(3)

where $\mu$ is forceful viscosity, $k$ is thermic conductivity, $K^{*}$ is absorptivity, $T_{1}$ is the temperature of the lower frontier, $T_{2}$ is the temperature of the upper frontier, $H$ is the distance of the channel., B is magnetic field force, $\sigma$ is the electrical conductivity, $Q^{*}$ is temperature gradient heat source parameter and ϕ is the aligned angle. The radiation heat flux $q_{r}$ is accustomed by

$$q_{r} = \frac{{ - 4\gamma^{*} }}{{3\alpha^{*} }}\frac{{\partial T^{*4} }}{{\partial y^{*} }}$$

(4)

where $\gamma^{*}$, $\alpha^{*}$ are constants stands for Stephan-Boltzmann and mean immersion respectively. The temperature distinction within the fluid is sufficiently tiny thus $T^{*4}$ expanded in a Taylor series about the free torrent temperature T₁ so that after omitting higher order terms

$$T^{*4} \cong 4T_{1}^{3} T - 3T_{1}^{4}$$

(5)

The related non- dimensional quantities are

$$u = \frac{{u^{*} }}{{u_{0} }},\,\,\theta = \frac{{T^{*} - T_{1} }}{{T_{2} - T_{1} }},\,\,y = \frac{{y^{*} }}{H},\,\,K = \frac{{K^{*} }}{{H^{2} }}$$

(6)

In view of Eqs. (4–6) the Eqs. (1) and (2) become

$$\frac{{d^{2} u}}{{dy^{2} }} - M^{2} (\sin^{2} \phi )\,u + \frac{1}{K}u = 0$$

(7)

$$\left( {1 + \frac{4N}{3}} \right)\,\frac{{d^{2} \theta }}{{dy^{2} }} + Br\left( {\frac{du}{{dy}}} \right)^{2} + BrM^{2} (\sin^{2} \phi )\,u^{2} + Q\frac{d\theta }{{dy}} = 0$$

(8)

The subsequent conditions on the lower and upper boundary are

$$\left. \begin{gathered} u = - 1,\quad \theta = 0\quad when\quad y = 0\quad \hfill \\ u = \;\;\,1,\quad \theta = 1\quad \;when\quad y = 1 \hfill \\ \end{gathered} \right\}$$

(9)

where $M^{2} = \frac{{\sigma B_{0}^{2} H^{2} }}{\mu }$ is Hartmann number, $Br = \frac{{\mu u_{0}^{2} }}{{k\left( {T_{2} - T_{1} } \right)}}$ is Brinkman number, $Q = \frac{H}{k}Q^{*}$ is temperature gradient heat source parameter $\left( {Q > 0} \right)$ and $N = \frac{{4\gamma^{*} T_{1}^{3} }}{{\alpha^{*} k}}$ is emission parameter.

2.1 Entropy generation

Entropy analysis could be a medium to quantify the thermodynamics in any fluid flow procedure. The 1^st law of thermodynamics is an interpretation principle of the conservation of energy. Thermodynamics 2^nd law states that each real procedure is irreversible. As entropy generation takes place, the eminence of energy during a field flow manner are diminish the entropy generation with in the fluid, volume entropy generation in engineering systems rescinds existing work and then diminishes its productivity. Numerous studies are accessible in live the causes of irreversibility in workings and procedures. The entropy generation rate, characteristic entropy generation rate and characteristic temperature ratio relation are given by [12]

$$E_{G} = \frac{k}{{T_{1}^{2} }}\left[ {\left( {\frac{{dT^{*} }}{{dy^{*} }}} \right)^{2} + \frac{{16\gamma^{*} T_{1}^{3} }}{{3k\alpha^{*} }}\left( {\frac{{dT^{*} }}{{dy^{*} }}} \right)^{2} } \right] + \frac{\mu }{{T_{1} }}\left( {\frac{{du^{*} }}{{dy^{*} }}} \right)^{2} + \frac{{\sigma \,B^{2} \sin^{2} \phi \;}}{{T_{1} }}u^{{*^{2} }}$$

$$E_{{G_{0} }} = \frac{{k(T_{2} - T_{1} )^{2} }}{{H^{2} T_{1}^{2} }}$$

(11)

$$\omega = \frac{{T_{1} }}{{T_{2} - T_{1} }}$$

(12)

Entropy generation number is

$$\begin{gathered} Ns = \frac{{E_{G} }}{{E_{{G_{0} }} }} = \left( {1 + \frac{4}{3}N} \right)\,\left( {\frac{d\theta }{{dy}}} \right)^{2} + Br\omega \left[ {\left( {\frac{du}{{dy}}} \right)^{2} + \left( {M^{2} \sin^{2} \phi } \right)\,u^{2} } \right] \hfill \\ \quad \;\, = HTI + FFI \hfill \\ \end{gathered}$$

(13)

where $HTI = \left( {1 + \frac{4}{3}N} \right)\,\left( {\frac{d\theta }{{dy}}} \right)^{2}$ is the heat transferal irreversibility $FFI = Br\omega \left[ {\left( {\frac{du}{{dy}}} \right)^{2} + \left( {M^{2} \sin^{2} \phi } \right)\,u^{2} } \right]$ is the fluid friction irreversibility

The Bejan number $Be$ is the appropriate irreversibility parameter and is well-defined as

$$Be = \frac{HTI}{{N_{s} }}$$

(14)

The Bejan number range concerning 0 and 1. Where ever $Be = 1$ is that the limit, at that heat transfer irreversibility dominates, $Be = 0$ is that the limit at that fluid friction irreversibility dominates and $Be = 1/2$ implies that both of them contribute equally.

3 Solution of the problem

To explain the entropy generation & Bejan number on Couette flow with aligned magnetic in the manifestation of thermal radiation, temperature dependent heat source influence, dissipations (viscous and joules), it is requisite regimes of velocity and temperature. The governing equations are determined by systematic technique and it is solved by employing (7), (8) and (9). Initially, solution of the equation of momentum (7) is obtained which is used to solve equation of energy (8).

Explication of the reckonings (7) and (8) subjected to the periphery conditions (9) are attained as follows

$$u = c_{1} e^{{M_{1} \,y}} + c_{2} e^{{ - M{}_{1}\,y}}$$

(15)

$$\theta = c_{3} + c_{4} e^{{ - \,\frac{Q}{B}y}} + c_{5} e^{{2M_{1} \,\,y}} + c_{6} e^{{ - 2M_{1} \,\,y}} + c_{7}$$

(16)

$$\begin{gathered} Ns = \left( {1 + \frac{4}{3}N} \right)\,\left( {c_{4} \left( { - \frac{Q}{B}} \right)e^{{ - \frac{Q}{B}y}} + 2M_{1} c_{5} e^{{2M_{1} y}} - 2M_{1} c_{6} e^{{ - 2M_{1} y}} + c_{7} } \right)^{2} \hfill \\ \quad \;\;\; + Br\omega \left[ {c_{1}^{2} e^{{2M_{1} y}} \left( {2M_{1}^{2} } \right) + c_{2}^{2} e^{{ - 2M_{1} y}} \left( {2M_{1}^{2} } \right)\,} \right] \hfill \\ \end{gathered}$$

(17)

3.1 Skin friction

$$\tau = \left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0,\quad y = 1}$$

(18)

$$\tau_{y = 0} = c_{1} M_{1} - c_{2} M_{1}$$

(19)

$$\tau_{y = 1} = c_{1} M_{1} e^{{M_{1} }} - c_{2} M_{1} e^{{ - M_{1} }}$$

(20)

3.2 Nusselt Number

$$Nu = \left( { - \frac{\partial \theta }{{\partial y}}} \right)_{y = 0,\;y = 1}$$

(21)

$$Nu_{y = 0} = \frac{Q}{B}c_{4} - 2M_{1} c_{5} + 2M_{1} c_{6} + c_{7}$$

(22)

$$Nu_{y\, = 1} = \frac{Q}{B}c_{4} e^{{ - \,\frac{Q}{B}}} - 2M_{1} c_{5} e^{{2M_{1} }} + 2M_{1} c_{6} e^{{ - 2M_{1} }}$$

(23)

4 Results and discussion

The current examination is a continuation work of Sukumar and Varma [12] with porous medium K, aligned angle ϕ and temperature gradient heat source instead of temperature dependent heat source and with different boundary condition $u^{*} = - \,u_{0}$ instead of slip condition $\frac{{\partial u^{*} }}{{\partial y^{*} }} = \frac{\alpha }{\sqrt K }u^{*}$ at $y^{*} = 0$. The target of the current work is to contemplate the properties of temperature gradient heat source and entropy generation on aligned magnetic arena in the subsistence of thermal radiation, viscous dissipation and joules dissipation. The implications of physical parameters such as Brinkman number $Br$, Hartmann magnetic number $M$, radiation parameter $N$, permeability parameter K, aligned angle parameter ϕ, characteristic temperature ratio $\omega$ and temperature gradient heat source parameter $Q$ are probed on the velocity and temperature distributions, Bejan number and entropy generation. The closed method result procured for velocity and temperature are selected to enumerate entropy generation. The conclusions are interpreted by graphs using MATLAB program. The mutations in profiles of velocity $u$ for diverse values of aligned angle parameter ϕ and Hartmann number $M$ are conferred in Figs. 2 and 3. It is perceived that the velocity of the fluid increased in lower part of the channel whereas it contracts in the upper part of the channel with rising M or ϕ. The consequences of Brinkman number Br, Hartmann numbers M and temperature gradient-heat source $Q$ on temperature distribution are shown in Fig. 4. It was confirmed that the fluid temperature enriched with an escalation of temperature gradient heat source Q and Brinkman number Br. The enhancement in Brinkman number repercussions in enhanced convective transport and $Q$ result is very much eloquent for the fluid flow model where transfer of heat is given prime imperative, whereas the mounting values of Hartmann number M denigrate the fluid temperature.

Fig. 2

Velocity portrait for diverse values of M, when ϕ = π/3 and K = 0.5

Fig. 3

Velocity portrait for diverse values of aligned angle parameter ϕ when K = 0.5 and M = 10

Fig. 4

Temperature portrait for diverse values of Hartmann and Brinkman numbers Br and M and gradient heat source parameter Q when N = 1, K = 1 and ϕ = π/3

Figure 5 emphasizes the changes of θ-temperature distribution for diverse values of N radiation parameter and aligned angle parameter ϕ. It is noticed that the temperature distribution diminishes with intensifying N and ϕ values. This can be interpreted by the evidence that an escalation $N = \frac{{4\gamma^{*} T_{1}^{3} }}{{\alpha^{*} k}}$ for k and T₁ aids acceleration in the mean immersion constant $\alpha^{*}$. The deviation of radiative heat flux diminutions as $\alpha^{*}$ intensifications the rate of radiative heat transferred to the fluid and accordingly the fluid temperature decreases.

Fig. 5

Temperature portrait for diverse values of radiation parameter N and aligned angle parameter ϕ when K = 1, Q = 1 and M = 1

The diversity in entropy generation number $Ns$ for conflicting values of aligned angle ϕ, Hartmann magnetic number $M$, Brinkman number $Br$, permeability parameter K and temperature gradient heat source Q are shown in Figs. 6, 7, 8. From Fig. 6 it is witnessed that in the channel the entropy generation accelerates with accelerating values of M and K, this instigated by the transversely enforced hypnotic field retards the flow as well as Ohmic dissipation leads to intensification in heat in the channel with augmenting values of M. Figure 7 demonstrates the impact of Brinkman number Br and temperature gradient heat source Q on the entropy generation. From the figure, it was endorsed that dissimilar enrichment values of the temperature gradient heat source lead to stimulating the entropy generation rate. But by Brinkman number the amount of entropy generation rises in the down part of the channel and decays in the upper part of the channel. It is highlighted that Br is a part of fluid erosion in the dissipative flow pattern. Figure 8 elucidates the effect of aligned angle parameter ϕ against N_s entropy generation. It demonstrates that entropy accelerates in the conduit with escalating aligned angle. The difference in Bejan number Be for divergent values of flow parameters are exhibited in Figs. 9 and 10. Figure 9 demonstrates the influences of temperature gradient heat source Q as well as radiation parameter N on Bejan number. The Bejan number raised by the incremental values of temperature gradient heat source parameter Q near lower and upper part of the channel while the slackening effect occurs in the middle of the channel. Opposite effect occurred in case of radiation parameter N i.e.: the Bejan number is diminished by means of the incremental values of radiation parameter N near lower and upper part of the channel while the intensification effect occurs in the middle region of the channel. Figure 10 depict that the Bejan number declined in the channel with increasing values of characteristic ratio $\omega$ and aligned angle parameter ϕ.

Fig. 6

Ns for diverse values of Hartmann number M & porosity parameter K when Q = 1, N = 1, ω = 0.4, ϕ = π/3 and Br = 10

Fig. 7

source parameter Q when M = 2, K = 1, N = 1, ϕ = π/3 and ω = 0.4

Ns for diverse values of Brinkman number Br and temperature gradient heat

Fig. 8

Ns for diverse values of aligned angle parameter ϕ when K = 1, Q = 1, N = 1, M = 1, ω = 0.4 and Br = 10

Fig. 9

source when M = 2, ω = 0.4, Br = 10, K = 0.01 and ϕ = π/3

Bejan number for diverse values of N-radiation parameter and Q-temperature gradient heat

Fig. 10

Bejan number for diverse values of ω-characteristic temperature ration and ϕ-aligned angle parameter when N = 1, M = 2, K = 0.01, and Q = 1

Table 1 illustrates the shearing stress at the plates y = zero (0) and y = one (1). From this table it is noticed that the intensifying values of M and ϕ lead to raise shear stress at both plates. But conflicting influence was eventuated in case of porosity parameter K. Also we can see that shear stress is same at both plates (lower and upper plates). Table 2 represents the impacts of M-magnetic field parameter and K-permeability parameter on Nusselt number. It is perceived that the Nusselt number declines with an augment in M or K at wall y = zero (0), whereas at wall y = one (1), Nu decreases by increasing M or K. Table 3 elucidates that Nusselt number lessening by an rise in Q-temperature gradient heat source parameter or Brinkman number Br at y = zero (0) wall but reverse trend at the wall y = one (1). Table 4 shows that with increasing aligned angle ϕ or radiation parameter N, the Nusselt number Nu accelerates at lower plate y = zero (0) and decelerates at higher plate y = one (1).

Table 1 Skin friction at the plates $y = 0$ and $y = 1$

Table 2 Nusselt number for diverse values of Hartmann number M and porosity parameter K with $Br$ = 10, $N$ = 1,$Q$ = 1, $\varphi = \frac{\pi }{3}$ and $y = 0,\,1$

Table 3 Nusselt number for diverse values of brinkman number Br and temperature gradient heat source parameter Q with N = 1,$M$ = 1, $K$ = 1, $\varphi = \frac{\pi }{3}$ and $y = 0,\,1$

Table 4 Nusselt number for diverse values of aligned angle parameter ϕ, radiation parameter N with Br = 10, $M$ = 1, $K$ = 1, Q = 1 and $y = 0,1$

5 Conclusions

Entropy generation in a horizontal channel entrenched with permeable medium in the existence of aligned magnetic field, temperature gradient heat source, thermal radiation and dissipations (viscous and joules) have been studied and analyzed. The results obtained from our examination are the velocity of the fluid escalated in lower part of the channel while it contracts in the upper part of the channel with intensifying magnetic field parameter $M$ and aligned magnetic field parameter ϕ. Fluid temperature intensification with amplification of magnetic parameter M or temperature gradient heat source parameter Q. Brinkman number Br augments boundary layer density. Due to thermal radiation or aligned angle the thickness of thermal boundary layer becomes thinner. $Ns$ escalates with intensifying values of $M$, aligned angle ϕ, temperature gradient heat source parameter Q, characteristic temperature ration $\omega$ and permeability parameter K. But contrast result is occurred in the case of N- radiation parameter. Entropy generation increases in lower part of the channel whereas the reversal effect is occurred in the upper part of the channel by Brinkman number Br. When the magnetic parameter M accelerates the Bejan number diminished in the lower part of the channel and rises in the upper part channel. Bejan number will increase in lower and upper part of the channel with the cumulative values of Br whereas it decays in the middle region of the channel with the increasing values Br. Reinforcement of characteristic temperature ration $\omega$ or aligned angle parameter ϕ leads to decelerate in Bejan number. Spurring the values of temperature gradient heat source Q lead to Bejan number increases in lower & higher divisions of the conduit but in the central segment of the channel the reversed trend is witnessed. Bejan number decreases at both lower and upper channel except in central region of the channel, the reversed trend is witnessed in middle region of the channel due to enhancement in diverse values of radiation parameter N. Increasing M or ϕ the skin friction accelerates but decays by porosity K at both the lower and upper walls. As Brinkman number Br or temperature gradient heat source Q rises, the Nusselt number decays at lower (y = 0) wall and increases at upper (y = 1) wall.

The results that are obtained are helpful to study in what way to minimize or restrict energy wastages in the form of heat dissipation during energy generation, particularly in dealing with problems of heat transfer. This flow model can be extended to study for non-Newtonian fluid flows.

Appendix

$$\begin{aligned} c_{1} = & \frac{{1 + e^{{ - M_{1} }} }}{{e^{{M_{1} }} - \,e^{{ - M_{1} }} }}, \\ c_{2} = & - 1 - c_{1} , \\ c_{3} = & - c_{4} - c_{5} - c_{6} , \\ c_{4} = & \frac{{c_{5} (e^{{2M_{1} }} - 1) + c_{6} (e^{{ - 2M_{1} }} - 1) + c_{7} - 1}}{{1 - e^{{ - \,\frac{Q}{B}}} }}, \\ c_{5} = & \frac{{Brc_{1}^{2} (M^{2} \sin^{2} \phi - M_{1}^{2} )}}{{\left( {4BM_{1}^{2} + 2M_{1} Q} \right)}}, \\ c_{6} = & \frac{{Brc_{2}^{2} (M^{2} \sin^{2} \phi - M_{1}^{2} )}}{{\left( {4BM_{1}^{2} - 2M_{1} Q} \right)}}, \\ B = & 1 + \frac{4N}{3}, \\ M_{1}^{2} = & M^{2} \sin^{2} \phi + \frac{1}{K} \\ \end{aligned}$$