1 Introduction

Landing gear or in brief LG systems, support the structure of aircraft by trunnions, transmit decreased impact loads, hold aircraft stable during landing and taxiing phase, provide passenger comfort and make the aircraft to control on the runway [1]; An ideal LG can return aircraft to the equilibrium state rapidly, without any oscillation. There are three kinds of LG systems including passive, semi-active, and active. Passive LG systems do not have any tools for modifying their performance regarding landing condition and they are optimized only once in the factory and technicians must check the LG at the end of a certain period to ensure that there is no fault in the system. semi-active LG systems usually benefit from dampers and control the system by adjusting the area of the main orifice. However, active LG is equipped by an electro-hydraulic system producing an external force for tackling ground excitation and improving the performance of absorber in real-time. Many useful types of research were performed about semi-active control systems, but this paper is concentrated on active systems and investigates only researches that were carried out around this kind of LGs.

In 1982, the concept of an active control system was proposed by Ross and Edson for reducing vibrations and landing loads under different runway conditions [2]. As Ross and Edson started their survey, Karnopp was simultaneously working on the concept of semi-active control of LG [3]. In 1987, Freymann experimentally proved the reduction of 42% in vertical acceleration in an active control system [4, 5]. Researchers could show the advantages of an active control system versus other control strategies. They could analytically and experimentally show the effectiveness of an active control system in reducing the vibrations, jerks and aircraft loads in landing time [6, 7]. The researchers dedicated upper chamber for oil transferring and an accelerometer was located on top of the LG for measuring vertical acceleration. In addition, a linear potentiometer and a pressure gauge were utilized to evaluate impact of the shock strut and hydraulic pressure of the actuator, respectively. External signals of the transmitters were sent to control system as feedbacks and the controller analized them to calculate suitable flow quantity. Moreover, a servovalve was applied for adjusting the flow quantity which was injected to LG or exited from it.

Until present, a range of control methods is used for control of LG. For instance, PID control [1, 8], optimal control [9], backstepping control [10], predictive control [11, 12], H-infinity Control Approach [13] and fuzzy control [9,10,11,12] are presented by researches that many of them were around semi-active control approach and some of them concentrated on active control. The goal of the majority of these studies was tackling the body oscillations after landing or passing bumps. In [1, 14] a PID controller is designed to actively control the LG in which the coefficients are adjusted by Ziegler-Nichols tuning rules. But the authors mentioned that the proposed control systems lack robustness against large uncertainties. This is because of an inadequate number of parameters to deal with the independent specifications of time-domain response like settling time and overshooting. Moreover, in some studies, a PID controller was used with variable coefficients. These coefficients can be tuned by intelligent manners such as bee algorithm, PSO, or other methods [15,16,17,18,19,20].

An important fact here and in many types of research that used the PID controller in LG is that regardless of using constant or variable PID coefficients, there is a huge question on this method. The actual LG system is highly nonlinear [21, 22]. While the system is nonlinear, linearization will result in adding different sources of error to the system. An imprecise model, in the linearization process, will provide an incorrect equilibrium point and the PID controller will not work well. Concerning this fact that the disturbance in the linearized model is too large, any disturbance can push the system far away from the equilibrium point. This issue is mentioned in [8] strictly. Therefore, simplifications and linearizations are not suitable in this case. So, PID controllers seem to be not an efficient solution for this type of highly nonlinear system.

Recently, to achieve a reasonable performance including good passenger comfort and good aircraft handling, an impedance fuzzy controller was proposed for LG. The control system was comprised of three interior loops named impedance loop, position loop, and force loop. A transfer function was presented for the impedance loop that can regulate the dynamic behavior of LG. A PD-like fuzzy and a simple classic PI controller was designed for position and force loops, respectively. Although the control system succeeded to decrease the vibrations and improve both comfort and handling, the controllers were not robust and uncertainties were not considered in this study [23]. Also, in another research, aircraft handling and passenger comfort were promoted using variable mechanical admittance while aircraft is taxiing on the ground [24]. The research is utilized a three dimensional mass-spring-damper model for landing gear and neglects the nonlinearity of the system.

It is worth noting that the control system should be efficient in both landing moment and during taxiing phase. In the previous papers, the effect of the proposed controllers at touchdown and passing bumps, was not investigated separately. Based on the above description, a new manner should be presented to be robust against a range of uncertainties (that include landing impact, bump stroke, unmodeled dynamics, measurement errors and external disturbance of actuator) and dose not have the mentioned PID controllers’ issues.

In this paper, the operation of landing gear is proposed in Sect. 2. After that, the dynamics of the system is clearly described and the equations of the forces are well proposed. Regarding all the aspects mentioned previously, RNCS is selected in this study. In Sect. 4, the RNCS design is investigated and in the next sections, displacement control and force control are widely described. After that, the control system was applied to the model using MATLAB software and performance of the controllers are studied under a lumped uncertainty at landing moment and during taxiing phase, separately and their results are completely expressed.

2 Mathematical model of LG

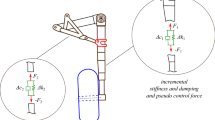
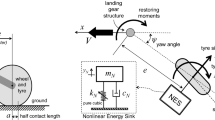
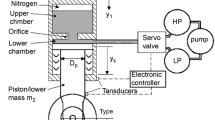
As Fig. 1 illustrates, an active LG system is comprised of the main absorber and some additional electro-hydraulic devices. In theoretical researches, a vibration model is usually used for reviewing the performance of LG. Figure 2 indicates a two DOF vibration model of an active LG where m1 is aircraft mass and m2 is mass of tire and shock absorber. K1, C1, Kt, and Ct are the parameters that represent the stiffness and the damping coefficients of the absorber and tire, respectively. y1, y2 are positions of m1 and m2, respectively and yg is ground input displacement.

Fig. 1
figure 1

Active landing gear system [8]

Full size image
Fig. 2
figure 2

Two DOF model of active LG system [23]

Full size image

The dynamic equations describing the LG system is presented as [8]:

$$\left\{ {\begin{array}{*{20}l} {m_{1} \ddot{y}_{1} = m_{1} g - L - F_{a} - F_{l} - f - F_{Q} } \hfill \\ {m_{2} \ddot{y}_{2} = m_{2} g - F_{t} + F_{a} + F_{l} + f + F_{Q} } \hfill \\ \end{array} } \right..$$
(1)

In which L is the aerodynamic lift and g is the gravitational acceleration constant. Fa, Fl, Ft, f, and FQ represent the spring force of the shock absorber, damping forces of the shock absorber, the tire force, the friction force, and the active control force, respectively.

The forces of the dynamic equations are defined as below [8]:

  • The spring force Fa which is generated by the pressure of the nitrogen gas can be described as:

    $$F_{a} = \frac{{P_{0} A}}{{\left( {1 - \frac{{y_{1} - y_{2} }}{{y_{0} }}} \right)^{n} }}$$
    (2)

    where \(y_{0} = \frac{{V_{0} }}{A}\) and P0, V0, y0 are initial gas pressure, volume, and length of the gas cylinder, respectively. A is the cross-sectional area of the piston and n is the gas constant of value normally.

  • Damping force is produced by the oil flowing through the orifice and can be given by:

    $$F_{l} = P_{l} A$$
    (3)

    here \(y_{3} = \dot{y}_{1}\), \(y_{4} = \dot{y}_{2}\) and \(P_{l} = \frac{{0.5\rho A^{2} \left( {y_{3} - y_{4} } \right)\left| {y_{3} - y_{4} } \right|}}{{\xi^{2} A_{0}^{2} }}\) is the difference between the pressures of the lower and upper chambers. A0, \(\rho\) and \(\xi\) denote the orifice area, the mass density of the oil, and an orifice discharge coefficient, respectively.

  • Tire force is an applied force on the tire from the runway and is in the following form:

    $$F_{t} = K_{t} \left( {y_{2} + y_{g} } \right) + C_{t} \left( {y_{4} + \dot{y}_{g} } \right).$$
    (4)

  • In this type of LG, the friction force is due to two different sources. Friction \(F_{OW}\) stems from the offset wheel and friction \(F_{sael}\) is generated by the tightness of the seal. These forces are formulated as:

    $$F_{seal} = K_{m} \left( {y_{3} - y_{4} } \right) - {\text{sgn}} \left( {y_{3} - y_{4} } \right)K_{n} \left( {y_{3} - y_{4} } \right)^{2}$$
    (5)
    $$F_{OW} = \frac{{F_{t} \mu l}}{{y_{1} - y_{2} + B}}$$
    (6)

    where B is one-half of the thickness of the lower bearing, \(\mu\) is the coefficient of friction on the interface between the cylinder and the piston. l represents the distance between the tire force and the centerline of the piston. Km and Kn are two positive coefficients. Therefore, the total friction force f in the LG will be as follows:

    $$f = F_{seal} + F_{OW} .$$
    (7)

  • The active control force is the same force that is generated by an external hydraulic actuator such as a servo valve. This force is a function of the flow quantity which is adjusted by the displacement of the servo valve. There is no exact relationship between the active control force and the flow quantity from the servo valve and it is often determined through experiments or by the empirical formula. The force can be given by:

    $$F_{Q} = K_{a} Q + K_{b} Q\left| Q \right|$$
    (8)

where

$$Q = C_{d} wx\sqrt {\frac{{\left| {P_{s} - P_{l} } \right|}}{\rho }}$$
(9)

here Q represents the flow quantity in which Cd is the discharge coefficient, w defines the gradient of the area of the servo valve port, Ps is the pressure of oil reservoir and x is the displacement of the servo valve. Ka and Kb are the characteristic constants. Assume the oil pressure in the low-pressure reservoir is denoted Psl and the oil pressure in the high-pressure reservoir is denoted Psh, then we have:

$$P_{s} = \left\{ {\begin{array}{*{20}l} {P_{sh} } \hfill & {x \ge 0} \hfill \\ {P_{sl} } \hfill & {x < 0} \hfill \\ \end{array} } \right.$$
(10)

whenever the servo valve is opened positively (\(x \ge 0\)), the oil is transferred from the high-pressure reservoir into the LG and generates a positive flow quantity and a positive active force. If the servo valve is opened negatively (\(x < 0\)), then the oil is sent from LG into the low-pressure reservoir. Thus, both the flow quantity and active force are negative.

3 Robust nonlinear control system design

The designed control system includes two loops. The outer loop is responsible for controlling the vertical displacement of the LG and the inner loop is designed to control the external actuator force by determining the displacement of a servo valve. The output of the displacement controller determines the desired external actuator force and it is applied to the inner loop as a reference signal. Thus, the force loop should be able to track the desired force exactly. Any error produced by the inner loop will be compensated by the outer loop through negative feedback. Also, this control system can overcome uncertainties including parametric errors, measurement noise, disturbance due to runway excitation, and other disturbances, since RNCS used in both the displacement loop and the force loop. Small uncertainties will be omitted by a small force while counteracting to larger uncertainties needs a larger active control force. The structure of the control system is shown in Fig. 3.

Fig. 3
figure 3

The structure of the control system

Full size image

3.1 Displacement control

The dynamics model of LG can be written as follow:

$$\left\{ {\begin{array}{*{20}l} {\ddot{y}_{1} = g - \frac{L}{{m_{1} }} - \frac{1}{{m_{1} }}\left( {F_{a} + F_{l} + f + F_{Q} } \right)} \hfill \\ {\ddot{y}_{2} = g - \frac{{F_{t} }}{{m_{2} }} + \frac{1}{{m_{2} }}\left( {F_{a} + F_{l} + f + F_{Q} } \right)} \hfill \\ \end{array} } \right..$$
(11)

According to equations of forces, the dynamics model of LG shows that the system is highly coupled and nonlinear. Thus, an advanced controller should be designed to overcome these nonlinearities. The LG deflection ys is defined as:

$$\ddot{y}_{s} = \ddot{y}_{2} - \ddot{y}_{1} = \frac{L}{{m_{1} }} - \frac{{F_{t} }}{{m_{2} }} + \left( {\frac{1}{{m_{1} }} + \frac{1}{{m_{2} }}} \right)\left( {F_{a} + F_{l} + f + F_{Q} } \right)$$
(12)

Now, by defining:

$$\left\{ {\begin{array}{*{20}l} {\overline{C} = \frac{{m_{1} m_{2} }}{{m_{1} + m_{2} }}} \hfill \\ {\overline{D} = \frac{{ - m_{2} }}{{m_{1} + m_{2} }}L + \frac{{m_{1} }}{{m_{1} + m_{2} }}F_{t} - F_{a} - F_{l} - f} \hfill \\ \end{array} } \right..$$
(13)

Equation (12) can be rewritten as:

$$\overline{C} \ddot{y}_{s} + \overline{D} = F_{Q} .$$
(14)

The real terms \(\overline{C}\) and \(\overline{D}\) are not completely known, because an exact model is not available. However, the nominal terms can be used in the model system. Hence, Eq. (14) changes to:

$$C\ddot{y}_{s} + D + F_{u} = F_{Q}$$
(15)

here C and D are the nominal terms for \(\overline{C}\) and \(\overline{D}\) respectively, and Fu is an unknown function that represents the lumped uncertainty. It is assumed C and D have the structure as \(\overline{C}\) and \(\overline{D}\) respectively. A suitable control law can be proposed based on the feedback linearization as:

$$Cu_{p} + D + \hat{F}_{u} = F_{Q}$$
(16)

where \(\hat{F}_{u}\) denotes the estimation of lumped uncertainty and up is a new control input. Substituting (16) into (15) yields:

$$u_{p} - \ddot{y}_{s} = C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right).$$
(17)

Now, a control law for up can be proposed as:

$$u_{p} = \ddot{y}_{sd} + K_{d}^{D} \left( {\dot{y}_{sd} - \dot{y}_{s} } \right) + K_{p}^{D} \left( {y_{sd} - y_{s} } \right)$$
(18)

where \(\ddot{y}_{sd}\) is desired LG deflection and the two terms \(K_{d}^{D}\) and \(K_{p}^{D}\) are positive constants for displacement controller, which are called proportional and differential coefficient respectively. Substituting (18) into (17) gives

$$\left( {\ddot{y}_{sd} - \ddot{y}_{s} } \right) + K_{d}^{D} \left( {\dot{y}_{sd} - \dot{y}_{s} } \right) + K_{p}^{D} \left( {y_{sd} - y_{s} } \right) = C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right).$$
(19)

If the tracking error is defined as e = ysd − ys then Eq. (19) can be changed to:

$$\ddot{e} + K_{d}^{D} \dot{e} + K_{p}^{D} e = C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right).$$
(20)

The direct method of Lyapunov is then applied to obtain a suitable robust control law. The state-space form of (20) is expressed as follows:

$$\dot{E} = AE + B\left( {C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right)} \right)$$
(21)

where \(E = \left[ {\begin{array}{*{20}c} e & {\dot{e}} \\ \end{array} } \right]^{T}\) is the space vector and \(C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right)\) can be supposed as the input of the system. A is the state matrix and B is gain of input vector which are defined as:

$$A = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - K_{p}^{D} } & { - K_{d}^{D} } \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right].$$
(22)

A Lyapunov function candidate is considered for guaranteed stability as:

$$V_{p} \left( E \right) = E^{T} PE\quad \left( {for:E \ne 0} \right),\quad V_{p} \left( 0 \right) = 0$$
(23)

here Vp(E) denotes the Lyapunov function candidate and P is a positive definite symmetric matrix. Taking the time derivative of (23) yields in:

$$\dot{V}_{p} \left( E \right) = \dot{E}^{T} PE + E^{T} P\dot{E}.$$
(24)

From (21) we have:

$$\dot{E}^{T} = E^{T} A^{T} + \left( {C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right)} \right)^{T} B^{T} .$$
(25)

Substituting (25) and (21) into (24) gives:

$$\begin{aligned} \dot{V}_{p} \left( E \right) & = E^{T} A^{T} PE + \left( {C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right)} \right)^{T} B^{T} PE \\ & & \quad + \;E^{T} PAE + E^{T} PB\left( {C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right)} \right). \\ \end{aligned}$$
(26)

The Eq. (26) can be simplified as:

$$\dot{V}_{p} \left( E \right) = E^{T} \left( {A^{T} P + PA} \right)E + 2E^{T} PB\left( {C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right)} \right).$$
(27)

Assuming Q is a positive definite symmetric matrix that satisfies the Lyapunov equation, as stated in the "Appendix".

$$A^{T} P + PA = - Q.$$
(28)

Then from (27) and (28):

$$\dot{V}_{p} \left( E \right) = - E^{T} QE + 2E^{T} PB\left( {C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right)} \right).$$
(29)

And asymptotic stability is achieved if \(\dot{V}_{p} \left( E \right) \le 0\). Thus it is sufficient that:

$$E^{T} PB\left( {C^{ - 1} \left( {F_{u} - \hat{F}_{u} } \right)} \right) \le 0.$$
(30)

Hence, this is sufficient so long as:

$$E^{T} PBC^{ - 1} F_{u} \le E^{T} PBC^{ - 1} \hat{F}_{u} .$$
(31)

Assume that we can calculate an upper bound on the uncertainty Fu as:

$$\left| {F_{u} } \right| \le \phi \left( t \right)$$
(32)

where φ(t) is a known scalar. Using (32) and the Cauchy–Schwartz inequality can be written as:

$$E^{T} PBC^{ - 1} F_{u} \le \left| {E^{T} PBC^{ - 1} } \right| \cdot \left| {F_{u} } \right| \le \left| {E^{T} PBC^{ - 1} } \right|\varphi \left( t \right).$$
(33)

Therefore, to establish (31), it is sufficient to have:

$$E^{T} PBC^{ - 1} \hat{F}_{u} = \left| {E^{T} PBC^{ - 1} } \right|\varphi \left( t \right).$$
(34)

Thus, if \(E^{T} PB \ne 0\), robust control can be proposed as:

$$\hat{F}_{u} = \frac{{E^{T} PB}}{{\left| {E^{T} PB} \right|}}\varphi \left( t \right)\quad \left( {if:E^{T} PB \ne 0} \right).$$
(35)

If ETPB = 0, then form (29):

$$\dot{V}_{p} \left( E \right) = - E^{T} QE.$$
(36)

As a result, the control system will be stable regardless of robust control \(\hat{F}_{u}\). Hence it can be proposed:

$$\hat{F}_{u} = 0\quad \left( {if:E^{T} PB = 0} \right).$$
(37)

Generally, the robust control law is provided by (35) and (37) [25], but this is discontinuous on ETPB = 0 and may cause chattering. It can also excite high-frequency dynamic modulation in the modeling which degrades the performance of the control system and may even lead to instability. If ε is a small positive constant for eliminating possible chattering, discontinuous robust control law can be modified using a suitable approximation as:

$$\hat{F}_{u} = \left\{ {\begin{array}{*{20}l} {\frac{{E^{T} PB}}{{\left| {E^{T} PB} \right|}}\varphi \left( t \right)} \hfill & {\left( {if:E^{T} PB \ge \varepsilon } \right)} \hfill \\ {\frac{{E^{T} PB}}{\varepsilon }\varphi \left( t \right)} \hfill & {\left( {if:E^{T} PB < \varepsilon } \right)} \hfill \\ \end{array} } \right..$$
(38)

Besides, a simple low pass filter can be designed to create a better control system and reduce the impress of chattering in (38).

Detecting a proper function for φ(t) is too difficult, but it can be determined by the upper bound of the parameters based on an expert’s knowledge about the model of the system. Anyway, the safe uncertainty bound parameter can be obtained from nominal terms in the equation of the system. From (14) and (15) we have:

$$(\overline{C} - C)\ddot{y}_{s} + (\overline{D} - D) = F_{u} .$$
(39)

Hence, lumped uncertainty is a function of the dynamics model of LG. By taking the norm 2 of (39), it can be realized that it is bounded as follows:

$$\left| {F_{u} } \right| \le \left| {(\overline{C} - C)} \right| \cdot \left| {\ddot{y}_{s} } \right| + \left| {(\overline{D} - D)} \right|.$$
(40)

Now, suppose that the nominal terms in the equation of system are adequately close to real terms such as \(\left| {(\overline{C} - C)} \right| \le \left| C \right|\) and \(\left| {(\overline{D} - D)} \right| \le D\). Thus by substituting these assumptions into the relation, it can easily be obtained that:

$$\left| {F_{u} } \right| \le \left| C \right| \cdot \left| {\ddot{y}_{s} } \right| + \left| D \right|.$$
(41)

And concerning (41) and (32), uncertainty bound parameter can be chosen as:

$$\varphi \left( t \right) = \left| C \right| \cdot \left| {\ddot{y}_{s} } \right| + \left| D \right|.$$
(42)

Although the nominal terms C and D are completely known for us but \({\ddot{y}}_{s}\) should be measured by feedback. It is worth noting, an upper bound on the uncertainty Fu can be found in a better manner.

3.2 External force control

Substituting (8) into (9) gives:

$$F_{Q} = a_{1} x + a_{2} x\left| x \right|$$
(43)

where a1 and a2 are defined as:

$$\left\{ {\begin{array}{*{20}l} {a_{1} = K_{a} C_{d} w\sqrt {\frac{{\left| {P_{s} - P_{l} } \right|}}{\rho }} } \hfill \\ {a_{2} = K_{b} C_{d}^{2} w^{2} \frac{{\left| {P_{s} - P_{l} } \right|}}{\rho }} \hfill \\ \end{array} } \right..$$
(44)

The external actuator system of (43) is nonlinear and nonaffine. Therefore, at first, we will change it to an affine system. Now it can be defined:

$$\delta = x + \tau \dot{x}.$$
(45)

Thus,

$$\dot{x} = \frac{\delta - x}{\tau }$$
(46)

where τ is a positive constant. The time derivative of (43) yields:

$$\dot{F}_{Q} = \dot{a}_{1} x + a_{1} \dot{x} + \dot{a}_{2} x\left| x \right| + 2a_{2} \dot{x}\left| x \right|.$$
(47)

From (46) and (47):

$$\dot{F}_{Q} = \dot{a}_{1} x + a_{1} \left( {\frac{\delta - x}{\tau }} \right) + \dot{a}_{2} x\left| x \right| + 2a_{2} \left( {\frac{\delta - x}{\tau }} \right)\left| x \right|.$$
(48)

Hence, (48) can be rewritten as:

$$\dot{F}_{Q} = \dot{a}_{1} x + \dot{a}_{2} x\left| x \right| - \left( {\frac{{a_{1} + 2a_{2} \left| x \right|}}{\tau }} \right)x + \left( {\frac{{a_{1} + 2a_{2} \left| x \right|}}{\tau }} \right)\delta .$$
(49)

Equation (49) can be presented in the simple form of:

$$\overline{R} \dot{F}_{Q} + \overline{S} = \delta$$
(50)

where \(\overline{R}\) and \(\overline{S}\) are defined as:

$$\left\{ {\begin{array}{*{20}l} {\overline{R} = \frac{\tau }{{a_{1} + 2a_{2} \left| x \right|}}} \hfill \\ {\overline{S} = - \frac{{\dot{a}_{1} + \dot{a}_{2} \left| x \right|}}{{a_{1} + 2a_{2} \left| x \right|}}\tau x + x} \hfill \\ \end{array} } \right..$$
(51)

It should be noted that \(a_{1} + 2a_{2} \left| x \right|\) must be unequal to zero so that \(\overline{R}\) and \(\overline{S}\) will be bounded. The model is an affine system and δ is its input. The real \(\overline{R}\) and \(\overline{S}\) are unknown for us because the exact model is not available. However, the nominal model can be used as:

$$R\dot{F}_{Q} + S + \delta_{u} = \delta$$
(52)

S and R are the nominal terms of \(\overline{R}\) and \(\overline{S}\) respectively and δu represents lumped uncertainty. A control law can be proposed as:

$$Ru_{f} + S + \hat{\delta }_{u} = \delta$$
(53)

uf denotes a new control input and \(\hat{\delta }_{u}\) is the estimation of lumped uncertainty. Substituting (53) into (52) obtains:

$$u_{f} - \dot{F}_{Q} = R^{ - 1} \left( {\delta_{u} - \hat{\delta }_{u} } \right).$$
(54)

Now the new control input uf can be offered as:

$$u_{f} = \dot{F}_{Qd} + K_{p}^{F} \left( {F_{Qd} - F_{Q} } \right)$$
(55)

where \(K_{p}^{F}\) is a positive constant, which is called the proportional coefficient for force controller and FQd is the desired signal for the actuator. Substituting (55) into (54) gives:

$$\left( {\dot{F}_{Qd} - \dot{F}_{Q} } \right) + K_{p}^{F} \left( {F_{Qd} - F_{Q} } \right) = R^{ - 1} \left( {\delta_{u} - \hat{\delta }_{u} } \right).$$
(56)

Now, assume that the force error is defined as ef = FQd − FQ. Thus, it can be written:

$$\dot{e}_{f} + K_{p}^{F} e_{f} = R^{ - 1} \left( {\delta_{u} - \hat{\delta }_{u} } \right).$$
(57)

The direct method of Lyapunov is utilized for asymptotic stability analysis of the robust controller. Equation (57) can be changed as:

$$\dot{e}_{f} = - K_{p}^{F} e_{f} + R^{ - 1} \left( {\delta_{u} - \hat{\delta }_{u} } \right).$$
(58)

A simple Lyapunov candidate can be proposed as follows:

$$V_{f} \left( e \right) = \frac{1}{2}e_{f}^{2}$$
(59)

here Vf represents the Lyapunov candidate. The time derivative of (59) gives:

$$\dot{V}_{f} \left( e \right) = e_{f} \dot{e}_{f} = - K_{p}^{F} e_{f}^{2} + e_{f} R^{ - 1} \left( {\delta_{u} - \hat{\delta }_{u} } \right).$$
(60)

To achieve asymptotic stability, it is sufficient that:

$$e_{f} R^{ - 1} \left( {\delta_{u} - \hat{\delta }_{u} } \right) \le 0.$$
(61)

Hence, it is enough:

$$e_{f} R^{ - 1} \delta_{u} \le e_{f} R^{ - 1} \hat{\delta }_{u} .$$
(62)

Assume that an upper bound on the uncertainty δu can be calculated as:

$$\left| {\delta_{u} } \right| \le \psi \left( t \right)$$
(63)

where ψ(t) is a known scalar and from the two last relations it can be written:

$$e_{f} R^{ - 1} \delta_{u} \le \left| {e_{f} R^{ - 1} } \right| \cdot \left| {\delta_{u} } \right| < \left| {e_{f} R^{ - 1} } \right|\psi \left( t \right).$$
(64)

Consequently, to satisfy \(\dot{V}_{f} \left( e \right) < 0\) can be selected as:

$$e_{f} R^{ - 1} \hat{\delta }_{u} = \left| {e_{f} R^{ - 1} } \right|\psi \left( t \right)$$
(65)

Thus, if \(e_{f} R^{ - 1} \ne 0\), a robust controller can be proposed as:

$$\hat{\delta }_{u} = \frac{{e_{f} R^{ - 1} }}{{\left| {e_{f} R^{ - 1} } \right|}}\psi \left( t \right)\quad \left( {if:e_{f} R^{ - 1} \ne 0} \right).$$
(66)

If \(e_{f} R^{ - 1} = 0\) then from (60) we have:

$$\dot{V}_{f} \left( e \right) = - k_{p} e_{f}^{2} .$$
(67)

Thus, the control system is independent of robust control \(\hat{\delta }_{u}\) and it will be always stable. Hence, it can be considered as:

$$\hat{\delta }_{u} = 0\quad \left( {if:e_{f} R^{ - 1} = 0} \right).$$
(68)

The robust control law is obtained from (66) and (68) but is discontinuous on \(e_{f} R^{ - 1} = 0\). To attenuate the chattering problem, a suitable approximation can be used as:

$$\hat{\delta }_{u} = \left\{ {\begin{array}{*{20}l} {\frac{{e_{f} R^{ - 1} }}{{\left| {e_{f} R^{ - 1} } \right|}}\psi \left( t \right)} \hfill & {\left( {if:e_{f} R^{ - 1} \ge \varepsilon } \right)} \hfill \\ {\frac{{e_{f} R^{ - 1} }}{\varepsilon }\psi \left( t \right)} \hfill & {\left( {if:e_{f} R^{ - 1} < \varepsilon } \right)} \hfill \\ \end{array} } \right..$$
(69)

In which, ε is a small positive constant. Also, a simple low pass filter can be designed to have a better control system and reduce the effect of chattering in (69).

ψ(t) can be realized by the upper bound of the parameters according to our knowledge about the system. However, the safe uncertainty bound parameter can be obtained from nominal terms in the equation of the system. Substituting (52) into (50) gives:

$$(\overline{R} - R)\dot{F}_{Q} + (\overline{S} - S) = \delta_{u} .$$
(70)

So, the lumped uncertainty depends on the dynamic model of the actuator. Taking the norm 2 of (70) clarifies that it is bounded as:

$$\left| {\delta_{u} } \right| \le \left| {(\overline{R} - R)} \right| \cdot \left| {\dot{F}_{Q} } \right| + \left| {(\overline{S} - S)} \right|.$$
(71)

Suppose that the nominal terms in the equation of actuator are sufficiently close to real terms such as \(\left| {(\overline{R} - R)} \right| \le \left| R \right|\) and \(\left| {(\overline{S} - S)} \right| \le S\). Thus, according to (71), it can be written that:

$$\left| {\delta_{u} } \right| \le \left| R \right| \cdot \left| {\dot{F}_{Q} } \right| + \left| S \right|.$$
(72)

Finally, from (72) and (63) uncertainty bound parameter can be selected as:

$$\psi \left( t \right) = \left| R \right| \cdot \left| {\dot{F}_{Q} } \right| + \left| S \right|.$$
(73)

The values of R and S are known, but the \(\dot{F}_{Q}\) will be determined by online measurement.

4 Simulation and results

The control system is simulated using MATLAB software. In this simulation, an aircraft is investigated which has an upper mass 4832.7 kg, lower mass 145.1 kg, and aerodynamic lift 7500 N taxing at 78 m/s. Table 1 presents the values of other parameters used in this simulation.

Table 1 The values of the parameters used in the simulation [8]
Full size table

Equations 1 to 10 are used for simulating the system. To have a good comparison, three LG systems including passive system, simple PID control, and the RNCS are simulated which are shown in Figs. 4, 5 and 6, respectively. First of all, passive systems are simulated to show the performance of the LG. Then, a simple PID controller with suitable coefficients is added to the system to indicate the effectiveness of active control for the LG. Finally, RNCS is simulated to indicate advantages of the control system versus other systems.

Fig. 4
figure 4

Simulink model of passive system

Full size image
Fig. 5
figure 5

Simulink model of PID control system

Full size image
Fig. 6
figure 6

Simulink model of RNCS

Full size image

In order to investigate the performance of proposed control system, the LG is simulated subject to lumped uncertainty. As it is mentioned earlier, it should involve parametric errors, unmodeled dynamics, and external disturbances. In this simulation, to consider the parametric errors the nominal parameters are given as 0.9 of their real value. Also, a signal as 100sin(t) is added to the actuator force for covering the unmodeled dynamics and the measurement errors. External disturbance can be supposed as 50(1 − cos(tπ/0.5)) for actuator force. This disturbance is different from runway disturbance or bump. Runway disturbance is called ground input in this study and considered in the tire force equation.

The RNCS coefficients and PID controller coefficients are given in Table 2. In this research, for designing the PID controller, the trial and error method is used for finding suitable coefficients. Several coefficients are tested and the best coefficients are selected for comparison to the RNCS method. Also, the value of ε is chosen as 0.01. A low pass filter with transfer function 1/(0.01 s + 1) is used after FQd and x to remove the unwanted high frequencies. Here, the filter time constant is chosen to be 0.01 s. Hence, the cutoff frequency is fc = 1/(2π(0.01)) = 15.915 Hz. This can be an alternative approach to attenuate chattering.

Table 2 RNCS coefficients and PID controller coefficients
Full size table

Passive and active LG systems are compared in body position, body velocity, body acceleration, LG displacement, LG velocity, LG acceleration, LG forces, and active external force. Two causes are considered as runway disturbances in the vertical body position of the aircraft. The first cause is due to the landing impact. During the process of landing, the LG experiences compression and extension. This oscillation continues until all landing impact energy is dissipated. The second cause is due to ground input. In the taxiing process when the aircraft passes the bump, the LG oscillates. These oscillations are damped by internal forces of the LG. It is expected that an aircraft rapidly returns to its original equilibrium state and have minimum vertical displacement when influenced by a runway excitation such as bumps and caves [26].

In this paper, to investigate the effects of the mentioned causes, the LG systems are simulated for two different conditions. In the first condition, the ground is assumed quite flat and the aircraft don’t face any bump or puddle while it is taxiing on the runway. Thus, the effect of landing impact can be reviewed lonely. The other simulation is dedicated to investigating the performances of the systems when the ground input is supposed as an unknown irregular signal with several peaks and troughs.

4.1 Simulation 1

The goal of this simulation is to review the performances of the LG systems at the landing process. Hence, the runway is supposed quite flat. The body position, body velocity, and body acceleration are shown in Figs. 7, 8 and 9, respectively.

Fig. 7
figure 7

The body position at touch down

Full size image
Fig. 8
figure 8

The body velocity at touch down

Full size image
Fig. 9
figure 9

The body acceleration at touch down

Full size image

Also, Figs. 10, 11 and 12 indicate LG deflection and its derivatives that are LG velocity and LG acceleration. The figures show that at the landing process, the passive system experiences multiple oscillations and PID based system have better condition and number of oscillations is reduced, but the RNCS can control system without any oscillation and it causes the system return to equilibrium state rapidly. Also, the amplitude of overshoots and undershoots in the passive system is very large. But the PID based system is reduced the amplitude and RNCS have the best performance and it succeeds significantly to tackle the overshoots and the undershoots. For instance, according to Fig. 10, the percentage of maximum overshoot in the passive system is 58% and the diagram shows several oscillations. In the PID based system, the percentage of maximum overshoot is decreased to 38%, and the number of oscillations is reduced. However, in RNCS the percentage of maximum overshoot is 0.5% and the oscillations approximately vanish. Thus, RNCS responses are considerably better than that of the PID controller and the passive LG.

Fig. 10
figure 10

LG deflection

Full size image
Fig. 11
figure 11

First derivative of LG deflection

Full size image
Fig. 12
figure 12

Second derivative of LG deflection

Full size image

The internal forces of the LG systems including damping force, spring force, friction force, and tire force can be observed in Figs. 13, 14, 15 and 16 respectively. Figures show in the passive system, LG tolerates forces with larger amplitude and several oscillations. But the condition of the PID control system is better and the controller can reduce amplitude and number of oscillations. However, in RNCS, the diagrams are so smooth and the forces meet the steady states rapidly without any oscillation. Moreover, there is ether no overshoots or a small overshoot in the diagrams.

Fig. 13
figure 13

Damping force of LG

Full size image
Fig. 14
figure 14

Spring force of LG

Full size image
Fig. 15
figure 15

Friction force of LG

Full size image
Fig. 16
figure 16

Tire force of LG

Full size image

The external active control forces which are needed in PID based system and RNCS can be compared in Fig. 17. Regarding the diagrams, the active force in both systems experiences a large undershoot of about 2300 N, 0.1 s to 0.15 s after the first moment of landing. Then, in the RNCS, the force reaches to zero rapidly while in the PID based system, the force has a significant overshoot and some oscillations.

Fig. 17
figure 17

Comparison of active control force between PID and RNCS

Full size image

All in all, as a result, it would be said that the performance of the LG system is improved by using RNCS.

4.2 Simulation 2

A bounded ground input can be proposed as shown in Fig. 18. As it indicates, a signal is considered as ground input that has multiple peaks and multiple indents. The ground input reaches the largest indent and the largest peak that have the minimum and the maximum amplitudes almost − 0.08 at t = 1.58 s and 0.08 at t = 4.59 s, respectively.

Fig. 18
figure 18

The ground input

Full size image

Figure 19 shows that the performance of all three systems is influenced by the ground input. The passive system experiences oscillations with significant magnitude and PID based system have better condition and magnitude of oscillations is reduced, but the RNCS can control the system with smaller oscillation and causes the system to return to equilibrium state much faster. The maximum value of body position in passive system, PID based system, and RNCS is 0.34 m, 0.29 m, and 0.25 m, respectively. According to Figs. 20 and 21, body velocity and body acceleration in all three systems reach to zero after some oscillations. But the diagram of RNCS has the smallest values while the largest values are allocated to the passive system.

Fig. 19
figure 19

Body position in presence of different controllers

Full size image
Fig. 20
figure 20

Body velocity in presence of different controllers

Full size image
Fig. 21
figure 21

Body acceleration in the presence of different controllers

Full size image

The LG deflection, the velocity of LG, and the LG acceleration are indicated in Figs. 22, 23 and 24, respectively. As it can be observed in these figures, the diagrams have a similar condition to Figs. 19, 20 and 21. In other words, in the passive system, there are oscillations with large magnitudes. However, the PID system reduced the magnitudes of the oscillations. On the other hand, RNCS has better performance rather than passive and PID based systems and the magnitudes of the oscillations are small.

Fig. 22
figure 22

Lnding gear deflection

Full size image
Fig. 23
figure 23

Velocity of landing gear

Full size image
Fig. 24
figure 24

Acceleration of landing gear

Full size image

Figures 25, 26, 27 and 28 show damping force, spring force, friction force, and tire force respectively. The forces in the passive system face intense oscillations that can harm the LG and tire. But both PID based and RNCS succeed to avoid large oscillations. However, RNCS can decrease the magnitude forces of LG more. As a result, it can help LG to be safe and work properly for a long period. Figure 28 clearly shows that the maximum overshoot of tire force in the passive system and PID based system is higher than 4.8 × 104 N and about 4.5 × 104 N, respectively. But in the RNCS it is less than 4.3 × 104 N. To assure the vehicle’s safety, the firm uninterrupted contact of wheels to ground should be ensured, and the dynamic tire load should be small [27]. On the other hand, during the taxiing process, the aircraft’s behavior is similar to a simple vehicle. The tire force should be minimized to have well handling [25]. According to Fig. 28, in RNCS, aircraft handling reaches the acceptable condition in a short time after passing the bumps. Thus, the performance of the RNCS is better in this case.

Fig. 25
figure 25

Damping force in presence of different controllers

Full size image
Fig. 26
figure 26

Spring force in presence of different controllers

Full size image
Fig. 27
figure 27

Friction force in presence of different controllers

Full size image
Fig. 28
figure 28

Tire force in presence of different controllers

Full size image

In Fig. 29 the actuator force of the RNCS and PID based systems can be compared. The RNCS can provide a suitable condition for the LG by lower active external force and the performance of the RNCS is generally better than the PID controller. To implement the PID controller, an actuation force of more than 3.9 × 103 N is required. Establishing this force may be difficult and expensive. But for RNCS, the maximum magnitude of the external force is almost 1.8 × 103 N.

Fig. 29
figure 29

Comparison of actuator force between RNCS and PID based system

Full size image

All in all, based on simulation results, it can be concluded that the desired RNCS has a good performance and it can strongly overcome uncertainty.

5 Conclusions

In this research, a robust control approach is developed for active control of LG. The control system includes two different loops, one for the displacement of LG and the other for the force of the external actuator.

This study shows that the novel model presented in this study for overcoming uncertainties and the control rule can be widely used in other case studies. Specifically, in the systems that are highly nonlinear and nonaffine, using the advantages of this method can be very helpful. There is a significant difficulty in the robust control system that it needs a priori information about the bounds on these uncertainties. In this paper, the upper bound of lumped uncertainties in both displacement and force control loops are properly calculated.

It is obvious from the results that the RNCS gives a better response than the PID controller for the actuator forces. Providing this amount of force might be sometimes difficult or might have cost considerations. Therefore, the controller which needs less force would be a better choice. As it is shown in the graphs, the tire force in the PID based system has a larger amplitude. Moreover, it is obvious in the graphs, that the forces rapidly reach over the peak amplitudes in a very short time. This can result in irreversible damage or high wear to the LG system, specifically the tires. A short cycle can result in a shorter tire lifetime.

The aircraft’s displacement performance is also considerably better in this method. There are fewer waves in the graphs shown previously and the whole system is more stable than other methods.

The simulation results show that the proposed robust controller can provide a considerable improvement in the performance of the LG and improve aircraft handling. In future works, this control approach can be tested experimentally, and also, the extended 3D model can be considered, including the whole 3D model of the aircraft with an in-depth extended model of the suspension system.