Abstract
Atmospheric variability at the intraseasonal timescale remains of great concern in tropical Africa because of the vulnerability of the population to variations in the distribution and amount of rainfall within a season. Then, the parameterization of the processes that induce the intraseasonal variability of the rainfall is still a challenge for the sub-seasonal-to-seasonal forecast in the tropics. In the study of intraseasonal oscillations (ISOs) in Central Africa, almost all of the authors focused only on the amplitude of the oscillations, even though the frequency is also very important because it also undergoes strong spatiotemporal variations. The novelty of this study is that we applied wavelet transform on the 2.5° × 2.5° daily Outgoing Long-wave Radiation (OLR) to extract the frequency (period) of intraseasonal oscillations (ISO) and then study its spatiotemporal variations over Central Africa (CA) within the period 1981–2015 (35 years). By the algorithm used, we obtained a dataset of daily ISO Period Indices (ISOPI) within the study period, with the same dimensions as the original OLR datasets. The analyses showed that the mean ISOPI globally fluctuates between 32 and 52 days, but undergoes strong day-to-day variations. The ISO frequency is highly seasonal, with high ISOPI (low frequency) during December–February and June–August, and short low ISOPI (high frequency) during March–May and September–November. The composites of OLR and 850 hpa zonal winds revealed that the low-frequency ISOs (LFISOs) are predominant in Eastern Central Africa and around the Cameroon Volcanic Line, while the long-frequency events (HFISOs) are mostly found in Western Central Africa, especially around the Congo basin. The plots of yearly mean ISOPI showed that the ISO period exhibits strong interannual variations with years of very high ISOPI such as 1983, 1985, 1987, 1989, 1999, 2002 and 2009, and years of lower ISOPI as 1988, 1994, 1995. Finally, it was proved in this study that there is an enhancement of rainfall during LFISOs, especially in northern hemisphere, while HFISOs are generally associated with normal or suppressed rainfall regime.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In Central Africa (CA), rainfall is a crucial resource because the socioeconomic activities of the population such as agriculture, livestock and energy are highly rainfall dependent. In recent years, for instance, many African countries have been affected by rainfall variability and long-term changes, in terms of amount and spatial and temporal distributions. The distribution of rainfall within the season is then of great interest to the local socioeconomic actors since it allows them to plan their activities throughout the year.
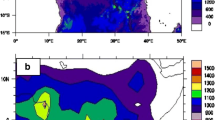
In terms of climate, CA (15°S–15°N; 0–50°E) is a particular region because of its geographical location, topography and surface cover. It extends mainly over the land and part of Atlantic and Indian oceans on its edges. The topography of the region is also diversified, including highlands, mountains and plateaus. The gradient in the surface elevation between the East and West boundaries can reach up to 3000 m (Fig. 1a). CA features varied vegetation types ranging from desert landscapes to humid tropical forest (Fig. 1b). Rainfall distribution is also varied, exhibiting a strong gradient from western to the eastern boundaries of the region (Fig. 1c). The Congo basin embedded in CA was proved to be the third most extensive region of deep convection, globally, after the West Pacific warm pool region and Amazonia [1, 2].
a Surface elevation over the study area based on 30-min topographic data (meter) from digital elevation model (DEM) of the US Geological Survey. The study area is shown as solid box. b Mean distribution of vegetation (NDVI), the density of the vegetation here can be interpreted as the green level of the surface. c Annual mean rainfall (mm), the plot is based 2.5° × 2.5° pentad GPCP precipitation for the period 1981–2000
Rainfall variability in CA is complex, ranging from diurnal cycle of rainfall to the interannual variability [3,4,5]. However, the intraseasonal timescale is of relatively great interest because it provides the information about the distribution of rainfall within the season, allowing the farmers to plan their activities throughout the year. Intraseasonal variability (ISV) refers to the atmospheric oscillations with that a period less than the length of a season (less than 90 days). But practically, to make a difference with the synoptic scale (less than about 10 days), the intraseasonal variability is more often referred to the cycle with a timescale between the synoptic scale and a season (10–90 days).
Until the years 1960s, in many climate variability studies, the authors focused mainly on the annual cycle of rainfall as well as the interannual variability because they were limited by the poor resolution of the data available those days [6, 7]. But since the beginning of 1970s, the advent of satellite-based rainfall products and advanced mathematical tools used in signal processing allowed the investigation of rainfall variability in the tropics at shorter timescales. The notion of ISV raised in the scientific community in the early 1970s, and since then, many authors used different datasets and techniques to document the ISV of some atmospheric variables in different geographical areas around the world (e.g., [8,9,10,11,12]).
Unfortunately until recent years, many of these studies on ISV were carried in some particular regions around the world because of the availability of gauge data [8, 13, 14]. But since the advent of reliable satellite data, Africa has drawn more attention of researchers, and many authors attempted to investigate the intraseasonal atmospheric variability in different regions in Africa. For instance, Janicot and Mounier [15] applied spectral analysis on OLR data in West Africa and found two peaks at intraseasonal timescales, centered around 15 and 40 days; some authors analyzed West African rainfall and showed that it is dominated by two frequency bands (10–25 and 25–60 days) at intraseasonal timescales (e.g., [15,16,17]). The work of Pohl [18] addressed the influence of the Madden–Julian Oscillation (MJO) on East African rainfall and showed that MJO phases leading to wet spells in the eastern (coastal) region are often those associated with overall suppressed deep convection in the Africa/Indian Ocean region.
However, many of these studies carried out in Africa at intraseasonal timescales have so far been biased toward West or East Africa [15, 17, 19, 20]. Only very few of them addressed the characterization of ISV in CA, even though it is an interesting zone in climate variability studies because it undergoes the phenomena that induce rainfall variability both in western and eastern Africa. Since the ending of 2010s, some authors started the investigation of ISV in CA. For example, Mark and Jury [21] investigated the spatial and temporal structures of intraseasonal oscillations over central Africa using 21 years (1980–2000) of pentad (5 day) rainfall and low-level wind, documenting three dominant modes for intraseasonal rainfall with the periods around 40–50 days. Three main modes were found in convection and rainfall over CA with centers over Northern Congo, South Ethiopia and Southwestern Tanzania, and the power spectrum of the respective principal components peaked around a period of 40 days [3, 22, 23].
Many of the above-mentioned authors who attempted to study the ISO in the tropics focused only on the amplitude (or intensity) of the oscillations [3, 24, 25]. But the characterization of ISO activity in terms of frequency also can be of great importance as it might help to develop a method by which the period of oscillations should be set. Moreover, these few authors who attempted to address the ISO frequency using the classical spectral analysis allowed them to obtain an optimal frequency for each grid point, but not its variations. This technique was limited, because it led to a unique peak frequency for a given time series. Unfortunately, this method was very limiting when it comes to study the variations in the ISO frequency at different timescales (e.g., seasonal and annual).
The wavelet analysis (WA) is a very powerful tool to overcome the issue, because unlike the Fourier analysis which allows just the transformation of time series from the time–space into the time–frequency space, the WA is able to determine both the dominant frequencies of variability and how they vary with time. An illustration of the comparison between the classical Fourier analysis and WA is shown in Fig. 2. In this figure, the major information that can be extracted from the classical power spectrum (Fig. 2a) is that the intraseasonal variability in CA is dominated by 25–70-day timescales (which corresponds to the frequencies 0.015–0.04 day−1 on the spectrum). However, the wavelet spectrum provides some additional information about the intraseasonal variability. For instance, Fig. 2b clearly reveals two frequency bands at intraseasonal timescales (10–25 days and 25–70 days). Moreover, the seasonality of oscillations is also evident, showing the high amplitude during November–May and very low amplitude during June–October.
a Power spectrum (solid black), red noise curve (green solid) of OLR in Central Africa, and curves indicating the upper (red dashed) and lower (blue dashed) confidence bounds. b Wavelet spectra (W2.m−4) of the OLR anomalies averaged over Central Africa. A 120-day cutoff low-pass filter was applied to long-term anomalies in order to remove any aspect of seasonal cycle and interannual variability
In this study, we use the WA technique to build a dataset of the daily ISO frequencies indices in CA and then investigate the space–time variations in these daily indices using appropriate mathematical and statistical tools. The paper is organized as follows: the data and methods are described in Sect. 2. The main results and comments are presented in Sect. 3, and finally, the summary and conclusions are found in Sect. 4.
2 Data and methods
As stated earlier, one of the great obstacles for the study of the intraseasonal rainfall variability in Africa has so far been the availability of high-resolution rainfall data. But since the advent of satellite measurements, the satellite-based data are of great interest. Amongst these products, some are very attractive because of their good temporal and spatial resolutions. Moreover, some satellite data have been proved to have a linear relationship with rainfall and are then more often used as rainfall proxy. One of these rainfall proxies, used in this study, is the daily Outgoing Long-wave Radiation (OLR) at 2.5° x 2.5° latitude–longitude resolution [26]. It is well known that in the tropics, deep convection and rainfall can be estimated through low OLR values. This observation led many authors to the use of OLR in the estimation of rainfall in some tropical areas [27, 28].
The Global Precipitation Climatology Project 2.5° × 2.5° rainfall data is also used in this study. In fact, it is a merged product obtained by combining the satellite estimates and gauge measurements using a weighted average [29, 30]. The GPCP products have been validated by many authors at regional and global scales [31] and are more and more used in place of gauge observations or supplement to gauge observations. But they are not generally used for long-term studies because of short time coverage.
To characterize the large-circulation dynamics over CA, we used the 2.5° × 2.5° daily zonal and meridional components of winds from the National Centers for Atmospheric Prediction (NCEP) reanalysis [32]. Even though the reanalysis data cannot be considered as the most reliable data, they have many advantages over observation data. For example, they are available on regular grids, and their spatial resolutions are most often high (up to 0.5° for some). Additionally, a sufficiently long history of these data is generally available. The NCEP-NCAR reanalysis data can be freely downloaded on the website https://www.esrl.noaa.gov/psd/data/.../data.ncep.reanalysis.html.
Fourier transform is a technique that allows us to know the contribution of different frequencies to a given signal. This process is called as the spectral analysis. The Fourier transform, X(f), of a given function x(t) can be written as:
In atmospheric sciences, we generally deal with time series, not an analytical function that we can be easily integrated. This means that taking a Fourier transform of discrete data simply turns into taking the discrete approximation to the Fourier integrals. For a given signal x(n), the discrete Fourier transform X(n) can be calculated as follows:
where N is the number of signal samples. In general, x(n) and X(n) have the same dimensions.
By this process, the Fourier transform will generate values of amplitudes and phases averaged over the entire time series for each frequency component. At last, the amplitude and phase of the signal can then be represented as a function of the frequency.
In many studies in geophysics, some frequencies are of greater interest than others. The filtering technique is then used to isolate the desired frequencies and attenuate the others generally called noise. In this study, we used the Lanczos filter [33]. Its main advantage is the reduction of Gibb’s oscillation. Unlike classical filtering technique (using Fourier transform), the simplicity of calculating the weights and the adequate response make Lanczos filtering an attractive filtering method.
The WA is very useful in signal processing for numerical analysis of discrete time series [34, 35]. Its main feature is the time–frequency decomposition. It is a very powerful tool for harmonic analysis, because unlike the classical Fourier analysis which allows just the transformation of time series from the time–space into the time–frequency space, the WA is able determine both the dominant time scales of variability and how they vary with time. The detailed literature on wavelet transform can be found in [35].
For a discrete sequence x(n), the wavelet transform Wn(s) is defined as the inner convolution of x(n) with a scaled and translated version of ψ(t).
where s is the “dilation” parameter used to change the scale, and n is the translation parameter used to slide in time [36]. δt is the constant time interval between two consecutive values. The asterisk (*) denotes complex conjugate. Then, by varying the wavelet scale s and translating along the localized time index n, one can plot an image representing both the amplitude at any scale and how this amplitude evolves with time (Fig. 2).
Wavelet functions ψ have many kinds. But for our study, we used the Morlet wavelet, which has better local character both in time domain and in frequency domain. For ω0 > 5, the Morlet wavelet is defined as:
We extracted the ISOPI in this study using a technique based on WA. From the spectral analysis (Fig. 2a), we firstly filtered our daily OLR time series between 25 and 70 days. After the filtering process, the wavelet transform is applied to the filtered OLR time series. We then obtained for each grid point the wavelet spectrum that gives for each frequency value and each day, the value of wavelet power. The notion of bandwidth is used here to determine the ISOPI. In fact from the wavelet spectrum obtained at each grid point, the average power spectrum is plotted, and the maximum spectral power is detected. The bandwidth then consists of the frequencies between two extreme values (fmin and fmax) and for which the wavelet power is higher than the half of the maximum value. Finally to compute the daily ISOP, we simply averaged all the bandwidth periods corresponding to this day. An illustration of the ISOPI calculation is shown in Fig. 3, where the bandwidth is shaded with gray color. This procedure is applied to all grid points in the study area to obtain the daily ISOPI. By this algorithm, we have built the daily ISOPI dataset, with the same dimensions as the original time series.
3 Results and discussion
3.1 Intra-annual variations
In this section, we investigate the variations of ISO frequency within the year. Then, we start by a brief overview of seasonal ISO patterns in CA. Since it has been proved by many studies that rainfall in CA is highly seasonal, we plotted the composites of 25–70-day filtered OLR and 850 hPa horizontal winds for each of the four seasons (DJF, MAM, JJA and SON). Figure 4 shows the time sequence of the composite of OLR anomalies (shaded) and the 850 hPa horizontal winds (vectors) from t0-30 to t0 + 20 days in 10-day steps and for the four seasons (DJF, MAM, JJA and SON). To achieve this, we first selected active phases of ISO events (AIEs). AIEs are detected when the area-averaged value of 25–70-day filtered OLR anomaly is higher (lower) than 1.5 ( − 1.5) times their respective standard deviations.
Composites of 25–70-day filtered OLR anomalies (shaded contours, in W/m2) and 850 hPa horizontal winds (in m/s) during the active phase of the intraseasonal events and for the four seasons (December–February, March–May, June–August, September–November). Only significant anomalies at the 90% confidence level are plotted
During December–February (DJF), at the early stage (t0-30), CA is marked by some spots of positive OLR anomalies, which grows to reach the mature stage at t0-20 and then extends to cover the whole Congo basin and part of Indian Ocean at East Africa borders. This positive anomaly vanishes progressively in the next days and completely disappears few days (approximatively 5 days, not shown here) before t0. Subsequently, negative OLR anomalies emerge over the same area that develops and reaches the mature stage at t0. This negative anomaly over CA increases gradually after date t0 and disappears on around t0 + 15 (not shown here). For the 850 hPa horizontal winds, during DJF, we observe at t0-30 that the significant winds are mostly southwestward over northern Congo (around 10°N latitude) and southward over southern Congo (around 10°S latitude). At t0-20, significant westward winds are found all over the study area. In addition, an anticyclonic circulation anomaly is seen cover the South Congo. At t0-10, the situation is almost opposed to t0-30, and the significant wind anomalies are mostly northeastward over the North Congo and northwestward over the South Congo. The magnitude and direction of winds evolve, and they are approximately eastward over the study area at t0, and the directions are reversed afterward. The situation in March–May (MAM) is quite similar to DJF, but the wind speeds are smaller and their directions have changed slightly. For June–August (JJA) and September–November (SON) seasons, the cyclonic/anticyclonic center has moved eastward and can be located over the land around south Congo. It can also be noticed that during almost the four seasons there is a cyclonic/anticyclonic circulation centered on the Indian Ocean, which generates an anomalous easterly winds that blow from the Indian Ocean, reverses around East African borders and blows back into the ocean. This anomalous circulation may possibly be responsible for the modulation of the atmospheric anomalous convection at intraseasonal timescales, especially in ECA.
The plot of the composites at 1-day time step (not shown here) showed that the duration of a complete cycle of OLR and 850 hPa horizontal winds anomalies varies between 40 and 50 days, but the averaged value is highest during JJA season (about 45 days) and lowest during MAM season (about 40 days). These observations suggest the strong annual variations in the ISOPI.
To further investigate the variations in the ISO frequency, we applied the technique described in Sect. 2 to extract the daily ISOPI. Figure 5 shows the day-to-day variations in the ISOPI, averaged over CA within the study period (1981–2015). It is well observed that the ISOPI undergoes strong variations from day to another. Globally the ISOPI is ranged between 32.28 days (minimum) and 51.6 days (maximum), suggesting the dominance of MJO signal. As can be noticed on the figure, the ISOPI undergoes large intra-annual and interannual variations.
Variations of the daily period (in days) averaged over the study area, within 1981–2015. The two horizontal solid black lines determine ± 1.5 standard deviation, and the dashed gray line the average value. The HFISOs are shaded with blue color and the LFISOs with orange color. The linear trend is represented by the red line
The intra-annual variations can further be illustrated by plotting the mean annual cycle of ISOPI throughout the study period (Fig. 6). In this figure, the seasonality of ISO periods is clear, showing two seasons of high ISOPI, intercepted by two seasons of low ISOPI. Indeed, these results differ significantly from those of Anderson et al. [24], based on a smaller sample and shorter time series, who found that there was a total absence of seasonality in amplitude as well as the period of the ISO, because it is clearly seen from the figure that the ISOPI is higher during June–September (JJAS) and lowest during MAM. Moreover, the month-to-month variations of the MJO (ISO) frequency have been studied by Pohl [18] and established that in general, the MJO appears shorter during the equinox seasons (March–May and September–November) and longer during winter and summer seasons (December–February and June–August) of both hemispheres.
To characterize the extreme-frequency events, we defined in this study a short-frequency event (LFISO) when the area-averaged ISOPI is greater than 1.5 times the standard deviation and the long-frequency event (HFISO) when the area-averaged ISOPI is less than -1.5 times the standard deviation. Figure 7 shows the spatial distribution of mean ISOPI during LFISOs and HFISOs shown in Fig. 5. The mean ISOPI is obtained by taking at each grid point the average ISOPI corresponding to selected days (SEFs or HFISOs). During SEFs, the spatial mean ISOPI exhibits a bipolar structure, since the high periods are predominantly observed over two major areas. The first area covers East African highlands and extends to the Indian Ocean at East African borders, and the second can be located around the Cameroon Volcanic Line (CVL) that covers Cameroon and neighboring areas. As for HFISOs, it is well observed in Fig. 7 that the low frequencies are mainly observed over WCA, but globally, the whole CA exhibits low ISOPI during HFISOs. The lowest ISOPI values are observed over Soudan and neighboring countries. Moreover, it should be noted that during both LFISOs and HFISOs, the Congo basin experienced low ISOPIs (high frequencies).
3.2 Interannual variations
One of the most notable features of the MJO (ISO) is its fluctuations from year to another. A number of authors have observed year-to-year variability in the strength and character of the ISO [3, 36,37,38]. However as stated in the introduction, almost all the authors who attempted to address the issue focused mainly on the intensity of the oscillations, even though the frequency of the oscillations is also a key parameter in the investigation of ISO patterns.
The interannual variations in the ISO frequency can be observed in Fig. 5. This figure reveals severe year-to-year variations in the ISO frequency (period), with some years of high ISOPI as 1983, 1985, 1987, 1989, 1999, 2002 and 2009, and years of lower ISOPI as 1988, 1994, 1995. Within the study period, the maximum ISOPI is observed in 1985 and the minimum in 1994. It is also observed that the ISOPI decreased from one decade to another, as can be seen from the linear trend in Fig. 4. In Table 1 are listed the statistics of the ISOPI for each year within the study period. From this table, it is once more noticeable that although the yearly mean period of oscillation remains between 40 and 50 days, there is a pronounced interannual variability that can be well observed in the mean, standard deviation, minimum and maximum values of the ISOPI.
Figure 8 further illustrates the year-to-year variations in the ISOPI, by showing the spatial distribution of the yearly mean ISOPI within 1981–2015. This figure clearly reveals that the spatial distribution of the mean ISOPI strongly varies from year to another. As could be expected from Fig. 7, the maximum values of ISOPI are most often observed over East African highlands and around the CVL in WCA. In addition, the other relevant information that can be extracted from Fig. 7 is that the ISOPI values were high all over the study area during some particular years as 1982, 1985 and 2003. Similarly, the ISOPI were low all over the study area during the years 1986, 1987, 1995, 1996, 1998, 2006 and 2009. Once more the decadal variations are also clear, because the decade 1981–1990 is characterized by higher ISOPI over most of the study area, followed by 1991–2000.
3.3 Relationship with large-scale circulation
It is well known that for a typical MJO life cycle, the convective envelopes initiate from the western Indian Ocean, strengthen over the central Indian Ocean, bifurcate while passing through the Maritime Continent, re-intensify upon reaching the western Pacific and finally dissipate around date line. The key processes identified over the Indian Ocean may not be of equal importance in other regions, depending on some geographical features. To further understand the modulation of the ISO frequency over CA by large-scale circulation, we plotted lagged/lead composites of OLR and 850 hPa horizontal winds anomalies corresponding to the extreme frequencies (LFISOs and HFISOs). The construction of the composites is based on the method described in Sect. 3.1 for each anomaly field. The reference vector used here is the area-averaged ISOPI. Once more, the evolutions of these anomalies are taken from t0 − 30 to t0 + 20.
Figure 9 shows the spatial patterns of intraseasonal oscillations during LFISOs. It is well seen that in the convection (OLR anomalies), the oscillations are predominantly observed over ECA and the Indian Ocean during LFISOs. The early stage (t0-30) is marked by positive OLR anomalies mainly over the Eastern Central Africa, which extends to cover part of Indian Ocean around the East African borders. This positive anomaly decreases progressively in the next days and completely disappears few days (approximatively 7 days, not shown here) before t0. Subsequently, negative OLR anomalies emerge over the same area that develops and reaches the mature stage at t0. This negative anomaly over CA increases gradually after date t0 and completely disappears on around t0 + 15 (not shown here). At t0, one it is evident that high negative OLR anomalies are observed over East African Highlands and around the CVL. From the circulation point of view, at lag − 30, the lower atmosphere around CA is dominated by some discrete centers of cyclonic/anticyclonic activity that develop over the Indian ocean and extends to the East African borders. On the other hand, almost no significant wind is observed over northern Congo (above the equator). However, the Southern Congo is characterized by relatively high horizontal winds that are mostly westward between the equator and the latitude of 15°S.
Composites of 25–70-day filtered OLR anomalies (shaded contours, in W/m2) and 850 hPa horizontal winds (vectors, in m/s) corresponding to the LFISOs. A day is selected if the averaged ISOPI is higher than 1.5 times the standard deviation and only OLR anomalies statistically significant at the 90% level are selected.
Similarly, Fig. 10 shows the spatial patterns of intraseasonal oscillations during HFISOs. Unlike the LFISOs, the oscillations are predominantly observed over WCA (West of Rift valley, located around the longitude of 30°N). The early stage (t0-30) is marked by negative OLR anomalies over the northern Congo, which extends northward to cover part of African Sahel and westward over the Atlantic Ocean around West Africa borders. This negative anomaly increases progressively in the consecutive days and re-appears few days before t0. It is also noticeable that a minor center of low-frequency ISO is observable over Southwestern Tanzania, which experiences suppressed convection at t0-30 and enhanced convection around t0. At t0, the entire Congo basin is characterized by negative OLR anomalies indicating an enhancement in the convective activity. For the 850 hPa horizontal winds, we observe at t0-30 that the horizontal winds are mostly inward over in the WCA (eastward in the southern hemisphere and southwestward in the northern hemisphere), while the ECA is characterized by outward fluxes. Once more, cyclonic/anticyclonic centers are observed in the study area. The major center is located over northern Africa (around the latitude of 20°N and a minor cyclonic circulation around the east African corner. The magnitude and direction of winds then evolve hereafter, and at t0, the cyclonic/anticyclonic centers disappear and there is a flux convergence over CA between − 10°N and 10°N. In short, Figs. 9 and 10 reveal that the ISOPI is high over the regions of higher surface elevation. These results clearly suggest the influence of topography on the ISO frequency. Indeed, some studies have shown that the topography and land-sea contrast strongly modulate the MJO convective envelopes as they pass through. The topographic blocking and mountain wave-making effect create extra lifting and sinking within the large-scale circulation of the MJO. Consequently, the MJO convection amplifies and becomes stationary around mountainous land area than in the open sea or flat, and then, the duration of a cycle increases [39, 40]. Further investigations are required to fully document the mechanisms that drive the ISO frequency variations around the regions of complex topography.
Same with Fig. 6, but for the HFISOs. A day is selected if the averaged ISOPI is lower than -1.5 times the standard deviation and only OLR anomalies statistically significant at the 90% level are selected
Now we discuss the impact of the ISO frequency on rainfall in this section. Some authors investigated the influence ISO on rainfall in some tropical areas [41, 42], and they generally focused on the relationship between ISO intensity and rainfall. In the actual study, we examine the impact of ISOPI on rainfall. Hence to quantify the impact of ISO frequency on rainfall, we used as index a quantity called the impact rate (IR). The IR here is defined at each grid point as the ratio of the average daily precipitation for LFISOs (resp. HFISOs) to the average daily precipitation corresponding to the entire time series. For instance, for a LFISO, IR is defined as:
where PLFISO is the average daily precipitation of the days belonging to LFISOs (from the onset day to the demise day) and PT the average daily precipitation corresponding to the entire time series. A value of IR greater than one implies an enhancement of rainfall and a value less than one a suppression of rainfall during LFISOs.
Figure 11 shows the spatial distribution of IR over CA for LFISOs and HFISOs. Overall, the influence of ISO frequency on rainfall varies considerably for LFISOs and HFISOs. During LFISOs, the IR ranges from 0 to about 6. The maximum IR is observed over the north Congo (around the latitude of 15°N) and over the Atlantic Ocean around the West African borders (near 15°S), where the IR reaches up to 6, implying that the daily rainfall during LFISOs can reach up to 6 times the average value. This result clearly revealed an enhancement of rainfall rate during LFISOs. On the other hand during HFISOs, the IR is relatively low over most of the study area. The value is globally less than one over the northern Africa (above the equator), indicating a suppression of rainfall during HFISOs. These results suggest that during LFISOs and HFISOs, some large-scale mechanisms are great contributors, such as wind regime (Figs. 9 and 10), which converges the moisture flux in the regions of high IR and then diverges in the regions of low IR.
4 Summary and conclusions
In this study, we used wavelet-based indices to study the spatiotemporal variations in the frequency of 25–70-day intraseasonal atmospheric oscillations in CA. For this purpose, we used as rainfall proxy, the 2.5° × 2.5° daily OLR datasets within the period 1981–2015 (35 years).
To extract our wavelet-based frequency indices, we applied the wavelet transform on the 25–70-day filtered OLR anomalies at each grid point in the study area and then used afterward the notion of bandwidth to retain the relevant ISO frequencies (period). In fact for each day, we averaged all frequencies for which the wavelet power is greater than the half of the maximum value to obtain the daily frequency index. Through this algorithm, we then built dataset of the daily ISOPI, with the same dimensions as the original OLR time series.
The analyses revealed that the mean daily ISOPI mainly fluctuates between 32 and 52 days, in accordance with some previous studies. The plots of the annual variations in the ISOPI showed that unlike some previous studies, the ISO frequency is highly seasonal with maximum ISOPI during December–February and June–August and minimum values during March–May and September–November. The composite analysis revealed that in the OLR, the LFISOs are predominantly observed over ECA and the Indian Ocean, while HFISOs are mostly found over WCA. The interannual variations of ISOPI have also been investigated, and we found that the ISO frequency undergoes strong year-to-year variations with years of very high ISOPI such as 1983, 1985, 1987, 1989, 1999, 2002 and 2009, and years of very low ISOPI as 1988, 1994, 1995. Finally, we studied the influence of ISO frequency on rainfall. For this purpose, we use a parameter called impact rate, which is defined at each grid point as the ratio of the average daily precipitation for LFISOs (resp. HFISOs) to the average daily precipitation corresponding to the entire time series. The plot of IR over CA for LFISOs and HFISOs showed that during LFISOs, there is a strong enhancement of rainfall, especially over northern Congo, around the latitude of 15°N, while the HFISOs are generally associated with normal rainfall rate (IR close to one).
In sum in this study, we have shown that the ISO frequency undergoes strong spatial and temporal variations in Central Africa. Short-frequency oscillations are generally observed in Eastern Central Africa, while long-frequency oscillations are mostly found in WCA. Moreover, ISOPI undergoes large interannual variations. The construction of wavelet-based indices then allowed us to study the variations patterns in the ISO frequency both spatially and temporally and their relationship with large-scale circulation.
References
Shem WO, Dickinson RE (2006) How the Congo Basin deforestation and the equatorial monsoonal circulation influences the regional hydrological cycle. Paper presented at the 86th Annual AMS Meeting, January 2006
Todd MC, Washington R (2004) Climate variability in central equatorial Africa: influence from the Atlantic sector. Geophys Res 31:L23202. https://doi.org/10.1029/2004GL020975
Tchakoutio AS, Nzeukou A, Tchawoua C (2012) Intraseasonal atmospheric variability and its interannual modulation in central Africa. Meteorol Atmos Phys 117:167–179
Vondou DA, Yepdo ZD, Steve TR, Tchakoutio SA, Lucie DT (2017) Diurnal cycle of rainfall over Central Africa simulated by RegCM. Model Earth Syst Environ 3:1055–1064. https://doi.org/10.1007/s40808-017-0352-6
Gbobaniyi E, Sarr A, Sylla M, Diallo I, Lennard C, Dosio A, Dhiédiou A, Kamga A, Klutse NAB, Hewitson B, Nikulin G, Lamptey B (2014) Climatology, annual cycle and interannual variability of precipitation and temperature in CORDEX simulations over West Africa. Int J Climatol. https://doi.org/10.1002/joc.3834
Conrad V (1941) The variability of precipitation. Mon Weather Rev 69:5–11
Rubin MJ (1956) The associated precipitation and circulation patterns over southern Africa. Notos 5:53–59
Madden RA, Julian PR (1971) Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J Atmos Sci 28:702–708
Knutson TR, Weickmann KM (1987) 30-60 day atmospheric oscillations: composite life cycles of convection and circulation anomalies. Mon Weather Rev 115:1407–1436
Hendon HH, Liebmann B (1990) The intraseasonal (30–50 day) oscillation of the Australian summer monsoon. J Atmos Sci 47:2909–2923
Madden RA, Julian PR (1994) Observations of the 40–50 day tropical oscillation: a review. Mon Weather Rev 122:814–837
Matthews M (2000) Propagating mechanisms for the Madden-Julian oscillation. Quart J Roy Meteor Soc 126:2637–2652
McPhaden MJ, Taft BA (1988) Dynamics of seasonal and intra-seasonal variability in the eastern equatorial Pacific. J Phys Oceanogr 18:1713–1732
Enfield D (1987) The intraseasonal oscillation in eastern Pacific sea levels: How is it forced. J Phys Oceanogr 17:1860–1876
Janicot S, Mounier F (2004) Evidence of two independent modes of convection at intraseasonal timescale in the West African summer monsoon. Geophys Res Lett 31:L16116. https://doi.org/10.1029/2004GL020665
Sultan B, Janicot S (2003) The West African monsoon dynamics. Part II: the pre-onset and onset of the summer monsoon. J Climate 16:3407–3427
Janicot S, Sultan B (2001) Intra-seasonal modulation of convection in the West African monsoon. Geophys Res Lett 28:523–526
Pohl B (2007) L'Oscillation de Madden-Julian et la variabilité pluviométrique régionale en Afrique Subsaharienne. Climatologie. PhD thesis, Université de Bourgogne, Dijon, France.
Pohl B, Camberlin P (2006) Influence of the Madden–Julian oscillation on East African rainfall. I: intraseasonal variability and regional dependency. Quart J Roy Meteor Soc 132:2521–2539. https://doi.org/10.1256/qj.05.104
Pohl B, Camberlin B (2006) Influence of the Madden–Julian oscillation on East African rainfall: II March–May season extremes and interannual variability. Quart J Roy Meteor Soc 132(621):2541–2558. https://doi.org/10.1256/qj.05.223
Tazalika L, Jury MR (2008) Intraseasonal rainfall oscillations over central Africa: space-time character and evolution. Theor Appl Climatol 94:67–80
Tchakoutio AS, Nzeukou A, Tchawoua C, Kamga FM, Vondou D (2013) A comparative analysis of intraseasonal variability in OLR and 1DD GPCP data over central Africa”. Theor Appl Climatol 116(1–2):37–49
Tchakoutio AS, Nzeukou A, Tchawoua C, Sonfack B, Tengeleng S (2014) On the differences in the intraseasonal rainfall variability between Western and Eastern Central Africa: case of 10_25-Day oscillations. J Climatol. https://doi.org/10.1155/2014/434960
Anderson JR, Stevens DE, Julian PR (1984) Temporal variations of the tropical 40–50-day oscillation. Mon Weather Rev 112(2431–2438):1984
Tchakoutio AS, Wamba C, Vondou A, Nzeukou A, Pokam MW (2020) Interannual variations in the amplitude of 25–70-day intraseasonal oscillations in Central Africa and relationship with ENSO. Bull Atmos Sci Technol. https://doi.org/10.1007/s42865-020-00016-3
Liebmann B, Smith CA (1996) Description of a complete (Interpolated) outgoing longwave radiation dataset. Bull Am Meteorol Soc 77:1275–1277
Arkin PA, Xie P (1997) Global monthly precipitation estimates from satellite-observed outgoing longwave radiation. J Climat 9:840–858
Yoo JM, James C (1988) Spatial dependence on the relationship between rainfall and outgoing longwave radiation in the Tropical Atlantic. J Climat 7:1047–1054
Huffman GJ, Adler RF, Arkin PA, Chang A, Ferraro R, Gruber A, Janowiak JE, McNab A, Rudolf B, Schneider U (1997) The global precipitation climatology project (GPCP) combined precipitation dataset. Bull Am Meteorol Soc 78:5–20
Huffman GJ, Adler RF, Morrissey M, Bolvin D, Curtis S, Joyce R, McGavock B, Susskind J (2001) Global precipitation at one-degree daily resolution from multi-satellite observations. J Hydrometeor 2:36–50
McCollum J, Nelkin E, Klotter D, Berte Y, Diallo BM, Gaye I, Kpabeba G, Ndiaye O, Noukpozounkou JN, Tanu MM, Thiam A, Toure AA, Traore AK, Nicholson SE, Some B (2003) Validation of TRMM and other rainfall estimates with a high-density gauge dataset for West Africa Part I validation of GPCC rainfall product and pre-TRMM satellite and blended products. J Appl Meteor 40:1355–1368
Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo KC, Ropelewski C, Wang J, Leetmaa A, Reynolds R, Jenne R, Joseph D (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteor Soc 77:437–470
Duchon CE (1979) Lanczos filtering in one and two dimensions. J Appl Meteor 18:1016–1022
Daubechies I (1990) The wavelet transform time-frequency localization and signal analysis. IEEE Trans Inform Theory 36:961–1004
Daniel TLL and Yamatoto A (1994) Wavelet Analysis: Theory and Applications. Hewlett Packard Journal, December: 44–52
Zhang C, Hendon HH, Glick J (1999) Interannual variation of the Madden-Julian oscillation during austral summer. J Climat 12:2538–2550
Harry HH, Matthew CW (2004) An all-season real-time multivariate MJO Index: development of an index for monitoring and prediction. Mon Weather Rev 132:1917–1932
Tchakoutio AS, Nzeukou A, Tchawoua C, Sonfack B, Siddi T (2013) Comparing the patterns of 20–70 days intraseasonal oscillations over Central Africa during the last three decades. Theor Appl Climatol. https://doi.org/10.1007/s00704-013-1063-1
Wu C-H, Hsu H-H (2009) Topographic influence on the MJO in the maritime continent. J Climat 22:5433–5448. https://doi.org/10.1175/2009JCLI2825.1
Hung CS, Sui CH (2018) A Diagnostic Study of the Evolution of the MJO from Indian Ocean to maritime continent: wave dynamics versus advective moistening processes. J Climat 31(10):4095–415. https://doi.org/10.1175/JCLI-D-17-0139.1
Farnaz P, Tomoki T, Hooshang G, Pascal O (2014) Influences of the MJO on intraseasonal rainfall variability over southern Iran: MJO and rainfall variation over southern Iran. Atm Sci Lett. https://doi.org/10.1002/asl2.531
Mayta VC, Ambrizzi T, Espinoza JC, Silva Dias PL (2018) The role of the Madden–Julian oscillation on the Amazon Basin intraseasonal rainfall variability. Int J Climatol. https://doi.org/10.1002/joc.5810
Acknowledgements
Most of the figures in this study were produced using NCL software. The NCEP and OLR data were obtained from the NOAA websites, http://www.cdc.noaa.gov for the NCEP zonal winds and http://www.esrl.noaa.gov for the OLR. All the administrator members of these websites are gratefully acknowledged for maintaining the updated data.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interests regarding the publication of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tchakoutio Sandjon, A., Djiotang Tchotchou, A.L., Vondou, D.A. et al. On the variations in the frequency of 25–70-day intraseasonal oscillations in Central Africa using wavelet-based indices. SN Appl. Sci. 3, 304 (2021). https://doi.org/10.1007/s42452-021-04285-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-021-04285-1