Numerical simulations and experiments on droplet coalescence dynamics over a liquid–air interface: mechanism and effect of droplet-size/surface-tension

Abstract

Present study is on partial/complete coalescence dynamics of a droplet (surrounded by air) over a horizontal pool of the same liquid. Experimental and numerical studies are presented for both isopropanol and glycerol droplet of a constant diameter. Numerical study is presented in more detail for the isopropanol droplet to study the effect of diameter ($D=0.035-6.7 mm$) and surface tension coefficient ($\gamma =2-200 mN/m$) on the coalescence dynamics. For partial coalescence of an isopropanol droplet and complete coalescence of a glycerol droplet, excellent agreement is demonstrated between our numerically and experimentally obtained interface dynamics; and a qualitative discussion on the mechanism of the partial and complete coalescence is presented. Three regimes of partial coalescence − viscous, inertio-capillary and gravity − proposed in the literature for a liquid-liquid system are presented here for the present liquid-air system while studying the effect of diameter of the isopropanol droplet. Probably for the first time in the literature, our numerical study presents a flow and vorticity dynamics based quantitative evidence of the coalescence-mechanism, analogy with a freely vibrating Spring-Mass-Damper System, the gravity regime for a liquid-gas system, and the effect of surface tension coefficient $\gamma$ based coalescence dynamics study. The associated novel $\gamma$ based droplet coalescence regime map presents a critical Ohnesorge number $Oh_{c}$ and critical Bond number $Bo_{c}$ for a transition from partial to full coalescence; and such critical values are also presented for the transition under effect of the droplet diameter. The critical values based transition boundaries, obtained separately for the varying D and varying $\gamma$, are demonstrated to be in excellent agreement with a correlation reported in the literature.

1 Introduction

Droplet coalescence on a planar liquid-gas interface is widely studied due to its importance in many physical processes like raindrop dynamics [1], droplet emulsion [2], microfluidics applications [3], separation of oil phase from water phase in emulsion [4], and production of ocean mists [5]. For designing the efficient oil-water extraction device, it is important to have great insight on the smallest components that affect the outcome of drop-drop and drop-interface interactions [6]. When a liquid droplet comes in contact with its pool, it either generates a secondary droplet before merging in the pool or the droplet completely gets absorbed in the liquid pool without formation of secondary droplet. The former phenomenon is called as partial-coalescence while the latter is termed as full-coalescence. In partial-coalescence case, the surface tension force plays an important role, stretching the droplet surface upwards due to propagation of capillary waves over the liquid-gas interface. Whereas, in the full-coalescence, the gravity or viscous force dominates and suppresses the wave propagation, causing the full merging of droplet with the pool. A detailed review of different stages of coalescence of liquid on planar interface was presented by Kavehpour [6], with emphasis on the different types of types of stresses (viscous, Marangoni, and electric field) affecting the outcome of the process. In the following sections, we describe various experimental as well as numerical investigations reported in the literature for the droplet coalescence on its liquid pool.

For the coalescence dynamics, before presenting the literature survey on experimental and numerical work in separate paragraphs below, the four dimensionless groups that govern the process are presented; given as

$$\begin{aligned} Oh\equiv \frac{\mu _{1}}{\sqrt{\rho _{1}\gamma D}};\,Bo\equiv \frac{\rho _{1}gD^{2}}{\gamma };\,\chi \equiv \frac{\rho _{2}}{\rho _{1}};\,\eta \equiv \frac{\mu _{2}}{\mu _{1}} \end{aligned}$$

(1)

where the heavier fluid-1 is considered as the characteristic fluid and its thermophysical properties ($\rho _{1}$ and $\mu _{1}$) are used for non-dimensionalization. Here, D is the diameter of the droplet (at the onset of coalescence), $\gamma$ is the surface tension coefficient, $\rho$ is density, and $\mu$ is dynamic viscosity. The Ohnesorge number Oh and Bond number Bo indicate the relative importance of viscous and gravity force with respect to the inertia force (generated by the interfacial tension), respectively. For the above non-dimensional numbers, the characteristic length scale is $l_{c}=D$ and velocity scale is capillary-velocity $u_{c}=\sqrt{ {\gamma }/{\rho _{1}D}}$ for $Oh<1$ and $u_{c}= {\gamma }/{\mu }$ for $Oh>1$. Furthermore, non-dimensional time is represented here by scaling with the time scale $t_{c}= {l_{c}}/{u_{c}}$. Thus, non-dimensional representation of length (droplet height and secondary droplet diameter), velocity (contours), and time (secondary drop pinch-off time) are presented here as a function of above four governing parameters, i.e., $f(Oh,\,Bo,\,\chi ,\,\eta )$.

Initial experiments by Cockbain and Roberts [2] were for coalescence of oil and water drops on a liquid-liquid interface under the presence of different types of surface active agents. Using high-speed visualization, Charles and Mason [7] investigated the partial coalescence for liquid droplet at a liquid-liquid interface and the experimental results were analyzed with the help of Rayleigh’s theory of unstable liquid columns. Using a high-speed imaging, coalescence dynamics at a liquid-air interface was studied by Thoroddsen and Takehara [8] for water, ethanol and mercury droplet; and by Aryafar and Kavehpour [9] and Honey and Kavehpour [11] for water, methanol, and silicon-oil. The former work [8] reported that coalescence process is not instantaneous but takes place in self-similar cascade while the latter work [9] presented the condition of coalescence based on the Ohnesorge number: $Oh<1$ corresponds to dominance of surface tension or inertia forces leading to partial-coalescence while $Oh>1$ corresponding to the dominance of viscous forces causes full-coalescence. Honey and Kavehpour [11] explored the bouncing height of the secondary droplet during a series of partial coalescence, and developed a theory for maximum height of the bouncing drop which matched well with the experimental results. For coalescence of water and water-glycerol droplet at liquid-liquid interface, Chen et al. [10] reported three sub-regimes within the partial coalescence regime and presented scaling relationship for the drop size ratio and the coalescence time. For coalescence of ethanol-water and ethanol-glycerin droplet at liquid-air interface, Blanchette and Bigioni [12] identified a narrow range of droplet diameters for which viscosity and gravity forces are negligible and emphasized the importance of capillary force using ultra-high speed video in partial coalescence process; and presented a phase diagram, as a function of Ohnesorge number (Oh) and Bond number (Bo), for partial and full coalescence. Later, they presented a detailed study on the coalescence events for the liquid-air system at various values of Ohnesorge and Bond numbers [14].

For coalescence at liquid-liquid interface, Gilet et al. [13] reported a record number of 11 steps cascade for mercury and less-viscous droplets in their experiments. The rest time of drops coalescing at a fluid interface under AC/DC electric fields was investigated with high-speed photography [15]. Aarts and Lekkerkerker [16] studied the coalescence of a drop with its bulk phase in fluid-fluid demixing colloid-polymer mixtures. Particle Image Velocimetry (PIV) experiments by Kassim and Longmire [17] were used to quantify the velocity and vorticity fields during the coalescence events of drops in different viscous fluids. Using the high speed shadowgraphy, Dong et al. [18] observed the evolution of the interfaces and drop size ratios during a partial coalescence of an aqueous drop with an organic-aqueous interface with and without surfactant. They used PIV for velocity profiles and vorticity structures in the coalescing drops. Effect of surfactants on the coalescence of a drop at a flat aqueous-organic interface was studied by Weheliye et al. [19] using high-speed PIV. For the various experimental work reported in the literature, Table 1 presents the experimental method and the range of non-dimensional parameters investigated.

Numerical work on the coalescence dynamics is challenging since it involves rigorous interface dynamics as well as different small-scale phenomenon like pinch-off of droplet, film drainage, capillary wave propagation etc. Different numerical methods have been used to study the physics of droplet coalescence mechanism which are broadly categorized as interface-tracking and interface-capturing methods. Coalescence of different droplets in liquid-air system had been tracked by using Boundary Integral Method (BIM) [12, 14, 20]. Using phase field method, Yue et al. [22, 23] studied coalescence of water droplet at planar interface in Newtonian and viscoelastic fluids; and found that viscoelastic effects delay the pinch-off mechanism. Using a coupled level set and volume of fluid method (CLSVOF), Ray et al. [24] investigated the conditions and the outcomes of the coalescence events. Using VOF method coupled with front tracking [?]. Martin and Blanchette [29] performed numerical simulations to study the partial coalescence in presence of surfactant. Ghost Fluid Method (GFM), proposed by Fedkiw et al. [25, 26], models the surface tension more realistically as surface force (used as an interfacial jump conditions while solving the pressure Poisson equation) that leads to a reduction in spurious currents near the interface; reported for the other methods that models the surface tension as a volumetric force [27, 28]. Along with the fixed grid methods such are LS, VOF and CLSVOF for the multiphase flow, there are certain methods on moving grids such as arbitrary Lagrangian-Eulerian (ALE) (Kamran et al. [30]), purely Lagrangian (Saksono and Peric [31]), and embedded Eulerian-Lagrangian (Jarauta et al. [32]). A detailed review on experimental techniques and modeling approaches for the coalescence phenomenon of drops in liquid/liquid systems was presented by Kamp et al. [33]. For the various numerical work on the coalescence dynamics, Table 2 presents the numerical method and the range of non-dimensional governing parameters considered in the simulations reported in the literature and the present work.

Table 1 Summary of the experimental measurement performed on droplet coalescence. Experimental Methods (EMs) are HSC: High speed camera and PIV: Particle image velocimetry)

Table 2 Summary of the numerical studies on droplet coalescence. Numerical methods (NMs) are BIM: Boundary Integral Method, VOF: Volume of Fluid, LSM: Level Set Method, CLSVOF: Coupled Level Set Method and Volume of Fluid and FT: Front tracking

Advancement in the imaging technology led to refinement in the earlier experimental work and advanced numerical techniques led to a more detailed study of the coalescence dynamics. For the droplet coalescence on a planar interface, Table 1 presents the experimental work using high-speed camera and PIV, and Table 2 presents the numerical work consisting of interface-tracing and interface-capturing methods. Most of the numerical study have been done using a diffuse-interface as compared to a more-realistic sharp-interface method which is attempted here. The sharp-interface as compared to diffuse-interface level set method leads to a substantially reduction in the unphysical spurious velocity (near the interface) and results in better accuracy on the same grid size [37]. From the literature survey for coalescence with liquid-liquid system, it is found that the four governing parameter commonly reported [13, 24] are $Oh_{1}$, $Oh_{2}$, $Bo_{12}\equiv (\rho _{1}-\rho _{2})gD^{2}/\gamma$, and Atwood number$At=(\rho _{1}-\rho _{2})/(\rho _{1}+\rho _{2})$. For a liquid-gas system, $At\approx 1$ (since $\rho _{1}\gg \rho _{2}$); and thus, the Oh, Bo, $\chi$, and $\eta$ (Eq.1) are the four governing parameters for the coalescence with liquid-gas system considered here. Furthermore, from Tables 1 and 2, it is found that most of the experimental and numerical studies are done for a liquid-liquid system and few such studies [8, 9, 11, 12] are reported for a liquid-gas system; thus, the present work is proposed for a liquid-air system. Also, the recent review paper by Kavehpour [6] mentions that more experiments and numerical simulation are needed to investigate the effect of surfactants on the coalescence dynamics. Thus, the effect of varying the surface tension coefficient $\gamma$ on the coalescence dynamics is studied here numerically. Considering a particular liquid-gas combination, the variation in $\gamma$ leads to a variation in both Ohnesorge number Oh and Bond number Bo (Eq. 1) at a constant density ratio $\chi$ and viscosity ratio $\eta$. Similar variations in Oh and Bo can also be achieved by varying the droplet diameter D. Thus, another objective of the present numerical work is to study the effect of simultaneous variation of Oh and Bo, done by varying $\gamma$ as compared to varying D, on the coalescence dynamics.

In the present work, the coalescence mechanism of a droplet for liquid-air system is studied using experimental and computational methods for two different fluids: isopropanol $(Oh<1)$ and glycerol $(Oh>1)$. The computations are performed using Ghost Fluid Method (GFM) based Sharp-Interface Level Set Method (SI-LSM) in which Sharp Surface-tension Force (SSF) model [26] is implemented for an accurate computation of capillary force along with reduction in spurious currents as well as mass-error in the level set method. A dual-grid approach based Sharp-Interface Dual-Grid Level Set Method (SI-DGLSM) [38], proposed originally for a diffuse-interface level set method [39], is used here for studying the physics of droplet coalescence on the planar liquid surface (Table 2). Using a high-speed camera, our experimental results are used to validate our computational results of isopropanol and glycerol droplets coalescence on the respective liquid pools. Numerically, coalescence dynamics is studied for a wide range of $Oh\,\left( 0.004-0.04\right)$ and $Bo\,\left( 0.01-15\right)$, with respect to propagation of capillary waves over the droplet surface and dampening effect due to viscous and gravity forces. A regime map is presented for the effect of droplet-diameter and surface-tension based on the transition from full to partial coalescence for a wider range of Oh and Bo for liquid-air coalescence, which is not available in the literature to the best of our knowledge. Vortex rings, as observed in experiments [17] are captured numerically across the interface, are also quantified for different surface tension forces.

2 Experimental and numerical details

The experimental and numerical details for the present work are presented in separate subsections below.

2.1 Experimental details

Fig. 1

Experimental set-up for the droplet coalescence study: a liquid droplet, gently placed over its pool. The liquid considered here are isopropanol and glycerol

The schematic of the experimental setup, along with associated instrumentation, is shown in Fig. 1. The figure shows an isopropanol/glycerol droplet that is generated using a micro-syringe (with 31 gauge needle), surrounded by air, and gently placed on a container filled up with the same liquid. The diameter is $1.55\pm 0.05$ mm for isopropanol and $1.6\pm 0.05$ mm for glycerol [41] droplet and the dimensions of the container is $14\times 8\times 8$ cm. The liquid is filled up to the rim of the container − to negate the effect of liquid meniscus disturbance during a sidewise visualization on the wall of container. The height of the syringe is adjusted such that the generated droplet touches to the liquid surface inside the container without any impact velocity, i.e., droplets are generated just above the liquid surface.

The figure also shows a white LED lamp (back light source) for illumination and high-speed camera for visualization of the coalescence phenomenon. The camera (MotionPro, Y-3 classic), with long distance working objective (Qioptiq Inc.), was used on a similar setup to study impact-dynamics of a droplet on the solid surface [41]. The selected magnification corresponds to $14\mu m$ per pixel, which implies dimensional error of $\pm 28\,\mu m$. The images of $320\times 344$ pixels, at 3000 frames per second, are captured in all our experiments. All measurements are performed in air, with an ambient temperature of $26\pm 1^{o}C$ and relative humidity of $36\pm 5\%$. Considering the isopropanol and glycerol droplet of the constant diameter, experimental results are presented below for a validation study and a discussion on mechanism for coalescence dynamics. The time-scales for a droplet-impact and droplet-evaporation phenomena are of the order of milliseconds and seconds, respectively. For example, an impact of a 3 microliter isopropanol droplet with 0.37 m/s velocity takes around 7 ms to spread on a fused silica surface [49], and around 200s for the evaporation. Thus, the time duration for the coalescence phenomenon is much smaller than the evaporation time-scale. Furthermore, there is almost no variation in the ambient temperature during the short-duration of the coalescence process and thus, there is no temperature-dependent variation in the surface tension over the interface. Also, the diameter of the isopropanol droplet considered here is small enough for any buoyancy effect inside the droplet. Thus, the effects of volatility of isopropanol, Marangoni and buoyancy are ignored in the present work.

2.2 Numerical details

Fig. 2

Droplet coalescence a non-dimensional computational set-up and b geometrical parameters characterizing the unsteady interface dynamics

The numerical study and the results are presented here mostly in non-dimensional form, considering the initial diameter of the droplet D as the non-dimensional length scale and the velocity scale $u_{c}$ as capillary-velocity $\sqrt{\gamma /\rho _{1}D}$ for isopropanol $\left( Oh<1\right)$ and $u_{c}=\gamma /\mu$ for glycerol $\left( Oh>1\right)$. For the liquid-air system here, the liquid is considered as the reference fluid. Figure 2a shows a non-dimensional axi-symmetric (${R-Z}$) computational domain and initial as well as boundary conditions. The initial condition is seen as the liquid droplet touching the horizontal free-surface of the liquid pool and both the fluids are stagnant. The boundary conditions are seen as axi-symmetric at the left, no-slip at the bottom, free-slip at the right, and outflow at the top boundaries. The figure also shows the non-dimensional height of the pool as 2.5, and the size of computational domain is $\left[ 4\times 8\right]$; obtained after a domain-size independence study. This study was done for the isopropanol droplet and resulted in a non-dimensional pinch-off time as $\tau =5.79,\,5.83,\,5.82$ on a non-dimensional domain size of $\left[ 3\times 6\right]$, $\left[ 4\times 8\right]$, and $\left[ 5\times 10\right]$, respectively. The dimensional value of the length and velocity scales are presented in Table 3, along with the physical properties of the two liquids and air; considered in the present experimental and numerical work.

Table 3 Physical properties of the fluids, dimensional value of the characteristic length and velocity scales ($u_{c}=\sqrt{\gamma /\rho _{1}D}$ for isopropanol and $u_{c}=\gamma /\mu$ for glycerol), and non-dimensional governing parameters considered in our experimental and numerical study. All the dimensional variables are presented below in SI units except D which is in mm

Our Ghost Fluid Method (GFM) based Sharp-Interface Dual-Grid Level set method (SI-DGLSM) [37] is used for simulating the droplet coalescence phenomenon. The non-dimensional momentum equation is given as

$$\begin{aligned} \frac{\partial \overrightarrow{U}}{\partial \tau }+\nabla \cdot \left( \overrightarrow{U}\overrightarrow{U}\right) =-\frac{\nabla P}{\chi _{i}}+\frac{Oh}{\chi _{i}}\nabla \cdot \left( 2\eta _{i}{\mathbf {D}}\right) -\chi _{i}Bo{\hat{j}} \end{aligned}$$

(2)

where $Oh=\mu _{1}/\sqrt{\rho _{1}\gamma D}\,\text { and }Bo=\rho _{1}gD^{2}/\gamma$. Here, $\rho _{1}$ is density and $\mu _{1}$ is viscosity of the heavier fluid (liquid). Furthermore, $\chi _{i}$ and $\eta _{i}$ are the non-dimensional density and viscosity; $\chi _{1}=\eta _{1}=1$ in fluid-1 (liquid) while $\chi _{2}=\rho _{2}/\rho _{1}$ and $\eta _{2}=\mu _{2}/\mu _{1}$ in fluid-2 (air). Also, rate of deformation tensor ${\mathbf {D}}=0.5\left[ \nabla \overrightarrow{U}+\left( \nabla \overrightarrow{U}\right) ^{T}\right]$ and ${\hat{j}}$ is the unit vector for gravity (${\hat{j}}=<0,-1>$).

In this present work, a semi-explicit projection method [40] is used in the present work that results a restriction on maximum value of time-step. The restrictive time-step depends on the modeled physical phenomena, governing parameters and grid size and is given as

$$\begin{aligned} \Delta \tau =0.025min\left( \Delta \tau _{CFL},\Delta \tau _{CAP},\Delta \tau _{GFN}\right) \end{aligned}$$

where $\Delta \tau _{CFL},\Delta \tau _{CAP},\,and\,\,\Delta \tau _{GFN}$ are stable time-step sizes due to Courant-Friedrichs-Lewy, capillary and grid Fourier number stable time-step criteria, respectively.

Here, for the SI-LSM, a dual-grid methodology [38] is used in which Navier-Stokes equations are solved on a uniform grid size $m\times n$ and the level set equations are solved on the double refined uniform grid $2m\times 2n$. The advection terms in the Eq. 2 are treated explicitly using 3rd-order Lin-Lin TVD schemes, whereas the diffusion terms are solved using central diffusion scheme. The velocity across the interface is considered as continuous (without any jump condition) i.e. $\left[ \overrightarrow{U}\right] _{\Gamma }=0$. After a grid independence and a validation study (with our experiments on isopropanol and glycerol droplets), presented below, a grid size with $m=200$ and $n=400$ is used in the present work.

3 Experimental and numerical study: coalescence dynamics of isopropanol and glycerol droplets

This section presents a validation study and a qualitative as well as quantitative discussion on the mechanism of partial coalescence of an isopropanol droplet $(D=1.55mm)$ and full coalescence of a glycerol droplet $(D=1.6mm)$ using our experimental and numerical study.

3.1 Code validation and grid independence study

A validation of our SI-DGLSM based code is done by comparing our numerical results with in-house experiments (using high-speed camera) for isopropanol and glycerol liquid droplets in air. For a coalescence dynamics in the liquid-air system, the physical properties, dimensional values of characteristic scales, and non-dimensional governing parameters are presented in Table 3. The detailed description of the method along with its performance and computational time for various two-phase problems is presented by Shaikh et al. [38].

For the coalescence dynamics of two different liquid-droplets in air, the validation study is demonstrated in Fig. 3 (Multimedia view). The figures show an excellent agreement between our numerical and our experimental results. The agreement is shown for the unsteady results corresponding to temporal variation of instantaneous interface, non-dimensional droplet-height H, and contact/neck radius $C_{R}$/$N_{R}$; $C_{R}$ for the full-coalescence of glycerol droplet in Fig. 3d and $N_{R}$ for the partial-coalescence of the isopropanol droplet in Fig. 3c. The unsteady parameters $\left( H,C_{R}\text { and }N_{R}\right)$ which characterizes the time wise varying dimensions of the droplet are shown schematically in Fig. 2b − H is the height of the droplet from the horizontal free-surface of the unperturbed liquid pool, contact-radius $C_{R}$ is the radius of the droplet at the unperturbed pool, and neck-radius $N_{R}$ is the minimum radius of the droplet. These parameters are computed using a change in the sign of the level set function across the interface [37]. Over the time interval considered here for the numerical as compared to experimental results, shown in Fig. 3c-d (Multimedia view), the maximum percentage error is $2.2\,\%$ ($9\,\%$) in H and $6\,\%$ (7 %) in $N_{R}\left( C_{R}\right)$ for isopropanol (glycerol) droplet. Also, for the SI-DLSM on the grid-size of $200\times 400$, the mass error − which is the biggest disadvantage of a level set method − is $0.92\%$ for isopropanol droplet and $1.62\,\%$ for glycerol droplet simulations. For the partial coalescence of the isopropanol droplet, excellent agreement is also found for non-dimensional pinch-off time $\tau _{p}$ and non-dimensional secondary droplet diameter $\xi$ − our numerical and our experimental results as $\tau _{p}=0.6$ and 0.62 and $\xi =0.58$ and 0.55, respectively.

Fig. 3

For the coalescence dynamics of the (a, c) isopropanol $(D=1.55\,mm)$ (b, d) glycerol $(D=1.6\,mm)$ droplet, comparison between our numerical and our experimental results: variation of (a, b) instantaneous interface shape with time (ms), and (c, d) non-dimensional height and contact radius of the interface with non-dimensional time. Dotted line in (a, b) represents numerically obtained interface overlapped with the experimental image. The arrows in (a2) represent the upward and radially-outward traveling capillary waves. The numerical results presented in (a, b) are on a grid size $\left[ 200\times 400\right]$ while that in (c, d) are for three different grid-sizes. (Multimedia view, separately for (a, c) and (b, d))

Our numerical results are also validated with the experimental results of Blanchette and Bigioni [12], for a partial coalescence of an ethanol droplet. Excellent agreement is found between our numerical and the published results [43] for the temporal variation of the instantaneous interface as well as the height H of the droplet. This validation study corresponds to the ethanol droplet of diameter $D=1.07mm$ surrounded by air that corresponds to $Oh=0.011$ and $Bo=0.09$. Since the $Bo=0.09$ for the ethanol droplet is much smaller compared to $Bo=0.85$ for the isopropanol droplet, note that the validation presented above for the partial coalescence regime corresponding to sufficiently different Bond numbers.

Along with the validation of our in-house code, Fig. 3c,d also shows a grid-independence study for the partial-coalescence of isopropanol droplet on three different uniform grids. The figure shows almost same results on the two finer as compared to the coarsest grid. Thus, the intermediate grid size of $200\times 400$ is used in our non-dimensional parametric study for various diameters and various surface tension coefficients of the isopropanol droplet; presented in the Sect. 4.

3.2 Mechanism of partial and full coalescence

Mechanism of partial and full coalescence is presented below in separate sub sections for interface dynamics, flow dynamics and vorticity dynamics. The mechanism for the partial coalescence of a droplet is well reported, with a qualitative discussion on the experimentally/numerically obtained interface dynamics [10, 17, 23, 24]. However, a quantitative evidence of a well known qualitative discussion that is missing in the literature is presented here, with the help of numerically obtained flow dynamics and vorticity dynamics. Although the flow and stress fields were presented earlier by Yue et al. [23] for drop coalescence on an interface involving Newtonian and Viscoelastic fluids, a much more detailed temporal variation of flow field and vorticity field is presented below for a more clear quantitative evidence of the mechanism.

3.2.1 Interface dynamics: experimental and numerical results

For the isopropanol droplet, Fig. 3a (Multimedia view for (a,c)) shows partial coalescence − formation of the first vertically elongated columnar shape (seen at $4.67\,ms$) and then neck-formation (seen at $6\,ms$), leading to break-up (at $6.68\,ms$; not shown here) and a secondary-droplet (seen at $8.33\,ms$) which bounces up before completely merging with the pool (not shown here). Yue et al. [23] reported a qualitative discussion on the mechanism of partial-coalescence as a two stage process: first, capillary waves propagating along the drop and transforming it into a fluid column; and second, neck formation on the column and pinch-off of the secondary droplet. For the partial-coalescence case, Ray et al. [24] discussed that a breakage of the thin fluid-2 (air here) film between the droplet and pool (both consisting of fluid-1) surface leads to the onset of capillary waves in upward and radially outwards directions. These two waves are observed in our experiments as well as in the simulations, shown by arrows in Fig. 3a at $1.33\,ms$. Furthermore, as the figure shows that the upward traveling wave induced upward-flow leads to the elongated columnar shape of the droplet, and the surface-tension induced inward-radial-push near the base results in the neck formation. The upward inertia induced elongation is resisted by the surface-tension induced downward-pull at the top of the droplet − there is a competition between the downward-pull at the top and the inward-radial-push at the neck of the droplet; note that both downward pull and radial push are induced by surface-tension. The two upward capillary waves from the two side of the droplet (shown by upward arrows) in Fig. 3a2 converge to stretch the droplet vertically upward; thus, the vertical downward collapse (induced by the surface-tension as well as gravity induced downward-pull) is delayed, as observed by Blanchette and Bigioni [12]. This is seen in the temporal variation of droplet-height H (Fig. 3c), with a slight increase (around $10\%$ at intermediate time-duration) in the decreasing trend of variation of H; notice that the initial decrease is much smaller ($<5\%$) as compared to the sharp decrease at the later time instant $\left( \tau >0.4\right)$. The upward capillary wave induced upward stretching delays the vertical collapse and a neck-formation during the delay leads to the formation of secondary droplet which bounces up before completely merging with the pool. Whereas, the radially outward moving capillary waves perturbs the horizontal pool surface finally leading to a shallow cavity on the pool surface after the breakup of the secondary drop, shown in Fig. 3a8. The figure (Multimedia view) also shows good agreement between the numerical and experimental results, for the shape and size of the secondary droplet.

For the glycerol droplet, Fig. 3b shows full-coalescence − characterized quantitatively by a monotonic decrease in the temporal variation of droplet-height H and increase in the contact-radius $C_{R}$ (Fig. 3d). For validating the full coalescence, glycerol is used due to high viscosity ($Oh=3.5$) that leads to the viscous damping of the capillary waves and no columnar as well as neck-formation along with much smaller perturbation of the horizontal pool surface. Figure 3a,b (Multimedia view) shows a good agreement between our experimental and our numerical results.

3.2.2 Flow dynamics: numerical results

From our experimental results, the contact of the droplet (with the pool surface) induced onset of upward and radially outward capillary-waves was presented schematically (as arrows in Fig. 3a2) and discussed above for the mechanism of partial or full coalescence − without any quantitative evidence. Some such evidence of the mechanism are presented here, probably for the first time from our numerical results, as contours of non-dimensional flow-field (radial-velocity U, axial-velocity V and pressure P) and vorticity $\omega _{\theta }$ field; overlapped with the interface contours. They are shown in Fig. 4a for the partial-coalescence of an isopropanol droplet, and Fig. 4b for full-coalescence of a glycerol droplet.

Fig. 4

Temporal variation of instantaneous interface, overlapped with the non-dimensional velocity (radial U and axial V), pressure P and normalized vorticity $\overline{\omega _{\theta }}$ contours, for coalescence of a isopropanol $\left( D=1.55\,mm\right)$ and b glycerol droplet $\left( D=1.65\,mm\right)$. Streamlines are also shown overlapped with the pressure contours. Arrows in the figure represents a local maxima in the velocity contours, seen at the interface

At the onset of contact of the droplet, the rupture of the thin layer of air leads to a perturbation induced upward and radial capillary waves. The waves propagates with a wave velocity $v_{w}\approx \sqrt{\gamma \kappa /\rho }$, where $\kappa$ is wave number. After the contact, the larger/block arrows (near the line of contact) on the velocity contours at $\tau =0.1$ (Fig. 4a,b) points to the maximum value of positive radial-velocity U (outward) and positive axial-velocity V (upward) at the interface, as an evidence to the radial and axial flow induced due to the onset of the radially-outward and upward capillary waves, respectively; however, it can be seen that the magnitude of the radial flow velocity are much larger for the isopropanol $\left( U_{max}=2\right)$ as compared to the glycerol droplet case $\left( U_{max}=0.2\right)$.

For the isopropanol droplet, slightly above the outward block - arrow in the $U-$velocity contour at $\tau =0.1$, the inward smaller arrow in Fig. 4a points to a local maxima in the inward radial-velocity which shifts downward with time, with a value $U_{max}=1.25$ at $\tau =0.4$ that corresponds to an inflection-point on the interface; and finally, leads to the neck-formation. Similarly, local maxima for $V-$velocity contour at the interface is shown by the upward smaller-arrow in Fig. 4a. It can be seen that this maxima shifts upward with time and reaches to the top of columnar shaped interface at $\tau =0.3$. The larger axial-velocity $V_{max}\approx 2$ based upward stretching at the top (that leads to the columnar-formation) is more than the larger radially inward velocity $U_{max}=1.3$ based push at the neck of the droplet. The upward stretching delays the downward collapse and the radial push based neck formation during the delay causes the breakup and formation of the secondary drop. Similar phenomenon was observed and described qualitatively for the partial coalescence of an ethanol droplet by Blanchette and Bigioni [12] - the capillary waves are vigorous enough to delay the vertical collapse and the horizontal collapse at the neck causes the secondary droplet.

The upward movement of the capillary waves set up a downward pressure gradient inside the drop and across the neck. This is evident from the pressure contours in Fig. 4a at $\tau =0.2$ and 0.3, with larger pressure near the top of the droplet and smaller pressure near the neck. The pressure difference leads to the drainage of the liquid from the droplet to the pool, through the opening of the droplet at the base, shown by the streamlines in Fig. 4a; the interface in the figure also shows a reduction of the opening with time. At $\tau =0.3$ and 0.4, the interface shows the movement of the droplet in upward direction as the capillary waves move upwards on the droplet surface; indicated by the increase in the upward $V-$velocity, toward the top of the droplet. Once the capillary waves reach the top, over the time duration $\tau =0.4-0.57,$ the pressure contour in Fig. 4a shows a much larger pressure difference $\Delta P\approx 12$ across the interface in the columnar-region as compared to the neck-region of the droplet. Similar large pressure gradient in the liquid column is also reported in the numerical studies of Dong et al. [18] and Martin and Blanchette [29]. Thus, the pressure-force induced upward pull on the droplet is more than the radial push at the neck, leading to the shrinkage of the droplet near the neck at faster rate than the downward-collapse that results in the break-up near the neck and formation of secondary drop at $\tau =0.58$. For the partial coalescence case of isopropanol, the height-to-diameter ratio of the fluid column is less than $\pi$ which is a required condition for growth of surface perturbations according to Rayleigh Plateau instability [44], as reported by Yue et al. [23].

For the glycerol droplet, at the onset of the contact of the droplet with the pool surface, the rupture of thin air-film induced capillary-waves are damped due to extremely large viscous-force $(Oh=3.5)$ as compared to the inertia and surface forces. Thus, the interface shape in Fig. 4b shows a time-wise expansion of the base of the droplet, no columnar as well as neck formation, and monotonic downward fall of the top of the droplet. The pressure contour shows that the downward gradient of pressure is larger in the lower as compared the upper half of the droplet which causes the continuous drainage of the fluid into the pool. This sets up a larger downward axial velocity near the center as compared to the top of the droplet, seen by the negative values of the $V-$velocity contours in Fig. 4b. However, due to large viscosity of glycerol, the outward movement of the base of the droplet is extremely slow − leading to almost uniform negative $V-$velocity based vertical collapse of the droplet on the pool, refer Fig. 4b from $\tau =$ 0.7 to 1.25. The interface corresponding to the pool surface is seen in the figure as almost horizontal at various time instant that indicates the suppression of the radial capillary waves generated over the surface.

The velocity at which droplet expands over the liquid surface after touching the liquid surface is found to be maximum just after contact of the droplet with the liquid pool [17]. It is found that the maximum velocity of droplet over the liquid pool is strong function of the viscosity ratio [7, 45]. In our liquid-air system, the maximum radial U-velocity is found is $U_{max}=2$ for isopropanol $\left( \eta =0.009\right)$ and 0.2 for glycerol $\left( \eta =4.5\times 10^{-5}\right)$ droplets. The maximum velocity of receding edge was measured by Kassim and Longmire [17] in the PIV experiments of a liquid-liquid coalescence as $U_{max}=20$ for $\eta =3$ and $U_{max}=40$ for $\eta =7.5$. The difference in our and their $U_{max}$ is due to the larger ambient viscosity and a bigger size of droplet $\left( 1.03\,cm\right)$ used in their experiment. Charles and Mason [7] measured maximum speed up to 67 in their liquid-liquid experiments for $\eta =1.5$. Hartland’s experiments [45] reported the velocities are much lower i.e. $U_{max}=0.04$ and 0.6 for a viscosity ratio of $\eta =0.02$ and $\eta =0.2$, respectively. Recently, Dong et al. [18] captured the 2D time-resolved velocity fields inside the droplet using PIV with the maximum resultant as 0.06 m/s for $\eta =0.18$ which is increased to 0.08 m/s after addition of surfactant for liquid-liquid coalescence.

3.2.3 Vorticity dynamics: numerical results

At the onset of liquid-liquid droplet coalescence, just after the film breaks up, two counter rotating vortices are reported in various experimental work [17-19] Another experimental work [46] reported downward evolution of the vortex rings when the impact velocity of the droplet is very low or negligible. Their study mainly focused on the evolution of downward moving vortex rings in the liquid pool. The curved drop surface at the contact region turned the moving drop fluid towards the contact region. Hence, the curved streamline generates vorticity to maintain zero viscous stress at the free surface. The upward and radial capillary wave motion also sets up two vortices across the interface, shown in Fig. 4 by the non-dimensional vorticity contours $\left( \overline{\omega _{\theta }}=\omega _{\theta }D/u_{c}\right)$. Here, $\omega _{\theta }$ is vorticity, $u_{c}$ is the velocity scale and D is initial droplet diameter for the isopropanol and glycerol droplets.

For the isopropanol droplet, at non-dimensional time $\tau =0.1$, the vorticity contours in Fig. 4a shows that the curvature at the junction of the droplet and liquid pool generates a positive/counter-clockwise vortex that initially moves upwards on the upper side of the droplet surface and negative/clockwise vortex that moves radially outward on the pool surface. The figure at $\tau =0.1$ shows the maximum non-dimensional vorticity $\overline{\omega _{\theta }}=\pm 1$ indicating that the magnitude of the positive and negative vortices is $\omega _{\theta }\sim u_{c}/D$ obtained. The figure shows that both the vortices move with the capillary waves across the interface. It can be seen that the upper-side vortex moves slightly upward initially with a reduction in the vorticity magnitude and then moves downward later − the downward collapse increases the positive-vortex strength and attains maximum value to $\omega _{\theta }=2.2u_{c}/D$ at the neck region before pinching-off at $\tau =0.57$. The radially outward moving negative vortex $\omega _{\theta }=0.2\,u_{c}/D$ diffuses while traveling over the pool surface (not shown in the figure).

For the glycerol droplet, the vorticity contours in Fig. 4b shows that the monotonic expansion of the base causes drainage of the fluid into the pool and the high shear stress in the droplet suppresses the capillary wave movement and the neck formation, which also dampens the formation of vortex rings and its movement across the drop. The figure shows a much smaller strength of vortex $\omega _{\theta }=\approx u_{c}/D$ at the base region at $\tau =0.1$ which later diffuses due to high viscous forces of the glycerol droplet to $\omega _{\theta }=0.1u_{c}/D$. For bigger droplet size $\left( 1.03\,cm\right)$ and with viscous surrounding fluid, Mohamed-Kassim and Longmire [17] reported the maximum vorticity in the surrounding fluid as $\omega _{\theta }=87u_{c}/D$ and $34u_{c}/D$ for a viscosity ratio $\eta =3.3$ and $\eta =7$, respectively; and found the dampening of the droplet vortex rings due to high viscous dissipation of droplet fluid, as observed in the present case of glycerol.

3.3 Analogy of the oscillations of the coalescing droplet with a freely vibrating spring-mass-damper System

This section present a scaling analysis of the damping of interface-oscillations during the present Coalescence Dynamics. During the coalescence, the damped oscillations of the isopropanol and glycerol droplet (Fig. 3) can be explained by a scaling analysis that is based on drawing an analogy of the present oscillating droplet with a freely vibrating mass-spring-damper system. The freely damped system is governed by an equation $m\ddot{x}+c{\dot{x}}+kx=0$, where m is the mass of the suspended solid, c is the damping coefficient of the damper, and k is stiffness of the spring. For this system, a damping ratio $c_{r}$ and time period of the damped oscillation $t_{d}$ are given [47] as

$$\begin{aligned} c_{r}&=\frac{c}{c_{c}}\text { where }c_{c}=2\sqrt{km} \end{aligned}$$

(3)

$$\begin{aligned} t_{d}&=\frac{1}{f_{n}\sqrt{1-c_{r}^{2}}}\text { where }f_{n}=\frac{1}{2\pi }\sqrt{\frac{k}{m}} \end{aligned}$$

(4)

where $c_{c}$ is a critical damping coefficient (threshold between an over-damped and underdamped system) and $f_{n}$ is the natural frequency of the system.

The present viscosity or gravity based damped oscillation of the coalescing droplet system is considered here analogous to the above viscously damped freely vibrating solid system, with the mass of the droplet $\rho _{1}\pi D^{3}/6$ and its surface tension coefficient $\gamma$ for the damped droplet-system analogous to the mass m and stiffness k for the damped solid-system, respectively; thus, $m\sim \rho _{1}D^{3}$ and $k\sim \gamma$. Further analogy results in representation of the scaling for the damping coefficient c by the viscosity $\mu _{1}$ of the droplet and gravitational acceleration g for the viscous and gravity regimes of the droplet coalescence, respectively; thus, $c\sim \mu _{1}D$ and $c\sim \rho _{1}D^{3}g/\sqrt{\gamma /(\rho _{1}D)}$ for the respective regimes. Substituting the scales for m, k and c in Eq. 3, the damping ratio $c_{r}\sim Oh/2$ for the viscosity dominated damping and $c_{r}\sim Bo/2$ for the gravity dominated damping.

Since the droplet size $D=1.55 mm$ is small enough for the above coalescence dynamics of the isopropanol and glycerol droplet, the damping of the droplets is dominated by viscosity as compared to gravity. Thus, for $Oh=0.012$ for isopropanol and $Oh=3.5$ for glycerol droplet (Table 3), $c_{r}\sim Oh/2$ results in $c_{r}=0.006$ and 1.75 for the respective droplets. The $c_{r}\ll 1$ results in the isopropanol droplet coalescence as an underdamped system while the $c_{r}>1$ results in the glycerol droplet coalescence as an over-damped system. This implies that there are oscillation at the free surface for isopropanol droplet and almost no-oscillations for glycerol droplet, consistent with the above observation in the present measurements and simulations. Furthermore, for the present isopropanol case, substituting $m\sim \rho _{1}D^{3}$, $k\sim \gamma$ and $c_{r}=0.006$ in Eq. 4 results in $t_{d}\sim \sqrt{\rho _{1}D^{3}/\gamma }$ . Substituting $\rho _{1}$, D and $\gamma$ from Table 3, $t_{d}\approx 11.53 ms$ that is consistent with the pinch-off time obtained here experimentally as $t_{p}=6.68 ms$ and numerically as $t_{p}=7.15 ms$. The scaling $t_{d}\sim \sqrt{\rho _{1}D^{3}/\gamma }$ is consistent with time period of free surface oscillations of a droplet impacting on a liquid and solid surfaces; reported earlier [48, 49] .

4 Numerical study: effect of droplet size and surface tension coefficient on coalescence dynamics of isopropanol droplet

After our experimental and numerical study demonstrates the validation of our SI-DGLSM and a qualitative as well as quantitative discussion on mechanism of coalescence dynamics of isopropanol and glycerol droplet, the isopropanol droplet is considered for a detailed numerical study. The study is done for the effect of droplet size and capillary force, with a wide range of dimensional and non-dimensional governing parameters as shown in Table 4. With reference to the $D=1.55 mm$ and $\gamma =22 mN/m$ in our experiments for the isopropanol droplet (Tables 3, 4 shows smaller as well as larger D and $\gamma$ considered in our simulations for the parametric study. Further, it can be seen that the effect of D and $\gamma$ is studied separately at the constant experimental values of $\gamma =22 mN/m$ and $D=1.55 mm$, respectively.

Table 4 For coalescence dynamics of isopropanol droplet in air, dimensional/non-dimensional governing parameters considered in the present numerical work to study the effect of droplet diameter D and surface tension coefficient $\gamma$ at a constant density ratio $\chi =1.55\times 10^{-3}$ and viscosity ratio $\eta =8.9\times 10^{-3}$

4.1 Effect of droplet size

There are numerous studies reported in the literature for the effect of droplet size on the coalescence dynamics; however, for the liquid-air system studied numerically here, most of the earlier studies are experimental (refer Tables 1 and 2). For a liquid-liquid system, partial coalescence at the intermediate range of D, and full-coalescence at the smaller as well as larger D has been reported experimentally [9, 10] as well as numerically [23]. The smaller D or larger $Oh\,(\mu _{1}/\sqrt{\rho _{1}\gamma D})$ corresponds to the domination of the viscous-force, and the larger D or larger $Bo\,(\rho _{1}gD^{2}/\gamma )$ corresponds to the domination of gravity force; the domination of viscous/gravity force leads to the transition from partial to full coalescence. For coalescence of water, ethyl alcohol and mercury droplet in air, experimental study by Thoroddsen and Takehara [8] presented partial coalescence in a self-similar regime (at insignificant Oh and Bo) that corresponds to a constant secondary droplet size ratio $\xi$ ($=D_{s}/D$) $\approx 0.5$ through successive cycles of partial coalescence. The range of D was extended later in an experimental work by Chen et al. [10] that led to their proposition of non self-similar regimes of partial coalescence as viscous regime for smaller D or larger Oh and gravity regime for larger D or larger Bo, along with the self-similar regime called as inertio-capillary regime at intermediate D. For the range of D in the self-similar inertio-capillary regime, they also reported that the non-dimensional pinch-off time $\tau _{p}$ ($=t_{p}/t_{c}$, where $t_{c}$ is capillary time) also remain constant along with the constant secondary drop ratio $\xi \approx 0.5$.

Fig. 5

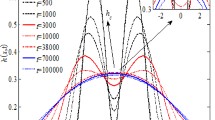
For partial-coalescence regime of the isopropanol-droplet in air, variation of the non-dimensional (a) pinch-off time $\tau _{p}$ ($=t_{p}/t_{c}$, where $t_{c}$ is capillary time) and (b) secondary-drop size ratio $\xi$ (=$D_{s}/D$) with increasing initial diameter D of the droplet (varying from $0.2\,mm$ to $4.6\,mm$). The $x-$axes at the top also shows the variation with increasing Bo and decreasing Oh. Here, VR: viscous regime; ICR: inertio-capillary regime; and GR: gravity regime. The dashed and solid lines corresponds to a scaling analysis based correlation [10] for the viscous and gravity regime, respectively

The three regimes for the partial coalescence, originally proposed by Chen et al. [10] for a liquid-liquid system, are presented here in Fig. 5 for the liquid-gas system; considering various diameters (Table 4) of the isopropanol droplet in air. The figure is shown for the partial coalescence of the isopropanol droplet at the intermediate range of D varying from $0.2\,mm\text { to }4.6\,mm$ while full-coalescence is found at smaller $D\le 0.18\,mm$ as well as larger $D\ge 4.7\,mm$. For the partial coalescence, Fig. 5a shows a smaller critical diameter $D_{c,1}=0.35\,mm$ (critical Ohnesorge-number $Oh_{c}=0.0257$) of the isopropanol droplet for the transition from inertio-capillary to viscous regime at $D<D_{c,1}$, and also a larger critical diameter $D_{c,2}=3.1\,mm$ (critical bond-number $Bo_{c}=3.37$) for the transition from the inertio-capillary to gravity regime at $D>D_{c,2}$; the critical values are decided by a diameter at which there is change in the trend from almost constant to a variation in both $\tau _{p}$ and $\xi$ (inflection point) with increasing diameter [10].

The viscous and gravity force acting a coalescing droplet increases with decreasing D and increasing D, respectively. The domination of viscous (gravity) force over the capillary increases with decreasing (increasing) D at smaller (larger) range of D. This leads to the transition from the inertio-capillary to the viscous (gravity) partial-coalescence-regime and further decrease (increase) in D leads to the transition from partial to full coalescence. Both viscous and gravity force dampens the vigorous movement of capillary waves over the droplet surface, leading to a slow and fast drainage of the droplet-fluid with increasing viscous and gravity force, respectively. However, the dampening of capillary waves with increasing viscous/gravity force suppresses the columnar formation that leads to a decrease in the size of secondary droplet. Thus, the figure shows that $\tau _{p}$ increases and $\xi _{p}$ decreases with decreasing D in viscous regime; whereas, with increasing D, both $\tau _{p}$ and $\xi$ decreases in gravity regime. The pinch-off occurs due to the two reasons: (a) movement of capillary waves over the droplet surface due to opening of the neck in the early stage of coalescence and (b) radial collapse due to the neck formation. In the gravity regime, for the droplet size $D>3.5mm$ (Fig. 5), the gravity force starts to dominate with increasing D and increases the rate of liquid drainage into the pool which reduces the upward momentum of capillary waves and increases the momentum of radially inward collapse due to the neck formation. This radial collapse is able to reach faster that leads to the pinch-off and reduces the pinch-off time as well as the secondary droplet size with increasing D in the gravity regime (Fig. 5). Similar results were reported by Chen et al. [10] for a liquid-liquid system.

The figure shows a good agreement of our SI-DGLSM based numerical results for isopropanol-air system with the published experimental results of Thoroddsen and Takehara [8] for a liquid-air system and Chen et al. [10] for a liquid-liquid system; and a phase filed method based numerical results of Yue et al. [23] for a liquid-liquid system. The figure also shows a reasonably good agreement of our results with a scaling analysis based correlations proposed by Chen et al. [10] for a liquid-liquid system separately in the viscous and gravity regime. For the inertio-capillary regime, our numerically obtained almost constant secondary droplet size ratio $\xi \approx 0.5$ also matches with the published experimental results [8, 10, 13].

4.2 Effect of surface tension coefficient

The effect of surface tension coefficient is presented with respect to coalescence and vorticity dynamics of isopropanol droplet in air in the following sections.

4.2.1 Coalescence dynamics

Fig. 6

Effect of Oh on coalescence behavior (a) Effect of surface tension on top height of droplet (b) Effect of surface tension on neck radius of droplet (P: Partial Coalescence, F: Full Coalescence)

The effect of capillary forces is investigated by varying surface-tension coefficient from $\gamma =2-200\,mN/m$ (Table 4) for the isopropanol droplet of initial diameter $D=1.55\,mm$ in air. Thus, as shown in Table 4, non-dimensional simulations are done for the various Oh ($0.004-0.04$) and $Bo\,$ $(0.09-9.25)$ at a constant $\chi =1.55\times 10^{-3}$ and $\eta =8.9\times 10^{-3}$. The decreasing $\gamma$ (increasing Oh) led to a transition from partial to full coalescence for $\gamma \ge X\,mN/m\,(Oh\ge 0.027).$ Vice-versa, with increasing $\gamma$ (decreasing Oh), the larger (smaller) value of $\gamma \left( Oh\right)$ sets up vigorous capillary waves which is found here to elongates the columnar shape of the droplet by $15-20\%$ before the pinch-off of the secondary droplet. Blanchette and Bigioni [12] and Gilet et al. [13] observed almost $30\%$ increase in column size due to capillary induced stretching. In the PIV experiments [18], the rise of columnar size was found about $4\%-10\%$ of the initial drop diameter. Figure 6 (a) shows an almost constant droplet-height initially followed by a slightly-increasing trend at intermediate time-duration and finally a decreasing trend of variation. For the transition from partial to full coalescence at the critical Ohnesorge number $Oh_{c}=0.027$ and also at the slightly larger $Oh=0.3$, Fig. 6b show that the neck radius oscillates twice due to a competition between viscous and capillary force before resulting in the full coalescence. Similar double oscillations was reported by Ray et al. [24] who presented the oscillation as the deciding factor for the transition from partial to full coalescence. Furthermore, for the partial-coalescence regime, Fig. 6b shows an increasing trend (due to expansion at the contact of the droplet with the pool liquid) that is followed by a decreasing (due to surface tension based radial push at neck) trend in variation of the neck-radius at all the values of Oh. Larger surface tension coefficient or smaller Oh results in vigorous surfaces waves which perturbs the droplet surface with larger droplet stretching (Fig. 6a) that causes a reduction in the neck size (Fig. 6b). For the full-coalescence regime, the temporal variation of the droplet-height in Fig. 6a shows an almost monotonic decreasing trend with a smaller rate of decrease initially as compared to the later time-duration; and the rate of decrease of the height or the rate of downward collapse of the droplet increases with decreasing $\gamma$ or increasing Oh.

Fig. 7

Effect of surface tension on coalescence of isopropanol droplet in air (a) variation of the pinch-off time time with respect to surface tension (b) variation of droplet ratio (secondary to primary) with increasing surface tension of the isopropanol-droplet in air, surface-tension − varying from $\gamma =2-200\,mN/m$. The $x-$axes at the top also show the variation with increasing Bo and decreasing Oh, with non-dimensional correlation for droplet ratio

As discussed earlier, the increase in the droplet-height or upward stretching of the droplet for the partial-coalescence is due to the larger velocity of upward capillary wave − the wave velocity increases with increasing $\gamma$, leading to the increase in the maximum upward stretching of the droplet. At smaller $\gamma$ or larger Oh, the viscous force is dominant over the smaller capillary force that dampens the upward capillary waves and accelerates the downward collapse of the droplet into the pool without any upward stretching.

For the partial-coalescence cases with increasing surface tension coefficient $\gamma$ or decreasing Oh, Fig. 7a shows an almost constant pinch-off time $\left( \tau _{p}\right)$ and an almost asymptotic increase in droplet size ratio $\xi$. The constant pinch-off time for all values of surface tension in Fig. 7a shows that the radial push at the neck is independent of velocity of capillary wave propagation. The primary effect of surface tension is to produce capillary waves over the droplet surface which pushes the fluid towards the droplet top surface and elongates the height of the columnar structure. With increasing $\gamma$, the capillary waves gets strengthened and the resulting increased stretching of the columnar structure increases the size of secondary droplet as shown in Fig. 7b. The figure shows that the size of secondary droplet increases from $\xi =0.47\,\text {at}\,\gamma =2mN/m$ to $\xi =0.62\,\text {at}\,\gamma =100\,mN/m$. With further increase in surface tension $\gamma \ge 100mN/m$, the size of secondary droplet remains almost constant at $\xi =0.62$ which matches with the Kavehpour first-order relationship [6]. The trend of $\xi$ versus Oh in Fig. 7b matches well with the experimental results of presented by Gilet et al. [13] for different fluid combinations at smaller $\gamma$. Whereas, the difference in our and their results at larger $\gamma$ is probably due to liquid-air coalescence considered here as compared to liquid-liquid coalescence considered by them [13].

The effect of surface tension on the characteristics of capillary wave dynamics is shown in Fig. 8. The figure shows the interface shape at $\tau =0.2$ for three different surface tension coefficients $\gamma =3\,mN/m$, $22\,mN/m$ and $120\,mN/m$. The arrows in the figure are used for an approximate quantification of the wavelength $\left( \lambda \right)$ of the capillary waves generated over the droplet surface and the distance between the two arrows is approximated here as half of the wavelength $\left( \lambda /2\right)$. As shown in Fig. 8, $\lambda /2$ is approximately equal to 0.25, 0.3, 0.4 for $\gamma =3\,mN/m,\,22\,mN/m$ and $120\,mN/m$. Thus, with the increase in surface tension, the wavelength along with wave-velocity (proportional to the wavelength) increases that leads to the above discussed strengthening of the capillary wave.

Fig. 8

Capillary waves dynamics over the droplet at a non-dimensional time of $\tau =0.2$, under the effect of surface tension coefficients: (a) $\gamma =3\,mN/m$, (b) $\gamma =22\,mN/m$ and (c) $\gamma =120\,mN/m$, corresponding to $Oh=0.03$, 0.004, 0.006, respectively

4.2.2 Vorticity dynamics in Droplet coalescence on the liquid surface

During the droplet coalescence over its liquid pool, liquid drainage from the droplet produces vortex rings in the surrounding fluid near the neck region due to propagation of capillary waves. The droplet coalescence induced surrounding vortices in air are shown schematically in Fig. 9c. The effect of varying $\gamma$/Oh based capillary forces on the unsteady vorticity dynamics is presented in Fig. 9. For both partial and full coalescence, Fig. 9a,b shows that the variation of the strength $\omega _{\theta }$ of the surrounding counter-clockwise vortex (represented here by the maximum value of positive vortex [50]) decreases sharply at the beginning, remains almost constant at the intermediate time-duration, and increases sharply at the end of the partial/full coalescence process. It is interesting to notice that the constant value of $\omega _{\theta }$ is much larger (around five times) for the full coalescence as compared to the partial coalescence. The temporal variation of instantaneous vorticity contours in Fig. 9a,b shows that the initial rush of fluid from droplet to the pool causes circulation in the surrounding air near the neck region. This results in the generation of the vorticity whose strength decreases due to reduction in the fluid drainage rate into the pool. Later, the upward moving capillary wave pushes the fluid towards the top of the droplet due to rigorous capillary waves generation that decreases the strength of the vortices. After the column formation, the downward pull at the top of the droplet leads to an increase in the strength of vortex and become maximum at the end of coalescence process. The vortex rings in the surrounding air are produced due to drainage of fluid in the liquid pool, however, the strength of the vortex depends on the rate of propagation of capillary waves. The larger strength of the positive-vortex for the full as compared to the partial coalescence is probably due to the larger drainage rate for the full coalescence, as shown in Fig. 9a. The direction of vortices is judged by the color of the vorticity-contours as seen in Fig. 8, where the downward drainage of droplet-fluid into the pool causes counter-clockwise vortices near the neck and the wave dynamics over the liquid pool creates the clockwise vortices over the pool surface.

Fig. 9

Temporal variation of the strength $\omega _{\theta }$ of the positive/counter-clockwise vortex (formed near the neck in air) for (a) partial and (b) full coalescence at $Oh=0.0065$ and $Oh=0.035$, respectively. Figure (c) shows a schematic representation of the vortex formation; and (d) shows the temporal variation of the vortex strength for various Ohnesorge numbers, with F: Full coalescence and P: Partial coalescence. The four discrete time instants in (d) corresponds to that for which the vorticity contours are shown in (a) and (b)

Figure 9c shows a schematic of the formation of the counter rotating vortices that is induced by the upward and radial movement of the capillary wave movement and fluid drainage. For the intermediate time duration of the partial/full coalescence $\tau =0.1-0.5$. Figure 9d shows the increase in vorticity strength at the later time is more profound for full as compared to partial coalescence due to the difference in the rate of drainage of fluid into the pool. With increase in $\gamma$, the stronger capillary waves moves upward with larger wave velocity and pushes more fluid to the top − causing the less fluid drainage into the pool which decreases the positive-vortex strength. Whereas, decrease in $\gamma$ results in the domination of viscous forces over the smaller capillary forces which slows down the convergence of capillary-waves over the droplet surface and results in faster drainage of droplet fluid into the pool that leads to the increase in the strength of vortex.

4.3 Regime map

The effect of droplet diameter D and surface tension coefficient $\gamma$ on the partial/full coalescence regime is presented in Fig. 10 as a regime map. For the effect of varying D as well as varying $\gamma$, the figure shows the present simulated combinations of Oh and Bo that leads to partial and full coalescence by filled and unfilled symbols, respectively. It is interesting to notice that the line − corresponding to a correlation proposed by Blanchette and Bigioni [14] for a liquid-liquid system − almost demarcates the present combinations of Oh and Bo that leads to partial coalescence with those leading to full coalescence, for both D and $\gamma$ based transitions in coalescence dynamics.

Fig. 10

Regime map: effect of droplet diameter D and coefficient of surface tension on the partial and full coalescence of isopropanol droplet in air ($\chi =1.55\times 10^{-3}$, and $\eta =8.9\times 10^{-3}$) on $Oh-Bo$ phase diagram. The dashed line corresponds to a correlation $Oh_{c}=-0.005Bo+0.029$, proposed by Blanchette and Bigioni [14] for a liquid-liquid system with nearly matched densities and viscosities

For the decreasing Oh and increasing Bo number under the effect of increasing droplet-diameter D, Fig. 10 shows the transition from partial to complete coalescence at a lower and higher critical diameters $D_{c,L}=0.18\,mm$ and $D_{c,U}=4.7\,mm$, respectively. The respective critical diameters lead to the associated critical non-dimensional parameter as critical Ohnesorge number $Oh_{c}=0.036$ for the viscosity based transition and critical Bond number $Bo_{c}=7.74$ for the gravity based transition to full coalescence. Increasing viscous-damping for the larger $Oh\ge Oh_{c}$ while increasing gravitational-force for larger $Bo\ge Bo_{c}$ leads to the suppression of the upward capillary wave induced upward flow that leads to the downward collapse and full-coalescence of the droplet before forming the columnar shape as well as neck. Whereas, for the intermediate Oh and Bo, the effect of inertia and capillary forces are much larger as compared to viscous and gravity forces resulting in the partial coalescence as shown in Fig. 10; and also shown in Fig. 5 for both self-similar inertio-capillary regime and non self-similar viscous/gravity regimes. Note that the full coalescence is found here at $D\le D_{c,L}$ and $D\ge D_{c,U}$ while partial coalescence occurs at $D_{c,L}<D<D_{c,U}$.

Our critical values of $Oh_{c}=0.036$ and $Bo_{c}=7.74$ are found to have good agreement with $Oh_{c}=0.035$ and $Bo_{c}=7$ reported numerically by Ray et al. [24] for a liquid-liquid coalescence. The minimum droplet diameter for partial coalescence is found numerically here as $D_{c}=0.2\,mm\,\left( Oh=0.034\right)$ which is in good agreement with the Blanchette and Bigioni [12] experimental value $D_{c}=0.19\,mm\,\left( Oh=0.026\right)$ for coalescence of ethanol droplet in air. They also presented various droplet-diameters based regime map from their numerical simulations as well as experiments; however, their study was for smaller $Bo\le 1$ as compared to $Bo\le 15$ considered in the present work. Thus, their regime map does not present the transition reported here at the larger bond number $Bo\ge 7.7$ or $D\ge 4.7\,mm$; reported here for the first time for a liquid-air system although both smaller and larger diameter based transitions are well reported for a liquid-liquid system ( [10, 23]).

Furthermore, under the effect of varying surface tension coefficient $\gamma$, Fig. 10 shows a single transition from partial to full coalescence at a critical $\gamma _{c}=4\,mN/m$ that corresponds to $Oh_{c}=0.027$ and $Bo_{c}=4.22$. The figure shows increasing and decreasing surface tension coefficient $\gamma$ of the isopropanol droplet as compared to its standard value $\gamma =22\,mN/m$ at $25^{\text {o}}C$, with the suppression of the capillary waves and the resulting transition from partial to full coalescence at smaller $\gamma \le 4\,mN/m$. Whereas, the increase in $\gamma$ leads to strengthening of the capillary waves that results in an increased stretching of the columnar structure and the increase in the size of secondary droplet (Fig. 7).

The full coalescence obtained after a critical Bo can be explained as the characteristics of an over-damped spring-mass system, as discussed in Subsect. 3.3. It was discussed that the damping ratio $c_{r}\sim Oh/2$ for the isopropanol droplet results in an underdamped system; whereas, $c_{r}\sim Bo/2$ for the gravity dominated damping with $c_{r}>1$ or $Bo>2$ corresponds to an over-damped system that is consistent with the $Bo_{c}=4.22$ and $Bo_{c}=7.74$ reported above by the present simulations.

5 Conclusions

The conclusions drawn from the present work are as follows:

• 1. The application of the ghost fluid method based sharp interface level set method for the droplet coalescence is presented here for the first time in literature; and is demonstrated as an accurate computational method to capture the rigorous unsteady interface dynamics by a code validation with our experimental results on partial coalescence for isopropanol droplet and full coalescence for glycerol droplet. Furthermore, the interface dynamics shows waviness at the interface, variation in the interface-height and neck formation that led to a mechanism of partial/full coalescence; discussed qualitatively. Further, a quantitative evidence of the well-reported interface dynamics based qualitative discussion on the mechanism is presented numerically, with the time wise variation of the radial/axial velocity, pressure, and vorticity fields. The flow and vorticity dynamics are discussed quantitatively, with regard to propagation and damping of capillary waves, for the partial (full) coalescence of isopropanol (glycerol) droplet.

• 2. A scaling analysis is presented for the viscous and gravity based dampening of the oscillations of the interface during the droplet coalescence, by drawing an analogy with a freely vibrating mass-spring-damper system. The analysis demonstrates the isopropanol and glycerol droplet coalescence as underdamped and over-damped system, respectively.

• 3. For the effect of diameter D (of the isopropanol droplet) on the coalescence dynamics, our numerical study resulted in full coalescence at smaller D as well as larger D and partial coalescence at the intermediate D. Furthermore, considering the variation of non-dimensional pinch-off time $\tau _{p}$ and secondary droplet diameter ratio $\xi$ with increasing D, the partial coalescence regime is classified as viscous regime at smaller D, inertio-capillary regime at intermediate D and gravity regime at larger D. For the various regimes, a good agreement is found with the published experimental and numerical results.

• 4. For the effect of surface tension coefficient $\gamma$ of the isopropanol droplet, full coalescence at smaller $\gamma$ and partial coalescence at larger $\gamma$ is found numerically. Effect of surface tension is found on the variation of secondary droplet ratio $\xi$ but the pinch-off time $\tau _{p}$ remains almost constant. Vortex rings formed due to propagation of capillary waves are demonstrated in the surrounding fluid, with a larger strength of the surrounding vortex for full coalescence as compared to the partial coalescence cases.

• 5. Non-dimensional governing parameters Ohnesorge number Oh and Bond number Bo based regime map is presented that demarcates the combination of $Oh\,\left( 0.004-3.5\right)$ and $Bo\,\left( 0.0005-15\right)$ that leads to the partial coalescence with those for full coalescence. The critical values for the transition from partial to full coalescence is found as $Oh_{c}=0.034$ and $Bo_{c}=7.74$ for various isopropanol droplet-diameters; whereas, for various surface tension values, the critical values are $Oh_{c}=0.027\,and\,Bo_{c}=4.22$. The demarcation of the transition envelope, passing through the critical values, is found to match with a correlation proposed by Blanchette and Bigioni [12] for a liquid-liquid system. Based on this observation, it is hypothesized that the enveloping correlation is applicable for any liquid-liquid and any liquid-air droplet coalescence; and will be explored in our future study.