1 Introduction

Waterborne diseases generally spread through the consumption of contaminated water. Every year, waterborne diseases caused millions of deaths and disabilities. In particular, cholera alone caused \(100,000-120,000\) deaths globally [25]. The situation is far more serious in the developing and underdeveloped countries. In these countries, the majority of the population is deprived of clean drinking water and proper sanitary conditions. Some of the waterborne diseases (e.g., giardia, cholera, campylobacter, hepatitis A, hepatitis E, etc.) emerge periodically in different parts of the globe. Each outbreak of waterborne diseases disturbed the economy of countries where such outbreaks take place. Therefore, controlling the outbreaks of waterborne diseases is one of the major challenges of the current time. Hence, researchers and health agencies are working to develop some robust policies and programs which can help to reduce the burden of waterborne diseases.

The understanding of the transmission mechanism of an infectious disease is the primary requirement to control these diseases. The rapidly changing climatic and environmental conditions provide a conducive environment for the disease-causing agents (i.e., bacteria, viruses, etc.). Further, the human invasion of new environmental conditions, environmental pollution, and increased travel (from one part of the globe to other) provide an opportunity for disease-causing agents to survive and travel from one place to another [15]. Mathematical models are very successful in providing some crucial information about the spread of infectious diseases. Due to this, the application of mathematical models to gather key insight into the disease dynamics is an exciting research area these days. The foundation of compartmental models was led by Kermack and McKenrick in 1927. Since then, a variety of mathematical models have been formulated and deployed to study the spread of different diseases [15, 16]. Recently, some authors modify the classic SIR and SEIR models by incorporating fractional derivatives [18, 19]. The works demonstrate that the order of fractional derivatives plays an important role in the disease dynamics. Mathematical model has also been deployed to plan some optimal control strategies to control an infectious disease [1, 6, 17]. Further, the availability of vast literature of mathematical models pertaining to different infectious diseases underlines their importance in the field of epidemiology [20].

Due to their catastrophic impacts on human health and periodic occurrence, a number of mathematical models pertaining to waterborne diseases have been formulated and analyzed [10, 14, 23, 24, 26, 30, 32, 37, 40]. The primary aim of these studies is to identify the key parameters and role of different intervention strategies in controlling the outbreaks of waterborne diseases. Codeço [10] used a mathematical model to investigate the influence of the aquatic reservoir on the persistence of endemic cholera. The study also derives minimum conditions under which cholera becomes endemic and epidemic. Hartley et al. [14] modify the model proposed in [10] by introducing hyperinfectious (HI) state. The study further shows that the inclusion of HI state results in a better fit with the pattern of cholera. Tien and earn [32] extended the generic SIR model by incorporating a new compartment (W) to keep track of water to human transmission. Mukandavire et al. [23] formulate an epidemic model to estimate the value of the basic reproduction number for Zimbabwe. The model considers multiple transmission pathways (i.e., from water to human and human to human). Mukandavire et al. [24] obtained the value of the basic reproduction number for the disastrous outbreak of cholera that takes place in Haiti during 2010. To achieve this task, the author used the model proposed in [23]. Posny et al. [26] formulated a compartmental epidemic model to investigate the role of different health interventions (e.g., treatment, vaccination, and sanitation) in controlling the spread of cholera. The work conducted by Zhou et al. [37] proposed a mathematical model to understand the role of vaccination in the prevention of cholera. The study assumes that vaccination is perfect and no transmission from vaccinated class to infected class is possible, while the work carried out by Zhou et al. [40] investigates the role of vaccination by considering imperfect vaccination. As environmental conditions play an important role in the transmission of cholera, the study proposed by Sharma et al. [30] used a mathematical model to investigate the same. The model consists of a separate compartment containing individuals with lower immunity (or high disease transmission) due to the regular exposure to environmental pollution. The study concludes that environmental pollution supports the spread of the disease.

The main objective of epidemic modeling is to determine threshold conditions under which a disease can be eliminated or persist. The basic reproduction number (\(R_0\)) is a fundamental quantity whose expression is the primary requirement in the study of mathematical epidemiology. Due to this, a number of researchers used mathematical models to estimate the value of \(R_0\) for certain disease [8, 9, 23, 24]. It is believed for long that making \(R_0 < 1\) is sufficient for disease eradication while the disease will persist if \(R_0 > 1\). But the work carried out in [12] brought forth an important phenomenon known as backward bifurcation. The work carried out in [12] obtains the conditions under which a simple disease may exhibit backward bifurcation. In the case of backward bifurcation, disease eradication is not guaranteed when \(R_0 < 1\) [13]. Under the conditions of backward bifurcation, a mathematical model may exhibit complicated dynamics due to the existence of multiple equilibrium points. Consequently, many works investigate the possibility and conditions under which a mathematical model exhibits backward bifurcation (e.g., [2,3,4,5, 13, 33] and references cited therein). As the treatment plays a pivotal role in the elimination of a particular epidemic, a number of mathematical models have been used to understand the impact of treatment on the transmission mechanism of an infectious disease. In case of an outbreak, it is a common perception that every infected individual should be treated. This standard condition holds true when we have a small number of infected individuals. But, once this number increases, it will be difficult to meet this standard condition. This is due to several factors, such as the availability of hospitals and trained health workers. Due to this, a variety of treatment functions have been proposed (see Song et al. [31], Zhong and Liu [35] Zhou and Fan [36], Wang et al. [34] and references cited therein). The analysis of these models reveals that once we incorporate a nonlinear-type treatment function, the model exhibits complex dynamics despite its simple structure. This includes the existence of different bifurcations and bi-stability. Therefore, the use of such treatment functions certainly provides a clear understanding of disease transmission. In the case of a bifurcation scenario, health agencies require more effort to eliminate the disease from a region.

Despite its popularity in infectious disease models, the backward bifurcation is generally absent in waterborne pathogen models [21, 26, 27, 29, 30, 37, 40]. However, recently some mathematical models pertaining to waterborne diseases with limited treatment facilities exhibit backward bifurcation [28, 39]. This shows that there is a possibility of backward bifurcation for a waterborne disease model if it involves a saturated treatment function. In this work, we use the central manifold theorem to obtain the result on the backward bifurcation of a cholera model with a decreasing treatment function. Since the cholera outbreak mostly occurs in developing and underdeveloped countries [38], the incorporation of such treatment function is realistic. We believe that the results obtained in this work will certainly enhance the understanding of the disease dynamics.

2 Mathematical model

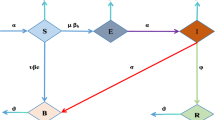
In this paper, we consider a mathematical model comprising four differential equations. The first three equations of the model system refer to the human population N(t) which is divided into three compartments, namely susceptible S(t), infected I(t), and recovered R(t). The fourth equation consists of pathogen population P(t).

$$\begin{aligned} \begin{aligned} \frac{dS}{dt} &=\Lambda - \frac{\beta S P}{L + P} - d S\\ \frac{dI}{dt} &=\frac{\beta S P}{L + P} - (r + \alpha + d) I - I g(I)\\ \frac{dR}{dt} &=r I + I g(I) - d R\\ \frac{dP}{dt} &=\theta I - \theta _0 P. \end{aligned} \end{aligned}$$
(1)

In model system (1), \(\Lambda\) represents the recruitment rate of susceptible individuals. The disease transmission rate is represented by \(\beta\), and L is the concentration of pathogens in water that yields a 50 % chance of catching the disease [10]. The natural death rate of the human population is d, and \(\alpha\) is the disease-induced mortality rate for infected individuals. Similar to the work carried out in [39], it is also assumed that infected individuals also recovered at a rate r naturally. We also assume that the growth rate of the pathogen population is directly proportional to the infected individuals and the growth rate of the pathogen population is \(\theta\) and \(\theta _0\) is the decay rate for the pathogen population. Since total medical resources are fixed and, in general, all infected individuals are equal access to the medical facilities, the treatment function is a function of the number of infected individuals. The per capita treatment rate is denoted by g(I). If g(I) is density dependent, then the number of individuals treated for a unit of time is g(I)I. Further, as discussed in [33], g(I) is satisfying the following properties:

  1. (i)

    \(g(0) > 0, \frac{dg}{dI} \ne 0,\)

  2. (ii)

    \(g(I) \ge 0\) for \(I > 0\).

Since R is not involved in any other equation of model system (1), it is sufficient to study the following reduced system

$$\begin{aligned} \begin{aligned} \frac{dS}{dt} &=\Lambda - \frac{\beta S P}{L + P} - d S\\ \frac{dI}{dt} &=\frac{\beta S P}{L + P} - (r + \alpha + d) I - I g(I)\\ \frac{dP}{dt} &=\theta I - \theta _0 P. \end{aligned} \end{aligned}$$
(2)

The study of model system (2) is performed with the following initial conditions:

$$\begin{aligned} S(0) > 0, ~~~~ I(0) \ge 0, ~~~~ P(0) \ge 0. \end{aligned}$$

Next, we give the feasible region for model system (2). First, we obtain the feasible region \(\Omega _H\) for the human population

$$\begin{aligned} \Omega _H = \left\{ (S,I): (S + I) \le \frac{\Lambda }{d}, S > 0, I \ge 0 \right\}. \end{aligned}$$

Similarly, the feasible region for the pathogen population is obtained as

$$\begin{aligned} \Omega _P = \left\{ P : P \le \frac{\theta \Lambda }{\theta _0 d} \right\}. \end{aligned}$$

Finally, the positive invariant region for model system (2) is obtained as \(\Omega = \Omega _H \times \Omega _P\).

3 The basic reproduction number

The model system possesses a unique disease-free equilibrium \(E_0 = (\frac{\Lambda }{d}, 0, 0)\). Next, we use the next-generation matrix method described in [11] to calculate the expression of the basic reproduction number (\(R_0\)). We obtain matrices F and V as

$$\begin{aligned} F = \begin{pmatrix} 0 &{} \frac{\beta \Lambda }{Ld}\\ 0&{}0 \end{pmatrix}, \quad V = \begin{pmatrix} (r + \alpha + d) + g(0) &{} 0\\ - \theta &{} \theta _0 \end{pmatrix}. \end{aligned}$$

Now, the inverse of the matrix V can be obtained as

$$\begin{aligned} V^{-1} = \frac{1}{\theta _0 \{(r + \alpha + d) + g(0) \}} \begin{pmatrix} \theta _0 &{} 0\\ \theta &{} (r + \alpha + d) + g(0) \end{pmatrix}. \end{aligned}$$

Next, we can obtain \(FV^{-1}\) as

$$\begin{aligned} FV^{-1} = \frac{1}{\theta _0 \{(r + \alpha + d) + g(0) \}} \begin{pmatrix} \frac{\beta \Lambda \theta }{Ld} &{} \frac{\beta \Lambda \theta \{(r + \alpha + d) + g(0) \}}{Ld}\\ 0&{} 0 \end{pmatrix}. \end{aligned}$$

Further, the largest eigenvalue of the matrix \(FV^{-1}\) gives the basic reproduction number (\(R_0\)). Hence,

$$\begin{aligned} R_0 = \frac{\beta \Lambda \theta }{L d \theta _0\{(r + \alpha + d) + g(0) \}}. \end{aligned}$$
(3)

4 Backward bifurcation

We use the theory of central manifold and normal forms to derive the conditions for the backward bifurcation. In particular, we use the popular result given in [7] to achieve this task.

Let us consider the following system

$$\begin{aligned} \begin{aligned} F_1 &=\Lambda - \frac{\beta S P }{L+P} - dS\\ F_2 &=\frac{\beta S P}{L + P} - (r + \alpha + d) I - I g(I)\\ F_3 &=\theta I - \theta _0 P. \end{aligned} \end{aligned}$$

Next, to explore the possibility of backward bifurcation at \(R_0 = 1\), we consider the transmission rate \(\beta\) as the bifurcation parameter. Further, we obtain the value of \(\beta\) corresponding to \(R_0 = 1\) as

$$\begin{aligned} \beta ^* = \frac{L d \theta _0 \{(r + \alpha + d) + g(0)\}}{\Lambda \theta }. \end{aligned}$$

The Jacobian of model system (2) at the disease-free equilibrium point and \(\beta = \beta ^*\) is

$$\begin{aligned} \begin{pmatrix} - d &{} 0 &{} - \displaystyle \frac{\beta \Lambda }{L d}\\ 0 &{} - (r + \alpha + d) - g(0) &{} \displaystyle \frac{\beta \Lambda }{L d}\\ 0 &{} \theta &{} - \theta _0 \end{pmatrix}. \end{aligned}$$

Next, we obtain the right eigenvector \(a = (a_1, a_2, a_3)^T\) by solving the following system of equations:

$$\begin{aligned} \begin{aligned}& - d a_1 - \left( \displaystyle \frac{\beta \Lambda }{L d}\right) a_3= 0\\ &-\left( (r + \alpha + d) + g(0) \right) a_2 + \left( \displaystyle \frac{\beta \Lambda }{L d}\right) a_3= 0\\ &\theta a_2 - \theta _0 a_3= 0 \end{aligned} \end{aligned}$$

and the same is obtained as

$$\begin{aligned} a_1 = -\left( \displaystyle \frac{\beta \Lambda }{L d^2}\right) ,~~ a_2 = \frac{\theta _0}{\theta },~~ \text {and}~~a_3 = 1. \end{aligned}$$

Similarly, the left eigenvector \(b = (b_1, b_2, b_3)\) satisfying \(a.b = 1\) can be obtained by solving the following system:

$$\begin{aligned} \begin{aligned}& -d b_1= 0\\ &-\left( (r + \alpha + d) + g(0) \right) b_2 + \theta b_3= 0 \\ &- \left( \displaystyle \frac{\beta \Lambda }{L d}\right) b_1 + \left( \displaystyle \frac{\beta \Lambda }{L d}\right) b_2 - \theta _0 b_3= 0. \end{aligned} \end{aligned}$$

Thus, we get the b as

$$\begin{aligned} b_1 = 0,~~~ b_2 = \frac{\theta \theta _0 L d}{\theta _0^{2} L d + \theta \beta \Lambda },~~ \text {and}~~~ b_3 = \frac{\theta \beta \Lambda }{\theta _0^{2} L d + \theta \beta \Lambda }. \end{aligned}$$

Now, using the result given in [7], we calculate the two bifurcation parameters \(\xi\) and \(\psi\) as

$$\begin{aligned} \xi = \sum _{k,i,j=1}^3 b_k a_i a_j \frac{\partial ^2 F_k}{\partial x_i \partial x_j}(E_0, \beta ^{*}) ~~~~~~~ \text {and}~~~~~~~~~~ \psi = \sum _{k,i=1}^3 b_k a_i\frac{\partial ^2 F_k}{\partial x_i \partial \beta }(E_0, \beta ^{*}). \end{aligned}$$

Using the left and right eigenvectors and the nonzero second-order partial derivatives, we obtain

$$\begin{aligned} \xi = - \frac{ 2 \theta \theta _0 L d}{\theta _0 ^{2} L d + \theta \beta ^* \Lambda } \left\{ \frac{\theta _0^{2}}{\theta ^2} g^{'}(0) + \frac{\beta ^* \Lambda }{L d} \right\} ~~~~~ \text {and}~~~~ \psi = \frac{\Lambda \theta \theta _0}{\theta _0^{2} L d + \theta \beta \Lambda }. \end{aligned}$$

From the expressions of \(\xi\) and \(\psi\), it is easy to observe that \(\psi\) is always positive and \(\xi\) is positive if

$$\begin{aligned} \frac{\theta _0^{2}}{\theta ^2} g^{'}(0) + \frac{\beta ^* \Lambda }{L d} < 0 \end{aligned}$$

which holds true when

$$\begin{aligned} R^* = - \displaystyle \frac{\theta _0 g^{'} (0)}{\theta \{(r + \alpha + d) + g(0)\}} > 1. \end{aligned}$$
(4)

Next, we state the following result on the backward bifurcation of model system (2).

Theorem 1

Model system (2) exhibits backward bifurcation at \(R_0 = 1\) when \(R^* > 1\), where the expression of \(R^*\) is given in equation (4).

5 Stability analysis

In this section, we obtain the condition on local stability of disease-free and endemic equilibrium points. First, we perform the stability analysis of the disease-free equilibrium point followed by endemic equilibrium point.

Theorem 2

The disease-free equilibrium point \(E_0\) is locally asymptotically stable provided \(R_0 < 1\).

Proof

As discussed in section (4), the Jacobian matrix of model system (2) around the disease-free equilibrium point \(E_0\) can be obtained as

$$\begin{aligned} M_0 = \begin{pmatrix} - d &\quad 0 &\quad - \displaystyle \frac{\beta \Lambda }{L d}\\ 0 &\quad - (r + \alpha + d) - g(0) &\quad \displaystyle \frac{\beta \Lambda }{L d}\\ 0 &\quad \theta &\quad - \theta _0 \end{pmatrix}. \end{aligned}$$

The characteristic equation of the matrix \(M_0\) is

$$\begin{aligned} (d+\lambda )\left[ \{(r+\alpha +d)+g(0)+\lambda )(\theta _{0} + \lambda )\}-\frac{\beta \Lambda \theta }{L d}\right]. \end{aligned}$$

From the above equation, it is easy to observe that one eigenvalue (\(-d\)) is negative and the remaining two eigenvalues are negative if \(R_0 < 1\). Hence, the theorem.

Next, we obtain the following result pertaining to the local stability of the endemic equilibrium point.

Theorem 3

If \(R_0 > 1\), a unique endemic equilibrium exists and is locally asymptotically stable.

Proof

From the third equation of model system (2), we obtain

$$\begin{aligned} P^* = \frac{\theta I}{\theta _0}. \end{aligned}$$

Next, using \(P^*\) in the first equation of model system (2), we get

$$\begin{aligned} S^* = \frac{(\theta _0 L + \theta I){(r + \alpha + d) + g(I)}}{\beta \theta }. \end{aligned}$$

Further, using \(P^*\) and \(S^*\) in the second equation of model system (2), we derive

$$\begin{aligned} P(I) = I H(I) - F(I) = 0 \end{aligned}$$
(5)

where

$$\begin{aligned} H(I)&= (\beta \theta + d \theta ) \{ (r + \alpha + d) + g(I)\}\\ F(I)&= \Lambda \beta \theta - d \theta _0 L \{(r + \alpha + d) + g(I)\}. \end{aligned}$$

Now, from equation (5), it is easy to note that \(lim_{I \rightarrow \infty } P(I) = \infty\) and \(P(0) = - F(0) < 0\) when \(R_0 > 1\). Therefore, we have a unique endemic equilibrium \(E^* =(S^*,I^*,P^*)\), provided \(R_0 > 1\).

Next, to deduce the local stability of the endemic equilibrium point \(E^*\), we obtain the Jacobian of model system (2) about \(E^*\). For simplicity, we introduce the following notations \(T = \frac{\beta P^*}{L+ P}, Q= \frac{\beta S^* L}{(L+P^*)^2}\) and \(R = (r + \alpha + d) + g(I)\).

Using the above notations, we obtain the Jacobian as

$$\begin{aligned} M^* = \begin{pmatrix} T- d &{} 0 &{} - Q\\ T &{} - R &{} Q\\ 0 &{} \theta &{} - \theta _0. \end{pmatrix} \end{aligned}$$

The characteristic equation of the Jacobian matrix can be obtained as

$$\begin{aligned} \lambda ^3 + a_2 \lambda ^2 + a_1 \lambda + a_0 = 0 \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} a_0 &=(T+ d) \theta _0 R\\ a_1 &=(\theta _0 R + TR + T \theta _0 + dR + d \theta _0) \\ a_2 &=(T+ R + \theta _0 + d) \end{aligned}. \end{aligned}$$

Now, using the Routh–Hurwitz criterion, all the eigenvalues of \(M^*\) have negative real part if \(a_0, a_1, a_2 > 0\) and \(a_1a_2 - a_0 > 0\). From the expressions of \(a_i s\), it is easy to observe that both the conditions are satisfied. Hence, the theorem.

6 Numerical simulation

In this section, we discuss some numerical results by considering special types of treatment functions. First, we consider the saturated treatment function \(g_1(I) = \frac{\delta _0}{1 + \delta _1 I}\), which is proposed by Zhang and Liu [35]. In this function, \(\delta _0\) is the cure rate and the parameter \(\delta _1\) gauges the effect of the delay in treatment.

Now, with the above treatment function, model system (2) can be written as

$$\begin{aligned} \begin{aligned} \frac{dS}{dt} &=\Lambda - \frac{\beta S P}{L + P} - d S\\ \frac{dI}{dt} &=\frac{\beta S P}{L + P} - (r + \alpha + d) I - \frac{\delta _0 I}{1 + \delta _1 I}\\ \frac{dP}{dt} &=\theta I - \theta _0 P. \end{aligned} \end{aligned}$$
(6)

For the above model system, the expression of the basic reproduction number is obtained as \(R_0 = \frac{\beta \Lambda \theta }{L d \theta _0 (r + \alpha + d + \delta _0)}\). Similarly, the expression of \(R^*\) can be obtained as \(R^* = \frac{\delta _1 \delta _0 \theta _0}{\theta (r + \alpha + d + \delta _0)}\).

Further, the endemic equilibrium point \(E^* = (S^*, I^*, P^*)\) can be obtained as

$$\begin{aligned} &P^* = \frac{\theta I}{\theta _0} and\\ &S^* = \frac{1}{\beta \theta } \left\{ (r + \alpha + d) + \frac{\delta _0}{1+\delta _1 I} \right\} (L \theta _0 + \theta I). \end{aligned}$$
Fig. 1
figure 1

Bifurcation diagram for model system (6)

Full size image

Now, \(I^*\) can be obtained from the following quadratic equation:

$$\begin{aligned} Q_1 I^{*2} + Q_2 I^* + Q_3 = 0 \end{aligned}$$
(7)

and \(Q_i,\)s, \(i = 1,2, ~ \& ~ 3\), has the following expressions:

$$\begin{aligned} \begin{aligned} Q_1 &=\delta _1 \theta (r + \alpha + d)(\beta + d)\\ Q_2 &=\left\{ (r + alpha + d) (\beta \theta + d \delta _1 L \theta _0 + d \theta ) + \beta \theta \delta _0 + d \theta \delta _0 - \beta \theta \Lambda \delta _1 \right\} \\ Q_3 &=d L \theta _0 (r + \alpha + d + \delta _0) (1 - R_0). \end{aligned} \end{aligned}$$

From Eq. (7), it is clear that model system (6) may have zero, one, or two endemic equilibrium points depending on the values of \(Q_i\)s. The same result is summarized in the following theorem.

Theorem 4

Model system (6) has

  1. (i)

    only one endemic equilibrium point if \(R_0 > 1\) or \(R_0 = 1\) and \(Q_2 < 0\);

  2. (ii)

    two endemic equilibrium points if \(R_0 < 1\), \(Q_2 < 0\) and \(Q_2^{2} - 4 Q_1 Q_3 > 0\);

  3. (iii)

    no endemic equilibrium point otherwise.

From Theorem (4), it is easy to conclude that multiple equilibrium points may exist for model system (6).

To explore the possibility of backward bifurcation numerically for model system (6), we use the following set of parameter values.

Table 1 Parameter values used in simulation of model system (6)
Full size table

It can be checked that for the parameter values given in Table (1), the value of \(R^* = 3.2974\) which is greater than one. Hence, the condition for the existence of backward bifurcation, stated in Theorem (1), is satisfied. And the same is also observed from Fig. 1.

Next, we consider another saturated treatment function \(g_2(I) = \frac{\delta _0}{\delta _1 + I}\) proposed by Zhou and Fan [36]. In fact, it is a modification of the treatment function proposed by Zhang and Liu [35] (studied in model system (6)). This function considers that the supply of medical resources (\(\delta _0\)) also plays an important role. In this function, \(\delta _0\) measures the maximal supply of medical resources and \(\delta _1\) is half saturation constant.

Similar to model system (6), model system (2) with the treatment function \(g_2\) can be written as

$$\begin{aligned} \begin{aligned} \frac{dS}{dt} &=\Lambda - \frac{\beta S P}{L + P} - d S\\ \frac{dI}{dt} &=\frac{\beta S P}{L + P} - (r + \alpha + d) I - \frac{\delta _0 I}{\delta _1 + I}\\ \frac{dP}{dt} &=\theta I - \theta _0 P. \end{aligned} \end{aligned}$$
(8)

Now, using expression (3), the expression of the basic reproduction number is obtained as \(R_0 = \frac{\beta \Lambda \theta \delta _1}{L d \theta _0 \lbrace \delta _1 (r + \alpha + d + \delta _0 \rbrace }.\). Similarly, the expression of \(R^*\) can be obtained as \(R^* = \frac{\delta _0 \theta _0}{\delta _1 \theta \lbrace (r + \alpha + d + \delta _0 \rbrace }.\).

Fig. 2
figure 2

Bifurcation diagram for model system (8)

Full size image

The endemic equilibrium point can be obtained using a similar calculation performed for model system (6). Therefore, we obtain the components of the endemic equilibrium point \(E^* = (S^*, I^*, P^*)\) as

$$\begin{aligned} P^* = \frac{\theta I}{\theta _0} and \\ S^* = \frac{1}{\beta \theta } \left\{ (r + \alpha + d) + \frac{\delta _0}{\delta _1+ I} \right\} (L \theta _0 + \theta I). \end{aligned}$$

Now, \(I^*\) can be obtained from the following quadratic equation

$$\begin{aligned} R_1 I^{*2} + R_2 I^* + R_3 = 0 \end{aligned}$$
(9)

where \(R_1, R_2\) and \(R_3\) have the following expressions:

$$\begin{aligned} \begin{aligned} R_1 &=\theta (r + \alpha + d)(\beta + d)\\ R_2 &=\left\{ (r + alpha + d) (\beta \theta + d L \theta _0 + d \theta \delta _1 ) + \beta \theta \delta _0 + d \theta \delta _0 - \beta \theta \Lambda \right\} \\ R_3 &=d L \theta _0 \lbrace \delta _1 (r + \alpha + d + \delta _0 \rbrace (1 - R_0). \end{aligned} \end{aligned}$$

Now, the following theorem ascertains the possible number of endemic equilibrium points for model system (8).

Theorem 5

Model system (6) has

  1. (i)

    only one endemic equilibrium point if \(R_0 > 1\) or \(R_0 = 1\) and \(R_2 < 0\);

  2. (ii)

    two endemic equilibrium points if \(R_0 < 1\), \(R_2 < 0\) and \(R_2^{2} - 4 R_1 R_3 > 0\);

  3. (iii)

    no endemic equilibrium point otherwise.

The result stated in Theorem (5) speculates about the possibility of the existence of multiple equilibrium points.

To inquire about the possibility of backward bifurcation numerically for model system (8), we use the parameter set given in Table 2.

Table 2 Parameter values used in simulation of model system (6)
Full size table

For the parameter set given in Table 2, it can be checked that the value of \(R^*\) is 1.0994. Hence, the condition under which model system (8) exhibits backward bifurcation [see Theorem (1)] is satisfied. And the same is confirmed from Fig. 2.

7 Conclusion

A general nonlinear cholera model with treatment has been formulated and analyzed. In general, the outbreaks of cholera take place in developing and underdeveloped countries. In these countries, the availability of medical resources is not up to the mark [22]. Moreover, each outbreak of cholera results in a surge of patients, which creates a huge burden on the limited medical facilities of such countries. Therefore, to make the model realistic, we consider a treatment function g(I) such that \(g(0) = 0\) and \(\frac{dg}{dI} \ne 0\) and \(g(I) \ge 0\) for \(I > 0\). In particular, the analysis of the proposed model reveals that the backward bifurcation occurs if the treatment function g(I) is decreasing. The result obtained on backward bifurcation shows that the model exhibits backward bifurcation for a large class of treatment functions satisfying the above conditions. Despite its celebrated place in the epidemic models, backward bifurcation is not so popular in mathematical models pertaining to waterborne diseases. To the best of our knowledge, there are very few models that exist in the literature addressing the backward bifurcation for a cholera model [28, 39]. The biological importance of the current work lies in the fact that it provides a general condition for the occurrence of backward bifurcation in a cholera model with a nonlinear treatment function. The occurrence of backward bifurcation leads to the existence of multiple equilibrium points. In such a scenario, the classical condition of disease eradication (i.e., making \(R_0 < 1\)) will not work and the number of infected individuals at the initial time also plays an important role.

The result obtained in this work is of particular interest for the region where medical facilities are limited which is largely true for cholera. Therefore, the current work can be utilized to frame some robust policies to reduce the impact of outbreaks of fatal waterborne disease cholera.