Numerical simulation of periodic MHD casson nanofluid flow through porous stretching sheet

Abstract

The perspective of this paper is to characterize a Casson type of Non-Newtonian fluid flow through heat as well as mass conduction towards a stretching surface with thermophoresis and radiation absorption impacts in association with periodic hydromagnetic effect. Here heat absorption is also integrated with the heat absorbing parameter. A time dependent fundamental set of equations, i.e. momentum, energy and concentration have been established to discuss the fluid flow system. Explicit finite difference technique is occupied here by executing a procedure in Compaq Visual Fortran 6.6a to elucidate the mathematical model of liquid flow. The stability and convergence inspection has been accomplished. It has observed that the present work converged at, P_r ≥ 0.447 indicates the value of Prandtl number and L_e ≥ 0.163 indicates the value of Lewis number. Impact of useful physical parameters has been illustrated graphically on various flow fields. It has inspected that the periodic magnetic field has helped to increase the interaction of the nanoparticles in the velocity field significantly. The field has been depicted in a vibrating form which is also done newly in this work. Subsequently, the Lorentz force has also represented a great impact in the updated visualization (streamlines and isotherms) of the flow field. The respective fields appeared with more wave for the larger values of magnetic parameter. These results help to visualize a theoretical idea of the effect of modern electromagnetic induction use in industry instead of traditional energy sources. Moreover, it has a great application in lung and prostate cancer therapy.

1 Introduction

This is indispensable to study the non-Newtonian type of fluid in order to the vast application of engineering, especially in manufacturing processes and industry. But it is impossible to establish a liner model to express this type of fluid in fluid dynamics because of non-linearity pattern of this fluid. Researcher proposed a number of complex models to explain different type of fluid which carried the non-Newtonian mechanism. Casson liquid exemplary is one of them which was at first introduced by Casson [1] at 1959 in case of pigment-oil. Basically, scientist focused on these rheological characteristics type fluid owing to significant application in arena of bioengineering, metallurgy, drilling, and food industry. Therefore, Shima et al. [2] investigated gas bubble behavior in Casson fluid by using numerical calculation. The Casson fluid flow (entry and exit) is examined by Pham et al. [3]. Recently, Mukhopadhyay et al. [4] analyzed Casson fluid for unsteady periphery layer drift on a widening surface with the help of similarity transformation. It was found that the velocity field declines with swelling value of Casson factor. Chemically reactive types Casson fluid model was inspected by Makanda et al. [5] by using Runge–Kutta-Fehlberg (RKF) scheme. Akbar and Butt [6] explored Casson fluid property in consider with peristaltic type motion of this fluid. Tamoor et al. [7] explored a numerical model of Casson fluid with combined effect of MHD on stretching cylinder. Recently, lReddy et al. [8] worked on entropy generation from Casson liquid drift on a radiative type vertical cylinder where implicit technique is used to solve non-linear time dependent couple equation. Hussanam et al. [9] achieved an arithmetical elucidation of Casson fluid with MHD effect in porous medium applying Laplace transform. It was found that velocity field suppresses with an increase of Casson parameter. Later, Abro and Khan [10] inspected the tide of Casson liquid over a vacillating plumb plate in permeable medium. Numerical solution of the same fluid by the effect of chemical reaction on a distending piece was observed by the author Khan et al. [11]. Ullah et al. [12] explored in terms of liquid flow over non-linearity stretching sheet by applying Keller-box method where Soret and Dufour influence was considered. Moreover, by using RKF 4^th-5^th power align with shooting method, Kumar et al. [13] analyzed non-linear radiative type Casson flow over perpendicular with plate. Khan et al. [14] examined Homogeneous and heterogeneous types of fluid on a stretching sheet. However, the nanoparticles interaction were observed in Casson fluid [15] and it was discovered that thermal radiation accelerated the heat transfer rate significantly. Again, Khan et al. [16] inspected the behavior of Casson fluid with the assistance of Newtonian heating where Sodium Alginate was used as nanoparticle. In addition, the flow characteristics of a Rayleigh-Bénard Convection (RBC) Casson fluid were investigated by Aghighia et al. [17].

Moreover, numerically Runge–Kutta based shooting technique gives more accurate and stable outcomes. Because of that nature, the simulation of the following authors [18,19,20,21] was carried out numerically by Runge–Kutta based shooting technique. It has been investigated that single wall carbon nanotubes transfer low heat rather than double wall carbon nanotubes. However, the flow characteristics of the Casson fluid was also analyzed by considering the physical impact of slip, Stefan blowing, and thermal radiation on a shrinking/stretching surface. The stability of Darcy-Forchheimer Casson nanofluid drift was also been inspected. Again on a vertical surface, Sulochana and Poornima [22] have inspected the drift of Casson nanofluid with the impression of Hall current. It was concluded that the heat transfer characteristics of Casson fluid is superior to the Newtonian fluid. However, the heat transfer characteristics of Newtonian nanofluid has been discussed extensively recently by many authors. For details, one can refer to the following inspections [23]. Nanomaterial mixed with Casson fluid flow in oblique manner effect of convection boundary condition was analyzed by Nadeem et al. [24]. Malik et al. [25] found a solution of Casson nanofluid by applying RKF method where fluid flow was investigated on exponentially stretching cylinder. After that, Abolbashari et al. [26] explored the same nanofluid on stretching surface for entropy generation.

In 1962, Turcotte and Lyons [27] first introduced the periodic boundary layer flow of MHD. Then Sadiqa et al. [28] conducted research on this condition by the help of implicit FDM formulation. Recently, Reza-E-Rabbi et al. [29] and Biswas et al. [30] determined numerical solution of periodic MHD effect on Casson and Jeffery nanofluid using explicit finite difference method (EFDM). A detail simulation of Newtonian and non-Newtonian fluids flow have been presented in their work by considering diverse physical quantity. Other researchers have also applied the same method to study different types of fluid flow, we mention the significant contributions of the following authors [31].

The above-discussed work on Casson nanofluid flow has motivated us to conduct our research. Most of the works were related to the regular pattern of magnetic field. The novel purpose of this work is to use the periodic effect of MHD on Casson nanofluid flow. The magnetic field is considered herein sinusoidal form. The updated visualization of the fluid flow has been presented in this work in vibrating form. Moreover, the velocity fields are exhibited here in sinusoidal form to discuss the impact of various physical parameters like Casson fluid, magnetic field, Darcy number, chemical reaction and thermophoresis. It is also noticed that Lorentz force behaves in a significant way when the values of magnetic parameter develop. However, it is also analyzed from the velocity field that due to the presence of periodic magnetic field, the interaction between the nanoparticles got increased. These discussed incidents represent the novel inspection of this work. Again, the current work has great application in the field of medical science. Nowadays, nanoparticles are used in cancer therapy, and it has also seen that with the presence of periodic magnetic field, it is easier to control the nanoparticles. In modern era, nanoparticles are used for the treatment of lung cancer and prostate cancer. Moreover, we know the MHD play a vital role in nanofluid flow for the development of industrial application as well as cooling gadget in reactor analysis. However, the current work has been described in the following way.

• Firstly, a time dependent fundamental set of equations, i.e. momentum, energy and concentration have been established to discuss the fluid flow system. Then it is solved numerically by imposing an explicit scheme.

• Then we have examined the accuracy of optimizing parameters by performing the stability and convergence test.

• Further, we have explored the behavior of different physical parameters in vibrating form on velocity profiles as well as the usual form is also depicted on the temperature and concentration profiles.

• Finally, some systemic profiles are also illustrated on different physical fields. Moreover, the updated visualization of the flow field is also exhibited through streamlines and isothermal lines.

2 Mathematical fluid flow model

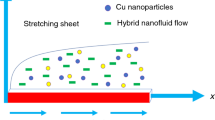
The transportation of incompressible Casson fluid with nanoparticles are explored with the impression of thermal radiation, radiation absorption, chemical reaction, heat generation and periodic MHD through a porous stretching sheet. The flow is considered here as a time dependent flow. The applied uniform magnetic field is taken as ${\text{B}}_{y} { = }\,{\text{B}}_{{0}} {\text{sin}}\left( {{\pi x}/{\uplambda }} \right)$(where,${\text{B}}_{{0}}$ is constants) [29]. The fluid flow takes place at y = 0 While, $u = U_{0} = bx$ is the stretching velocity and b is the constant. $T( = T_{\infty } )$ and $C( = C_{\infty } )$ represent the fluid temperature and concentration away from the wall surface respectively. For Casson fluid flow the rheological equation can be considered as [31],

$$ \tau_{ij} = \left\{ {\begin{array}{*{20}c} {2\left(k_{c} + \frac{{\tau_{0} }}{{\sqrt {2\pi } }}\right)e_{ij} \,\,\,\,if\,\,\,\pi > \pi_{c} } \\ {2\left(k_{c} + \frac{{\tau_{0} }}{{\sqrt {2\pi_{c} } }}\right)e_{ij} \,\,\,\,if\,\pi < \pi_{c} \,} \\ \end{array} } \right. $$

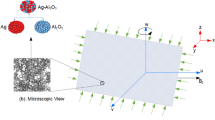
where $e_{ij} = \frac{1}{2}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)$ is strain tensor rate,$\tau_{ij}$, stress tensor element, $k_{c}$,viscosity factor, $\pi_{cc} = e_{ij}$,strain tensor product rate, $\pi_{c}$, critical value for rate of strain tensor, $\tau_{0}$ is output stress and $u_{i}$, velocity components (Fig. 1).

Fig.1

Image of a fluid flow in terms of physical patent [30]

Under these assumptions the governing equations in the dimensional form are considered as, [29]

Continuity equation:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0 $$

(1)

Momentum equation:

$$ \begin{aligned} \frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = & \upsilon \left( {1 + \frac{1}{{k_{c} \sqrt {2\pi_{c} } /\tau_{0} }}} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + g\beta (T - T_{\infty } ) + g\beta^{*} (C - C_{\infty } ) \\ & - \frac{{\sigma B_{0}^{2} }}{\rho }\sin^{2} (\pi x)u - \frac{\upsilon }{K^{\prime}}u \\ \end{aligned} $$

(2)

Energy equation:

$$ \begin{aligned} \frac{\partial T}{{\partial t}} + u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = & \frac{\kappa }{{\rho \,c_{p} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{\upsilon }{{\,c_{p} }}\left( {1 + \frac{1}{{k_{c} \sqrt {2\pi_{c} } /\tau_{0} }}} \right)\left( {\frac{\partial u}{{\partial y}}} \right)^{2} - \frac{1}{{\rho \,c_{p} }}\frac{{\partial q_{r} }}{\partial y} + \frac{{Q_{0} }}{{\rho \,c_{p} }}(T_{w} - T_{\infty } ) \\ & + \frac{{Q_{1}^{*} }}{{\rho \,c_{p} }}(C_{w} - C_{\infty } ) + \tau \left\{ {D_{B} \left( {\frac{\partial T}{{\partial y}}\frac{\partial C}{{\partial y}}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right\} \\ \end{aligned} $$

(3)

Concentration equation:

$$ \frac{\partial C}{{\partial t}} + u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial y^{2} }}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - K_{c} (C - C_{\infty } )^{P} $$

(4)

with,

$$ \begin{gathered} t = 0,u = bx,\,v = 0,\,T = T_{w} ,\,\,C = C_{w} \,\,\,\,{\text{every}}\,{\text{where}} \hfill \\ t \ge 0,\,u = 0,v = 0,T = T_{\infty } ,C = C_{\infty } \,\,\,\,\,\,\,{\text{at}}\,\,\,\,\,\,x = 0 \hfill \\ u = U_{0} = bx,\,v = 0,\,T = T_{w} ,\,\,C = C_{w} \,\,\,\,{\text{at}}\,\,\,\,\,\,y = 0\, \hfill \\ u = 0,T \to T_{\infty } ,\,C \to C_{\infty } \,\,{\text{at}}\,\,\,\,\,\,y \to \infty \, \hfill \\ \end{gathered} $$

(5)

wherever velocity element is symbolized by u and v, factor of magnetic field is indicated by B₀, coefficient in terms of thermal is symbolized by β, T_w is wall temperature, β^*, concentration expansion, C_w, species concentration, b is the stretching constant, ʋ, kinematic viscosity, κ, thermal conductivity, $\tau = (\rho c)_{p} /(\rho c)_{f}$,here numerator indicate the capacity of heat mixed with nanoparticle type materials and denominator indicate the capacity of heat of fluid and $\alpha = k_{c} \sqrt {2\pi_{c} } /\tau_{0}$ is non-Newtonian Casson factor, ρ is density.

3 Mathematical formulation

The dimensional Eqs. (1, 2, 3, 4, 5) must be founded in a finite-difference manner, and it is vital to find the solution with no dimension. Due to that fact, the subsequent dimensionless quantities are considered as, [30, 31, 33]

$$ u = \frac{\upsilon }{\lambda }Gr^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} U,v = \frac{\upsilon }{\lambda }Gr^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}}} V,Y = \frac{y}{\lambda }Gr^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}}} ,X = \frac{x}{\lambda },\tau = \frac{\upsilon }{{\lambda^{2} }}Gr^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} t,\,\phi = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }},\,\theta = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}. $$

where Gr = Grashof number, λ = wave length, τ = dimensionless time, φ = dimensionless concentration, θ = dimensionless temperature, U = V = dimensionless velocity component, u = v = dimensional velocity, t = dimensional time.

Hence the fundamental equations turn into the following form,

Continuity equation:

$$ \frac{\partial U}{{\partial X}} + \frac{\partial V}{{\partial Y}} = 0 $$

(6)

Momentum equation:

$$ \frac{\partial U}{{\partial \tau }} + U\frac{\partial U}{{\partial X}} + V\frac{\partial U}{{\partial Y}} = \left(1 + \frac{1}{\alpha }\right)\frac{{\partial^{2} U}}{{\partial Y^{2} }} - M^{2} \sin^{2} (\pi x)U + Gr\varphi \,\, + Gm\theta - \frac{1}{Da}U $$

(7)

Energy equation:

$$ \begin{aligned} \frac{\partial \theta }{{\partial \tau }} + U\frac{\partial \theta }{{\partial X}} + V\frac{\partial \theta }{{\partial Y}} = & \frac{1}{\Pr }\left( {1 + \frac{4}{3}R} \right)\frac{{\partial^{2} \theta }}{{\partial Y^{2} }} + Q\theta + Q_{1} \phi + N_{b} \left( {\frac{\partial \theta }{{\partial Y}}.\frac{\partial \varphi }{{\partial Y}}} \right) + N_{t} \left( {\frac{\partial \theta }{{\Delta Y}}} \right)^{2} \\ & + (1 + \frac{1}{\alpha }\,)E_{c} \left( {\frac{\partial U}{{\partial Y}}} \right)^{2} \\ \end{aligned} $$

(8)

Concentration equation:

$$ \frac{\partial \varphi }{{\partial \tau }} + U\frac{\partial \varphi }{{\partial X}} + V\frac{\partial \varphi }{{\partial Y}} = \frac{1}{{L_{e} }}\left[ {\frac{{\partial^{2} \varphi }}{{\Delta Y^{2} }} + \left( {\frac{{N_{t} }}{{N_{b} }}} \right)\frac{{\partial^{2} \theta }}{{\Delta Y^{2} }}} \right] - K_{r} \phi^{P} $$

(9)

With corresponding boundary conditions,

$\begin{gathered} \tau \le 0,U = 0,V = 0,\theta = 0,\varphi = 0\,\,\,{\text{every}}\,{\text{where}} \hfill \\ \tau > 0,U = 0,V = 0,\theta = 0,\varphi = 0\,\,\,{\text{at}}\,X = 0 \hfill \\ \end{gathered}$.

$$ \begin{gathered} U = 1,\,\,\,\theta = 1,\,\,\varphi = 1\,\,\,\,\,at\,\,\,\,\,\,y = 0 \hfill \\ U = 0,\,\,\theta = 0,\,\varphi = 0\,\,\,\,\,at\,\,\,\,\,\,y \to \infty \, \hfill \\ \end{gathered} $$

(10)

where, magnetic parameter, $M = \frac{{\sigma^{^{\prime}} B_{0}^{2} \lambda^{3} }}{{\rho \upsilon^{2} }}$, Grashof number,$G_{r} = \frac{{g\beta_{T} \left( {T_{w} - T_{\infty } } \right)\lambda^{3} }}{{\upsilon^{2} }}$,mass Grashof number $G_{c} = \frac{{g\beta_{c} \left( {C_{w} - C_{\infty } } \right)\lambda^{3} }}{{\upsilon^{2} }}$, Darcy number, $D_{a} = \frac{{K^{\prime}U_{0}^{2} }}{{\upsilon^{2} }}$, Prandtl number, $P_{r} = \frac{{\rho \,c_{p} \upsilon }}{\kappa }$, radiation parameter,$R = \frac{{4\sigma_{0} T_{\infty }^{3} }}{{\kappa (a + \sigma_{s} )}}$, heat source parameter,$Q = \frac{{Q_{0} \upsilon }}{{U_{0}^{2} \rho \,c_{p} }}$, radiation absorption parameter, $Q_{1} = \frac{{Q_{1}^{*} \upsilon }}{{U_{0}^{2} \rho \,c_{p} }}$, Eckert number, $E_{c} = \frac{{U_{0}^{2} }}{{c_{p} (T_{w} - T_{\infty } )}}$, Dufour number, $D_{u} = \frac{{D_{m} \kappa_{T} }}{{c_{s} c_{p} \upsilon }}\left( {\frac{{C_{w} - C_{\infty } }}{{T_{w} - T_{\infty } }}} \right)$, Lewisl number, $L_{e} = \frac{\upsilon }{{D_{m} }}$, thermophoresis parameter, $N_{t} = \frac{{\tau D_{T} }}{{T_{\infty } \upsilon }}(T_{w} - T_{\infty } )$, Brownianl parameter,$N_{b} = \frac{{\tau D_{B} (C_{w} - C_{\infty } )}}{\upsilon }$, chemicall reaction, $K_{r} = \frac{{\upsilon K_{c} (C_{w} - C_{\infty } )^{p - 1} }}{{U_{0}^{2} }}$ and Power of chemical reaction is indicated by Pl.

Stream function $\psi$ contents the equation of continuity and is allied with the speed parts in customary way as,

$U = \frac{\partial \psi }{{\partial Y}},\,V = - \frac{\partial \psi }{{\partial X}}$.

The factors of scientific attention due to the current problem are the native skin-friction local Sherwood and Nusselt number, which are elucidated as:

Skin-friction,$C_{f} Gr^{ - 3/4} = - \left( {1 + \frac{1}{\alpha }} \right)\left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0}$,

Sherwood number, $S_{h} = \frac{1}{2\sqrt 2 }G_{r}^{ - 3/4} \left( {\frac{\partial \phi }{{\partial Y}}} \right)_{Y = 0} .$

Nusselt number, $N_{u} Gr^{ - 1/4} = \left( {1 + \frac{4}{3}Rd} \right)\left( {\frac{\partial \theta }{{\partial y}}} \right)_{y = 0}$.

4 Numerical analysis of the model

The implementation of an explicit technique has been done for Eqs. (6, 7, 8, 9, 10). A fluid flow field is being considered in a rectangular form where the gridlines are distributed (Fig. 2). For this investigations, the following thing is taken into consideration.

Fig. 2

The finite scheme grid [31]

Grid distance: n = 200, m = 200, Plates level: Y_max = 50, X_max = 20 as Y → ∞,

Mesh shape: $\Delta X = 0.2\left( {0 \le X \le 20} \right),\,\,\,\Delta Y = 0.25\left( {0 \le Y \le 50} \right)$.Time difference: Δτ = 0.005.

Hence Eqs. (6, 7, 8, 9, 10) converted into the following form,

Equation of continuity:

$$ \frac{{U^{\prime}_{i,j} - U^{\prime}_{i - 1,j} }}{\Delta X} + \frac{{V_{i,j} - V_{i,j - 1} }}{\Delta Y} = 0 $$

(11)

Equation in terms of momentum:

$$ \begin{aligned} \frac{{U^{\prime}_{i,j} - U_{i,j} }}{\Delta \tau } & + U_{i,j} \frac{{U_{i,j} - U_{i - 1,j} }}{\Delta X} + V_{i,j} \frac{{U_{i,j + 1} - U_{i,j} }}{\Delta Y} = (1 + \frac{1}{\alpha }\,)\frac{{\left( {U_{i,j + 1} - 2.0\,U_{i,j} + U_{i,j - 1} } \right)}}{{\left( {\Delta Y} \right)^{2} }} \\ & - M^{2} sin^{2} \left( {\pi X(i)} \right)U_{i,j} + Gm\,\varphi_{i,j} + Gr\theta_{i,j} \,\, - \frac{1}{{D_{a} }}U_{i,j} \\ \end{aligned} $$

(12)

Equation in terms of energy:

$$ \begin{aligned} \frac{{\theta^{\prime}_{i,j} - \theta_{i,j} }}{\Delta \tau } + U_{i,j} \frac{{\theta_{i,j} - \theta_{i - 1,j} }}{\Delta X} + V_{i,j} \frac{{\theta_{i,j + 1} - \theta_{i,j} }}{\Delta Y} = & \left( {1 + \frac{4}{3}R} \right)\frac{1}{{P_{r} }}\frac{{\theta_{i,j + 1} - 2\theta_{i,j} + \theta_{i,j - 1} }}{{\left( {\Delta Y} \right)^{2} }}{\text{ + Q}}\theta_{i,j} \\ + & Q1\varphi_{i,j} { + }(1 + \frac{1}{\alpha }\,)E_{c} \left( {\frac{{U_{i,j + 1} - U_{i,j} }}{\Delta Y}} \right)^{2} { + }Nb\left( {\left( {\frac{{\theta_{i,j + 1} - \theta_{i,j} }}{\Delta Y}} \right)\left( {\frac{{\varphi_{i,j + 1} - \varphi_{i,j} }}{\Delta Y}} \right)} \right) \\ & { + }Nt\left( {\frac{{\theta_{i + 1,j} - \theta_{i,j} }}{\Delta Y}} \right)^{2} \\ \end{aligned} $$

(13)

Equation in terms of concentration:

$$ \begin{aligned} \frac{{\phi_{i,j}^{^{\prime}} - \phi_{i,j} }}{\Delta \tau } + U_{i,j} \frac{{\phi_{i,j} - \phi_{i - 1,j} }}{\Delta X} + V_{i,j} \frac{{\phi_{i,j + 1} - \phi_{i - 1,j} }}{\Delta Y} &= - K_{r} (\phi_{i,j} )^{P} \frac{1}{{L_{e} }}\left[\frac{{\phi_{i,j + 1} - 2\phi_{i,j} + \phi_{i,j - 1} }}{{(\Delta Y)^{2} }} \right.\\ &\quad\left. + \left( {\frac{{N_{t} }}{{N_{b} }}} \right)\frac{{\theta_{i,j + 1} - 2\theta_{i,j} + \theta_{i,j - 1} }}{{(\Delta Y)^{2} }}\right] \\ \end{aligned} $$

(14)

with

$$ U(i,j) = 1,\,\,V(i,j) = 0,\,\theta (i,j) = 1,\,\,\varphi (i,j) = 1\,\,{\text{at}}\,\,y = 0 $$

$$ U(i,j) \to 0,\,\,\theta (i,j) \to 0,\,\,\overline{\varphi } (i,j) \to 0\,\,\,{\text{as}}\,y \to \infty $$

(15)

Here, subscript $i\,,j$ and superscript n represents grid points with $X\,and\,Y$ co-ordinate and the value of time $\tau$ respectively, where $\tau = n\Delta \tau ,\,n = \,1,2,3,\ldots$.

5 Stability test and convergence criteria of the model

Meanwhile, an explicit procedure is being applied, so that to complete the analysis, it is badly needed discussion about the stability and convergence of explicit finite difference scheme. On behalf of persistent lattice sizes, the stability criteria of the system may be introduced as follows.

The Eq. (11) is not considered since Δτ is absent. The common parameters of known lFourier expansion for U, θ and φ at fixed time randomly called t = 0 are all $e^{i\alpha X} e^{i\beta Y}$, separately from a constant, where,$i = \sqrt { - 1}$. At time t = τ, these relations become; [32, 34]

$$ \left. \begin{gathered} U:\psi (\tau )e^{i\alpha X} e^{i\beta Y} \hfill \\ \theta :\theta (\tau )e^{i\alpha X} e^{i\beta Y} \hfill \\ \varphi :\varphi (\tau )e^{i\alpha X} e^{i\beta Y} \hfill \\ \end{gathered} \right\} $$

(16)

And later the time-phased changes these relations become;

$$ \left. \begin{gathered} U^{\prime}:\psi^{\prime}(\tau )e^{i\alpha X} e^{i\beta Y} \hfill \\ \theta^{\prime}:\theta^{^{\prime}} (\tau )e^{i\alpha X} e^{i\beta Y} \hfill \\ \varphi^{\prime}:\varphi^{^{\prime}} (\tau )e^{i\alpha X} e^{i\beta Y} \hfill \\ \end{gathered} \right\} $$

(17)

Now substituting (16) and (17) in the above Eqs. (12, 13, 14, 15), the resulting equations over simplified have been obtained as;

Momentum equation:

$$ \begin{aligned} \frac{{\psi^{\prime}(\tau ) - \psi (\tau )}}{\Delta \tau } + U\frac{{\psi (\tau )(1 - e^{ - i\beta \Delta Y} )}}{\Delta X} + V\frac{{\psi (\tau )(e^{i\beta \Delta Y} - 1)}}{\Delta Y} = & G_{r} \theta (\tau ) + G_{m} \phi (\tau ) - \psi (\tau )M^{2} Sin^{2} X(i) \\ & - \frac{1}{{D_{a} }}\psi (\tau ) + \left( {1 + \frac{1}{\alpha }} \right)\frac{2\psi (\tau )(\cos \beta \Delta Y - 1)}{{(\Delta Y)^{2} }} \\ \end{aligned} $$

$$ \begin{aligned} \psi^{\prime}(\tau ) - \psi (\tau ) = & \Delta \tau G_{r} \theta (\tau ) + \Delta \tau G_{m} \phi (\tau ) - \Delta \tau \psi (\tau )M^{2} Sin^{2} X(i) - \frac{1}{{D_{a} }}\Delta \tau \psi (\tau ) \\ + \left( {1 + \frac{1}{\alpha }} \right)\frac{2\psi (\tau )\Delta \tau (\cos \beta \Delta Y - 1)}{{(\Delta Y)^{2} }} - U\frac{{\Delta \tau \psi (\tau )(1 - e^{ - i\beta \Delta Y} )}}{\Delta X} - V\frac{{\Delta \tau \psi (\tau )(e^{i\beta \Delta Y} - 1)}}{\Delta Y} \\ \end{aligned} $$

$$ \begin{aligned} \psi \prime (\tau ) = & \psi (\tau )\Delta \tau [1 - U\frac{{(1 - e^{ - i\beta \Delta Y} )}}{\Delta X} - V\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y} - M^{2} {\text{Sin}}^{2} X(i) - \frac{1}{{D_{a} }} \\ & + \left( {1 + \frac{1}{\alpha }} \right)\frac{2(\cos \beta \Delta Y - 1)}{{(\Delta Y)^{2} }} + \Delta \tau G_{r} \theta (\tau ) + \Delta \tau G_{m} \varphi (\tau ) \\ \end{aligned} $$

$$ \psi^{\prime} = A_{1} \psi + A_{2} \theta + A_{3} \varphi $$

(18)

$$ A_{1} = \Delta \tau \left[ {1 - U\frac{{(1 - e^{ - i\beta \Delta Y} )}}{\Delta X} - V\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y} - M^{2} Sin^{2} X(i)} \right.\left. { - \frac{1}{{D_{a} }} + \left( {1 + \frac{1}{\alpha }} \right)\frac{2(\cos \beta \Delta Y - 1)}{{(\Delta Y)^{2} }}} \right] $$

$A_{2} = G_{r} \Delta \tau$ and $A_{3} = G_{m} \Delta \tau$.

Energy equation:

$$ \begin{aligned} \frac{{\theta^{\prime}(\tau ) - \theta (\tau )}}{\Delta \tau } & + U\frac{{\theta (\tau )(1 - e^{ - i\alpha \Delta X} )}}{\Delta X} + V\frac{{\theta (\tau )(e^{i\beta \Delta Y} - 1)}}{\Delta Y} = \frac{1}{{P_{r} }}(1 + \frac{4}{3}R)\frac{2\theta (\tau )(\cos \beta \Delta Y - 1)}{{(\Delta Y)^{2} }} + Q\theta (\tau ) \\ + Q_{1} \theta (\tau ) + \left( {1 + \frac{1}{\alpha }} \right)E_{c} \left( {\frac{{\theta (\tau )(e^{i\beta \Delta Y} - 1)}}{\Delta Y}} \right)^{2} + Nb\left( {\frac{{\theta (\tau )(e^{i\beta \Delta Y} - 1)}}{\Delta Y}} \right)^{2} + Nt\left( {\frac{{\theta (\tau )(e^{i\alpha \Delta X} - 1)}}{\Delta Y}} \right)^{2} \\ \end{aligned} $$

$$ \begin{aligned} \theta^{\prime}(\tau ) = & \theta (\tau )\Delta \tau \left[ 1 \right. - U\frac{{(1 - e^{ - i\alpha \Delta X} )}}{\Delta X} - V\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y}\frac{1}{{P_{r} }}(1 + \frac{4}{3}R)\frac{2(\cos \beta \Delta Y - 1)}{{(\Delta Y)^{2} }} + Q \\ + \left( {1 + \frac{1}{\alpha }} \right)E_{c} \left( {\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y}} \right)^{2} + \theta (\tau )Nb\left( {\frac{{\varphi (\tau )(e^{i\beta \Delta Y} - 1)}}{\Delta Y}} \right)^{2} + \theta (\tau )Nt\left( {\frac{{(e^{i\alpha \Delta X} - 1)}}{\Delta Y}} \right)^{2} ] + Q_{1} \varphi (\tau ) \\ \end{aligned} $$

$$ \theta ^{\prime} = A_{4} \theta + A_{5} \varphi $$

(19)

$$ \begin{aligned} A_{4} = & \Delta \tau \left[ 1 \right. - U\frac{{(1 - e^{ - i\alpha \Delta X} )}}{\Delta X} - V\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y}\frac{1}{{P_{r} }}(1 + \frac{4}{3}R)\frac{2(\cos \beta \Delta Y - 1)}{{(\Delta Y)^{2} }} + Q \\ & + \left( {1 + \frac{1}{\alpha }} \right)E_{c} \left( {\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y}} \right)^{2} + \theta (\tau )Nb\left( {\frac{{\varphi (\tau )(e^{i\beta \Delta Y} - 1)}}{\Delta Y}} \right)^{2} + \theta (\tau )Nt\left( {\frac{{(e^{i\alpha \Delta X} - 1)}}{\Delta Y}} \right)^{2} ] \\ \end{aligned} $$

$$ A_{5} = Q_{1} \varphi (\tau ) $$

Concentration equation:

$$ \begin{aligned} \frac{{\varphi_{i,j}^{^{\prime}} - \varphi_{i,j} }}{\Delta \tau } + U_{i,j} \frac{{\varphi_{i,j} - \varphi_{i - 1,j} }}{\Delta X} + V_{i,j} \frac{{\varphi_{i,j + 1} - \varphi_{i - 1,j} }}{\Delta Y} = & - K_{r} (\varphi_{i,j} )^{P} \frac{1}{{L_{e} }}[\frac{{\varphi_{i,j + 1} - 2\varphi_{i,j} + \varphi_{i,j - 1} }}{{(\Delta Y)^{2} }} \\ + & \left( {\frac{{N_{t} }}{{N_{b} }}} \right)\frac{{\theta_{i,j + 1} - 2\theta_{i,j} + \theta_{i,j - 1} }}{{(\Delta Y)^{2} }}] \\ \end{aligned} $$

$$ \varphi ^{\prime} = A_{6} \varphi + A_{7} \theta $$

(20)

$$ \begin{aligned} \frac{{\varphi^{\prime}(\tau ) - \varphi (\tau )}}{\Delta \tau } + U\frac{{\varphi (\tau )(1 - e^{ - i\alpha \Delta X} )}}{\Delta X} + V\frac{{\varphi (\tau )(e^{i\beta \Delta Y} - 1)}}{\Delta Y} & = \frac{1}{{L_{e} }}\frac{2\varphi (\cos \beta \Delta Y - 1)}{{\Delta Y^{2} }} \\ & + \frac{{N_{t} }}{{N_{b} }}\frac{2\theta (\cos \beta \Delta Y - 1)}{{\Delta Y^{2} }} - K_{r} \varphi^{P} \\ \end{aligned} $$

$$ \begin{aligned} \varphi^{\prime}(\tau ) = & \varphi (\tau )\Delta \tau [1 - U\frac{{(1 - e^{ - i\alpha \Delta X} )}}{\Delta X} - V\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y} + \,\frac{1}{{L_{e} }}\frac{2(\cos \beta \Delta Y - 1)}{{\Delta Y^{2} }} - K_{r} \varphi^{P} ] \\ + \theta (\tau )\Delta \tau \frac{{N_{t} }}{{N_{b} }}\frac{2(\cos \beta \Delta Y - 1)}{{\Delta Y^{2} }} \\ \end{aligned} $$

$$ A_{6} = \Delta \tau [1 - U\frac{{(1 - e^{ - i\alpha \Delta X} )}}{\Delta X} - V\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y} + \,\frac{1}{{L_{e} }}\frac{2(\cos \beta \Delta Y - 1)}{{\Delta Y^{2} }} - K_{r} \varphi^{P} ] $$

$$ A_{7} = \Delta \tau [\frac{{N_{t} }}{{N_{b} }}\frac{2(\cos \beta \Delta Y - 1)}{{\Delta Y^{2} }}] $$

$$ \psi^{\prime}(\tau ) = A_{1} \psi (\tau ) + A_{2} \theta (\tau ) + A_{3} \varphi (\tau ) $$

$$ \theta ^{\prime}(\tau ) = A_{4} \theta (\tau ) + A_{5} \varphi (\tau ) $$

$$ \varphi ^{\prime}(\tau ) = A_{6} \varphi (\tau ) + A_{7} \theta (\tau ) $$

$$ \left[ {\begin{array}{*{20}c} {\psi^{\prime}} \\ {\theta^{\prime}} \\ {\varphi^{\prime}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A_{1} } & {A_{2} } & {A_{3} } \\ 0 & {A_{4} } & {A_{5} } \\ 0 & {A_{7} } & {A_{6} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \psi \\ \theta \\ \varphi \\ \end{array} } \right] $$

$$ \eta^{\prime} = T\eta $$

where $\eta^{\prime} = \left[ {\begin{array}{*{20}c} {\psi^{\prime}} \\ {\theta^{\prime}} \\ {\varphi^{\prime}} \\ \end{array} } \right]$;$T = \left[ {\begin{array}{*{20}c} {A_{1} } & {A_{2} } & {A_{3} } \\ 0 & {A_{4} } & {A_{5} } \\ 0 & {A_{7} } & {A_{6} } \\ \end{array} } \right]$ and $\eta = \left[ {\begin{array}{*{20}c} \psi \\ \theta \\ \varphi \\ \end{array} } \right]$.

For attaining the constancy condition, the Eigenvalues of the intensification matrix T will be apprehended. This is a fourth-order square matrix. Due to this explicit scheme Δτ inclines to zero. Beneath this situation $A_{2} \to 0,A_{3} \to 0,A_{5} \to 0\,\,{\text{and}}\,A_{7} \to 0$.

$$ T = \left[ {\begin{array}{*{20}c} {A_{1} } & 0 & 0 \\ 0 & {A_{4} } & 0 \\ 0 & 0 & {A_{6} } \\ \end{array} } \right] $$

Thus, T are gained as $A_{1} = \lambda_{1} ,A_{4} = \lambda_{2} \,$ and $A_{6} = \lambda_{3}$. For stability check, each of the Eigenvalues must not exceed unity in terms of modulus. Beneath this concern, the stability must follow the below criteria:

$\left| {A_{1} } \right| \le 1,\left| {A_{4} } \right| \le 1$ and $\left| {A_{6} } \right| \le 1$.

Let,$a_{1} = \Delta \tau ,\,\,\,d_{1} = 2\frac{\Delta \tau }{{\left( {\Delta Y} \right)^{2} }}\,\,{,}\,\,\,d_{2} = \frac{\Delta \tau }{{\Delta Y}}\,{\text{, d}}_{{3}} = \left| { - \varepsilon } \right|\frac{\Delta \tau }{{\Delta Y}}\,\,{\text{and}}\,\,d_{4} = \frac{\Delta \tau }{{\Delta Y^{2} }}$,

The coefficients ac, b and c are wholly positive. Thus the max modulus of $A_{1}$,$A_{4}$ and $A_{5}$ ensues when $\alpha \Delta Y = n\pi$, where $n$ is indicated by an integer value and here $A_{1}$, $A_{4}$ also $A_{6}$ are showed as absolute value. The magnitudes of $\left| {A_{1} } \right|$,$\left| {A_{4} } \right|$ and $\left| {A_{6} } \right|$ are larger while $n$ is odd type integer, in this case,

$$ \begin{aligned} A_{4} = & \Delta \tau \left[ 1 \right. - U\frac{{(1 - e^{ - i\alpha \Delta X} )}}{\Delta X} - V\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y} + \frac{1}{{P_{r} }}(1 + \frac{4}{3}R)\frac{2(\cos \beta \Delta Y - 1)}{{(\Delta Y)^{2} }} + Q \\ & + \left( {1 + \frac{1}{\alpha }} \right)E_{c} \left( {\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y}} \right)^{2} + \theta (\tau )Nb\left( {\frac{{\varphi (\tau )(e^{i\beta \Delta Y} - 1)}}{\Delta Y}} \right)^{2} + \theta (\tau )Nt\left( {\frac{{(e^{i\alpha \Delta X} - 1)}}{\Delta Y}} \right)^{2} ] \\ \end{aligned} $$

$$ a_{1} = \Delta \tau \,,{\text{d}}_{{1}} = \frac{\Delta \tau }{{\Delta X}},\,\,d_{2} = 2\frac{\Delta \tau }{{\left( {\Delta Y} \right)^{2} }}\,\,{,}\,\,\,d_{3} = \frac{\Delta \tau }{{\Delta Y}}\,\,\,,\,\,d_{4} = \frac{\Delta \tau }{{\Delta Y^{2} }}{\text{and}}\,\,d_{5} = \frac{\Delta \tau }{{\left( {\Delta Y} \right)^{2} }} $$

$$ A_{4} = \left[ {a_{1} - Ud_{1} - Vd_{3} + \frac{1}{{P_{r} }}(1 + \frac{4}{3}R)d_{2} + Q + \left( {1 + \frac{1}{\alpha }} \right)E_{c} d_{5} + \theta N_{b} d_{5} + \theta N_{t} d_{5} } \right] $$

$$ A_{6} = \Delta \tau \left[ {1 - U\frac{{(1 - e^{ - i\alpha \Delta X} )}}{\Delta X} - V\frac{{(e^{i\beta \Delta Y} - 1)}}{\Delta Y} + \frac{1}{{L_{e} }}\frac{2(\cos \beta \Delta Y - 1)}{{\Delta Y^{2} }} - K_{r} \varphi^{P} } \right] $$

$$ A_{6} = \left[ {1 - Ud_{1} - Vd_{3} + \,\frac{1}{{L_{e} }}d_{2} - K_{r} } \right] $$

$$ A_{7} = \left[ {\frac{{N_{t} }}{{N_{b} }}d_{2} } \right] $$

Here, the values are $A_{1} = - 1$ $A_{4} = - 1$ and $A_{6} = - 1$. thus the stability conditions off the techniques are,

$$ \begin{aligned} A_{4} = & \frac{1}{{P_{r} }}(1 + \frac{4}{3}R)\frac{\Delta \tau }{{(\Delta Y)^{2} }} + Q\frac{\Delta \tau }{2} - \frac{U}{\Delta X} - \frac{V}{\Delta Y} \\ & + \left( {1 + \frac{1}{\alpha }} \right)E_{c} \Delta \tau \left( {\frac{1}{\Delta Y}} \right)^{2} + \theta (\tau )Nb\Delta \tau \left( {\frac{\varphi }{\Delta Y}} \right)^{2} + \theta (\tau )Nt\Delta \tau \left( {\frac{1}{\Delta Y}} \right)^{2} ] \\ \end{aligned} $$

$$ A_{4} = \left[ {a_{1} - Ud_{1} - Vd_{3} + \frac{1}{{P_{r} }}(1 + \frac{4}{3}R)d_{2} + Q + \left( {1 + \frac{1}{\alpha }} \right)E_{c} d_{5} + \theta N_{b} d_{5} + \theta N_{t} d_{5} } \right] $$

$$ \begin{aligned} \frac{1}{{P_{r} }}(1 + \frac{4}{3}R)\frac{\Delta \tau }{{(\Delta Y)^{2} }} & + Q\frac{\Delta \tau }{2} - \frac{U}{{2\left( {\Delta X} \right)}} - \frac{V}{{2\left( {\Delta Y} \right)}} \\ + \left( {1 + \frac{1}{\alpha }} \right)\frac{{E_{c} }}{2}\Delta \tau \frac{1}{{\left( {\Delta Y} \right)^{2} }} + \theta (\tau )\frac{Nb}{2}\Delta \tau \left( {\frac{\varphi }{\Delta Y}} \right)^{2} + \theta (\tau )\frac{Nt}{2}\Delta \tau \left( {\frac{1}{\Delta Y}} \right)^{2} ] \le 1 \\ \end{aligned} $$

(21)

and $A_{6} = \left[ {1 - Ud_{1} - Vd_{3} + \frac{1}{{L_{e} }}d_{2} - \frac{{\Delta \tau K_{r} }}{2}} \right]$

$$ \left[ {\frac{1}{Le}\frac{\Delta \tau }{{\left( {\Delta Y} \right)^{2} }} - \Delta \tau \frac{{K_{r} }}{2} - U\frac{\Delta \tau }{{2\left( {\Delta X} \right)}} - V\frac{\Delta \tau }{{2\left( {\Delta Y} \right)}}} \right] \le 1 $$

(22)

With primary boundary conditions $U = V = T = C = 0$ and for $\Delta \tau = 0.005$, $\Delta X = 0.2$ and $\Delta Y = 0.25,$ the problem would be converged at $P_{r} \ge 0.447$ and j $Sc \ge 0.163$.

6 Results and discussion

In order to characterize the impact of different physical terms on velocity, concentration, temperature, Sherwood number, skin friction as well as Nusselt number along with isotherm, streamlines have been depicted from Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19. In addition, the updated visualization of the fluid flow has been presented in this work in vibrating form. Moreover, the velocity fields are exhibited here in sinusoidal form to discuss the impact of various physical parameters like Casson fluid, magnetic field, Darcy number, chemical reaction and thermophoresis. The ongoing investigation has significant importance in daily life due to its great applications in the field of medical science. Nowadays, nanoparticles are used in cancer therapy, and it has also seen that with the presence of periodic magnetic field, it is easier to control the nanoparticles. Here, the nanoparticle interactions have also been inspected theoretically with the presence of periodic magnetic field. Moreover, in modern era, nanoparticles are also used for the treatment of lung cancer and prostate cancer.

Fig. 3

Velocity illustration for various values of $\alpha$

Fig. 4

Velocity illustration for various values of M

Fig. 5

Velocity illustration for various values of Da

Fig. 6

Velocity illustration for various values of Kr

Fig. 7

Velocity illustration for various values of Nt

Fig. 8

Concentration illustration for various values off Kr

Fig. 9

Concentration illustration for various values off Le

Fig. 10

Concentration illustration for difference values off Nb

Fig. 11

Temperature illustration for various values off Nb

Fig. 12

Temperature illustration for various values off R

Fig. 13

Sherwood number illustration for various values off Le

Fig.14

Skin friction illustration for various values off R

Fig. 15

Nusselt number illustration for various values of R

Fig. 16

Isotherm lines for M = 0.50

Fig. 17

Isotherm lines for M = 1.00

Fig. 18

Streamlines for M = 0.50

Fig. 19

Streamlines for M = 1.00

Moreover, the average computational time (CPU) was observed for seven different fluid fields. For velocity, temperature and concentration fields, the CPU run time was 10.8493 s. Again, for the skin friction, Nusselt number and Sherwood number profiles, the CPU run time was 3.5743 s. Finally, the CPU run time for streamlines and isothermal lines was 2.1675 s. For this analysis, the following default data have been considered i.e. Gr = 10, Gm = 5, Nb = Nt = 0.5, Le = 2.0, Kp = 1.0, p = 2.0, Ec = 0.01, Pr = 1.0, Kr = 0.2, Q₁ = 1.0, m = 200, n = 200,$\Delta X = 0.2,$$\Delta Y = 0.25,$$\Delta \tau = 0.005$, τ = 6.0, 1.0, 0.5. However, the validity of the current investigation with Reza-E-Rabbi et al. [29] is self-evident in Table 1 (see ‘Appendix’ for residual error). Both mentioned parameters give an identical impact on the respective fluid fields, and the numerical data is relatively closer to each other.

Table 1 Comparison of C_f and Nu when, Gm = 1.0, Gr = 5.0, γ = Nb = Nt = 0.5, Le = 5.0, Kp = 1.0, p = 2.0, Ec = 0.01, Pr = 1.0, Kr = 0.2, and Q₁ = 0

Figure 3 depicts the impression of Casson fluid parameter on velocity profiles, where the sinusoidal pattern of velocity profiles increased for the rising values of $\alpha$. So, the fluid parameter has created an accelerated force. This force diminishes the viscosity of fluid and increases the fluid velocity. The investigations of Lund et al. [21] also came out with the similar outcome for Casson fluid parameter although they imposed a regular pattern magnetic field. They observed the identical impact on the velocity filed slightly away from the surface. Again in our work it has been seen that, due to the presence of periodic magnetic field the Casson fluid parameter has significant impact on the respective field. The influence of magnetic scheme in term of velocity is displayed in Fig. 4. The oscillating pattern diminishes for the enhancing values of M. In this figure, the peak value of sinusoidal pattern varies at Y = 5 with every step 213.88%, 211.66%, 96.8%, 47.64%, 25.8% and 16.02% numerically. However, the obtained outcomes are similar with the result of Reza-E-Rabbi et al. [29]. It reveals that Lorentz force resists the flow of nanofluid. Owing to the cause, magnetic field originates a resistant power on the wall periphery known as Lorentz force, which eventually impedes the movement of liquid.

Figure 5 depicts the variation of velocity with Darcy number where ascending values of Darcy number increase the values of velocity. The increasing rate of the fluid field for this case is 145.75, 74.88, 44.89, 29.91, 21.36 and 16.01% respectively as the data of Darcy number enhances from 1.0 to 7.0. This happens physically because Darcy number is directly proportional to the fluid velocity. The velocity of fluid is decreased with chemical reaction, which is presented in Fig. 6. It is examined that positive value of chemical reaction indicated the impact of destructive chemical reaction. Kinematic viscosity and chemical reaction are proportional to each other. Therefore, the viscosity of the fluid get increase due to the development of chemical reaction factors and because of that, it diminishes the fluid field. The work of Biswas et al. [30] appeared with the identical physical impact on the velocity fields for both Darcy number and chemical reaction.

Figure 7 depicts an oscillatory pattern of the impression of thermophoresis parameter on velocity field. The numerical variations at Y = 5 are 4.29, 4.73, 5.18 and 5.62 as the data of Nt develops from 0.3 to 0.9. It is asserted that thermophoresis parameter enhances the velocity profiles. Thermophoresis factor is inversely proportional to kinematic viscosity. Again, enhancing data of thermophoresis parameter develops the motion of the fluid particles, as a result, the improvement is visible in velocity distribution.

In addition, Reza-E-Rabbi et al. [29] have also showed the same impact of nanoparticle parameters in their work. However, the influences of destructive and constructive chemical reactions have been discussed by Ullah et al. [15] and Reza-E-Rabbi et al. [31] in their respective work. The current investigation (Fig. 8) also gives identical result on the same field and represent a good agreement with the mentioned authors.

We observed that the field of concentration get diminishes for both cases. The interesting fact is that destructive chemical reactions (Kr = 0.2, 0.4) decline the fluid concentration more significantly rather than the constructive ones (Kr = − 0.4, − 0.2). This happens because the motions of the molecules are usually high for destructive chemical reactions.

Nadeem et al. [24] and Ullah et al. [15] observed the impressions of Brownian motion parameter on concentration and temperature fields respectively. Additionally, Ullah et al. [15] also discussed the physical impact of Lewis number and radiation parameter on concentration and temperature fields. The present investigations have also depicted the impression of same physical parameters on the mentioned fluid fields (see Figs. 9, 10, 11, 12) and it has illustrated a good agreement with Nadeem et al. [24] and Ullah et al. [15].

Figure 9 outlines the characteristics of concentration field for the variation of Lewis number. The decrement of concentration field is observed for the greater values of Lewis number. The physical cause behind this behavior is that the thermal diffusion increases for larger Lewis number so that the concentration of the fluid get decrease. The decreasing rate is 0.15, 0.08, 0.09, 0.06 and 0.04% as Le varies from 5 to 16. The effect Brownian motion on concentration field is illustrated in Fig. 10. It is shown that for the larger data of Brownian motion, the fluid concentration diminishes. The Brownian motion of the particle is usually high when the value of Nb is large because of that the increasing data of Nb accelerates the fluid motion and eventually diminishes the concentration fields. Due to this physical phenomena, the temperature field of the fluid flow also increases for higher values of Brownian parameter (Fig. 11). Because the accelerating particles will collide with each other significantly and eventually increases the temperature of the fluid particles.

The influences of radiation parameter (R) on temperature profile is plotted in Fig. 12. The temperature field is increased for larger data of radiation parameter. This incident happened physically because radiation enhances the diversity of heat flux. The increment rates are 4.12, 1.98, 1.94%, 1.89, 1.85 and 1.83% as R varies from 0 to 0.7.

Figure 13 displayed the impression of Lewis number on the field of Sherwood number. Here, the increasing rates are 4.08, 7.3, 6.52, 5.97, 5.56 and 5.23% over the period of time as Lewis number varies from 5.0 to 16.0. Increase in Lewis number boosts the Sherwood number, which obeys the natural phenomena of increasing thermal diffusion directed towards rising concentration field.

The impact of radiation parameters on skin friction is captured in Fig. 14, where radiation parameters developed the motion of the particles near the wall. Numerically, the developing rates are 28.37%, 25.86%, 0.81%, 0.34%, 28.72% and 0.37% from R = 0.30 to 1.30 at Y = 2.00. But, in case of Nusselt number (Fig. 15), the radiation parameter behaved inversely. For this case, the diminishing values are 0.55%, 0.6%, 0.54%, 0.24%, 0.43% and 0.19% as R changes from 0.30 to 1.30 at Y = 2. The radiation parameter increases the diversity of the heat flux and develops the fluid motion at the wall but behaved differently for the Nusselt number profile.

The isothermal lines are presented with contour level for magnetic parameter M (Figs. 16, 17). As a result, more wave nature is visualized for a larger magnetic parameter. The larger values of magnetic parameter increased the temperature between fluid molecules. Again, for different values of M, the streamlines are also presented with contour lines in Figs. 18 and 19. Here, the higher values of magnetic parameter created a more sinusoidal pattern of the streamlines. Physically it happens because of a resistive force (Lorentz force) of a magnetic parameter. The same phenomena was also seen for larger magnetic field parameter in the work of Siddiqa et al. [28] and here in both work the streamlines and isothermal lines exhibit identical physical impact for periodic magnetic field parameter.

7 Conclusions

The current investigation exhibits the simulation of periodic hydromagnetic Casson nanofluid flow resulting from a stretching surface. The fundamental equations were transformed into a dimensionless form and solved numerically with the implementation of explicit finite difference method. The main aim of this investigation was to induce a magnetic field in sinusoidal form instead of regular pattern of magnetic field. One of the novel concern was to observe theoretically, how the presence of periodic magnetic field affects the interaction of the nanoparticles. Again, the updated exhibition of fluid fields (streamlines and isothermal lines) have also been observed in periodic form. It has been inspected newly that for larger values of magnetic parameter the Lorentz force affects the velocity fields, streamlines and isothermal lines more effectively. However, for further investigation the present study can be extended. The periodic form of wall friction, Nusselt number profiles and Sherwood number profiles can be exhibited graphically to observe how fluid particle behaves at the wall surface in the presence of a periodic magnetic field. Moreover, the current numerical simulation can also be done by using the Runge–Kutta based shooting method also known as similarity transformations. However, other key findings are stated below as:

Velocity profiles increase due to the increment in Casson fluid parameter, Darcy number, and thermophoresis parameter. On the other hand, velocity field diminishes when the values of magnetic parameter and chemical reaction get develop. Therefore, concentration profile declines for larger values of three significant parameters which are chemical reaction, Lewis number, and Brownian motion. Moreover, temperature fields have represented a directly proportional behavior for greater values of Brownian motion and radiation parameters. Similarly, Lewis number profile increases for increasing data of Sherwood number. Radiation parameter increases the skin friction profiles but exhibits an inverse relation with Nusselt number profiles. Finally, the isotherm lines exhibit an accelerating behavior for larger magnetic parameter whilst streamlines represent a reverse behavior.

Appendix

Regression analysis is performed on the Nusselt number values shown in Table 1 to determine the residual error, i.e., the differences between the previous and the predicted data values. From the study, the coefficient of determination (R square) and the coefficient of correlation (Multiple R) were 0.999973 and 0.999986, respectively, with a standard error of 0.00421.

See Fig. 20.

Fig. 20

The Residual vs the Nusselt number (Table 1)