1 Introduction

Functionally graded materials (FGMs) are composite materials that their mechanical properties are varied through thickness. This material was first discovered by a Japanese group [1]. Thick-walled cylinders are one of the practical problems in industries as pressure vessels, pipes, tubes, etc. FGM cylinders have a non-homogeneity along the thickness direction, like multi-layered composite cylinders. It should be noted that unlike the conventional composite cylinders, the stress concentration in the layer connection zones does not occur in the FGM cylinders due to the fact that the material properties alter continuously.

In many of the previous studies, the researchers used plane elastic theory (PET) to solve the cylindrical problems. Then, the influence of shear deformation in thick structures was investigated by many researchers. Reddy [2] proposed a higher order shear deformation theory (HSDT) of plates and validate it with classical and first order plate theories, this theory can be generalized for other structures such as beam and shell. Soldatos [3, 4] considered the effect of thickness-shear deformation for analysis of homogeneous isotropic non-circular cylindrical shells, cylindrical panels and cylindrical of antisymmetric angle-ply construction. A generalization of shear deformation theories for axisymmetric multi-layered shells is proposed by Touratier [5]. Additionally, Soldatos and Timarci [6] formulated a general theory that unifies most of the variational classical and shear deformable cylindrical shell theories. Also, some studies are carried out for composite beams and plates by several researchers [7,8,9,10]. According to the importance of using the shear deformation effects to explain the behavior of composite structures, this paper employs a general form of shear deformation function to generalize the obtained formulations. In other words, the shape function can be easily changed in accordance with the desired shear deformation type.

Analysis of FGM thick cylinder under different pressure loading was presented by several published papers in the literature. Chen et al. [11] investigated the free vibration of a thick FG piezoelectric hollow cylinder filled with compressive fluid. Tutuncu [12] presented solutions of stresses and displacements in thick-walled FG cylindrical vessels subjected to internal pressure. Also, an analytical solution for calculating the stresses in an FGM thick cylinder under combined pressure and temperature loading was presented by Abrinia et al. [13]. Chen and Lin [14] acquired an elastic analysis for FGM thick cylinders, the obtained result shows that the property of FGMs has a significant influence on the stress distribution. Three-dimensional thermo-elastic analysis of FG cylindrical shell with piezoelectric layers under the effect of cosine form and ring pressure loadings and various boundary conditions were obtained by the differential quadrature method [15]. Wu [16] presented an analysis of the thick cylinder temperature field based on the thermal–fluid–solid coupling. An analytical analysis of FG thick cylinder with finite length was studied by Khoshgoftar et al. [17]. There are also many published papers in similar fields such as, nonlinear dynamics analysis of clamped FGM cylinder subjected to an external excitation and uniform temperature change [18], and analysis of wave propagation in FG thick hollow cylinder [19].

Shear deformation effects can be observed in the structures such as beams, plates, shells, etc. with considerable thickness. Thus, it is imperative to consider the shear deformation effects on thick-walled cylinders. There are several studies which deal with the shear deformation effects especially in a general shear deformation theory form [20,21,22,23,24]. In fact, the necessity of considering the shear deformation effects is demonstrated in the present study, and it is illustrated that ignoring these effects can result in considerable errors. Khoshgoftar [25] employed the second-order shear deformation theory (which is conventional for shells) to analyze FG thick shells. The current study utilizes the third-order and sinusoidal theories which are common in thick beams or plates and illustrates how they can be accurate for thick cylinders, too.

This study aims at applying the general shear deformation theory to derive a general form of nonlinear equations for thick-walled FG cylinders and using non-uniform internal pressure to acquire the stress resultants. For this reason, the current paper is organized in the following manner. In Sect. 2, the material properties distribution for an FG cylinder is defined based on a power-law function, the displacement field is defined based on the general shear deformation theory, and the governing differential equations and boundary conditions are derived using the principle of stationary potential energy. In Sect. 3, the implementation of GDQM to discretize the equation is expressed. Section 4 presents the numerical results obtained by the present solution and a commensurate discussion for each of them. Finally, Sect. 5 contains a summary and some general conclusions.

2 Elastic analysis of FG thick cylinders

In this study, distribution of FG properties is considered along thickness direction, as follows [22]:

$$p(z) = (p_{c} - p_{m} )\left( {\frac{1}{2} + \frac{z}{t}} \right)^{n} + p_{m}$$
(1)

where p is a function of material properties for FGM cylinder (such as Young’s modulus). Also, the subscripts m and c denote the metallic and ceramic components, respectively. In fact, the real number n is called the power-law index, and z is the distance from the mid-surface of the FGM cylinder. It should be noted that the Poisson’s ratio is considered constant due to the fact that the difference of the Poisson’s ratio at the top (ceramic) and the bottom (metal) surface of the cylinder is negligible.

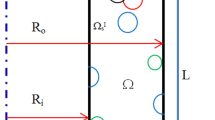
The governing equations for circular thick-walled cylinder made of FGM with finite length, are obtained in this section. The geometry of the studied cylinder is shown in Fig. 1. To write the local displacement components based on the general shear deformation theory, a shape function f(z) should be used. The shape function describes the shear deformation across the thickness for each theory. The displacement field based on general shear deformation theory is defined as follow:

$$\begin{aligned} U(x,z) & = u(x) + f(z)\varphi (x) \\ W(x,z) & = w(x) + f(z)\psi (x) \\ \end{aligned}$$
(2)

where U and W are longitudinal and radial displacements, respectively. Also, u, w, \(\varphi\) and \(\psi\) are longitudinal displacement, radial displacement, longitudinal and radial rotations, respectively.

Fig. 1
figure 1

The geometry of the cylinder

Full size image

The strain–displacement relations according to small deformation and cylindrical coordinate system are written as [26]:

$$\begin{aligned} \varepsilon_{x} & = \frac{\partial U}{\partial x} = \frac{du}{dx} + f(z)\frac{d\varphi }{\partial x} \\ \varepsilon_{\theta } & = \frac{W}{r} = \frac{w}{r} + f(z)\frac{\psi }{r} \\ \varepsilon_{z} & = \frac{\partial W}{\partial z} = f^{\prime } (z)\psi \\ \gamma_{xz} & = \frac{\partial U}{\partial z} + \frac{\partial W}{\partial x} = f^{\prime } (z)\varphi + \frac{dw}{dx} + f(z)\frac{d\psi }{\partial x} \\ \end{aligned}$$
(3)

Also, the stress field can be obtained by Hook’s law:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{\theta } } \\ {\sigma_{z} } \\ {\tau_{xz} } \\ \end{array} } \right\} = \frac{E(z)}{(1 + \nu )(1 - 2\nu )}\left[ {\begin{array}{*{20}l} {1 - \nu } \hfill & \nu \hfill & \nu \hfill & 0 \hfill \\ \nu \hfill & {1 - \nu } \hfill & \nu \hfill & 0 \hfill \\ \nu \hfill & \nu \hfill & {1 - \nu } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\frac{1 - 2\nu }{2}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\varepsilon_{z} } \\ {\gamma_{xz} } \\ \end{array} } \right\}$$
(4)

where E(z) is Young’s modulus that varies as a power function, and v is Poisson’s ratio that is held constant.

To obtain the governing differential equations, we need the potential energy functional. This energy for FGM cylinder under the internal pressure p(x) is given from Eq. (5).

$$\begin{aligned} U & = \int_{0}^{2\pi } {\int_{0}^{L} {\int_{ - t/2}^{t/2} {(\sigma_{x} \varepsilon_{x} + \sigma_{\theta } \varepsilon_{\theta } + \sigma_{z} \varepsilon_{z} + \gamma_{xz} \gamma_{xz} )rdzd\theta dx} } } \\ & \quad -\, \int_{0}^{2\pi } {\int_{0}^{L} {p(x)\left( {R - \frac{t}{2}} \right)} \left( {w(x) + f\left( { - \frac{t}{2}} \right)\psi (x)} \right)dxd\theta .} \\ \end{aligned}$$
(5)

By applying the principle of stationary potential energy, we have:

$$\delta U = 0.$$
(6)

By using the Eqs. 3, 5 and 6, Eq. 7 obtains as follow;

$$\begin{aligned} & \int_{0}^{L} \int_{ - t/2}^{t/2} \left[{\sigma_{x} \delta \left( {\frac{du}{dx} + f(z)\frac{d\varphi }{dx}} \right) + \sigma_{\theta } \delta } \left( {\frac{w}{r} + f(z)\frac{\psi }{r}} \right) + \sigma_{z} \delta (f^{\prime } (z)\psi ) \right.\\ & \left.\quad +\, \tau_{xz} \delta \left( {f^{\prime }(z)\varphi + \frac{dw}{dx} + f(z)\frac{d\psi }{dx}} \right)\right](R + z)dzdx \\ & \quad -\, \int_{0}^{L} {p(x)\left( {R - \frac{t}{2}} \right)\delta \left( {w + f\left( { - \frac{t}{2}} \right)\psi } \right)} dx = 0. \\ \end{aligned}$$
(7)

Equation 7 comes in the form of Eq. 8, when the variational principle is applied.

$$\begin{aligned} & \int_{0}^{L} \int_{ - t/2}^{t/2} \left[{\sigma_{x} \left( {\frac{d}{dx}\delta u + f(z)\frac{d}{dx}\delta \varphi } \right) + \sigma_{\theta } } \left( {\frac{1}{r}\delta w + f(z)\frac{1}{r}\delta \psi } \right) + \sigma_{z} (f^{\prime } (z)\delta \psi ) \right.\\ & \left.\quad + \,\tau_{xz} \left( {f^{\prime } (z)\delta \varphi + \frac{d}{dx}\delta w + f(z)\frac{d}{dx}\delta \psi } \right)\right](R + z)dzdx \\ & \quad -\, \int_{0}^{L} {p(x)\left( {R - \frac{t}{2}} \right)\left( {\delta w + f\left( { - \frac{t}{2}} \right)\delta \psi } \right)} dx = 0. \\ \end{aligned}$$
(8)

Applying integration by parts, Eq. 8 is rewritten as follow:

$$\begin{aligned} & \int_{0}^{L} \int_{ - t/2}^{t/2} \left[{\left( { - \frac{{d\sigma_{x} }}{dx}} \right)\delta u + \left( { - f(z)\frac{{d\sigma_{x} }}{dx} + f^{\prime } (z)\tau_{xz} } \right)\delta \varphi + } \left( {\frac{{\sigma_{\theta } }}{r} - \frac{{d\tau_{xz} }}{dx}} \right)\delta w \right.\\ & \left.\quad +\, \left( {f(z)\frac{{\sigma_{\theta } }}{r} + \sigma_{z} f^{\prime } (z) - f(z)\frac{{d\tau_{xz} }}{dx}} \right)\delta \psi \right](R + z)dzdx \\ & \quad +\, \left. {\int_{ - t/2}^{t/2} {(\sigma_{x} \delta u + f(z)\sigma_{z} \delta \varphi + \tau_{xz} \delta w + f(z)\tau_{xz} \delta \psi )} (R + z)dz} \right|_{x = 0}^{x = L} \\ & \quad - \,\int_{0}^{L} {p(x)\left( {R - \frac{t}{2}} \right)\left( {\delta w + f\left( { - \frac{t}{2}} \right)\delta \psi } \right)} dx = 0. \\ \end{aligned}$$
(9)

The governing equations are obtained from Eq. 9 as follow.

$$\begin{aligned} & \delta u{:}\,\,\,\,\,\int_{ - t/2}^{t/2} {\frac{{d\sigma_{x} }}{dx}(R + z)dz = 0} \\ & \delta \varphi{:}\,\,\,\,\int_{ - t/2}^{t/2} {\left( { - f(z)\frac{{d\sigma_{x} }}{dx} + f^{\prime } (z)\tau_{xz} } \right)(R + z)dz = 0} \\ & \delta w{:}\,\,\int_{ - t/2}^{t/2} {\left( {\frac{{\sigma_{\theta } }}{r} - \frac{{d\tau_{xz} }}{dx}} \right)(R + z)dz = } \left( {R - \frac{t}{2}} \right)p(x) \\ & \delta \psi{:}\,\,\int_{ - t/2}^{t/2} {\left( {f(z)\frac{{\sigma_{\theta } }}{r} + f^{\prime } (z)\sigma_{z} - f(z)\frac{{d\tau_{xz} }}{dx}} \right)(R + z)dz = f\left( { - \frac{t}{2}} \right)\left( {R - \frac{t}{2}} \right)p(x)} . \\ \end{aligned}$$
(10)

Substituting Eqs. 3 and 4 into Eq. 10, we have:

$$\begin{aligned} & A\left( {\left( {\int_{ - t/2}^{t/2} {E(z)(R + z)dz} } \right)\frac{{d^{2} u}}{{dx^{2} }} + \left( {\int_{ - t/2}^{t/2} {E(z)f(z)(R + z)dz} } \right)\frac{{d^{2} \varphi }}{{dx^{2} }}} \right) \\ & \quad +\, B\left( {\left( {\int_{ - t/2}^{t/2} {E(z)dz} } \right)\frac{dw}{dx} + \left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)dz} } \right) + \left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)(R + z)dz} } \right)} \right)\frac{d\psi }{dx}} \right) = 0 \\ \end{aligned}$$
(11a)
$$\begin{aligned} & C\left( {\left( {\int_{ - t/2}^{t/2} {E(z)(f^{\prime } (z))^{2} (R + z)dz} } \right)\varphi + \left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)(R + z)dz} } \right)\frac{dw}{dx}} \right. \\ & \quad + \,\left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)(R + z)dz} } \right)\frac{d\psi }{dx} - A\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)(R + z)dz} } \right)\frac{{d^{2} u}}{{dx^{2} }}} \right. \\ & \quad \left. { + \left( {\int_{ - t/2}^{t/2} {E(z)(f(z))^{2} (R + z)dz} } \right)\frac{{d^{2} \varphi }}{{dx^{2} }}} \right) - B\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)dz} } \right)\frac{dw}{dx}} \right. \\ & \quad \left. { + \left( {\left( {\int_{ - t/2}^{t/2} {E(z)f^{2} (z)dz} } \right) + \left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)(R + z)dz} } \right)} \right)\frac{d\psi }{dx}} \right) = 0 \\ \end{aligned}$$
(11b)
$$\begin{aligned} & A\left( {\left( {\int_{ - t/2}^{t/2} {\frac{E(z)}{(R + z)}dz} } \right)w + \left( {\int_{ - t/2}^{t/2} {\frac{E(z)f(z)}{(R + z)}dz} } \right)\psi } \right) + B\left( {\left( {\int_{ - t/2}^{t/2} {E(z)dz} } \right)\frac{du}{dx}} \right. \\ & \quad +\, \left. {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)dz} } \right)\frac{d\varphi }{dx} + \left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)dz} } \right)\frac{d\psi }{dx}} \right) \\ & \quad - \,C\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)(R + z)dz} } \right)\frac{d\varphi }{dx} + } \right.\left( {\int_{ - t/2}^{t/2} {E(z)(R + z)dz} } \right)\frac{{d^{2} w}}{{dx^{2} }} \\ & \quad +\, \left. {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)(R + z)dz} } \right)\frac{{d^{2} \psi }}{{dx^{2} }}} \right) - p(x)\left( {R - \frac{t}{2}} \right) = 0 \\ \end{aligned}$$
(11c)
$$\begin{aligned} & A\left( {\left( {\int_{ - t/2}^{t/2} {\frac{E(z)f(z)}{(R + z)}dz} } \right)w + \left( {\left( {\int_{ - t/2}^{t/2} {\frac{{E(z)(f(z))^{2} }}{(R + z)}dz} } \right) + \left( {\int_{ - t/2}^{t/2} {E(z)(f^{\prime } (z))^{2} (R + z)dz} } \right)} \right)\psi } \right) \\ & \quad +\, B\left( {\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)dz} } \right) + \int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)(R + z)dz)} } \right)\frac{du}{dx}} \right. \\ & \quad + \,\left( {\left( {\int_{ - t/2}^{t/2} {E(z)(f(z))^{2} dz} } \right) + \left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)(R + z)dz} } \right)} \right)\frac{d\varphi }{dx} \\ & \quad \left. { + \left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)dz} } \right)w + 2\left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)dz} } \right)\psi } \right)\, - C\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)(R + z)dz} } \right)\frac{d\varphi }{dx}} \right. \\ & \quad + \,\left( {\int_{ - t/2}^{t/2} {E(z)f(z)(R + z)dz} } \right)\frac{{d^{2} w}}{{dx^{2} }}\, + \left. {\left( {\int_{ - t/2}^{t/2} {E(z)(f(z))^{2} (R + z)dz} } \right)\frac{{d^{2} \psi }}{{dx^{2} }}} \right) - p(x)f\left( { - \frac{t}{2}} \right)\left( {R - \frac{t}{2}} \right) = 0 \\ \end{aligned}$$
(11d)

where coefficients A, B and C define as follow:

$$A = \frac{1 - \nu }{(1 + \nu )(1 - 2\nu )};\quad B = \frac{\nu }{(1 + \nu )(1 - 2\nu )};\quad C = \frac{1}{2(1 + \nu )}.$$

The boundary conditions that must be satisfied at the both ends of cylinder, are shown in Eq. 11.

$$\left. {\int_{ - t/2}^{t/2} {(\sigma_{x} \delta u + f(z)} \sigma_{z} \delta \varphi + \tau_{xz} \delta w + f(z)\tau_{xz} \delta \psi )(R + z)dz} \right|_{x = 0}^{x = L} = 0.$$
(12)

3 Implement of GDQM

3.1 GDQM

The generalized differential quadrature (GDQ) method is a numerical technique for solving the ordinary and partial differential equations, which was proposed by Shu [27]. The GDQ is a very powerful and accurate method that some basic features of this method such as error and stability have been analysed in Ref. [27]. More information and details about the GDQ method were proposed by Shu and Richard [28]. In this method, we do as follow:

nth order derivative with respect to x, at the grid point \(x_{i}\) as;

$$f_{x}^{(n)} (x_{i} ) = \sum\limits_{k = 1}^{N} {c_{ik}^{(n)} f(x_{k} )} ,\quad n = 1,. \ldots .,N - 1.$$
(13)

Weighting coefficients for the first order derivative;

$$c_{ij}^{(1)} = \frac{{A^{(1)} (x_{i} )}}{{(x_{i} - x_{j} )A^{(1)} (x_{j} )}},\quad i,j = 1, \ldots ,N_{x} ,i \ne j$$
(14)

where

$$A^{(1)} (x_{i} ) = \prod\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{N} {(x_{i} - x_{j} )} .$$
(15)

Weighting coefficients for the second and higher order derivatives;

$$c_{ij}^{(n)} = n\left( {c_{ii}^{(n - 1)} c_{ij}^{(1)} - \frac{{c_{ij}^{(n - 1)} }}{{x_{i} - x_{j} }}} \right),\quad i,j = 1,2, \ldots ,N;\,n = 2,3, \ldots ,N - 1.$$
(16)

When i = j, the weighting coefficients given by

$$c_{ii}^{(n)} = - \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{N} {c_{ij}^{(n)} } ,\,\,\,\,\,\,\,i = 1, \ldots ,N - 1;\,\,n = 1,2, \ldots ,N - 1.$$
(17)

In this method, the region is discretized into several sample points. The sample points are obtained from the Chebyshev–Gauss–Lobatto:

$$X_{i,m} = \frac{1}{2}\left( {1 - \cos \left( {\frac{(m - 1)\pi }{N - 1}} \right)} \right).$$
(18)

3.2 Discreted governing equations

The obtained governing equations in Eqs. 11, are discreted by the GDQM as Eqs. 19 for N sample points.

$$\begin{aligned} & A\left( {\left( {\int_{ - t/2}^{t/2} {E(z)(R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(2)} u_{j} } + \left( {\int_{ - t/2}^{t/2} {E(z)f(z)(R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(2)} \varphi_{j} } } \right) \\ & \quad + \,B\left( {\left( {\int_{ - t/2}^{t/2} {E(z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} w_{j} } + \left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)dz} } \right) + \left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)(R + z)dz} } \right)} \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} \psi_{j} } } \right) = 0 \\ \end{aligned}$$
(19a)
$$\begin{aligned} & C\left( {\left( {\int_{ - t/2}^{t/2} {E(z)(f^{\prime } (z))^{2} (R + z)dz} } \right)\varphi_{i} + \left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)(R + z)dz} } \right)} \right.\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} w_{j} } \\ & \quad + \,\left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)(R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} \psi_{j} } - A\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)(R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(2)} u_{j} } } \right. \\ & \quad \left. { + \left( {\int_{ - t/2}^{t/2} {E(z)(f(z))^{2} (R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(2)} \varphi_{j} } } \right) - B\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} w_{j} } } \right. \\ & \quad \left. { + \left( {\left( {\int_{ - t/2}^{t/2} {E(z)f^{2} (z)dz} } \right) + \left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)(R + z)dz} } \right)} \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} \psi_{j} } } \right) = 0 \\ \end{aligned}$$
(19b)
$$\begin{aligned} & A\left( {\left( {\int_{ - t/2}^{t/2} {\frac{E(z)}{(R + z)}dz} } \right)w_{i} + \left( {\int_{ - t/2}^{t/2} {\frac{E(z)f(z)}{(R + z)}dz} } \right)\psi_{i} } \right) + B\left( {\left( {\int_{ - t/2}^{t/2} {E(z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} u_{j} } } \right. \\ & \quad + \,\left. {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} \varphi_{j} } + \left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} \psi_{j} } } \right) \\ & \quad - \,C\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)(R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} \varphi_{j} } + } \right.\left( {\int_{ - t/2}^{t/2} {E(z)(R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(2)} w_{j} } \\ & \quad + \,\left. {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)(R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(2)} \psi_{j} } } \right) - p(x)\left( {R - \frac{t}{2}} \right) = 0 \\ \end{aligned}$$
(19c)
$$\begin{aligned} & A\left( {\left( {\int_{ - t/2}^{t/2} {\frac{E(z)f(z)}{(R + z)}dz} } \right)w_{i} + \left( {\left( {\int_{ - t/2}^{t/2} {\frac{{E(z)(f(z))^{2} }}{(R + z)}dz} } \right) + \left( {\int_{ - t/2}^{t/2} {E(z)(f^{\prime } (z))^{2} (R + z)dz} } \right)} \right)\psi_{i} } \right) \\ & \quad + \,B\left( {\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)dz} } \right) + \int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)(R + z)dz)} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} u_{j} } } \right. \\ & \quad + \,\left( {\left( {\int_{ - t/2}^{t/2} {E(z)(f(z))^{2} dz} } \right) + \left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)(R + z)dz} } \right)} \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} \varphi_{j} } \\ & \quad \left. { + \left( {\int_{ - t/2}^{t/2} {E(z)f^{\prime } (z)dz} } \right)w_{i} + 2\left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)dz} } \right)\psi_{i} } \right) \\ & \quad - \,C\left( {\left( {\int_{ - t/2}^{t/2} {E(z)f(z)f^{\prime } (z)(R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(1)} \varphi_{j} } } \right. \\ & \quad + \,\left( {\int_{ - t/2}^{t/2} {E(z)f(z)(R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(2)} w_{j} } \, + \left. {\left( {\int_{ - t/2}^{t/2} {E(z)(f(z))^{2} (R + z)dz} } \right)\sum\limits_{j = 1}^{N} {c_{ij}^{(2)} \psi_{j} } } \right) \\ & \quad - \,p(x)f\left( { - \frac{t}{2}} \right)\left( {R - \frac{t}{2}} \right) = 0. \\ \end{aligned}$$
(19d)

The applied boundary conditions for the study are shown in Eqs. 20.

$$\left\{ \begin{aligned} u_{i} = 0 \hfill \\ w_{i} = 0 \hfill \\ \end{aligned} \right.\quad i = 0,N.$$
(20)

The governing differential equations are transformed to the discreted governing equations. The set of discreted governing equations (Eq. 21) are solved by Newton–Raphson method.

$$\left[ {Coefficient\,Matrix} \right]_{16 \times 16} \left\{ {\begin{array}{*{20}c} {\left\{ u \right\}_{3 \times 1} } \\ {\left\{ \varphi \right\}_{5 \times 1} } \\ {\left\{ w \right\}_{3 \times 1} } \\ {\left\{ \psi \right\}_{5 \times 1} } \\ \end{array} } \right\}_{16 \times 1} = \left\{ 0 \right\}.$$
(21)

4 Numerical results and discussion

To investigate the significance of the shear deformation on this study, we consider an FGM cylinder with mechanical properties that can be seen in Table 1 and variation of Young’s modulus by the non-homogeneity parameter is shown in Fig. 2. Also for validation, the radial displacement along the thickness by FSDT and PET are computed for a homogeneous cylinder with \(\nu = 0.3\), R =0.05 m, t =0.02 m and E =200 GPa under internal pressure of 80 MPa, and compared with Ref. [29] (see Fig. 3). In this section, the numerical results of the FG cylinder have been obtained at the inner surface of the cylinder. The geometry of the cylinder is assumed as; L =1 m and R =0.05 m. Both of the longitudinally constant and non-linear distributed pressures are shown in Fig. 4. Additionally, the higher-order shear deformation theories (HSDT) used in this paper, are Reddy [2] and Touratier [5] theories (see Table 2).

Table 1 Material properties [17]
Full size table
Fig. 2
figure 2

Young’s modulus along thickness for different non-homogeneity

Full size image
Fig. 3
figure 3

Variation of radial displacement versus non-dimensional radius for FSD and PE theories under constant pressure

Full size image
Fig. 4
figure 4

Both of pressure constant and non-linear distributions

Full size image
Table 2 Shear deformation theories used in this study
Full size table

Axial and radial displacements along the x-direction are respectively shown in Figs. 5 and 6, for both FSDT and HSDT (Reddy and Touratier theories). Figures 7 and 8 show axial and radial rotations along the x-direction under FSDT and HSDT, respectively. Also, axial and radial displacements under HSDT are plotted in Figs. 9 and 10, for different non-homogeneity parameters. These figures illustrate that the linear shear deformation assumptions have considerable difference with the higher order shear deformation assumptions. As expected, they indicate that type of internal pressure distribution has much fewer effects on the axial displacement of the cylinder compared with the radial ones. Moreover, the significance of using higher-order shear deformation becomes more obvious when the pressure distribution is not constant. This did not show before in the published literature.

Fig. 5
figure 5

Comparison of axial displacement distribution for FSDT and HSDT under a constant and b non-linear distributed pressure (n = 1)

Full size image
Fig. 6
figure 6

Comparison of radial displacement distribution for FSDT and HSDT under a constant and b non-linear distributed pressure (n = 1)

Full size image
Fig. 7
figure 7

Comparison of axial rotation distribution for FSDT and HSDT under a constant and b non-linear distributed pressure (n = 1)

Full size image
Fig. 8
figure 8

Comparison of axial rotation distribution for FSDT and HSDT under a constant and b non-linear distributed pressure (n = 1)

Full size image
Fig. 9
figure 9

Comparison of axial displacement distribution for different non-homogeneity parameters under a constant and b non-linear distributed pressure

Full size image
Fig. 10
figure 10

Comparison of radial displacement distribution for different non-homogeneity parameters under a constant and b non-linear distributed pressure

Full size image

Normal and hoop stresses of the FG cylinder are respectively shown in Figs. 11 and 12, where the first and higher order shear deformation theories are compared with each other. Figures 11 and 12 demonstrate that the solution of the FG cylinder under FSDT, estimates lower stresses than HSDT. This difference is somewhat remarkable that we should be careful against using the FSDT. It is interesting to note that the FSDT has more error to predict the stresses in comparison with the displacements. Additionally, this error is more obvious in the normal stresses of the thick-walled cylinder, and the hoop stresses predicted by the FSDT is closer to the HSDT (whereas, this trend gets reversed for the displacements).

Fig. 11
figure 11

Comparison of axial stress distribution for FSDT and HSDT, under a constant and b non-linear distributed pressure (n = 1)

Full size image
Fig. 12
figure 12

Comparison of hoop stress distribution for FSDT and HSDT, under a constant and b non-linear distributed pressure (n = 1)

Full size image

Also, the normal and hoop stresses under HSDT are shown in Figs. 13 and 14, for different non-homogeneity parameters. In these figures, the homogeneous material (Zirconia and Ti6AlV) curves overlapped, because the stress does not depend on material for homogeneous components, but this clause is not correct for non-homogeneous components. Additionally, the values of axial and radial displacements and the values of normal and hoop stresses increased by increasing the non-homogeneity parameter, because the strength of material diminishes by increasing this parameter. It is noted that both constant and non-linear pressure distributions are evaluated in Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14.

Fig. 13
figure 13

Comparison of axial stress distribution for different non-homogeneity parameters, under a constant and b non-linear distributed pressure

Full size image
Fig. 14
figure 14

Comparison of hoop stress distribution for FSDT and HSDT, under a constant and b non-linear distributed pressure

Full size image

5 Conclusions

In this paper, a general shear deformable solution is carried out to show the elastic behavior of thick-walled cylinders made of FG materials. A nonlinear internal pressure is assumed to apply to the cylinder and the obtained results are compared to those acquired by constant internal pressure. The main objective of the present study is that both third-order and sinusoidal shear deformation theories (as higher-order shear deformation theories) are employed to consider shear deformation influences occurred through the thick walls. The results indicate that neglecting the higher-order shear deformation can lead to a wide range of under- or overestimation in the calculation of the stresses and displacements. Also, both Reddy and Touratier theories show good responses for the present study. This study is a static analysis and it would be a very good idea to use the same procedure for dynamic analyses. Also, the non-classical continuum theories can be imposed on the current study to capture a size-dependent analysis.