1 Introduction

Traffic loads on bridges are an important topic that has been actively studied during the last decade [4, 20, 28], as the extension of the design life of the infrastructure stock is currently required.

Indeed, the operation life of bridges of all types can be affected by the growth of traffic, both in mass or volume. Research has shown that even a small annual growth, for example of 1%, in the traffic flow significantly affects the traffic load models for European bridges (i.e. in the Netherlands, [13]). Parallely, works (for example [16, 27]) based on numerical simulations show a significant increase of the maximum lifetime traffic load effects with the increase of single truck weights. However, the growth of truck volume and proportion of heavy trucks within the whole traffic cause a relatively moderate increase in load effects.

For both Ultimate Limit State (ULS) and Fatigue Limit State (FLS), monitoring data-based analysis is the most efficient method in order to observe the real situations. Indeed, it has been shown (i.e. [12]) that monitoring of loads and stresses can successfully be used for fatigue reliability. But in order to answer the question of which type of monitoring data is required, it is necessary to know the type of structure. For example, for bridges with steel orthotropic decks, critical structural details of a deck are exposed to fatigue and have a shorter life than the other structural elements [17].

Work based on Weigh-in-Motion (WIM) or Bridge Weigh-in-motion (BWIM) data [8] gives some insights on the fatigue reliability index, that stays much higher than values required in the European Norms (EN) [9]. In this case, the reliability analysis is done based on the probability of failure as a joint function of both the exceedance of Constant Amplitude Fatigue Limit (CAFL) (by high amplitudes of stresses using weekly block maximum approach) and fatigue damage accumulation (using Miner’s rule). Moreover, the use of the BWIM-based probabilistic model is suggested for simple bridge models. Finally, the verification with reliability indexes of EN [9] is made and gives conclusions on higher reliability levels depending on geometry and load cases.

The work [14] validates the EN modelling for fatigue based on BWIM data, and suggests more consistent reliability levels. It also identifies the welds in joints of orthotropic decks as critical structural details with shorter fatigue life. Therefore target values of reliability indexes for FLS in the welds of an orthotropic deck have to be reanalyzed. For the case of load models based on traffic counts, [11] suggests an advanced methodology for fatigue reliability levels considering uncertainties. A comparison between a Finite Element (FE) model and a model based on Weigh-in-motion (WIM) data shows the importance of accuracy in load models for reliability analysis. In a case when direct monitoring is not available, the FE model is built to obtain stresses in critical structural details, using rules of the EN for definition of the loading cases.

For the evaluation of extreme traffic loads on bridges, usually, the Extreme Value Theory (EVT) is used. One of the challenges of the current study lays in applying the EVT to the number of fatigue cycles caused by different vehicles and axles of trucks.

We can cite several similar studies carried out in other areas of expertise: For instance, in the area of composites, the stiffness-based model is introduced by [25] for fatigue damage and life prediction . Moreover, [1] compares a new probabilistic fatigue assessment with a deterministic approach for railway bridges. As stated recently [5], the extreme value approaches can be used for different aspects of material fatigue: for a certain observed structure, it is important to understand which case is the most unfavorable for a bridge: high amplitude stresses caused by rare extreme events or small stresses by a high number of cycles.

In this study, the Peaks Over Threshold (POT) approach is chosen to extrapolate fatigue damage in time. Indeed, its applicability has been stated for several domains, like wind engineering [2], precipitation predictions with non-stationary data [23], electricity demand estimation with a time-varying threshold [26], and other fields. Moreover, this method is also efficient for the estimation of traffic effects [21, 28]. In addition, it does not assume the data to be Gaussian.

2 Methodology

This study considers the combined application of traffic loads and wind loads to a given structure, whose response is then computed. The extrapolated effects in time, given on one side by the conventionnal methodology (Sect. 2.1), and by the metholodogy that is proposed here on the other side (Sect. 2.3) are compared, see Fig. 1.

Fig. 1
figure 1

General methodology, from monitoring to reliability

Full size image

2.1 General application of POT approach

The POT approach has recently been proven to be a good solution for predictions of extreme traffic actions [28, 29]. As time-series, the peak values of Load Effets (LE), which lay above a certain threshold, are fitted to the Generalized Pareto distribution (GPD).

Let X be a random variable representing a LE. Let \(Y= X-u\) be a random variable representing the threshold excesses, which are denoted by \(Y_i\) so that \(Y_i = X_i - u\). The conditional cumulative distribution function of Y, given \(X > u\), denoted by \(F_u (y)\), can be expressed as:

$$\begin{aligned} F_u (y) = P[Y \le y | X>u] = \frac{F(y+u)-F(u)}{1-F(u)}. \end{aligned}$$
(1)

The main principle of the POT approach was described a few decades ago [22], and is based on the following expression: \(F_{u} (y)\) tends to the upper tail of a GPD with given shape and scale parameters (\(\sigma\) and \(\xi\)). Under the following hypothesis’, i) \(y = x-u \ge 0\), ii) \(x > u\) for \(\xi \ge 0\), and \(u \le y \le u-\sigma /\xi\) for \(\xi <0\), iii) \(\sigma >0\), we have,

$$\begin{aligned} G(x; \xi ; \sigma ;u)= {\left\{ \begin{array}{ll} (1-[1+\xi \left( \dfrac{x-u}{\sigma }\right) ]^{-1/\xi }, &{}\xi \ne 0, \\ 1-\exp \left( -\dfrac{x-u}{\sigma }\right) , &{}\xi = 0. \end{array}\right. } \end{aligned}$$
(2)

The following assumptions have to be made for the application of the EVT:

  • There is an identical probability distribution for the random variables \(X_i\),

  • the random variables \(X_i\) are independent,

  • the threshold u is sufficiently high.

For a long period, the observations can be based on the cumulative distribution function of extreme values over a shorter period [7]. Then, for the probability \(P[Y \le y\vert X>u]\) with the probability of exceedance \(\zeta _u=P\{X>u\}\), the return level can be written as [6]:

$$\begin{aligned} S^{return}_{pot}(p)= {\left\{ \begin{array}{ll} u + \dfrac{\sigma }{\xi } \left[ (p \zeta _u)^{\xi }-1\right] , &{}\xi \ne 0, \\ u + \sigma \log (p \zeta _u), &{}\xi = 0, \end{array}\right. } \end{aligned}$$
(3)

where \(S^{return}_{pot}(p)\) is p-observation return level - a quantile that exceeds once every p observations with large enough p to provide \(S^{return}_{pot}(p)>u\). The POT approach has also its drawbacks, such as the selection of an optimized threshold [21]. On one side, it should be reasonably high so that extreme event types are not mixed, in order to obtain their convergence. On the other side, the threshold must be low enough to provide a necessary number of peaks for obtaining reliable results. In the current study, thresholds are estimated using a recently proposed graphical method [18].

2.2 Reliability method

To assess the reliability of a given structural detail to a specific loading, a Limit State Function (LSF) is needed.

Let \(R \sim \mathcal {L} (\mu _R; s_R)\) be a real-valued random variable representing the initial resistance of material with a mean value \(\mu _R\) and a standard deviation \(s_R\), which is assumed to follow a Log-normal distribution \(\mathcal {L}\).

Let S(x) be the real-valued random variable representing a load effect, depending on the nature of load X.

A basic LSF \(G(x)=0\) with:

$$\begin{aligned} G(x) = R - S(x), \end{aligned}$$
(4)

is defined by comparison of R and S(x).

The numerical value of the reliability index \(\beta\) and the probability of failure \(P_f\) are found for example by using First Order Reliability Method (FORM).

For each case of load effect, modeled by the real-valued random variable X, the reliability index \(\beta\) is found for the corresponding probability of failure \(P_f\):

$$\begin{aligned} \beta = - \varPhi ^{-1} ( P_f ) = - \varPhi ^{-1} \left( \int _{G(x) \le 0} q(x) dx \right) , \end{aligned}$$
(5)

where q(x) is the probability density function of the load effect X and \(\varPhi (a)\) is the Cumulative Distribution Function (CDF) of the normalized Gaussian distribution:

$$\begin{aligned} \varPhi (a) = \dfrac{1}{\sqrt{2\pi }} \displaystyle \int _{-\infty }^{a} e^{-y^2/2} dy. \end{aligned}$$
(6)

2.3 Fatigue damage accumulation

Fig. 2
figure 2

Relation between stress and number of cycles: (I)-no damage, (II)-fatigue damage, (III)-extreme load effects

Full size image

Fatigue verification is essential to cover while evaluating the reliability of a given steel structure.

Values of stress cycles of low and medium amplitudes (Fig. 2, zones I and II) that are repeated millions of times can cause material fatigue in a structural detail. While stress of very high amplitude takes place quite rarely, it is close to the critical value (Fig. 2, zone III) and it may affect highly the reliability of the detail.

Either stress amplitudes can cause damage in the future, therefore predictions for both cases have to be made.

In order to assess fatigue in an existing structure, the EN [10] provide S-N curves for diverse structural details or elements.

The fatigue damage accumulation based on Palmgren-Miner’s rule and two-slopes S-N curve for a detail of class K can be written as:

$$\begin{aligned} D_{f}&= R_p \left( \dfrac{1}{2 \times 10^6 (K^3)} \sum \limits _{\ge 0.74K} dS_i^3 N_i + \dfrac{1}{5 \times 10^6 ((0.74K)^5)} \sum \limits _{0.4K}^{0.74K} dS_j^5 N_j \right) , \end{aligned}$$
(7)

where \(dS_i\) is a considered stress range, such that \(dS_i \ge 0.74K\) with the corresponding number of cycles \(N_i\), \(dS_j\) is a considered stress range such that \(0.74K > dS_j \ge 0.4K\) with the corresponding number of cycles \(N_j\).

The LSF based on the two-slopes S-N curve can be written as:

$$\begin{aligned} G_{f} = D_{cr} - R_p \left( \dfrac{1}{A} \sum \limits _{i} dS_i^m N_i + \dfrac{1}{B} \sum \limits _{j} dS_j^n N_j \right) , \end{aligned}$$
(8)

where \(A = 2 \times 10^6 K^m\) and \(B = 5 \times 10^6 (0.74K)^n\), m and n are the slopes of the S-N curve, K is the detail category according to the EN [10]. \(R_p = 365.25 Y / d_m\) is the ratio of the number of years Y of interest and the number of monitored days \(d_m\), \(D_{cr}\) is the critical damage accumulation, \(dS_i\) is a considered stress range, such that \(dS_i \ge 0.74K\) with the corresponding number of cycles \(N_i\), \(dS_j\) is a considered stress range, such that \(0.74K > dS_j \ge 0.4K\) with the corresponding number of cycles \(N_j\).

Therefore, the LSF (8) gives a value of reliability index \(\beta _f\) (see Fig. 1) based on the model suggested in the EN.

2.4 POT approach for numbers of fatigue cycles

Let \(\varDelta = \{\varDelta ^{(1)}, \ldots ,\varDelta ^{(i)}, \ldots , \varDelta ^{(r)}\}\) be the sequence of r stress ranges defined according to the dataset. Let \(C^{(i)} = \{c_1, \ldots , c_j, \ldots , c_z \}\) be the daily number of cycles, counted for each stress range \(\varDelta ^{(i)}\), where z is the number of available days of monitoring (in case of traffic loads, weekdays are counted separately from weekends and national holidays).

Then, the probability distribution of each \(C^{(i)}\) may be exposed to the application of the POT approach (Sect. 2.1). The resulting value of P-years return level \(C_r^{(i)}\) for each \(\varDelta ^{(i)}\) is an updated value of number of stress cycles for the P-years return period. Finally, the fatigue damage \(G_{f*}\) is computed according to [10] using the updated values of \(C_r^{(i)}\) for \(i = 1, \ldots, r\) and for given k and j (see Fig. 3), which leads to Eqs. (9) and (10):

$$\begin{aligned}&G_{f*} = D_{cr} - \left( \dfrac{1}{A} \sum \limits _{i} d S_{k,i}^m C_r^{(i)} + \dfrac{1}{B} \sum \limits _{i} d S_{j,i}^n C_r^{(i)} \right) , \end{aligned}$$
(9)
$$\begin{aligned}&G_{f*} = D_{cr} - \dfrac{1}{A} \sum \limits _{i=1}^{b} d S_{k,i}^m \left[ u_i + \dfrac{\sigma _i}{\xi _i} ((p \zeta _i)^{\xi _i}-1) \right] \nonumber \\&\quad \quad - \dfrac{1}{B} \sum \limits _{i=b}^{w} d S_{j,i}^n \left[ u_i + \dfrac{\sigma _i}{\xi _i} ((p \zeta _i)^{\xi _i}-1) \right] , \end{aligned}$$
(10)

where A, B, m, n and K have the same definitions as in Eq. (8), \(D_{cr}\) is the critical damage accumulation, \(dS_k\) is a considered stress range, such that \(dS_k \ge 0.74K\) with the corresponding number of cycles \(N_k\), \(dS_j\) is a considered stress range, such that \(0.74K > dS_j \ge 0.4K\) with the corresponding number of cycles \(N_j\). The algorithm is detailed in Sect. 3, applied to the case of the orthotropic deck of the Millau viaduct.

Fig. 3
figure 3

Extrapolation of number of fatigue cycles, schematic graph

Full size image

Therefore, the LSF (Eq. 9), is used to assess the alternative value of a reliability index \(\beta _{f*}\), see Fig. 1. The use of the GPD with its shape and scale parameters makes it possible to assess values of return levels for the number of fatigue cycles at different levels of loading.

3 Application to Millau viaduct

The Millau viaduct is a cable-stayed bridge with a steel orthotropic deck, located in Southern France. It consists of 8 spans with a total length of 2460 m, see Fig. 4. The object of this study is the deck between second and third spans to take into account the wind actions on pile P2 with its pylon [18]. The data on traffic actions were obtained with the BWIM system (”BWIM” in Fig. 4) that was installed in the middle of the first span of the viaduct between October 2016 and June 2017 with a total 180 days. Traffic flow on the second and third spans is assumed to be the same as on the first span. Wind velocities at different heights (”SHM” in Fig. 4) were collected by the bridge management system and a national weather station located nearby [18, 19].

Fig. 4
figure 4

Millau viaduct, position of SHM and BWIM systems

Full size image

3.1 Cycles counting based on BWIM data

First, speaking about fatigue of a steel bridge and using the methodology described above, stresses and number of cycles for each stress range are needed. Therefore, critical elements subjected to fatigue loading have to be chosen.

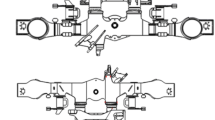
For the current study, the critical detail is the welded connection between a longitudinal stiffener and the plate of the orthotropic deck that is located right under a truck wheel, assuming the vehicle is passing in the middle of the slow lane, see Fig. 5.

The finite element model is created by combining the detailled modelling of several sub-systems, [15].

Fig. 5
figure 5

Finite element model of the part of the deck

Full size image

In the case of the Millau bridge, values of stresses in the deck are not measured directly. Therefore, it is not possible to observe the presence of dynamic effects. However, for the evaluation of fatigue, the use of long-term BWIM data is possible even though it does not directly give stress cycles. Indeed, the system provides axle weights [kN] and spacing [m], vehicle speed [m/s], axles configuration of heavy vehicles. Moreover the absence of data for light vehicles does not cause a problem for this study, as such vehicles do not cause much stress in an orthotropic deck, and do not contribute to the fatigue damage accumulation.

Knowing the exact action applied to the bridge, stress in the whole cross-section might be evaluated, for example, by FE modelling of the deck. The FE model takes into account the self-weight of the bridge deck with its asphalt layer, the type of passing vehicle and amplitudes of axle loads from each axle and as well, wind actions.

However, fatigue cycles are equal to absolute values of stress, a difference between the maximum and minimum values of stress that occur in the same detail. Therefore ”rainflow” counting [3] is done in order to compute number of cycles of each stress range from a given stress timeseries.

Fig. 6
figure 6

Main types of axles groups and their induced stresses

Full size image

The value of the stress given by a group of axles is usually higher than the one caused by each axle separately and lower than their sum. Therefore, in a case of a group of axles, instead of counting separately stress cycles from each axle load in a group, the maximum value produced by the group is considered, see Fig. 6.

There are various possible combinations of axles: some of them are grouped by two or three. For example, for vehicles of type ”113”, to calculate stress cycles, the common action of three rear axles have to be considered. Also for the type ”122”, the group of two axles are taken into account.

Then, using the FE model and by taking into account the shape of the influence lines of longitudinal local bending of the longitudinal stiffeners in orthotropic decks, the stress cycles in MPa are obtained by summing the cycles for every axle or axle group, see histogram Fig. 7.

Fig. 7
figure 7

Histogram of stress cycles for the studied detail of the deck of Millau viaduct and the recorded traffic data

Full size image

3.2 Fatigue load model according to standards

Fig. 8
figure 8

Stress cycles histogram

Full size image

In order to assess fatigue in the structural detail of the deck which is of category \(K=71\) (according to Table 8.8 of [10]), the corresponding S-N curve is used: For the structural detail \(K=71\), according to Figure 7.1 of [10], the stress value at \(2\times 10^6\) of cycles is \(S_K= 71\) MPa. The constant-amplitude fatigue limit (the point where the slope of the S-N curve changes from \(m=3\) to \(m=5\)) is defined as \(S_D=0.738\times S_K= 52\) MPa, and the cut-off limit as \(S_L=0.549 \times S_D = 28\) MPa. All stresses \(S < S_L\) do not contribute to the fatigue damage accumulation.

Figure 8 shows the counted stress cycles in the chosen structural detail. Based on only a half a year of data, the values of stress cycles are far from the S-N curve. Therefore, fatigue damage \(D_f\) is much smaller than its critical value:

$$\begin{aligned} D_{f} \ll D_{cr}. \end{aligned}$$
(11)

In order to assess the damage \(D_f\) at the end of the operational life, an extrapolation is needed. When damage is estimated according to the EN, a linear extrapolation of the damage is made. Let \(R_p\) be a reference value for the extrapolation in time with the desired number of years Y and monitored days \(d_m\):

$$\begin{aligned} R_p = 365.25 \times \dfrac{Y}{d_m}. \end{aligned}$$
(12)

3.3 Extrapolation in time of the number of stress cycles

As it was briefly explained in Sect. 2.4, an alternative methodology is proposed here to assess reliability to fatigue. The methodology is based on fitting the GPD (see Eq. 2), with its shape and scale parameters to a number of fatigue cycles at different levels of stresses.

The algorithm of the proposed method is summarized in Fig. 9: The return period \(R_p = z\times dt\) corresponds to a number z of chosen time ranges dt during the period of interest. The array of stresses \(S=[S_1,\ldots,S_q,\ldots,S_Q]\) recorded during J time ranges \(dt_j\) in the certain detail of category K is considered. It is subdivided into H stress ranges \(\varDelta ^{(i)}\) in order to be studied separately. Firstly, the first chosen range \(\varDelta ^{(1)}\) is taken. Secondly, for the first time range \(dt_1\) is studied, a number of cycles \(c_1^{(1)}\) is counted. Then, \(c_j^{(1)}\) is obtained for every following time range \(dt_j\) until \(j=J\). In that case, for the array \(C^{(1)} = c^{(1)}, \ldots , c_j^{(1)}, \ldots c_J^{(1)}\) that consist of J obtained numbers of cycles, the POT approach is used (see Sect. 2.1). It provides parameters of a fitted GPD \(\mathcal {G} (u_i,\sigma _i, \xi _i)\) which are used to assess a return level of daily number of cycles \(C_r^{(1)}\) for every \(z=1, \ldots, Z\) so that \(R_p=Z\times dt\). The procedure is repeated for all ranges \(\varDelta ^{(i)}\) until \(i=H\). The final step is to compute the fatigue damage according to Eq. (14), and to compare it with a critical value of damage accumulation.

Fig. 9
figure 9

Proposed algorithm for the use of POT for the FLS

Full size image

The category of chosen detail is \(K=71\) that brings following values: \(S_K = 71\) MPa, \(S_D = 52\) MPa, and \(S_L = 28\) MPa, see Fig. 7. Therefore, stress ranges of \(28\le dS_1 < 52\) and \(dS_2 \ge 52\) are defined according to the data set. It is done this way as the stress distribution is almost linear between \(S_L\) and \(S_D\), Fig. 7, and there is not much data for values greater than \(S_D\) to divide this part into smaller ranges.

Fig. 10
figure 10

Histogram of stress cycles with equivalent stresses of 65.7 MPa and 37.9 MPa

Full size image

Let \(C^{(1)}\) and \(C^{(2)}\) be arrays of length J representing daily number of cycles counted for each range \(dS_1\) and \(dS_2\), where \(J=129\) days of available data from monitoring. In a case of traffic loads, to respect weekly stationarity of the loading, weekdays must be counted separately from weekends and national holidays, so not the total of 180 days are considered, but 129 week days. Histograms for \(C^{(1)}\) and \(C^{(2)}\) are shown in Fig. 10. Results of the application of the POT approach (Sect. 2.1) are shown in Table 1 and Fig. 11. The resulting value of P-years return level \(C_r^{(i)}\) for each \(\varDelta ^{(i)}\) is an updated value of number of stress cycles for the P-years return period.

Table 1 Values of return level for daily number of fatigue cycles \(C^{(1)}\) and \(C^{(2)}\)
Full size table
Fig. 11
figure 11

Example of POT results for the range \(dS_2\): (i) fitting GPD to histogram of \(C^{(2)}\), (ii) probability plot, (iii) return level plot

Full size image

The equivalent stresses are competed for ranges \(dS_1\) and \(dS_2\) to the stress ranges in order to apply the method. Let \(s = s_1, \ldots, s_i, \ldots, s_{max}\) be the set of stress ranges of 1 MPa with the maximum recorded value \(s_{max}\). Let \(\eta = \eta _1, \ldots, \eta _i, \ldots, \eta _{max}\) be the set of corresponding number of cycles for s. Then, the equivalent stress is found as:

$$\begin{aligned} S^{eq} = \left[ \dfrac{\displaystyle \sum \eta _i s_i^{m\text { or } n} }{\displaystyle \sum \eta _i}\right] ^{\dfrac{1}{m\text { or } n}}. \end{aligned}$$
(13)

It is found that mean values for \(dS_1\) and \(dS_2\) equivalent stresses are respectively \(S_1^{eq}=37.9\) MPa, \(S_2^{eq}=65.7\) MPa. Finally, fatigue damage is computed according to the EN [10] using updated values of \(C_r^{(i)}\) for \(i = 1, 2\), see Fig. 3.

$$\begin{aligned}&D_{f*} = \dfrac{1}{A} \sum \limits _{z=1}^{Z} (S_1^{eq})^3 C_{r,z}^{(1)} + \dfrac{1}{B} \sum \limits _{z=1}^{Z} (S_2^{eq})^5 C_{r,z}^{(2)}, \end{aligned}$$
(14)
$$\begin{aligned}&D_{f*} = \dfrac{1}{5 \times 10^6 (52^5)} (37.9^5 \times \sum _{z=1}^{Z} C_{r,z}^{(1)}) \nonumber \\&\quad \quad + \dfrac{1}{2 \times 10^6 (71^3)} (65.7^3 \times \sum \limits _{z=1}^{Z} C_{r,z}^{(2)}). \end{aligned}$$
(15)

3.4 Estimated fatigue damage and comparison with standards

Based on the obtained results, a comparison of damage accumulation assessed with both methods is presented in Table 2:

Table 2 Fatigue damage obtained with linear extrapolation of \(D_0\) and POT
Full size table

The value of \(D_0\) is the value of fatigue damage accumulation during available 180 days of monitoring. Years 50 and 120 correspond to the year 2054 and 2124 since the moment of the opening of the bridge. As it can be seen in Table 2, the values of fatigue damage are slightly higher when applying the EVT to the daily number of cycles, which brings attention to a possible grow in traffic volume with time, see Fig. 12. In both cases, the values of fatigue damage \(D_f\) and \(D_{f*}\) are smaller than \(D_{cr} = 1\).

Fig. 12
figure 12

Fatigue damage accumulation during the operational life of the viaduct, comparison of two methods

Full size image

The extrapolation of number of cycles which is proposed here is a more conversative approach than the conventional, linear approach. It leads to a higher fatigue damage.

It should be noted that one approach does not give a necessarily better approximation of the fatigue accumulation than the other: indeed, this depends on the initial signal and cycles with which the whole analysis is made.

If these cycles are of a long period of time and represent correctly all the phenomena happening in the detail, than the linear approach may be supposed sufficient. Nevertheless, for short signals, the POT-approach would make it possible to infer what could be observed in a longer signal.

Without more information et in all generality, none of these two approaches can be called more accurate than the other. Indeed, this would depend on the duration of the measurement, the expected life of the structure and the initial signal. Nevertheless, these methods give some numerical bounds for the fatigue damage calculated with the S-N curve and Miner approach. The POT-approach also makes it possible to assess the representativity and the length of the initial signal.

3.5 Reliability of the detail based on the proposed approach

Taking into account the results of the fatigue calculations made in Sect. 2.3, the reliability analysis is made for the case of linear extrapolation (Eq. 8) and for the case of POT-based approach (Eq. 9).

Table 3 lists all the random variables for each method, with the chosen probability distributions, as found in litterature (for example [24]).

In this case, FORM is used to obtain the values of probability of failure \(P_f\) and reliability index \(\beta\).

The convergence for the reliability indexes \(\beta\) is reached for both the traditional approach (Fig. 13) and the POT-based approach (Fig. 14).

Fig. 13
figure 13

Convergence for the reliability index \(\beta\), fatigue by EN

Full size image
Fig. 14
figure 14

Convergence for the reliability index \(\beta\), fatigue by POT

Full size image

Then, for both reference periods of 50 and 120 years, reliability indexes obtained with the POT-based approach and with the traditional approach, see Table 4 and Fig. 15.

Table 3 Random variables for the fatigue reliability analysis
Full size table
Table 4 Results of the fatigue reliability analysis
Full size table

The reliability indexes, obtained for the various return periods, are lower when calculated with the proposed POT-approach than with the usual, linear extrapolation approach: those calculated with the POT approach are equal to approximatively 60% to 75% of those calculated with the linear approach.

Moreover, the numerical values of the realiability indexes calculated with the POT approach come close to the minimum value stated by the Eurocodes (4.3 for 50 years and structures with high level of consequence \(RC_3\), see [9]), but remain still greater than this minimum value, even for 120-year calculation.

Fig. 15
figure 15

Evaluation of reliability index with time, for fatigue

Full size image

4 Conclusions

Several limits states, as ULS and FLS here, should be verified for steel structural details of bridge decks. Usually, fatigue damage accumulated in a detail during a monitoring period is linearly extrapolated in time. A methodology has been proposed for predicting the numbers of fatigue cycles with the POT approach. It is based on fitting the GPD to a number of fatigue cycles.

Comparison of the proposed approach with the classical method has been carried out on the example of the orthotropic deck of Millau viaduct.

The fatigue damage has been computed, based on 180 days of monitoring data, and has been extrapolated linearly (as it is usually done) and by POT-based approach. Both methods prove that at the end of the design life of the viaduct, reliability of the structural details due to fatigue is higher than required by the EN value for the reference period of 50 years. The suggested probabilistic approach gives a slightly lower reliability level of the studied structural detail. It can be explained by the change of traffic in volume and vehicles weight over the measured period.

This work can be followed by several additional studies in order to observe how the proposed method works for various structural details of different types of bridges. This study can also be extended by using longer monitoring of loads or load effects. This can demonstrate how the duration of monitoring influences the results of extrapolating fatigue damage in time with the proposed probabilistic method.