1 Introduction

Heterogeneous customer requirements and growing competition urge companies to offer more and more product variants [1]. Therefore, they increasingly produce small series, small batches or single pieces [2]. Due to the small quantities, Statistical Process Control (SPC) is no longer applicable as large sample sizes of approximately 125 values are required to achieve reliable estimations and information [3]. Companies can no longer make quality relevant decisions or prove their process capability to their customer. The control limits of control charts become too large to detect instabilities and are therefore—in practice—no longer useful. Another reason is that the required confidence intervals of the capability indices are dependent on the sample size and become too large to be informative. To overcome the problem of too small sample sizes different approaches exist [4]. Change point models [5], control charts with greater sensitivity [6], self-starting charts [7], pre-control-charts [8], Bayesian approaches [9], control charting process and parameters instead of product features [10] are exclusively for control charts. Normalizing and grouping of similar features (grouping) [11] as well as bootstrapping [12] are methods for the general application of SPC. This is advantageous, as we cannot only use the enlarged dataset for control charts but also for more informative process capability analyses with more reliable confidence limits due to an enlarged sample size. Whereas grouping is preferable, as according to Ryan, bootstrapping does not work well with SPC applications for example when distributions are skewed [12]. When grouping, the data originates from real production data and we do not artificially enlarge the data, which makes the SPC results more trustworthy and applicable in a production environment. In addition, the ISO 7870-8 Control charts—Part 8: Charting techniques for short runs and small mixed batches suggests to group data for enlarging the sample size for the application to SPC, but does not provide a sufficient technique how to do so. For these reasons, this paper scrutinizes grouping approaches. Especially grouping algorithms—automated grouping approaches—are of interest as the time and the knowledge of what to group as well as methods on how to group are often not available within companies. Additionally, grouping algorithms provide more objective results compared to expert knowledge.

The requirements on grouping and respectively on grouping algorithms originate from the application of SPC. The idea of SPC is monitoring the variation of product features to distinguish between natural variation and variation due to assignable causes originating from a production process. By identifying and eliminating an assignable cause, we reduce the overall variation and thus optimize the process [13]. SPC is obliged to a great number of data of the corresponding products to achieve significant statements on which we can base decisions. Therefore, for low volume production, grouping is a solution to achieve the required data [14]. When grouping data, we add a third type of variation: variation due to grouping. The different product properties (e.g. different materials) and the different process set-ups (e.g. different clamping) cause this variation. Grouping can obscure the variation due to assignable causes and lead to either false alarms or no alarms at all in control charts. To minimize variation due to grouping, grouping algorithms are applied which only combine statistically similar groups. We use following definitions regarding grouping algorithms in the further context of this paper:

  • Similar features are features of the same type produced by processes of the same technology and have quality characteristics with the same distribution, homogenous spread and location [11].

  • Grouping of similar features means combining similar features descending from different products [11].

  • Grouping algorithms automatically identify and combine similar features to increase the database by using historical measurement data of similar features and statistical methods [11].

Not many grouping algorithms exist and furthermore they have not been compared systematically yet. In this paper, we firstly introduce the state of the art regarding grouping algorithms. Secondly, we set up requirements on grouping algorithms. Thirdly, we introduce statistical methods used within grouping algorithms. Fourthly, we present four different grouping algorithms, which we developed ourselves, in consideration of the requirements and different criteria deducted from the concepts of discretization processes. Furthermore, we also vary two of the four grouping algorithms slightly. Fifthly, we test the algorithms for their reliability and usefulness. We choose or design performance indices based on the requirements. By conducting a full-factorial Design of Experiments, which is based on a simulation with artificial data on the grouping algorithms, performance indices are calculated. Sixthly, with these performance indices we evaluate the requirements for their fulfillment. Seventhly, a summary and conclusion is provided which grouping algorithm and which setting parameters are the best.

2 State of the art on grouping algorithms

In literature, two grouping algorithms for the application of SPC to small quantities exist: by Al-Salti et al. and by Wiederhold. In the following, we provide a short review on these grouping algorithms.

2.1 Grouping algorithm according to Al-Salti et al

The grouping algorithm by Al-Salti et al. is based on Group Technology (GT) [15] and similar to the works of Cheng [16]. GT is a manufacturing technique. GT reduces the costs of manufacturing small batches. When using GT component groups are created based on similarities in design and manufacturing for example by grouping components with a similar geometry. The following procedures to group components according to GT exist:

  • Visual search, where an expert defines variants based on part geometry [17].

  • A Coding and Classification System, which experts create depending on the components of the company. The experts give each property of the component a number, e.g. the material, clamping, etc. Like this, each variant receives a specific number (Opitz-code) [18]. The similarity of the sequence of numbers indicates the similarity of the variants [17].

  • The cladistics originates from biology. In manufacturing, it includes the evolutionary development of a component and its relationship to similar components. An expert creates a tree about the relationship of similar component features [19].

A deficit of GT is that it is a systematic approach, which only classifies components mostly according to their geometry. GT does not take into consideration, whether this classification also corresponds to empirical analyses with historical measurement data of the features.

Al-Salti et al. extend GT by the mentioned missing empirical analysis and assume that the features of those grouped components have similar quality characteristics as well as statistical properties and therefore use GT to increase the database for applying SPC [15]. The idea is that the data of similarly manufactured components (e.g. equal work plans) also possess similar statistical properties.

Al-Salti et al.’s approach consists of two steps. Firstly, an expert creates a Classification and Coding System. Hereby each property of a component gets a digit for example each material. The expert encodes all the properties of each component accordingly and creates a database with the codes and the historical measurements of the components.

Secondly, if data for an SPC analysis of a component’s feature is needed it is firstly evaluated if sufficient data is available. If not one or several digits of the code freed. An expert makes the decision, which digit is freed, by testing the potentially similar components with statistical methods. Therefore, the expert retrieves historical measurement data of the components’ features from the database and creates samples based on the code. Hypothesis tests for homogeneity of spread by using the F-test and for homogeneity of location by using a one-way Analysis of Variance (ANOVA) tests these groups. To compensate varying dimensions of potentially similar features the deviation from nominal (DNOM) of the features is formed. If the test proves homogeneity, the expert groups the components’ features. This means these digits/properties of the components are not relevant any longer, meaning more components have the same code and the database is larger. Result are statistically similar features for the application to SPC [15].

2.2 Grouping algorithm according to Wiederhold

Wiederhold groups individual similar features of components according to factor and factor levels in order to apply SPC. The grouping algorithm allows an automated analysis of non-parametric empirical process data [11]. The algorithm consists of three steps. The algorithm repeats the three steps until it has considered all factors and formed all groups.

In the first step, an expert creates the required database. It contains historical measurement data and possibly relevant factors and factor levels about the process and the product (material, tool, etc.) meant to cause variation due to grouping. Expert knowledge determines these factors and factor levels. The expert answers following question to identify these: “What are differences of similar features that could prevent a grouping? Possible differences identified by experts could be the material, the geometric element, the tool, clamping etc. the feature has been produced in. These differences are translated to factor and factor levels and used to preprocess the data for the application to the algorithms. Additionally from the historical measurement data, the DNOM is calculated. The resulting database serves as input for the next step [11].

The second step involves checking all factors and factor levels for their homogeneity of spread and location by using the Levene- and the Kruskal–Wallis-test. The algorithm sees the factor with the smallest p value as the one causing the highest inhomogeneity and chooses it first. On the factor levels of this factor, a cluster analysis is applied. As input for the cluster analysis, the spread and location of the factor levels are used. On the first run, the algorithm forms two clusters. If the tests show that these clusters are not homogeneous, the algorithms increases the number of clusters by one and repeats the cluster analysis. If both, spread and location are homogeneous, the algorithm forms the groups [11].

The third step consists of recursively calling the entire grouping algorithm. On each recursion, the algorithms examines the most significant—not yet examined—factor. It is possible that the groups split up further. To realize the recursion calls, all so far created groups are selected one after the other and used as database. The grouping algorithm terminates as soon as it has considered all factors [11].

2.3 Conclusion

Al-Salti et al.’s grouping algorithm is not suitable for data with arbitrary distribution, as the incorporated ANOVA requires the residuals of data to be normally distributed. Furthermore, the algorithm is not fully automatic. Both grouping algorithms are costly for a practical application in a production environment, because they require a lot of expert process knowledge to determine possibly relevant factors, for creating a Coding and Classification System or pre-processing the required database. This knowledge is often not available or its creation and application very time-consuming for companies. Furthermore, the performance of these algorithms has never been tested or compared. Within this paper, new automatic grouping algorithms are developed and compared. In the following, we describe the methods used within these algorithms.

3 Commonly used methods within grouping algorithms

In the following, we introduce the building blocks for grouping algorithms. According to these building blocks, we design new easy-to-use grouping algorithms and introduce them in the subsequent chapter. Grouping algorithms need to successfully measure if potential groups possess a homogenous spread and location. We adopt Wiederhold’s assumption, that the distributions of features originating from the same technology are always the same; we do not include Goodness-of-fit-tests in the grouping algorithms [11]. To measure the homogeneity of spread and location we use the p value.

The p value is the probability to achieve the same or extreme result by a sample if the null hypothesis is true [13]. The grouping algorithms heuristically use the p value as a measure of homogeneity. The higher the p value the more homogenous the combined groups [11]. Consequently, a group with a p value smaller than the significance level is inhomogeneous. In the following, we introduce the statistical tests applied to check the homogeneity of spread and location within our grouping algorithms and choose the best fitting ones as building blocks.

3.1 Testing the homogeneity of spread

Tests of homogeneity of spread aim to check whether the spreads of groups are the same. The following null hypothesis \( H_{0} : \sigma_{1}^{2} = \sigma_{2}^{2} = \cdots = \sigma_{n}^{2} \) and alternative hypothesis \( H_{1} : At\;least\;two\;variances\;are\;different \) are tested. Possible candidates to do so are the Brown-Forsythe-, Barlett- and Levene-test. To make the grouping algorithm applicable for features with arbitrary distributions and as the Brown–Forsythe-test and the Barlett-test require a normal distribution, we choose the Levene-test. The Levene-test examines the equality of group deviations from a population [20]. It calculates the deviations of each dependent variable from the arithmetic mean of the group for the test. The Levene-test performs an ANOVA on the calculated variances. The ANOVA determines if \( H_{0} \) is accepted or not [20].

3.2 Testing the homogeneity of location

ANOVA, Median test and Kruskal–Wallis test check whether two or more samples come from a population with the same location parameter. The null hypothesis \( H_{0} :\mu_{1}^{2} = \mu_{2}^{2} = \cdots = \mu_{n}^{2} \) and alternative hypothesis \( H_{1} : At \, least \, two \, means \, are \, different \) are tested. For the algorithms, we choose the Kruskal–Wallis-test as the ANOVA requires residuals of the distributions to be normally distributed and the Median-test has low power [20]. The Kruskal–Wallis-test uses the mean of the ranking values of groups to check the homogeneity of location. First, the Kruskal–Wallis-test examines all measured values without their group membership, sorts them in order and assigns them a rank. With those ranks and by considering the group membership again it conducts a one-way ANOVA. The Kruskal–Wallis-test requires the distributions of the groups to be of the same type and form. This requirement is met with the assumption that distributions of features originating from the same technology always have the same distribution [11].

4 Developed grouping algorithm alternatives and adaption of existing grouping algorithms for evaluation

This paragraph gives an overview on properties to develop grouping algorithms, the process of grouping, requirements on grouping algorithms and variations to test for homogeneity of location and spread. We then use these to create the new grouping algorithms.

We deduct the properties and process of grouping from discretization algorithms for continuous data. Lui et al. generalized these properties for these discretization algorithms [21]. Due to their similarity to grouping algorithms, we take on the properties and slightly adapt them for grouping. We deduct the following properties from discretization algorithms and transfer them as general properties to construct new grouping algorithms:

  • Supervised/unsupervised: Supervised methods consider continuous data as well as a class information. Unsupervised methods only consider the continuous data without a class information.

  • Splitting/merging: Splitting methods consider the whole dataset and split it into groups. Merging methods take each group separately and try to merge them into bigger groups.

  • Direct/incremental: Direct methods have an information about how many groups they should create. Incremental methods possess a stopping criterion according to which they stop creating further groups.

  • Univariate/multivariate: Univariate methods discretize one continuous feature at a time. Multi-variate methods discretize multiple features simultaneously.

We can simplify the process of grouping into three steps. In these steps, we integrate the above-mentioned properties to create new grouping algorithms. The steps are:

  • Evaluation: For splitting methods, the process seeks the best separation. For merging methods, the process seeks the best combination of groups. Therefore, an evaluation function is used. Typically, the process uses measures like entropy or statistical measures like homogeneity (p value).

  • Splitting/Merging: The process splits or merges the data to smaller or bigger groups.

  • Stopping: In this step, the process analyses if it has met a stopping criteria. The stopping criteria is a trade-off of the size of the groups and the required homogeneity.

We deducted the following requirements on grouping algorithms by discussions with industry and by analyzing several datasets from real production processes, which companies, which produce in low volumes, provided. Grouping algorithms need to fulfill following requirements within a production environment:

  • Grouping algorithms must be capable of working with variable sample sizes to enable them to process real data from small series production.

  • Grouping algorithms must be capable of working with different distributions. Therefore, an expert does not have to make an assumption about the distribution of the measurements.

  • Grouping algorithms must be able to keep the groups as homogeneous as possible to avoid alpha errors and beta errors.

  • Grouping algorithms should require as little expert knowledge as possible to enable an easy automation of the process of grouping.

  • The significance level of grouping algorithms should be variable to make the risk of rejecting a hypothesis adjustable.

We developed four different grouping algorithms according to the process of grouping and the requirements. As evaluation criteria, we use the p value and as stopping criteria we use the significance level of the Levene- and Kruskal–Wallis-test.

  • Grouping based on cluster analysis and splitting

  • Grouping based on ChiMerge and splitting

  • Grouping based on comparison and merging

  • Grouping based on splitting

Differently to the grouping algorithms by Al-Salti et al. and Wiederhold our four grouping algorithms do not require expert knowledge [11, 15]. This is an advantage as often within companies, this knowledge is not fully available and integrating the knowledge into the dataset by pre-processing the dataset is often too time-consuming for companies. We achieve this by only using class information for equal features. Therefore, the only expert knowledge and data pre-processing, which our algorithms require is the division of the features in different feature classes like length, diameter, etc. Furthermore, all feature regardless of their feature class have a unique ID. The unique ID contains all information about the feature like material, tolerance etc. The algorithms then perform the division of the features into groups only based on statistical variability.

For creating grouping algorithms, two options to use p values are possible. The Levene-test must always be applied before the Kruskal–Wallis-test as the Kruskal–Wallis-test requires a homogenous spread as a condition to be applicable. According to this condition, two options to create grouping algorithms are possible:

  1. 1.

    Testing p values of spread and location separately First conducting the whole algorithms with the p value of the Levene-test and group accordingly. In the second step, using the groups created as input for re-running the algorithm but this time applying the Kruskal–Wallis-test to calculate the p values and split groups further to achieve the homogeneity of location.

  2. 2.

    Pooling the p values of spread and location To get the set of p values the algorithm firstly conducts the Levene-test. If the spread proves to be homogeneous according to the Levene-test the algorithm conducts the Kruskal–Wallis-test and its p value is used instead. The p values of the Levene-test, which rejected the null hypothesis and the ones of the Kruskal–Wallis-test are pooled. From that pool, the algorithm chooses the smallest p value to split the group.

In the following, we explain the algorithms based on the defined principles and the simplified grouping process. We do not compare the algorithms with the algorithm Al-Salti et al. as this algorithm is based on an ANOVA and only handles data with normally distributed residuals. We conduct a comparison with a simplified version of Wiederhold (algorithm based on cluster analysis and splitting) as the original algorithm firstly requires data (factor and factor levels), which are then no longer comparable with the other algorithms (chapter 5 and 6) and secondly for the real datasets was not available due to a lack of expert knowledge (chapter 7).

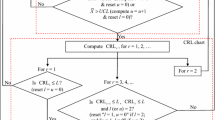
4.1 Algorithm based on cluster analysis and splitting

The algorithm based on cluster analysis and splitting is an adaptation of Wiederhold’s algorithm, which only takes the class information into consideration [11]. The algorithm is depicted in Fig. 1.

Fig. 1
figure 1

Flowchart for algorithm based on cluster analysis and splitting. The p value for the whole data is calculated. If the p value is smaller than the significance level, cluster analysis is used to create groups. If these are above the significance level they are homogenous

Full size image

First step consists of calculating the DNOM and creating the database. The p values are calculated by using this database and applying the Levene-test and Kruskal–Wallis-test. If the p value is below the significance level, the cluster analysis, which is also used by Wiederhold, is applied on the spread and the location of the features [11].

Wiederhold’s grouping algorithm uses the divisive hierarchical DIANA clustering [11]. Differently to any other clustering all data is in one cluster at the beginning and divided into clusters by following approach [22]:

  1. 1.

    In the beginning, all observations are in one cluster;

  2. 2.

    Choose the cluster with the largest distance metric and divide it into two subclusters.

    1. (a)

      Find the object with the largest mean distance to all other objects. This object is the first element of the new splitter group.

    2. (b)

      For each object in the larger cluster, calculate the mean distance to the remaining objects and compare it with the mean distance to the objects in the splitter group. The objects closer to the splitter group are assigned to the splitter group.

  3. 3.

    Repeat this process until each cluster contains only a single observation.

As a distance metric, the Euclidean or the Manhattan distance are possible choices. The Euclidean distance is a straight-line distance between two points in Euclidean space. The Manhattan distance is a grid-like distance represented by the sum of absolute differences of the Cartesian coordinates. Wiederhold proposes the Manhattan since the estimated mean and standard deviation are independent of each other [11]. As an output, the algorithm creates a dendrogramm, which orders possible clusters according to similarity.

After the group is split for each created subcluster the p value is calculated again with the Levene-test and Kruskal–Wallis-test. If the lowest p value of any subcluster still proves to be below the significance level the subcluster is split further by increasing the amount of clusters by one. This is repeated until a homogenous state is achieved and all lowest p value are above the significance level.

4.2 Algorithm based on ChiMerge and splitting

The algorithm based on ChiMerge and splitting in Fig. 2 is explained by dividing it into three steps. In the first step, the database is created. For each measurement, the deviation between the target value and the measured value is calculated and assigned to the feature (DNOM). The database is sorted according to the size of the deviation. It serves as input for the second step.

Fig. 2
figure 2

Flowchart for the algorithm based on ChiMerge and splitting. The ChiMerge-algorithm is used to create intervals. These intervals are used as input for a frequency table from which groups are deducted according to the class frequency

Full size image

In the second step, using the sorted database the algorithm forms intervals. The creation of the intervals is divided into three sub-steps. First, the algorithm splits the sorted database from the first step between changes of different features. This results in intervals. In the next sub-step, the algorithms performs the Chi square-test for all adjacent intervals and saves the Chi square-statistic. In the second sub-step—after all Chi square-statistics have been calculated and saved—the algorithms combines the units with the smallest Chi square-statistic. This results in new intervals in each run. In the third sub-step, the algorithm only joins adjacent intervals if the Chi square-statistic is below the Chi square-threshold determined by a specified significance level. If all values are above the significance level, the intervals generated so far serve as input for this step.

In the third step, the grouping algorithm meets the requirement that it has assigned all measurements of a feature to the same group. During the creation of the intervals this assignment of the measurements to the features is ignored [20]. The algorithm assigns each characteristic value to the interval in which the characteristic is most frequently represented by using a frequency table. Once the algorithm has assigned all characteristic values to an interval, it regards them as a group. The algorithm checks the groups using the Levene-test and Kruskal–Wallis-test. If the hypothesis tests show that the formed groups are still inhomogeneous, the algorithm splits them up by applying the algorithm again. All steps are recursively repeated until the Levene-test and Kruskal–Wallis-test prove the homogeneity of spread and location for each group.

4.3 Algorithm based on comparison and merging

The algorithm based on comparison and merging in Fig. 3 is a greedy algorithm, it selects the best result without considering future steps. It consists of three steps. In the first step, it generates the database containing the DNOM of the features. The resulting database serves as input for the next step.

Fig. 3
figure 3

Flowchart for algorithm based on comparison and merging. Pairwise combinations are created. For each combination a p value is calculated. The combination with the largest p value is merged to a group

Full size image

In this second step, the algorithm applies the Levene-test. Its aim is to create a pre-grouping for the Kruskal–Wallis-test. The second step consists of two sub-steps. First, the algorithms forms all possible combinations of two features. Second, the algorithm applies the Levene-test to each of these combinations. The p value resulting from the tests are stored. Third, after the algorithm has saved all p values, it selects the combination with the highest p value. If the p value is below the specified significance level, it dissolves the combination into its original parts, because the p value indicates a significant difference between the variances. The algorithm repeats the second step using the new groups until the highest calculated p value is lower than the significance level. The groups created up to this point serve as input for the third step.

In the third step, the homogeneity of the location is tested. For this purpose, the Kruskal–Wallis-test is used. The second and third steps are almost identical. The difference is that the algorithm uses the Kruskal–Wallis-test instead of the Levene-test to check the homogeneity of the location and calculate the p value. Each step resulting from the second step serves as input for the third step.

We created a variation of this grouping algorithm, where the algorithm pools the p values of spread and location. Accordingly the third step is dropped. The variation is referred to as algorithm based on comparison and merging 2.

4.4 Algorithm based on comparison and splitting

The algorithm based on comparison splitting in Fig. 4 is a greedy algorithm. The algorithm consists of three steps. In the first step, the database containing all features and DNOM is created. The database from the first step serves as input for the second.

Fig. 4
figure 4

Flowchart for algorithm based on comparison and splitting. Combinations are created by taking out each class out of the group once. For each combination a p value is calculated. The combination with the largest p value is grouped

Full size image

The second step consists of sub-steps. First, the algorithm forms various combinations of features. To do this, the algorithm examines entire database and excludes one feature. n different combinations with n + 1 features exist. After the algorithm has created all the combinations, each p value of the Levene-test is determined and stored. That means the algorithm calculates the p value of each combination without considering the excluded group. The Levene-test checks the sample for its homogeneity of spread. After the algorithm has performed all Levene-tests and stored all p values, it selects the combination with the largest p value. It assumes that this sample is the most homogeneous. The algorithm saves the feature excluded in this combination separately with other features. If the p value of the considered combination is above the significance level, the algorithm forms the group with all included features. If this is not the case, the algorithm repeats the process of excluding a feature, whereas the previously excluded feature is no longer considered. If the algorithm achieves and saves a homogeneous group, the excluded features are the new database and the algorithm repeats the second step with those features.

In the third step, the algorithm checks the homogeneity of location of the found groups of the second step. The algorithm repeats the second step, except that it uses the Kruskal–Wallis-test instead of the Levene-test. Output of this test are groups with homogenous spread and location.

A variation of this grouping algorithm exists, where the p values of spread and location are pooled. Accordingly the third step is dropped. The variation is referred to as algorithm based on comparison and splitting 2.

5 Performance metrics and evaluation method

To evaluate the different algorithms a full factorial Design of Experiments (DoE) is applied. We define two performance metrics showing the quality of the grouping by using the main requirements the grouping algorithms have to fulfill. We identified influences on the grouping by firstly scrutinizing datasets with real measurements and secondly by conducting expert discussions on what factors (chosen significance level, group size, etc.) might affect the grouping algorithms. According to these effects, a simulation with the programming language R was set up.

5.1 Influences on groupings

We conducted a DoE to determine the effects between influencing factors and our target variables size of created groups, separation and compactness. In order to be able to recognize the interrelationships of the individual parameters, we selected a higher number of factor levels. We used the factor and factor levels listed in Table 1 to test how well the algorithms perform.

Table 1 Factor, factor levels and the reason for choosing them for testing different algorithms
Full size table

5.2 Target variables: figures of evaluation

For a successful application of SPC to low volume production the following requirements have to be fulfilled:

  • The algorithms should provide as large groups as possible to provide a sufficiently large database for further statistical methods like control charts or process performance evaluations.

  • The algorithms should provide as homogeneous groups as possible regarding location and spread to realize a good average run length for control charts to prevent false alarms due to groups with differing location and spread.

Deducted from those two requirements to evaluate the grouping algorithms, we chose following performance indices size of created groups, separation and compactness (SDbw):

5.2.1 Size of created groups

The index shows the average sizes of groups in relation to sizes of groups created by the algorithm. The following formula is used:

$$ t = \frac{{\frac{{\mathop \sum \nolimits_{i = 1}^{n} x_{deposited groups, i} }}{{n_{deposited groups} }}}}{{\frac{{\mathop \sum \nolimits_{j = 1}^{m} x_{created groups by algorithm, j} }}{{n_{created groups by algorithm} }}}} $$

x: size of group; n: amount of deposited groups; i: number of deposited groups; m: amount of the created groups; j: number of created groups.

t can be between 0 and 1 whereas a smaller number indicates that group sizes increased by grouping whereas 1 indicates that group sizes stayed the same and no groups were grouped.

5.2.2 SDbw: compactness and separation

SDbw is made up of two measures: compactness and separation. A small value says the measured values within a group are very similar. SDbw takes on values between 0 and 2. A SDbw-value close to 0 indicates a high separation and compactness. SDbw consists of following formula according to Liu et al. [23]:

$$ SDbw = Dens\_bw\left( {NC} \right) + Scat\left( {NC} \right) $$

SDbw: Compactness and Separation; Dens_bw: Compactness; Scat: Separation; NC: number of clusters.

Compactness The compactness of a group determines how similar the individual measured values within a group are. It shows how close the measured values are. The compactness of a group is determined without placing it in relation to other groups. It shows how well the individual measurements within a group fit. To evaluate the compactness, we chose the formula by Liu et al., as it proved the best according to simulations conducted by Liu et al. [23].

$$ Scat\left( {NC} \right) = \frac{1}{NC}\mathop \sum \limits_{i} \frac{\|{\sigma \left( {C_{i} } \right)}\|}{\|\sigma \left( D \right)\|} $$

Scat: Separation; NC: number of clusters; σ: variance; Ci: the i-th cluster; D: dataset.

Separation The separation of groups indicates how clearly the groups differ from each other. It shows, if points are clearly assigned to a group, or if there are overlaps or inconsistencies between groups. The separation is evaluated in relation to other groups. If only one group exists, no separation measure is calculated. To evaluate the separation, we chose the formula by Liu et al., as it proved the best according to simulations conducted by Liu et al. [23]:

$$ Dens\_bw\left( {NC} \right) = \frac{1}{{NC\left( {NC - 1} \right)}}\mathop \sum \limits_{i} \left[ {\mathop \sum \limits_{j,j \ne i} \frac{{\mathop \sum \nolimits_{{x \in C_{i } \cup C_{j} }} f\left( {x, u_{i,j} } \right)}}{{max\left\{ {\mathop \sum \nolimits_{{x \in C_{i} }} f\left( {x, c_{i} } \right), \mathop \sum \nolimits_{{x \in C_{j} }} f\left( {x, c_{j} } \right)} \right\}}}} \right] $$

D: dataset; n: number of objects in D; c: center of D; P: attributes number of D; NC: number of clusters; Ci: the i-th cluster; ni: number of objects in Ci; Ci: center of Ci; (Ci): variance vector of Ci; (x, y): distance between x and y; \( X_{i} = \left( {X_{i}^{T} \cdot X_{i} } \right)^{{\frac{1}{2}}} \)

6 Evaluation of grouping algorithms

We used the programming language R and the development environment RStudio to implement the grouping algorithms as well as the simulation according to a full factorial DoE using the factors and their corresponding factor levels recorded in Table 1. We conducted the simulation twelve times and averaged the results. For their implementation, following functions in R were used: Levene-test, Kruskal–Wallis-test, ChiMerge of the R package Discretization and SDbw of the R package NbClust.

In Fig. 5 the main effects of the DoE are depicted. The ordinate axis shows the SDbw means of the main effects. The abscissa axis shows the examined factors and factor levels. If the mean of the SDbw are low it indicates a good separation and compactness.

Fig. 5
figure 5

Main effect diagram of SDbw. The different grouping algorithms are compared. The lower the SDbw-value the more homogenous are the groups created by the grouping algorithm. According to the evaluation the algorithm based on cluster analysis and splitting creates the most homogenous groups

Full size image

From Fig. 5 and the DoE, we deduct the following about the factors and the algorithms:

  • The amount of groups has a major effect on the SDbw. The more groups exist the better the SDbw. With an increasing amount of groups, the SDbw decreases, as the probability to form more homogenous groups increases.

  • As the size of groups increases, the SDbw increases, as groups become less compact and less separable. Variable group sizes do not have a big effect (Variable group sizes were comparable to the group sizes of 5).

  • The type of distribution does not have a great effect on the grouping algorithms, except the uniform distribution, as separation and compactness are hard to distinguish for this distribution.

  • The location has a big effect on the SDbw. The further the distance between the groups the smaller the SDbw due to a better separation of the groups.

  • The spread has a major effect on the SDbw. With increasing spread, SDbw increases due to less compactness and decreased separation.

  • With increasing significance level, SDbw decreases slightly as groups become more compact.

  • Pooling p values or evaluating them separately does not have a major effect on the SDbw as can be seen by the algorithms based on splitting or comparison.

  • The algorithm based on cluster analysis and splitting forms groups with the lowest SDbw. Therefore the algorithm outperforms the other algorithms in achieving the most compact and separable groups.

  • The algorithms based on comparison and splitting achieve the highest SDbw, which indicates that they perform worst.

  • The algorithm based on the ChiMerge and splitting achieves a high SDbw.

  • The algorithms based on comparison and merging perform similar to each other and are second after the algorithm based on the cluster analysis and splitting.

In Fig. 6 the main effects of the simulation for t are depicted. The ordinate axis shows the means of the SDbw regarding the main effects. The abscissa shows the examined factors and factor levels.

Fig. 6
figure 6

Main effect diagram of t. The lower the t-value larger the groups created by the grouping algorithm. According to the evaluation the Algorithm based ChiMerge and splitting creates the largest groups

Full size image

From Fig. 6 and the simulation, we deduct the following about the factors and the algorithms:

  • As the amount of groups increases, t decreases. This indicates that it is more likely to cluster groups if more groups are available.

  • As the group size increases, t increases. It shows the more values within a group are available the less likely it is to cluster groups. A reason could be that the location and spread of a group can be better estimated leading to less clustered groups.

  • As the location between groups increases, the less groups are clustered. It shows that the algorithms fulfill the requirement of identifying homogenous groups.

  • As the spread of the groups, increases the more groups are clustered. It shows that wide spreads affect the algorithms, which obscure finding homogenous groups.

  • With increasing significance level, the less groups are clustered. It shows that the p value fulfills the requirement of being a heuristic for homogeneity.

  • Pooling p values or evaluating them separately has an effect on t. Pooling leads to larger group sizes for the algorithms based on splitting and smaller groups for algorithms based on comparison.

  • The algorithms based on comparison and splitting cluster and the algorithm based on cluster analysis and splitting form the least groups and behave similar.

  • The algorithms based on comparison and merging behave very similar and cluster the second most groups.

  • The algorithm based on the Chi square-statistic clusters the most groups.

In conclusion, we deduct the following from Figs. 5 and 6: The simulation results suggest that the algorithm based on cluster analysis and splitting is the most optimal one to find compact and separable groups. The algorithm based on the Chi square-statistic clusters the most groups, but achieves a bad SDbw. To create groups for SPC the homogeneity of the groups is more important than the group sizes therefore we suggest using the algorithm based on cluster analysis and splitting. In the further progress of this paper, the focus is set on the algorithm based on cluster analysis and splitting.

In Figs. 7 and 8, the interaction diagram of the algorithm based on cluster analysis and splitting is depicted which provides information about how factors behave to each other. As the interaction diagrams of the other algorithms are very similar, we use the interaction diagram of the algorithm based on cluster analysis and splitting as example.

Fig. 7
figure 7

Interaction diagram of SDbw of the algorithm based on cluster analysis and splitting. Size of groups/significance level have an interaction. Location/Spread have an interaction

Full size image
Fig. 8
figure 8

Interaction diagram for t of the algorithm based on cluster analysis and splitting. No interactions are found

Full size image

Within an interaction diagram, two factors have an influence on each other if their lines do not run parallel to each other. Therefore, only the interactions between those factors are considered. From Figs. 7 and 8 and the simulation, following can be deducted:

  • Significance level/Amount of groups: For small amount of groups a smaller significance level lead to a smaller SDbw and less groups are clustered. A larger amount of groups and a larger significance level lead to a smaller SDbw and less clustered groups. Reason is that compactness and separation are estimated higher due to the less amount of data points.

  • Size of groups/Significance level: The larger the significance level and the larger the size of groups the lower the SDbw the less groups are clustered. The larger the significance level and the smaller the size of groups the larger the SDbw and the more groups are clustered. Nonetheless, the SDbw and consequently the homogeneity does not worsen or improve a lot. By changing the significance level from 0.05 to 0.9, an improvement of approximately \( \frac{0.6935 - 0.5550}{2 - 0} \) = 7% (figures as highlighted in Fig. 7 divided by the maximum SDbw = 2) of the SDbw is possible. We propose a clustering with a significance level of 0.05 to achieve homogenous groups with a sufficient size of groups for the application to SPC.

  • Spread/Location: Groups with a small spread and with wider distanced locations lead to a smaller SDbw. Close distanced locations and wide spreads lead to clustering of groups. Therefore, the algorithms work better if location and spread are separable.

7 Application of grouping algorithms to Statistical Process Control

The usual application of control charts consists of phase I and phase II. Phase I has the objective to provide valid control limits by calculating them with data under statistical control. Therefore, the process owner collects data, which the process owner analyzes by constructing trial control limits to scrutinize if the process was in control while the data was gathered. If not, the process owner removes the assignable causes and repeats the collection of data until control limits with data under statistical control can be calculated. Phase II follows after achieving the objective of phase I. It uses the control chart to monitor the process and maintain its capability [13]. The usage of the grouping algorithms is during phase I. For every removal of an assignable cause and repeated calculation of control limits, the features must be regrouped to identify if the groups still exist after the assignable cause was removed or when the process is in control. This ensures that the groups and control limits are based on valid data and do not happen to be blurred by instabilities like a change of location or spread.

In order to test the applicability of the grouping algorithms and to investigate, whether we can group homogeneous features in small series production, we apply the grouping algorithms to data of turned parts. The data was generated within the framework of the research project “GriPS: Software-supported grouping of similar characteristics for process control in small quantities” and “APProVe: App-based effort reduction for adaptive inspection in variant production” at a participating company. One of the companies produces turned parts in small series with different dimensions. One of the features of interest is the inner diameter. Table 2 shows an excerpt of the provided anonymized data, which we applied to the grouping algorithms. The data is for a phase I application of SPC.

Table 2 Excerpt of the historical real-world data from an application scenario with the relevant factors for grouping being “Variant” and “Deviation”
Full size table

In Fig. 9, the data of Table 2 is once applied to a “Variable aim, individual and moving range chart” proposed by ISO 7870-8 without grouping. The control chart highlights the different groups by using different colors. The data is instable as it belongs to phase I of SPC application. Nonetheless, it is visible that we cannot group all variants.

Fig. 9
figure 9

Application of the data without grouping to a “Variable aim, individual and moving range chart” proposed by ISO 7870-8. Different colors highlight the variants within the control charts

Full size image

In Fig. 10, we exemplary applied the data to two different algorithms using a p value of 0.05 to show the performance differences of the algorithms. We achieve four groups with the algorithm based on cluster analysis and splitting. We achieve three groups when using the algorithm based on ChiMerge and splitting. Differences in the mean and variance of the variants’ deviation indicate that the solution with four groups and therefore the algorithm based on cluster analysis and splitting is preferable. This is compliant with the simulation results in chapter 5.

Fig. 10
figure 10

Application of the data with grouping to a “Variable aim, individual and moving range chart” proposed by ISO 7870-8. The algorithm based on cluster analysis splitting and the algorithm based on ChiMerge and splitting created the groups at the proposed p value of 0.05. Their different grouping results (four groups vs. three groups) are depicted in the figure. Different colors highlight the grouped variants within the control charts

Full size image

In Fig. 11, we show the effect of how different p values lead to different amount of groups on the example of the algorithm based on cluster analysis and splitting. As visible, the algorithm creates more groups the higher the p value (0.001 vs. 0.05). Therefore, the homogeneity of the groups is controllable by the p value. To achieve sufficiently homogenous groups a p value of 0.05 is proposed as shown by the simulation.

Fig. 11
figure 11

Effect of different p values on the amount of created groups. The higher the p value the more groups the grouping algorithms create. The effect is shown on the example of the algorithm based on cluster analysis and splitting using the “Variable aim, individual and moving range chart” proposed by ISO 7870-8. Different colors highlight the grouped variants within the control charts

Full size image

The data of the process depicted in Figs. 9, 10 and 11 is for a phase I application of SPC and not stable. Within this use case, using the grouping algorithm the process owner could assign some of the special causes to an unsuitable clamping of some variants. In the next step, the process owner has to apply the grouping algorithm again and revise the formed groups after changing the clamping. The process owner has to collect data and regroup the variants using the grouping algorithms until the stability of the process is proven.

8 Discussion

In this study, we presented grouping algorithms to combine samples from different similar production processes. We analyzed what statistical properties the grouping algorithms possess and if they enable the application of SPC to low volume production processes.

Mainly two different approaches exist to enlarge the sample size for SPC. The approaches by Wiederhold and Al-Salti et al.—contrary to our approach—require a lot of knowledge and work force [11]. Experts either need to decide upon which data of which variant can be combined or at least, which factors are important to consider when grouping similar features of variants, e.g. if the variants are made of the same material. This also requires costly data preprocessing. Both, knowledge and work force are often not available in small and medium sized enterprises.

Our approach necessitates little data preprocessing and little expert knowledge, as our grouping algorithms only require historical measurement data of features and a feature category, which shows if features belong to the same entity, e.g. a diameter. The required database and database management is therefore significantly smaller than the one proposed by Zhu et al. Zhu et al. propose a database framework to apply SPC to low volume production based on GT [24]. Conceptual downside of our approach, compared to the other approaches, is, that our approach does not produce process knowledge in the sense that it can be easily comprehended what factors lead to new groups.

Contrary to the work of Al-Salti et al. and Zhu et Al., we tested our grouping algorithms using a full-factorial DOE and simulation data as well as real production data. Al-Salti et al. only tested their approach on one real production data example [15]. Wiederhold tested his algorithm using a simulation and real production data as well, but did not use a full-factorial DOE [11]. Therefore, the quality of his algorithm and the groups it produces are not fully comprehensible yet. The results in the previous two sections show, that the grouping algorithms, and especially the algorithm based on cluster analysis and splitting successfully enlarge the sample sizes. Furthermore, we could show, by using real production data, that an application of SPC for low volume production in phase 1 is possible and allows a detection of special causes.

To analyze grouping algorithms further, works of Lin et al. are promising. Lin et al. analyze what ratio of standard deviations are allowable within grouped features. They use the simulations to find out which average run lengths control charts achieve with grouped data [25]. In future, a combination with their approach and grouping algorithms makes sense for further validating grouping results.

9 Summary and conclusion

From discretization methods, we deducted grouping properties and a grouping process, which can be used to develop further grouping algorithms. We developed four algorithms based on different statistical methods and tested them with a simulation and a DoE. We used the factors amount of groups, size of groups, distribution, location and spread to test the grouping algorithms for their suitability to find homogenous groups. To assess the performance of the algorithms, we used two indices: the SDbw, which assesses the separation and compactness of clustered groups. The index t assesses how many groups are clustered to larger groups. The algorithm based on cluster analysis and splitting proved best at successfully detecting homogeneous groups for an application to SPC. For clustering groups, it performs mediocre compared to the other algorithms according to the evaluation with t, but performs best in finding homogenous groups according to the evaluation with SDbw. We rate the homogeneity of groups as more important than the size of groups for successfully applying SPC. Otherwise alpha and beta errors occur when applying control charts leading to a poor average run length, which would incur high costs due to a needless failure analysis in practice. Furthermore, by scrutinizing interactions between the factors a significance level, we propose a significance level of 0.05 to find homogenous groups with a sufficient size of groups (Figs. 7, 8). Within an application example we showed the applicability of the groups to “Variable aim, individual and moving range chart” proposed by ISO 7870-8.