Dielectric relaxation and magnetodielectric response of mesoporous terbium manganate nanopaticles

Abstract

We report here the investigation on dielectric response, charge transport mechanism and magnetocapacitance of mesoporous perovskite Terbium Manganate (TMO) nanoparticles. TMO NPs possess relatively high specific surface area (20.9 m² g⁻¹) than that of general perovskite-type metal oxides. To study the dielectric/magnetodielectric response in TMO material, a capacitive system is fabricated. Impedence spectroscopy shows electrically heterogeneous nature of the material. Due to the existence of inhomogeneity at electrode-TMO interface, ideality factor is larger than unity. Various Schottky diode electrical parameters are obtained here from temperature dependent capacitance–voltage (C–V) measurements. The function of Au/TMO/Au Schottky diode system is well explained from current–voltage (I–V) characteristics study. Ferroelectric-like hysteretic behaviour is observed at and above room temperature from non-ferroelectric TMO. Presence of defect states at TMO interface layer dominates the charge conduction phenomenon. Negative magnetodielectric effect arises in heterogeneous TMO sample due to the effect of magnetic field on Maxwell–Wagner space charge at the interface.

Graphic abstract

The thermionic current–voltage (I–V) characteristics of the Au/TMO/Au Schottky diode have been measured within the voltage range ± 40 V. Ferroelectric type hysteretic behaviour is observed in non-ferroelectric TMO sample.

1 Introduction

Rare-earth manganites are a major class of perovskite structured multiferroic materials due to the co-existance of both ferroelectricity and magnetism [1, 2]. Due to their multifunctional properties, they have potential applications for smaller and faster electronic devices as well as high energy storage devices [3, 4]. Terbium manganate (TbMnO₃) is an interesting rare-earth manganite multiferroic material, that exhibits orthorhombically distorted perovskite structure at room temperature [5, 6]. Perovskite-type metal oxide compounds [general formula = ABX₃] are considered to be an important class of materials for catalytic oxidations and reductions and solar cell applications [7, 8]. But the major challenge is that perovskite-type materials generally show very small surface area (< 2 m² g⁻¹), which in turn lowers the specific catalytic activity [9]. Researchers are interested to achieve nanomaterials with higher specific surface area. Ahmad et al. reported high specific surface area (304 m² g⁻¹) of multiferroic YMnO₃ nanoparticles [10]. Silva et al. investigated the catalytic activity of perovskite-type oxides with different surface areas of 33–44 m² g⁻¹ [7]. They can be utilised in various applications such as non-volatile memories, solar cells, photovoltaics and light polarisers [11]. Size-morphology dependent magnetic-dielectric behaviour study of multiferroics are in trend [12]. As differed from the properties present in bulk materials, it is very much important to investigate the magnetic and electrical behaviours of the materials at nanoscale region. Discovery of ferroelectric control of magnetic order in perovskite TbMnO₃ invoked intensive researches in the field of magnetodielectric materials [13]. Gupta et al. [14] reported magneto-structural and magneto-electric coupling in multiferroic BiFeO₃–TbMnO₃ composite. Acharya et al. [12] reported the multiferroic behaviour of hydrothermally prepared TbMnO₃ nanoplates. Lu et al. [15] reported the dielectric characteristics of polycrystalline Si-added and Si-doped TbMnO₃ materials. Izquierdo et al. [16] reported the dielectric response of Al-subsitituted multiferroic TbMnO₃ at high temperatures. But there are very few articles on the investigation of dielectric response and defect state contribution in the electrical transport properties of TMO NPs.

The present article reports the morphological, electrical and magnetodielectric characteristics of TbMnO₃ (TMO) NPs. BET (Brunauer–Emmett–Teller) analysis and BJH (Barrett–Joyner–Halenda) analysis are done to get the idea of surface morphology of the material. Here frequency dependent dielectric response of TMO NPs is studied above room temperature and the behaviours have been well explained by suitable theories. Voltage dependent capacitance (C–V) and voltage dependent current (I–V) measurements of the sample are done above room temperature. In this work, various electrical parameters are evaluated to get the information about the current conduction mechanism in the material. Further at room temperature, we have observed significant negative magnetodielectric (MD) response of the material.

2 Experimental details

Detailed synthesis procedure of mesoporous Terbium manganate (TMO) NPs and its physical characterisations are reported earlier [17]. In the present work, room temperature Fourier transform infrared spectrum (FTIR) of the sample (in pellet form milled with KBr) is recorded with FT-IR spectrometer (Thermo Nicolet iS10) in the region of 400–4000 cm⁻¹. The porosity and Brunaur–Emmett–Teller (BET) surface area of the sample is determined by N₂ physisorption measurements by Autosorb IQ gas sorption analyser (Quantachrome Instruments Cooperation). Electrical measurements of the sample are studied by making pellet of sample of area 2.83 × 10⁻⁵ m² and thikness 9.2 × 10⁻³ m. Conducting layer of silver is coated on opposite sides of the pellet to serve as electrodes. To study the electrical properties of the sample above room temperature, an oven with a temperature controller cryostat is used above room temperature. Dielectric measurements are carried out at frequencies ranging from 20 Hz–2 MHz on Agilent E 4980A LCR meter. The capacitance–voltage (C–V) is measured under 2 MHz frequency above room temperature. The I–V characteristic of the sample is obtained by applying a DC field and using computer controlled Keithley source meter (SMU). Susceptibility measurement of TMO NPs is carried out by Magnetic Susceptibility Balance (Sherwood). Using an electromagnet (EM-250), magnetodielectric measurements are done with the variation of the external transverse magnetic field (H ≤ 1 T).

3 Results and discussions

Figure 1 shows FESEM micrograph of TMO NPs of non-uniformly distributed grains. Less dense microstructure is obsereved. The grains are mesoporous in nature.

Fig. 1

FESEM image of TMO NPs

FT-IR study is performed here to substantiate the formation of TMO NPs and the organic residue on the sample (Fig. 2). The absorption peaks centered at 492 cm⁻¹ and 590 cm⁻¹ are the characteristic peaks of Mn–O–Mn bond bending vibration and Mn–O bond stretching vibration of perovskite-type structured Terbium Manganate respectively [18, 19]. A peak centered at 1645 cm⁻¹ comes from the bending vibration of O–H bond of adsorbed water molecule in the sample [19]. A strong absorption band centered at 3430 cm⁻¹ corresponds to the O–H stretch vibration of water [18]. Peaks centered at 1110 cm⁻¹ and 2356 cm⁻¹ come from the CO₂ content present in the atmosphere [20].

Fig. 2

Room temperature FT-IR spectrum of the sample

The surface morphology is observed from BET analysis and the N₂ adsorption/desorption isotherms. The total mass of the sample present during this analysis was approximately 3.78 mg. The isotherms are measured under the relative pressure region $\left( {{p \mathord{\left/ {\vphantom {p {p_{0} }}} \right. \kern-0pt} {p_{0} }}} \right)$ from 0.1 to 1.0 and back. Isotherm is a physisorption experiment that provides the information about the surface and porosity of the material [21]. Figure 3a exhibits N₂ adsorption/desorption isotherms of TMO NPs at 77 K. The measured isotherm can be classified as Type II isotherm in Brunauer classification [22, 23]. This type isotherm generally represents unrestricted monolayer-multilayer adsorption [24]. From the graph, it can be shown that the adsorption and desorption isotherms superpose to each other indicating mostly micropore related adsorption [25]. The increase in adsorbed gas volume at high value of ${p \mathord{\left/ {\vphantom {p {p_{0} }}} \right. \kern-0pt} {p_{0} }}$ takes place due to the capillary condensation [21]. Brunauer–Emmett–Teller (BET) specific surface area $\left( {S_{BET} } \right)$ and monolayer adsorption volume $\left( {V_{m} } \right)$ are calculated using BET equation as follows [26],

$$ \frac{p}{{V_{ads} \left( {p_{0} - p} \right)}} = \frac{1}{{V_{m} C_{B} }} + \frac{{C_{B} - 1}}{{V_{m} C_{B} }}\left( {\frac{p}{{p_{0} }}} \right), $$

(1)

where $V_{ads}$ is the adsorbed N₂ volume, $p$ and $p_{0}$ are the equilibrium and saturated vapour pressure of adsorbates at adsorption temperature respectively, $C_{B}$ is a constant and $V_{m}$ is the monolayer adsorbed N₂ volume. BET specific surface area $\left( {S_{BET} } \right)$ is determined using the relation $S_{BET} = 4.355 \times V_{m}$. Considering the particle to be spherical, average particle size $\left( {D_{BET} } \right)$ can be calculated using the following equation [25, 26],

$$ D_{BET} = \frac{6000}{{\rho \times S_{BET} }}, $$

(2)

where $\rho$ = 7.36 g/cc, the crystallographic density of TMO NPs. BET plot of the NPs is exhibited in Fig. 3b. Parameter $C_{B}$ can be calculated as,

Fig. 3

a N₂ adsorption–desorption isotherms of TMO NPs at 77 K (the inset displays the enlarged view of the isotherm at high ${p \mathord{\left/ {\vphantom {p {p_{0} }}} \right. \kern-0pt} {p_{0} }}$), b BET plot of the sample at 77 K

$$ C_{B} = \frac{Slope}{Intercept} + 1. $$

(3)

The $_{{}} C_{B}$ parameter measures the strength of the interaction of the adsorbate (N₂) with the surface of the material [27].

The calculated parameters such as specific surface area $\left( {S_{BET} } \right)$, monolayer adsorbed N₂ volume $\left( {V_{m} } \right)$ and average particle size $\left( {D_{BET} } \right)$ are indexed in Table 1. In case of multilayer adsorption, on the pore walls, an adsorbed layer has formed which is responsible for capillary condensation at higher ${p \mathord{\left/ {\vphantom {p {p_{0} }}} \right. \kern-0pt} {p_{0} }}$ [26]. The adsorbed layer thickness $\left( t \right)$ is derived from the adsorption isotherm data as follows [28],

Table 1 The derived surface parameters of TMO NPs derived from BET plot, $t - plot$ and pore size distribution (BJH plot) analysis

$$ t = \left( {\frac{13.99}{{ - \log \left( {{p \mathord{\left/ {\vphantom {p {p_{0} }}} \right. \kern-0pt} {p_{0} }}} \right) + 0.034}}} \right)^{1/2} . $$

(4)

The plot of $V_{ads}$ versus $t$ is known as $t - plot$, which is shown in Fig. 4a. The slope of the straight portion gives the value of cumulative pore surface area $\left( {S_{t - plot} } \right)$ for multilayer adsorption because $S_{t - plot}$ is related by the equation,

Fig. 4

a t- plot for TMO NPs at 77 K (the inset displays the linear portion of $t - plot$ curve), b differential pore size distribution curve (BJH plot) of TMO NPs for adsorption and desorption branch

$$ t = {\raise0.7ex\hbox{${V_{ads} }$} \!\mathord{\left/ {\vphantom {{V_{ads} } {S_{t - plot} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${S_{t - plot} }$}}. $$

(5)

Pore size distribution from both the adsorption and desorption branches of isotherm data generally is described by Barrett–Joyner–Halenda (BJH) analysis [21]. In general, the pores of the material can be categorised as micropores (size < 2 nm), mesopores (2–50 nm) and macropores (> 50 nm) [29]. To fit BJH model, the pores are considered here as cylindrical. The average pore diameter $\left( {r_{p} } \right)$ can be calculated using Kelvin equation and $t - plot$ equation such as [21],

$$ r_{p} = r_{K} + t, $$

(6)

where $r_{K}$ is the Kelvin radius i.e. the radius of the condensed adsorbate and $t$ is the adsorbed layer thickness. The differential pore size distribution curve (BJH plot) of TMO NPs is shown in Fig. 4b, which clearly indicates the mesoporosity present in the sample. This is single modal distribution centred at ~ 7 nm for adsorption branch (~ 9 nm for desorption branch).The pore size distribution derived from adsorption branch is quite similar with that obtained from the adsorption branch. These unique pores can effectively provide disorder-free paths for oxygen vacancies for catalytic performances [29]. Based on $t - plot$ and BJH analysis, the values of cumulative surface area of pore $\left( {S_{t - plot} } \right)$, cumulative pore volume $\left( {V_{BJH} } \right)$ and average pore diameter $\left( {d_{BJH} } \right)$ are evaluated and listed in Table 1 [27]. Soleymani et al. [30] reported the synthesis of nano-sized La_0.6Ca_0.4MnO₃ with high specific surface area (40.7 m² g⁻¹) by low temperature pyrolysis of a modified citrate gel method. Rabelo et al. [31] reported the synthesis of pure phase perovskite La_1−xSr_xMnO_3±δ with specific surface area of 34.3 m² g⁻¹ which is potentially applicable for solid oxide fuel cells (SOFC). In the present work, we have achieved the specific surface area of 20.9 m² g⁻¹ of the synthesised TMO NPs.

Further the dielectric response of this sample to an alternating applied electric field is recorded. The application of electric field produces/alters the net dipole moment density in the material. In this case, the change in the positive–negative charge orientations will not be instantaneous. The frequency dependent dielectric constant is expressed as,

$$ \varepsilon^{*} \left( f \right) = \varepsilon^{\prime } \left( f \right) - i\varepsilon^{\prime \prime } \left( f \right). $$

(7)

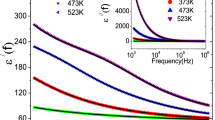
The frequency dependent real part [$\varepsilon^{\prime}\left( f \right)$] and imaginary part [$\varepsilon^{\prime\prime}\left( f \right)$] of dielectric constant respectively (Fig. 5a, b). The $\varepsilon^{\prime}\left( f \right)$ and $\varepsilon^{\prime\prime}\left( f \right)$ values are high in the lower frequency region due to the effect of electrode polarisation. In the higher frequencies, the free ions in the material cannot find sufficient time to direct themselves along the field direction. As a result th values of $\varepsilon^{\prime}\left( f \right)$ and $\varepsilon^{\prime\prime}\left( f \right)$ become lower in this range. At lower temperature region, size of the micro domains increases as they fuse together. As a result delay of the response to the applied field takes place. The experimental data of dielectric relaxation process can be described by the following Cole–Cole function [32, 33],

$$ \varepsilon^{*} \left( f \right) = \varepsilon_{\infty } + \frac{{\varepsilon_{S} - \varepsilon_{\infty } }}{{1 + \left( {i\omega \tau } \right)^{\beta } }} - \frac{{i\sigma^{*} }}{{\varepsilon_{0} \omega^{p} }}, $$

(8)

where $\beta$ and $p$ describe the ‘skewdness’ and the ‘depression’ of relaxation time distribution respectively. $\varepsilon_{S}$ and $\varepsilon_{\infty }$ are the static and infinite dielectric constant respectively, the dielectric relaxation time is $\tau$. The expression of $\varepsilon^{\prime}\left( f \right)$ and $\varepsilon^{\prime \prime } \left( f \right)$ can be further expanded as,

$$ \varepsilon^{\prime } \left( f \right) = \varepsilon_{\infty } + \left[ {\frac{{\left( {\varepsilon_{S} - \varepsilon_{\infty } } \right)\left\{ {1 + \left( {\omega \tau } \right)^{\beta } \cos \left( {{\raise0.7ex\hbox{${\beta \pi }$} \!\mathord{\left/ {\vphantom {{\beta \pi } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right)} \right\}}}{{1 + 2\left( {\omega \tau } \right)^{\beta } \cos \left( {{\raise0.7ex\hbox{${\beta \pi }$} \!\mathord{\left/ {\vphantom {{\beta \pi } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right) + \left( {\omega \tau } \right)^{2\beta } }}} \right] + \frac{{\sigma_{sp} }}{{\varepsilon_{0} \omega^{p} }} $$

(9)

and

$$ \varepsilon^{\prime \prime } \left( f \right) = \left[ {\frac{{\left( {\varepsilon_{S} - \varepsilon_{\infty } } \right)\left\{ {1 + \left( {\omega \tau } \right)^{\beta } \sin \left( {{\raise0.7ex\hbox{${\beta \pi }$} \!\mathord{\left/ {\vphantom {{\beta \pi } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right)} \right\}}}{{1 + 2\left( {\omega \tau } \right)^{\beta } \cos \left( {{\raise0.7ex\hbox{${\beta \pi }$} \!\mathord{\left/ {\vphantom {{\beta \pi } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right) + \left( {\omega \tau } \right)^{2\beta } }}} \right] + \frac{{\sigma_{fc} }}{{\varepsilon_{0} \omega^{p} }}, $$

(10)

where $\sigma_{fc}$ and $\sigma_{sp}$ are the free charge carrier and space charge carrier conductivity respectively. In Fig. 5a, b, using modified Cole–Cole model, the green lines are fitted with the experimental curves. The calculated values of the parameters are summerised in Table 2. $\beta$ values are closer to unity indicating limited distribution of dielectric relaxation time. Both $\sigma_{fc}$ and $\sigma_{sp}$ increase with increasing temperature. Dielectric relaxation time $\left( \tau \right)$ gets smaller with the rise in temperature. This happens due to the increase in mobility of the ions with increasing temperature.

Fig. 5

a The frequency variation of $\left[ {\varepsilon^{\prime } \left( f \right)} \right]$ of the sample at different temperatures, b the frequency variation of $\left[ {\varepsilon^{\prime \prime } \left( f \right)} \right]$ of the sample at different temperatures, c the frequency variation of real part $\left( {M^{\prime } } \right)$ of complex electric modulus of the sample at different temperatures, d the frequency variation of imaginary part $\left( {M^{\prime \prime } } \right)$ of complex electric modulus of the sample at different temperatures

Table 2 The derived electrical parameters [relaxation time ($\tau$), parameter ($\beta$), exponent ($p$), space charge conductivity ($\tau$), free charge conductivity ($\tau$)] of the TMO sample from dielectric spectra analysis

Dielectric response and dielectric relaxation process in dielectric materials can be further explained by complex electric modulus [34]. Electric modulus is defined as,

$$ M^{*} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\varepsilon^{*} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\varepsilon^{*} }$}} = \frac{{\varepsilon^{\prime } }}{{\left( {\varepsilon^{\prime } } \right)^{2} + \left( {\varepsilon^{\prime \prime } } \right)^{2} }} + \frac{{\varepsilon^{\prime \prime } }}{{\left( {\varepsilon^{\prime } } \right)^{2} + \left( {\varepsilon^{\prime \prime } } \right)^{2} }} = M^{\prime } + iM^{\prime \prime } , $$

(11)

Figure 5c, d exhibit the frequency variation of $M^{\prime }$ and $M^{\prime \prime }$ of the sample respectively. $M^{\prime }$ is almost zero in lower frequencies due to minor electrode polarisation effect. With the increase in frequency, $M^{\prime }$ increases with a transition but shows no characteristic peak. This is an intrinsic behaviour of highly capacitive system [35]. Loss peaks are observed in the curves of $M^{\prime \prime }$ spectra. This characteristic peak depicts the presence of ionic conduction relaxation. In the lower frequency region of the peak, immobilised charge carriers pass easily without any obstruction but in the higher frequency side of the peak, the charge carriers are restricted to the potential well [35]. Interfacial polarisation arises due to the dielectric difference between the surface shell and the core material [36]. With temperature rise, free charge accumulates at the interface in the sample. as a result relaxation time decreases. The measured data of $M^{\prime \prime }$ spectra can be fitted using a general solution of Modified Kohlrausch–Williams–Watts (KWW) decay function as follows,

$$ M^{\prime \prime } \left( f \right) = \frac{{M_{\hbox{max} }^{\prime \prime } }}{{\frac{{\left( {1 - \left| {a - b} \right|} \right)}}{a + b}\left[ {b\left( {{\raise0.7ex\hbox{$f$} \!\mathord{\left/ {\vphantom {f {f_{\hbox{max} } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${f_{\hbox{max} } }$}}} \right)^{ - a} + a\left( {{\raise0.7ex\hbox{$f$} \!\mathord{\left/ {\vphantom {f {f_{\hbox{max} } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${f_{\hbox{max} } }$}}} \right)^{b} } \right] + \left| {a - b} \right|}}, $$

(12)

where the values of shape parameters ‘$a$’ and ‘$b$’ typically lie in between 0 and 1 (summerised in Table 3). Non-Debye type dielectric relaxation is present in the sample. The values of shape parameters become higher with temperature.

Table 3 The derived electrical parameters [shape parameters ($a$) and ($b$)] of TMO sample from electrical modulus spectra analysis

Electrode-dielectric material (the sample) junction i.e. metal–semiconductor junction forms Schottky Barrier Diode (SBD). Capacitance–bias voltage (C–V) characteristics study is a significant tool to get the idea about different Schottky parameters of SBD such as built in voltage $\left( {V_{bi} } \right)$, Fermi energy $\left( {E_{F} } \right)$, donor concentration $\left( {N_{D} } \right)$, image force lowering $\left( {\Delta \varphi_{b} } \right)$, barrier height $\left( {\varphi_{C - V} } \right)$ and depletion width $\left( {W_{D} } \right)$. Well known Mott-Schottky analysis can be implied in the bias dependent depletion region of SBD. By this above-mentioned analysis, the depletion capacitance is stated as follows [37,38,39],

$$ \frac{1}{{C^{2} }} = \frac{{2\left( {V_{bi} - V} \right)}}{{q\varepsilon_{S} \varepsilon_{0} A^{2} N_{D} }}, $$

(13)

where $A$ is the effective area, $\varepsilon_{S}$ and $\varepsilon_{0}$ are the dielectric constants of the material and of the free space respectively. Plot of $C^{ - 2}$ versus $V$ characteristics at different temperatures is exhibited in Fig. 6. Linear fitting of the plot determines the values of $V_{bi}$ and $N_{D}$ which are listed in Table 4. From these values, further, the Fermi energy $\left( {E_{F} } \right)$, effective carrier density $\left( {N_{C} } \right)$, image force lowering $\left( {\Delta \varphi_{b} } \right)$, barrier height $\left( {\varphi_{C - V} } \right)$ and depletion width $\left( {W_{D} } \right)$ can be evaluated using the following equations.

$$ N_{C} = 2\left( {\frac{{2\pi m_{e}^{*} k_{B} T}}{{m_{0} h^{2} }}} \right)^{3/2} $$

(14)

where the effective mass of an electron $m_{e}^{*} = 0.98m_{0}$ and $m_{0}$ is the rest mass of electron.

$$ E_{F} = \frac{{k_{B} T}}{q}\ln \left( {\frac{{N_{C} }}{{N_{D} }}} \right), $$

(15)

$$ \Delta \phi_{b} = \left( {\frac{{q^{3} V_{bi} N_{D} }}{{8\pi^{2} \varepsilon_{S}^{3} }}} \right)^{1/4}, $$

(16)

$$ \phi_{C - V} = V_{bi} + E_{F} + \Delta \phi_{b} , $$

(17)

and

Fig. 6

${1 \mathord{\left/ {\vphantom {1 {C^{2} }}} \right. \kern-0pt} {C^{2} }}$ versus $V$ plot with a Mott–Schottky fit to the depletion capacitance

Table 4 The derived Schottky parameters [built in voltage $\left( {V_{bi} } \right)$, Fermi energy $\left( {E_{F} } \right)$, donor concentration $\left( {N_{D} } \right)$, image force lowering $\left( {\Delta \phi_{b} } \right)$, barrier height $\left( {\phi_{C - V} } \right)$ and depletion width $\left( {W_{D} } \right)$] of Au/TMO Schottky Barrier Diode from C–V measurements

$$ W_{D} = \sqrt {\frac{{2\varepsilon_{S} V_{bi} }}{{qN_{D} }}} . $$

(18)

The calculated Schottky parameters values are summerised in Table 4. Barrier height $\left( {\phi_{C - V} } \right)$ slightly increases with temperature. $W_{D}$ decreases with increase in temperature as excess capacitance exists at metal–semiconductor junction interface. This unique property makes the material suitable for photocatalytic and solar cell applications.

The thermionic current–voltage (I–V) characteristics of the Au/TMO/Au Schottky diode have been measured within the voltage range ± 40 V. Figure 7a shows $\ln I$ versus $V$ plots at different temperatures. The sample exhibits hysteresis loop in I–V characteristics curve. Here the least value of current shifts from zero voltage. Generally, the ferroelectric property of the material shifts the curves from their original position because of polarisation hysteresis. But in this case, TMO exhibits ferroelectricity only below its Neel temperature (~ 41 K). The electrical hysteresis in I–V curve probably comes from the irreversible charge transport in the schottky barriers. Kim et al. [40] observed the similar ferroelectric-like hysteresis loop originated from non ferroelectric effects. Even in the absence of polarisation switching effect; several factors such as electrostatic interaction, electrochemical strain etc. are responsible for the charge injection between forward and reverse bias sweep. Due to this unique property, the sample may pose electrical memory effect. Using thermionic emission (TE) theory, rectifying nature of I–V characteristics of a SBD is stated by Richardson formalism [41],

$$ I = I_{S} \left[ {\exp \left\{ {q\left( {V - IR} \right)/nk_{B} T} \right\} - 1} \right], $$

(19)

where $I$ is the forward current. Reverse saturation current $\left( {I_{S} } \right)$ is written as

$$ I_{S} = AA*T^{2} \exp \left( { - \frac{{q\phi_{b} }}{{k_{B} T}}} \right), $$

(20)

where $A$ is the area of the sample, $A^{*}$ is a constant, $n$ is the ideality factor, $\phi_{b}$ is the barrier height and $k_{B}$ is Boltzmann’s constant. Reverse saturation current increases with rise in temperature. Figure 7b shows the temperature variation of ideality factor and barrier height. With temperature, $\phi_{b}$ increases but $n$ decreases. For ideal Schottky diode $n$ = 1, but in practical case $n$ is always greater than 1. The barrier inhomogeneity of SBD interface causes the high value of n [42]. Richardson plot of $\ln \left( {{\raise0.7ex\hbox{${I_{S} }$} \!\mathord{\left/ {\vphantom {{I_{S} } {T^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T^{2} }$}}} \right)$ versus ${\raise0.7ex\hbox{$q$} \!\mathord{\left/ {\vphantom {q {k_{B} T}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${k_{B} T}$}}$ is shown in the inset of Fig. 7a. The plot is linear in nature because of the inhomogeneous nature of the sample [43]. The obtained value of $\phi_{b}$ from I–V study is greater than that from C–V analysis. The presence of excess capacitance and heterogenous barrier at Au–TMO interface are the responsible factors [37]. From the temperature dependent current–voltage characteristics in forward bias, the parameters such as series resistance ($R_{S}$), ideality factor ($n$) can be evaluated using the model of Cheung and Cheung [44]. According this model, current–voltage characteristics of a SBD can be expressed as,

Fig. 7

a $\ln I$ versus $V$ curves at different experimental temperatures (the inset displays the Richardson plot of $\ln \left( {{{I_{S} } \mathord{\left/ {\vphantom {{I_{S} } {T^{2} }}} \right. \kern-0pt} {T^{2} }}} \right)$ versus ${q \mathord{\left/ {\vphantom {q {kT}}} \right. \kern-0pt} {kT}}$ of the sample), b variation of barrier height and variation of ideality factor with temperature

$$ \frac{dV}{d\ln I} = IR_{S} + \frac{{nk_{B} T}}{q}, $$

(21)

Figure 8a shows the linear variation of ${\raise0.7ex\hbox{${dV}$} \!\mathord{\left/ {\vphantom {{dV} {d\ln I}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${d\ln I}$}}$ versus $I$ plots at various measuring temperatures. The parameters i.e. $R_{S}$ and $n$ are evaluated from the linear plots in Fig. 8a. The temperature variation of $R_{S}$ and $n$ is shown in Fig. 8b. The values of ideality factor from Cheung’s approach are almost similar to those evaluated from Richardson’s equation in TE theory. This result implies the validity and the consistency of these models. From the results, it can be depicted that the defect states present in the TMO interface layer are the dominant responsible factor for the charge transport phenomenon. The series resistance value increases with the decrease in temperature. Here, defect state density decreases with lowering temperature [37].

Fig. 8

a Temperature dependent plot of ${\raise0.7ex\hbox{${dV}$} \!\mathord{\left/ {\vphantom {{dV} {d\ln I}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${d\ln I}$}}$ versus $I$ at different experimental temperatures, b variation of series resistance and ideality factor with temperature

To measure magnetic susceptibility of the material, Evans balance method is used here. Mass magnetic susceptibility, $\chi_{g}$, is written as [45],

$$ \chi_{g} = {{\left[ {C_{bal} L\left( {R - R_{0} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {C_{bal} L\left( {R - R_{0} } \right)} \right]} {\left( {m \times 10^{9} } \right)}}} \right. \kern-0pt} {\left( {m \times 10^{9} } \right)}}, $$

(22)

where $C_{bal}$ is a constant, $L$ is sample height, $m$ is sample mass.$R$ and $R_{0}$ are the digital readings for sample filled tube and empty tube respectively. Room temperature effective magnetic moment $\left( {\mu_{eff} } \right)$ is calculated using the following equation,

$$ \mu_{eff} = 2.828 \times \sqrt {M\chi_{g} T} \mu_{B} , $$

(23)

where $M$ is the molar mass of TMO, $\mu_{B}$ is Bohr magneton. $\mu_{eff}$ of the sample is ~ 0.11 $\mu_{B}$ showing paramagnetic behaviour of TMO at room temperature. The paramagnetic nature of the sample may discard the possibility of multiferroicity of the sample at room temperature. Wang et al., Rai et al. and Ponomarev et al. [46,47,48] reported the presence of magnetoelectric coupling in the paramamagnetic state of metal–organic framework and rare earth molybdates respectively. In the present sample, further study is done to observe the nature of magnetoelectric coupling at room temperature. An applied magnetic field affects the magnetic order as well as the dielectric constant of a magnetoelectric material [49]. Figure 9a and the inset of Fig. 9a shows frequency dependence of dielectric constant $\left( {\varepsilon^{/} } \right)$ and dielectric loss $\left( {\tan \delta } \right)$ with and without magnetic field respectively. With the application of magnetic field, there exists a slight change in dielectric constant. With the application of magnetic field, dielectric loss (leakage current) slightly decreases throughout the probing frequency range. The change in the value of $\varepsilon^{/}$ and $\tan \delta$ is higher in low frequency region than that of high frequency range. It suggests that the grain boundaries are more sensitive to the magnetic field than the intrinsic grains [48]. Figure 9b shows the magnetic field dependence of dielectric loss $\left( {\tan \delta } \right)$ at different frequencies. The loss reduces with the increase in applied magnetic field. The room temperature magnetocapacitance/magnetodielectric (MD) response as a function of applied magnetic field $H$ measured at different frequencies is shown in Fig. 9c. Magnetodielectric response can be expressed using the following equation,

$$ MD = \frac{{\varepsilon^{/} \left( H \right) - \varepsilon^{/} \left( 0 \right)}}{{\varepsilon^{/} \left( 0 \right)}} \times 100, $$

(24)

where $\varepsilon^{/} \left( H \right)$ and $\varepsilon^{/} \left( 0 \right)$ represent the value of dielectric constant corresponding to the magnetic field $H$ and zero respectively. The increasing magnetic field gives rise to the enhanced negative magnetocapacitance at room temperature. To explain the magnetic field dependency of dielectric constant, a recently proposed model of a two-phase inhomogeneous system can be introduced [50]. According to this model, a composite medium having different conductivities possesses Maxwell–Wagner polarisation between the interface which in turn causes magnetodielectric effect without multiferroicity. In the present case, considering TMO sample as a inhomogeneous medium, the magnetodielectric effect arises not because of multiferroicity, but due to the Maxwell–Wagner space charge at the interface and the effect of magnetic field thereon. When magnetic field is applied, it generates an electric field which influences the polarisation of the system by reducing the accumulated charge in the interface. As a result, the value of dielectric constant also decreases [51].

Fig. 9

a The frequency variation of dielectric constant $\left( {\varepsilon^{/} } \right)$ at different applied magnetic fields (the inset display the frequency variation of dielectric loss $\left( {\tan \delta } \right)$ at different applied magnetic fields), b magnetic field dependence of dielectric loss $\left( {\tan \delta } \right)$ at different frequencies, c magnetic field dependence of magnetodielectric (MD) effect at different frequencies

4 Conclusion

To summarise, we have investigated dielectric and magnetodielectric properties of mesoporous Terbium Manganate (TMO) nanoparticles (NPs). The sample exhibits relatively high surface area (20.9 m² g⁻¹) and narrow pore size distribution. Dielectric response of the material to the external alternating field is described by modified Cole–Cole model. Modified Electric modulus spectra is well explained by KWW function. The capacitive system of electrode-TMO junction forms Schottky Barrier Diode (SBD) which is well explained by thermionic emission theory from the I–V measurements. Ferroelectric-type hysteretic behaviour is observed in the sample. Different barrier properties are well explained by Mott–schottky analysis in the depletion region. Although TMO exhibits paramagnetic nature at room temperature, it responds to the applied transverse magnetic field by showing significant change in dielectric constant over a broad frequency window. The negative magnetodielectric effect may be attributed to the presence of inhomogeneity in the sample. These observations demonstrate that the perovskite TMO is a promising multifunctional material, showing dielectric, magnetodielectric properties at room temperature.