1 Introduction

Nowadays, the understanding of non-Newtonian behavior is very essential due to its broad applications in the engineering, technology and science fields. Few particular examples of non-Newtonian materials are jams, blood, Soups, jelly, waxy crude oils and synthetic lubricants. The properties of these liquids are not represented by a single (unaccompanied) basic equation. The rate of stress and strain linear connection of these liquids exists. The Casson liquids are the prominent one amongst the non-Newtonian liquids. It is worthy mentioned that a mathematical model is diminished into a Newtonian liquid if the yield stress is smaller than the wall stress [1,2,3,4,5]. Ramesh et al. [6] executed the nature of Casson fluid numerically by considering the dust and nanoparticles. Three-dimensional (3D) transport of Casson nanoliquid is reported by Sulochana et al. [7]. Archana et al. [8] scrutinized the nonlinear radiative heated Casson nanofluid flow. Mustafa et al. [9] modeled the magneto Casson nanoparticles fluid flow. The nature of Casson nanofluid flow with linear radiation is elaborated by Gireesha et al. [10]. Ullah et al. [11] executed the porous media aspects in the above problem. Heat dissipation in Casson fluid flow is investigated by Konda et al. [12]. Three-dimension flow analysis of this model is addressed by Nadeem et al. [13]. The Casson flow behavior with absorption and generation of heat is elaborated by Sreenivasulu et al. [14]. Poornima et al. [15] described the slip flow and variable conductivity phenomenon of Casson fluid.

Parabolic revolution about its axis otherwise described like thin needle adding the varying thickness into its feature. If the thickness does not surpass the boundary, then it is considered to be thin. Recently, vast work is going about this booming topic. Axisymmetric heat transportation process in the boundary layer analysis has achieved special importance due to its technological and engineering implications. Thin needle problem is one category of axisymmetric. Parabolic revolution of slendering object is known as geometry of thin needle. Realistic importance is given to the problem of variable thickness slendering needle in the present years because of its implications in the field of applied mechanics specifically, the blood transport problems, cancer therapy phenomena, and aerodynamics etc. Lee [16] represented this phenomenon firstly. The Brownian and thermophoretic aspects in magneto Sakiadis flow over thin needle is discussed by Sulochana et al. [17]. Krishna et al. [18] described the nature of magnetohydrodynamic Blasius–Sakiadis nanofluids flows induced by horizontal needle. Ishak et al. [19] reported the thin needle analysis in parallel free stream situation.

The nanofluid mechanism is a topic of abundant investigations in the modern world of nano-technology and industrial products. There exist versatile features of nanoparticles based on the physical and thermal nature of these particles. The one of the types of nanoparticles is the carbon nanotubes. Hexagonal structures of carbon atoms are termed as carbon nanotubes (CNTs) as they are trolled like cylinder shape. Because of its unique behavior and strength, it has remarkable industrial applications like transistors with CNTs, speakers using microwave amplifiers, sensors and in medicinal field especially in artificial body part manufacturing, genomic effect due to drug and so on. Classification of CNTs is MWCNTs and SWCNTs. Mahantesh et al. [20] investigated the CNTs immersed MHD nanofluid along with Marangonic effect. Later, he extended his work by incorporating varying heat source [21]. Khan et al. [22] explored the heat transfer impact past a moving wedge. Reddy et al. [23] studied the MHD flow past non-linear stretching sheet. Reddy et al. [24] worked on the analysis of single wall and multi wall CNTs over a vertical cone. Ramzan et al. [25] reported the entropy production induced by the vertical cone under radiation aspects.

Hydromagnetic flows and slip phenomenon receives much attention of the explorers because of its distinct and wider involvement in manufacturing and industrial processes. In general, no-slip condition creates erroneous reports like MEMs, like in systems, the no-slip situation is no longer valid. Sheikholeslami et al. [26] addressed the numerical behavior of magnetic nanofluid flow under convective heating process. Souayeh et al. [27] discussed the magnetic field characteristics of non-Newtonian Casson nanofluid flow induced by the movement of thin needle. Second law implications on ferrofluid flow in presence of Lorentz forces generated by the semi-annulus has been described by Sheikholeslami et al. [28]. Poornima et al. [29] reported the heterogeneous and homogeneous reactive flow of magnetized Williamson fluid over moving surface. A comparative analysis of non-magnetic and magnetic nanoparticles in viscous fluid flow induced by the moving wedge has been presented by Hassan et al. [30]. Ellahi et al. [31] discussed the Couette–Poiseuille power law fluid flow under entropy production and magnetic field aspects. Sreenivasulu et al. [32] executed the nature of Lorentz force in Maxwell non-Newtonian nanofluid flow under heat generation and absorption phenomenon. Ismail et al. [33] reported the features of magnetized heat transport in micropolar fluid flow generated by the movement of rectangular duct.

The role of radiation in heat transportation has wider involvement in distinct branches of thermal engineering and industrial processes like gas turbines, aero-space vehicles, aircraft propulsion processes, missiles, nuclear power (thermal) plants and satellites. Sreenivasulu et al. [34] discussed the phenomenon of radiative heat transportation in dissipated micropolar fluid flow through variation of heat flux. Yousif et al. [35] reported the exponentially stretched flow of radiated micropolar fluid flow under heat sink and source. Radiative plane Poiseuille nanofluid flow through porosity and slip aspects has been demonstrated by Alamri et al. [36]. Khan et al. [37] introduced the radiative aspects in magnetized viscoelastic non-Newtonian nanofluid flow induced by permeable movement of sheet through finite element procedure. Gupta et al. [38] employed the nonlinear radiative aspects in magneto Williamson nanofluid flow under variable thickness.

To the authors’ comprehension, major of the literary work reveals the study of Casson nanoliquid with general geometries like plates and cylinders. But, the hydromagnetic slip flow of Casson nanoliquid through a thin needle comparing the efficiency of SWCNTs and MWCNTs has not been yet considered. It is the booming topic of research now as it has the substantial applications in medicinal and industrial fields such as micro-fluidic machinery and nanofluidic pumps. So, in the current investigation, we explored the numerical behavior of magneto-hydrodynamic flow of Casson nanofluid embedded a thin needle with the radiation and Navier slip effects. The impact of pertinent physical controlled variables on velocity, friction, temperature factor (Nusselt number) and the streamlines are portrayed and analyzed applying shooting technique.

2 Mathematical analysis

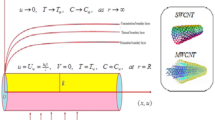
We assumed the two-dimensional (2D), laminar and boundary-driven slip Casson nanofluid flow through a horizontal needle with thermal radiation is considered. The slender needle has radius \(\bar{r} = \bar{R}(\bar{x})\), where \(\bar{r}\) and \(\bar{x}\) denote the radial and axial coordinates. It is presumed that leading edge of the needle is thinner while its thickness may not exceed the thickness of boundary layer over it. Furthermore, the needle transports horizontally through uniform velocity \(\bar{U}(\bar{x})\) and subjected to changeable heat flux (see Fig. 1). The thermophysical properties for present problem are presented in Table 1.

Fig. 1
figure 1

Flow configuration and physical model

Full size image
Table 1 Thermo-physical features of nanotubes and water
Full size table

The rheological expression of Casson fluid can be reported as [39]:

$$\tau_{ij} = \left\{ {\begin{array}{*{20}l} {2\left( {\mu_{B} + p_{y} /\sqrt {2\pi } } \right)e_{ij} ,} \hfill & {\pi > \pi_{c} ,} \hfill \\ {2\left( {\mu_{B} + p_{y} /\sqrt {2\pi_{c} } } \right)e_{ij} ,} \hfill & {\pi < \pi_{c} ,} \hfill \\ \end{array} } \right.$$

where πc represents the empirical value of the product regarding to non-Newtonian situation, \(\pi = e_{ij} e_{ij}\) denotes the deformation rate product with itself, \(e_{ij}\) the \(\left( {i,j} \right)\) components of deformation rate, μB the plastic dynamic viscosity and Py the yield stress of liquid.

The modeled equations of continuity (mass), momentum (flow) and energy conservation are respectively in dimensional form as

$$\frac{\partial }{{\partial \bar{r}}}(\bar{r}\,\bar{v}) + \frac{\partial }{{\partial \bar{x}}}(\bar{r}\,\bar{u}) = 0,$$
(1)
$$\bar{v}\frac{{\partial \bar{u}}}{{\partial \bar{r}}} + \bar{u}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} = \bar{U}\frac{{d\bar{U}}}{{d\bar{x}}} + \nu_{nf} \left( {1 + \frac{1}{\beta }} \right)\frac{1}{r}\frac{\partial }{{\partial \bar{r}}}\left( {\bar{r}\frac{{\partial \bar{u}}}{{\partial \bar{r}}}} \right),$$
(2)
$$\bar{v}\frac{{\partial \bar{T}}}{{\partial \bar{r}}} + \bar{u}\frac{{\partial \bar{T}}}{{\partial \bar{x}}} = \alpha_{nf} \frac{1}{{\bar{r}}}\frac{\partial }{{\partial \bar{r}}}\left( {\bar{r}\frac{{\partial \bar{T}}}{{\partial \bar{r}}}} \right) - \frac{1}{{(\rho C_{p} )_{nf} }}\frac{1}{{\bar{r}}}\frac{\partial }{{\partial \bar{r}}}\left( {\bar{r}\,q_{r} } \right),$$
(3)

and the physical boundary conditions are imposed as:

$$\begin{aligned} \bar{u} & = \bar{u}(\bar{x}) + N\mu_{nf} \left( {\frac{{\partial \bar{u}}}{{\partial \bar{r}}}} \right),\quad \bar{v} = 0,\quad \frac{{\partial \bar{T}}}{{\partial \bar{r}}} = - \frac{{\bar{q}_{w} (\bar{x})}}{{k_{nf} }}\quad at\quad \bar{r} = \bar{R}(\bar{x}), \\ \bar{u} & \to 0,\quad \bar{T} \to \bar{T}_{\infty } \quad as\quad \bar{r} \to \infty . \\ \end{aligned}$$
(4)

The expression of radiation heat flux through Rosseland’s theory is given by:

$$q_{r} = - \frac{4}{3}\frac{\sigma *}{k*}\frac{{\partial T^{4} }}{{\partial \bar{r}}}.$$
(5)

Rosseland’s model needs optically dense media as radiation travels only a short space before dispersed or immersed. When material has a great extinction coefficient, it can be treated as optically thick. We have a taken a fluid model in which the energy transfer through radiation within optically dense Casson fluid exists before the heat is dispersed, so, radiative heat transfer is taken into account. By employing the Rosseland’s approximation, the temperature contrasts inside the stream are adequately little, at that point condition Eq. (5) can be linearized by extending \(T^{4}\) into the Taylor arrangement about T∞, which in the wake of ignoring higher-arrange terms takes the frame

$$T^{4} \cong 4T_{\infty }^{3} \bar{T} - 3T_{\infty }^{4} .$$
(6)

In interpretation of Eqs. (5) and (6) in Eq. (3), we obtain

$$\bar{u}\frac{{\partial \bar{T}}}{{\partial \bar{x}}} + \bar{v}\frac{{\partial \bar{T}}}{{\partial \bar{r}}} = \left( {\alpha_{nf} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} (\rho C_{p} )_{nf} }}} \right)\frac{1}{{\bar{r}}}\frac{\partial }{{\partial \bar{r}}}\left( {\bar{r}\frac{{\partial \bar{T}}}{{\partial \bar{r}}}} \right).$$
(7)

A few researchers have been presented the nanofluid models are legitimate just for rotational or spherical curved particles with little pivotal proportion and these models may not depict the features of carbon nanotubes space distribution on thermal conductivity. But, the carbon nanotubes can be viewed as judicious curved model with extensive hub proportion. A hypothetical model in light of Maxwell hypothesis incorporating rotational curved nanotubes with expansive pivotal proportion and repaying the impacts of room appropriations on CNTs was proposed by Xue [40]:

$$\begin{aligned} \rho_{nf} & = \phi \rho_{CNT} + (1 - \phi )\rho_{f} ,\quad \alpha_{nf} = \frac{{k_{nf} }}{{\rho_{nf} (Cp)_{nf} }},\quad \rho_{nf} (C_{p} )_{nf} = (1 - \phi )(\rho C_{p} )_{f} + \phi (\rho C_{p} )_{CNT} , \\ \frac{{k_{nf} }}{{k_{f} }} & = \frac{{1 + 2\phi \frac{{k_{CNT} }}{{ - k_{f} + k_{CNT} }}\ln \frac{{k_{f} + k_{CNT} }}{{2k_{f} }} - \phi }}{{1 + 2\phi \frac{{k_{f} }}{{ - k_{f} + k_{CNT} }}\ln \frac{{k_{f} + k_{CNT} }}{{2k_{f} }} - \phi }},\quad \mu_{nf} = \frac{{\mu_{f} }}{{(1 - \phi )^{2.5} }}. \\ \end{aligned}$$
(8)

Here, ϕ represents the volume fraction of nanotubes, the subscripts nf, f and CNTs represent the thermos-physical nature of the nanofluids, water and nanotubes respectively.

Now, we employing the following dimensionless variables:

$$\begin{aligned} & x = \frac{{\bar{x}}}{L},\quad r = \text{Re}^{1/2} \left( {\frac{{\bar{r}}}{L}} \right),\quad u = \frac{{\bar{u}}}{{U_{0} }},\quad v = \text{Re}^{1/2} \left( {\frac{{\bar{v}}}{{U_{0} }}} \right),\quad U(x) = \frac{{U(\bar{x})}}{{U_{0} }}, \\ & q_{w} (x) = \frac{{\bar{q}_{w} (\bar{x})}}{{q_{0} }},\quad R(x) = \text{Re}^{1/2} \left( {\frac{{\bar{R}(\bar{x})}}{L}} \right),\quad T = \frac{{k_{f} \text{Re}^{1/2} \left( {\bar{T} - T_{\infty } } \right)}}{{q_{0} L}}. \\ \end{aligned}$$
(9)

By utilizing Eq. (9) in Eqs. (1), (2), (7) and (4) and which are transfromed to:

$$\frac{\partial }{\partial r}(rv) + \frac{\partial }{\partial x}(ru) = 0,$$
(10)
$$v\frac{\partial u}{\partial r} + u\frac{\partial u}{\partial x} = U\frac{dU}{dx} + \nu_{nf} \left( {1 + \frac{1}{\beta }} \right)\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial u}{\partial r}} \right),$$
(11)
$$v\frac{\partial T}{\partial r} + u\frac{\partial T}{\partial x} = \left( {\alpha_{nf} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} (\rho C_{p} )_{nf} }}} \right)\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T}{\partial r}} \right),$$
(12)

and the related conditions of these equations are

$$\begin{aligned} u & = u(x) + N\mu_{nf} \left( {\frac{\partial u}{\partial r}} \right),\quad v = 0,\quad \frac{\partial T}{\partial r} = - \frac{{q_{w} (x)}}{{k_{nf} }}\quad at\quad r = R(x), \\ u & \to 0,\quad T \to 0\quad as\quad r \to \infty . \\ \end{aligned}$$
(13)

Similarity variables and stream function which satisfies continuity identically are below:

$$\begin{aligned} & \eta = x^{m - 1} r^{2} ,\quad U(x) = x^{m} ,\quad q_{w} (x) = x^{(5m - 1)/2} ,\quad \psi = xf(\eta ), \\ & T(x) = x^{2m} \theta (\eta ),\quad N(x) = N_{1} x^{(1 - m)/2} ,\quad u = \frac{1}{r}\frac{\partial \psi }{\partial r},\quad v = - \frac{1}{r}\frac{\partial \psi }{\partial x}. \\ \end{aligned}$$
(14)

The constant surface η = a changes to revolutionary surface and signifies the needle wall. Now, Setting η = a in Eq. (14) elaborates both size and shape of the body having surface defined by

$$R(x) = a^{1/2} x^{{\frac{1 - m}{2}}} .$$
(15)

Then the Eqs. (11) and (12) can be transformed as:

$$\frac{8}{{\left( {1 - \phi + \phi (\rho_{CNT} /\rho_{f} )} \right)}}\left( {1 + \frac{1}{\beta }} \right)\left( {\eta f^{{\prime \prime }} } \right)^{{\prime }} + (1 - \phi )^{2.5} \left[ {4ff^{{\prime \prime }} + m\left( {1 - 4(f^{{\prime }} )^{2} } \right)} \right] = 0,$$
(16)
$$2\left( {\frac{{k_{nf} }}{{k_{f} }} + \frac{4}{3}R} \right)\left( {\eta \theta^{{\prime }} } \right)^{{\prime }} + \Pr [1 + \phi \rho_{CNT} (Cp)_{CNT} /\rho_{f} (Cp)_{f} - \phi ](f\theta^{{\prime }} - 2mf^{{\prime }} \theta ) = 0,$$
(17)

and the associated dimenionless boundary conditions (4) are:

$$\begin{aligned} & f^{{\prime }} (a) = \frac{1}{2} + \frac{2\delta }{{\left( {1 - \phi } \right)^{2.5} }}\left( {1 + \frac{1}{\beta }} \right)\,f^{{\prime \prime }} (a),\quad f(a) = \left( {1 - m} \right)af^{{\prime }} (a),\quad \theta^{{\prime }} (a) = - \frac{1}{2}\frac{{k_{f} }}{{k_{nf} }}a^{ - 1/2} , \\ & f^{{\prime }} (\infty ) \to 0,\quad \theta (\infty ) \to 0\,. \\ \end{aligned}$$
(18)

The quantities of engineering interest, the skin-friction \(C_{f}\) and the local Nusselt number \(Nu_{x}\) which are described by

$$C_{f} = \frac{{\mu_{nf} }}{{\rho_{f} \bar{U}(\bar{x})^{2} }}\left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial \bar{u}}}{{\partial \bar{r}}}} \right)_{{\bar{r} = \bar{R}}} ,\quad and\quad {\text{Nu}}_{x} = \frac{{\bar{x}k_{nf} }}{{k_{f} (\bar{T}_{w} - T_{\infty } )L}}\left( { - \frac{{\partial \bar{T}}}{{\partial \bar{r}}}} \right)_{{\bar{r} = \bar{R}}} .$$
(19)

Using the similarity transformation (6), the above expression in dimensionless form can be expressed as

$$\text{Re}_{x}^{1/2} C_{f} = \frac{{4a^{1/2} }}{{(1 - \phi )^{2.5} }}\left( {1 + \frac{1}{\beta }} \right)f^{{\prime \prime }} (a),\quad \text{Re}_{x}^{ - 1/2} \,{\text{Nu}}_{x} = - \frac{{2k_{nf} }}{{k_{f} }}a^{1/2} \theta^{{\prime }} (a).$$
(20)

3 Numerical method

The govern physical expressions are nonlinear in nature. The problem is solved using Shooting method initially and then solved by R-K method using Mathematica software.These expression are tackled by the implemenatation of numerical procedure namely Runge–Kutta method with fourth order through shooting criteria. The procedure of numerical scheme for final expressions is described below. The first order ODEs are converted as:

$$\left. {\begin{array}{*{20}l} {f^{{\prime }} = X,} \hfill \\ { f^{{\prime \prime }} = X^{{\prime }} = s} \hfill \\ {f^{{{\prime \prime \prime }}} = X^{{\prime \prime }} = s = t} \hfill \\ {\theta^{{\prime }} = Y} \hfill \\ {\theta^{{\prime \prime }} = Y^{{\prime }} = p} \hfill \\ \end{array} } \right\}$$
(19)

Equations (16) and (17) take the following forms:

$$\left. \begin{aligned} \frac{8}{{\left( {1 - \phi + \phi (\rho_{CNT} /\rho_{f} )} \right)}}\left( {1 + \frac{1}{\beta }} \right)\left( {\eta s} \right)^{{\prime }} + (1 - \phi )^{2.5} \left[ {4fs + m\left( {1 - 4(z)^{2} } \right)} \right] = 0 \hfill \\ \left( {\frac{{k_{nf} }}{{k_{f} }} + \frac{4}{3}R} \right)\left( {\eta w} \right)^{{\prime }} + \Pr [1 - \phi + \phi (\rho Cp)_{CNT} /(\rho Cp)_{f} ](fw - 2mz\theta ) = 0 \hfill \\ \end{aligned} \right\}$$
(20)

and the corresponding Eq. (18) becomes,

$$\begin{aligned} z(a) & = \frac{1}{2} + \frac{2\delta }{{\left( {1 - \phi } \right)^{2.5} }}\left( {1 + \frac{1}{\beta }} \right)\,s(a),\quad f(a) = a\left( {1 - m} \right)z(a),\quad w(a) = - \frac{1}{2}\frac{{k_{f} }}{{k_{nf} }}a^{ - 1/2} , \\ z(\infty ) & \to 0,\quad \theta (\infty ) \to 0. \\ \end{aligned}$$
(21)

The determination of η∞ is the first process in this technique. To find this, firstly we adopt distinct values of physical variables presented in Eqs. (20) and (21), to compute the values of f″(a) and θ(a). Then we choose another higher value of η∞ up to the iterative values of f″(a) and θ(a) distinct in specified digit order. That set of variables is selected as the final value of η∞. The η∞ can be changed for other set of constraints and resultant IVP is treated with Runge–Kutta method of fourth order along the criterion of 10−5 accuracy. The variable values are taken as \(\beta = 2.0,a = 0.4,\delta = 0.3,\phi = 0.1\), \(\Pr = 2.0,R = 0.6,m = 1.0\) throughout the study. Table 2 displays the appraisal of our present analysis with the published works of Ishak et al. [19], Chen and Smith [41], Grosan and Pop [42] and good agreement is seen.

Table 2 The values of \(f^{{\prime \prime }} (a)\) and \(- \theta^{{\prime }} (a)\) for m = 0 and β → ∞
Full size table

4 Graphical analysis

The graphical representation for the flow field velocity, temperature, wall shear stress and Nusselt number are computed and illustrated through graphs 2–13.

Fig. 2
figure 2

Variations of Casson parameter \(\beta\) on velocity \(f^{{\prime }} \left( \eta \right)\)

Full size image

Figure 2 represents the influence of Casson parameter on \(f^{{\prime }} \left( \eta \right)\). The flow velocity descends with ascending Casson fluid parameter. Physical insight escalating β values, gives rise to resistance force which resists the motion of the liquid and this is due to increase in the dynamic viscosity which means reducing the yield stress. This reduces the momentum boundary layer thickness and thereby decreasing the fluid movement and escalating absolute surface velocity gradient. MWCNTs are better than SWCNTs. Fluid velocity converges faster in the case of thin needle (cylinder) rather than paraboloid geometry case. Figure 3 shows the impact of varying radius of the needle on the fluid velocity. Momentum of the Casson nanofluid descends as the needle thickness ascends. Since the thickness of the needle is close to the boundary layers of the fluid present inside, the boundary layer separation is delayed and the thickness decreases. We evidently showed that the velocity of the fluid dominates in the case of MWCNTs when compared to SWCNTs. We observed that nanofluid motion in cylinder geometry dominates paraboloid.

Fig. 3
figure 3

Variations of \(a\) on velocity \(f^{{\prime }} \left( \eta \right)\)

Full size image

We showed that the varying slip increases the motion of the nanofluid till η ~ 3 and after that the lower branch turns and shows a reverse trend (Fig. 4). Velocity of the Casson CNTs immersed nanofluid with multi-wall shows superiority than that of the single walled and also you can observe that the displacement rate values of cylinder are higher than paraboloid. A comparative analysis of Figs. 3 and 4 depict that both \(a\) and \(\delta\) have opposite influence on fluid velocity. Improving ϕ, the size of CNTs accelerates the viscous nature of the liquid, so high viscosity liquids moves with lesser ease. Therefore, we observe a deceleration of the flow movement (Fig. 5). We illustrated clearly that the inflection point is seen near η = 0.75 and before that point the trend seems reversed. In view of fluid motion MWCNTs predominant SWCNTs. The values of displacement gradient in the flow field for cylinder are dominating paraboloid case values.

Fig. 4
figure 4

Variations of \(\delta\) on velocity \(f^{{\prime }} \left( \eta \right)\)

Full size image
Fig. 5
figure 5

Variations of nanoparticles volume-fraction \(\phi\) on velocity \(f^{{\prime }} \left( \eta \right)\)

Full size image

The profiles of nano-flow temperature are diminishing as the Prandtl number escalates (Fig. 6). It signifies that the thickness of the thermal boundary layer is equal to that of velocity boundary layer when Pr = 1. For the rest cases i.e., Pr > 1, the fluid flow slows because of thermal diffusivity which in turn reduces temperature. Growing Prandtl number decreases the thermal dispersion from the fluid to surface leading to fall in energy profiles. Interesting fact one can observe here is, if the surface is paraboloid then heat transfer is faster rather than needle surface. Heat transfers faster in MWCNTs compared to SWCNTs. Figure 7 portrays the influence of radiation on the temperature of the fluid. Radiation increases the temperature of the fluid and transfers the heat effectively. Enhancing radiation releases more energy inside the fluid along with increase in thermal diffusivity as present in the thermal boundary layer Eq. (7), thus increasing the thermal boundary layer thickness. SWCNT showcast a fabulous performance in transferring heat compared to MWCNT. The needle thickness impact on temperature is significant (Fig. 8). Figure 9 shows temperature profiles for varying slip parameter. Temperature rises as the slip parameter escalates. In this case, MWCNTs transfer heat more effectively than SWCNTs. The parabolic revolution surface is more suitable than cylindrical surface for transferring heat from the fluid.

Fig. 6
figure 6

Variations of Prandtl number \(\Pr\) on temperature \(\theta \left( \eta \right)\)

Full size image
Fig. 7
figure 7

Variation of radiative constraint \(R\) on temperature \(\theta \left( \eta \right)\)

Full size image
Fig. 8
figure 8

Variations of \(a\) on temperature \(\theta \left( \eta \right)\)

Full size image
Fig. 9
figure 9

Variations of \(\delta\) on temperature \(\theta \left( \eta \right)\)

Full size image

Nanotube volume fraction impact on surface shear stress along with fluid parameter is described in Fig. 10. As the volume fraction improves surface skin friction decreases when it swifts rapidly for increasing fluid parameter. The friction is more in cylindrical needle surface than curvy surface. Rather than parabolic surface, Smoothness is good in cylindrical surface. Single walled tubes act as smoothening factor. Figure 11 exhibited the variations of radiation parameter \(R\) and Prandtl number Pr on local heat transfer rate. We observe here that increase in both the Prandtl number and radiation decreases the heat transfer rate. Cylindrical surface with multi walled nanotubes act as coolers for systems.

Fig. 10
figure 10

Variations of nanoparticles volume-fraction \(\phi\) and Casson parameter \(\beta\) on \(C_{fx}\)

Full size image
Fig. 11
figure 11

Variations of radiative parameter \(R\) and Prandtl number \(\Pr\) on \({\text{Nu}}_{x}\)

Full size image

We notice that from Fig. 12a–d, when the fluid parameter is escalated, the fluid particle traces a definite curve along x-direction past a parabolic revolution. We observe that growth in the flow pattern due to the fluid parameter increases for single and multi-walled nanotubes. MWCNTs are less shaded than SWCNTs.

Fig. 12
figure 12

a Isotherms for SWCNTs when \(m = 0,\beta = 0.1\), b isotherms for MWCNTs when \(m = 0,\beta = 0.1\), c isotherms for SWCNTs when \(m = 0,\beta = 2.0\), d isotherms MWCNTs when \(m = 0,\beta = 2.0\), e isotherms for SWCNTs when \(m = 1,\beta = 0.1\), f isotherms for MWCNTs when \(m = 1,\beta = 0.1\), g isotherms for SWCNTs when \(m = 1,\beta = 2.0\), h isotherms for MWCNTs when \(m = 1,\beta = 2.0\)

Full size image

From Fig. 12e–h streamlines for needle surface with varying Casson parameter is seen. Due to increment in Casson fluid constraint, a pattern of increasing behavior isotherms is observed clearly. The enhancement in magnitude of fluid constraint creates the wider gaps between isotherms. The fluid flow pattern for varying slip and needle thickness under parabolic revolution is portrayed in Fig. 13a–d. Multi walled nanotubes are dis-intensified than SWCNTs. As the slip and radius of the needle increases, the gap decreases within the isotherms. It is seen that stream lines are regular for β = 1.0. Stream plots for cylindrical revolution are illustrated through the Fig. 13e–h. Increasing fluid flow pattern is visible from the graphs for increasing a and δ values. The gap of the isotherms is small due to increasing a.

Fig. 13
figure 13

a Isotherms for SWCNTs when \(m = 0,\delta = 0.5,a = 0.3\), b isotherms for MWCNTs when \(m = 0,\delta = 0.5,a = 0.3\), c isotherms for SWCNTs when \(m = 0,\delta = 1.5,a = 1.0\), d isotherms for MWCNTs when \(m = 0,\delta = 1.5,a = 1.0\), e isotherms for SWCNTs when \(m = 1,\delta = 0.5,a = 0.3\), f isotherms for MWCNTs when \(m = 1,\delta = 0.5,a = 0.3\), g isotherms for SWCNTs when \(m = 1,\delta = 1.5,a = 1.0\), h isotherms for MWCNTs when \(m = 1,\delta = 1.5,a = 1.0\)

Full size image

5 Conclusions

The aspects of non-linear radiative Casson nanofluid with suspension of CNTs under Navier thermal condition are executed in this work. The surface of geometry is taken as parabolic and needle shape. The following are the major features of this work:

  • The wall friction is more significant in cylindrical shape of needle surface than parabolic form of surface.

  • Usage of multi wall carbon nanotubes acts as a decreasing friction factor.

  • MWCNTs with needle surface eliminate more heat from the fluid.

  • Fluid velocity retards with increasing Casson fluid parameter while the surface shear stress enhances.

  • As needle thickness increases, both the fluid motion and temperature decreases.

  • Nanofluid temperature increases by enhancing radiative constraint while heat transportation rate decay for rising radiation parameter.

  • Shear stress reduces while nanofluid velocity enhanced due to the increase in nanotube volume fraction.