Abstract
In this study, the inharmonicity of bass guitar strings with and without areas of lowered and raised mass near the saddle is studied. Using a very high sample rate of over 900 kHz enabled finite difference time domain simulation to be applied for strings that simultaneously have nonzero stiffness and linear density which varies along the length of the string. Results are compared to experiments on specially constructed strings. Perturbation theory is demonstrated to be sufficiently accurate (and much more computationally efficient) for practical design purposes in reducing inharmonicity. The subject of inharmonicity is well known in pianos but has not been studied extensively in bass guitar strings. Here, the inharmonicity is found to be low in the lowest (open string) pitch on the five string bass guitar (\({B}_0\)) given typical standard construction. Conversely, the inharmonicity is high (around 100 cents at the 10th partial) when that string is sounded when stopped at the 12th fret and very high (around 100 cents at the 6th partial) when that string is stopped at the 21st fret. Bass guitar strings were constructed with three different constructions (standard, tapered and lumped) in order to demonstrate how incorporating a lump of raised mass near the saddle can achieve close to zero inharmonicity for the lower frequency partials. This also has potential in terms of improving the use of higher fret numbers for musical harmony (reducing beating) and also in controlling pitch glide that has, with some exceptions, often been attributed solely to nonlinear behaviour.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The physics of guitar strings have been studied recently using the linear wave equation for transverse wave motion, giving new insight into the sensitivity to player control for unwound and wound strings [17, 25]. Lower pitch strings such as bass strings on pianos are known to demonstrate significant inharmonicity. This arises from the finite stiffness of the string and results in the resonance frequencies being progressively higher in resonant frequency than the simple integer multiples implied by the wave equation, and this inharmonicity is significantly worse for strings of wider core and shorter sounding length [14]. While most research in the field of inharmonicity has focussed on the piano, it is known that inharmonicity can be perceptually significant for string instruments tones in general [24] and that inharmonicity of the lowest pitch string on the steel strung acoustic guitar is clearly perceptible [23]. This study is motivated by the inharmonicity of lower pitch strings on the bass guitar as this is expected to be significant, particularly when playing at high fret numbers.
The wound bass strings on pianos typically have exposed cores near the ends of the sounding length. Such two part stepped/tapered, stiff strings have inharmonicity which is raised in comparison with uniform strings [7,8,9]. The fundamental frequencies of bass notes on pianos are tuned progressively flat so that their (relatively sharp) overtones/resonances are harmonious with the notes in the mid-range and high-pitched notes are similarly tuned progressively sharp. This is known as stretch tuning. Some inharmonicity is desirable when synthesising piano tones in order to produce a realistic result [29]. On the other hand, too much inharmonicity has a detrimental effect on tone quality and pitch perception and this is one cause of the generally poorer sound quality of bass notes on smaller instruments with shorter bass strings such as upright pianos and baby grand pianos (in comparison with full sized concert grand pianos). It has also been noted that inharmonicity may be less important than the spectrum bandwidth in such cases, with the depth of the bass response dependent on the soundboard size [16]. It should also be noted that, occasionally, extreme inharmonicity has been utilised for deliberate musical purposes [21, 22]. In contrast, an area of raised mass near the end of piano strings has been proposed in theory by Miller [26] and demonstrated in practical terms in patents by Sanderson [30, 31] and marketed as Sanderson Accu-Strings. Sanderson achieved an “ideal inharmonicity” where the effect of the raised mass near the string end is calculated to compensate for the effect of the exposed winding at the very ends of the sounding length. Similarly, Dalmont and Maugeais have very recently suggested reducing the inharmonicity for piano strings using raised mass near the string end [11]. These methods can be understood in terms of the perturbation theory formulated by Lord Rayleigh to treat variable density along the length of ideal strings [28, p. 170].
Inharmonicity in guitar tones has been detected and utilised for automatic guitar and bass guitar string detection in transcribing tablature from recorded audio since inharmonicity is known to vary from string to string and vary significantly with fret number [1, 2]. No research has been conducted in reducing the inharmonicity of strings on bass guitar and other instruments with low sounding pitches such as six, seven and eight string guitars to the best of the knowledge of the current author. Inharmonic resonances could lead to poor tone quality, secondary beats and, since higher-frequency resonances decay faster, inharmonicity can also lead to a downward pitch glide during note sustains as investigated later in this work. Sympathetic resonance within the instrument, differences between boundary conditions and magnetic drag [13] for different polarisations of motion, torsional waves, nonlinear behaviour (whether due to harmonic distortion in amplifiers, loudspeakers, effects units, pickup behaviour [18] or mode mixing [10]) all have the potential to generate extra spectral peaks that may clash or beat with others. It should be noted that slow beating between nearby partials may be beneficial in producing an organic tone quality, while larger differences in frequency may generate undesirable dissonance.
The field of finite difference modelling has included treatment of string stiffness [5, 6, 19, 20] and the treatment of variations in mass density [3]. Combining these two aspects (simulation of stiff strings with variable mass per unit length), the aim of this paper is to:
Validate finite difference time domain modelling for typical bass string designs whose mass per unit length varies along the length of the string.
Validate the perturbation method for strings of variable density for modifying the tuning of stiff strings.
Exploring possible advantages of an alternative design with a raised mass profile near the bridge (similar in concept to the designs of Sanderson [30, 31] for bass piano strings but with the aim of reduced inharmonicity rather than “ideal inharmonicity”).
2 Uniform stiff strings
The equation of motion for transverse waves of displacement y for a string of finite stiffness under tension T (whose central core is on the x axis at equilibrium) is given by [14]:
where E is the Young’s modulus of the material responsible for stiffness (nominally \(E = E_\mathrm{core}\) is the cross-sectional area of the core), S is the cross-sectional area of the material responsible for stiffness (nominally \(S = S_\mathrm{core}\), the cross-sectional area of the core), \(\kappa\) is the radius of Gyration (nominally \(\kappa = d_1/4\) for a circular strings of core diameter \(d_1\) and nominally \(\kappa = \sqrt{5/6}(d_1/4)\) for hex core strings if the distance between the points or maximum diameter is \(d_1\)) and the mass per unit length for the core of the string is \(\mu _\mathrm{core}\). Following the notation of previous work [25], the ratio of the total mass of the string to the mass of the core is \(\tau\) (such that \(\tau = 1\) for a plain string and \(\tau \mu _\mathrm{core}\) is the total mass per unit length of a wound string). The contribution to tension due to the windings of a wound string will be assumed to be negligible, something that has been proved to be reasonable [25]. Stiffness, on the other hand, may have an appreciable contribution from the windings, with the value of \(E S \kappa ^2\) around 7% higher than \(E_\mathrm{core} S_\mathrm{core} (d_1/4)^2\) according to measurements on circular core piano strings by Fletcher [14]. The value of \(E S \kappa ^2\) should be checked experimentally, as discussed below, for the string construction in question, particularly in the context of hexagonal core bass guitar strings with multiple layers of windings.
For a string with a core of maximum diameter \(d_1\), the cross-sectional area of the core is \(S_\mathrm{core} = \gamma _\mathrm{core} (d_1/2)^2\) where, for a circular cross section core, \(\gamma _\mathrm{core} = \pi\), and for a hexagonal cross section core, \(\gamma _\mathrm{core} = 3 \sqrt{3}/2\). It should be noted that specifications for hex cores are generally given as the distance between the flat surfaces of the hex cores (or minimum diameter), labelled here as \(d_\mathrm{spec}\), and the maximum diameter for a given diameter specification can be approximated geometrically as being \(d_1 = (2/\sqrt{3}) d_\mathrm{spec}\).
The mass per unit length of a circular cross section core and the total mass per unit length of a string consisting of a circular cross section core and a single winding is given in Chumnantas [7, p.47]. The ratio \(\tau\) (the ratio between the mass of the entire string and the mass of the core) is similarly given for strings hex or circle cores and single windings previously [25]. Extending this to the case of a string of M layers (one core and \(M-1\) windings) gives:
where \(\rho _\mathrm{core}\) is the volumetric density of the core, \(\rho _w\) is the volumetric density of the windings, \(d_1\) is the maximum diameter of the core, \(d_2\) is the outside diameter of the string after the first layer of circular cross section winding is applied, \(d_3\) is the outside diameter of the string after the second layer of circular cross section winding is applied, etc. The specification of the diameter of the first winding will be approximately \((d_2 - d_1)/2\) and so on.
The solution for the pth mode frequency, including the effect of stiffness, has been given by Fletcher [14] as:
with
where L is the sounding length, \(f_0\) is the fundamental frequency of the linear wave equation (as would result from setting the fourth-order differential stiffness term to be equal to zero in Eq. 1) and is given by:
The effect of harmonics becoming progressively sharp of the harmonic series has been illustrated in the work of Fletcher [14].
The resonant frequencies from Eq. 3 are higher in frequency (or equivalently, sharper in pitch) than those from the true harmonic series, and this effect becomes pronounced for high-frequency resonances for strings which have shorter sounding lengths and are of wider core. This occurs because \(S \kappa ^2\) will be (at least approximately) proportional to the diameter of the core to the power of four and this is divided by \(L^4\) in Eq. 4. The inharmonicity, \({\mathbb {I}}\), in cents (per cent of an equally tempered semitone by which the pth mode frequency differs from the ideal harmonic which is the lowest resonance frequency \(f_1\) multiplied by p) may then be graphed for each harmonic using the formula:
3 Finite difference time domain modelling of strings with multiple steps
Strings consisting of multiple sections of different mass per unit length can be assessed by physical modelling synthesis using the finite difference time domain (FDTD) technique. Such a model will be discussed and then run in MATLAB with the resulting resonant frequencies determined using discrete Fourier transforms. This has allowed for meaningful verification of the method against Fletcher’s formula for a uniform string and Chumnantas’ method for two part stepped strings. In addition to this, the FDTD method can predict resonances for stiff, stepped or tapered strings of three or more parts for the first time and the results compared to experiment as presented here.
3.1 Lossy model
Losses occur for various reasons in strings, including air drag, internal friction due to the viscoelasticity of the string material, temperature changes (due to thermoelasticity) being conducted away, conduction of vibrational energy at the supports and dry friction between windings. Such loss models are frequency dependent, and the literature on this topic is summarised in Desvages [pp. 49–55] [12] and in Valette and Cuesta [32, pp. 91–123]. A convenient and effective method set out in Bilbao [3, pp. 177–180, pp. 399–400] uses the equation of motion Eq. 1 and adds the frequency-dependent loss to give:
with \(\sigma _0\) being the loss coefficient for frequency-independent damping and \(\sigma _1\) being the loss coefficient for frequency-dependent damping.
Defining \(y_{n,l}\) as the transverse displacement at time domain sample number n and spatial sample number l, the resulting time domain model is implicit which means that the displacement at the next time step \(y_{n+1,l}\) depends on the displacement of neighbouring spatial sample points at that same time step (such as \(y_{n+1,l-1}\) and \(y_{n+1,l+1}\)). This problem can be solved using the matrix method described in Bilbao [3, p. 180, pp. 399–400]:
where \(\mathbf {y}_{n} = \{ y_{n,2}, y_{n,3}, \ldots y_{n,N_x-2}, y_{n,N_x-1}\}^{\intercal }\) is the column vector of displacements at all spatial samples for time sample number n excluding the fixed spatial samples \(y_{n,1} = y_{n,N_x} = 0\). The matrices are given by [3, p. 180, pp. 399–400]:
with \(k = 1/F_\mathrm{s}\) being the time domain sample period for sample rate \(F_\mathrm{s}\), \({\mathbf {I}}\) being the identity matrix, \({\mathbf {G}}\) being a diagonal matrix with the diagonal entries \(g_2, g_3, \ldots , g_{N_x-2}, g_{N_x-1}\), where \(g_l = T/(\tau _l \mu _\mathrm{core})\) is the square of the speed of wave propagation at spatial sample l (if the stiffness were zero) and \({\mathbf {Q}}\) being a diagonal matrix with the diagonal entries \(q_2, q_3 \ldots q_{N_x-2}, q_{N_x-1}\) where \(q_l = \left( E S_\mathrm{core}\kappa ^2 \right) _l/(\tau _l \mu _\mathrm{core})\) is the stiffness coefficient divided by the mass per unit length at spatial sample l. The second-order differential operator matrix is given by
(where the entries more than one place away from the diagonals are equal to zero) and the fourth-order differential operator matrix is given by
(where the entries more than two places away from the diagonals are equal to zero) with h being the distance between spatial samples (in metres) along the x axis. This is assuming that the ends of the string have the ideal fixed conditions \(y_{n,1} = 0\) for all n and \(y_{n,N_x} = 0\) for all n. The corner elements in Eq. 13 are 5 rather than 6 due to the second-order spatial differential at the fixed ends being zero (which means that the nonexistent points outside the string that are required in calculating \(D_{xxxx}\) are assumed to be \(y_{n,0} = - y_{n,2}\) and \(y_{n,N_x + 1} = - y_{n,N_x - 1}\)). All matrices are of dimension \(N_x -2 \times N_x -2\).
Note that Eq. 8 assumes that the spatial sample rate is constant. Numerical stability, however, requires that the minimum size for the distance between spatial samples is given by Bilbao [3, p.176]:
where the label j denotes the section of the (tapered) string under consideration. If numerical sound synthesis in real time was required then further work would be advisable to achieve efficient use of bandwidth [3, pp. 206–208]. For the current application (non-real-time analysis of resonant frequencies), all spatial samples will be set equidistant and equal to the maximum value of \(h_j\) along the string:
where J is the number of different sections of string (\(J = 1\) for a uniform string, \(J = 2\) for a two part stepped string, etc.). In practice, the value of h will therefore equal \(h_j\) for the section of string of lowest mass per unit length (as this will have the largest minimum value for \(h_j\)).
We will analyse the case of strings that are uniform along most of their length and may have a section or sections of contrasting construction close to the start (low numbers for l). The number of spatial samples along the string can be set to \(N_x =\) round(L/h) + 1, with the rounding error reducing linearly with the sample rate chosen. Assuming that the longest section of string has \(j = J\), the sounding frequency of the fundamental if there was no stiffness will then be approximated by:
Initialisation involves creating an initial shape for the string at the first two time steps (\(n=1\) and \(n=2\)) for use in Eq. 8. The exact nature of the initialisation is unimportant for the goal of assessing mode frequencies as long as all mode shapes of interest were given nonzero excitation and very high-frequency components outside the usable bandwidth are suppressed. In practice, a forward going travelling wave with a raised cosine shape was used:
where \(N_w = \mathrm {round}(2 N_x/3)\) was chosen as the length of the pulse in spatial samples, \(l_w\) was chosen such that the pulse was initially centred in the middle of the string, so \(l_w = \mathrm {round}(N_x/2) - \mathrm {round}(N_w/2)\), and
is the (less than or equal to unity) distance in samples for wave propagation in the low-frequency limit assuming the pulse is created entirely in the main section of string where \(j=J\).
4 Bass strings in measurement and simulation
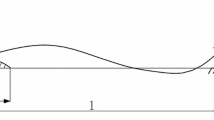
As demonstrated in the work of Chumnantas for two part piano strings [7,8,9] and confirmed here for multi-part bass guitar strings, introducing an area of lowered mass per unit length near an end of the sounding length increases the inharmonicity. Strings with lowered mass near the bridge are common in commercially available bass guitar strings in order to allow the string to bend around the saddle more effectively. It follows that introducing an area of larger mass per unit length near an end of a string will lower the inharmonicity. With this in mind, a string has been designed for this study to provide low inharmonicity when playing at high fret numbers on the bass guitar. Raised mass near the ends of the sounding length have been used for inharmonicity control in bass piano string construction [11, 30, 31] but not been used for bass guitar until this study to the best of the author’s knowledge. A diagram of the construction of such as string is shown in Fig. 1 where the sounding length begins at the saddle on the left hand side (of the \(j = 1\) section). The right hand most section (\(j = 4\) in this example) constitutes by far the longest section of string (and finishes far to the right of the figure).
Cross section of a tapered bass guitar string with an area of raised mass near the saddle comprising a core and three layers of winding (not to scale). The diameters of the different layers of windings \(d_{w1}\), \(d_{w2}\) and \(d_{w3}\) are numbered in the order they would be applied during manufacture, and the four sections are numbered \(j = 1, 2\), 3 and 4 sequentially along the length of the string. Shades of grey are used to differentiate the successive layers of windings though they were constructed from the same material (nickel-plated steel)
As is standard in the guitar string industry, wire specifications will be quoted in inches. These diameters must be converted to metres before use in the equations within this paper. The hexagonal cross section core has a specified minimum diameter of \(d_\mathrm{spec} \approx 0.028\)”, and hence, the diameter at the points of the hexagon is a factor of \(2/\sqrt{3}\) larger at \(d_1 \approx 0.032\)”. The first (innermost) winding in the “lumped” design was a short section of circular cross section nickel-plated steel of gauge \(d_{w1} \approx 0.013\)” (wound over approximately 21 mm of the core, starting 15 mm from the saddle and finishing 36 mm from the saddle). Next, a winding of circular cross section nickel-plated steel of gauge \(d_{w2} \approx 0.022\)” was wound over the core. This 0.022” winding begins beyond the nut finishes 9 mm short of the saddle (after running over the entirety of the short 0.013” winding). The final (outermost) layer of circular cross section winding of gauge \(d_{w3} \approx 0.028\)” starts at the knot which ties the core onto the ball end and runs on top of both the first layers of winding. This arrangement means no exposed ends for winding layers, with every layer of winding starting on the hex core (with the pointed corners of the hex core thus preventing the windings slipping out of place).
For the “tapered” and “standard” designs, the short section of \(d_{w1} \approx 0.013\)” winding was omitted. The thinner section of the “tapered” design results from the \(d_{w2} \approx 0.022\)” winding running from behind the nut and finishing 23 mm from the saddle (while still overwinding all the way from the ball end to beyond the nut with the \(d_{w3} \approx 0.028\)” winding). In the case of the “standard” string design, the \(d_{w2} \approx 0.022\)” winding finished at the ball end knot such that both the \(d_{w2} \approx 0.022\)” and \(d_{w3} \approx 0.028\)” windings ran over the entirety of the sounding length. The dimensions for the lumped, tapered and standard strings designs are described in Tables 1, 2 and 3.
A Sadowsky Bass Guitar Metroline MV5-NAT was used for experiments. The nominal scale length of this instrument (which is slightly less than the sounding length for unfretted notes due to strings going sharp when fretted) is \(L_0 = 34''\) or around 864 mm. Once the positions of the saddles were adjusted to set the intonation (so the sounding pitch of the 12th fret is an octave higher than the open string at pitch), the open B string has a sounding length of 874 mm and pressing the string behind the highest (21st) fret gives a sounding length of around \(L_{21} = 267\) mm.
4.1 FDTD simulations
Simulations of lossy string motion were performed within MATLAB at a very high sample rate of \(f_\mathrm{s} = 902.4\) kHz in order to give high spatial resolution (\(h \approx 1\) mm) in the resulting simulations when using the measured dimensions of the string given in Table 1. The loss coefficients, \(\sigma _0\) and \(\sigma _1\), were chosen to achieve a 60 dB drop in amplitude (\(T_{60}\) time) of 0.4 s at 8000 Hz for all fret numbers and to give a \(T_{60}\) time of 10 s at 600 Hz for the 21st fret simulations and a \(T_{60}\) time of 13 s at 600 Hz for simulations of both the open string and 12th fret (in order to approximately match the experimental results described in the subsequent section). This was achieved using the formulation set out in Bilbao [3, p. 178, pp. 399–400]. The inharmonicity in cents was observed to be insensitive to the exact choice of loss coefficient as realistic values require the effects of losses to be evident only over a very large number of cycles.
While unsuitable for real-time synthesis at present, the high sample rate allows different designs to be assessed. The approximate sounding length, L, is given by:
but due to variations in tension, etc., when the string is displaced on fretting, the string length was instead measured on the real instrument for better accuracy, giving \(L_0 = 0.873\) m and \(L_{12} = 0.442\) m and \(L_{21} = 0.267\) m. The value of T chosen to result in FDTD output having the same fundamental frequency (to within 0.1 Hz) as the corresponding experiments (and these tension values were obtained iteratively by assuming tension is proportional to sounding frequency squared).
It was assumed that the Young’s modulus for the steel core was \(E_\mathrm{core} = 207\) GPa and that the volumetric density of the steel was \(\rho _\mathrm{core} = 7860\hbox { kg/m}^3\) as in [25]. The windings were nickel-plated steel (approximately 8% nickel by weight), but the increase in volumetric density due to nickel content was only around 0.5% so, for simplicity, it was assumed that \(\rho _w = \rho _\mathrm{core}\).
The precise value of the stiffness coefficient \(E S \kappa ^2\) is critical to achieving good agreement between theory and experiment for the inharmonicity of higher-frequency resonances (and has a negligible impact on the fundamental frequency). While most of the stiffness is due to the core, assuming a value of \(E_\mathrm{core} S_\mathrm{core} \kappa _\mathrm{core}^2\) for the stiffness coefficient can be expected to underestimate the stiffness for strings due to the behaviour of the multiple layers of windings. Simulations were therefore run with a variety of values of the ratio \(\xi = (E S \kappa ^2)/(E_\mathrm{core} S_\mathrm{core} \kappa _\mathrm{core}^2)\) in order to obtain a good fit between experiment and theory for the string under consideration. It was assumed that \(E S \kappa ^2\) was constant along the length of the string because the effect of small variations in stiffness within the short stepped or tapered section is dwarfed by the effect of stiffness on the longest section of string.
These simulations were performed using the three string designs described in Tables 1, 2 and 3. The resulting waveform for each simulation was extracted at the nonzero spatial sample nearest the bridge (\(y_{n,2}\), where \(n = 1,2,3\ldots , N_t\) are the time sample numbers with \(N_t = 1000 f_\mathrm{s}/f_0\) rounded up to give the integer number of samples for 1000 cycles where \(f_0\) is taken from Eq. 16). Extracting the signal as close as possible to the bridge has the advantage that it is not at a nodal position for any of the standing wave shapes of interest. This was then analysed using a discrete Fourier transform (DFT) using the fft command in MATLAB. Since losses were included, the signals were self-windowing (i.e. no multiplication by a time domain window was required). Resonant peaks were then detected using a custom MATLAB script which searches recursively for maxima in the absolute value of the discrete Fourier transform in approximately harmonic frequency ranges starting with the region around Eq. 16. The inharmonicity within the resulting series of peak frequencies was then calculated for graphing using Eq. 6.
4.2 Experiments
Experiments were performed by plucking the string 20 mm from the bridge on the Sadowsky bass and recording the output from the magnetic pickups using a guitar cable plugged into an instrument input on a RME UFX soundcard connected to an Apple MacBook using USB. The bass was left in passive mode to bypass the tone controls, and the pickup fader was set to provide a signal consisting of the neck pickup output plus approximately a third of the output from the bridge pickup (by setting the pickup fader approximately five sixths of the way from the bridge to the neck pickup side of the range of travel on the dual MN taper potentiometer) as this arrangement was found to give a reasonably strong signal for nearly all harmonics of interest when playing at all frets of interest. Experiments were carried out for the open string, the octave (pressing the string behind the 12th fret) and the highest note on the string (pressing the string behind the 21st fret) for the “lumped”, “standard” and “tapered” strings (dimensions given in Tables 1, 2 and 3). Resonant frequencies peaks were then measured in each case using the same peak detection method as for the simulated string vibrations.
4.3 Results
The inharmonicity in cents (calculated using Eq. 6 based on the frequency of the peaks in the DFT) was compared for the experimental recordings and for the FDTD simulations for each geometry. Since the exact stiffness coefficient of the string may exceed the theoretical stiffness coefficient of the core (due to a contribution to stiffness from the multiple layers of windings for instance), it is necessary to run the simulation for a variety of stiffness coefficient values to determine a range for this parameter that produces good agreement (low root mean square error in cents) between the inharmonicity of the experimentally measured waveform and the inharmonicity of the simulated waveforms. Simulations were performed for values in the range \(1.1 \le \xi \le 1.7\) where \(\xi\) is the ratio between the stiffness coefficient used in the FDTD simulation and the theoretical stiffness coefficient of the core such that
where, for hex strings, \(S_\mathrm{core} = \gamma _\mathrm{core} (d_1/2)^2\) with \(\gamma _\mathrm{core} = 3 \sqrt{3}/2\) and \(\kappa _\mathrm{core} = (d_1/4) \sqrt{5/6}\) and the theoretical maximum distance between points can be worked out from the minimum (or specification) diameter as \(d_1 = (2/\sqrt{3}) d_\mathrm{spec}\). Open string inharmonicity values were observed to be too low for sensitive determination of the stiffness coefficient so measurements and simulations of notes played at the 12th fret and 21st fret were used for this purpose.
Taking the inharmonicity for the experimental data for the pth resonance as \({\mathbb {I}}_p^\mathrm{EXP}\) and the inharmonicity for the finite difference time domain data for the pth resonance for different values of \(\xi\) as \({\mathbb {I}}_p^\mathrm{FDTD}(\xi )\), the root mean squared error in cents was calculated using:
where P was the total number of resonances being analysed in this case and the root mean square error is a function of the offset value \(\delta\) used to account for the uncertainty in cents in the tuning of the string in the experimental data. Seven resonances (\(P=7\)) were used in the determination of the best fit because the eight resonance was difficult to measure accurately at the 21st fret due to the plucking position being at a node for this mode number.
The minimum value of \(\mathrm {RMSE}(\xi ,\delta )\) was found for integer values of \(\delta\) in the range \(-50\) cents \(\le \delta \le\) 50 cents for multiple values of \(\xi\). Resulting values of \(\mathrm {RMSE}(\xi )\) for different string constructions sounding at 12th fret and the 21st fret are shown in Fig. 2 with the range \(1.3 \le \xi \le 1.6\) giving minima for the root mean squared error. This range of values for \(\xi\) equates to the effective diameter used in the calculation of stiffness being around 7% and 12% larger than the measured core diameter given that \(E S \kappa ^2 \propto d_1^4\). This result is not expected to be generalisable to all hexagonal core strings due to the variety of constructions available and uncertainty in the exact value of variables such as the ratio of total string mass to core mass (\(\tau\)). Values of \(\xi = 1.3\) to \(\xi = 1.6\) thus give realistic maximum and minimum stiffness coefficients for use in simulations.
Root mean squared error inharmonicity in cents for the “lumped”, “standard” and “tapered” bass guitar strings between experimental measurement and for finite difference time domain simulation. Results are graphed for different ratios of \(\xi = (E S \kappa ^2)/(E_\mathrm{core} S_\mathrm{core} \kappa _\mathrm{core}^2)\). The 12th fret and the 21st fret were used, and the strings had dimensions given in Tables 1, 2 and 3
The results shown in Fig. 3 give the inharmonicity in cents for the “lumped” string, “standard” string and “tapered” bass guitar string measured experimentally and simulated using the FDTD method when fretted at the 21st fret (and thus vibrating between the 21st fret and the saddle). Simulations using \(\xi = 1.3\) gave the minimum values, and simulations using \(\xi = 1.6\) gave the maximum values of inharmonicity as represented in the error bars. For comparison, the inharmonicity according to the Fletcher formula of Eq. 3 is also given for the case of a uniform string of the same total sounding length (and the same construction as the longest section of the string). The theoretical (blue) lines showing the Fletcher formula for the different constructions are essentially coincident and show good agreement with the experimental results for the standard string construction as expected.
Inharmonicity for the “lumped”, “standard” and “tapered” bass guitar strings (approximately 132 gauge) described in Tables 1, 2 and 3 for experiment and finite difference time domain simulation. Results are shown for fretting at the 21st fret. The theoretical inharmonicity of uniform strings of the same total sounding length (and the same construction as the main \(j=J\) section of the string) according to the Fletcher formula, Eq. 3, is also given
Figures 4 and 5 show the same process repeated for the 12th fret and open string, respectively.
Inharmonicity for the “lumped”, “standard” and “tapered” bass guitar strings (approximately 132 gauge) described in Tables 1, 2 and 3 for experiment and finite difference time domain simulation. Results are shown for fretting at the 12th fret string. The theoretical inharmonicity of uniform strings of the same total sounding length (and the same construction as the main \(j=J\) section of the string) according to the Fletcher formula, Eq. 3, is also given
Inharmonicity for the “lumped”, “standard” and “tapered” bass guitar strings (approximately 132 gauge) described in Tables 1, 2 and 3 for experiment and finite difference time domain simulation. Results are shown for the open string. The theoretical inharmonicity of uniform strings of the same total sounding length (and the same construction as the main \(j=J\) section of the string) according to the Fletcher formula, Eq. 3, is also given
The experimental data show that, as expected, the inharmonicity is greater for a given resonant mode number for shorter sounding lengths (i.e. at higher frets). For open strings, the inharmonicity is not very significant for the first ten modes. It is clear that the “tapered” string (that has lowered mass near the bridge) has raised inharmonicity in comparison with the standard construction string in all cases (except for a very slight anomaly in the 2nd partial on the open string). The “lumped” design (with a lower mass very close to the saddle and raised mass nearby) generates significantly lower inharmonicity when playing at higher fret numbers (with spurious data for the eighth mode when playing the 21st fret due to negligible amplitude measured).
5 Perturbation theory
The effect of a perturbation in linear mass density on a string was established by Lord Rayleigh [28, p.170] and used to propose mass loading for inharmonicity reduction in piano strings by Miller [26]. If we make the perturbations add \(\delta \mu (x)\) to the mass per unit length in certain regions of the string then the frequency of the pth mode, \(f^\mathrm{(pert)}_p\) in terms of the unperturbed mode frequencies, \(f_p\), is given by [28, p.170]:
where s is given by the integral [28, p.170]:
This is usually applied to ideal strings rather than stiff strings. However, the mode shapes of uniform stiff strings with ideal fixed ends are the same as those of uniform strings of zero stiffness with fixed ends. It follows that the perturbation method can be applied as a first-order correction to the analytic mode frequencies for the uniform stiff string if the frequency ratio change is small (as is the case here because the length of the perturbed section is small in comparison with the total length of the string). This has a huge advantage in computation time for mode frequency prediction in comparison with high sample rate FDTD approach used elsewhere in the paper.
The integral in Eq. 24 can be computed resulting in a summation over the different sections of string (assuming \(j = J\) is the longest section):
where J is the number of different sections. The vector \(x_j\) contains the x coordinates of the discrete changes in density with \(x_0 = 0\) and the other entries calculated from the lengths of the sections, \(a_j\), using
In order to compute the results, first the stiff string mode frequencies, \(f_p\), from the Fletcher formula, Eq. 3, where calculated assuming the ratio of total mass of string to core mass was \(\tau = \tau (J)\) and Eq. 21 was used with \(\xi = 1.45\) (as the mid point in the range \(1.3< \xi < 1.6\) used previously). These were substituted into Eq. 23 (and taking the solution of the integral, s, from Eq. 25) to obtain the mode frequencies according to the perturbation method, \(f^\mathrm{(pert)}_p\), for the “lumped”, “standard” and “tapered” string designs. The inharmonicity in cents for the mode frequencies according to the perturbation method was then calculated by substitution into Eq. 6. The results are shown in Fig. 6 for the 21st fret measurement along with the FDTD and experimental results shown previously. Agreement between the perturbation method and the FDTD method is good, being well within the error bars produced by consideration of uncertainties in the exact diameters, mass ratios and contribution to stiffness due to the windings. This demonstrates that, for significant changes to the density localised near the end of the string, the perturbation method delivers results which are sufficient for analysing and optimising string designs. No losses were involved in the derivation of the mode frequencies according to the perturbation method, hence reinforcing the fact that losses have negligible impact on the frequencies of the modes.
Inharmonicity for the “lumped”, “standard” and “tapered” bass guitar strings (approximately 132 gauge) described in Tables 1, 2 and 3 for experiment, finite difference time domain simulation and perturbation theory. Results are shown for fretting at the 21st fret. Perturbation theory results were obtained from the Fletcher formula, Eq. 3, modified by perturbation theory, Eq. 23
6 Controlling pitch glide through inharmonicity reduction
Pitch glide is known to occur partly due to nonlinear oscillation as high amplitudes at the start of notes lead to raised tensions for part of the oscillation cycle. This can be expected to increase the resonance frequencies of all resonances (including the fundamental) near the start of the note [15]. Pitch tracking in humans and in electrical tuners depends on the amplitude and frequency of multiple partials. It is therefore important to also consider how the higher-frequency resonances decay much more quickly than the lower frequency resonances of strings. The higher pitched resonances (which are sharp of true harmonics of the fundamental resonant frequency) have a larger effect on the observed pitch at the start of a pluck, while the lower partials (which are closer to harmonic and thus flatter in pitch) have a larger effect on the observed pitch later in the sustain of the note. Pitch glide can therefore be expected to occur for inharmonic strings even if there was no pitch glide due to nonlinearity (with all the resonance frequencies essentially static in frequency). Pitch glides related to inharmonicity have been observed previously in bass piano notes [27, 29]. This kind of pitch glide can be expected to be reduced for strings of lower inharmonicity.
In order to investigate the effect, pitch tracking was performed on the recordings of the constructed strings by extracting the pitch contour obtained using the default settings (autocorrelation method) in Praat 6.0.29 software [4]. Following this, the audio was low pass filtered using “Filter (pass Hann band)” (with a corner frequency of approximately 1.5 times the fundamental frequency and smoothing of around a sixth of the fundamental frequency) in Praat software to remove the second and higher resonances. Pitch tracking was then performed on the resulting data to obtain pitch tracking data on the fundamental. Both sets of pitch tracking data were then overlaid on the spectrograms of the same recordings obtained using the spectrogram function in MATLAB (with a sample rate of 44.1 kHz and Hamming windows of length 65536 samples used, giving a window length of 1.4 s and an overlap between windows of 0.7 s and the colour map set with a dynamic range of 30 dB) for comparison. Zooming in to the area around the fundamental enables the any glide in pitch and fundamental frequency to be observed. For clarity in terms of pitch, dotted horizontal lines have been overlaid to indicate the frequencies corresponding to 20 cent intervals of pitch relative to the pitch observed in the later stages of the pitch tracking data. The results are plotted in Fig. 7.
Spectrogram (background image) and pitch tracking (magenta line) of the unfiltered audio recordings. Also shown is the pitch tracking of the fundamental frequency (black line) calculated by low pass filtering to remove second and higher resonances before running pitch tracking analysis. Results are shown for the “lumped”, “standard” and “tapered” bass guitar strings (approximately 132 gauge) constructed as described in Tables 1, 2 and 3 when playing the open string, 12th fret and 21st fret
In general, the (magenta) pitch tracking data shows significant downward pitch drift that is accentuated at higher fret numbers. This is not accompanied by any downward pitch glide for the (black) fundamental pitch tracking data or spectrogram data. For this experiment, the significant downward glide in the (magenta) pitch tracking data is therefore due to inharmonicity, not due to nonlinear oscillation.
The value for “glide” in cents per second is shown above each subplot, and this was calculated by taking the median of the pitch in cents between 0 and 1 s in the (magenta) pitch tracking data and subtracting the median of the pitch in cents between 1 second and 2 s in the (magenta) pitch tracking data. High values of pitch glide are associated with the “tapered” and “standard” string designs for high fret numbers. In general, the “lumped” string design (of lowest inharmonicity) shows the lowest values of pitch glide (less than 4 cents per second at all positions). It should be noted that the “tapered” string (that has the highest inharmonicity levels) has the lowest observed glide for the open string (at 1.75 cents per second) with the pitch tracking data consistently 20 cents above the fundamental frequency. Due to the higher resonances being strongly excited by the plucking position (2cm for the bridge), the inharmonic resonances were significant throughout the sustain at larger levels than would be typical in normal playing. The values of glide clearly depend on how strongly upper resonances are excited and how long they sustain and these are not central topics of the current paper. Analysing the effect inharmonicity on pitch glide during typical playing techniques is clearly worthy of future work, and lumped string designs clearly show promise in enabling lower pitch glides to be obtained throughout different neck positions (or fret numbers).
It is interesting to note that the (black) fundamental pitch tracking data at higher fret numbers show evidence of a mild upward pitch glide in the fundamental (the opposite of the glide in the fundamental expected from nonlinear theory) and may be related to magnetic drag [13]. This subtle effect is completely obscured by the downward pitch glide in the (magenta) pitch tracking data. The fluctuations in the pitch tracking data of the fundamental after around 4 s are due to the signal to noise ratio reducing as energy is lost from the vibration.
7 Conclusions
Assessing the resonant modes of lossy stiff bass guitar strings of varying cross section using the finite difference time domain method has been demonstrated to give good agreement with the experimental results for significant changes of mass density located near the bridge. This is encouraging in itself for applications such as musical sound synthesis of a wide range of string instruments although more advanced treatment of varying density would be necessary for real-time applications given current computational power. Starting from a lossless stiff string of constant mass per unit length and modifying the resonant frequencies using Rayleigh’s method for variation in mass per unit length (referred to as perturbation theory in this work) results in good agreement within reasonable error bounds. This demonstrates that this perturbation theory is acceptable for string design purposes while taking a tiny fraction of the programming and computation time. Due to the good agreement between lossy finite difference time domain simulation and lossless perturbation theory, the inclusion of losses is demonstrated to have negligible impact on inharmonicity for realistic bass guitar string simulations.
All the strings designs tested here demonstrated lower sustain when playing at high fret numbers. This is always expected for string instruments due to losses generally being larger for higher resonant frequencies and shorter wavelengths. The low sustain and high fundamental frequency high up the neck increases the relevance of maintaining low inharmonicity for the first few modes in order to maintain optimal timbre and harmony in musical contexts such as supporting chordal work.
The inharmonicity of strings is increased by conventional tapered or stepped string designs. On the other hand, the inharmonicity may be decreased by using a lumped string design (through introducing a section of raised mass per unit length near to the end of the sounding length). This may be expected to improve pitch perception, increase the sense of consonance with other instruments in musical context and improve the timbre of notes played through nonlinear systems such as distortion effects. Pitch glide can be problematic when tuning instruments in addition to potentially interfering with musical harmony and note quality. This problem is also reduced by increasing the mass near the saddle. Lower pitch bass guitar strings that typically have large inharmonicity at higher fret numbers are expected to benefit from this lumped design. Further work is required to validate the extent to which such constructions result in perceptually significant changes in musical context, including on the higher pitched strings on bass guitar. In addition to this, it is worth investigating to what extent pitch glide is caused by inharmonicity in musical contexts involving plucked strings.
References
Abeßer J (2013) Automatic string detection for bass guitar and electric guitar. In: Aramaki M, Barthet M, Kronland-Martinet R, Ystad S (eds) From sounds to music and emotions. Springer, Berlin, pp 333–352
Barbancho I, Tardon LJ, Sammartino S, Barbancho AM (2012) Inharmonicity-based method for the automatic generation of guitar tablature. IEEE Trans Audio Speech Lang Process 20(6):1857–1868. https://doi.org/10.1109/TASL.2012.2191281
Bilbao S (2009) Numerical sound synthesis: finite difference schemes and simulation in musical acoustics. Wiley, New York
Boersma P, Weenink D (2019) Praat: doing phonetics by computer [computer program]. version 6.0.29. http://www.praat.org/
Chaigne A, Askenfelt A (1994) Numerical simulations of piano strings. i. A physical model for a struck string using finite difference methods. J Acoust Soc Am 95(2):1112–1118. https://doi.org/10.1121/1.408459
Chaigne A, Askenfelt A (1994) Numerical simulations of piano strings. ii. Comparisons with measurements and systematic exploration of some hammer string parameters. J Acoust Soc Am 95(3):1631–1640. https://doi.org/10.1121/1.408549
Chumnantas P (1995) Inharmonicity in the natural mode frequencies of overwound strings. Ph.D. dissertation, The University of Edinburgh. http://www.era.lib.ed.ac.uk/handle/1842/13393
Chumnantas P, Greated CA, Campbell DM (1993) Inharmonicity of stepped stiff strings. Proc Inst Acoust 15(3):665–672
Chumnantas P, Greated CA, Parks R (1994) Inharmonicity of nonuniform overwound strings. J Phys IV 4(C5):C5–649
Conklin HA Jr (1999) Generation of partials due to nonlinear mixing in a stringed instrument. J Acoust Soc Am 105(1):536–545
Dalmont JP, Maugeais S (2019) Piano strings with reduced inharmonicity. Acta Acust United Acust 105(4):714–717. https://doi.org/10.3813/AAA.919350
Desvages CGM (2018) Physical modelling of the bowed string and applications to sound synthesis. Ph.D. dissertation, The University of Edinburgh . https://www.era.lib.ed.ac.uk/handle/1842/31273
Feinberg J, Yang B (2018) Natural-frequency splitting of a guitar string caused by a non-uniform magnetic field. J Acoust Soc Am 144(5):EL460–EL464. https://doi.org/10.1121/1.5080465
Fletcher H (1964) Normal vibration frequencies of a stiff piano string. J Acoust Soc Am 36(1):203–209. https://doi.org/10.1121/1.1918933
Fletcher N (2000) Inharmonicity, nonlinearity and music. The Physicist 37(5):171–175
Galembo A, Askenfelt A, Cuddy LL, Russo FA (2004) Perceptual relevance of inharmonicity and spectral envelope in the piano bass range. Acta Acust United Acust 90(3):528–536
Grimes DR (2014) String theory–the physics of string-bending and other electric guitar techniques. PLoS ONE 9(7):1–9. https://doi.org/10.1371/journal.pone.0102088
Guadagnin L, Lihoreau B, Lotton P, Brasseur E (2017) Analytical modeling and experimental characterization of a magnetic pickup for electric guitar. J Audio Eng Soc 65(9):711–721
Hiller L, Ruiz P (1971) Synthesizing musical sounds by solving the wave equation for vibrating objects: part 1. J Audio Eng Soc 19(6):462–470
Hiller L, Ruiz P (1971) Synthesizing musical sounds by solving the wave equation for vibrating objects: part 2. J Audio Eng Soc 19(7):542–551
Hobby K, Sethares W (2016) Inharmonic strings and the hyperpiano. Appl Acoust 114:317–327. https://doi.org/10.1016/j.apacoust.2016.07.029
Hopkin B (2018) Overtones harmonic and inharmonic. http://barthopkin.com/overtones-harmonic-and-inharmonic/. Accessed 12 Mar 2020
Järveläinen H, Karjalainen M (2006) Perceptibility of inharmonicity in the acoustic guitar. Acta Acust United Acust 92(5):842–847
Järveläinen H, Välimäki V, Karjalainen M (2001) Audibility of the timbral effects of inharmonicity in stringed instrument tones. Acoust Res Lett Online 2(3):79–84. https://doi.org/10.1121/1.1374756
Kemp JA (2017) The physics of unwound and wound strings on the electric guitar applied to the pitch intervals produced by tremolo/vibrato arm systems. PLoS ONE 12(9):1–25. https://doi.org/10.1371/journal.pone.0184803
Miller F (1949) A proposed loading of piano strings for improved tone. J Acoust Soc Am 21(4):318–322. https://doi.org/10.1121/1.1906515
Podlesak M, Lee A (1989) Effect of inharmonicity on the aural perception of initial transients in low bass tones. Acta Acust United Acust 68(1):61–66
Rayleigh JWSB (1877) The theory of sound, vol 1. Macmillan and Co., London
Rocchesso D, Scalcon F (1999) Bandwidth of perceived inharmonicity for physical modeling of dispersive strings. IEEE Trans Speech Audio Process 7(5):597–601. https://doi.org/10.1109/89.784113
Sanderson AE (1998) Wound strings for musical instruments characterized by reduced inharmonicity and method for making the same. https://patents.google.com/patent/US5817960A. US Patent 5,817,960
Sanderson AE (1999) Method for making wound strings for musical instruments characterized by reduced inharmonicity. URL https://patents.google.com/patent/US5984226A. US Patent 5,984,226
Valette C, Cuesta C (1993) Mécanique de la corde vibrante. Hermes, Paris
Acknowledgements
I wish to thank Prof Clive Greated, Prof. Murray Campbell and Dr. Raymond Parks of the University of Edinburgh including for supervision of my undergraduate honours Project on piano string inharmonicity in the 1997–1998 academic year. The late Clive Greated (1940–2018) suggested I look at bass guitar string inharmonicity at that time, a topic I hope I am finally doing justice to. Thanks also to Dr. Charlotte Desvages, Dr. Michele Ducceschi, Tom Groves and Pete Sukanjanajtee for helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kemp, J.A. On inharmonicity in bass guitar strings with application to tapered and lumped constructions. SN Appl. Sci. 2, 636 (2020). https://doi.org/10.1007/s42452-020-2391-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-020-2391-2