1 Introduction

In the transportation electrification, the pure electric vehicles (EVs) are becoming an emerging technology and power sector because of their zero emission [1]. The interest in increasing the EVs running on alternate and renewable sources of energy has led to a spurt of research in the direction of improving the technologies involved in the EVs [2,3,4]. Various initiatives have been undertaken by several government organizations across the globe along with the improvement of these EV technologies to push for the usage of vehicles which run on alternate source of energy. Various organizations, such as IEEE, the Society of Automotive Engineers (SAE), and the Infrastructure Working Council (IWC) are preparing standards and codes concerning the utility/customer interface. To electrifying commercial vehicles, several policies have been brought by various governments [1, 5].

EVs have been enhanced significantly to allow for a long driving range using novel battery technologies and fast-charging stations. The growth of the EV market has led to the significant issues of coming up with novel and innovative ideas to charge them [6,7,8]. Three significant barriers of EVs are high cost and cycle life of batteries, a complication of chargers, and the lack of charging infrastructures [9]. The chargers are an integral part of EV grid-to-vehicle (G2V) drivetrain efficiency. The G2V efficiency for EVs should be close to 45–50%. In order to improve the G2V energy efficiency, a high efficiency, high reliability, high power density, and cost-effective charger design are mandatory [5]. The battery chargers can introduce deleterious harmonic effects on electric utility distribution systems which is another drawback. The introduction of harmonics in the input line current causes low power factor of the fast-charging stations, thus drawing more current from utility, increasing line losses, and reducing the life of the distribution transformers [10].

Based on the power ratings, the chargers are classified as Level 1, Level 2, and Level 3. Level 1 and Level 2 chargers are typically designed for home charging with power less than 2 kW with a standard voltage of 120/230 V and public charging stations with power 20 kW with a standard voltage of 120/230 V, respectively [11]. The EV charging plug and the adapter for both Level 1 and Level 2 chargers typically comply with the SAE J1772 standard [12]. Level 3 chargers are typically designed for a fast charging using DC with the power rating around 100 kW with a charging time of less than 30 min. Level 3 chargers are used in commercial charging stations. They are normally connected directly to the medium-voltage three-phase systems. The DC fast-charging station’s standards are presented in [13].

Further information for all the levels of charging is provided in Table 1. As a test case, the Nissan Leaf® 24 kWh Li-ion battery pack is considered [14].

Table 1 Standard EV charging levels (SAE J1772)
Full size table

The review of available Level 3/DC fast-charging techniques is the cornerstone of this paper. The advantages and limitations are also highlighted for better clarity.

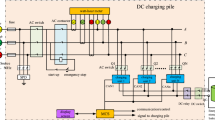
Generally, DC fast-charging stations for EVs are designed to supply about 50 kW of power [15]. The established trend is to place these chargers off-board as these stations are bulky. The general block diagram of a DC fast-charging station is shown in Fig. 1, and the charger is connected to a common AC link.

Fig. 1
figure 1

General block diagram of DC fast-charging station

Full size image

EV battery chargers can be integrated into an EV as an on-board charger or separated as an off-board charger. The power flows between the grids, and EV batteries can be unidirectional or bidirectional. The unidirectional power flow chargers are used as grid-to-vehicle charger applications, and bidirectional power flow chargers are used as grid-to-vehicle and vehicle-to-grid charger applications [16]. Unidirectional chargers can be controlled to charge the EV battery from the grid [17,18,19].

As per the previous review papers [20,21,22,23,24,25], they have reviewed two-level AC–DC converters, conventional boost rectifier, zero-voltage transition (ZVT) converters, zero-current transition (ZCT) converters, ZVT-ZCT converters, interleaved boost PFC converters, bridgeless boost PFC converters, and bridgeless interleaved boost PFC converters for the EV charging stations based on the efficiency, power factor, and input current THD and this paper reviews the practical viability of the energy-efficient converters based on the efficiency, power factor, power density, input current THD, and simulation analysis of Vienna rectifier for EV charging stations is carried out.

This paper presents a review of the recent battery-charging infrastructure for EVs in terms of converter topologies and power control strategies. From the analysis, the suitable converter has selected and simulated with a suitable controller based on the requirement of DC fast charger. In addition, three topologies of Vienna rectifier have been simulated. Based on the results of input current harmonics, output voltage, output current, and efficiency of three topologies of Vienna rectifier are analysed, and the graphs are plotted.

2 DC fast-charging converter topologies

There are several numbers of converter topologies available for the rapid charging of batteries or ultra-capacitors. Some feasible options are highlighted in this paper. They are:

2.1 Unidirectional boost converter

The unidirectional boost converter is shown in Fig. 2, and these converters are employed where the output voltage has to be boosted up for loads which require higher voltage [26].

Fig. 2
figure 2

Unidirectional boost converter [26]

Full size image

The primary goal of using a boost converter instead of the conventional diode bridge rectifier is to improve power factor, to reduce the harmonics at the end, and to have a controlled DC voltage at the output if unwanted perturbations occur at the AC end.

2.2 SWISS rectifier

The SWISS rectifier is shown in Fig. 3, and these rectifiers are employed where the efficiency has to be increased based on the application requirements [27].

Fig. 3
figure 3

SWISS rectifier [27]

Full size image

The significant achievement in using the SWISS rectifier is to provide better efficiency compared to the conventional rectifiers. Compared to boost-type converter, buck-type system provides a wide output voltage control range, while maintaining PFC capability in the input, enables direct start-up, and allows for dynamic current limitations at the output.

2.3 Matrix converter

The matrix converter is shown in Fig. 4, and these rectifiers are used for the regenerative operation of charging stations where it has to be used for the vehicle-to-grid applications with high efficiency [28].

Fig. 4
figure 4

Matrix converter [28]

Full size image

Matrix converter is a forced commutated converter that uses an array of controlled bidirectional switches which allows high-frequency operations. This type of converter does not require DC-link circuit and any large energy storage element. It can improve the power factor and reduce the harmonics in the line current at the end.

2.4 Vienna Rectifier

Another famous power converter for power quality improvement is the Vienna rectifier, as shown in Fig. 5. This is the popular choice when the aim is to achieve a high power factor and to attain lower harmonics distortion. The switching losses in Vienna rectifier are low because of low voltage stress in the switches [29, 30]. This converter consists of only one active switch per phase which makes the Vienna rectifier easier to control and makes it more dependable. This converter is basically a PWM converter [31], and the boost inductor at the input plays the role in ascertaining power factor correction. Basically, the stored energy acquired by the inductor when the switch is OFF is transmitted to the load through the diodes whenever the switch is ON. The advantage of employing this topology includes the absence of a neutral point connection [32].

Fig. 5
figure 5

Vienna rectifier [26]

Full size image

3 Performance comparison of energy-efficient converters

3.1 Comparative Analysis of Charging Converter Topologies

Some of the features of the converter topologies are discussed and are highlighted in Table 2. From the detailed review of the few converter topologies, it can be concluded that the use of the Vienna rectifier for the implementation of the charging station is appropriate, due to the following reasons:

  • It has less number of switches per phase.

  • Harmonic contents are compensated.

  • Good efficiency when compared to the PWM rectifier, SWISS rectifier, and matrix converter.

  • Higher power factor, around 0.99, compared to the PWM rectifier, SWISS rectifier, and matrix converter.

Table 2 Performance comparison of DC fast-charging converter topologies [33]
Full size table

The features of converter topologies are highlighted in Table 2. From the analysis, both the SWISS rectifier and Vienna rectifier have high efficiency with less than 5% THD. However, the Vienna rectifier is the most optimal converter topology for the charging stations as it has the advantages of high power density (12 kW/dm3) [37, 38] compared to the SWISS rectifier (4 kW/dm3) [32]. It is evident that the Vienna rectifier has been selected for designing DC fast charger as it has the advantage of high power density. The comparison of energy-efficient converters based on practical applications is given in Table 3. It can be seen from Table 3 that the Vienna rectifier can be used for EV charging system as it features high efficiency, high power density, unity power factor, and low total harmonic distortion, and the size of the system is small compared to other converters.

Table 3 Comparison of energy-efficient converters based on practical applications
Full size table

4 Control strategies of energy-efficient converters

Various control algorithms have been developed to improvise the power factor due to the harmonic distortions, different types of power controllers such as hysteresis current controller [47], SPWM controller [48], a direct power control (DPC) [49, 50]. The direct power control requires high inductance and sample frequency. The hysteresis controller is most commonly used but with more switching loss due to variable switching frequency, and in [51], it is originally used for thermostatically controlled loads [52] and is used for plug-in electric vehicle (PEV) charging to actively control the consumption of a higher number of chargers. In addition, several studies have established that model predictive control (MPC) reduces the harmonics in the line current and a smaller mean absolute current reference tracking error as compared to other controllers. In [53], the author presented a predictive current control method for reducing the total harmonic distortion (THD) by using a switching frequency of 8 kHz with a voltage source inverter. In [54], the researcher applied the model predictive control algorithm for a four-leg converter to observe the reduction in THD and switching frequency at low values of the filter parameters. In [55], a comparative study between a finite-control-set MPC (FCS-MPC) and synchronous proportional–integral (PI) controller with space vector modulation (PI-SVM) has been established; it was observed that the FCS-MPC is able to generate waveforms with fewer lower-order harmonics than the PI-SVM. The MPC method is able to operate with different voltage/frequency values while maintaining a lower THD value [56,57,58]. However, MPC requires complex implementation as compared to linear controllers. Meanwhile, in the single-phase on-board bidirectional charger proposed by [17], PI controllers were employed in AC/DC converters and DC/DC converters which provide constant voltage and constant current charging, as well as reactive power compensation. However, the THD of the line current was high.

In this paper, the PFC consisting of PI controller has been analysed for improving the power quality such as harmonics and power factor. The PFC with the PI controller is shown in Fig. 6. Other control strategies such as adaptive control, fuzzy logic control, sliding mode control, predictive control, or neural network control can be applied to improve the performance of the charging stations.

Fig. 6
figure 6

PFC with PI controller for EV applications [17]

Full size image

The PFC controller consists of three PI controllers which can regulate the DC output voltage based on the reference voltage. Small overshoot, good damping of oscillations, and fast response are the three fundamental goals of the designer for the synthesis of the involved PI controller in a control loop. This PFC controller has two outer voltage loops and one inner current loop. The evaluation of PI controller parameters is one of the key issues in the design of a cascaded structure where the inner loop is designed to achieve fast response and outer loops are designed to achieve optimum regulation and stability [59].

5 Topologies of Vienna rectifier for charging stations

5.1 Topology of the Vienna rectifiers

A single-phase Vienna rectifier topology employed in this study is shown in Fig. 7. The input filter of these topologies is composed of an inductor, L. The resistor R, means the resistive components in the inductor. The converter stated in this paper is similar to that of a single-phase T-type inverter, with the outer switches of the inverter having been replaced by the diodes in the rectifier. The rectifier topologies include the inner switch, which only operates when the top capacitor is charging. The circuit with fewer switches leads to less THD in the line current due to the frequency of switching, which leads to an improvement in the power factor at the source side. The key characteristics of this converter known as split capacitor consists of two capacitors being placed at the output side, that reduces the voltage stress on to the power semiconductor switches. The voltage across each capacitor is \(+ \frac{{V_{0} }}{2}\) and \(- \frac{{V_{0} }}{2}\) which detects the output voltage of the circuit. So, Vienna rectifier has three voltages such as \(+ \frac{{V_{0} }}{2}\), 0, and \(- \frac{{V_{0} }}{2}\). The capacitors at the output side are to reduce the voltage stress on the switches and also used to prevent the rapid voltage change at the output side. So, the cost of the converter can be reduced. The ratings used in this topological analysis are shown in Table 4.

Fig. 7
figure 7

Different topologies of Vienna rectifier

Full size image
Table 4 Rating of load for the analysis of 95% efficiency
Full size table

5.2 Mathematical Formulations for the Analysis

5.2.1 Topology 1

In this topology, the power factor correction controller is used to control the output voltage to a constant value and to make the input current sinusoidal. However, this topology has only one semiconducting switch and six diodes which reduce the efficiency of the system. Due to this connection, one of the most outstanding merit can be achieved which is low voltage stress on each component that will reduce half of the total DC bus voltage at each interval. By using analytical approximations, the average and the RMS current ratings of the semiconductor have been calculated [60]. By using the inductor present in the input side, these types of converter can increase the DC output voltage and improve the power quality in the input side as well.

The diode average (\(I_{{{\text{D}}_{{2, {\text{avg}}}} }}\)) and RMS current (\(I_{{{\text{D}}_{{2, {\text{avg}}}} }}\)) are calculated using Eqs. (1) and (2).

$$I_{{{\text{D}}_{{2, {\text{avg}}}} }} = \frac{1}{\pi }\hat{I}_{N}$$
(1)
$$I_{{{\text{D}}_{{2, {\text{RMS}}}} }} = \frac{1}{2}\hat{I}_{N}$$
(2)

The diode D3 average (\(I_{{{\text{D}}_{{3, {\text{avg}}}} }}\)) and RMS current (\(I_{{{\text{D}}_{{3, {\text{RMS}}}} }}\)) are calculated as in Eqs. (3) and (4).

$$I_{{{\text{D}}_{{3, {\text{avg}}}} }} = \left( {\frac{1}{\pi } - \frac{1}{2\sqrt 3 M}} \right)\hat{I}_{N}$$
(3)
$$I_{{{\text{D}}_{{3, {\text{RMS}}}} }} = \sqrt {\frac{1}{4} - \frac{4}{3\sqrt 3 M}\frac{1}{M}} \hat{I}_{N}$$
(4)

The diode D3 average (\(I_{{{\text{D}}_{{1, {\text{avg}}}} }}\)) and RMS current (\(I_{{{\text{D}}_{{1, {\text{RMS}}}} }}\)) are calculated as in Eqs. (5) and (6).

$$I_{{{\text{D}}_{{1, {\text{avg}}}} }} = \frac{1}{2\sqrt 3 M}\hat{I}_{N}$$
(5)
$$I_{{{\text{D}}_{{1, {\text{RMS}}}} }} = \sqrt {\frac{4}{3\sqrt 3 \pi }\frac{1}{M}} \hat{I}_{N}$$
(6)

The MOSFET average (\(I_{{{\text{S}}_{\text{avg}} }}\)) and RMS current (\(I_{{{\text{S}}_{{ {\text{RMS}}}} }}\)) are calculated by using Eqs. (7) and (8).

$$I_{{{\text{S}}_{\text{avg}} }} = \left( {\frac{2}{\pi } - \frac{1}{\sqrt 3 M}} \right)\hat{I}_{N}$$
(7)
$$I_{{{\text{S}}_{\text{RMS}} }} = \sqrt {\frac{1}{2} - \frac{8}{3\sqrt 3 \pi }\frac{1}{M}} \hat{I}_{N}$$
(8)

The capacitor ripple current (\({\text{I}}_{{{\text{C}}_{{ {\text{out}}, {\text{RMS}}}} }}\)) is calculated using Eq. (9).

$$I_{{{\text{C}}_{{{\text{out}},{\text{RMS}}}} }} = \sqrt {\frac{10\sqrt 3 M}{8\pi } - \frac{{9M^{2} }}{16}} \hat{I}_{N}$$
(9)

where \(\hat{I}_{N}\) is the peak line current, \(M = \frac{{U_{o} }}{{\sqrt 3 \hat{U}_{N} }}\) is the transformation ratio, \(U_{o}\) is the DC output voltage, and \(\hat{U}_{N}\) is the peak phase voltage.

5.2.2 Topology 2

In Topology 2, the freewheeling diode currents ID2 and ID4 and the capacitor ripple current IC remain the same as the Topology 1, and the MOSFET current is divided into two MOSFETs. To reduce the voltage stress on the switches, two capacitors are connected in parallel to minimize the losses in the switches [61].

The diode average (\(I_{{{\text{D}}_{{7,{\text{avg}}}} }}\)) and RMS current (\(I_{{{\text{D}}_{{7, {\text{RMS}}}} }}\)) are calculated using Eqs. (10) and (11).

$$I_{{{\text{D}}_{{7,{\text{avg}}}} }} = \frac{1}{2\sqrt 3 M}\hat{I}_{N}$$
(10)
$$I_{{{\text{D}}_{{7,{\text{RMS}}}} }} = \sqrt {\frac{4}{3\sqrt 3 \pi }\frac{1}{M}} \hat{I}_{N}$$
(11)

The diode D10 average (\(I_{{{\text{D}}_{{10,{\text{avg}}}} }}\)) and RMS current (\(I_{{{\text{D}}_{{10, {\text{RMS}}}} }}\)) are in Eqs. (12) and (13).

$$I_{{{\text{D}}_{{10,{\text{avg}}}} }} = \frac{1}{\pi }\hat{I}_{N}$$
(12)
$$I_{{{\text{D}}_{{10,{\text{RMS}}}} }} = \frac{1}{2}\hat{I}_{N}$$
(13)

The MOSFET average (\(I_{{{\text{S}}_{\text{avg}} }}\)) and RMS current (\(I_{{{\text{S}}_{\text{RMS}} }}\)) are calculated by using Eqs. (14) and (15).

$$I_{{{\text{S}}_{\text{avg}} }} = \left( {\frac{1}{\pi } - \frac{1}{2\sqrt 3 M}} \right)\hat{I}_{N}$$
(14)
$$I_{{{\text{S}}_{\text{RMS}} }} = \sqrt {\frac{1}{4} - \frac{4}{3\sqrt 3 \pi }\frac{1}{M}} \hat{I}_{N}$$
(15)

The capacitor ripple current (\(I_{{{\text{C}}_{\text{out,RMS}} }}\)) is calculated using Eq. (16).

$$I_{{{\text{C}}_{\text{out,RMS}} }} = \sqrt {\frac{10\sqrt 3 M}{8\pi } - \frac{{9M^{2} }}{16}} \hat{I}_{N}$$
(16)

5.2.3 Topology 3

The Topology 1 and Topology 2 have no redundancy states to balance the voltage of the capacitor continuously. This is the main drawback of above-mentioned topologies which leads to high voltage ripple at DC output. In Topology 2, the voltage ripple is minimized by balancing the voltage using two switches connected in anti-parallel to the neutral. In Topology 3, the freewheeling diode current remains the same as others. As the switch is made up of two MOSFETs, it is different from the Topology 1 which reduces the voltage stress on the switches and it has only two diodes in the circuit which reduces the losses in the diodes. Due to this design, the losses from the diodes have been reduced, and the rating of the switch has been reduced; it leads to a reduction in the cost of the device and increase in efficiency as well.

The diode average (\({\text{I}}_{{{\text{D}}_{{2,{\text{avg}}}} }}\)) and RMS current (\(I_{{{\text{D}}_{{2, {\text{RMS}}}} }}\)) are calculated using Eqs. (17) and (18).

$$I_{{{\text{D}}_{{2,{\text{avg}}}} }} = \frac{1}{2\sqrt 3 \pi }\hat{I}_{N}$$
(17)
$$I_{{{\text{D}}_{{2, {\text{RMS}}}} }} = \sqrt {\frac{2}{3} - \frac{8}{3\sqrt 3 }\frac{1}{M}} \hat{I}_{N}$$
(18)

The MOSFET average (\(I_{{{\text{S}}_{\text{avg}} }}\)) and RMS current (\(I_{{{\text{S}}_{\text{RMS}} }}\)) are calculated by using Eqs. (19) and (20).

$$I_{{{\text{S}}_{\text{avg}} }} = \left( {\frac{2}{\pi } - \frac{1}{\sqrt 3 M}} \right)\hat{I}_{N}$$
(19)
$$I_{{{\text{S}}_{\text{RMS}} }} = \sqrt {\frac{1}{2} - \frac{8}{3\sqrt 3 \pi }\frac{1}{M}} \hat{I}_{N}$$
(20)

In this topology, the switches are connected in the back–back connection of MOSFETs. During the positive half cycle, MOSFET S1 and diode of S2 conduct, and in negative half cycle MOSFET S2 and diode of S1 conduct.

Combined diode and MOSFET average (\(I_{{{\text{T}}_{\text{avg}} }}\)) and RMS current (\(I_{{{\text{T}}_{\text{RMS}} }}\)) are calculated by using Eq. (21)–Eq. (22).

$$I_{{{\text{T}}_{\text{avg}} }} = \left( {\frac{1}{\pi } - \frac{1}{2\sqrt 3 M}} \right)\hat{I}_{N}$$
(21)
$$I_{{{\text{T}}_{\text{RMS}} }} = \sqrt {\frac{1}{4} - \frac{4}{3\sqrt 3 \pi }\frac{1}{M}} \hat{I}_{N}$$
(22)

The capacitor ripple current (\(I_{{{\text{C}}_{\text{out, RMS}} }}\)) is calculated using Eq. (23).

$$I_{{{\text{C}}_{\text{out, RMS}} }} = \sqrt {\frac{10\sqrt 3 M}{8\pi } - \frac{{9M^{2} }}{16}} \hat{I}_{N}$$
(23)

5.2.4 Efficiency Computations

The conduction loss (\(C_{\text{L}}\)) for the diodes in the circuit is calculated using Eq. (24).

$$C_{\text{L}} = I_{\text{avg}} \times V_{\text{f}}$$
(24)

where Vf is the forward voltage drop of the diode at the particular Iavg as provided by the diode data sheet (Vf normally ranges from 0.6 to 1.1 V). The switching loss (SL) for the devices is given in Eq. (25).

$$S_{\text{L}} = \frac{1}{2}CV^{2} f$$
(25)

where C is the capacitance of the junction, V is the blocking voltage, and f is the switching frequency.

The conduction loss in the MOSFETs (\(C_{L1}\)) is calculated using Eq. (26).

$$C_{L1} = I_{\text{rms}}^{2} \times R_{{{\text{DS}}_{\text{ON}} }}$$
(26)

where \(R_{{{\text{DS}}_{\text{ON}} }}\) is the source-to-drain resistance at the operating temperature.

The switching loss during turn on and turn off is calculated using Eqs. (27) and (28).

$$S_{\text{on}} = \frac{1}{2}VI_{\text{rms}} t_{\text{r}} f_{\text{sw}}$$
(27)
$$S_{\text{off}} = \frac{1}{2}VI_{\text{rms}} t_{\text{f}} f_{\text{sw}}$$
(28)

where \(f_{\text{sw}}\) is the switching frequency, \(t_{\text{r}}\) is the rise time, and \(t_{\text{f}}\) is the fall time.

6 Results and analysis

6.1 Efficiency analysis

The number of switches, type, and the number of diodes for different topologies are given in Table 5, and it is observed that the number of components available in Topology 3 is low. The three topologies of the Vienna rectifier at 50 kHz are calculated for the efficiency values and are plotted in Fig. 8.

Table 5 Comparison of components in terms of number of devices
Full size table
Fig. 8
figure 8

Efficiency characteristics

Full size image

The Topology 1 has higher efficiency in between the input voltages of 320 V and 400 V, compared to Topology 2 and Topology 3, which is shown in Fig. 8. Beyond 400 V, due to the more number of switches in Topology 1, the switching losses will increase. So, the efficiency of Topology 3 overtakes the Topology 1, and for a wide range of input voltage, it is more efficient than other topologies. From Table 4, it is noted that the number of switches in Topology 3 is less compared to the other two topologies. Due to this, the losses in Topology 3 are very less, which leads to more efficiency.

6.2 Input Current Characteristics

It is noted that the input current waveform for three topologies is almost sinusoidal. The input current is shown in Fig. 9. In all three topologies, there are slight changes in the harmonics, which leads to minor variations in the sinusoidal waveform of input current. Compared to all three topologies, Topology 3 has the sinusoidal input current which indicates unity power factor at the input power supply.

Fig. 9
figure 9

Input current waveforms of three topologies of Vienna rectifier

Full size image

6.3 Input Current THD Spectrum

It is noted that the percentage input current THD for Topology 1 is 4.11, which is less than 5%, and it is meeting the IEEE standards. Due to the more number of switches in Topology 2, the harmonics on the input current are less compared to Topology 1 which is 6.45% and it fails to meet the IEEE standards. This leads to more losses in Topology 2, and the efficiency of the circuit has been reduced. The percentage input current THD for Topology 3 is 2.38, which is less than 5%, and it satisfies the IEEE standards. Among all the three topologies, it is evident from the analysis that the performance of Topology 3 is better compared to Topologies 1 and 2. The percentage input current THD for the three topologies is shown in Fig. 10.

Fig. 10
figure 10

THD for three topologies of Vienna rectifier

Full size image

6.4 Output Voltage of Vienna Rectifier Topologies

The DC output voltage is almost constant in all the topologies. The output DC voltage for three topologies is shown in Fig. 11.

Fig. 11
figure 11

Output DC voltage of three topologies of Vienna rectifier

Full size image

6.5 Performance Evaluations of the Vienna Rectifier Topologies

It can be seen from Table 6 that the Topology 3 is providing better performance in terms of THD value compared to other topologies. The introduction of harmonics is because of the number of diodes and controlled switches present in the converters. Topology 1 has more semiconductor switches compared to Topology 2 and Topology 3 which leads to more losses in Topology 1, and it reduces the efficiency of the system. Even though Topology 3 has the same number of controlled switches, the number of diodes is less compared to Topology 2. Due to this, the harmonics on the input current in Topology 2 increased to more than 5% which affects the power quality of the source. In Topology 3, the power factor has been improved to unity with the reduction of THD in the input current. It reduces the losses in the circuit and increases the efficiency of the system.

Table 6 Comparison of topologies in terms of THD and power factor
Full size table

7 Conclusion

This article comprehensively explore different types of energy efficient converter topologies for power factor assessment at the electric vehicle charging stations. It is understood from the literature review, the Vienna rectifier is a preferred choice in the high power applications, due to superior power factor and excellent capability to cancel out current harmonics.

In this paper, three topologies of the Vienna rectifier were compared using the following parameters.

  1. 1.

    Number of active/passive devices.

  2. 2.

    Total loss and efficiency.

  3. 3.

    Input current THD.

  4. 4.

    Power factor.

The losses for the three topologies of the Vienna rectifier have been calculated for the full load by using the formulas at different input voltages. The comparison of different topologies of Vienna rectifier for the efficiency has been made and plotted. From the analysis of three topologies of Vienna rectifier, it is observed that the Topology 3 using a minimum number of semiconductor switches is compared to other topologies. Topologies 1 and 3 are having the closest values of efficiency, and beyond 400 V, Topology 3 operates at higher efficiency at 99%. The performance of three topologies is simulated and analysed in terms of a number of active/passive devices, total loss and efficiency, power factor, and THD. It can be concluded that the Topology 3 is the most suitable converter for the electric vehicle charging stations and it is benchmarked for less complexity, high efficiency, high power density design, less input current THD, and improved power factor.