Measurements and calculations of the equilibrium adsorption amounts of CO₂–N₂, CO–N₂, and CO₂–CO mixed gases on 13X zeolite

Abstract

Pressure swing adsorption (PSA) is one practical process for CO₂ separation from the exhaust gases in various industries, such as blast furnace gas in steel works. For optimum design of the PSA process, precise estimation of the adsorption equilibrium of mixed gases is desired. The ideal adsorbed solution (IAS) model is a reliable model for this estimation. However, the IAS model requires convergent calculations, which significantly increase the calculation load, especially in dynamic PSA simulations. An analytical formula such as the extended Langmuir (EX-LM) equation is more useful for calculation of the equilibrium adsorption amounts of mixed gases. A drawback of this equation, however, is the uncertainty of the thermodynamic consistency and consequently the accuracy of the calculation results. In order to clarify the necessary conditions for application of the EX-LM equation as an approximation of the IAS model with Langmuir equation (IAS-LM model), both the analytical features and the estimation accuracy of these different methods were evaluated. To evaluate the accuracy of the equations, the equilibrium adsorption amount of mixed gases consisting of CO₂, N₂, and CO, which are the major gas components of blast furnace gas in steel works, on 13X zeolite were measured experimentally. The results confirmed that the accuracy of the EX-LM equation varies depending on the gas pressure and also the affinities of the adsorbates. Under higher gas pressure conditions, more reliable calculation results were obtained by the IAS-LM model.

Introduction

Adsorption-based gas separation processes such as Pressure Swing Adsorption (PSA) are expected to be a viable option for the separation of large amounts of CO₂ from waste gases. Owing to its simple mechanism utilizing the pressure dependency of the gas adsorption amount, PSA is already widely used in industrial gas production processes [1,2,3,4]. In studies of the adsorption equilibriums of single gases, various types of measured isotherms and fitted isotherm equations have been reported in previous work. These isotherm equations are used appropriately considering both the range of the gas concentration and the trend of the measured isotherms within the range of actual pressure variations. For example, the equilibrium adsorption amount of a dilute gas, which is substantially proportional to the gas partial pressure, can be expressed by a linear relationship such as Henry’s equation, while the well-known Langmuir equation, which has stronger nonlinearity and a saturation capacity in the higher gas concentration range, is used practically at higher gas concentrations [5]. The Langmuir equation has been widely applied to estimate the adsorption equilibrium of single gases owing to its simplicity with only two parameters and sufficient accuracy for various adsorbents [6]. The Sips equation [7] and the Toth equation [8] are also applicable as expanded forms of the Langmuir equation with additional parameters. These isotherms have the potential to improve estimation accuracy when the parameters are fitted properly [9,10,11,12], but the additional parameters generally increase the difficulty of parameter decision and also the deduction of the isotherm equations of mixed gases.

In the case of mixed gas adsorption, the Markham–Benton (M–B) equation, which is derived from the Langmuir equation, is a simple practical form that is readily applicable [13]. The advantages of using the M–B equation prior to other isotherm equations of mixed gases are the smaller number of parameters required for this equation and the fact those parameters are readily available as Langmuir parameters fitted to the measured single gas isotherms. The saturation capacity, q_∞, in the M–B equation means the number of adsorption sites, which is assumed to be constant and depends only on the type of adsorbent. In actual adsorption behavior, however, the saturation capacity of single gases, q_∞i, are not always constant, particularly when the molecular sizes and the affinities of the component gases are significantly different, which means that the number of adsorption sites changes depending on the gas species [14]. Therefore, the M–B equation cannot be applied for estimation of the adsorption equilibrium of mixed gases when the molecular sizes and the affinities of the component gases differ greatly. As a convenient solution to this problem, the extended multicomponent Langmuir (EX-LM) equation (also called the modified Markham–Benton equation) has been used as a substitute, as this equation considers the difference of q_∞i for each gas component [15,16,17]. However, the thermodynamic consistency of this equation has not been explained clearly due to the empirical procedure of rewriting from q_∞ to q_∞i [18].

Another method for estimating the adsorption equilibrium of mixed gases is the Ideal Adsorbed Solution (IAS) model [19,20,21]. This model can be applied to mixed gases in which each gas component has a different q_∞i. Furthermore, the IAS model is based on the Gibbs adsorption equation, which possesses thermodynamic consistency and therefore gives a more precise calculation result than the EX-LM equation [22]. The IAS model can be solved analytically when the gas adsorption equilibrium can be expressed by the Freundlich equation [23]. On the other hand, the IAS model with Langmuir equation requires convergent calculations due to the uncertainty of its analytic formula, and as a result, the calculation load becomes heavier, especially in simulations of dynamic processes like PSA, in which the equilibrium adsorption amount changes frequently within a split second. A dynamic PSA simulation model usually contains convergent calculations to solve both the pressure balance and the mass balance of the system. The equilibrium adsorption amounts should be recalculated in every step of these calculations. Therefore, if the adsorption equilibrium itself requires another convergent calculation, the iterative procedures are multiplied, resulting in a significant increase in the calculation load. Another problem of convergent calculations of the adsorption equilibrium is the uncertainty of the converged value, especially after sudden changes in the gas pressure, which sometimes occur in actual PSA operation. In order to avoid these inconveniences, certain types of analytical formulas, including the above-mentioned EX-LM equation, are preferably used instead of the IAS model in dynamic PSA simulations [24,25,26,27]. These analytical formulas are required to possess sufficient accuracy compared to the IAS model in estimation of the adsorption equilibrium of mixed gases. It is well-known that the adsorption equilibrium of mixed gases consisting of adsorbates having different affinities for the adsorbent shows significant deviation compared to that of single gases due to the effect of competitive adsorption [28,29,30]. Since the prediction accuracy of this specific behavior substantially defines the reliability of the calculated results of PSA simulations, the applicability of the analytical formulas of the adsorption equilibrium of mixed gases under various PSA operating conditions should be evaluated.

As a practical application of competitive adsorption of mixed gases, preferential CO₂ adsorption of CH₄–CO₂ mixed gas has been utilized positively for enhanced CH₄ recovery from shale rocks [31, 32]. Recently, the mechanism of this competitive adsorption has been studied using molecular simulations to confirm the effects of molecular size, pore structure, and adsorption affinity for the adsorbent [33]. Along with these simulation-based studies, precisely measured mixed gas equilibriums are also desired in order to verify the accuracy of the calculated values. However, experimental results are still scarce due to the difficulty of measuring actual mixed gas adsorption, which inevitably causes variations in the gas composition at equilibrium. The breakthrough test with measurement of gas phase change is a rather simple approach [34]. However, some difficulties remain in evaluating the effects of the gas mixing rates and partial pressures of the component gases at equilibrium. Therefore, the need for precise measurement of the equilibrium adsorption amount of mixed gas was another motivation of this work.

As the beginning of our research, the relationship between the IAS model with Langmuir equation (IAS-LM model) and the EX-LM equation was evaluated to clarify the several conditions required in order to apply the EX-LM equation as an approximation of the IAS-LM model. In this comparative study, the binary mixed gases of CO₂–N₂, CO–N₂, and CO₂–CO, all of which are major components of blast furnace gas in steel works, were considered. Then, the equilibrium adsorption amounts of these mixed gases on 13X zeolite were measured experimentally by using a volumetric adsorption apparatus, which enables precise measurement of the slightest variation of the mass balance after reaching the adsorption equilibrium, and compared with the calculated results in order to evaluate the prediction accuracy of these calculation methods.

Theory

The following Eqs. (1)–(4) are the numerical expressions of the IAS model. The superscript 0 means the value of a single gas, and the subscripts i and j mean the gas species. In the IAS model, the equilibrium adsorption amount is calculated by integrating the increment of adsorbed gas molecules under the assumption that the spreading pressure π, which is defined as the increment in the surface tension of a surface due to the spreading of an adsorbate over a surface, is assumed to have a relationship with the increment of the amount of adsorbates [19].

$$\Pi = \frac{\pi A}{RT} = \mathop \int \limits_{0}^{{p_{i}^{0} }} \frac{{q_{i}^{0} }}{{p_{i}^{0} }}dp_{i}^{0}$$

(1)

$$\frac{1}{{q_{t} }} = \mathop \sum \limits_{j = 1}^{n} \frac{{Z_{j} }}{{q_{j}^{0} }}$$

(2)

$$Z_{i} = \frac{{q_{i} }}{{q_{t} }}$$

(3)

$$Z_{i} = \frac{{p_{i} }}{{p_{i}^{0} }}$$

(4)

The various isotherm equations of single gases can be applied to the IAS model, setting aside the convergence property of the iterative calculation for the deduction of Π in Eq. (1). In this case, the IAS model with the following Langmuir equation Eq. (5) is considered.

$$q_{i}^{0} = \frac{{q_{\infty i} K_{i} p_{i}^{0} }}{{1 + K_{i} p_{i}^{0} }}$$

(5)

By integrating Eqs. (1) and (5), the following Eqs. (6) and (7) are obtained.

$$\Pi = q_{\infty i} { \ln }\left( {1 + K_{i} p_{i}^{0} } \right)$$

(6)

$${ \exp }\left( {\frac{\Pi }{{q_{\infty i} }}} \right) = 1 + K_{i} p_{i}^{0}$$

(7)

Since the right side of Eq. (7) becomes a direct substitution in the Langmuir equation, the gas adsorption amount of a single gas expressed by Eq. (8) can be obtained by the simultaneous equations of Eqs. (5) and (7).

$$q_{i}^{0} = \frac{{q_{\infty i} \left\{ {exp\left( {\frac{\Pi }{{q_{\infty i} }}} \right) - 1} \right\}}}{{exp\left( {\frac{\Pi }{{q_{\infty i} }}} \right)}}$$

(8)

The following Eq. (9) is obtained from Eqs. (2), (3), and (8).

$$1 = \mathop \sum \limits_{j = 1}^{n} \frac{{q_{j} \exp \left( {\frac{\Pi }{{q_{\infty j} }}} \right)}}{{q_{\infty j} \left\{ {\exp \left( {\frac{\Pi }{{q_{\infty j} }}} \right) - 1} \right\}}}$$

(9)

On the assumption that the mixed gas consists of two gas components having the same saturation capacity (q_∞1 = q_∞2), Eq. (9) can be deformed to Eq. (10) for derivation of the reduced spreading pressure Π.

$$\Pi = q_{\infty 1} { \ln }\left( {\frac{{ - q_{\infty 1} }}{{q_{1} + q_{2} - q_{\infty 1} }}} \right)$$

(10)

For gas component 1 (i = 1), the following Eq. (11) is obtained from Eqs. (6) and (10).

$$\frac{{ - q_{\infty 1} }}{{q_{1} + q_{2} - q_{\infty 1} }} = 1 + K_{1} p_{1}^{0}$$

(11)

When the mixed gas consists of two gas components, the total adsorption amount q_t equals the simple summation of q₁ and q₂ described as Eq. (12). Then, Eqs. (11), (12), and the following Eq. (13), which is derived from Eqs. (3) and (4), are integrated to obtain Eq. (14).

$$q_{t} = q_{1} + q_{2}$$

(12)

$$p_{1}^{0} = \left( {\frac{{q_{t} }}{{q_{1} }}} \right)p_{1}$$

(13)

$$p_{1} = \frac{{q_{1} }}{{K_{1} \left( {q_{\infty 1} - q_{t} } \right)}}$$

(14)

The same result can be obtained for gas component 2, and the following Eq. (15) is then obtained by using the pressure ratio of these gas components.

$$K_{2} p_{2} = \left( {\frac{{q_{2} }}{{q_{1} }}} \right)K_{1} p_{1}$$

(15)

The equilibrium adsorption amount given by Eq. (16) can be derived from Eqs. (12), (14), and (15).

$$q_{1} = \frac{{q_{\infty 1} K_{1} p_{1} }}{{1 + K_{1} p_{1} + K_{2} p_{2} }}$$

(16)

When the above equation is generalized, it becomes the M–B equation Eq. (17).

$$q_{i} = \frac{{q_{\infty } K_{i} p_{i} }}{{1 + \mathop \sum \nolimits_{j} K_{j} p_{j} }}$$

(17)

This means that the IAS-LM model is completely equivalent to the M–B equation when the saturation capacity q_∞ is uniform, regardless of the type of adsorbate. This result has the clear advantage of using the M–B equation prior to the IAS-LM model because it has the same thermodynamic consistency as the IAS-LM model but a smaller calculation load, as its analytical formula does not require convergent calculations.

On the other hand, a generalized equation including q_∞i is desired in cases having different q_∞i for each gas component (q_∞1 ≠ q_∞2). In these cases, the following approximation can be applied in the calculation.

The relationship expressed by Eq. (18) can be obtained by using the first and second terms of the Taylor expansion of the left side of Eq. (7).

$$\begin{aligned} { \exp }\left( {\frac{\Pi }{{q_{\infty i} }}} \right) & = 1 + \frac{{\frac{\Pi }{{q_{\infty i} }}}}{1!} + \frac{{\left( {\frac{\Pi }{{q_{\infty i} }}} \right)^{2} }}{2!} + \frac{{\left( {\frac{\Pi }{{q_{\infty i} }}} \right)^{3} }}{3!} + \ldots \cong 1 + \frac{\Pi }{{q_{\infty i} }} \\ 1 + \frac{\Pi }{{q_{\infty i} }} & = 1 + K_{i} p_{i}^{0} \\ \end{aligned}$$

(18)

Substitution of Eq. (13) in Eq. (18) gives the following Eq. (19).

$$\begin{aligned} & 1 + \frac{\Pi }{{q_{\infty 1} }} = 1 + \left( {\frac{{q_{t} }}{{q_{1} }}} \right)K_{1} p_{1} \\ &\Pi = \frac{{q_{t} K_{1} p_{1} q_{\infty 1} }}{{q_{1} }} \\ \end{aligned}$$

(19)

The approximation of Eq. (18) can also be applied to Eq. (9) and gives Eq. (20).

$$\Pi = \frac{{q_{\infty 1} q_{\infty 2} q_{t} }}{{q_{\infty 1} q_{\infty 2} - q_{1} q_{\infty 2} - q_{2} q_{\infty 1} }}$$

(20)

Equation (21) can be obtained from Eqs. (19) and (20).

$$K_{1} p_{1} = \frac{{q_{1} q_{\infty 2} }}{{q_{\infty 1} q_{\infty 2} - q_{1} q_{\infty 2} - q_{2} q_{\infty 1} }}$$

(21)

Because Eq. (19) is equally valid for gas component 2, the following Eq. (22) can be derived from the ratio of q₁ and q₂.

$$q_{2} = \frac{{q_{1} K_{2} p_{2} q_{\infty 2} }}{{K_{1} p_{1} q_{\infty 1} }}$$

(22)

The following Eq. (23) can be obtained by substitution of Eq. (21) in Eq. (22).

$$q_{1} = \frac{{q_{\infty 1} K_{1} p_{1} }}{{1 + K_{1} p_{1} + K_{2} p_{2} }}$$

(23)

When the above equation is generalized, it becomes the EX-LM equation shown in Eq. (24). In the case of having equal saturation capacities q_∞, Eq. (24) is identical to the M–B equation.

$$q_{i} = \frac{{q_{\infty i} K_{i} p_{i} }}{{1 + \mathop \sum \nolimits_{j} K_{j} p_{j} }}$$

(24)

Equation (24) is a more generalized equation than Eq. (17) because it allows the difference of the saturation capacity q_∞i for the component gases. According to the above relationship, the EX-LM equation that was derived by approximation of Eq. (18) is also applicable as an analytical formula of the IAS-LM model that has thermodynamic consistency for calculation of mixed gas adsorption. Similar derivations of the explicit forms of the IAS model with various single gas isotherms were attempted by Tarafder et al. [35]. However, they assumed strict uniformity of the saturation capacity q_∞i for all the component gases in order to eliminate the logarithmic form derived after the integration of the right side of Eq. (1). This assumption restricts the use of their equations to limited cases. As mentioned previously, the saturation capacity q_∞i is generally not constant and depends on the gas species. Therefore, the EX-LM equation can be used more generally than their equations. The fact that fewer parameters are required for the calculation is also an advantage of this model. As a result, the EX-LM equation is preferably used for calculation of the equilibrium adsorption amount of mixed gases in dynamic simulations owing to its analytical formula, which does not require convergent calculations.

Experiment

In order to evaluate the accuracy of both the EX-LM equation and the IAS-LM model, the equilibrium adsorption amounts of CO₂–N₂, CO–N₂, and CO₂–CO mixed gases were measured by using the following experimental apparatus and distinctive measurement procedure. As a suitable CO₂ adsorbent for CO₂-PSA, 13X zeolite with Si/Al = 1.4 (Zeolum F-9HA, Tosoh Corp., Japan) was used in these measurements (Fig. 1). This adsorbent was prepared as 1.5 mm diameter cylindrical pellets weighing 1 g. The physical properties of this adsorbent are listed in Table 1. The crystallographic structure of the adsorbent is 13X zeolite, which defines the size of the micro pores (0.9 nm as diameter). The average pellet length was measured for 50 randomly-selected pellets. The total macro–meso pore volume and the average macro–meso pore diameter were measured by the mercury penetration method, which is used in measurements of macro–meso pore distribution [36]. The measuring apparatus was an AutoPoreIV9520 (Micrometrics Inc.). The average macro–meso pore diameter was calculated from the measured pressure and Washburn’s equation [37]. The Brunauer–Emmett–Teller (BET) surface area was measured by the standard nitrogen adsorption method [38] by using a BELSORP-mini (MicrotracBEL Corp., Japan).

Fig. 1

Photo of pellets of 13X zeolite adsorbent (Zeolum F-9HA, TOSOH)

Table 1 Physical properties of adsorbent

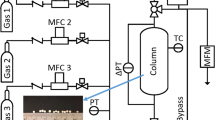
The equilibrium adsorption amounts of both the single gases and the mixed gases were measured by a multi-component gas adsorption system, BELSORP-VC (MicrotracBEL Corp., Japan), which is equipped with both an automatic gas sampler and a gas chromatograph connected directly to a sample column. In this experimental apparatus, the amount of gas adsorbed from the mixed gas was measured by using a combination of volumetric adsorption and gas concentration analysis. Figure 2 shows a schematic drawing of this experimental apparatus. The gas cylinders of all gas components including the purge gas He (99.999% purity) were connected individually to inlet gas lines. Before introduction into the sample column, the mixed gas was prepared by using a pre-column having a circulation pump which enabled precise calculations of the gas mixing rates. The pre-column consisted of two zones having known volumes, A and B. When the mixed gas was prepared, these two zones were filled with a primary gas at a specific pressure as a first step. Then, the B zone was isolated by shutting the valves, and the A zone was vacuumed by a vacuum pump. Subsequently, a secondary gas was introduced into the A zone at the pressure necessary to obtain the objective gas mixing rate and gas pressure. The A zone filled with the secondary gas was combined with the B zone filled with the primary gas by opening the separating valve, and the gases were mixed by the circulation pump. The gas mixing time by the circulation pump necessary to ensure sample uniformity was defined automatically. After preparing the mixed gas, it was introduced into a stainless sample column having a diameter of 6 mm and length of 100 mm, in which 1 g of the adsorbent pellets were inserted. The dead volume of the sample column was measured previously by He gas expansion. The compressibility factors of the component gases were also measured previously by the same equipment to ensure the accuracy of the measured gas concentrations. The connected gas chromatograph for gas concentration analysis was a 490 Micro-GC (Agilent Technologies), which enables fast and precise measurements within seconds.

Fig. 2

Experimental setup for measurement of equilibrium gas adsorption amounts (BELSORP-VC)

As the first step of these measurements, the adsorbent sample pellets were pretreated in a sample column at 623 K in a vacuum state for 4 h in order to remove adsorbed water and gases completely. Following this, the equilibrium adsorption amounts of the CO₂, N₂, and CO single gases were measured at the temperatures of 283 K, 298 K, and 313 K under thermostatic control. The equilibrium adsorption amounts of the gas 1-gas 2 mixed gases were measured by the following procedure. After the same pretreatment of the adsorbent as described above, the pre-adsorbed mixed gas with the various gas mixing rates was prepared and introduced into the sample column. The measurement was started from the lower gas 1 partial pressure, and the gas 1 ratio was gradually increased to observe the effect of gas mixing. The equilibrium gas pressure was adjusted to become atmospheric pressure P_a (101.3 kPa) because the gas pressure of the adsorption step in vacuum-type pressure swing adsorption (VPSA) processes such as CO₂-PSA is around P_a, and the equilibrium adsorption amount of the feed gas (i.e. mixed gas) at this pressure is closely related to the gas balance during VPSA operation. The pressure of the pre-adsorbed mixed gas was set to be higher than P_a to obtain an equilibrium gas pressure around P_a under each experimental condition. After reaching the adsorption equilibrium, part of the gas was introduced into the gas chromatograph to measure the gas composition that decides the partial pressure and the adsorbed gas amount of each component gas at equilibrium. Since the equilibrium gas pressure usually does not reach P_a precisely because of the effect of the pressure drop caused by gas adsorption, the equilibrium adsorption amount q_i at the equilibrium gas pressure P_a was obtained by the following Eq. (25) as a linear interpolation of the measured results when equilibrium was reached at a pressure around P_a [P₁ and P₂ in Eq. (25)].

$$q_{i} \left( {P_{a} } \right) = q_{i} \left( {P_{1} } \right) + \left( {q_{i} \left( {P_{2} } \right) - q_{i} \left( {P_{1} } \right)} \right) \cdot \frac{{P_{a} - P_{1} }}{{P_{2} - P_{1} }}\quad \therefore P_{1} < P_{a} < P_{2}$$

(25)

After measuring both the equilibrium gas pressure and the adsorbed gas amount of one mixed gas, the adsorbent was pretreated again in a sample column at 623 K in a vacuum state for 4 h to eliminate the effect of the previously adsorbed gases, especially the strongly adsorbed CO₂ remaining inside the adsorbent. This pretreatment was conducted every time before proceeding to the next measurement with another mixed gas. Although this was a time-consuming procedure by which required about 1–2 days to obtain only one point of the graph, this treatment was unavoidable for maintaining sufficient precision for our study. For this reason, the temperature effect was evaluated only for limited cases and was not included as a parameter of the isotherm equations in this study.

Results and discussion

Comparison of EX-LM equation and IAS-LM model

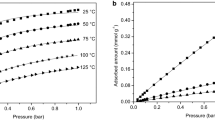
Figures 3, 4 and 5 show the CO₂, N₂, and CO single gas adsorption isotherms of 13X zeolite measured at 283 K, 298 K, and 313 K, respectively. Within these three isotherms, the CO₂ isotherm shows a higher CO₂ capacity than the other gases, which means that this adsorbent can be used preferably for CO₂ separation. The lines in these graphs are the isotherms calculated by the Langmuir equation with fitted parameters. It was observed that the measured isotherms can be expressed by the Langmuir equation for these gases. Table 2 shows the Langmuir parameters obtained from the fitted lines of Figs. 3, 4 and 5. The values of K in Table 2 indicate the adsorption affinity of these gases. Thus, the significantly higher value of K for CO₂ means the adsorption affinity of CO₂ is relatively stronger than those of the other gases.

Fig. 3

Measured equilibrium CO₂ adsorption amounts of 13X zeolite with fitted lines of Langmuir isotherms (temperature conditions: 283 K, 298 K, 313 K)

Fig. 4

Measured equilibrium CO adsorption amounts of 13X zeolite with fitted lines of Langmuir isotherms (Temperature conditions: 283 K, 298 K, 313 K)

Fig. 5

Measured equilibrium N₂ adsorption amounts of 13X zeolite with fitted lines of Langmuir isotherms (Temperature conditions: 283 K, 298 K, 313 K)

Table 2 Langmuir parameters

In order to evaluate the effect of the above-mentioned approximation, the calculation results of the IAS-LM model and the EX-LM equation were compared by using the Langmuir parameters in Table 2. In the following calculations, three cases of total gas pressure, namely, 20 kPa, 100 kPa, and 500 kPa at the temperature of 298 K, and three cases of temperature, namely, 283 K, 298 K, and 313 K at the pressure of 100 kPa, were considered. The equilibrium adsorption amount of the EX-LM equation was calculated by Eq. (24) according to its definition. When using the IAS-LM model, the equilibrium adsorption amount was calculated by the following set of equations. Firstly, Eq. (26) is obtained from Eq. (4). Then, as a second procedure, Eq. (7) is modified for substitution in Eq. (26) to derive Eq. (27). In this Eq. (27), the reduced spreading pressure Π is decided by convergent calculations, and Π is substituted in Eqs. (5) and (8) to derive p₀ and q₀. Finally, these values are used in the mixed gas equations Eqs. (28) and (29) to derive the equilibrium adsorption amount of each gas component.

$$\mathop \sum \limits_{j} Z_{j} = 1 = \mathop \sum \limits_{j} \frac{{p_{j} }}{{p_{j}^{0} }} = \mathop \sum \limits_{j} \frac{{K_{j} p_{j} }}{{K_{j} p_{j}^{0} }}$$

(26)

$$\mathop \sum \limits_{j} \frac{{K_{j} p_{j} }}{{K_{j} p_{j}^{0} }} = \mathop \sum \limits_{j} \frac{{K_{j} p_{j} }}{{{ \exp }\left( {\frac{\Pi }{{q_{\infty i} }}} \right) - 1}} = 1$$

(27)

$$q_{1} = \frac{{p_{2}^{0} q_{1}^{0} q_{2}^{0} }}{{p_{2}^{0} q_{2}^{0} + xp_{1}^{0} q_{1}^{0} }}\quad x = \frac{{p_{2} }}{{p_{1} }}$$

(28)

$$q_{2} = x\frac{{p_{1}^{0} }}{{p_{2}^{0} }}q_{1}$$

(29)

The calculation results are as follows. Figure 6 shows the calculation results of the CO₂–N₂ mixed gas. From the K values in Table 2, this mixed gas consists of gases having a relatively larger difference of adsorption affinities for the adsorbent. In the graphs in Fig. 6, the blue lines are the calculation results of the IAS-LM model, and the red lines are the results of the EX-LM equation. The two horizontal axes show the partial pressures of the component gases under the constant equilibrium gas pressure. The scale of the vertical axis of Fig. 6a is plotted as a half scale of Fig. 6b, c because of its lower adsorption amount. The green lines in these graphs show the single gas adsorption isotherms calculated by Eq. (5) with the Langmuir parameters in Table 2 as references. From the graphs in Fig. 6, the equilibrium adsorption amounts of CO₂ obtained by these different calculation methods are almost equal within the whole range of the total gas pressure considered in this work. In addition, it is observed that the result of the CO₂ in the mixed gas is almost equal to the result of the CO₂ single gas and thus is not affected by the coexisting N₂ owing to the higher value of K_CO2 in Table 2, which results in a smaller effect of the coexisting N₂ on the summation of the denominator in Eq. (24). In contrast, the equilibrium adsorption amounts of N₂ shown by the red and blue dotted lines differ significantly depending on the calculation method except for cases of lower total gas pressures. The maximum difference is observed around the left side of each graph in Fig. 6, and becomes larger as the total gas pressure increases. This difference contains not only the absolute error caused by the increased adsorption amount but also the relative error that can be evaluated by the ratio of the heights of these dotted lines at the same CO₂ partial pressure. The relative error is caused by the insufficient approximation of the IAS-LM model. At the lower gas pressure, the amount of adsorbed gas is small, and thus Π also becomes small compared to the saturation capacity q_∞i. The approximation accuracy of Eq. (18) is improved at the lower value of Π/q_∞i, which explains the similarity of the results of the IAS-LM model and the EX-LM equation in Fig. 6a.

Fig. 6

Equilibrium adsorption amounts of CO₂–N₂ mixed gas calculated by IAS-LM model and EX-LM equation (temperature: 298 K, Total gas pressure conditions: a 20 kPa, b 100 kPa, c 500 kPa)

In comparison with the calculation results for the single gases, the equilibrium adsorption amounts of N₂ in the mixed gases shown by the red and blue dotted lines decrease intensively compared to the single gases shown by the green dotted lines in each graph, and in particular, the gap becomes larger at higher total gas pressures. This specific behavior is due to the effect of competitive adsorption between gas components having different adsorption affinities, which could be predicted from the mixed gas isotherms calculated previously with the IAS model [39].

Figures 7 and 8 are the results of the same calculations for the CO–N₂ and the CO₂–CO mixed gases. From the K values in Table 2, the CO–N₂ mixed gas consists of gas components having relatively smaller adsorption affinities compared to CO₂, and the CO₂–CO mixed gas consists of gas components that have a larger difference of adsorption affinities, which is similar to the CO₂–N₂ mixed gas. The single gas isotherms calculated by the Langmuir equation Eq. (5) with the values in Table 2 are also drawn in these graphs as references. As a common trend of these graphs, the equilibrium adsorption amounts of the mixed gases are smaller than those of the single gases due to the effect of competitive adsorption. In Fig. 7, the equilibrium adsorption amount calculated by the EX-LM equation is almost equal to that calculated by the IAS-LM model within the whole range of the total gas pressure considered in this study. Unlike the case of Fig. 6, the pressure increase has a negligibly small effect on the difference of these calculation results. The component gases CO and N₂ in Fig. 7 both have weaker adsorption affinities, which give lower values of Π/q_∞i even at higher pressure. This assures a good approximation of Eq. (18) within a wider range of gas pressures, resulting in the smaller difference between these calculation methods. This result demonstrates the possibility of precise estimation of the equilibrium adsorption amount of CO–N₂ mixed gas by using the EX-LM equation. In Fig. 8, on the other hand, the difference of these results becomes larger as the total gas pressure increases. This tendency is similar to the case of the CO₂–N₂ mixed gas in Fig. 6, which can be estimated from the difference of the K values in Table 2.

Fig. 7

Equilibrium adsorption amounts of CO–N₂ mixed gas calculated by IAS-LM model and EX-LM equation (temperature: 298 K, Total gas pressure conditions: a 20 kPa, b 100 kPa, c 500 kPa)

Fig. 8

Equilibrium adsorption amounts of CO₂–CO mixed gas calculated by IAS-LM model and EX-LM equation (temperature: 298 K, Total gas pressure conditions: a 20 kPa, b 100 kPa, c 500 kPa)

Figure 9 shows the temperature dependency of the adsorption equilibrium of the CO₂–N₂ mixed gas at the pressure of 100 kPa. The difference between the results of the IAS-LM model and the EX-LM equation becomes smaller as the temperature increases. This specific behavior is due to the effect of the reduced CO₂ adsorption at higher temperature, which also causes a decrease of Π/q_∞i, contributing to improvement of the approximation accuracy of Eq. (18). This result implies the possibility of practical application of the EX-LM equation at higher temperatures.

Fig. 9

Equilibrium adsorption amounts of CO₂–N₂ mixed gas calculated by IAS-LM model and EX-LM equation (temperature conditions: a 283 K, b 298 K, c 313 K, total gas pressure: 100 kPa)

Measured adsorption equilibriums of mixed gases and discussion

Figures 10, 11 and 12 show the prediction accuracy of both the IAS-LM model and the EX-LM equation compared to the experimental results. In these graphs, the experimental results are plotted with open symbols. It is commonly said that the equilibrium adsorption amount of CO₂, which has a strong adsorption affinity for the adsorbent, can be estimated properly regardless of the calculation method. On the other hand, the prediction accuracy of CO and N₂, both of which have weaker adsorption affinities compared to CO₂, differs significantly depending on the coexisting gas. For both the CO₂–N₂ mixed gas in Fig. 10 and the CO₂–CO mixed gas in Fig. 12, the IAS-LM model shows better accuracy than the EX-LM equation in estimation of the equilibrium adsorption amounts of CO and N₂, even with coexistence of CO₂, although some deviations from the experimental results still remain at lower CO₂ partial pressures. During the desorption step of the VPSA operation for CO₂ separation, the adsorbent is not regenerated to the level of full vacuum in order to maintain productivity and cost efficiency. Thus, the deviation of the equilibrium adsorption amount at lower pressure might have a smaller effect on the results of VPSA simulations depending on the actual operating conditions. In the case of the CO–N₂ mixed gas in Fig. 11, on the other hand, the results of these different calculations are equally in good agreement for both component gases. This means that there is still a possibility of using the EX-LM equation for precise estimation of the adsorption equilibrium of mixed gases under certain conditions. Thus, these two different calculation methods should be used appropriately depending on the purpose of the simulation. That is, in rough estimations of adsorption behavior and remaining impurity gases, the EX-LM equation is a convenient analytical formula for calculating mixed gas adsorption, and is readily applicable to dynamic PSA simulations owing to its simple description with fewer parameters. Moreover, if the mixed gas consists of gases having weaker adsorption affinities, the results of calculations by this equation are quantitatively reliable within a wider range of pressures and temperatures. However, because the accuracy of this equation depends on the PSA operating conditions, the reliability of dynamic PSA simulations using this equation should be investigated carefully. For more precise estimation, the IAS-LM model is definitely preferable, in spite of the higher calculation load owing to convergent calculations. This is especially true when the mixed gas contains an object gas having stronger adsorption affinity.

Fig. 10

Equilibrium adsorption amounts of CO₂–N₂ mixed gas obtained by calculations and experiments (temperature conditions: a 283 K, b 298 K, c 313 K, total gas pressure: 101.3 kPa)

Fig. 11

Equilibrium adsorption amounts of CO–N₂ mixed gas obtained by calculations and experiments (temperature conditions: a 283 K, b 298 K, c 313 K, total gas pressure: 101.3 kPa)

Fig. 12

Equilibrium adsorption amounts of CO₂–CO mixed gas obtained by calculations and experiments (temperature conditions: a 283 K, b 298 K, c 313 K, total gas pressure: 101.3 kPa)

The effect of competitive adsorption becomes prominent when the mixed gas includes gases having stronger adsorption affinities, such as CO₂ or H₂O on zeolites. The overestimation by the EX-LM equation in calculations of the adsorption equilibrium of weakly adsorbed gases appears similarly in other mixed gases such as CH₄–CO₂ on coals [40], although the adsorption affinities of the component gases are affected by the oxygen functionalities of the adsorbent in case of adsorption on coals [41]. Thus, the degree of deviation cannot be compared simply with other adsorbents. Regarding experimental and modelling approaches for competitive adsorption of CO₂–N₂ mixed gas on zeolites, Harlick et al. [42] and Hefti et al. [43] conducted exhaustive investigations of the applicability of the mixed gas isotherm equations and IAS models. It is worth noting that both of their calculation results obtained by mixed gas isotherm equations showed the trend of overestimation of weakly adsorbed gases compared to the experimentally measured adsorption equilibrium, which is consistent with our results, even though their experiments were conducted with different measurement methods. Harlick et al. failed to fit the IAST model with the experimental results and concluded that this failure was due to the electrostatic properties of CO₂ on the cationic sites of zeolite adsorbent. On the other hand, Hefti et al. successfully estimated the trend of CO₂–N₂ mixed gas adsorption on 13X zeolite with IAS models complemented by activity coefficients. The range of application for their model is sufficiently wide owing to the advantage of strictly defined parameters, but this might become a drawback if the adsorbent still has various options and many parameter estimations are required. In the present work, the EX-LM equation and the IAS-LM model, both of which have fewer parameters compared to other isotherm equations or models, were applied with the aim of facilitating the parameter decision and easy incorporation of the mixed gas adsorption equilibriums into dynamic PSA simulations. It is sometimes difficult to explain the trend of strongly nonlinear isotherms such as CO₂ on 13X zeolite completely by using isotherm equations with fewer parameters. Nevertheless, it is meaningful that these calculation methods possess a sufficient capability for estimating the adsorption equilibrium of mixed gases on the condition that the method is selected appropriately depending on the component gases and the range of PSA operating conditions.

Conclusion

The relationship between the IAS-LM model and the EX-LM equation was evaluated by comparing the equilibrium adsorption amounts of CO₂–N₂, CO–N₂, and CO₂–CO mixed gases on 13X zeolite obtained by these different calculation methods. As features of the calculations, the M–B equation can be applied as an analytical formula of the IAS-LM model when all the component gases have the same saturation capacity q_∞. However, considering more generalized cases having different q_∞ for each gas component, the EX-LM equation can be applied as an approximated form of the IAS-LM model. For CO₂–N₂ mixed gas, which consists of two gases having significantly different adsorption affinities, the equilibrium adsorption amount of CO₂ calculated by the EX-LM equation is almost equal to that calculated by the IAS-LM model. On the other hand, the equilibrium adsorption amount of N₂ calculated by these calculation methods differs significantly except at lower total gas pressure due to the effect of the increased approximation error of the exponential functions. The gap between these calculation results also tends to increase with the total gas pressure, which means that the applicability of the EX-LM equation as an approximated form of the IAS-LM model is related to both the adsorption affinities of the component gases and the gas pressures. Furthermore, the difference between the results of these calculation methods becomes smaller as the temperature increases.

The equilibrium adsorption amounts of CO₂–N₂, CO–N₂, and CO₂–CO mixed gases under various pressure and temperature conditions of PSA operation were measured experimentally by using a volumetric adsorption apparatus and compared with the calculated results. The result of this comparative study confirmed that the equilibrium adsorption amounts of these mixed gases were estimated more precisely by using the IAS-LM model compared to the EX-LM equation under the pressure and temperature ranges considered in this work.