1 Introduction

Using the capability of smart materials to generate different modes of deformations has always been a concern for researchers to reduce the volume and price of actuators. Actuators made with smart materials are used in applications such as microscope platforms, and precise positioners. Bending actuators are more likely to be considered due to their relatively high displacements and forces. Bending actuators are often presented as bimorph beams. The variability of these actuators is significant in terms of the excitation energy, the mechanism of motion, the range of displacements and forces. Marth and Gloess [1] developed a precise bending actuator as an optical instrument in which four-layered piezoelectric was used. Honda et al. [2] introduced a linear motor using the Tb–Fe and Sm–Fe bimorph actuators. Roh et al. [3] proposed an ultrasonic linear motor using the traveling wave properties. Johansson et al. [4] presented a linear walking actuator. Müller et al. [5] introduced an actuator using shear piezoelectrics, which improved the speed, accuracy, and strength of walking actuators. The micro bending actuators using shape memory alloys have been presented by Abuzaitar et al. [6]. Ghodsi et al. [7, 8] developed a bending actuator and a positioner using magnetostrictive materials. Wang et al. [9] presented a bending actuator to deform a rectangular glass using a coated film of the Terfenol-D. Karafi et al. [10] presented a resonant torsional bulk actuator using a permendur rod. They developed a longitudinal- torsional bulk actuator using an exponential shape permendur [11]. Longitudinal and torsional actuators are used in ultrasonic applications such as sonars, positioners, cleaners, machining processes, ultrasonic assisted manufacturing processes, NDE (Non destructive evaluation), medical, health monitoring and etc. None of the previous researches have used a bulk material to generate bending deformations. As magnetostrictive materials can deform in different modes, in this paper, a new bending actuator is presented using a bulk magnetostrictive material. The bulk bending actuator can be used to fabricate precise positioners. For instance, platforms of the TEM (transmission electron microscope), STM (scanning tunneling microscope) or AFM (atomic force microscopy) can be fabricated with this actuator. Bending vibrations of the actuator can be used to fabricate motors.

After designing the actuator, the numerical simulations conducts using Comsol software to compute magnetic fields in the material. Furthermore, displacements and forces of the actuator computes in the software. Then, the actuator fabricates, and the results of experimental tests are presented.

2 Structure of the actuator

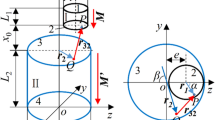
Magnetic fields should pass through a thin layer of a magnetostrictive rod to generate bending deformations. A comb shape magnetic core and coils are used to generate magnetic fields in the rod. The configuration of the actuator is presented in Fig. 1.

Fig. 1
figure 1

The structure of the bulk bending magnetostrictive actuator

Full size image

Due to the positive magnetostriction of the permendur, the thin layer which is excited with axial magnetic fields stretches and causes the bending of the rod. The magnetic core cross-section is a square with the dimension of 3 mm, the inner radius of bobbins is 2.15 mm, and the outer radius is 3.15 mm. Base on the capacity of laboratory power supplies, the maximum excitation current is considered as 2.5 A. Since the magnetic field intensity which the permendur reaches its magnetic saturation is 20 kA/m, the number of wire turns of the coils is considered as 170 turns. Since the maximum current density for the lacquered wire is 8 A/mm2, the wire cross-section could be as follow:

$${\mathrm{A}}_{\text{w}} = \frac{\text{I}}{\mathrm{J}} \cong 0.3\;{\text{mm}}^{2}$$
(1)

Values of the magnetic fields inside the permendur are computed using the numerical simulations.

3 The numerical simulations

The 2D model of the actuator has been used to simulate the magnetic fields. The simulations have been performed using the magnetostrictive module of the Comsol 5.3 software (i.e. The combination of the structural and magnetic physics). B-H and S-H (strain vs magnetic field) curves of the permendur are given to the software [12]. The number of elements in the 2D analysis is 36,017 and the quality of the meshes is 0.86. The physical properties of the permendur are listed in Table 1.

Table 1 The properties of the vanadium permendur
Full size table

The magnetic core and the base plate are made up of CK 45 steel. The B-H curve of the CK45 is shown in Fig. 2.

Fig. 2
figure 2

the B-H curve of the CK45 [13]

Full size image

The values of strains, stresses, and magnetic fields are computed under the DC and AC excitations. Figure 3 shows the 2D model of the actuator in the Comsol software.

Fig. 3
figure 3

2D model of the bulk bending actuator in the Comsol software 1-permendur rod 2-comb shape magnetic core 3-coil 4-bobbin 5-base plate 6-ambient (air)

Full size image

3.1 The simulation of the actuator under DC excitations

Figure 4 shows the magnetic flux in the actuator. The distribution of the magnetic flux is significant in the outer surface of the magnetostrictive rod. The penetration depth of the magnetic flux depends on the distance between two opposing poles. The penetration depth decreases by decreasing the distance. This distance should be selected in such a way that the value of fluxes in the axial direction be enough to bend the actuator.

Fig. 4
figure 4

Contour of the magnetic flux under the excitation current of 2.5 A

Full size image

The maximum axial magnetic field occurs between two opposing poles. Therefore, in this region, the maximum strain and displacement take places. While in the vicinity of poles, due to neutralizing the axial component of the magnetic field, the strain has its minimum value. Moreover, the radial component of the magnetic field causes stress and strain in the radial direction. Figure 5 shows the strain in the actuator.

Fig. 5
figure 5

Contour of the strain under the excitation current of 2.5 A

Full size image

The deflection of the actuator at the point A and C is computed under the excitation current of 2.5 A. The deflection of the points A and C are 0.31 and 0.9 µm, respectively. Figure 6 shows the deflection of the point A versus excitation currents.

Fig. 6
figure 6

Bending deflections of the point A versus DC excitation currents

Full size image

As the excitation currents increase, the deflection also increases. The rate of the increase reduces due to the magnetic saturation of the permendur. By blocking the point C and exciting the actuator, the force at the tip of the actuator is computed. Figure 7 shows the generating force versus excitation currents.

Fig. 7
figure 7

Generating forces of the point C versus excitation currents

Full size image

3.2 The simulation of the actuator under the AC excitations

The resonance frequency of the actuator is computed using the Comsol software. Figure 8 shows the result of the modal analysis of the permendur rod in COMSOL software.

Fig. 8
figure 8

First natural bending mode of the actuator at 276 Hz

Full size image

By applying different currents near the resonance frequency, the value of the axial magnetic fields, and stress are computed. Figure 9 shows the magnetic fields contour.

Fig. 9
figure 9

The contour of the magnetic field at the frequency of 138 Hz by applying a 2.5 A RMS current

Full size image

Under AC excitations, the generation of the eddy currents causes the reduction of the penetration depth of the magnetic fluxes. The magnetic fields has the maximum value at the outer surface of the material. The bending deformation increases as the magnetic field concentrates at the outer surface. The values of the deflection at points A and C are 17 µm and 82 µm, respectively. The strain of the actuator at the frequency of 138 Hz by applying a 2.5 A RMS current is shown in Fig. 10.

Fig. 10
figure 10

the contour of the strain at 138 Hz by applying 2.5 A RMS current

Full size image

Figure 11 shows the deflection of the point C versus the RMS currents at the frequency of 138 Hz.

Fig. 11
figure 11

Bending deflections of the point C versus RMS currents at the frequency of 138 Hz

Full size image

At the constant frequency, increasing of the RMS current increases the deflection of the actuator. As discussed earlier, the concentration of the magnetic fluxes in a thin layer, as well as the excitation at the resonance frequency, causes the increase of the deflection in the AC excitations compared to the DC excitations.

4 The analytical model of the unloaded actuator

The analytical model intents to explain the principle of the deformation of the actuator under free conditions. The piezo magnetic equation of the magnetostrictive materials is as follow:

$$\left[ \begin{aligned}\upvarepsilon_{1} \hfill \\\upvarepsilon_{2} \hfill \\\upvarepsilon_{3} \hfill \\\upvarepsilon_{4} \hfill \\\upvarepsilon_{5} \hfill \\\upvarepsilon_{6} \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {{\text{d}}_{ 1 3} } \hfill \\ 0 \hfill & 0 \hfill & {{\text{d}}_{ 1 3} } \hfill \\ 0 \hfill & 0 \hfill & {{\text{d}}_{ 3 3} } \hfill \\ 0 \hfill & {{\text{d}}_{51} } \hfill & 0 \hfill \\ {{\text{d}}_{51} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {{\text{H}}_{ 1} } \\ {{\text{H}}_{ 2} } \\ {{\text{H}}_{ 3} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {S_{11}^{H} } \hfill & {S_{12}^{H} } \hfill & {S_{13}^{H} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {S_{12}^{H} } \hfill & {S_{11}^{H} } \hfill & {S_{13}^{H} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {S_{13}^{H} } \hfill & {S_{13}^{H} } \hfill & {S_{33}^{H} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {S_{44}^{H} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {S_{44}^{H} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {S_{66}^{H} } \hfill \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}l} {\upsigma_{1} } \hfill \\ {\upsigma_{2} } \hfill \\ {\upsigma_{3} } \hfill \\ {\upsigma_{4} } \hfill \\ {\upsigma_{5} } \hfill \\ {\upsigma_{6} } \hfill \\ \end{array} } \right]$$
(2)

where \(\upvarepsilon_{\text{i}}\), \({\text{d}}_{\text{ij}}\), \({\text{H}}_{\text{i}}\), \(s_{ij}^{H}\), and \(\upsigma_{\text{i}}\) are the strain tensor, the magnetostriction coefficients, the magnetic field intensity, the compliance coefficients at the constant magnetic field intensity, and the stress tensor, respectively. Index 1, 2, and 3 represent x-, y- and z-axis in the Cartesian coordinate system, respectively. Index 4, 5 and 6 stand for rotation around x, y and z respectively. Since the actuator is excited under free conditions, the applied stress was considered to be zero. Therefore, the stress tensor in Eq. (2) would be zero. Since the required excitation magnetic field should be along the z-axis, \({\text{H}}_{1}\) and \({\text{H}}_{2}\) were considered to be zero. Therefore, the resulting strain would be as follow:

$$\upvarepsilon_{1} =\upvarepsilon_{\text{x}} = {\text{d}}_{13} {\text{H}}_{3}$$
(3)
$$\upvarepsilon_{2} =\upvarepsilon_{y} = {\text{d}}_{13} {\text{H}}_{3}$$
(4)
$$\upvarepsilon_{3} =\upvarepsilon_{\text{z}} = {\text{d}}_{33} {\text{H}}_{3}$$
(5)

By exciting the material along the z-axis, the actuator would deform in all three axes. The value of the \(d_{13}\) coefficient of the permendur alloy is half of the \(d_{33}\) [14]. The bending deflection of the actuator only depends on the elongation along the z-axis, while strains along the x- and y-axis do not affect the actuator’s deflections. Therefore, only the strain along the z-axis was considered in calculations. The deflection of the actuator could be determined as follow:

$$\varepsilon_{z} = \frac{{\sigma_{z} }}{E}$$
(6)
$$\sigma_{{z_{ \hbox{max} } }} = \frac{MC}{I} \Rightarrow \delta_{A} = \frac{{ML^{2} }}{2EI}$$
(7)

where \(E\) is Young’s module, \(M\) is the bending moment, \(I\) is the second moment of area, \(C\) is the maximum distance from the neutral axis, \(L\) is the actuator’s length, \(\sigma_{{z_{ \hbox{max} } }}\) is the maximum normal stress, and \(\delta_{A}\) is the actuator’s deflection at the point \(A\).

Since the deflection of the actuator required calculations of the magnetic fields, it is necessary to estimate the magnetic flux penetration depth in the material. For this purpose, the numerical simulation results is used. After computing the magnetic fields and its equivalent penetration radius, to simplify the calculation, the value of the equivalent magnetic field in the penetration area is considered as a constant excitation magnetic field in this area. The values of the magnetic fields out of the penetration area are considered to be zero. Figure 12 shows the penetration depth of the magnetic fluxes.

Fig. 12
figure 12

The magnetic flux penetration depth

Full size image

The equation of the equivalent penetration radius and the equivalent magnetic field are as follows:

$$r_{e} = \frac{{\sum H_{i} r_{i} }}{{\sum H_{i} }}$$
(8)
$$H_{e} = \frac{{\sum H_{i} r_{i} }}{{\sum r_{i} }}$$
(9)
$$\gamma_{p} = R - r_{e}$$
(10)

where \(\varvec{H}_{\varvec{e}}\), \(\varvec{\gamma}_{\varvec{p}}\), \(\varvec{r}_{\varvec{e}}\), and R are the equivalent magnetic field of each cross-section, the penetration depth, the equivalent penetration radius of each cross-section, and the radius of the permendur rod, respectively. The equivalent magnetic field and equivalent penetration radius are computed at 15 different cross-sections of the numerical model of the actuator, and their mean values are taken into account as the excitation magnetic field and penetration radius. The mean value of the equivalent penetration radiuses is 2.25 mm by applying a 2.5 A current, and the mean value of the equivalent magnetic field is 4673 A/m.

First, the elongation strain of the penetration depth is calculated. Then bending moments and the actuator’s deflections would be obtained. Knowing the stress distribution in the cross-section, and considering the equilibrium of the forces along the z-axis, the location of the neutral axis can be calculated. Figure 13 shows the stress distribution in the actuator’s cross-section.

Fig. 13
figure 13

The stress distribution in the cross section of the bending actuator

Full size image

In Fig. 13, A and \({\mathbf{A^{\prime}}}\) are the penetration area and the bending area, respectively. \(\varvec{N}_{\varvec{T}}\) is the neutral axis of the bending area, and \(\bar{\varvec{y}}_{{\varvec{A^{\prime}}}}\) is the distance between the neutral axis and the center of the cross-section.

$$h = \bar{y}_{{A^{\prime}}}$$
(11)
$$A^{\prime} = \pi R^{2} - A$$
(12)
$$\bar{y}_{{A^{\prime}}} \cdot A^{\prime} = - \bar{y}_{A} \cdot A$$
(13)

By knowing the magnetic field penetration depth, the location of the neutral axis can be calculated. Considering the equilibrium of the force along the z-axis, following equations can be expressed.

$$\sum F_{z} = F_{A} + \int \sigma_{{A^{\prime}}} dA^{\prime} = 0 \Rightarrow - \frac{E}{\rho }\bar{y}_{{A^{\prime}}} \cdot A^{\prime} = F_{A} \Rightarrow - \bar{y}_{{A^{\prime}}} \cdot A^{\prime} = \frac{{F_{A} \cdot \rho }}{E}$$
(14)
$$\varepsilon_{z} = \frac{{ - \left( {h + r_{e} } \right)}}{\rho }$$
(15)
$$F_{A} = E \cdot \varepsilon_{z} \cdot A$$
(16)
$${\text{h}} = \frac{{E \cdot \varepsilon_{z} \cdot A \cdot \frac{{h + r_{e} }}{{\varepsilon_{z} }}}}{{E \cdot A^{\prime}}} = \frac{{Ah + Ar_{e} }}{{A^{\prime}}} \Rightarrow h = \frac{{Ar_{e} }}{{A^{\prime} - A}}$$
(17)

where \(\varvec{F}_{\varvec{A}}\) is the tensional force at the area A, and ρ is the bending radius of the neutral axis. Axial strain at \(\varvec{r}_{\varvec{e}}\) could be calculated using the piezo-magnetic equations. The values of A and \(\bar{\varvec{y}}_{\varvec{A}}\) can be calculated considering the penetration depth. The values of \(\varvec{A^{\prime}}\) and \(\bar{\varvec{y}}_{{\varvec{A}{\prime }}}\) would be determined using Eqs. (11) and (12). The bending moment can be obtained as follow:

$$\varepsilon_{z} = \frac{{M \cdot \left( {r_{e} + h} \right)}}{{EI_{{A^{\prime}}} }}$$
(18)
$${\text{M}} = \frac{{\varepsilon_{z} \cdot E \cdot I_{{A^{\prime}}} }}{{\left( {r_{e} + h} \right)}}$$
(19)

Deflections of the actuator at the point A can be calculated using Eq. (7). Finally, the deflection and slope of the actuator are determined at the point C using geometrical relations.

$$\uptheta_{\text{A}} = \frac{\text{ML}}{{{\text{EI}}_{{A^{\prime}}} }}$$
(20)
$$\updelta_{c} = \frac{{{\text{ML}}^{2} }}{{2{\text{EI}}_{{A^{\prime}}} }} + \frac{\text{ML}}{{{\text{EI}}_{{A^{\prime}}} }} \times L$$
(21)
$$\uptheta_{c} =\uptheta_{\text{A}}$$
(22)

The actuator’s deflection is calculated by applying a 2.5 A current. The value of the mean equivalent magnetic fields, the magnetostriction coefficient at this magnetic field, and the axial strain of the material are 4673 A/m, 0.22 × 10−7 m/A [12], and 0.1, respectively. The actuator’s deflection at the point A is calculated as follows:

$$\updelta_{A} = \frac{{{\text{ML}}^{2} }}{{2{\text{EI}}_{{A^{\prime}}} }} = 0.13\;\upmu{\text{m}}$$
(23)
$$\updelta_{c} = \frac{{3{\text{ML}}^{2} }}{{2{\text{EI}}_{{A^{\prime}}} }} = 0.39\;\upmu{\text{m}}$$
(24)

Table 2 shows the deflection of the actuator at different currents.

Table 2 The actuator’s deflection at different currents
Full size table

5 The fabrication and experimental tests of the actuator

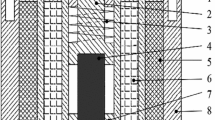
The fabricated parts and assembly of the actuator have been shown in Figs. 14 and 15, respectively.

Fig. 14
figure 14

Components of the actuator 1-magnetostrictive rod 2-comb shape magnetic core 3-bobbin 4-base plate 5-coil

Full size image
Fig. 15
figure 15

The assembled view of the actuator

Full size image

The coils shown in Fig. 14 are connected in series mode. The direction of their magnetic flux are shown in Fig. 1.

5.1 Experimental tests

The actuator has been tested under the DC and AC excitations. The displacement of the actuator has been measured under loaded and unloaded conditions. An eddy current gap sensor model AEC-5509, applied electronics, Japan is used to measure the actuator’s deflections. This sensor measures the deflection of the actuator at the point C. The sensitivity of the eddy current sensor is 0.4 mm/v, and its accuracy is 0.2 µm.

5.1.1 The results of the deflection measurements under the DC excitations

The deflection of the actuator is relatively small under the DC excitation. In this test, by applying a 3.8 A current, the deflection of the point C under free conditions is 1.6 µm. Figure 16 shows the test setup.

Fig. 16
figure 16

The DC test setup 1-oscilloscope 2-DC power supply 3-actuator 4-gap sensor

Full size image

To determine the performance of the actuator under loaded conditions in DC excitations, a spring with known stiffness (\(K_{L} = 502\;{\text{N}}/{\text{m}}\)) is engaged with the actuator at the point C, and the deflection is measured. Figure 17 shows the test setup under loading conditions.

Fig. 17
figure 17

DC test’s setup under loading conditions

Full size image

By applying a DC current of 3.8 A, the deflection of the actuator is 1.2 µm at the point C. Therefore the actuator force is 0.6 mN.

5.1.2 The results of the deflection measurement under the AC excitations

The resonance of the actuator occurs about the excitation frequency of 130 Hz. Since vanadium permendur has the positive magnetostriction property, both positive and negative directions of the magnetic fields cause elongations in the material. It can be found from the butterfly graph of the magnetostrictive strain versus magnetic fields. It means that the magnetostrictive material stretches two times in each period of the exciting magnetic field. Therefore, the frequency of the elongation is two times the excitation frequency. By exciting the actuator at the frequency of 130 Hz, the material vibrations frequency doubles and becomes 260 Hz which is fairly near the numerical resonance frequency of the actuator.

By varying the RMS currents, the deflection of the actuator has been measured at the point C under free conditions. Figure 18 shows the deflection of the point C in the experimental tests and simulations.

Fig. 18
figure 18

Deflections of the point C in the numerical analysis and experiments under free conditions

Full size image

The bending displacement increases with the increase of the RMS current. In the AC excitations, the deflection of the actuator is much more than the DC excitations. The reaction force of the actuator has been calculated by engaging a spring with known stiffness (\(k_{L} = 502\;{\text{N}}/{\text{m}})\) to the actuator. Table 3 shows the deflection of the actuator under free and loading conditions.

Table 3 The deflection of the actuator under free and loading conditions at the frequency of 130 Hz
Full size table

6 Discussion

The input and output power of the actuator at 2.5 RMS current and the exciting frequency of 130 Hz are 15.75 W and 0.034 W, respectively. The power dissipations of the actuator are magnetic, electric, and mechanical. Magnetic dissipations are flux leakages and hysteresis losses. The electrical dissipations are eddy current and joule losses of the coils.

The characteristic curve of the actuator (e.g. Bending deformations versus excitation currents or forces versus currents) shows that the actuator is a nonlinear system. Therefore there are three ways to control the bending deformations. The first way, is setting a working point on the characteristic curves and swinging the excitation current around the point. In this case, it is possible to use a linear controller for the approximate linear system. The second way is using nonlinear controller for wide range of the deformations. If there is an accurate model of the actuator, it is possible to have an open loop control system.

7 Conclusion

In this paper, a bulk magnetostrictive bending actuator has been presented using a permendur rod. This actuator consists of 8 coils, a comb shape magnetic core, and a magnetostrictive rod. The rod has been fixed on a metallic base plate. The actuator’s components have been designed in such a way that magnetic fluxes pass through a thin layer of the rod. The elongation of the thin layer causes the bending of the actuator. The actuator’s deflections and block forces are simulated in COMSOL software. The concentration of the magnetic fields in a thin layer under AC excitations, due to the generation of eddy currents in the material is much suitable for generating large deflections. Therefore AC mode operation is promising to use in rotary motors. Exciting the actuator with four comb shape magnetic cores with appropriate time shifts can generate elliptical motions to rotate a rotor. The deflection of the actuator is minimal under the DC excitation which is suitable to use in wireless precise positioners. For instance, platforms of the TEM, STM or AFM microscopes can be fabricated with this actuator. By adding axial and circumferential magnetic fields to this actuator, it is possible to generate multi-mode displacements.