1 Introduction

Space modulation techniques (SMTs) are unique multiple input multiple output (MIMO) transmission techniques that exploit the indices of the active antennas in order to map information bits, and utilize the differences among different channel paths to convey additional bits. However, in single radio frequency (RF) chain SMTs such as spatial modulation (SM) and space shift keying (SSK) schemes, one transmit antenna is activated at one particular time instant, while the other antennas are turned off [1]. These schemes have attracted lots of research interests due to the rapidly increasing demand of enhancing both the reliability and the capacity of the future wireless networks. Multi-user MIMO (MU-MIMO) systems play a key role in the fifth generation (5G) wireless communication networks [2] due to the substantial gains that obtained over conventional single input single output (SISO) techniques [3]. In the fourth generation (4G) cellular systems and mobile long term evolution (LTE) applications, small MIMO in base stations (BSs) terminals are used with few antennas. In this correspondence, the BSs in the fifth generation (5G) wireless networks are expected to equip massive MIMO stations with a high number of antennas in the order of hundreds or even more than the active users per each time–frequency slot. Additionally, the benefits of massive MIMO systems include the enormous spectral efficiency, and the lower Inter-user interference (IUI) [4]. Moreover, device-to-device (D2D) communications are also enabled in 5G cellular networks in order to increase the number of active users per time–frequency slot. In [5, 6] for example, the number of active users per slot was maximized to improve both the spectral and energy efficiencies by enabling the D2D communications in 5G networks.

The performance of SM and SSK modulation schemes in MU scenarios has been studied extensively in the literature (e.g., [7,8,9,10]). The authors in [7] have studied the performance of SSK scheme in the presence of multiple access interference, and showed that SSK scheme outperforms the conventional MIMO systems for various channel conditions and setups. Later, the proposed MU-SSK framework in [7] is generalized to MU-SM in [8]. In [9], the author has proposed an antenna-hoping spatial division multiple access for SSK modulation technique which is capable of providing transmit diversity gains. In addition, an orthogonal frequency division multiplexing (OFDM) based downlink MU-SM is considered in [10], where the data of each user is conveyed on different sub-channel, and it is shown that MU-SM-OFDM scheme is capable of outperforming Alamouti-coded OFDM scheme in some scenarios.

Generally, one of the most important issues in MU-MIMO systems is the number of users that can be supported by the BSs. However, it is revealed that the number of antennas at the transmitter and receiver sides and the channel scattering play a pivotal role in determining the number of users that can be simultaneously served in MU-MIMO systems [11]. For instance, increasing the number of instantaneous users beyond a certain limit with the existence of fixed number of antennas at the BSs leads to reduce the achievable data rate in the wireless networks. As a result, user selection techniques have emerged as a promising technology in order to substantially improve the performance of MU-MIMO systems with large number of simultaneously supportable users. In particular, the BSs can select the best set of users to be communicated with, when a partial or complete channel knowledge exists.

There are several promising user selection algorithms have been designed based on linear algebra concepts, matrix theory, and different cost metrics to select optimal set of users. However, throughput maximization algorithms based on zero-forcing (ZF) beamforming [12,13,14,15,16] and dirty paper (DP) beamforming [12, 17, 18] can be enhanced when the number of single-antenna users is larger than the number of transmit antennas at the BSs (K > Nt). Therefore, exploiting the multiuser diversity can be achieved by selecting a set of active users whose channel characteristics lead to a performance enhancement [19]. Over the last two decades, a large amount of research and several published work have focused on the asymptotic sum rate of MIMO broadcast systems with user selection algorithms (e.g., [13, 14, 16, 17]). In [20], two low complexity user selection algorithms were proposed, namely, the capacity-based user selection and Frobenius norm-based user selection algorithms using block diagonalization (BD) precoding technique in order to select a subset of users to maximize the total throughput and reduce the computational complexity. The former algorithm uses the total throughput as the selection criteria, while the selection criteria of the latter is based on the Frobenius norm of the effective channel matrix. In these two algorithms, a new user is selected iteratively to maximize the given user selection criteria with the previously selected users in each selection step. Furthermore, it is found in [20] that the norm-based user selection algorithm can significantly reduce the complexity with keeping the throughput performance. In [21], the authors proposed an improved norm-based user selection algorithm for traditional MU-MIMO systems with BD precoding technique based on heuristic Gram–Schmidt orthogonalization in the design of the precoding matrix that reduced the complexity of the original norm-based user selection algorithm [20] without evident performance loss under low signal-to-noise ratio (SNR) values. In addition, the authors in [22] applied the norm-based user selection and the signal-to-interference plus noise ratio (SINR)-based user selection algorithms in the norm-based transmit antenna selection (TAS) systems in order to allocate multiple transmit antennas to selected users based on the Gram–Schmidt orthogonalization algorithm. The results of this paper showed that the best performance is achieved by the norm-based user selection method. In a recent work, the authors in [23] proposed a Frobenius norm-based user selection method for MU-MIMO based on OFDM to further reduce the computational complexity.

In MU-MIMO systems with user selection algorithms, digital precoding methods are needed in order to eliminate other user’s interfering signals. This is due to the fact that multiplying each user’s signal by a precoding matrix before transmission results in removing all the IUI. The most frequently applied precoding schemes in MU-MIMO systems are BD and ZF precoding methods [11]. On the other side, unlike conventional MIMO techniques, the conventional ZF and minimum mean square error (MMSE) precoding techniques cannot be used in MU-SMTs, due to the fact that a part of the data in SMTs is also encoded into the channel impulse responses, which results in losing the data transmitted [24,25,26]. In addition, the singular value decomposition (SVD)-based precoding is well-established in MIMO systems where the whole MIMO channel is decomposed into several SISO channels with different channel gains [27, 28]. However, the geometric mean decomposition (GMD)-based precoding scheme is proposed in [29] in order to remove the inter-antennas interference that produces due to the use of multiple transmit and receive antennas. The advantage of GMD-based precoding scheme is to decompose the channel into a number of SISO channels with the same gain. Recently, the GMD-based precoding scheme is presented in [30] for millimeter-wave (mmWave) massive MIMO systems to avoid the complicated bit-allocation problem that caused by the unequal gains of the different sub-channels in SVD-based precoding technique. The authors in [30] showed that GMD-based precoding schemes outperform the SVD-based precoding methods, as well as the problem of the high energy consumption in mmWave massive MIMO systems that caused by the large number of required RF chains [31] is resolved. In a more recent work [32], GMD-based hybrid beamforming is applied in generalized spatial modulation (GSM) scheme with norm-based user selection algorithm, and showed a significant improvement compared to the conventional schemes with single-user scenario. Furthermore, the generalized triangular decomposition (GTD) method is exploited in [33] to design hybrid precoding scheme for mmWave massive MIMO systems.

Inspired by the norm-based user selection method that proposed in [20] for MU-MIMO systems, and the performance enhancement obtained in [20] and [22], this paper aims to apply Frobenius norm-based user selection algorithm with fully digital GMD-based precoding scheme for the emerging SMTs with single-RF chain in order to eliminate the interference at the transmitter, and successfully reconstruct the transmitted symbols at the receiver side.

To the best of author’s knowledge, there has been no research activities on user selection algorithms for MU-SMTs, and this paper is the first attempt to apply both GMD-based precoding scheme and norm-based user selection algorithm in MU-SMTs with single-RF chain. More specifically, the Frobenius norm-based user selection algorithm is applied to MU-SMTs-MIMO with single-RF chain using the fully digital GMD-based precoding scheme. Simulation results showed a significant improvement as compared to the conventional systems with single-user scenario. In addition, the effect of the channel estimation errors (CSEs) on the bit error rate (BER) performance of the proposed schemes is presented.

To this end, the rest of this paper is organized as follows. Section 2 presents the system model of SMTs with fully digital SVD- and GMD-based precoding schemes. The Frobenius norm-based user selection technique with GMD-based precoding scheme in SSK and SM systems is discussed in Sect. 3. Simulation results of the BER performance and comparisons are demonstrated and discussed in Sect. 4, and finally the paper is concluded in Sect. 5.

Notation

The following notations are used throughout the paper. Lower- and upper-case letters a and A denote a vector and a matrix, respectively. tr{A}, AH, and \(A _{F}\) denote the trace, the conjugate transpose, and the Frobenius norm operations, respectively. \({\mathbb{C}}^{m \times n}\) denotes a matrix with m rows and n columns, and \({\mathcal{C}\mathcal{N}}\left( {\upmu,\sigma^{2} } \right)\) denotes the complex normal distribution of a random variable having mean \(\upmu\) and variance σ2.

2 SMTs with fully digital SVD- and GMD-based precoding schemes

In MIMO systems, there are many digital precoding schemes that can be used to improve the system performance and to reduce the interference. Some precoding algorithms are based on the channel matrix decomposition which decomposes the complex channel matrix into corresponding transmitter precoding and receiver post-coding matrices. In this section, the fully digital SVD- and GMD-based precoding schemes are discussed in order to improve the error performance of single-RF SMTs.

Consider that SM and SSK systems are with Nt transmit antennas and Nr receive antennas. The SVD of the channel matrix \(H \in {\mathbb{C}}^{{N_{r} \times N_{t} }}\) can be written as in [29]

$$H = USV^{H} ,$$
(1)

where \(U \in {\mathbb{C}}^{{N_{r} \times N_{r} }}\) and \(V \in {\mathbb{C}}^{{N_{t} \times N_{t} }}\) are orthogonal and unitary matrices, and VH is the Hermitian transpose of the unitary matrix V. The diagonal matrix \(S \in {\mathbb{C}}^{{N_{r} \times N_{t} }}\) consists of the largest singular values of the complex channel matrix H are on its diagonal. It is, however, a real-valued diagonal matrix of the positive square roots of the eigenvalues of the matrix HHH sorted in a descending order.

SVD algorithm is considered as a complex algorithm due to the several generated sub-channels with different gain values which varies widely, and hence increasing the complexity either at the transmitter or the receiver side. In order to circumvent this issue, GMD algorithm is proposed in [34], where it can decompose the complex-valued MIMO channel into a number of identical sub-channels with equal gain as depicted in Fig. 1, and the sub-channel’s energies tend to converge together. Moreover, more energy will be assigned to smaller eigenvalue sub-channels, and the various sub-channel energies can be eventually made equal to the geometric mean of the positive non-zero singular values of the complex channel. Therefore, the fully digital GMD-based precoding scheme leads to avoid the complicated bit allocation issue that caused by the unequal SNRs for different sub-channels in the SVD-based algorithm [30]. The GMD of the channel matrix \(H \in {\mathbb{C}}^{{N_{r} \times N_{t} }}\) can be written as in [35]

$$H = QRP^{H} .$$
(2)
Fig. 1
figure 1

Illustration of sub-channel gains in a SVD-based precoding and b GMD-based precoding [30]

Full size image

In this algorithm, the two unitary matrices \(Q \in {\mathbb{C}}^{{N_{r} \times N_{r} }}\) and \(P^{H} \in {\mathbb{C}}^{{N_{t} \times N_{t} }}\) have orthonormal columns, while \(R \in {\mathbb{C}}^{{N_{r} \times N_{t} }}\) is an upper triangular matrix with diagonal real elements equal to the geometric mean of the positive singular values of the complex matrix H.

In the fully digital SVD- and GMD-based precoding schemes, the transmitted signal is multiplied by the transmit digital precoder matrix V or P, and the received signal is multiplied by the digital post-coder matrix UH or QH, respectively, with assuming that the channel state information (CSI) is available at both the transmitter and the receiver. In fact, the digital transmit precoder is designed in order to eliminate the inter-symbol interference at the transmitter, while the digital combiner which is also well-known as the digital post-coder or the receiver shaping is designed to successfully reconstruct the transmitted symbols at the receiver.

In this paper, the SVD and GMD algorithms are exploited to design the fully digital precoding schemes in single-RF SMTs. However, the SVD-based precoding technique is applied in MIMO systems to execute the singular value decomposition to the channel matrix H as in (1). The received signal equation with applying the SVD algorithm to the channel matrix in single-user SMTs with single-RF chain can be expressed as.

$$y = USV^{H} x_{t} + n,$$
(3)

where xt is the Nt—length transmitted vector, and n is an Nr—dimensional additive white Gaussian noise (AWGN) vector with zero mean and covariance matrix of \(\sigma_{n}^{2} I_{{N_{r} }}\), \(n\sim {\mathcal{C}\mathcal{N}}\left( {0_{{N_{r} }} , \sigma_{n}^{2} I_{{N_{r} }} } \right)\), where \(I_{{N_{r} }}\) is the Nr × Nr identity matrix, and σ 2n is the noise variance per dimension.

By multiplying the channel matrix H by both UH and V matrices, an equivalent channel matrix is obtained after applying the SVD-based precoding scheme as follows

$$H_{SVD} = U^{H} USV^{H} V = S \in {\mathbb{C}}^{{N_{r} \times N_{t} }} .$$
(4)

Therefore, the received signal equation of single-user SMTs employing the fully digital SVD-based precoding scheme can be expressed as

$$y = U^{H} \left( {USV^{H} Vx_{t} + n} \right) = H_{SVD} x_{t} + U^{H} n.$$
(5)

The noise term UHn will be eliminated by the maximum likelihood (ML) detector which is used to jointly estimate the spatial symbol \(\hat{\ell }\) and the signal symbol \(\hat{X}_{\ell }\) with taking the effective channel HSVD into consideration as follows

$$\left[ {\hat{\ell },\hat{X}_{\ell } } \right] = \mathop {\arg \hbox{min} }\limits_{{X_{\ell } \in X}} \left\| {y - H_{SVD} X_{\ell } } \right\|_{F}^{2} ,$$
(6)

where X is a set that containing all possible transmitted vector combinations between transmit antennas and data symbols.

Similarly, the GMD-based precoding scheme can be employed by executing the GMD algorithm to the channel matrix H in single-user SMTs with single-RF chain as written in (2). With applying the GMD algorithm to the channel matrix in single-RF SMTs, the received signal equation can be written as

$$y = QRP^{H} x_{t} + n.$$
(7)

By multiplying the complex channel matrix H by the precoder and post-coder matrices, P and QH, respectively, an equivalent channel matrix is obtained after applying the GMD-based precoding, where the effective channel matrix in (7) can be transformed into a real upper triangular matrix as follows

$$H_{GMD} = Q^{H} QRP^{H} P = R \in {\mathbb{C}}^{{N_{r} \times N_{t} }} .$$
(8)

The received signal equation of single-RF SMTs utilizing the fully digital GMD-based precoding scheme is expressed as

$$y = H_{GMD} x_{t} + Q^{H} n.$$
(9)

The ML detector is used in SMTs with GMD-based precoding scheme to jointly estimate both the spatial symbol \(\hat{\ell }\) and the signal symbol \(\hat{X}_{\ell }\) can be written as

$$\left[ {\hat{\ell },\hat{X}_{\ell } } \right] = \mathop {\arg \hbox{min} }\limits_{{X_{\ell } \in X}} \left\| {y - H_{GMD} X_{\ell } } \right\|_{F}^{2} .$$
(10)

3 Norm-based user selection technique for SMTs with GMD-based precoding

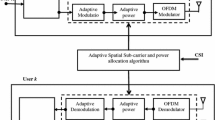
One common assumption adopted in [36,37,38] is that the number of the power-hungry RF chains at the transmitter side of MIMO systems cannot be smaller than the number of transmitted streams. Moreover, user selection technique is an important and critical aspect for maintaining good performance and optimizing MIMO systems. In this paper, single-RF SMTs with fully digital GMD-based precoding scheme employing the Frobenius norm-based user selection technique is presented with the system model shown in Fig. 2 for downlink MU-MIMO. In this scheme, there are Ka active users out of K users in the system, where the number of receive antennas for the Kth user is denoted by \(N_{{r_{k} }}\), and the BS is equipped with Nt > 1 transmit antennas and one RF chain.

Fig. 2
figure 2

Block diagram of SVD- and GMD-based precoding scheme for single-RF SMTs with norm-based user selection technique

Full size image

In downlink MU-SMTs systems with the Frobenius norm-based user selection technique, the Ka active users are selected based on the channel energy that indicated by the Frobenius norm, where a number of Ka users with the highest norm values are selected using the squared Frobenius norm after ordering the K norm values in a descending order. In this scheme, the channel matrix of MU-SMTs has the size of \(KN_{{r_{k} }} \times N_{t}\).

Applying the GMD algorithm to the channel matrix \(H \in {\mathbb{C}}^{{KN_{{r_{k} }} \times N_{t} }}\) in MU-SMTs with single-RF chain is as previously explained in Sect. 2. Moreover, applying the Frobenius norm-based user selection technique for SM or SSK systems with the fully digital GMD-based precoding scheme can be expressed as

$$H_{u} = \mathop {\text{arg max}}\limits_{{k \in \left\{ {1, 2, \ldots , K} \right\}}} \left\| {H_{GMD} } \right\|_{\,F}^{2} = \mathop {\text{arg max}}\limits_{{k \in \left\{ {1, 2, \ldots , K} \right\}}} \left\{ {tr\left( {H_{GMD} H_{GMD}^{H} } \right)} \right\}.$$
(11)

The received signal vector of the jth selected user with taking the used effective channel matrix Hu-a into consideration with \(K_{a} N_{{r_{k} }}\) rows of \(H_{u} \in {\mathbb{C}}^{{KN_{{r_{k} }} \times N_{t} }}\) are selected is expressed as

$$y_{j} = H_{{u - a_{j} }} x + \underbrace {{\mathop \sum \limits_{q \ne j}^{{K_{a} }} H_{u - a} x_{t} }}_{ \approx 0} + n_{j} = H_{{u - a_{j} }} x_{t} + n_{j} ,$$
(12)

where \(H_{{u - a_{j} }} \in {\mathbb{C}}^{{N_{{r_{k} }} \times N_{t} }}\) is the effective channel matrix for user j, \(n_{j} \in {\mathbb{C}}^{{N_{{r_{k} }} \times 1}}\) is the AWGN vector at the jth selected user, and j = 1, 2, …, Ka.

Employing the fully-digital GMD-based precoding scheme in MU-SMTs ensures that the interference imposed by the other users at the jth user is canceled. Moreover, the overall received signal vector of (12) can be represented by single vectors for all selected users as

$$\underbrace {{\left[ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ \vdots \\ {y_{{K_{a} }} } \\ \end{array} } \right]}}_{y} = \underbrace {{\left[ {\begin{array}{*{20}c} {H_{{u - a_{1} }} } \\ {H_{{u - a_{2} }} } \\ \vdots \\ {H_{{u - a_{{K_{a} }} }} } \\ \end{array} } \right]}}_{{H_{u - a} }}x_{t} + \underbrace {{\left[ {\begin{array}{*{20}c} {n_{1} } \\ {n_{2} } \\ \vdots \\ {n_{{K_{a} }} } \\ \end{array} } \right]}}_{n},$$
(13)

where \(y \in {\mathbb{C}}^{{K_{a} N_{{r_{k} }} \times 1}}\) is the received signal vector, \(H_{u - a} \in {\mathbb{C}}^{{K_{a} N_{{r_{k} }} \times N_{t} }}\) is the overall effective channel matrix between the BS and all selected users, and \(n \in {\mathbb{C}}^{{K_{a} N_{{r_{k} }} \times 1}}\) is the overall noise vector at all selected users.

The spatial symbol \(\hat{\ell }\) and the signal symbol \(\hat{X}_{\ell }\) are jointly estimated by the optimum ML detector as follows

$$\left[ {\hat{\ell },\hat{X}_{\ell } } \right] = \mathop {\arg \hbox{min} }\limits_{{X_{\ell } \in X}} \left\| {y - H_{u - a} X_{\ell } } \right\|_{F}^{2} .$$
(14)

4 Simulation results

In this section, the simulation results of the BER performance of single-RF SMTs with fully digital SVD- and GMD-based precoding schemes over Rayleigh fading channel are provided. The main purpose of these simulation results is to compare the BER performance of SMTs in single-user scenario with SVD- and GMD-based precoding algorithms. In addition, in order to obtain a good balance of BER performance across channels, the GMD algorithm is introduced to replace the SVD algorithm for precoding in the downlink MU-SMTs with single-RF chain. The simulation results of MU-SMTs with Frobenius norm-based user selection technique and employing GMD-based precoding scheme are presented for various numbers of transmit antennas and selected users. Throughout the simulation of this paper, all SM schemes employ 4-QAM technique.

4.1 Single-RF SMTs with fully digital SVD- and GMD-based precoding schemes

The BER performance of SM 2 × 4 scheme employing 4-QAM technique with fully digital SVD- and GMD-based precoding schemes is shown in Fig. 3. It can be clearly seen from this figure that the required SNR value to achieve the BER of 10−6 in SM system with SVD-based precoding scheme is about 21.4 dB. It is also clear that SM scheme with GMD-based precoding technique requires an SNR value of almost 15 dB at the BER performance of 10−6, while the conventional SM system requires about 16.7 dB at the same BER performance. This demonstrates that the fully digital GMD-based algorithm in SM 2 × 4 with 4-QAM technique shows an improvement of approximately 1.7 dB and 6.4 dB over the conventional SM system and SM with SVD-based precoding scheme, respectively.

Fig. 3
figure 3

BER performance of SM 2 × 4 employing 4-QAM with fully digital SVD- and GMD-based precoding schemes

Full size image

Figure 4 depicts the error performance of SM 4 × 4 scheme employing 4-QAM technique with SVD- and GMD-based precoding schemes. The improvement of SM system with GMD-based precoding scheme appears after the BER of 10−3, and it can be seen that the improvement equals to almost 1.7 dB at the BER of 10−6, because the required SNR value for the conventional SM system is about 17.5 dB and for SM system with GMD-based precoding scheme is approximately 15.8 dB to achieve the same BER performance. On the other hand, it is clear that SM system with SVD-based precoding scheme requires a very high SNR value to achieve the BER performance of 10−6 which leads to a performance degradation as compared to the conventional SM system.

Fig. 4
figure 4

BER performance of SM 4 × 4 employing 4-QAM with fully digital SVD- and GMD-based precoding schemes

Full size image

The error performance of SSK 2 × 4 with SVD- and GMD-based precoding schemes is shown in Fig. 5. As it can be clearly seen from this figure, the required SNR value for the conventional SSK system to achieve the BER performance of 10−6 is about 15.8 dB, while employing SVD- and GMD-based precoding techniques in SSK 2 × 4 scheme requires almost 11 dB and 9 dB, respectively, to achieve the same BER performance. This shows a performance improvement of approximately 4.8 dB and 6.8 dB with fully digital SVD- and GMD-based precoding algorithms, respectively.

Fig. 5
figure 5

BER performance of SSK 2 × 4 with fully digital SVD- and GMD-based precoding schemes

Full size image

In Fig. 6, the BER performance of SSK 4 × 4 scheme with fully digital SVD- and GMD-based precoding techniques is depicted to illustrate the effect of increasing the number of transmit antennas to Nt = 4. This figure shows that the required SNR value for the conventional SSK system is about 16.3 dB to attain the BER of 10−6, while the required SNR value for SSK system with SVD-based precoding scheme to achieve the same BER performance is almost 20 dB. Thus, this shows that SVD algorithm leads to a performance degradation of about 3.7 dB. Therefore, increasing the number of transmit antennas to Nt = 4 makes the SVD-based precoding scheme is not preferred because it requires higher SNR value than the

Fig. 6
figure 6

BER performance of SSK 4 × 4 with fully digital SVD- and GMD-based precoding schemes

Full size image

conventional SSK system. In addition, it is obvious from these results that the improvement in SSK system with fully digital GMD-based precoding scheme is observed after the BER of 10−3 at the SNR value of almost 9 dB, and it requires about 13.0 dB to obtain the BER performance of 10−6. This provides an improvement of approximately 2.4 dB over the conventional SSK scheme.

To summarize, applying the fully digital SVD- and GMD-based precoding schemes in single-user SMTs with various numbers of transmit antennas showed that employing the SVD-based precoding scheme in SM and SSK systems with single-RF chain and perfect CSI knowledge at the receiver caused a higher degradation in the BER performance with Nt = 4 than that with Nt = 2, while only SSK 2 × 4 system has showed a performance improvement with fully digital SVD-based precoding technique over the conventional SSK system. More importantly, employing the fully digital GMD-based precoding scheme in single-user SM and SSK techniques with assuming that a perfect CSI is available at the receiver provides an improvement in the system error performance due to avoiding the complicated bit allocation problem in SVD-based precoding algorithm.

4.2 MU-SM with GMD-based precoding scheme and norm-based user selection technique

The BER performance of MU-SM 2 × 4 system employing 4-QAM technique with fully digital GMD-based precoding scheme and Frobenius norm-based user selection algorithm is evaluated for various numbers of selected users as shown in Fig. 7. It can be clearly seen from this figure that the conventional SM system requires an SNR value of about 14.2 dB to achieve the BER performance of 10−5, while single-user SM system with GMD-based precoding technique outperforms the conventional SM system by just less than 1 dB at the same BER performance. Moreover, MU-SM system employing norm-based user selection algorithm with only one selected user out of ten available users requires an SNR value of almost 7.5 dB at the BER of 10−5 which shows an improvement of about 6.7 dB as compared to the conventional SM system. It is also clear that increasing the number of selected users improves the BER performance. On the other hand, MU-SM 2 × 4 system with fully digital GMD-based precoding scheme requires an SNR value of approximately – 2.7 dB to attain the BER performance of 10−5 with any number of selected users, and this scheme outperforms MU-SM system with selecting all available users (Ka = K = 10) by just less than 0.2 dB. This also reveals that MU-SM 2 × 4 system with GMD-based precoding scheme outperforms the conventional SM system by about 16.9 dB due to applying the fully digital GMD-based precoding scheme, regardless of how many users have been selected.

Fig. 7
figure 7

BER performance of MU-SM 2 × 4 employing 4-QAM and K = 10 users with GMD-based precoding scheme and various numbers of active users

Full size image

In Fig. 8, the BER performance of MU-SM 4 × 4 system employing 4-QAM technique with fully digital GMD-based precoding scheme and Frobenius norm-based user selection technique is evaluated and compared to the conventional SM system. This figure shows that the conventional SM scheme requires an SNR value of about 15 dB to attain the BER performance of 10−5, while single-user SM system with fully digital GMD-based precoding technique outperforms the conventional SM system by almost 1 dB at the same BER performance. It is also shown in Fig. 8 that selecting one user out of ten available users in MU-SM 4 × 4 system requires about 10.7 dB to achieve the BER performance of 10−5, and this performance is further improved as the number of selected users increased. Additionally, MU-SM system with GMD-based precoding scheme and selecting any number of users out of the ten available users requires almost – 2.5 dB to achieve the BER of 10−5, which is similar to the performance of MU-SM system with selecting all available users (Ka = K = 10). This shows that a significant improvement of almost 17.5 dB is obtained over the conventional SM system. It is also obvious from these results that the BER performance of MU-SM systems with Frobenius norm-based user selection algorithm is significantly improved by applying the fully digital GMD-based precoding scheme as compared to MU-SM systems without GMD-based precoding scheme.

Fig. 8
figure 8

BER performance of MU-SM 4 × 4 employing 4-QAM and K = 10 users with GMD-based precoding scheme and various numbers of active users

Full size image

4.3 MU-SSK with GMD-based precoding scheme and norm-based user selection technique

Figure 9 depicts the simulation results of MU-SSK 2 × 4 system with Frobenius norm-based user selection algorithm and fully digital GMD-based precoding scheme. It is clear from this figure that the required SNR value for the conventional SSK scheme is almost 13 dB to obtain the BER performance of 10−5, and SSK system with GMD-based precoding scheme outperforms the conventional SSK system by about 5.5 dB at the same BER performance. In addition, MU-SSK system with selecting only one user out of ten available users requires an SNR value of about 6 dB at the BER performance of 10−5, and this performance improves as the number of selected users increases. Moreover, MU-SSK system with fully digital GMD-based precoding scheme and selecting any number of users out of the ten available users requires an SNR value of about – 4 dB at the BER performance of 10−5. This shows that an enhancement of almost 17 dB and 11.5 dB are obtained over the conventional SSK system and single-user SSK with GMD-based precoding scheme, respectively. Additionally, it is clear that the best BER performance is achieved in MU-SSK system with GMD-based precoding scheme and selecting any number of users, and it outperforms the MU-SSK system with selecting all available users (Ka = K = 10) by approximately 1 dB at the BER performance of 10−5.

Fig. 9
figure 9

BER performance of MU-SSK 2 × 4 and K = 10 users with GMD-based precoding scheme and various numbers of active users

Full size image

On the other hand, the BER performance of MU-SSK \(4 \times 4\) system with fully digital GMD-based precoding scheme and Frobenius norm-based user selection technique is evaluated in Fig. 10 with various numbers of selected users out of ten total users. As it can be noticed from this figure, the conventional SSK scheme requires an SNR value of almost 13.8 dB to attain the BER of 10−5, while SSK system with fully digital GMD-based precoding scheme outperforms the conventional SSK system by about 1.6 dB at the same BER performance. In addition, MU-SSK scheme with selecting one user out of ten users requires an SNR value of just less than 10 dB at the BER performance of 10−5, and this can be further improved as the number of selected users increased. Moreover, MU-SSK system with fully digital GMD-based precoding scheme requires an SNR value of approximately – 3 dB to attain the BER of 10−5, and this outperforms MU-SSK system with selecting all available users (Ka = K = 10) by about 0.2 dB. Additionally, it is clear from this comparison that the maximum BER improvement with the minimum required SNR value of almost – 3 dB is achieved with any number of selected users to attain the BER of 10−5. This provides an improvement of about 16.8 dB as compared to the conventional SSK system, and about 15.2 dB over the SSK system with GMD-based precoding scheme. It is also noticeable from these results that the BER performance of MU-SSK systems with applying norm-based user selection algorithm is significantly improved with fully digital GMD-based precoding technique as compared to MU-SSK schemes without GMD-based precoding scheme.

Fig. 10
figure 10

BER performance of MU-SSK 4 × 4 and K = 10 users with GMD-based precoding scheme and various numbers of active users

Full size image

4.4 MU-SMTs with GMD-based precoding scheme in the presence of channel estimation errors

In order to explore the effect of the imperfect CSI at the receiver of MU-SMTs with fully digital GMD-based precoding scheme on the BER performance, Figs. 11, 12, 13 and 14 are plotted. In these figures, the imperfect channel estimation is taken into consideration in order to be practical in decoding the transmitted information. The channel matrix H and its estimate \(\tilde{H}\) are assumed in this paper to be jointly ergodic and stationary processes, and an orthogonality between the CSEs and the channel estimate is also assumed. For the imperfect CSI scenario, the estimated channel matrix \(\tilde{H}\) in MU-SMTs with GMD-based precoding scheme with error is written as [39]

$$\tilde{H} = H - E,$$
(15)

where \(E \in {\mathbb{C}}^{{K_{a} N_{{r_{k} }} \times N_{t} }}\) represents the CSE matrix with independent and identically distributed (i.i.d.) entries that having zero mean and variance σ 2e , \(E\sim {\mathcal{C}\mathcal{N}}\left( {0_{{N_{r} }} , \sigma_{e}^{2} I_{{N_{r} }} } \right)\). This variance captures the channel estimation quality, and it can be chosen appropriately depending on the channel estimation and dynamics schemes. For orthogonal pilot designs, it is assumed in this paper that the estimation error reduces linearly as the number of pilots increases [39, 40], thus the error variance σ 2e is kept equal to the noise variance σ 2n .

Fig. 11
figure 11

BER performance of MU-SM 2 × 4 scheme employing 4-QAM with fully digital GMD-based precoding in the presence of CSEs

Full size image
Fig. 12
figure 12

BER performance of MU-SM 4 × 4 scheme employing 4-QAM with fully digital GMD-based precoding in the presence of CSEs

Full size image
Fig. 13
figure 13

BER performance of MU-SSK 2 × 4 scheme with fully digital GMD-based precoding in the presence of CSEs

Full size image
Fig. 14
figure 14

BER performance of MU-SSK 4 × 4 scheme with fully digital GMD-based precoding in the presence of CSEs

Full size image

Figure 11 compares the error performance of MU-SM 2 × 4 system employing 4-QAM technique with fully digital GMD-based precoding scheme, MU-SM scheme with selecting two users out of ten available users, SM scheme with GMD-based precoding technique, and the conventional SM scheme. All of these schemes are considered with the presence of CSEs, where an imperfect channel knowledge is assumed at the receiver. Similarly, Figs. 12, 13 and 14 are plotted for MU-SM 4 × 4, MU-SSK 2 × 4 and MU-SSK 4 × 4 schemes, respectively. It is clearly seen from these figures that a performance degradation of almost 3–3.5 dB is found in the conventional single-user SMTs with the presence of CSEs over the same schemes with perfect channel knowledge at the receiver, while a performance degradation of about 2.8 dB occurs with CSEs in MU-SMTs and GMD-based precoded schemes as compared to the perfect CSI case without CSEs.

5 Conclusions

In this paper, the fully digital GMD-based precoding scheme is employed in single-user SM and SSK systems with single-RF chain in order to circumvent the issue of the complicated bit allocation and the different SNR values of the sub-channels that generated in SVD-based algorithm. Additionally, the Frobenius norm-based user selection technique is performed in both MU-SM and MU-SSK schemes. The simulation results showed that applying the SVD algorithm in single-RF SMTs degrades the error performance, while the GMD algorithm provides an enhancement to all SMTs. On the other hand, SMTs with fully digital SVD-based precoding technique when Nt = 2 outperform that when Nt = 4. In general, increasing the number of transmit antennas in single-user SMTs with SVD- and GMD-based precoding schemes reduces the improvement of the error performance. This shows that transmit diversity is not exploited in SMTs even with SVD- and GMD-based precoding techniques. It is also found from the simulation results that the BER performance of MU-SMTs improves as the number of selected users increases. From the results of MU-SMTs with GMD-based precoding scheme, it is found that employing the Frobenius norm-based user selection technique with any number of selected users provides the same and best BER performance as compared to the conventional SMTs, and this error performance matches that of MU-SMTs without GMD-based precoding and selecting all available users. Broadly speaking, a significant enhancement in MU-SMTs with GMD-based precoding scheme can be obtained with any number of selected users as compared to the conventional systems. In other words, it is noticed that the performance improvement becomes constant with any number of selected users in single-RF MU-SMTs with GMD-based precoding technique. Additionally, a comparison between MU-SMTs with perfect and imperfect CSI knowledge at the receiver showed that the BER performance is degraded by about 2.8 dB in all proposed schemes with the presence of CSEs over the same schemes with perfect channel knowledge at the receiver, while a performance drop of almost 3–3.5 dB occurs in the conventional single-user SMTs with the presence of CSEs over the same schemes with perfect CSI at the receiver. These results show that the MU-SMTs and GMD-based precoded schemes provide lower performance degradation than that of the conventional schemes with the presence of CSEs over the same schemes with perfect CSI. Therefore, the proposed MU-SMTs with fully digital GMD-based precoding scheme can be effectively used in various 5G wireless networks.