1 Introduction

The ongoing improvement in nanoscience acquires a potential intrigue the centrality of nanoparticles as of late. It is tentatively advocated that annulling of metal nanoparticles in conventional base liquids, an energizing discussion of heat spread liquid, is accomplished identified as "nanofluid". As of late, the incomparable intrigue has been created by researchers toward the progression of nanofluids because of fascinating applications with regards to the mechanical and innovative divisions where the heat and mass transpiration get the main significance. Because of noticeable quality thermophysical assets, the noteworthiness of nanoparticles remembers numerous uses in cooling schemes, solar systems, heat exchangers, micro/nanoelectromechanical devices, destroying of cancer tissues, artificial lungs, treatment of various diseases, and so forth. Also, numerous fluids are utilized for heat transportation in different engineering and chemical productions. Choi [1] was planned the leading work on nanofluid which was additionally stretched out in different ways. These fluids with improved thermophysical properties were termed nanofluids. The motivation for Choi’s pioneering work was the realization that base fluids with their low thermal conductivities are not efficient for modern heat transfer needs. The fascinating slip highlights of Brownian movement and thermophoresis development related to the nanofluid were examined by Buongiorno [2].

The warmth move addition of nanofluids was affirmed in different cases by trial results [3]. Ghadikolaei et al. [4] inspected the Joule warming and irregular warm emission point of view in Casson nanofluid prompted by extended structure. Khan and Shehzad [5] decided to utilize a convergent method for thermophoretic parts of nanofluid in third-grade nano-material. Hayat and Nadeem [6] considered the thermal energy transfer characteristics of Ag-CuO/water nanofluid. They achieved that, hybrid nanoliquid displays a bigger heat transfer rate in contrast with the ordinary nanofluid. Waqas et al. [7] revealed various uses related to the progression of nanoparticles within the sight of gyrotactic microbes. They utilized a second-grade viscoelastic nanofluid pattern where the arithmetical arrangement has been determined by means of an implicit bvp4c calculation. A nanoliquid investigation of the third-grade liquid stream with the effect of viscid dispersal, warm radiation, and slip results was investigated by Abdelmalek et al. [8]. Eid et al. [9] completed electromagnetic highlights in blood movement CNTs in a permeable round chamber.

The existence of nanoparticles in a fluid upsurges its thermal conductivity and therefore significantly improves the heat transfer characteristics of the nanofluid. For this reason, nanofluids have the great advantage of enhanced thermal conductivity compared to base fluids which improves their utility as heat transfer fluids. In view of such added advantages, nanofluids find significant applications in vehicle cooling, heat exchangers, computer processors, nuclear reactors, air conditioners, etc. In light these beneficial properties, many researchers [10, 11] have studied the properties and potential uses of nanofluids for both Newtonian and non-Newtonian liquids. Fang and Tao [12] explored the laminar unstable stream over a flexible turning circle with negative acceleration. The first and second law investigates an electrically directing liquid past a turning disk within the sight of a uniform vertical attractive field that was considered by Rashidi et al. [13].The consistent 3D flow and warm move of dense liquid on a turning plate extending a spiral way was concentrated by Asghar et al. [14]. Turkyilmazoglu [15] explored the customary Bodewadt limit layer of the incompressible dense liquid stream and warmth move over a fixed circle given that the plate is permitted to radially extend. Hussain, et al. [16] acquired the arrangement of the issue built up by the progression of a micropolar liquid turning about an expedite circle. The steady progression of a condensed power-law liquid due to pivoting unending plate was concentrated by Ming et al. [17] and they gave the mathematical consequences of the liquid stream with warmth transport impact. Rashidi et al. [18] have built up a lot of nonlinear PDEs that related to the constant convective and magnetohydrodynamic slip stream that happened because of the turn of a plate in the presence of viscous dissemination and Ohmic warming. A Casson liquid stream yield by pivoting a rigid plate was created by Rehman et al. [19]. The magnetohydrodynamic viscous nanofluid 3D stream (flow) by turning disc with heat, Arrhenius vitality of activation, and the binary chemical reaction was concentrated by Asma et al. [20]

The unpredictable example of different microorganisms like microscopic organisms and green growth creates the wonder. Truth is told, the starting point of the bioconvection is related to the infinitesimal convection of microorganisms which showed up because of the density gradient. It is usually assessed that when microorganisms travel some particular way, the fluid thickness of such microbes improved. The bioconvection can be described as a gathering of microbes that are denser than water transfers a particular way, bringing about a density gradient that could prompt the development of the naturally visible radiative movement. Super fluidity and superconducting are crucial marvels that can be detectable on a macroscale. The usage of bioconvection incorporates various solicitations like enzymes, fertilizers, bio microsystems ethanol, oil recovery, and bioreactors. The bioconvection wonder experienced applications in different items in mechanical and organic productions. Normally, the developments of unicellular organisms are named taxis, and relying on the improvement and bearing of development; the taxis can additionally be subgrouping in gyrotaxis, gravitaxis, and phototaxis. Such esteemed solicitations demanded the examiners give some regular commitments on this theme. Kuznetsov [21] gave the bioconvection in nanostructures over the level layer. In this research article, the researchers have reduced the modeled equations to three coupled equations and then solved the reduced problem by employing homotopy perturbation method. The highlights of nanoparticles containing gyrotactic microorganisms arranged by a level surface were presented by Basir et al. [22].

An examination to research the bioconvection because of the gyrotactic microbes and nanoparticles which indicated that transmission increments with expanding the flexibility factor within the sight of the convective situation while simultaneously the concentration of nanoparticle expanded with the upgrade of the Brownian movement constraint was accounted by Khan et al. [23].The dual results for water-based nanofluid and gyrotactic microbes with warm emission on nonlinear contracting/extending slip were gotten by De [24]. Utilizing the 5th order Runge Kutta Fehlberg technique alongside the shooting technique for a solution, his discoveries uncovered that motile microbes work diminished for the upgrade of bioconvection Lewis number. An investigation that deliberated the gravity-driven nanofluid stream comprising gyrotactic microorganisms and nanoparticles was introduced by Palwasha et al. [25]. They tackled the issue through the HAM and investigated that the instantaneous movement of Williamson and Casson nanofluids diminished with a highly attractive field constraint. The aftereffects of the liquid stream, warmth move enclosing nanoparticles and gyrotactic microbes within the sight of non-Newtonian nanofluids were acquired by Khan et al. [26]. They indicated that nanofluid stream, warmth move, gyrotactic microbes concentrations, and nanoparticles had reasonable outcomes for latently organized nanofluid model boundary conditions contrasted with the effectively measured nanofluid model boundary conditions. The nanoparticles and gyrotactic microbes alongside the second-grade nanofluid stream (flow) and warmth move in which heat expanded with the thermophoresis constraint were explored by Zuhra et al. [27]. Riaz et al. [28] introduced the heat transmission procedure in a human body is a complex procedure comprising of heat move in the pores of membranes, as heat transfer in tissues, perfusion of an arterial-venous blood, emission of electromagnetic radiation from cell phones, generation of metabolic heat, and exterior interface. Thinking about the human thermoregulation framework and thermotherapy, the work is pointed toward portraying the effect of bio heat and mass exchange in the peristaltic movement of an Eyring-Powell ("non-Newtonian") liquid in a three-dimensional rectangular cross section. Anum et al. [29] reviewed the investigation of heat transmission rate, mass and motile microorganisms for convective second grade nanoliquid flow. The deliberated model contains of both gyrotactic micro-organisms as well as nanoparticles.

As a profound investigation of the above-referred to explore work, we plan to build up a bioconvection Casson Nanofluid flow model for the Darcy-Forchheimer flow related to the system of a rotating disk using the HAM technique [30,31,32,33].

The novelty of the present work is pointed out as:

  • The published work [20] is extended including the motile gyrotactic microorganisms.

  • Darcy-Forchheimer flow and the Casson model are used as extensions.

  • Convection and thermal radiation terminologies are also included in the present work to extend the existing work [20].

The mathematical formulation, analytical solution, graphical and numerical results are organized and discussed. The main findings are highlighted in the conclusion section.

2 Problem formulation

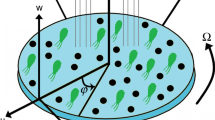
We scrutinize 3D bioconvection Darcy-Forchheimer flow of Casson nanoliquidis quipped above whirling plate for z > 0. Nanofluid comprises mobile microorganisms that are gyrotactic. Thermal radiation effects and Arrhenius activation vitality are furthermore exist. Magnetic field \(\beta_{0}\) moves in \(z\)-direction (see Fig. 1). Brownian diffusion and thermophoretic effects also exist.

Fig. 1
figure 1

Pictorial representation of the flow

Full size image

On behalf of the above flow assumptions, the governing equations can be recovered as [19, 20]:

$$ \frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{\partial w}{{\partial z}} = 0, $$
(1)
$$ \begin{gathered} u\frac{\partial u}{{\partial r}} + w\frac{\partial u}{{\partial z}} - \frac{{v^{2} }}{r} + \frac{1}{{\rho_{nf} }}p_{r} = \upsilon_{nf} \left( {1 + \frac{1}{\lambda }} \right)\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{{\partial r}} - \frac{u}{{r^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) - \frac{{\upsilon_{nf} }}{{k^{*} }}u - Fu^{2} \hfill \\ - \frac{{\sigma_{nf} }}{{\rho_{nf} }}\beta_{0}^{2} u + \frac{{\left( {\rho \beta } \right)_{nf} }}{{\rho_{nf} }}g\left( {T - T_{\infty } } \right), \hfill \\ \end{gathered} $$
(2)
$$ \begin{gathered} u\frac{\partial v}{{\partial r}} + w\frac{\partial v}{{\partial z}} + \frac{uv}{r} = \upsilon_{nf} \left( {1 + \frac{1}{\lambda }} \right)\left( {\frac{{\partial^{2} v}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial v}{{\partial r}} - \frac{v}{{r^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right) - \frac{{\upsilon_{nf} }}{{k^{*} }}v - Fv^{2} \hfill \\ - \frac{{\sigma_{nf} }}{{\rho_{nf} }}\beta_{0}^{2} v + \frac{{\left( {\rho \beta } \right)_{nf} }}{{\rho_{nf} }}g\left( {T - T_{\infty } } \right), \hfill \\ \end{gathered} $$
(3)
$$ u\frac{\partial w}{{\partial r}} + w\frac{\partial w}{{\partial z}} + \frac{1}{{\rho_{nf} }}\frac{\partial p}{{\partial z}} = \upsilon_{nf} \left( {1 + \frac{1}{\lambda }} \right)\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{{\partial r}} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right), $$
(4)
$$ \begin{gathered} u\frac{\partial T}{{\partial r}} + w\frac{\partial T}{{\partial z}} = \left( {\alpha_{nf} + \frac{{16\sigma^{0} T_{\infty }^{3} }}{{3k_{nf} \left( {\rho c_{p} } \right)_{nf} }}} \right)\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) \hfill \\ + \tau \left[ {D_{b} \left( {\frac{\partial T}{{\partial r}}\frac{\partial C}{{\partial r}} + \frac{\partial T}{{\partial z}}\frac{\partial C}{{\partial z}}} \right) + \frac{{D_{t} }}{{T_{\infty } }}\left( {\left( {\frac{\partial T}{{\partial r}}} \right)^{2} + \left( {\frac{\partial T}{{\partial z}}} \right)^{2} } \right)} \right], \hfill \\ \end{gathered} $$
(5)
$$ \begin{gathered} u\frac{\partial C}{{\partial r}} + w\frac{\partial C}{{\partial z}} = D_{b} \left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{{\partial r}} + \frac{{\partial^{2} C}}{{\partial z^{2} }}} \right) + \frac{{D_{t} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) \hfill \\ - k_{r}^{2} \left( {C - C_{\infty } } \right)\left( {\frac{T}{{T_{\infty } }}} \right)^{n} exp\left( { - \frac{{E_{a} }}{kT}} \right), \hfill \\ \end{gathered} $$
(6)
$$ u\frac{\partial n}{{\partial r}} + w\frac{\partial n}{{\partial z}} + \frac{{b^{*} W_{c} }}{{\left( {C_{w} - C_{\infty } } \right)}}\left( {\frac{\partial }{\partial z}\left( {n\frac{\partial n}{{\partial z}}} \right)} \right) = D_{m} \frac{{\partial^{2} n}}{{\partial z^{2} }}, $$
(7)

While BCs are [20]:

$$ \begin{gathered} u = L_{1} \frac{\partial u}{{\partial z}},v = r\Omega + L_{1} \frac{\partial v}{{\partial z}},w = 0,T = T_{w} + L_{2} T_{z} ,C = C_{w} + L_{3} \frac{\partial C}{{\partial z}},n = n_{w} \, + L_{4} \frac{\partial n}{{\partial z}}\,\,\,\,at\,\,z = 0, \hfill \\ \,\,\,\,\,\,\,u \to 0,v \to 0,T \to T_{\infty } ,C \to C_{\infty } ,n \to n_{\infty } \,\,at\,\,z \to \infty . \hfill \\ \end{gathered} $$
(8)

The variables for problem [20]

$$ \begin{gathered} u = r\Omega f^{\prime}\left( \xi \right),w = - \left( {2\Omega \upsilon } \right)^{\frac{1}{2}} f^{\prime}\left( \xi \right),v = r\Omega g\left( \xi \right), \hfill \\ \theta \left( \xi \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}\phi \left( \xi \right) = \frac{{C - C_{\infty } \,}}{{C_{w} - C_{\infty } }},h\left( \xi \right) = \frac{{n - n_{\infty } \,}}{{n_{w} - n_{\infty } }},\xi = \sqrt {\frac{2\Omega }{\upsilon }} . \hfill \\ \end{gathered} $$
(9)

Using Eq. (9) and Eqs. (1–8) take the form

$$ 2\left( {1 + \frac{1}{\lambda }} \right)f^{\prime\prime\prime} + 2\left( {1 + F_{1} } \right)ff^{\prime\prime} + g^{2} - f^{{\prime}{2}} - \left( {k_{1} + M} \right)f^{\prime} - \left( {\frac{{G_{r} }}{{Re_{r}^{2} }}} \right)\theta^{\prime} = 0, $$
(10)
$$ 2\left( {1 + \frac{1}{\lambda }} \right)g^{\prime\prime} + 2\left( {fg^{\prime} - f^{\prime}g} \right) - \left( {\frac{{G_{r} }}{{Re_{r}^{2} }}} \right)\theta^{\prime} - \left( {k_{1} + M} \right)g - F_{1} g^{2} = 0, $$
(11)
$$ \frac{1}{Pr}\left( {1 + \frac{3}{4}R} \right)\theta^{\prime\prime} + N_{b} \theta^{\prime}\phi^{\prime} + N_{t} \theta^{{\prime}{2}} + f\theta^{\prime} = 0, $$
(12)
$$ \phi^{\prime\prime} + Scf\phi^{\prime} + \frac{{N_{t} }}{{N_{b} }}\theta^{\prime\prime} - Sc\sigma_{1} \left( {1 + \delta \theta } \right)^{n} \phi \exp \left( { - \frac{E}{{\left( {1 + \delta \theta } \right)}}} \right) = 0, $$
(13)
$$ h^{\prime\prime} + 2\Pr L_{b} fh^{\prime} - 2P_{e} \left( {h^{\prime}\phi^{\prime} + \left( {h + \Omega_{1} } \right)\phi^{\prime\prime}} \right) = 0, $$
(14)

So Eq. (9) in Eq. (8) the modified boundary conditions are;

$$ \begin{gathered} f^{\prime} = \alpha f^{\prime\prime},f = 0,g = 1 + g^{\prime},\theta = 1 + \beta \theta^{\prime},\phi = 1 + \gamma \phi^{\prime},h = 1 + \varsigma h^{\prime}\,\,\,\,\,\,at\,\xi = 0, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f^{\prime} \to 0,g \to 0,\theta \to 0,\phi \to 0,h \to 0\,\,\,\,\,at\,\,\xi \to \infty . \hfill \\ \end{gathered} $$
(15)

The dimensionless quantities are [27, 28]:

$$ \begin{gathered} M = \frac{{\sigma \beta_{0}^{2} }}{{\Omega \rho_{f} }},\Pr = \frac{\upsilon }{\alpha },\alpha = L_{1} \sqrt {\frac{2\Omega }{\upsilon }} ,\gamma = L_{3} \sqrt {\frac{2\Omega }{\upsilon }} ,\varsigma = L_{4} \sqrt {\frac{2\Omega }{\upsilon }} ,L_{b} = \frac{\alpha }{{D_{m} }} \hfill \\ \sigma_{1} = \frac{{k_{r}^{2} }}{\Omega },Sc = \frac{\upsilon }{{D_{b} }},N_{b} = \frac{{\tau D_{b} \left( {C_{w} - C_{\infty } } \right)}}{\upsilon },\,\delta = \,\,\frac{{\left( {T_{f} - T_{\infty } } \right)}}{{T_{\infty } }},P_{e} = \frac{{bW_{c} }}{{D_{m} }}\,\,\,\, \hfill \\ N_{t} = \frac{{\tau D_{t} \left( {T_{w} - T_{\infty } } \right)}}{{\upsilon T_{\infty } }},\,E = \frac{{E_{a} \,}}{{kT_{\infty } }},\beta = L_{2} \sqrt {\frac{2\Omega }{\upsilon }} ,R = \frac{{4\sigma^{0} T_{\infty }^{3} }}{{3k\left( {\rho c_{p} } \right)}} \hfill \\ F_{1} = Fr,k_{1} = \frac{\upsilon }{{k^{*} \Omega }},G_{r} = \frac{{g\beta \left( {T_{w} - T_{\infty } } \right)r^{3} }}{{\upsilon^{2} }},Re_{r} = r\left( {\frac{r\Omega }{\upsilon }} \right) \hfill \\ \end{gathered} $$
(16)

Above the symbols \(\Pr ,\sigma_{1} ,M,F_{1} ,G_{r} ,\,L_{b} ,{\text{Re}}_{r} ,\beta ,P_{e} ,\alpha ,\,\varsigma ,\,N_{b} ,\gamma ,Sc,R,E,N_{t} ,\,\,k_{1} and\,\delta ,\,.\,\,\) respectively denote Prandtl number, chemical reaction parameter, magnetic parameter, inertia coefficient, Grashof number, bioconvection Lewis number, Reynolds number (local), thermal slip factor, bioconvection Peclet number, velocity slip parameter, motile microorganism slip parameter, Brownian movement, concentration slip factor, Schmith number, radiation factor, nondimensional activation energy, thermophoretic factor, porosity parameter and for temperature difference.

3 Physical quantities of interest

The non-dimensional Nusselt number, Sherwood number, the local density number of motile microorganisms and the skin friction are defined as follows [19, 27]:

$$ C_{f} = \left. {\left( {1 + \frac{1}{\lambda }} \right)\frac{{\left( {\mu \frac{\partial u}{{\partial z}}} \right)}}{\mu \Omega }} \right|_{z = 0} ,C_{f} = \left. {\left( {1 + \frac{1}{\lambda }} \right)\frac{{\left( {\mu \frac{\partial v}{{\partial z}}} \right)}}{\mu \Omega }} \right|_{z = 0} , $$
(17)
$$ Nu = \frac{{q_{w} }}{{\left( {T_{w} - T_{\infty } } \right)}},Sh = \frac{{q_{m} }}{{\left( {C_{w} - C_{\infty } } \right)}},Nn = \frac{{q_{n} }}{{\left( {n_{w} - n_{\infty } } \right)}} $$
(18)

Here

$$ \,q_{m} = - r\left( {\frac{\partial C}{{\partial z}}} \right)_{z = 0} ,\,\,\,q_{w} = - r\left( {\frac{\partial T}{{\partial z}}} \right)_{z = 0} \,\,\,,\,\,\,q_{n} = - r\left( {\frac{\partial n}{{\partial z}}} \right)_{z = 0} ,\,\,\, $$
(19)

Using Eq. (8), we obtains

$$ \begin{gathered} {\text{Re}}_{r}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} C_{f} = \left( {1 + \frac{1}{\lambda }} \right)f^{\prime\prime}\left( 0 \right),{\text{Re}}_{r}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} C_{g} = \left( {1 + \frac{1}{\lambda }} \right)g^{\prime}\left( 0 \right),{\text{Re}}_{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}} Nu = - \theta^{\prime}\left( 0 \right), \hfill \\ {\text{Re}}_{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}} Sh = - \phi^{\prime}\left( 0 \right),{\text{Re}}_{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}} Nn = - h^{\prime}\left( 0 \right) \hfill \\ \end{gathered} $$
(20)

4 Solution by HAM

The problem is solved through the HAM technique by utilizing the boundary conditions (15) the solutions of equations. HAM scheme in mathematica software is prescribed to solve the system of equations that form the flow. The initial assumptions are designated as follows

$$ L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}^{iv} ,L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}^{\prime\prime},{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} {(}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } {) = }\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }^{\prime\prime}{\text{,L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} {(}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } {) = }\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }^{\prime\prime} \, ,{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }} {(}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} {) = }\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h^{\prime\prime}} , $$
(21)

Linear operators \(L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} ,{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} \,and\,{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }}\) are indicated as

$$ \begin{aligned} & L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} (e_{1} + e_{2} \xi + e_{3} \xi^{2} + e_{4} \xi^{3} ) = 0,\;{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} (e_{5} + e_{6} \xi ) = 0,\;{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} (e_{7} + e_{8} \xi ) = 0, \\ & {\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} (e_{9} + e_{10} \xi ) = 0 \, ,\;{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }} (e_{11} + e_{12} \xi ) = 0 \\ \end{aligned} $$
(22)

The non-linear operators are reasonably nominated as \({\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} ,{\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} ,\,{\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} ,{\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} \, and\,{\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }} \, \,\) and classify in the system:

$$ \begin{gathered} \, {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )} \right] = 2\left( {1 + \frac{1}{\lambda }} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{\xi \xi \xi \xi } + 2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{\xi \xi \xi } - 2\left( {1 + F_{1} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{\xi } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{\xi \xi } + 2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{\xi } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{\xi }^{2} \hfill \\ - \left( {k_{1} + M} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{\xi \xi } - \left( {\frac{{G_{r} }}{{Re_{r}^{2} }}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{\xi } \hfill \\ \end{gathered} $$
(23)
$$ \begin{gathered} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )} \right] = 2\left( {1 + \frac{1}{\lambda }} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{\xi \xi } - 2\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{\xi } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{\xi } } \right) - \left( {k_{1} + M} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} \hfill \\ - \left( {\frac{{G_{r} }}{{Re_{r}^{2} }}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{\xi } - F_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}^{2} \hfill \\ \end{gathered} $$
(24)
$$ {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta )} \right] = \frac{1}{\Pr }\left( {1 + \frac{3}{4}R} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{\xi \xi } + N_{b} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\xi } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{\xi } + N_{t} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{\xi }^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{\xi } $$
(25)
$$ {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )} \right] = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\xi \xi } + Sc\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\xi } + \frac{{N_{t} }}{{N_{b} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{\xi \xi } - \frac{1}{2}Sc\sigma_{1} \left( {1 + \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } } \right)\phi \exp \left( { - \frac{E}{{\left( {1 + \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } } \right)}}} \right) $$
(26)
$$ {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta )} \right] = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{\xi \xi } + 2\Pr L_{b} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{\xi } - 2P_{e} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{\xi } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\xi } + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} + \Omega_{1} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\xi \xi } } \right) $$
(27)

So Eqs. (10–14) the 0th-order system is written as

$$ (1 - \zeta )L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{0} (\xi )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )} \right] $$
(28)
$$ (1 - \zeta )L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{0} (\xi )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \, \left[ {f(\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )} \right] $$
(29)
$$ (1 - \zeta ) \, L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{0} (\xi )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ,\zeta )} \right] $$
(30)
$$ (1 - \zeta ) \, L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{0} (\xi )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )} \right] $$
(31)
$$ (1 - \zeta ) \, L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{0} (\xi )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta )} \right] $$
(32)

where BCs are:

$$ \begin{gathered} \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta )} \right|_{\xi = 0} = 0, \, \left. {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta )}}{\partial \xi }} \right|_{\xi = 0} = \alpha \left. {\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta )}}{{\partial \xi^{2} }}} \right|_{\xi = 0} ,\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta )} \right|_{\xi = 0} = 1 + \left. {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta )}}{\partial \xi }} \right|_{\xi = 0} \hfill \\ \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )} \right|_{\xi = 0} = 1 + \beta \left. {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )}}{\partial \xi }} \right|_{\xi = 0} ,\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta )} \right|_{\xi = 0} = 1 + \beta \left. {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta )}}{\partial \xi }} \right|_{\xi = 0} ,\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ;\zeta )} \right|_{\xi = 0} = 1 + \varsigma \left. {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ;\zeta )}}{\partial \xi }} \right|_{\xi = 0} \hfill \\ \left. {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta )}}{\partial \xi }} \right|_{\xi = \infty } = 0,\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta )} \right|_{\xi = \infty } = 0\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta )} \right|_{\xi = \infty } = 0,\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )} \right|_{\xi = \infty } = 0,\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta )} \right|_{\xi = \infty } = 0,\,\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ;\zeta )} \right|_{\xi = \infty } = 0 \hfill \\ \end{gathered} $$
(33)

While the implanting constraint is \(\zeta \in [0,1]\), to regulate for the convergence \(\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }}\), \(\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }}\) and \(\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }}\) are utilized. When \(\zeta = 0{\text{ and }}\zeta = 1\) we have:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ){ ,}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ) $$
(34)

Enlarge the \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\eta ;\zeta ) \, ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta )\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\eta ;\zeta )\) over Taylor’s series for \(\zeta = 0\)

$$ \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{0} (\xi ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{n} (\xi )\zeta^{n} } \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{0} (\xi ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{n} (\xi )\zeta^{n} } \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{0} (\xi ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{n} (\xi )\zeta^{n} } \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{0} (\xi ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{n} (\xi )\zeta^{n} } \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{0} (\xi ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{n} (\xi )\zeta^{n} } \hfill \\ \end{gathered} $$
(35)
$$ \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{n} (\xi ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\xi ;\zeta )}}{\partial \xi }} \right|_{p = 0} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{n} (\xi ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta )}}{\partial \xi }} \right|_{p = 0} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{n} (\xi ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\xi ;\zeta )}}{\partial \xi }} \right|_{p = 0} , \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{n} (\xi ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\xi ;\zeta )}}{\partial \xi }} \right|_{p = 0} {,}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{n} (\xi ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} (\xi ;\zeta )}}{\partial \xi }} \right|_{p = 0} \, {. } \hfill \\ \end{gathered} $$
(36)

where as B Cs are:

$$ \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \left( 0 \right) = \gamma ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f^{\prime}} \left( 0 \right) = \alpha \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f^{\prime\prime}} \left( 0 \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} \left( 0 \right) = 1 + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g^{\prime}} , \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } \left( 0 \right) = 1 + \beta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta^{\prime}} \left( 0 \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } \left( 0 \right) = 1 + \gamma \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi^{\prime}} \,\left( 0 \right)\,,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} \left( 0 \right) = 1 + \varsigma \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h^{\prime}} \,\left( 0 \right)\,\, \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f^{\prime}} \left( \infty \right) = 0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \left( \infty \right) = 0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} \left( \infty \right) = 0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } \left( \infty \right) = 0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } \left( \infty \right) = 0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} \left( \infty \right) = 0 \hfill \\ \end{gathered} $$
(37)

Now

$$ \begin{gathered} \Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }} \left( \xi \right) = 2\left( {1 + \frac{1}{\lambda }} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{n - 1}^{iv} - 2\left( {1 + F_{1} } \right)\sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}^{\prime}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f^{\prime\prime}}_{j} } + 2\sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f^{\prime\prime\prime}}_{j} } + 2\sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}^{\prime}_{j} } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f^{\prime}}_{n - 1}^{2} \hfill \\ - \left( {\frac{{G_{r} }}{{Re_{r}^{2} }}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta^{\prime}}_{n - 1} - \left( {k_{1} + M} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f^{\prime\prime}}_{n - 1} , \hfill \\ \end{gathered} $$
(38)
$$ \Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( \xi \right) = 2\left( {1 + \frac{1}{\lambda }} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g^{\prime\prime}}_{n - 1} - 2\left( {\sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}^{\prime}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{j} } - \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}^{\prime}_{j} } } \right) $$
(39)
$$ \Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }} (\xi ) = \frac{1}{\Pr }\left( {1 + \frac{3}{4}R} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{n - 1}^{\prime \prime } + N_{b} R_{0} \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{w - 1 - j}^{\prime } } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{j}^{\prime } + N_{t} \theta_{n - 1}^{\prime 2} + \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{w - 1 - j}^{\prime } } \hat{f}_{j} $$
(40)
$$ \Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} \left( \xi \right) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }^{\prime\prime}_{n - 1} - Sc\sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }^{\prime}_{j} } + \frac{{N_{t} }}{{N_{b} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta^{\prime\prime}}_{n - 1} - \frac{1}{2}Sc\sigma \left( {\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{n - 1} + 1} \right)^{n} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{n - 1} \exp \left( { - \frac{E}{{\left( {\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }_{n - 1} + 1} \right)}}} \right) $$
(41)
$$ \Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }} \left( \xi \right) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h^{\prime\prime}}_{n - 1} + 2\Pr L_{b} \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}^{\prime}_{j} } - 2P_{e} \left( {\sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}^{\prime}_{j} } + \sum\limits_{j = 0}^{w - 1} {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h}_{w - 1 - j} + \Omega_{1} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi^{\prime\prime}}_{j} } } \right) $$
(42)
$$ {\text{While}}\;\chi_{n} = \left\{ \begin{gathered} 0,{\text{ if }}n \le {1} \hfill \\ 1,{\text{ if }}n > {1}{\text{.}} \hfill \\ \end{gathered} \right. $$
(43)

5 Results and discussions

We now discuss the outcomes of the present investigation from the relevant sketched graphical parameters on velocity, temperature, concentration and motile microorganism profiles.

5.1 Velocity profile

The influence of various factors upon axial \(f^{\prime}\left( \eta \right)\) and tangential velocity \(g\left( \eta \right)\) have shown in Figs. (2, 3, 4 and 5). Figure 2 delineates the variety of the outspread segments of velocity profiles for various Grash of numbers \(Gr\) because of the pivoting plate. This shows that velocity profiles expand with the growth of \(Gr\) both radiative nanofluids, trailed by overshoots close to the outside of the circle. Higher \(Gr\) records for the bigger varieties of the relative outspread speed parts contrasted with the littler \(Gr\) case. Figure 3 depicts the variety of the tangential components of velocity profiles \(g\left( \xi \right)\) for nanofluid past a pivoting plate. It is seen that \(g\left( \xi \right)\) increases because of the expansion of \(Gr\) for nanofluid. Be that as it may, noteworthy relative tangential velocity parts show up as we move from the outside of the plate towards the surrounding liquid. Figure 4 displays the distinguishing structures of \(f^{\prime}\left( \xi \right)\) for nanofluid for various Reynolds numbers \({\text{Re}}_{r}\) because of the turning plate. Clearly \(f^{\prime}\left( \xi \right)\) is a diminishing role of \({\text{Re}}_{r}\). Additionally,\(f^{\prime}\left( \xi \right)\) profiles decay monotonically because of increments in \({\text{Re}}_{r}\) for nanofluid. The comparative velocity of \(f^{\prime}\left( \xi \right)\) nanofluids shows a significant decrease with the increment of \({\text{Re}}_{r}\), because of the pivoting plate. Figure 5 represents the conduct of \(g\left( \xi \right)\) for for various Reynolds numbers \({\text{Re}}_{r}\) because of the extending of the turning plate. This situation \(g\left( \xi \right)\) is expanding the capacity of \({\text{Re}}_{r}\) the two kinds of nanofluid. Different values of \({\text{Re}}_{r}\) create dissimilar layers of profiles of \(g\left( \xi \right)\). Enlarged \({\text{Re}}_{r}\) improves \(g\left( \xi \right)\) profiles for nanofluid. Intensification is greater for bigger \({\text{Re}}_{r}\) for nanofluid. Somewhat larger comparative velocity of \(g\left( \xi \right)\) is attained for higher \({\text{Re}}_{r} .\)

Fig. 2
figure 2

Influence of \(G_{r}\) on \(f^{\prime}(\xi )\)

Full size image
Fig. 3
figure 3

Effect of \(G_{r}\) on \(g(\xi )\)

Full size image
Fig. 4
figure 4

Impact of \({\text{Re}}_{r}\) on \(f^{\prime}(\xi )\)

Full size image
Fig. 5
figure 5

Impact of \({\text{Re}}_{r}\) on \(g(\xi )\)

Full size image

5.2 Temperature profile \(\theta \left( \eta \right)\)

The Prandtl number \(\Pr\) impact on the temperature field is depicted in Fig. 6. A noteworthy decrease in liquid temperature happens with a higher estimation of the Prandtl number. Truly, the Prandtl number has a converse connection with warm diffusivity. Along these lines, the liquid having a higher Prandtl number gradually diffuses when contrasted with a liquid having lower estimations of Prandtl number. This contention brings about a decrease in the liquid temperature inside the nanofluid stream. Figure 7 describes the influence of thermophoresis constraint \(N_{t}\) on \(\theta \left( \xi \right)\). In the thermophoresis procedure, the warmed liquid particles advanced toward a moderately cool medium, and accordingly, temperature distribution increments. The Brownian movement factor \(N_{b}\) extends its effect on the temperature \(\theta \left( \xi \right)\) in Fig. 8. Brownian movement is the centeral goal of the current framework. Nanoparticles and nanofluids network affirms the Brownian movement commitment on an ongoing premise. Brownian movement is the consequence of the irregular movement of the nanoparticles which causes to build the temperature.

Fig. 6
figure 6

Impact of \(\Pr\) on \(\theta (\xi )\)

Full size image
Fig. 7
figure 7

Effect of \(N_{t}\) on \(\theta (\xi )\)

Full size image
Fig. 8
figure 8

Effect of \(N_{b}\) on \(\theta (\xi )\)

Full size image

5.3 Concentration profile \(\varphi \left( \eta \right)\)

From Fig. 9, we saw that the greater Schmidt constraint \(Sc\) shows decay in concentration \(\phi (\xi )\). Schmidt factor is on the other hand comparative with Brownian diffusivity. Expanding Schmidt \(Sc\) yields a progressively delicate Brownian diffusivity. This increasingly delicate Brownian diffusivity improvements concentration lesser \(\phi (\xi )\). Figure 10 demonstrates that how \(N_{t}\) effects concentration distribution \(\phi (\xi )\). By illuminating the thermophoresis limit \(N_{t}\), the concentration \(\phi (\xi )\) and allied layer are extended. Figure 11 portrays the impact of Brownian development \(N_{b}\) on concentration \(\phi (\xi )\). It is clearly seen that an increasingly delicate \(\phi (\xi )\) is framed by expending progressed Brownian development factor \(N_{b}\). Figure 12 clarifies the outcome of non-dimensional stimulation vitality \(E\) on concentration \(\phi (\xi )\). An overhauling in initiation vitality \(E\) deteriorations formed Arrhenius effort \(\left( {\frac{T}{{T_{\infty } }}} \right)^{n} e^{{ - E_{a} /KT}}\). This develops the generative engineered reaction due to which concentration \(\phi (\xi )\) updates. Figure 13 presents an improvement in the chemical reaction \(\sigma_{1}\) indicates a decline in concentration \(\phi (\xi )\) and its allied layer.

Fig. 9
figure 9

Effect of \(Sc\) on \(\phi (\xi )\)

Full size image
Fig. 10
figure 10

Effect of \(N_{t}\) on \(\phi (\xi )\)

Full size image
Fig. 11
figure 11

Effect of \(N_{b}\) on \(\phi (\xi )\)

Full size image
Fig. 12
figure 12

Influence of \(E\) on \(\phi (\xi )\)

Full size image
Fig. 13
figure 13

Effect of \(\sigma_{1}\) on \(\phi (\xi )\)

Full size image

5.4 Motile micro-organism profile

The impact of bio convection Lewis number \(L_{b}\) on microorganism \(h\left( \xi \right)\) is inspected in Fig. 14. The tense product exhibits that the motility distribution reduces because of the effect of \(L_{b}\) because of lower dispersion of microorganisms. Usually, we can say that \(L_{b}\) assumes a more grounded job to decline the \(h\left( \xi \right)\) of nanoliquid. Figure 15 recommends the effect of Peclet number on motile \(h\left( \xi \right)\). The advanced estimations of \(P_{e}\) compare to motile dissemination because of which a diminishing microorganism \(h\left( \xi \right)\) is decided. Figure 16 displays the effect of the difference factor of microorganism concentration \(\Omega_{1}\) on the motile thickness of microbes. It has appeared in the figure that both the limit layer thickness of microbes and thickness decreases for expanding values of \(\Omega_{1}\).

Fig. 14
figure 14

Influence of \(L_{b}\) on \(h\left( \xi \right)\)

Full size image
Fig. 15
figure 15

Effect of \(P_{e}\) on \(h\left( \xi \right)\)

Full size image
Fig. 16
figure 16

Impact of \(\Omega_{1}\) on \(h\left( \xi \right)\)

Full size image

5.5 Table discussions

Table 1 described the impact of \(\lambda ,M, \, k_{1} , \, G_{r} ,Re_{r}\) axial \(f^{\prime}\left( \eta \right)\) and tangential velocity \(g\left( \eta \right)\). For increasing value \(G_{r}\) axial velocity \(f^{\prime}\left( \eta \right)\) and tangential velocity \(g\left( \eta \right)\) are rises, for increasing value of \(Re_{r}\) tangential components of velocity \(g\left( \eta \right)\) is rises and decreases both axial \(f^{\prime}\left( \eta \right)\) and tangential velocity \(g\left( \eta \right)\) for increasing values of \(\lambda ,M, \, k_{1}\), for increasing value of \(Re_{r}\) axial velocity \(f^{\prime}\left( \eta \right)\) is reduces. Table 2 describes the influence of \(\Pr ,N_{b} ,R\) on \(\theta \left( \eta \right)\). By increasing values of \(\Pr ,N_{b} , \, R\) temperature profile is rises for \(N_{b} , \, R\) and decreases for \(\Pr\). Table 3 shows the outcome of \(Sc,\sigma_{1} ,\delta ,E\) on \(\phi \left( \eta \right)\). For increasing estimations of \(E\) concentration profile is rises and decreases for \(\,Sc,\sigma_{1} ,\delta\).Table 4 describes the impact \(L_{b} , \, P_{e} , \, \Omega\) on motile density distribution. For increasing values of \(L_{b} , \, P_{e} , \, \Omega\) motile density distribution is decreases Tables 5, 6, 7, 8 examine the influence of \({\text{C}}_{f}\),\(Nu\) and \(Sh\) in the effect of disparate limits. The possessions of \(M, \, k_{1} , \, \lambda ,G_{r} ,Re_{r}\) on skin friction for the unlike valuations are revealed in Table 5. It is thought that the increasing approximations of \(\lambda ,M, \, k_{1} ,Re_{r}\) upsurges the \({\text{C}}_{f}\), while \({\text{C}}_{f}\) is decreases function of \(G_{r}\). It is perceived that the increasing approximations of \(\lambda ,M, \, k_{1}\) expansions the \({\text{C}}_{g}\), while \({\text{C}}_{g}\) is decreases function of \(G_{r} ,Re_{r}\).The impacts of \(\Pr ,N_{b} ,R\) on \({\rm N}u\) is portrayed in Table 6. It is noticed that \({\rm N}u\) rises due to an increase in \(\Pr\), while increasing values of \(N_{b} ,R\) cause a decline in \({\rm N}u_{x}\). Table 7 shows that increasing values of \(Sc,\sigma_{1} ,\delta ,\) Sherwood number is upsurges and declines for increasing in \(E\).Table 8 shows that increasing values of \( \, P_{e} , \, \Omega ,L_{b}\) the local density number \(\left( {Nn_{x} } \right)\) is increases.

Table 1 Impact of various physical parameters over velocity profiles \(f(\xi ),\,\,f^{\prime}(\xi )\) and \(g(\xi )\) when \(F_{1} = 0.3,\, \in_{3} = 0.5,\Pr = 2,R = 0.5,N_{b} = 0.1,Nt = 0.1,Sc = 0.6,\alpha = 1,\beta = 1,\gamma = 1,\sigma_{1} = 1,\delta = 0.5,E_{1} = 0.4\)
Full size table
Table 2 Impact of various physical parameters over Temperature profile \(\theta (\xi )\) when \(\begin{gathered} \lambda = 0.2,F_{1} = 0.3,k_{1} = 0.4,M = 2.5,{\text{Re}}_{r} = 3, \in_{3} = 0.5,N_{b} = 0.2,N_{t} = 0.1,Sc = 0.6, \hfill \\ \alpha = 1,\beta = 1,\gamma = 1,\sigma_{1} = 1,\delta = 0.5,E_{1} = 0.4 \hfill \\ \end{gathered}\)
Full size table
Table 3 Impact of various physical parameters over concentration profile \(\phi (\xi )\) When \(\begin{aligned} & \lambda = 0.2,F_{1} = 0.3,k_{1} = 0.4,M = 1.5,{\text{Re}}_{r} = 3, \in_{3} = 0.5,\Pr = 0.7, \\ & R = 0.6,G_{r} = 2,N_{b} = 1,N_{t} = 0.1,\alpha = 1,\beta = 1,\gamma = 1; \\ \end{aligned}\)
Full size table
Table 4 Impact of various physical parameters over Skin fraction \({\text{Re}}_{r}^{1/2} C_{f} = f^{\prime \prime } (0)\) and \({\text{Re}}_{r}^{1/2} C_{g} = g^{\prime}(0)\) when \(F_{1} = 0.3,\, \in_{3} = 0.5,\Pr = 1,R = 0.5,N_{b} = 0.2,N_{t} = 0.1,Sc = 0.6,\alpha = 1,\beta = 1,\gamma = 1,\sigma_{1} = 1,\delta = 0.5,E_{1} = 0.4\)
Full size table
Table 5 Impact of various physical parameters over movement profile \(\xi (\eta )\) of the living micro-organism
Full size table
Table 6 Impact of various physical parameters over Nusselt Number \({\text{Re}}_{r}^{ - 1/2} Nu = - \frac{1}{Pr}\left( {1 + \frac{3}{4}R} \right)\theta^{\prime}(0)\) when \(\begin{aligned} & \lambda = 0.2,F_{1} = 0.3,k_{1} = 0.4,M = 2.5,{\text{Re}}_{r} = 3, \in 3 = 0.5,N_{b} = 1,N_{t} = 0.1,Sc = 0.6, \\ & \alpha = 1,\beta = 1,\gamma = 1,\sigma_{1} = 1,\delta = 0.5,E = 0.4 \\ \end{aligned}\)
Full size table
Table 7 Impact of various physical parameters over Sherwood number \({\text{Re}}_{r}^{ - 1/2} Sh = - \phi^{\prime}(0)\) When \(\begin{gathered} \lambda = 0.2,F_{1} = 0.3,k_{1} = 0.4,M = 2.5,{\text{Re}}_{r} = 3, \in 3 = 0.5,\Pr = 2, \hfill \\ R = 0.6,G_{r} = 0.9,N_{b} = 1,N_{t} = 0.1,\alpha = 1,\beta = 1,\gamma = 1; \hfill \\ \end{gathered}\)
Full size table
Table 8 Impact of various physical parameters over motile \(Nn_{x} {\text{Re}}_{x}^{ - 1/2} = - \xi^{\prime}(0)\) of the micro-organism
Full size table

6 Conclusions

The Darcy-Forchheimer and bioconvection Casson nanofluid flow over a turning disk is analyzed. The Arrhenius Activation Energy and thermal Radiation terminologies are also included in the modeled problem. The governing equations are altered to the ordinary differential equations (ODEs) and the solution is obtained through the analytical technique HAM. The main outcomes of the present work are pointed out as. Increments in inertia coefficient \(F_{1}\) and \(k_{1}\) produce a decrease in \(f^{\prime}\left( \xi \right)\) and \(g\left( \xi \right)\) for the Casson nanofluid. Temperature profile enhancing with larger values of the parameters \(N_{t}\) and \(N_{b} .\) Outcome shows that greater Magnetic field constraint displays a diminishing pattern for both \(f^{\prime}\left( \xi \right)\) and \(g\left( \xi \right).\) Both \(f^{\prime}\left( \xi \right)\) and \(g\left( \xi \right)\) decline with the larger magnitude of \({\text{Re}}_{r}\). Similarly, Concentration \(\phi \left( \xi \right)\) delineates diminishing conduct for bigger \(\delta\) and \(\sigma_{1}\). Concentrations \(\phi \left( \xi \right)\) are a diminishing element of higher values of \(Sc\). Concentration \(\phi \left( \xi \right)\) shows the inverse behavior for \(N_{b}\) and \(N_{t}\). The motility profile diminishes because of the implication of \(L_{b}\). Velocities \(f^{\prime}\left( \xi \right)\) and \(g\left( \xi \right)\) are increasing function of \(G_{r}\). The advanced estimations of \(P_{e}\) declining motile microorganism profile \(h\left( \xi \right)\).

6.1 Future directions

The current study can be extended using the variable viscosity and variable thermal conductivity. The extension of the present work is also possible through viscous dissipation, Joules heating’s, Hall current, Electric field, Marangoni convection, slip conditions, and so on.