1 Introduction

Time dependent displacements of structures founded in clayey soils due to their porous consolidation can have a serious effect on their structural performance. Terzaghi [56] was the first to investigate the consolidation problem in 1D field with elastic parameters. Subsequently, a number of papers have been published dealing with the 1D linear consolidation [2, 19, 28, 48] and nonlinear consolidation taking into account the alteration of permeability over time [17, 33, 60]. In order to have a more realistic approach to the porous consolidation of heterogeneous clays, 2D consolidation problems were studied by Huang et al. [22] . Various types of monotonic or cyclic loadings have been investigated with analytical solutions Kim et al. [29]. Numerical simulations have been also proposed leading to a variety of computational tools for estimating foundation settlements and pore pressures.

The stochastic finite element method is an important approach for the investigation of the consolidation of saturated porous media due to the uncertainties involved in the input parameters. Several investigations have studied the influence of the input variability, such as the Young modulus and the permeability on the actual displacements, the degree of consolidation and the stress distribution in the soil domain. Kim et al. [29], Huang et al. [22], Bong and Stuedlein [9], Ronold [46] and Houmadi et al. [21]. In the stochastic finite element method there are two ways of describing the spatial distribution of the input stochastic variables [5, 8, 12, 20, 24, 35, 37,38,39, 42, 49]. In the first approach the nodal points are considered as random variables and deterministic shape functions are used for providing the material spatial distribution [27, 39]. Subsequently, the spectral representation or the Karhunen Loeve expansion, has been applied for providing a random field of the variable under consideration. Ali et al.[3], Papadrakakis and Papadopoulos [42]. Then, for both methods, the standard Monte Carlo simulation can be implemented. Other methods to estimate variability are also used for porous consolidation problems, such as the subset simulation Houmadi et al. [21].

All studies performed so far refer to 1D or 2D problems, while the material stress-state law in most cases is considered linear elastic. Furthermore, the analytical solutions proposed are limited to specific loading and geometric conditions. In the present article a numerical simulation approach is proposed in order to provide accurate and reliable quantitative results. The implementation of the material yield model proposed by Kavvadas and Amorosi [25] is adopted, which is considered an accurate and reliable material model for clays Vrakas [57]. This material model implemented in connection with the finite element simulation method can be used in any type of 3D loading and geometric condition. The computational cost required by the Monte Carlo simulation method, which is particularly excessive for large models, can be addressed with efficient computational methods as proposed in Stavroulakis et al. [51, 52]. The goal of the present paper is to quantify the uncertainty of the output displacement in relation to the variability of the input parameters i.e., the spatial distribution of the material variables and the soil depth. The stochastic input variables to the porous consolidation problems are the compressibility factor \(\kappa \), the permeability k and the critical state line inclination c of the soil. Three spatial distributions of the material variables with respect to the depth Z of the soil domain are considered: The constant and linear variation, as well as the Karhunen Loeve random field with an exponential autocorrelation function. In the first two spatial distributions, the truncated normal random variable is considered at the nodal points. Different geometrical dimensions of the 3D soil domain and correlation lengths are considered and compared with respect to the corresponding solid problem without considering the pore pressure. The qualitative and quantitative results obtained in the present work agree with the published work in the field [5, 9, 21, 22, 29, 34, 37, 46]

2 Formulation of the dynamic soil-pore-fluid interaction

2.1 Consolidation problem of saturated soil

The problem of consolidation of clays in saturated soils is the Biot problem [1, 16, 31, 36, 47, 53, 62,63,64] which is described by the following set of equations

$$\sigma^{\prime}_{ij}= \sigma _{ij}+ \delta _{ij}p \quad {\mathrm{d}}\sigma^{\prime}=Dd\epsilon _{\mathrm{elastic}} $$
(1a)
$${\mathbf {S}}^{\mathrm{T}} {\varvec{\sigma}}-\rho {\mathbf {\mathord {\ddot{u}}}}-\rho _{f}({\mathbf {\mathord {\dot{w}}}}+{\mathbf {w}}\bigtriangledown ^{\mathrm{T}} {\mathbf {w}})+\rho {\mathbf {b}}={\mathbf {0}} $$
(1b)
$$\begin{aligned}&-\bigtriangledown p - {\mathbf {R}}-\rho _{f}{\mathbf {\mathord {\ddot{u}}}}-\rho _{f}(\mathbf {\mathord {\dot{w}}}+{\mathbf {w}}\bigtriangledown ^{\mathrm{T}} {\mathbf {w}})/n+\rho _{f}{\mathbf {b}}={\mathbf {0}} \end{aligned}$$
(1c)
$$\begin{aligned}&\mathbf {kR}=\mathbf {w} \end{aligned}$$
(1d)
$$\begin{aligned}&\bigtriangledown ^{\mathrm{T}} \mathbf {w}+ \alpha \mathbf {m\dot{\epsilon }}+ \frac{\dot{p}}{Q}+\frac{n\dot{\rho _{\mathrm{f}}}}{\rho _f}+\dot{s}=0 \end{aligned}$$
(1e)
$$\begin{aligned}&B=B_u U B_t \quad \mathbf {u}=\mathbf {u_0 }\quad in \quad B_u, \quad \mathbf {t=n}{\varvec{\sigma}}=\mathbf {t_0} \quad in \quad B_t \end{aligned}$$
(1f)
$$\begin{aligned}&B=B_p U B_w \quad p=p_0 \quad in \quad B_p, \quad \mathbf {w=n^{\mathrm{T}}}{\varvec{w}}=w_n \quad in \quad B_w \end{aligned}$$
(1g)

where \(\delta _{ij}\) is the Kronecker Delta which takes value of 1 for \(i=j\) and 0 otherwise, \(\sigma _{ij}\) and \(\sigma ^{'}_{ij}\) are the total and effective stresses, respectively, p the pore pressure of water and D is the tangent consistent matrix. \(\mathbf {S}\) is the deformation matrix such as \(\mathbf {d\epsilon }=\mathbf {S}*\mathbf {du}\) and \(\mathbf {b}\) is the external forces vector in means of measure of force per unit volume. \(u_i\) and \(w_i\) are the displacement of solid matrix and the average velocity of the water relative to the soil component, respectively. \(\rho _{\mathrm{f}} \) and \(\rho _{\mathrm{s}} \) are the density of the fluid and solid, respectively, and n is the porosity while, \(\rho =n\rho _{\mathrm{f}} +(1-n)\rho _{\mathrm{s}} \) is the total density of the mixture. \(\mathbf {R}\) are the viscous drag forces, while \(\mathbf {k}\) denotes the permeability in matrix representation ([length]\(^3\) [time]/[mass]). Each component k of \(\mathbf {k}\) is not the same as the hydraulic conductivity \(k_1\) that has units of velocity. They are related with equation \(k=k_1 /(\rho _{\mathrm{fg}}) \) where g is the gravitational acceleration. Also \(\frac{1}{Q} = \frac{n}{K_{\mathrm{f}}} + \frac{\alpha -n}{K_{\mathrm{s}}}\) where \(\alpha = 1- \frac{K_{\mathrm{T}}}{K_{\mathrm{s}}} \) and \(K_{\mathrm{f}}\) \(K_{\mathrm{s}}\) and \( K_{\mathrm{T}} \) are the bulk modulus of fluid, soil and average bulk modulus of the solid skeleton, respectively. \(B_{x}\) is the part of the boundary B that the variable x is a known function of time. The dot notation stands for differentiation over time, while the space differentiation is described with the assistance of Nabla symbol.

In the case of low frequency excitations or static loading conditions, the full Biot problem can be simplified considerably leading to a drastic reduction of the computational effort. Eqs. 1b and 1e can be written, respectively

$$\begin{aligned}&\mathbf {S}^{\mathrm{T}}{\varvec{\sigma}}-\rho \mathbf {\mathord {\ddot{u}}}+\rho \mathbf {b}=\mathbf {0} \end{aligned}$$
(2a)
$$\begin{aligned}&\bigtriangledown ^{\mathrm{T}} \mathbf {k}(-\bigtriangledown p-\rho _{f}\mathbf {\mathord {\ddot{u}}}+\rho _{f}\mathbf {b})+ \alpha \mathbf {m\dot{\epsilon }}+ \frac{\dot{p}}{Q}+\dot{s}=0 \end{aligned}$$
(2b)

Eqs. (1a, 1f, 1g, 2a, 2b) correspond to the \(u-p\) formulation of the Biot simulation of consolidation, in which the dynamic terms are omitted in low frequency phenomena or in static problems. In porous consolidation problems, water is assumed as incompressible. This assumption holds since the bulk modulus of soils is small compared to the bulk modulus of water. The validity of the \(u-p\) formulation depends on the relation of the excitation period to the natural period, taking into account the permeability of the soil. In the present work, the \(u-p\) formulation is implemented since static loading is applied to the clay soil domain.

2.2 Numerical solution of the problem.

The finite element discretization of the \(u-p\) formulation takes the form:

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {x}}+\mathbf {C}\dot{\mathbf {x}}+\mathbf {K}\mathbf {x}=\mathbf {F} \end{aligned}$$
(3)

where

$$\begin{aligned} \mathbf {M}= & {} \begin{bmatrix} \mathbf {M_1} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {0} \end{bmatrix} \mathbf {C}=\begin{bmatrix} \mathbf {C_1} &{} \mathbf {0} \\ \mathbf {Q^{\mathrm{T}}_c} &{} \mathbf {S} \end{bmatrix}\nonumber \\ \mathbf {K}= & {} \begin{bmatrix} \mathbf {K_1} &{} \mathbf {-Q_c} \\ \mathbf {0} &{} \mathbf {H} \end{bmatrix} \mathbf {F}=\begin{bmatrix} \mathbf {F_1} \\ \mathbf {0} \end{bmatrix} \mathbf {x}=\begin{bmatrix} \mathbf {u} \\ \mathbf {p} \end{bmatrix} \end{aligned}$$
(4)
$$\begin{aligned} \mathbf {Q_c}= & {} \int _{V} \mathbf {B}^{\mathrm{T}} \mathbf {m} \mathbf {N^p} {\mathrm{d}}v \quad \mathbf {H}=\int _{V} (\bigtriangledown \mathbf {N^p})^{\mathrm{T}} \mathbf {k} \bigtriangledown \mathbf {N^p} {\mathrm{d}}v \quad \nonumber \\ \mathbf {S}= & {} \int _{\mathbf {V}} \mathbf {N}^\mathbf {p} \frac{1}{Q}\mathbf { N^p } {\mathrm{d}}v \quad \end{aligned}$$
(5)
$$\begin{aligned} \mathbf {F_1}= & {} \int _{V} (\mathbf {N^p})^{\mathrm{T}} \bigtriangledown ^{\mathrm{T}} (\mathbf{k} \mathbf{b} ) {\mathrm{d}}v \end{aligned}$$
(6)

\(\mathbf {N^p}\) is the shape functions of pore pressure in matrix representation. \(\mathbf {M_1 , C_1 , K_1} \) are the standard mass, damping and stiffness matrices of the solid skeleton. Furthermore, \(\mathbf {Q_c , H, S} \) are the coupling, permeability and saturation matrices, respectively. Finally, \(\mathbf {F_1}\) corresponds to the equivalent forces due to the external loading. Numerical schemes, such as the Newmark direct integration method, are implemented to obtain the solution to the problem.

3 The yield stress model

3.1 Definition of plastic and bond strength envelope

The material model is based on the theory of incremental plasticity and the critical state concepts, where all stresses involved correspond to the effective stresses of the solid skeleton. The presented model is a modified Cam Clay type model with two characteristic surfaces: The plastic yield envelope (PYE) in which the stress points are in elasticity and the bond strength envelope (BSE) [10, 11, 23, 25, 26, 57, 61]. It holds that PYE is always inside BSE and the magnitude of the bond envelope is directly associated with the structure of the microtiles of the clay. If a stress point lies in BSE, the structure degradation rate of the clay is maximum. Both envelopes have ellipsoidal shape as depicted in Fig. 1. The mathematical representation of BSE is given by

$$\begin{aligned} F(p_{\mathrm{h}},\mathbf{s} ,a)=\frac{1}{c^2} \mathbf {s}:\mathbf {s}+(p_{\mathrm{h}}-a)^2-a^2=0 \end{aligned}$$
(7)

where \(p_{\mathrm{h}}\) is the hydrostatic component of the stress tensor, s is the deviatoric component of the stress tensor, c is the critical state line inclination and a is the half-size of the large diameter of the ellipse

Furthermore, PYE is described by the function

$$\begin{aligned}&f(p_{\mathrm{h}},\mathbf{s} ,p_{\mathrm{L}},\mathbf {s_L},a)\nonumber \\&\quad =\frac{1}{c^2} (\mathbf {s-s_L}):(\mathbf {s-s_L})+(p_{\mathrm{h}}-p_{\mathrm{L}})^2-(\xi a)^2=0 \end{aligned}$$
(8)

where \(p_{\mathrm{L}}\) is the hydrostatic component of the centroid of PYE , \(\mathbf {s_L}\) is the deviatoric component of the centroid of PYE and \(\xi \) is the similarity factor

Fig. 1
figure 1

Graphical representation of the constitutive model

Full size image

Finally, inside PYE the isotropic poroelasticity theory applies, where the bulk and shear moduli have constant ratio, with the assumption of constant Poisson ratio. The bulk modulus is given by:

$$\begin{aligned} K_{\mathrm{bulk}}=\frac{\nu p_{\mathrm{h}}}{\kappa } \end{aligned}$$
(9)

where \(\nu \) is the specific volume of the soil

3.2 Isotropic and kinematic hardening

Hardening, softening and plastic behavior can be simulated by this constitutive model.

Dafalias and Popov [15], Zienkiewicz and Shiomi [62], Dafalias [14], Kavvadas and Amorosi [25] and Kalos [23]. The hardening phenomenon consists of the isotropic hardening of the half-axis a of BSE and the kinematic hardening of the variation of the critical state line inclination and the translation of the centroid L of PYE.

The isotropic hardening rule illustrates the evolution of BSE and PYE in relation to the load history and the plastic strains. The variable a is given by the generalized expression:

$$\begin{aligned}&a = a^*[(B_0 -B_{\mathrm{res}} + \zeta ^p_v |\epsilon ^p| + \zeta ^p_q |\epsilon ^p_q|)\nonumber \\&\quad (\exp (-(\eta ^p_v |\epsilon ^p| + \eta ^p_q |\epsilon ^p_q|)))+B_{\mathrm{res}}] \end{aligned}$$
(10)

where \(B_0\) and \(B_{\mathrm{res}}\) are the initial and final values of the ratio \(B=\frac{a}{a^*}\) and \(a^*\) is the halfsize of the intrinsic strength envelope (ISE). This is the smallest possible BSE for a certain reference clay point. Furthermore, \(\epsilon ^p\) and \(\epsilon ^p_q\) are the total volumetric and deviatoric plastic strains and are expressed as follows:

$$\begin{aligned} \epsilon ^p_v=\epsilon ^p_{xx}+\epsilon ^p_{yy}+\epsilon ^p_{zz} \quad \dot{\epsilon }^p_q=\sqrt{\frac{2}{3}\dot{\mathbf {e^p}}:\dot{\mathbf {e^p}}} \end{aligned}$$
(11)

where \(\mathbf {e^p}\) is the deviatoric plastic strain tensor, while \(\eta ^p_v\) \(\eta ^p_q\) \(\zeta ^p_q\) \(\zeta ^p_v\) are constitutive calibration parameters. \(\zeta ^p_q\) and \(\zeta ^p_v\) are responsible for the smoother transition from \(B_0\) to \(B_{\mathrm{res}}\) [23, 25, 55]. \(\eta ^p_v\) and \(\eta ^p_q\) are governing the degradation of bonding attributed to the volumetric and deviatoric plastic strain component, respectively. For the computation of half-size a, the half-size \(a^*\) of the ISE needs to be calculated. The exponential relation is applied

$$\begin{aligned} a^*=\frac{1}{2}\exp \left( \frac{N_{{\mathrm{iso}}^*} -\nu - \kappa \ln p_h}{\lambda -\kappa }\right) \end{aligned}$$
(12)

Kavvadas and Amorosi [25], Kavvadas and Belokas [26] and Kalos [23], where \(N_{{\mathrm{iso}}^*}\) is the specific volume of the soil for \(p_{\mathrm{h}}=1\) KPa.

The kinematic hardening of the proposed criterion consists of two components. The critical state line inclination alteration and the translation of the secondary anisotropy tensor \({\varvec{\sigma_L}}\). The critical state line inclination is an exponential function of the deviatoric plastic deformation. Furthermore for \({\varvec{\sigma _L}}\), two distinct loading cases need to be considered. The BSE and the position of PYE evolve due to plastic straining and tend to the conjugate point. Consequently, in order to describe the kinematic hardening associated with \({\varvec{\sigma _L}}\) it is essential to define the conjugate point M’ on the BSE curve, depicted in Fig. 2 and is given by

Fig. 2
figure 2

Definition of the conjugate point \(M'\)

Full size image
$$\begin{aligned} {\varvec{\sigma _ {M'}}} =a {\varvec{I}}+\frac{1}{\xi } ({\varvec{\sigma}}-{\varvec{\sigma _L}}) \end{aligned}$$
(13)

where I is the identity Tensor.

The two cases portrayed in Fig. 2 for the evolution of \({\varvec{\sigma}}_L\): (a) The stress state lays simultaneously on BSE and PYE, the conjugate point coincides with the absolute stress point M”. Therefore, \({\varvec{\sigma}}_L\) is computed directly in closed form.

$$\begin{aligned}{\varvec{\sigma}}_L=(1-\xi ){\varvec{\sigma}}+\xi a {\varvec{I}} \end{aligned}$$
(14)

(b) the stress state lays on PYE but inside BSE, the evolution of the plastic yield envelope center \({\varvec{\sigma}}_L\) depends on the isotropic hardening parameter a and the evolution of the stress state toward the conjugate point, which is governed by Eq. (13). The following equation is implemented

$$\begin{aligned} d{\varvec{\sigma}}_L=\frac{da}{a} {\varvec{\sigma}}_L + {\varvec{\beta}} d\mu \end{aligned}$$
(15)

where \({\varvec{\beta}}\) = MM’ and the scalar variable d\(\mu \) is given by

$$\begin{aligned} d\mu =\frac{\frac{1}{c^2}({\varvec{s}}-{\varvec{s_{\mathrm{L}}}}) : \left( {\mathrm{d}}\varvec{s}-\frac{{\mathrm{d}}a}{a} \varvec{s})+(p_{\mathrm{h}}-p_{\mathrm{L}}\right) \left( {\mathrm{d}}p_{\mathrm{h}}-\frac{{\mathrm{d}}a}{a}p_{\mathrm{h}}\right) }{\xi a^2-\left[ \frac{1}{c^2}\left( \varvec{s}-\varvec{s}_{\mathrm{L}}\right) : \varvec{s}+(p_{\mathrm{h}}-p_{\mathrm{L}})(p_{\mathrm{h}}-a)\right] } \end{aligned}$$
(16)

3.3 Plastic hardening modulus

For the case (a) of the stress state, the calculation of plastic hardening modulus H is obtained by the closed form expressions

$$\begin{aligned} H & = 2 \xi p_{\mathrm{h}} h_0, \,\, h_{0}=h_{1}+h_{2}+h_{3} \end{aligned}$$
(17a)
$$\begin{aligned} h_{1}= & {} \frac{\nu }{\lambda -\kappa } a^* P_{\mathrm{hydr}} ({\mathrm{Part\,Exponent}}+B_{\mathrm{res}}) \end{aligned}$$
(17b)
$$\begin{aligned} h_{2}= & {} a^* (\zeta ^p_v|P_{\mathrm{hydr}}|+ \zeta ^p_q \sqrt{\frac{2}{3} ( P_{\mathrm{dev}}:P_{\mathrm{dev}})}) {\mathrm{Exponent}} \end{aligned}$$
(17c)
$$\begin{aligned} h_{3} & = -a^* ({\mathrm{Part Exponent}}) (\eta ^p_v |P_{\mathrm{hydr}}|+ \eta ^p_q \sqrt{\frac{2}{3} ( P_{\mathrm{dev}}:P_{\mathrm{dev}})}) \end{aligned}$$
(17d)

and

$$\begin{aligned} Part\,=\,& B_0 -B_{\mathrm{res}} + \zeta ^p_v |\epsilon ^p| + \zeta ^p_q |\epsilon ^p_q| \quad ,\nonumber \\&\quad {\mathrm{Exponent}}=\exp \left( -(\eta ^p_v |\epsilon ^p| + \eta ^p_q |\epsilon ^p_q|)\right) \quad \end{aligned}$$
(17e)
$$\begin{aligned} P_{\mathrm{Hydr}}= & {} \frac{\partial f}{\partial p} \quad , \quad P_{\mathrm{Dev}}=\frac{\partial f}{\partial \varvec{s}} \end{aligned}$$
(17f)

For the case (b) an ellipsoidal law of computing H in relation to the plastic hardening modulus of the conjugate point \(M'\) is adopted. This law takes into consideration the relative position of the stress state \(\varvec{\sigma }\) with the conjugate point \(\varvec{\sigma _{M'}}\) and the stress state at the onset of yielding \(\varvec{\sigma _0}\). H is given by

$$\begin{aligned} H=H_{M'}+ \left( \frac{\partial f}{\partial \varvec{\sigma }}:\varvec{C_e}: \frac{\partial f}{\partial \varvec{\sigma }}\right) \lambda ^* \left( \frac{{\mathrm{Nominator 1}}}{{\mathrm{Denominator 1}}}\right) ^\gamma \end{aligned}$$
(18a)

where \(\lambda ^*\) and \(\gamma \) comprise constitutive calibration parameters and

$$\begin{aligned}&{\mathrm{Nominator 1}}=\frac{1}{c^2}(\varvec{s_{M'}}-\varvec{s}) : (\varvec{s_{M'}}-\varvec{s})+(p_{M'}-p)^2 \end{aligned}$$
(18b)
$$\begin{aligned}&{\mathrm{Denominator 1}}=\frac{1}{c^2}(\varvec{s_{0}}-\varvec{s}) : (\varvec{s_{0}}-\varvec{s})+(p_{0}-p)^2 \end{aligned}$$
(18c)

The constitutive model is valid for clays, for static and dynamic loads, regardless of the overconsolidation ratio. Clays of friction angle between \(17^{\circ }\) and \(30^{\circ }\) can be simulated with accuracy. This range of friction angles corresponds to the majority of the natural clayey soils. Furthermore, it is proved to be numerically stable because the majority of the equations of the criterion are in a closed form.

4 Random fields and the truncated normal variables

4.1 The Karhunen Loeve series

A random field can be constructed either considering the nodal point values as random variables with deterministic shape functions, or by using stochastic random fields computed by Karhunen Loeve expansion [24], Liu et al. [58], Li and Kiureghian [32], Pryse and Adhikari [44], Peng et al. [43], Calamak and Yanmaz [13], Yue et al.  [59] and Papadopoulos and Giovanis [41]. In this work, in order to compare each approach influence in the output variability, both approaches are considered for the material variables in discussion. For the first method, which is analyzed plainly in Liu et al. [58] the random function f is approximated with the usage of shape functions \(N_i\) by

$$\begin{aligned} f(x)=\sum _{i=1}^{N_0} N_i(x)f_i \end{aligned}$$
(19)

where \(N_0\) is the total number of shape functions and the \(f_i\) are the values of f in the nodal points which can be random variables following a probability density function (PDF). In the present work, \(N_i\) are linear functions and the \(f_i\) follows the truncated normal distribution which is analyzed in Sect. 4.3.

For the Karhunen–Loeve implementation, let \(H_1(\mathbf{x} , \omega )\) be a zero-mean random field based on a known autocovariance function \(C_h(\mathbf {x_1},\mathbf {x_2})=\sigma (\mathbf {x_1}) \sigma (\mathbf {x_2}) \rho (\mathbf {x_1},\mathbf {x_2})\), where \(\rho (\mathbf {x_1},\mathbf {x_2})\) is the correlation function and \(\sigma (\mathbf {x_1})\) is the standard deviation of \(\mathbf {x_1}\). There is an orthogonal basis of eigenvalues \(\lambda _i\) and eigenfunctions \(\phi _i\) such that

$$\begin{aligned} C_h(\mathbf {x_1},\mathbf {x_2})=\sum _{i=1}^{\infty } \lambda _i \phi _i(\mathbf {x_1}) \phi _i(\mathbf {x_2}) \end{aligned}$$
(20)

This basis is the solution of the integro-differential Fredholm problem which is stated as

$$\begin{aligned} \int _{\varOmega } C_h(\mathbf {x_1},\mathbf {x_2}) \phi _i(\mathbf {x_2}) \mathbf {dx_2} =\lambda _i \phi _i(\mathbf {x_1}) \quad ,\quad \int _{\varOmega } \phi _i(\mathbf {x_1}) \phi _j(\mathbf {x_1}) \mathbf {dx_1}=\delta _{ij} \end{aligned}$$
(21)

where \(\delta _{ij}\) is the Kronecker Delta function. Therefore any realization \(H_1\) of the field can be expanded as:

$$\begin{aligned} H_1(\mathbf {x},\omega )=\mu (\mathbf {x})+\sum _{i=1}^{\infty } \sqrt{\lambda _i} \phi _i(\mathbf {x}) \xi _i(\omega ) \end{aligned}$$
(22)

where \(\xi _i \) is a set of random variables of zero mean and covariance function \( E(\xi _i ,\xi _j)=\delta _{ij} \). Finally, for a Gaussian random field, as implemented in the present study, the \(\xi _i\) functions are a set of standard normal random variables.

4.2 An analytical Karhunen Loeve expansion

An analytical solution of the Fredholm problem is presented below along with the K–L expansion Karhunen [24], Pryse and Adhikari [44]. Let the autocovariance function \(C_h\) be denoted as

$$\begin{aligned} C_h(x_1,x_2)=\sigma _d^2 e^{\frac{x_1-x_2}{b}} \end{aligned}$$
(23)

where b is the correlation length. Assuming a symmetrical space [\(-\alpha \),\(\alpha \)] for \(x_1\) and \(x_2\), the Fredholm integral of Eq. (21) becomes

$$\begin{aligned} \int _{-\alpha }^{\alpha } \sigma _d^2 e^{\frac{x_1-x_2}{b}} \phi _i(x_2) {\mathrm{d}}x_2 =\lambda _i \phi _i(x_1) \end{aligned}$$
(24)

In Eq. (24) there is an analytical solution.

For \(i=\) odd

$$\begin{aligned}&\lambda _i =\frac{2 \sigma _d^2 b}{1+(\omega _i b)^2},\quad \phi _i(x)=\alpha _i \cos (\omega _i x) \quad ,\nonumber \\&\alpha _i=\left( \alpha +\frac{\sin (2\omega _i\alpha )}{2\omega _i}\right) ^{-0,5} \end{aligned}$$
(25)

where \(\omega _i\) is the solution of the equation

$$\begin{aligned} \frac{1}{b}-\omega _i \tan (\omega _i \alpha )=0 \end{aligned}$$
(26)

in the range \([(i-1) \frac{\pi }{\alpha },(i-0,5) \frac{\pi }{\alpha }]\)

For \(i=\) even

$$\begin{aligned} \lambda _i =\frac{2 \sigma _d^2 b}{1+(\omega _i b)^2} \quad ,\quad \phi _i(x)=\alpha _i\sin(\omega _i x) \quad ,\quad \alpha _i=\left( \alpha -\frac{\sin \left( 2\omega _i\alpha \right) }{2\omega _i}\right) ^{-0,5} \end{aligned}$$
(27)

where \(\omega _i\) is the solution of the equation

$$\begin{aligned} \frac{1}{b}\tan (\omega _i \alpha )+\omega _i=0 \end{aligned}$$
(28)

in the range \([(i-0,5)\frac{\pi }{\alpha },i\frac{\pi }{\alpha }]\)

If the space is not symmetrical, which is applied in most random field realizations, the Fredholm integral is solved over the symmetrical space \(\varOmega _s=[b_1-T,b_2-T]\) where \(\varOmega _s\) is the symmetrical equivalent space of \(\varOmega =[b_1,b_2]\) and \(T=\frac{b_1+b_2}{2} \).

For M number of eigenfunctions the random field is calculated as

$$\begin{aligned} H_1(\mathbf {x},\omega )=\mu (\mathbf {x})+\sum _{i=1}^{M} \sqrt{\lambda _i} \phi _i(\mathbf {x}-T) \xi _i(\omega ) \end{aligned}$$
(29)

This type of expansion is the most common because it is strong and robust. If the Fredholm equations cannot be solved analytically, and this occurs when the autocovariance function is more complicated, numerical methods can be applied such as the Galerkin method [20, 44].

4.3 The truncated normal distribution

Due to physical restrictions for the material variables, the samples in the present study are in a closed space. The ratio \(\frac{\kappa _{z=\max }}{\kappa _{z=0}}\), which is considered as random in the present study, is in the space [0, 1]. Furthermore, the critical state line inclination should be in a closed space in order to be in the limits of validity for clays, as stated in the last paragraph of Sect. 3. In addition the experimental results fit to a Gaussian PDF of each material variable [4, 6]. Therefore, the truncated normal distribution is adopted.

Let X be a random variable normally distributed with mean \(\mu \) and standard deviation \({\sigma _d}\), defined into the space of [\(-\infty \),\(\infty \)], and let Y be equal to X in the subspace [a,b] and 0 elsewhere. The total area of the probability density function equals to 1, then for the PDF of Y it holds

$$\begin{aligned} g_1(x)=A_1 \frac{1}{\sqrt{2\pi }{\sigma _d}} {\mathrm{exp}}^{\frac{-(x-\mu )^2}{2{{\sigma _d}}^2}} I_{A\le x \le B} \end{aligned}$$
(30)

where \(A_1\) is constant and \(g_1\) is the PDF of Y. Also, \(I_{A\le x \le B}\) is the indicator function for the subspace [a, b]. Then \(g_1\) is calculated [7, 45] as

$$\begin{aligned} g_1(x)=\frac{\phi (X_0)}{{\sigma _d} (\varPhi (B)-\varPhi (A))} \end{aligned}$$
(31)

where \(\phi (X_0)\) and \(\varPhi (X_0)\) are the standard normal probability and cumulative distribution function for \(X_0\), respectively, and \(A=\frac{\alpha -\mu }{\sigma _d}\) and \(B=\frac{\beta -\mu }{\sigma _d}\) with \(X_0=\frac{x-\mu }{{\sigma _d}}\) . The cumulative distribution of \(g_1(x)\) is

$$\begin{aligned} G(x)=\frac{\varPhi (X_0)-\varPhi (A)}{\varPhi (B)-\varPhi (A)} \end{aligned}$$
(32)

The mean and standard deviation of Y denoted \(M_y\) and \({\sigma }_{y}\) are given by

$$\begin{aligned}&M_y=\mu +{\sigma _d} \frac{\phi (A)-\phi (B)}{\varPhi (B)-\varPhi (A)} \end{aligned}$$
(33)
$$\begin{aligned}&{\sigma }_{y}={\sigma _d} \sqrt{(1+\frac{A \phi (A)-B \phi (B)}{\varPhi (B)-\varPhi (A)}-(\frac{\phi (A)-\phi (B)}{\varPhi (B)-\varPhi (A)})^2)} \end{aligned}$$
(34)

The material random variables expressed by the PDF of Eq. (31) and the random fields realizations that occur from Eq. (29) influence the finite element system of Eqs. (3). The corresponding matrices \(\mathbf {C}\), \(\mathbf {K}\), and \(\mathbf {F}\) are changing due to the randomness of the compressibility factor \(\kappa \), the critical state line inclination c and the permeability k.

5 Numerical tests on stochastic consolidation with random linear and nonlinear material properties

5.1 Description of the problem

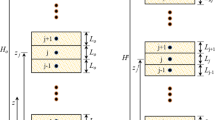
The presented approach is applied to porous problems, which are governed by the set of Eq. (3). The geometry of the problem is depicted in Fig. 3. A uniform vertical load \(q=150\) kPa is applied which leads to significant plastic deformations in nearly the whole soil domain. Three different depths are considered \(h=20, 40, 50\) m. The discretization of the soil domain is performed with 8 node hexahedral finite elements with linear shape functions for u and p, which is considered an adequate discretization for obtaining the requested results [40, 54]. The length in X and Y directions of the domain is taken 4 times the depth, in order to secure the full transfer of the load in the center of the field. The initial stresses due to geostatic loading are assumed as \(\sigma _v=\gamma z\), \(\sigma _x=\sigma _y=0.85 \sigma _v\) corresponding to stress point L of Fig. 1. The duration of the simulation in all cases is 0.5 d in order to have quasi-static conditions. The other deterministic properties of the soil defined in Sect. 3 are given in Table  1.

Here \(\nu _0\) stands for the initial specific volume of the soil. It should be noted that in all cases \(\lambda \) and \(\kappa \) are proportional. The boundary conditions are as follows: \(\mathbf {u}_{x}(z=h)=\mathbf {u}_{y}(z=h)=\mathbf {u}_{z}(z=h)=\mathbf {0}\) and the rest boundary surfaces are free of constraints. The stochastic material variables are the compressibility factor \(\kappa \), the critical state line inclination c and the permeability k.

Table 1 Deterministic parameters of the soil domain
Full size table
Fig. 3
figure 3

Graphical representation for the linear spatial distribution of the compressibility factor

Full size image
Fig. 4
figure 4

Geometry of the problem (\(h=20, 40, 50\) m)

Full size image

For the compressibility factor \(\kappa \), a linear and a constant spatial distribution along the depth of the soil domain is assumed. For the linear distribution of the compressibility factor denoted as \(\kappa _{L}\), \(\kappa _{z=0}=0.008686\) and the ratio \(R=\frac{\kappa _{z=\max }}{\kappa _{z=0}}\) follows the truncated normal distribution with PDF as described in Eq. (31). The mean value of the ratio is \(\mu _{R}=0.469\) and \(\sigma _{R}=0.25 \mu _{R}\), leading to \(\kappa _{z={\mathrm{max, mean}}}=0.004074\), which is chosen such as the mean compressibility of the soil to account for a shear velocity of 200 \(\frac{m}{s}\) and can be depicted in Fig. 3. Here it should be noted that since the bulk and shear moduli are assumed proportional, as a consequence of constant Poisson ratio, \(\kappa \) is directly related with the shear velocity. For the case of constant distribution of \(\kappa \) along the depth, denoted as \(\kappa _{{C}}\), the mean value of \(\kappa \) is \(\kappa _{\mu }=0.004074\) and the standard deviation is \(\kappa _{\sigma }=0.25 \kappa _{\mu }\).

In the case of a constant spatial distribution of the critical state inclination c along the depth, two possible numerical values for c are considered. In the first case, denoted as \(c_{R}\), the friction angle \(\phi \) follows the truncated normal distribution PDF of Eq. (31). The mean value is \(\mu _{\phi }=23^{\circ }\) and the standard deviation is \(\sigma _{\phi }=2^{\circ }\). These values are chosen in order for the friction angle \(\phi \) to be within an acceptable range for clays [25, 26]. Consequently, the samples of \(\phi \) are generated and c is calculated from \(c=\sqrt{\frac{2}{3}} \frac{6\sin (\phi )}{3-\sin (\phi )}\). In the second case, denoted as \(c_{D}\), the critical state line inclination has a deterministic value of c=0.7336 for friction angle \(\mu _{\phi }=23^{\circ }\).

Table 2 Non porous (solid) analyses performed
Full size table
Table 3 Porous analyses performed
Full size table

Two types of analyses are considered. The solid analyses, where the pore pressure of the soil domain is neglected and the porous analyses, where the water flow is calculated. The solid analyses performed, indicated with (\(\mathbf {S}\)) are given in Table 2, combining linear (L) or constant (C) distribution for \(\kappa \) and deterministic (D) or random variable (R) cases for c. The porous analyses performed are depicted in Table 3, combining linear (L), constant (C), and random field (RF) distribution for \(\kappa \), deterministic (D), random variable case (R) and random field (RF) distribution for c and random field distribution (RF) for k.

In the random field distributions the mean values are: \(\kappa _{\mathrm{mean}}\,=\,0.008686\), \(c_{\mathrm{mean}}\) = 0.7336 and \(k_{\mathrm{mean}}\,=\,10^{-8} \frac{{\mathrm{m}}^3\,{\mathrm{s}}}{{\mathrm{Mgr}}}\) [1, 47, 53, 64]. The standard deviations are: \(\sigma _{\kappa }\,=\,0.25\kappa _{\mathrm{mean}}\), \(\sigma _{\phi }=2^{\circ }\) and \(\sigma _k=0.25 k_{\mathrm{mean}}\). The autocorrelation function in all fields is taken according to Eq. 23, with correlation lengths \(b=75\) (\(k_{{\mathrm{RF}}{75}}\)) and \(b=100\) (\(k_{{\mathrm{RF}}{100}}\)). The linear (L) and constant (C) spatial distributions for \(\kappa \) as well as the random variable (R) distributions for all material variables refer to a random variable case analysis. Also, for c has been considered a constant deterministic analysis. The random field (RF) distributions correspond to the Karhunen Loeve series and are described by the set of Eqs. (20–22). This set combined with the autocovariance function, described in Eq. 23, becomes the set of Eqs. (25–29) which provide realizations of the random field.

All the analyses are static, while the number of eigenfunctions considered is eight. Each Monte Carlo simulation was applied for 500 samples, which were found sufficient in achieving convergence for the mean value and standard deviation of the monitored displacements.

5.2 Presentation of the results

The results are depicted in Tables 4, 5, 6 and 7 and in Figs. 5, 6, 7 and 8. In these tables the mean values of output displacements in the middle of the soil domain, depicted by point A in Fig. 4 are presented together with the standard deviation, the coefficient of variation (CoV), the maximum and minimum value of the Monte Carlo simulation.

Table 4 Monte Carlo results for the output displacement (m) for non-porous medium
Full size table
Fig. 5
figure 5

PDFs of displacements of solid analyses

Full size image

When the pore pressure is ignored, larger mean displacements and smaller CoV are obtained when \(\kappa _{L}\) is assumed compared to \(\kappa _{{C}}\), as can be observed from columns \(\mathbf {S}\)-\(\kappa _{L}\)-\(c_{D}\) , \(\mathbf {S}\)-\(\kappa _{{C}}\)-\(c_{D}\) of Table 4 for both depths considered. In the numerical tests performed, the largest possible CoV of the output is similar to the corresponding variation of the input, as can be seen in Table 4, columns \(\mathbf {S}\)-\(\kappa _{{C}}\)-\(c_{D}\). The mean value of the output displacement for the case \(\mathbf {S}\)-\(\kappa _{L}\)-\(c_{D}\) compared to the mean value in the \(\mathbf {S}\)-\(\kappa _{{C}}\)-\(c_{D}\) analysis of \(h=50\) m is about 76 \(\%\) greater, while the CoV of the output was found to be 5 times smaller. Similar conclusions can be drawn for the corresponding analyses of depth 20 m. Consequently, the critical spatial distribution of \(\kappa \) for the CoV of the output is the \(\kappa _{{C}}\) case and for the mean displacements is the \(\kappa _{L}\) distribution. The PDF’s of solid analyses are depicted in Fig. 5a, b. Between the \(\kappa _{L}\) and \(\kappa _{{C}}\) assumptions for \(\kappa \), the \(\kappa _{L}\) case gives greater mean displacements with less variability. This difference can be explained by the fact that in the \(\kappa _{L}\) case the upper layers of the soil, which are the most compressible, have low CoV of \(\kappa \) leading to low CoV for both displacements and strains.

Table 5 Monte Carlo results for the output displacements (m) for porous analyses with linear and constant distribution for \(\kappa \)
Full size table
Fig. 6
figure 6

PDFs of displacements of porous analyses \(\mathbf {P-}\) \(\kappa _{L}\)-\(c_{D}\)-\(k_{{RF}{{75-100}}}\), \(\mathbf {P-}\) \(\kappa _{{C}}\)-\(c_{D}\)-\(k_{{RF}{{75-100}}}\)

Full size image

The CoV of the monitored displacements in porous analyses was found to be affected by the change in the considered depth, unlike the solid problems, as can be seen in Tables 4 and 5. Also, for the same depth and analysis, in porous medium, smaller variability of the output is obtained compared to the non-porous medium. The largest output CoV in the case of porous problems was found 36 \(\%\) lower than the CoV of the input for the case of \(h=20\) m, and 46 \(\%\) lower than the variability of the input for \(h=50\) m, as opposed to zero variability reduction for the corresponding solid analyses. In the \(\mathbf {P-}\) \(\kappa _{L}\)-\(c_{D}\)-\(k_{{RF}}\) analyses, the output CoV is negligible in all depths. Thus, when considering the pore pressure in the soil domain, a reduction of the variability of the displacements occurs in all cases examined. This is in accordance with the results obtained in Huang et al. [22] This result is attributed to the fact that the bulk modulus, as described by Eq. 9 in porous problems, is smaller than the respective solid case. As a consequence, since the applied load is the same, lower values for deformations and displacements are expected and also lower variability. This observation is also depicted in Fig. 6a, b for the PDFs of \(\mathbf {P-}\) \(\kappa _{L}\)-\(c_{D}\)-\(k_{{\mathrm{RF}}{75-100}}\) and \(\mathbf {P-}\) \(\kappa _{{C}}\)-\(c_{D}\)-\(k_{{\mathrm{RF}}{75-100}}\) analyses.

Table 6 Monte Carlo results for the output displacements (m) for porous analyses with random field representation for all stochastic material variables
Full size table
Fig. 7
figure 7

PDFs of displacements of \(\mathbf {P-}\) \(\kappa _{{\mathrm{RF}}}\)-\(c_{{\mathrm{RF}}}\)-\(k_{{RF}}\) analyses

Full size image

The porous analysis with random field representations for all material variables is subsequently performed as a more general case, since it takes into consideration the spatial randomness of the material properties of the soil. In the case of porous random field analyses, the largest CoV of the output, was found 53 \(\%\) lower in relation to the input variability as can be seen in Table 6, \(\mathbf {P-}\) \(\kappa _{{\mathrm{RF}}}\)-\(c_{{\mathrm{RF}}}\)-\(k_{{\mathrm{RF}}{100}}\). In soil depth 50 m the monitored displacement variation is even smaller. The choice of the correlation length appears to have no significant effect on the PDF of the output displacement in all porous analyses. Furthermore, the comparison between the \(\mathbf {P-}\) \(\kappa _{{\mathrm{RF}}}\)-\(c_{{\mathrm{RF}}}\)-\(k_{{\mathrm{RF}}}\) analyses and the previous porous analyses indicate that the corresponding CoV of the monitored displacement is between the \(\mathbf {P-}\) \(\kappa _{L}\)-\(c_{D}\)-\(k_{{\mathrm{RF}}}\) and the \(\mathbf {P-}\) \(\kappa _{{C}}\)-\(c_{D}\)-\(k_{{\mathrm{RF}}}\) analyses, as it is shown in Tables 5 and 6. Consequently, the critical spatial distribution of \(\kappa \) is the assumption of constant variation over depth.

The mean value in porous analyses is greater in \(\mathbf {P-}\) \(\kappa _{{RF}}\)-\(c_{{\mathrm{RF}}}\)-\(k_{{\mathrm{RF}}}\) simulations, with maximum mean value 0.0214 m in \(\mathbf {P-}\) \(\kappa _{{\mathrm{RF}}}\)-\(c_{{\mathrm{RF}}}\)-\(k_{{\mathrm{RF}}{100}}\) analysis of depth 50 m (see Table 6). This mean value compared to the mean value for the \(\mathbf {P-}\) \(\kappa _{{C}}\)-\(c_{D}\)-\(k_{{\mathrm{RF}}{100}}\) is about 47 \(\%\) larger, while in the \(\mathbf {P-}\) \(\kappa _{L}\)-\(c_{D}\)-\(k_{{\mathrm{RF}}{100}}\) analysis is about 4 \(\%\) larger. Similar conclusions can be drawn with soil depth of 20 m. As a result, the critical spatial distribution of \(\kappa \) for maximizing the mean output displacement corresponds to the assumption of the random K–L field.

The PDFs of \(\mathbf {P-}\) \(\kappa _{{\mathrm{RF}}}\)-\(c_{{\mathrm{RF}}}\)-\(k_{{\mathrm{RF}}}\) analyses depicted in Fig. 7a, b confirm the small influence of the correlation length b on the variability of the output. Comparing the PDFs of Fig. 7a, b with the corresponding of the rest porous analyses, in which for different correlation lengths the output probability density functions are identically the same, it can be concluded that the K–L random field representation for \(\kappa \) influences to a lesser extent the PDF of the output.

These quantitative results, obtained from the aforementioned analyses, provide an insight into the effect of the randomness of each material parameter in porous consolidation problems. The poroelastic parameter \(\kappa \), influences the most both the mean value and the standard deviation of the displacement. This influence is more pronounced when the distribution of \(\kappa \) is considered constant along the depth of the domain in both solid and porous problems. This can be explained by the fact that the poroelastic variable \(\kappa \) is directly associated with the bulk modulus and therefore has a direct influence on the strains and displacements.

The porous variable of permeability k has a small effect to the monitored displacement. The numerical results indicate that the spatial variability of k does not affect the CoV of the output in all possible combinations for \(\kappa \) and c. This is because, for the same porous consolidation problem with the same depth, load and other deterministic parameters, the monitored output displacements are not influenced by the permeability since the pore pressures are fully dissipated.

Finally, the variability of critical state line inclination c of the material model appears to have a negligible effect on the probability density function of the output, regardless its spatial distribution and type of analysis. For this reason only the \(c_{D}\) case has been included in Tables 4, 5 and 6. This is explained by the fact that the deviatoric component of the stresses is sufficiently low due to the relatively small shear stresses in comparison to the normal stresses. As a consequence, there are negligible deviatoric strains and the volumetric strains, which are influenced by the bulk modulus, are not associated with c.

Fig. 8
figure 8

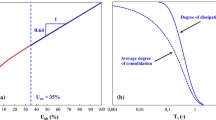
Histograms of output displacement in m and the normal distribution fitting for 3 randomly selected analyses. a Solid analysis of depth 20 m with linear distribution for \(\kappa \) and deterministic analysis for c referring to Fig. 4a continuous line. b Porous analysis of depth 20 m with constant distributions for \(\kappa \), deterministic analysis for c and random field representation for k referring to Fig. 5a dotted line. c Porous analysis of depth 20 m with random field representations for all stochastic material variables and \(b=75\) m referring to Fig. 6a continuous line

Full size image

For justifying the assumption that the output displacement follows the truncated normal distribution, the histograms of three Monte Carlo simulations for the output displacement with the normal distribution fitting are presented in Fig. 8. As can be seen graphically, the probability density functions estimated by the histograms can be approximated by the truncated normal PDF described in Eq. (31). The maximum and minimum values indicated in Tables 4, 5 and 6 are reliable values to set the subspace [a, b] of Eq. (31). Also, for providing a numerical justification of the aforementioned assumption, the Kolmogorov–Smirnov test is implemented [18, 30, 50]. In all output probability density functions, the null hypothesis \(H_0\), at the 5\(\%\) significance level is satisfied, as can be seen in Table 7, where for three randomly selected cases of Monte Carlo simulations performed are presented. In Table 7 the largest absolute difference from the data cumulative distribution function (CDF) and the theoretical CDF of the Monte Carlo simulations in Fig. 8 are presented and compared to the critical difference for accepting \(H_0\). Since the largest absolute difference in all three analyses is less than the critical value, the samples can be approximated by the truncated normal distribution. This comes in agreement with the previous research results [9, 22]

Table 7 Kolmogorov–Smirnov test results for the Monte Carlo simulations of Fig. 8
Full size table

Some additional observations regarding the results of the presented analyses are subsequently presented. The largest displacement of the simulations is 7.9 cm (see Table 4 column \(\mathbf {S-}\) \(\kappa _{L}\)-\(c_{D}\) depth 50 m) leading to an effective shear strain of \(1.5\,\times \,10^{-3}\), which is in the limit of validity for linear geometric analysis. The smallest displacement of the analyses is 0.55 cm and is found in columns \(\mathbf {P-}\) \(\kappa _{{C}}\)-\(c_{D}\)-\(k_{{\mathrm{RF}}{75-100}}\) of Table 5. This magnitude of displacement is capable in a typical structure-foundation system to change significantly the internal forces of the structure. Therefore for all analyses the soil-structure interaction phenomenon cannot be neglected. The largest ratio of maximum to mean value, which is common in all depths, is 1.82 and is found in solid problems in \(\mathbf {S-}\) \(\kappa _{{C}}\)-\(c_{D}\) (see Table 4). Consequently, a safety ratio of 2 is sufficient in static problems in order to predict the displacements in the most unfavorable situation and perform a soil-structure interaction analysis.

Furthermore, as the depth of the soil increases, all corresponding CoV values of the output decrease and the mean value increases. Specifically, in pure solid analyses, by increasing the depth by a factor of 2.5 the largest CoV is practically the same as the input variability of 0.25 and the largest mean value is 1.6 times greater. In porous analyses, by increasing the depth from 20 to 50 m the largest CoV is decreased by 20% and the largest mean displacement is practically the same. This can be explained by the fact that as the depth increases the soil domain is less stiff and therefore larger displacements are expected. Finally, the effect of randomness in the stress distribution was found to be negligible in all analyses and this applies to both normal and shear stresses of all three directions as the maximum CoV in Gauss points stresses is less than 0.01.

6 Conclusions

In the present work a stochastic analysis is presented for studying the consolidation phenomenon of clayey soils taking into consideration the pore pressure-soil interaction. The goal of the present paper is to present, not only qualitative insights, but reliable quantitative results on the prediction of the response for porous consolidation of 3D clay domains under uncertainty conditions on soil material properties. Also, the proposed model provides a more general numerical tool for investigating the uncertainty quantification of porous consolidation regardless of the geometry of the problem or other simplistic assumptions that are necessary for an analytical solution. In this context, a detailed finite element simulation, alongside with a sophisticated material constitutive model, is adopted.

The numerical results obtained indicate that the randomness of material poroelasticity plays the most important role in the output displacement, especially when it has a constant distribution along the depth of the soil domain. When a random Karhunen Loeve field is assumed for the material variables, greater mean displacements are obtained. The CoV of the output in porous problems was found to be less than the corresponding variability of the solid problems, indicating the smaller effect of k in the monitored displacements. The output variability reduction in relation to the respective variability of the input varies between 35 and 50 \(\%\).

The spatial variability of permeability expressed with the correlation length appears to have a minor influence on the monitored displacements. Furthermore, the randomness of a plasticity variable, such as the critical state line inclination, was found to have a negligible effect on the output displacement. In both solid and porous considerations, the truncated normal distribution was proved to be an adequate approximation for the probability density function of the output displacement estimated by the histograms. Thus, the Gaussian nature of the output value can be assumed to be preserved despite the material nonlinearity. As the depth of the domain increases, the CoV of the output decreases and the mean value increases in all corresponding analyses. The variability reduction of the output in porous analyses when the depth of the soil domain increases is about 20\(\%\). Consequently, the most critical layers for monitored displacement variability are in the vicinity of the surface.