Surfactant flooding is a well-known enhanced oil recovery (EOR) method that has been used worldwide for decades [1, 2]. In surfactant flooding, injected surfactants are supposed to participate in oil recovery processes, but loss of surfactants due to adsorption on the rocks in the reservoir can also lead to lower oil recoveries than expected. Because of this, one of the main challenges facing surfactant flooding is the adsorption of surfactant on the formation rock, something that can make the surfactant flooding process economically unfeasible [3, 4]. Low salinity water flooding is a quite new technique, implemented to adjust the salt content in sea water before injection to the reservoir. Therefore it has been considered by various research groups as one of the most inexpensive techniques of EOR [5, 6] and has been reported for both laboratory core floods and field tests [7,8,9,10]. The combination of low salinity water injection and surfactant flooding (LSW-SF) is considered to be an economically attractive EOR approach, as high oil recovery and low surfactant retention was reported in core flooding tests [11]. In recent years, there has been an increasing interest in conducting QCM measurements for increased oil recovery processes prior to performing more time consuming core flooding tests [12,13,14,15,16]. A major advantage of running QCM experiment is its relatively fast technique for screening significant experimental parameters such as surface properties and crude oil. Previously QCM has been successfully used to investigate the adsorption of surfactant and desorption of oil during simulated surfactant flooding and LSW-SF [12].

It is helpful to analyze the surfactant adsorption in terms of a theoretical model in order to find a molecular understanding of the parameters of such a model. This understanding can then be applied to match the adsorption behavior of different surfactant and to predict the surfactant adsorption in new systems. However, several efforts have been made to achieve a general model to explain the kinetics of adsorption on adsorbent surfaces for the liquid/solid system, and some models such as Langmuir [17], Freundlich [18], Temkin [19] and Henry’s Law [18] model have been developed and applied but so far the effect of oil properties and the surfactant\oil replacement process have not been considered separately and explained by them.

This paper details two methods that can be employed for the interpretation of frequency shifts in QCM experiments during surfactant flooding. The first method described an assumption that the surfactant adsorption is not sensitive to the oil type, and the surfactant adsorption is calculated by carrying out blank measurements wherein the crystals are exposed to the surfactant solution without prior adsorption of crude oil [12]. This paper introduces and describes a second method of analysis that can be used for the determination of the surfactant adsorption in surfactant flooding without running the blank tests. This analysis is more powerful, since it can be applied to different chemical EOR methods, such as surfactant flooding and low salinity water injection assisted with surfactant flooding, and also takes into account the effect of the characteristics of the crude oil.

In this study, the interfacial tension (IFT) gradient was considered as the driving force for surfactant\oil replacement and surfactant adsorption processes during surfactant flooding. Also, it is assumed that the adsorption of surfactants consists of two simultaneous processes, including surfactant replacement with oil and surfactant absolute adsorption to the underlying surface. To validate the analytical model, QCM tests were conducted using two well characterized sulfonate surfactants, sodium dodecylbenzene sulfonate (SDBS) and sodium dioctylsulfosuccinate (AOT) as anionic surfactants, and silica and aluminosilicate coated quartz crystals to simulate the surface of minerals in sandstone reservoirs.

1 Material and methods

The first method of analysis was previously explained by Nourani et al. [12], the second method is going to be introduced and explained in this paper.

1.1 Theory

Normally in surfactant flooding, higher adsorption of surfactant result in lower oil recovery [3]. But contrary to this, QCM results shows that the oil desorption can be higher when the surfactant adsorption is higher [12]. This observation may lead to the assumption that the surfactant adsorption consists of two simultaneous processes; surfactant replacement with oil and surfactant absolute adsorption (to the underlying surface). Surfactant absolute adsorption is associated with oil desorption in the surfactant replacement process, and is therefore favorable for EOR purpose whereas only surfactant adsorption takes place in the surfactant absolute adsorption process without any oil recovery.

To model these two simultaneous processes, we consider the total surfactant concentration, \({C}_{T}\), and a mix-wet crystal with an adsorbed oil layer as shown in Fig. 1a.

Fig. 1
figure 1

Schematic overview of the surfactant interaction with the adsorbed oil layer. a \({C}_{B}, {C}_{Ad}\) and \({C}_{s.}\) are the surfactant concentrations at the bulk, oil–water interface and on the crystal surface, respectively. Surfactant monomer approaching the adsorbed oil layer and \({C}_{Ad}\) increases, while \({C}_{B}\) decreases. b Replacement of oil by surfactant monomer. \({\mathrm{C}}_{\mathrm{S}}\) is zero. \({C}_{R}\) is the surfactant concentration adsorbed in the oil layer, and is approximately zero. The surfactant concentration difference between the “hole” and the interface is substantial and cause Marangoni flow into the “hole” to reduce this difference and form a channel toward the oil-solid interface. c Progression of oil replacement by surfactant over time. \({\mathrm{C}}_{\mathrm{R}}\) will increase from \({\mathrm{C}}_{\mathrm{B }}\) to \({\mathrm{C}}_{\mathrm{Ad}}\) since the \(\Delta C\) and \(\Delta {\gamma }_{r}\) will remain constant and equal to \({\mathrm{C}}_{\mathrm{Ad}}\) and \(\Delta {\upgamma }_{\mathrm{t}}\). d Maximum surfactant replacement reached in oil channel. Once the surfactant molecules reach the crystal surface, \({\mathrm{C}}_{\mathrm{R}}\) reaches the maximum value,\({\mathrm{C}}_{\mathrm{R}-\mathrm{Max}}\), and the oil replacement ends. e Direct surfactant adsorption on crystal surface when the surfactant monomers reach the surface. f Schematic overview of the maximum surfactant absolute adsorption. After the surfactant molecule reaches the crystal surface, the absolute adsorption process starts and \(\Delta {\upgamma }_{\mathrm{t}}\) distributes between absolute adsorption and replacement processes as demonstrated in Eq. (3)

Full size image

When surfactant is added to the oil-coated surface, some surfactant is adsorbed at the oil–water interface and interfacial tension is reduced. Due to adsorption the surfactant concentration at the oil–water interface,\({C}_{Ad},\) increases, while the bulk concentration (\({C}_{B}\)) decreases, and \({C}_{T}\) is the sum of \({C}_{B}\) and \({C}_{Ad}\).

Low interfacial tension causes that oil from the interface to be solubilized into micelles and detached from oil–water interface. This detachment could be initialized by turbulent flow or random energy fluctuation at the interface. When the first micelle is detached from interface the surfactant concentration difference between the “hole” and the interface is significant and cause Marangoni flow into the “hole” to reduce this difference. This flow causes additional disturbance which might cause detachment of other micelles with oil and formation of a channel toward the oil-solid interface as shown in Fig. 1b.

At earlier time the surfactant concentration on the crystal surface,\({\mathrm{C}}_{\mathrm{S}},\) is zero so the difference between surfactant concentrations on the surface of crystal and near to the oil layer is \({\mathrm{C}}_{\mathrm{Ad}}\). This difference in surfactant concentrations makes the total difference in IFT, \(\Delta {\gamma }_{t}\), between the crystal surface and the area near to the oil layer.

Initially, the surfactant concentration adsorbed in the oil layer \({,\mathrm{C}}_{\mathrm{R}},\) is approximately zero therefore the difference between \({\mathrm{C}}_{\mathrm{R}}\) and \({\mathrm{C}}_{\mathrm{Ad}}\) is the maximum value (\({\mathrm{C}}_{\mathrm{Ad}}\)). Consequently, the change in IFT of replacement,\(\Delta {\upgamma }_{\mathrm{r}}\), will be to the same as\(\Delta {\upgamma }_{\mathrm{t}}\). Over time \({\mathrm{C}}_{\mathrm{R}}\) will increase, and the surfactant concentration in the oil layer,\({\mathrm{C}}_{\mathrm{R}}\), will increase from \({\mathrm{C}}_{\mathrm{B }}\) to \({\mathrm{C}}_{\mathrm{Ad}}\) since the \(\Delta C\) and \(\Delta {\gamma }_{r}\) will remain constant and equal to \({\mathrm{C}}_{\mathrm{Ad}}\) and\(\Delta {\upgamma }_{\mathrm{t}}\), respectively as shown in Fig. 1c.

$$\Delta_{C} = (C_{Ad} + C_{R} ) - C_{R} = C_{Ad}$$
(1)

When the surfactant molecules reach the crystal surface, \({\mathrm{C}}_{\mathrm{R}}\) reaches the maximum value,\({\mathrm{C}}_{\mathrm{R}-\mathrm{Max}}\), and the oil replacement ends as depicted in Fig. 1d.

By increasing \({\mathrm{C}}_{\mathrm{S}}\) over time, \(\Delta C\) will increase.

$$\Delta_{C} = (C_{Ad} + C_{S} ) - C_{R}$$
(2)

As shown in Fig. 1e, after the surfactant molecule reaches the crystal surface, the absolute adsorption process starts and \(\Delta {\upgamma }_{\mathrm{t}}\) distributes between replacement and absolute adsorption processes as follows:

$$\Delta \gamma_{t} = \Delta \gamma_{r} + \Delta \gamma_{a}$$
(3)

where \(\Delta {\gamma }_{a}\) is the change in IFT of the absolute adsorption process. As one can see in Fig. 1f, when the \({\mathrm{C}}_{\mathrm{S}}\) equals the maximum \({\mathrm{C}}_{\mathrm{R}}\), the \(\Delta {\gamma }_{a}\) will be equal to the \(\Delta {\gamma }_{t}\) therefore the absolute adsorption will be maximum too.

1.1.1 The description of the replacement process

We assume that surfactants diffuse to the oil layer through an interfacial tension gradient, and we consider the surfactant diffusion channel in an oil layer to be cylindrical with a radius \({\mathrm{r}}_{0}\) and length L with its axis co-incident with the x-axis and assume that the IFT and velocity are function only of the distance and radius, dx and r respectively, as shown in Fig. 2. The IFT at the upstream end, 2, is \({\upgamma }_{\mathrm{r}}\) and at the downstream end, 1, has risen by \(\Delta {\upgamma }_{\mathrm{r}}\) to (\({\upgamma }_{\mathrm{r}}\)+\(\Delta {\upgamma }_{\mathrm{r}}\)). As the flow is in equilibrium, the driving force at upstream 1 and 2 due to IFT is equal to the retarding force due to the shear stress by the walls as follows:

$$2\pi r\gamma_{r} - (\gamma_{r} + \Delta \gamma_{r} )2\pi r = \tau 2\pi rdx$$
(4)
Fig. 2
figure 2

Schematic figure of the element the surfactant flow in a cylindrical channel used for developing the model

Full size image

Hence, the shear stress can be predicted by rearranging the Eq. (4) as:

$$\tau = - \frac{{\Delta \gamma_{r} }}{{\Delta {\text{x}}}}$$
(5)

A Newtonian fluid shows a linear relationship between shear stress and shear rate given in Eq. (6).

$$\tau = - \mu \frac{{{\text{du}}}}{{{\text{dr}}}}$$
(6)

where \(\tau\), \(\mu\), and \(\mathrm{u}\) are shear stress, viscosity, and velocity respectively. Equating Eqs. (5) and (6) and integrating with respect to \(r\) gives:

$$u = \frac{1}{\mu }\frac{{\Delta \gamma_{{\text{r}}} }}{{\Delta {\text{x}}}}\int\limits_{0}^{{r_{0} }} {dr} = \frac{1}{\mu }\frac{{\Delta \gamma_{{\text{r}}} }}{{\Delta {\text{x}}}} + C$$
(7)

The integration constant, \(C\), can be found by putting velocity zero in the boundary condition at the wall (\({\mathrm{r}=\mathrm{r}}_{0}\)) as:

$$u = - \frac{{r_{0} }}{\mu }\frac{{\Delta \gamma_{{\text{r}}} }}{{\Delta {\text{x}}}}\left( {1 - \frac{{\text{r}}}{{{\text{r}}_{0} }}} \right)$$
(8)

The flow rate can be predicted by integration once more respect to cross section area as:

$$Q = \int\limits_{0}^{{{\text{r}}_{0} }} {udA = - \frac{{2\pi {\text{r}}_{0} }}\mu{{{\text{ }}}}}\frac{{\Delta \gamma_{{\text{r}}} }}{{\Delta {\text{x}}}} \int\limits_{0}^{{{\text{r}}_{0} }} {r\left( {1 - \frac{{\text{r}}}{{{\text{r}}_{0} }}} \right)} dr$$
(9)

Rearranging the result of the integration gives the relationship between \(\Delta {\upgamma }_{\mathrm{r}}\) and mass flow rate,\(\frac{\partial \mathrm{m}}{\partial \mathrm{t}}\), in cylindrical channel as:

$$\Delta \gamma_{{\text{r}}} = - \frac{24\mu L}{{\pi \rho d^{3} }}^{{}} \frac{\partial m}{{\partial t}}$$
(10)

where \(d\), \(L\), and \(\rho\) are channel diameter, channel length and density, respectively. To simplify Eq. (10), we consider the parameters in \({\mathrm{K}}_{\mathrm{r}}\) constant as:

$${\text{K}}_{{\text{r}}} = - \frac{{\pi d^{3} }}{24\nu L}$$
(11)

where ν is kinematic viscosity. Therefore, the \(\Delta {\upgamma }_{\mathrm{r}}\) can be obtained as follows:

$$\Delta {\upgamma }_{\mathrm{r}}=-\frac{1}{{\mathrm{K}}_{\mathrm{r}}}\frac{\partial \mathrm{m}}{\partial \mathrm{t}}$$
(12)

1.1.2 The description of the absolute adsorption process

Experimentally determining the absolute surfactant adsorption is most commonly done by adding a known surfactant concentration to the system, waiting for the system to reach equilibrium, separating the dispersed solids and subsequently measuring the surfactant concentration in the solution. Surfactant adsorption can be then given by:

$$\Gamma = \frac{{(C_{0} - C)V}}{{{\text{ma}}_{{{\text{sp}}}} }}$$
(13)

where \(C\) is the surfactant concentration in solution, \({\mathrm{C}}_{0}\) is the initial surfactant concentration, \(V\) is the volume of solution, \(m\) is the mass of particles, \({\mathrm{a}}_{\mathrm{sp}}\) is the specific area of the particles and \(\Gamma\) is the amount adsorbed [17].

The amount of surfactant adsorption below system saturation is related to the surfactant concentration. It is also known that change in surfactant concentration below saturation causes changes in IFT. Consequently, assuming that the mass of absolute surfactant adsorption is linearly related to changes in IFT of absolute adsorption, the change in IFT of absolute adsorption can be predicted as:

$$\Delta \gamma_{{\text{a}}} = - \frac{{\text{m}}}{{{\text{K}}_{{\text{a}}} }}$$
(14)

where \({\mathrm{K}}_{\mathrm{a}}\) is the surfactant absolute adsorption’s constant and the negative sign shows that surfactant adsorbs from low IFT to high IFT sites.

1.1.3 Mathematical modeling

Hence, the differential equation. that models the surfactant adsorption process in QCM tests can be obtained by replacing Eqs. (12) and (14) into Eq. (3) as:

$$\frac{1}{{{\text{K}}_{{\text{r}}} }}\frac{{\partial {\text{m}}}}{{\partial {\text{t}}}} + \frac{{\text{m}}}{{{\text{K}}_{{\text{a}}} }} + \Delta \gamma_{{\text{t}}} = 0$$
(15)

Equation 15 is a first order non-homogeneous differential equation that can be solved as:

$$m(t) = {\text{B}}e^{{ - \frac{{{\text{K}}_{{\text{r}}} }}{{{\text{K}}_{{\text{a}}} }}t}} + {\text{K}}_{{\text{a}}} \Delta \gamma_{{\text{t}}} \left[ {e^{{ - \frac{{{\text{K}}_{{\text{r}}} }}{{{\text{K}}_{{\text{a}}} }}t}} - 1} \right]$$
(16)

where \(B\) is the initial condition at time zero. The liquid load effect can be considered as the initial mass in QCM tests so the solution can be developed as:

$$m(t) = - {\text{K}}_{{\text{a}}} \Delta \gamma_{t} + (m_{{{\text{LL}}}} + {\text{K}}_{{\text{a}}} \Delta \gamma_{t} )e^{{ - \frac{{{\text{K}}_{{\text{r}}} }}{{{\text{K}}_{{\text{a}}} }}t}}$$
(17)

where \({m}_{\mathrm{LL}}\) is the liquid loading mass imposed due to the injection of solutions with different densities and viscosities in QCM experiments. If we set \({(-\mathrm{K}}_{\mathrm{a}}\Delta {\upgamma }_{\mathrm{t}})\) to \({\mathrm{m}}_{0}\) and \({(\mathrm{m}}_{\mathrm{LL}}+{\mathrm{K}}_{\mathrm{a}}\Delta {\upgamma }_{\mathrm{t}})\) to \({\mathrm{m}}_{1}\), Eq. (17) can be written as:

$$m(t) = m_{o} + m_{1} e^{{ - \frac{{{\text{K}}_{{\text{r}}} }}{{{\text{K}}_{{\text{a}}} }}t}}$$
(18)

1.2 Experiments

1.2.1 Surfactant Solutions

The commercial surfactants SDBS (tech., Sigma Aldrich) and AOT (96%, VWR International AS) were used as received. The surfactant concentrations in the sample solutions were 435 ppm, 1000 ppm and 1500 ppm for SDBS and 500 ppm, 1098 ppm and 1500 ppm for AOT [12] in deionized water (mQ-water).

Brines Synthetic high salinity brine was made by dissolving NaCl (99.5%, Merk, Germany), CaCl2·2H2O (99.5% Merk, Germany) and MgCl2·6H2O (99.5% Merck, Germany) in mQ-water and used as the connate brine for all the QCM measurements whereas the amount of total dissolved solids (TDS) in high salinity brine were 65,272 ppm. Low salinity brine was prepared by dissolving NaCl (99.5%, Merk, Germany), in mQ-water. As tertiary low salinity water flooding reported for salinities lower than 5,000 ppm [20, 21], the TDS for low salinity brine was considered near to the limit, 4,675 ppm. The composition of the synthetic high and low salinity waters are listed in Table 1 [12].

Table 1 Composition of high and low salinity brines [12]
Full size table

1.2.2 Crude oil

The crude oils used in these experiments from offshore and onshore fields in the North Sea and Germany, respectively. The densities of the oils were measured in a temperature scan from 15 to 60 °C with a DMA-5000 density meter. The viscosity of each oil was measured in a temperature scan between (20 and 80) °C and at a shear rate around 10 s−1 with a Physica MCR301 (Anton Paar GmbH). The bulk composition of the oil was investigated by SARA (Saturates/Aromatics/Resins/ Asphaltenes) fractionation as described by Hannisdal [22]. The properties of the oils are given in Table 2 [23].

Table 2 Composition and properties of the crude oils [23]
Full size table

1.2.3 QCM measurements

QCM is an ultra-sensitive and in-situ real-time weighing device that is principally appropriate for measuring the adsorption and desorption of tiny masses. The sensitivity of QCM is about 100 times higher than that of a typical precise analytical balance, hence enabling detecting of mass variation at a nanogram level. The dissipation monitoring provides the opportunity to measure viscoelastic changes in the boundary layer in the closeness of the sensor, and changes in the viscosity or density in a solution [24, 25]. The QCM consists of a thin disk of single crystal quartz, with metal electrodes on each side of the disk [26]. The dissipative quartz crystal microbalance (QCM-D) measures simultaneously the changes in resonance frequency, \(f\), and dissipation, \(D\), due to adsorption on the crystal surface. When an AC voltage is applied over the electrodes the crystal starts to oscillate with a characteristic frequency, and this frequency changes when the oscillating crystal is brought into contact with solutions.

The Equation describing mass load (Sauerbrey Equation) is as follows [27]:

$$\Delta {f}_{ads.}=-\frac{2n{f}_{0}^{2}\Delta m}{{\rho }_{q}{v}_{q}A}$$
(19)

where \(n\) is the harmonic number, \({f}_{0}^{ }\) is the fundamental resonant frequency (5 MHz), \(\Delta m\) is the adsorbed mass, \(A\) is the active area of the crystal (\(0.785\times {10}^{-4}{m}_{ }^{2}\)), \({\rho }_{q}\) is the specific density of quartz (2650\(\frac{kg}{{m}_{ }^{3}}\)) and \({v}_{q}\) represents the shear wave velocity in quartz (3340\(\frac{m}{s{ }_{ }}\)) [28]. In this way the frequency shift if the crystal is directly linked to the mass adsorbed on it, and absorption of species introduced to the crystal can be directly estimated. Note that the QCM measures total mass and is not able to distinguish between different adsorbents. Hence, most QCM studies attempted to evaluate the effect of low-salinity brine and/or surfactant flooding on desorption of crude oil, have only tended to focus on one adsorbent [14, 16, 29,30,31]. It is assumed that the surfactant adsorption is the same in the presence and absence of oil components at the crystal surface. Therefore, conducting separate blank measurements are proposed to estimate the frequency decrease because of surfactant adsorption [12]. The frequency changes are registered as the QCM sensors are exposed to surfactant and brine solutions without previous adsorption of the crude oil components in blank measurements. The frequency change attributed to oil desorption upon surfactant flooding can be estimated using the following equation [12]:

$$\Delta {f}_{oil des,SF}=\Delta {f}_{meas,SF-} \Delta {f}_{meas,blank}$$
(20)

where \(\Delta {f}_{meas,SF}\) and \(\Delta {f}_{meas,blank}\) are the frequency shifts registered in the main measurement and blank test during surfactant flooding, respectively.

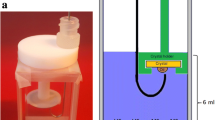
The surfactant adsorption on SiO2 (QSX 303, Q-sense) and AlSiOx QCM sensors (QSX 999, Q-Sense) were studied using a dissipative QCM-Z500 from KSV (Helsinki, Finland). Figure 3 a, b show the dimension of the QCM sensor and how to insert it into the QCM chamber, respectively. The temperature was kept at \(20\pm 0.1\mathrm{ C}\) in all experiments. The experimental procedure was as follows [12]:

Fig. 3
figure 3

a The dimension of the QCM sensor (1 cm). b Inserting the QCM sensor (crystal) into the QCM chamber

Full size image

(1) The chamber was flushed with pure toluene to obtain a stable baseline. (2) 2–2.5 mL of the crude oil was injected by gravitational flow into the temperature loop. (3) The crude oil was kept in the temperature loop for 5 min to equilibrate the temperature. (4) The crude oil was injected twice to the QCM chamber to ensure saturation of the crystal surface. (5) 4 mL toluene was flushed over the crystal with a relatively high flow rate to remove weakly bound oil components from the surface. (6) 4 mL of high saline brine were injected at its natural pH to simulate the connate brine of the reservoir. (7) 4 mL of low salinity brine was let into the measurement chamber as low salinity water flooding step. (8) Finally, 4 mL of surfactant solution were flooded through the QCM chamber. The procedure was repeated for two crystals, SiO2 and AlSiOx, using two surfactants, SDBS and AOT, with three different concentrations. Similarly to investigate the effect of different oils with different properties on the surfactant adsorption, some experiments were implemented by applying four characterized crude oils at LSW-SF process on silica crystal.

2 Results and discussion

By using Eq. (19), the apparent adsorbed mass on silica surface were calculated and depicted versus time in Fig. 4. The mass change was interpreted as a combination of oil desorption, surfactant adsorption, and liquid load effect. Running the blank tests (method 1) was suggested to calculate and extract each effect from the whole curve, and was done in a previous work [12]. A similar exponential decay curve to Eq. 18 was previously observed experimentally and reported for asphalt desorption from silica surface in QCM measurements [29]. Equation (18) was fitted to the experimental apparent adsorbed mass data, and Fig. 5 shows an example of the fitting.

Fig. 4
figure 4

The calculated mass by the Saubrey equation (Eq. 19) as a function of time for LSW-SF process on a silica crystal. Concentration of surfactant in the injected water, in ppm for SDBS and AOT respectively, is given in the figure. The time of surfactant injection into the systems is denoted with a green arrow

Full size image
Fig. 5
figure 5

Example fitting of Eq. (18) to QCM data. Experimental data is for oil A on a silica surface displaced with 1500 ppm AOT solution. The fitting shows good agreement with the experimental data (R2 = 0.94)

Full size image

The fitting constants (\({\mathrm{m}}_{0}\) and \(\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}}\)) for the different surfaces, and for different salt content are listed in Tables 3, 4 and 5. Analysis of these reveal the following: First, the power constant,\(\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}}\), increased with increasing surfactant concentration for LSW-SF process on silica (Table 3). Similar trends have been reported previously for asphalt recovery from silica crystals [29]. The adsorption of anionic surfactants on silica surface proceeds via favorable dispersion and surfactant monomer-surface interactions [12], and with increasing surfactant concentration, surfactant\oil replacement process overtakes the absolute adsorption process. The opposite trend was observed for the same process on aluminosilicate surfaces (Table 4) and high salinity-surfactant flooding on silica crystals (Table 5), indicating that more in these cases the absolute surfactant adsorption is dominating over the surfactant replacement.

Table 3 Summary of constants obtained through fitting mass versus time data with Eq. 18 for AOT\SDBS flooding after LSW on silica surface
Full size table
Table 4 Summary of constants obtained through fitting mass versus time data with Eq. (18) for AOT\SDBS flooding after LSW on aluminosilicate surface
Full size table
Table 5 Summary of constants obtained through fitting mass versus time data with Eq. 18 for AOT\SDBS flooding after high saline brine injection on silica surface
Full size table

The quite low values of power constants show that the values of \({\mathrm{K}}_{\mathrm{a}}\) are much greater than \({\mathrm{K}}_{\mathrm{r}}\) values. However, \({\mathrm{K}}_{\mathrm{r}}\) is increasing by increasing of surfactant concentration, the trend of power constant suggests that \({\mathrm{K}}_{\mathrm{r}}\) never could reach to \({\mathrm{K}}_{\mathrm{a}}\) and the power constant values are always less than one.

Second, SDBS showed lower power constant values than AOT for LSW-SF on silica crystals (Table 3). With its two hydrocarbon tails AOT has a totally longer tail length than SDBS which tends to produce more organized solubilization structures. In effect a larger interaction between AOT’s tails and the oil phase leads to more and better participation of AOT in surfactant\oil replacement process. Therefore \({\mathrm{K}}_{\mathrm{r}}\) values are higher for AOT with two tails and larger interactions at the interface.

Third, higher m0 values were observed for AOT than SDBS for all the measurements. According to Eq. (17), the maximum surfactant adsorption, when time approaches infinity, will be obtained as:

$$m_{\max } = - {\text{K}}_{{\text{a}}} \Delta \gamma t$$
(21)

This maximum surfactant adsorption is equal to the \({\mathrm{m}}_{0}\) constant in Eq. (18). The mass adsorbed on the surface starts at zero and build up exponentially to the final value of \({\mathrm{m}}_{0}\). At a time T \(= \frac{{\mathrm{K}}_{\mathrm{a}}}{{\mathrm{K}}_{\mathrm{r}}}\), mass reaches a value that is 63% of \({\mathrm{m}}_{0}\). This time is the constant time for surfactant adsorption process and at the end of 5 time constants (\(5\frac{{\mathrm{K}}_{\mathrm{a}}}{{\mathrm{K}}_{\mathrm{r}}}\)), the surface will be fully saturated with the surfactant.

As shown in Tables 3, 4 and 5, \({\mathrm{m}}_{0}\) increased with increasing surfactant concentrations for all the experiments due to the higher values of Δγt at the higher surfactant concentrations.

Also the higher amount of the surfactant adsorption on aluminosilicate surfaces at LSW-SF (Table 4) and surfactant flooding after high salinity brine injection on silica crystal (Table 5) comparing to LSW-SF on silica crystals (Table 3) at the same surfactant concentrations, can be explained by higher surfactant absolute adsorption’s constant \({(\mathrm{K}}_{\mathrm{a}})\) values for aluminosilicate crystal and high salinity condition. According to Eq. (21), the maximum surfactant adsorption is also a function of change in IFT and higher Δ \({\gamma }_{t}\) causes higher surfactant absolute adsorption. The generally lower IFT values of AOT comparing to SDBS have been observed and attributed to the two tailed structure of AOT, which independent of electrolyte causes a tighter packing and higher the critical packing parameter (CPP) than that of SDBS [23].

Taking the derivative of Eq. (17), leads to the surfactant mass flow rate,\(\dot{m}\), as:

$$\dot{m}=-\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}}\left({m}_{\mathrm{LL}}+{\mathrm{K}}_{\mathrm{a}}\Delta {\upgamma }_{\mathrm{t}}\right){ e}^{-\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}} t}$$
(22)

Since the maximum \(\dot{m}\) can be obtained at time zero as follows:

$${\dot{m}}_{max}=-\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}}\left({m}_{\mathrm{LL}}+{\mathrm{K}}_{\mathrm{a}}\Delta {\upgamma }_{\mathrm{t}}\right)$$
(23)

By neglecting the liquid load effect in Eq. (22), the maximum surfactant replacement rate can be achieved as:

$${\dot{m}}_{max}=-{\mathrm{K}}_{\mathrm{r}} \Delta {\upgamma }_{\mathrm{t}}$$
(24)

So \({\dot{\mathrm{m}}}_{\mathrm{max}}\) can be predicted by multiplying \({\mathrm{m}}_{0}\) with the power constant in Eq. (18). Therefore, higher absolute surfactant adsorption and higher \(\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}}\) values reason higher oil replacement rate as can be seen for high AOT concentrations (1098 and 1500 ppm) at LSW-SF process on silica crystal in Table 3. Conversely, lower replacement rates were seen for high saline environment and aluminosilicate surfaces because of lower \(\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}}\) values. The constants \({\mathrm{m}}_{0}\) and \(\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}}\) for different crude oils, A, B,C and D on silica surfaces are presented in Table 6, with the surfactant flooding done with a 1000 ppm SDBS solution after low salinity brine injection on silica surfaces. Results in Table 6 show varied surfactant adsorptions for different crude oils by the newly developed method whereas just one adsorption value was predicted by method 1 for different type of oils. As one can see in Table 6, the highest and the lowest surfactant adsorptions were reported for the crude oil C and crude oil A, respectively. However, method 1 is a useful and practical method to estimate the oil desorption and surfactant adsorption via running the blank tests, but it is not sensitive to oil properties and different oil types. Tichelkamp et al. measured and reported IFT values between SDBS/AOT solutions and the same crude oils, at 60 °C, as listed in Table 7 [23]. According to Eq. (21) and considering IFT and \({\mathrm{m}}_{0}\) values for different oils in Table 7,\({\mathrm{K}}_{\mathrm{a}}\) is the lowest for oil A.

Table 6 Summary of constants obtained through fitting mass versus time data with Eq. 18 for 1000 ppm SDBS flooding after LSW on silica surface saturated with different oils and the mass of adsorbed surfactant calculated by method 1 at the same condition
Full size table
Table 7 IFT values between SDBS/AOT solutions and four different crude oils at 60 °C [23]
Full size table

As Eqs. (11) and (24) predict properly, the maximum mass flow rates (listed in Table 6) are inversely related to the kinematic oil viscosities. Therefore, the oil D with the lowest kinematic viscosity shows the highest surfactant replacement whereas oil C with highest kinematic viscosity indicates a very low, 0.02 mg/sm2, replacement rate.

As shown in Fig. 6, between the power constant and the ratio \(\left(\frac{\mathrm{Resins }(\mathrm{wt\%})-0.4 \times \mathrm{Asphaltenes }(\mathrm{wt\%})}{\upnu }\right)\), a correlation coefficient of 0.99 was obtained, indicating proportionality between the \(\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}}\) and the ratio. Malkin et al. showed that the small concentrations of asphaltenes have a dominant influence on the viscosity, while much higher concentrations of resins and aromatics are required in order to cause a significant increase of oil viscosity [32]. Resins contribute to dispersion of asphaltene nanoaggregates, increase the solubility of asphaltenes in oil and decrease the effect of asphaltenes on viscosity through reducing the size of asphaltene aggregates [33,34,35]. In addition, Mousavi et al. showed that resin–asphaltene interactions are prominent only if the number of resin molecules is greater than the number of asphaltene molecules [36].

Fig. 6
figure 6

Empirical relation between the Kr/Ka and the ratio \(\left(\frac{\mathrm{Resins }(\mathrm{wt\%})-0.4 \times \mathrm{Asphaltenes }(\mathrm{wt\%})}{\upnu }\right)\)

Full size image

The empirical ratio \(\left(\frac{\mathrm{Resins }(\mathrm{wt\%})-0.4 \times \mathrm{Asphaltenes }(\mathrm{wt\%})}{\upnu }\right)\) involves and demonstrates the above-mentioned effects of resin and asphaltene on surfactant adsorption coefficients. Therefore, the \(\frac{{\mathrm{K}}_{\mathrm{r}}}{{\mathrm{K}}_{\mathrm{a}}}\) is much higher for crude A and D with higher empirical ratio values compared to crudes B and C.

3 Conclusion

A mathematically simple and reliable model is developed for surfactant adsorption in surfactant flooding and compared with experimental data from QCM measurements. The model considers two simultaneous processes; surfactant\oil replacement and absolute surfactant adsorption. By fitting the model to the experimentally obtained apparent adsorbed mass versus time, the maximum absolute surfactant adsorption in addition to the maximum surfactant replacement rate can be determined.

The power constant in the developed model is the ratio between the replacement coefficient (\({\mathrm{K}}_{\mathrm{r}})\) and the surfactant monomer absolute adsorption’s constant (\({\mathrm{K}}_{\mathrm{a}})\) whereas both coefficients are function of surfactant type, surfactant concentration and salinity. In addition, \({\mathrm{K}}_{\mathrm{a}}\) is dependent on the type of surface while \({\mathrm{K}}_{\mathrm{r}}\) is dependent on the thickness of the oil layer and its kinematic viscosity.

High saline environment and aluminosilicate surfaces showed higher \({\mathrm{K}}_{\mathrm{a}}\) values than low saline condition on silica surfaces. This would indicate that better results could be obtained on aluminosilicate surfaces at high saline condition using lower surfactant concentrations whereas higher oil desorption can be expected by applying higher surfactant concentrations at low saline condition on silica surfaces. The developed model also successfully manages to predict the relative mass flow of different oils based on their viscosity.

Based on the experimental results and model predictions from this study, it can be concluded that achieving very low IFT is not always favorable from an EOR perspective. It appears that applying a weaker surfactant (in terms of higher IFT), like SDBS comparing to AOT in this study, is more feasible and applicable especially for high salinities and in presence of aluminosilicate surfaces (clays). The developed analytical model explains this by the parameter \({m}_{0}\) which is a function of \({\mathrm{K}}_{\mathrm{a}}\) and change in IFT.