1 Introduction

Terahertz (THz) bandpass filters have wide applications in imaging, spectroscopy, molecular sensors, security systems and detection of materials [1]. One of the important parameters in such filters is the thickness of the metal film at higher frequencies (THz range) [2]. Changes in the metal film thickness have been the subject of many studies [3, 4]. Some geometric shapes such as square, circular, annular and pair of conductive rings have widely been investigated so as to determine the best structure for filters. The transmission coefficient of filters with ring-shaped arrays (patches) has been addressed in more than 70% of the research in the field [5]. This coefficient is not the same for different frequency ranges. For frequencies of 0.1–1 THz and 2–14 THz, the transmission coefficient ranges from 90% to 100% and 40% to − 70%, respectively [6].

A metal-mesh bandpass filter was designed and fabricated with a 12-um-thick copper film in the frequency range of 0.5–2.5 THz [7]. Using the CST simulation software, two same filters were placed in a row at various distances to improve the frequency bandwidth. This led to a lower frequency width at half maximum (FWHM) compared to cases with a single filter. Also, the effect of changes in the incident wave angle was investigated at several angles. In the following, a new type of asterisk filter was proposed. In its output spectrum, it was shown to have lower noise (or unwanted frequency) than other asterisk filter samples [8].

In recent years, the use of metamaterials and frequency selective surfaces (FSS) in the terahertz field has been of great importance, which has also been used for terahertz bandpass filters. These properties as well as the use of different substrates for achieving narrower bandwidth as well as frequency spectrum tunable have been used [9,10,11,12,13,14].

In the present study, a new bandpass filter called ‘spider’ is proposed through designing and simulation. It has proved to have a very good transmission coefficient (almost 100%) and, as shown by the output spectrum, much lower output noise (or unwanted frequencies) than the other bandpass filters ever designed and made.

2 Filter structure and the results

A check on the length, width and period of filter patches shows that certain changes in these dimensions lead to the change of the frequency peak (Fig. 1, Eq. 1) [2].

Fig. 1
figure 1

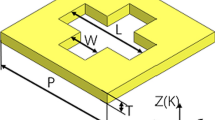
Dimensions of the plus bandpass filter to obtain the resonant frequency [2]

Full size image
$$\lambda_{R} = 2\left( {g - 2a - b} \right)$$
(1)

In the first stage of the study, a plus bandpass filter is simulated with the thickness of 0.3 Âµm on an air substrate by the CST software. The length (K), width (J) and period (G) of each filter structure (Fig. 2) are different for different resonance frequencies. In this simulation, a filter is produced with an output frequency peak near 1.54 THz, and G, K, and J are 154, 100 and 29 micrometers, respectively (Figs. 2 and 3). To verify the accuracy of the simulation with the CST software, these coordinates are evaluated according to the studies already conducted on plus bandpass filters. Indeed, the simulated sample is compared to the experimental samples of the filter [7].

Fig. 2
figure 2

Dimensions of a plus bandpass filter [7]

Full size image
Fig. 3
figure 3

Output frequency of a plus bandpass filter with the resonance frequency of 1.54 THz (comparison of the experimental results with the simulation)

Full size image

According to Fig. 2 and the coordinates taken from experimental studies [15,16,17] and a simulation work [7], the frequency peak lies at 1.54 THz, which indicates good agreement between simulations and experimental samples (Fig. 3).

In the next stage, to reduce the FWHM of the output spectrum, two same filters are placed in a row at various distances (distance x) (Fig. 4). This makes a considerable change in the frequency, as compared to the initial state (i.e., single-filter state). The value of (x) changes at distance \(\lambda\), \(\frac{\lambda }{2}\) and \(\frac{\lambda }{4}\) of the central wavelength (resonance frequency), and the most decrease of the FWHM occurs at the distance of \(\frac{\lambda }{2}\). In this state, the FWHM is about half of its initial value (Fig. 5).

Fig. 4
figure 4

Two same filters placed in a row at the distance of x

Full size image
Fig. 5
figure 5

FWHM at the central frequency of 1.54 THz for the distance \(x = \frac{{\lambda }}{2}\) in a single-filter state (solid line) and FWHM when two same filters are placed in a row (dashed line)

Full size image

According to the results obtained based on the Fabry–Perot principles, FWHM can be reduced if two filters are placed in a row at a distance which is a multiple of half-wavelength. The results of this simulation are consistent with the computational results in some other studies such as [17,18,19,20].

The next part of the study is dedicated to the investigation of an asterisk bandpass filter (Fig. 6) that consists of a copper film with the thickness of 0.3 Âµm on an air substrate. This filter is designed in dimensions identical to a plus bandpass filter so that their output frequency shapes can be compared together.

Fig. 6
figure 6

Two asterisk bandpass filter samples: a rectangular and b cylindrical (wire), which is the proposed type

Full size image

3 Analysis of two samples of asterisk bandpass filters

Two asterisk bandpass filters are designed and simulated: one with a rectangular surface and the other in a cylindrical (wire) shape. These two types of bandpass filters, as shown in Fig. 6, have transmission coefficients of 90% [8, 21,22,23] and 100%, respectively (Fig. 7). Cylindrical asterisk bandpass filters have the least noise (unwanted frequencies) among all the bandpass filters ever designed and fabricated (especially rectangular asterisk bandpass filters [8,9,10]). In a rectangular type, when the width of the filter (W) increases, the output spectrum coefficient decreases, while the noise (unwanted frequencies) increases (Fig. 7). In a cylindrical type, however, with an increase in the cylinder diameter (D), the FWHM changes in the range of 10–20 GHz.

Fig. 7
figure 7

The noise (unwanted frequencies) in the asterisk bandpass filters of rectangular type (solid line) and cylindrical types (dashed line)

Full size image

3.1 Analysis of the transmission coefficient

Through the simulation of different bandpass filters with the CST software, the output spectrum in the frequency range of 0.1–1 THz, the transmission coefficient is found to be almost 100%. In higher-frequency ranges, different transmission coefficients have been achieved [14, 24,25,26].

In this paper, the proposed filters are investigated in the frequency range of 0.5–2.5 THz. According to the simulation results, the transmission coefficient of the plus bandpass filter in this frequency range is almost 85–90%. In the asterisk bandpass filter of the cylindrical type, this value is about 95–100% (Fig. 7). Also, according to studies of circular filters by using the CST software [27,28,29,30], the transmission coefficient is 95–100%.

3.2 Investigation of the frequency width at half maximum (FWHM)

The plus bandpass filters designed with the CST software have an FWHM of about 5–10 GHz, while this value is about 10–20 GHz for other filters (Fig. 8).

Fig. 8
figure 8

The FWHM for a plus bandpass filter (dashed line) and the proposed asterisk bandpass filter (solid line)

Full size image

3.3 Analysis of noise (unwanted frequency)

The ratio of the original frequency to the unwanted frequencies in the output spectral range of the filter is the main advantage of the structure of this filter [31,32,33]. According to the literature on simulations, the amount of noise is investigated for different filters. The results are shown in Fig. 9. As it can be seen, the proposed asterisk bandpass filter of the cylindrical type has less noise than the other filters (especially plus and circular bandpass filters) in the frequency range of 0.1–1 THz.

Fig. 9
figure 9

The noise (unwanted frequencies) of a the proposed asterisk, b plus [7] and c circular [27,28,29] bandpass filters

Full size image

Although a plus bandpass filter has less noise and a lower FWHM than other bandpass filters, it has a lower transmission coefficient than the proposed cylindrical asterisk bandpass filter and circular bandpass filters.

4 The new proposed bandpass filter (spider filter)

In order to improve the fundamental factors in terahertz bandpass filters (including low FWHM, low noise and very high output intensity), a new bandpass filter called spider filter has been designed and simulated (Fig. 10).

Fig. 10
figure 10

Dimension of the proposed spider bandpass filter

Full size image

The proposed spider bandpass filter has dimensions b, x, A and k equal to 5, 10, 50 and 100 micrometers, respectively. These dimensions are determined in accordance with the wavelength (Fig. 1, Eq. 1) in the plus bandpass filter so as to compare the output spectra of the two filters.

In this simulation, each piece consists of a layer of copper with a thickness of 0.3 micrometers on the air substrate. The distance of each piece and its width vary according to Eq. 1 and the desired frequency. The desired frequency range in this simulation is from 0.1 to 3 terahertz, and it is possible to design a bandpass filter for each desired range. In this simulation, a module CST MICROWAVE STUDIO on the periodic structures—FSS and metamaterial—has been used.

According to Eq. 1, the width and distance of each piece are proportional to the frequency of 1.54 terahertz. The simulation results are completely consistent with the results expressed according to Eq. 1.

On this basis, the transmission coefficient, the noise (unwanted frequency) (Fig. 11) and the FWHM (Fig. 12) of the output spectra are investigated.

Fig. 11
figure 11

The effects of noise (unwanted frequencies) and transmission coefficient of a the proposed spider filter (dashed line) and b the plus bandpass filter (solid line)

Full size image
Fig. 12
figure 12

The FWHM of a the proposed spider filter (solid line) and b the plus bandpass filter (dashed line)

Full size image

Through a comparison of the properties of the proposed spider bandpass filter and the plus bandpass filter, it emerges that the former has a higher transmission coefficient (almost 100%) and lower noise (unwanted frequency) at all the frequencies in the range of 0.1–3 THz.

4.1 The effects of the incident wave angle on the filters

The change of the incident wave angle is investigated for its effect on filters, such as filters with grooved disks [21,22,23]. In this section, the effects of the incident wave angle are investigated for the plus bandpass and the proposed asterisk filters. The outputs from these filter samples are analyzed in the following sections.

The effect of angle variation on the incident waves of the spider filter in the TM and TE modes is also investigated. In the TE mode, as in the case of the plus bandpass filter, the change of the incident wave angle leads to a change in the frequency peak. In the TM mode, however, there is no change made in the frequency peak (Figs. 13 and 14).

Fig. 13
figure 13

Changes of the \(\theta\) angle in the TE mode: a, b, c, d and e represent 0, 20, 40, 60 and 80°

Full size image
Fig. 14
figure 14

Changes of the \(\theta\) angle (0 and 80°) in the TM mode

Full size image

Comparison of terahertz bandpass filters simulation results is shown in Table 1.

Table 1 Comparison of simulation results of terahertz bandpass filters (important options in each filter are shown in red)
Full size table

In order to find out optimum dimensions for the proposed spider bandpass filter, various dimension and shapes are checked and simulated by the CST software (Fig. 15).

Fig. 15
figure 15

Change of the dimensions in the proposed bandpass filter to obtain optimal values

Full size image

As the results of simulation suggest, the optimum distance of each piece, or a patch, in the filter structure should be equal to half of the dimension of the filter to obtain a good transmission coefficient. According to Fig. 10, it is as follows:

$$A = \frac{k}{2}$$
(2)

Also, according to the filter dimension (k), the optimum groove in each piece of the filter (\(x \times b\)) is considered equal to the following:

$$x = \frac{k}{10},\, b = \frac{k}{20}$$
(3)

By taking the optimal values of x, A and b into account, as indicated in Fig. 10, a filter can be designed with a transmission coefficient of 100% and an excellent signal-to-noise ratio.

5 Conclusion

In this paper, the frequency width at half maximum (FWHM) of bandpass filters was reduced through placing two such filters at different distances (the Fabry–Perot principles). A new bandpass filter called spider is also proposed with a transmission coefficient of almost 100%. It has less noise (unwanted frequency) than other filters in the frequency range of 0.1–3 THz. According to the simulation results, the incident wave angle of the filter is an important factor in that it moves the frequency peak of the output spectrum and makes other frequency peaks appear.