MHD instability of pressure-driven flow of a non-Newtonian fluid

Abstract

The effect of a uniform vertical magnetic field on the stability of pressure-driven flow of an electrically conducting non-Newtonian fluid in an isothermal channel is numerically investigated using the Chebyshev collocation method. The non-Newtonian fluid is modeled by the couple stress fluid theory, which permits for polar effects and encountered regularly in liquids with very large molecules. It is established that Squire’s theorem is valid and the modified Orr–Sommerfeld equation is derived by considering the fact that the magnetic Prandtl number P_m, for recognized electrically conducting liquids is too small. The triplets (R_c, α_c, c_c), where R_c is the critical Reynolds number, α_c is the critical wave number and c_c is the critical wave speed, are obtained for different values of couple stress parameter Λ and the Hartman number M. It is found that increasing M has a stabilizing effect on the system while an increase in the couple stress parameter shows twofold deeds. Individual aspects of the kinetic energy spectrum are observed and presented for different parametric values to obtain comprehensive information at the critical state of fluid flow.

1 Introduction

The pressure-driven flow in an isothermal channel has preoccupied fluid dynamicists for centuries. The ubiquitous nature of turbulence and its inability to give a universal theory have led many to try conceiving of the transition from laminar state to turbulent as a simple problem. It has many applications in engineering, geophysics, meteorology, oceanography and so on. The studies undertaken by many authors on this subject are very collectible in the book by Drazin and Reid [1].

The stability of hydromagnetic Poiseuille flow has additionally gotten equivalent significance in the literature. Lock [2] initiated this study by assuming P_m is exceptionally small and showed that the magnetic field has a stabilizing effect on the fluid flow. Later, Potter and Kutchey [3] re-examined the problem without any simplification and observed that the fluid flow becomes more stable as P_m increases. Takashima [4] re-considered the problem explored by Potter and Kutchey [3] under the appropriate boundary conditions on the magnetic field perturbations. The Lock’s arguments were supported by Lingwood and Alboussiere [5], who solved the problem numerically including all magnetic contributions and their results differed only a few percent from Lock’s results. Using the multi-deck asymptotic approach, the effect of transverse magnetic field on the stability of Poiseuille flow at high Reynolds number was investigated by Makinde [6]. Proskurin and Sagalakov [7] analyzed the effect of longitudinal magnetic field on the stability of Poiseuille flow. Later, Makinde and Mhone [8] extended the work of Takashima [4] to an isotropic porous domain case and subsequently to an anisotropic porous domain by Shankar and Shivakumara [9]. In the past, the stability of conducting fluid flows in a channel in the presence of a uniform magnetic field has attracted the attention of a host of researchers (Takashima [10], Kaddeche et al. [11], Balyaev and Smorodin [12], Adesanya et al. [13], Hayat et al. [14], Hudoba et al. [15], Hudoba and Molokov [16], Bhatti et al. [17], Shankar et al. [18], Ijaz et al. [19], Hassan et al. [20], Shankar et al. [21] and references therein).

The stability of forced convection in a fluid layer has been studied extensively. However, its counterpart for non-Newtonian fluids is in the much-to-be preferred state as these fluids bound to occur in many engineering applications. There exist various types of non-Newtonian fluids and the couple stress fluid, formulated by Stokes [22] based on micro-continuum theories, is one such non-Newtonian fluid which takes into account the size of fluid particles. These fluids are found to be useful in scientific and engineering applications. The effect of couple stresses on the stability of fluid flow was initially studied by Jain and Stokes [23] and its counterpart in a porous medium was examined by Shankar et al. [24]. In a slit channel with metrically astringent walls, the hydromagnetic flow of a couple stress fluid was investigated by Mekheimer [25]. The stability of free (natural) convection in a vertical couple stress fluid layer was investigated by Shankar et al. [18] while later this study was extended by Shankar et al. [26] and Shankar et al. [27] to include a uniform AC electric field and magnetic field, respectively. In addition, many researchers investigated the effect of couple stresses on fluid flows in different contexts (Rudraiah et al. [28], Shivakumar et al. [29], Turkyilmazoglu [30], Shivakumara and Naveen Kumar [31], Srinivasacharya and Rao [32], Ramesh [33], Tripathi et al. [34], Mahabaleshwar et al. [35], Layek and Pati [36], Nandal and Mahajan [37], Reddy et al. [38], Naveen Kumar et al. [39]).

To the best of our knowledge, the simultaneous presence of couple stresses and magnetic field on the pressure-driven stability of fluid flow in a channel is missing in the literature despite the study finds importance in biological fluid flows. The novelty of this paper is to unveil the validity of Squire’s theorem in analyzing the stability characteristics of the couple stress fluid in a channel in the presence of a uniform vertical magnetic field and undertaking energy budget analysis to understand the physical mechanisms involved in the flow transition.

2 Mathematical formulation

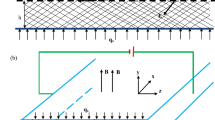
We consider fully developed pressure-driven steady flow of an electrically conducting incompressible couple stress fluid in an isothermal horizontal channel of thickness 2 h (Fig. 1). For modeling this flow, a Cartesian coordinate system (x, y, z)is used where the axes x, y and z denote the streamwise, spanwise, and wall-normal coordinates, respectively. The fluid layer is permeated by a uniform vertical magnetic induction $\vec{B}_{0} = (0,0,B_{0} )$. Following Stokes [22], Takashima [4] and Shankar et al. [27], the governing linear stability equations in the dimensionless form are

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 $$

(1)

$$ \begin{aligned}& \frac{\partial u}{\partial t} + u_{b} \frac{\partial u}{\partial x} + w\frac{{\partial u_{b} }}{\partial z} = - \frac{\partial P}{\partial x} + \frac{1}{R}\nabla^{2} u - \frac{1}{{R\,\varLambda^{2} }}\nabla^{4} u \\ &\quad+ \frac{{M^{2} }}{{R^{2} P_{m} }}\left[ {\left( {\frac{\partial }{\partial z} + RP_{m} B_{b} \frac{\partial }{\partial x}} \right)B_{x} + RP_{m} B_{z} \frac{{\partial B_{b} }}{\partial z}} \right] \end{aligned} $$

(2)

$$ \frac{\partial v}{\partial t} + u_{b} \frac{\partial v}{\partial x} = - \frac{\partial P}{\partial y} + \frac{1}{R}\nabla^{2} v - \frac{1}{{R\,\varLambda^{2} }}\nabla^{4} v + \frac{{M^{2} }}{{R^{2} P_{m} }}\left( {\frac{\partial }{\partial z} + RP_{m} B_{b} \frac{\partial }{\partial x}} \right)B_{y} $$

(3)

$$ \begin{aligned}& \frac{\partial w}{\partial t} + u_{b} \frac{\partial w}{\partial x} = - \frac{\partial P}{\partial z} + \frac{1}{R}\nabla^{2} w - \frac{1}{{R\,\varLambda^{2} }}\nabla^{4} w \\ &\quad+ \frac{{M^{2} }}{{R^{2} P_{m} }}\left( {\frac{\partial }{\partial z} + RP_{m} B_{b} \frac{\partial }{\partial x}} \right)B_{z} \end{aligned} $$

(4)

$$ \frac{{\partial B_{x} }}{\partial x} + \frac{{\partial B_{y} }}{\partial y} + \frac{{\partial B_{z} }}{\partial z} = 0 $$

(5)

$$ \begin{aligned} &\frac{{\partial B_{x} }}{\partial t} + u_{b} \frac{{\partial B_{x} }}{\partial x} + RP_{m} w\frac{{\partial B_{b} }}{\partial z} = \left( {\frac{\partial }{\partial z} + RP_{m} B_{b} \frac{\partial }{\partial x}} \right)u\\ &\quad + B_{z} \frac{{\partial u_{b} }}{\partial z} + \frac{1}{{RP_{m} }}\nabla^{2} B_{x} \end{aligned} $$

(6)

$$ \frac{{\partial B_{y} }}{\partial t} + u_{b} \frac{{\partial B_{y} }}{\partial x} = \left( {\frac{\partial }{\partial z} + RP_{m} B_{b} \frac{\partial }{\partial x}} \right)v + \frac{1}{{RP_{m} }}\nabla^{2} B_{y} $$

(7)

$$ \frac{{\partial B_{z} }}{\partial t} + u_{b} \frac{{\partial B_{z} }}{\partial x} = \left( {\frac{\partial }{\partial z} + RP_{m} B_{b} \frac{\partial }{\partial x}} \right)w + \frac{1}{{RP_{m} }}\nabla^{2} B_{z} $$

(8)

Fig. 1

Schematic of the problem considered

The relevant boundary conditions are

$$ u = u^{{{\prime \prime }}} = v = v^{{{\prime \prime }}} = w = w^{{{\prime \prime }}} = 0,\,B_{x} = B_{y} = \frac{{\partial B_{z} }}{\partial z} = 0\;{\text{at}}\;z = \pm 1. $$

(9)

The basic flow is fully developed, unidirectional, steady and laminar. Under these circumstances, the governing equations reduce to

$$ \frac{{d^{2} u_{b} }}{{dz^{2} }} - \frac{1}{{\,\varLambda^{2} }}\frac{{d^{4} u_{b} }}{{dz^{4} }} + \frac{{M^{2} }}{{RP_{m} }}\frac{{dB_{xb} }}{dz} = R\frac{{dP_{b} }}{dx} $$

(10)

$$ \frac{{du_{b} }}{dz} + \frac{1}{{RP_{m} }}\frac{{d^{2} B_{xb} }}{{dz^{2} }} = 0 $$

(11)

Equations (10) and (11) are solved using the boundary conditions

$$ u_{b} = u^{\prime\prime}_{b} = 0,\,B_{xb} = 0\;{\text{at}}\;z = \pm 1. $$

(12)

The solution is found to be

$$ u_{b} = \frac{{ - b^{2} \cosh \left( {\frac{az}{\sqrt 2 }} \right)\cosh \left( {\frac{b}{\sqrt 2 }} \right) + \cosh \left( {\frac{a}{\sqrt 2 }} \right)\left[ {2\sqrt {\varLambda^{4} - 4M^{2} \varLambda^{2} } \cosh \left( {\frac{b}{\sqrt 2 }} \right) + a^{2} \cosh \left( {\frac{bz}{\sqrt 2 }} \right)} \right]}}{{ - b^{2} \cosh \left( {\frac{b}{\sqrt 2 }} \right) + \cosh \left( {\frac{a}{\sqrt 2 }} \right)\left[ {a^{2} + 2\sqrt {\varLambda^{4} - 4M^{2} \varLambda^{2} } \cosh \left( {\frac{b}{\sqrt 2 }} \right)} \right]}} $$

(13)

$$ B_{xb} = \frac{{\sqrt 2 \left[ {b^{3} \cosh \left( {\frac{b}{\sqrt 2 }} \right)\left( { - z\sinh \left( {\frac{a}{\sqrt 2 }} \right) + \sinh \left( {\frac{az}{\sqrt 2 }} \right)} \right) + a^{3} \cosh \left( {\frac{a}{\sqrt 2 }} \right)\left( {z\sinh \left( {\frac{b}{\sqrt 2 }} \right) - \sinh \left( {\frac{bz}{\sqrt 2 }} \right)} \right)} \right]}}{{ab\left[ { - b^{2} \cosh \left( {\frac{b}{\sqrt 2 }} \right) + \cosh \left( {\frac{a}{\sqrt 2 }} \right)\left( {a^{2} + 2\sqrt {\varLambda^{4} - 4M^{2} \varLambda^{2} } \cosh \left( {\frac{b}{\sqrt 2 }} \right)} \right)} \right]}} $$

(14)

where $a = \sqrt {\varLambda^{2} - \sqrt {\varLambda^{4} - 4M^{2} \varLambda^{2} } } \,\,$, $\,\,b = \sqrt {\varLambda^{2} + \sqrt {\varLambda^{4} - 4M^{2} \varLambda^{2} } }$. We note that $u_{b} = \frac{\cosh M - \cosh Mz}{\cosh M - 1}$ and $B_{xb} = \frac{\sinh Mz - z\sinh M}{M(\cosh M - 1)}$ as $\varLambda \to \infty$ which coincide with the expression obtained by Takashima [4]. Since u_b and B_xb are real, from Eqs. (13) and (14) it follows that Λ > 2 M. We look for normal mode solution of Eqs. (1)–(8) in the form

$$ \begin{aligned} \left( {u,v,w,P} \right)& = \left( {\hat{u},\hat{v},\hat{w},\hat{P}} \right)(z)e^{{i\left( {\alpha \left( {x - ct} \right) + \beta y} \right)}} ,\;\left( {B_{x} ,B_{y} ,B_{z} } \right) \\ &= R\left( {\hat{B}_{x} ,\hat{B}_{y} ,\hat{B}_{z} } \right)\,(z)\,e^{{i\left( {\alpha \left( {x - ct} \right) + \beta y} \right)}} . \end{aligned} $$

(15)

Substituting Eq. (15) into Eqs. (1)–(8), we obtain

Using Eq. (15), Eqs. (1)–(8) become,

$$ D\hat{w} + i\left( {\alpha \hat{u} + \beta \hat{v}} \right) = 0 $$

(16)

$$ \begin{aligned} & i\alpha \left( {u_{b} - c} \right)\hat{u} + \hat{w}Du_{b} = - i\alpha \hat{P} + \frac{1}{R}\left( {D^{2} - \alpha^{2} - \beta^{2} } \right)\hat{u} \\ & \quad - \frac{1}{{R\,\varLambda^{2} }}\left( {D^{4} + \alpha^{4} + \beta^{4} + 2\alpha^{2} \beta^{2} - 2\alpha^{2} D^{2} - 2\beta^{2} D^{2} } \right)\hat{u}\\ &\quad + M^{2} \left( {\frac{{D\hat{B}_{x} }}{{RP_{m} }} + i\alpha B_{b} \hat{B}_{x} + \hat{B}_{z} DB_{b} } \right) \\ \end{aligned} $$

(17)

$$ \begin{aligned} & i\alpha \left( {u_{b} - c} \right)\hat{v} = - i\beta \hat{P} + \frac{1}{R}\left( {D^{2} - \alpha^{2} - \beta^{2} } \right)\hat{v} \\ & \quad - \frac{1}{{R\,\varLambda^{2} }}\left( {D^{4} + \alpha^{4} + \beta^{4} + 2\alpha^{2} \beta^{2} - 2\alpha^{2} D^{2} - 2\beta^{2} D^{2} } \right)\hat{v} \\ &\quad+ M^{2} \left( {\frac{{D\hat{B}_{y} }}{{RP_{m} }} + i\alpha B_{b} \hat{B}_{y} } \right) \\ \end{aligned} $$

(18)

$$ \begin{aligned} \begin{aligned} & i\alpha \left( {u_{b} - c} \right)\hat{w} = - D\hat{P} + \frac{1}{R}\left( {D^{2} - \alpha^{2} - \beta^{2} } \right)\hat{w} \\ & \quad - \frac{1}{{R\,\varLambda^{2} }}\left( {D^{4} + \alpha^{4} + \beta^{4} + 2\alpha^{2} \beta^{2} - 2\alpha^{2} D^{2} - 2\beta^{2} D^{2} } \right)\hat{w} \\ &\quad+ M^{2} \left( {\frac{{D\hat{B}_{z} }}{{RP_{m} }} + i\alpha B_{b} \hat{B}_{z} } \right) \\ \end{aligned} \end{aligned} $$

(19)

$$ D\hat{B}_{z} + i\left( {\alpha \hat{B}_{x} + \beta \hat{B}_{y} } \right) = 0 $$

(20)

$$ \begin{aligned}& i\alpha R\left( {u_{b} - c} \right)\hat{B}_{x} + RP_{m} \hat{w}DB_{b} = \left( {D\hat{u} + i\alpha RP_{m} B_{b} \hat{u} + R\hat{B}_{z} Du_{b} } \right) \\ &\quad+ \frac{1}{{P_{m} }}\left( {D^{2} - \alpha^{2} - \beta^{2} } \right)\hat{B}_{x} \end{aligned} $$

(21)

$$ i\alpha R\left( {u_{b} - c} \right)\hat{B}_{y} = \left( {D\hat{v} + i\alpha RP_{m} B_{b} \hat{v}} \right) + \frac{1}{{P_{m} }}\left( {D^{2} - \alpha^{2} - \beta^{2} } \right)\hat{B}_{y} $$

(22)

$$ i\alpha R\left( {u_{b} - c} \right)\hat{B}_{z} = \left( {D\hat{w} + i\alpha RP_{m} B_{b} \hat{w}} \right) + \frac{1}{{P_{m} }}\left( {D^{2} - \alpha^{2} - \beta^{2} } \right)\hat{B}_{z} $$

(23)

Let us introduce the following modified Squire’s transformation

$$ \tilde{\alpha } = \sqrt {\alpha^{2} + \beta^{2} } ,\quad \tilde{u} = \frac{{\alpha \hat{u} + \beta \hat{v}}}{{\tilde{\alpha }}},\quad \tilde{w} = \hat{w},\;\tilde{P} = \frac{{\tilde{\alpha }\hat{P}}}{\alpha },\quad \tilde{B}_{x} = \frac{{\alpha \hat{B}_{x} + \beta \hat{B}_{y} }}{{\tilde{\alpha }}},\;\tilde{B}_{z} = \hat{B}_{z} ,\quad \tilde{R} = \frac{\alpha R}{{\tilde{\alpha }}},\;\tilde{\varLambda } = \varLambda , $$

$$ \tilde{M} = M,\tilde{P}_{m} = P_{m} $$

(24)

so that the exceeding 3D equations can be reduced to an equivalent 2D ones.

Equations (16)–(20), using Eq. (24), become

$$ D\tilde{w} + i\tilde{\alpha }\tilde{u} = 0 $$

(25)

$$ \begin{aligned}& i\tilde{\alpha }\left( {u_{b} - c} \right)\tilde{u} + \tilde{w}Dw_{b} = - i\tilde{\alpha }\tilde{P} + \frac{1}{{\tilde{R}}}\left( {D^{2} - \tilde{\alpha }^{2} } \right)\tilde{u}\\ &\quad - \frac{1}{{\tilde{R}\tilde{\varLambda }^{2} }}\left( {D^{2} - \tilde{\alpha }^{2} } \right)^{2} \tilde{u} + \tilde{M}^{2} \left( {\frac{{D\tilde{B}_{x} }}{{\tilde{R}\tilde{P}_{m} }} + i\tilde{\alpha }B_{b} \tilde{B}_{x} + \tilde{B}_{z} DB_{b} } \right) \end{aligned} $$

(26)

$$ \begin{aligned}& i\tilde{\alpha }\left( {u_{b} - c} \right)\tilde{w} = - D\tilde{P} + \frac{1}{{\tilde{R}}}\left( {D^{2} - \tilde{\alpha }^{2} } \right)\tilde{w} - \frac{1}{{\tilde{R}\tilde{\varLambda }^{2} }}\left( {D^{2} - \tilde{\alpha }^{2} } \right)^{2} \tilde{w}\\ &\quad + \tilde{M}^{2} \left( {\frac{{D\tilde{B}_{z} }}{{\tilde{R}\tilde{P}_{m} }} + i\tilde{\alpha }B_{b} \tilde{B}_{z} } \right) \end{aligned} $$

(27)

$$ D\tilde{B}_{z} + i\tilde{\alpha }\tilde{B}_{x} = 0 $$

(28)

$$ \begin{aligned} &i\tilde{\alpha }\tilde{R}\left( {u_{b} - c} \right)\tilde{B}_{x} + \tilde{R}\tilde{P}_{m} \tilde{w}DB_{b} = \left( {D\tilde{u} + i\tilde{\alpha }\tilde{R}\tilde{P}_{m} B_{b} \tilde{u} + \tilde{R}\tilde{B}_{z} Du_{b} } \right)\\ &\quad + \frac{1}{{\tilde{P}_{m} }}\left( {D^{2} - \tilde{\alpha }^{2} } \right)\tilde{B}_{x} \end{aligned} $$

(29)

$$ i\tilde{\alpha }\tilde{R}\left( {u_{b} - c} \right)\tilde{B}_{z} = \left( {D\tilde{w} + i\tilde{\alpha }\tilde{R}\tilde{P}_{m} B_{b} \tilde{w}} \right) + \frac{1}{{\tilde{P}_{m} }}\left( {D^{2} - \tilde{\alpha }^{2} } \right)\tilde{B}_{z} . $$

(30)

The relevant boundary conditions are

$$ \tilde{u} = D\tilde{u} = D^{3} \tilde{u} = \tilde{w} = 0,\,\,D\tilde{B}_{z} = \tilde{B}_{x} = 0\;{\text{at}}\;z = \pm 1. $$

(31)

It is viewed that Eqs. (25)–(30) and Eqs. (16)–(23) display the same mathematical structure if β = v = B_y = 0. The transformation involving the Reynolds number suggests that 2D disturbances are more unstable than 3D ones. The velocity stream function ϕ(x, z, t)and the magnetic stream function ψ(x, z, t)are introduced through (neglect the tilde in the subsequent analysis)

$$ u = \frac{\partial \phi }{\partial z},\;w = - \frac{\partial \phi }{\partial x},\;B_{x} = \frac{\partial \psi }{\partial z},\;B_{z} = - \frac{\partial \psi }{\partial x} $$

(32)

and eliminate P from the Eqs. (26) and (27) to obtain

$$ \begin{aligned} & \left( {u_{b} - c} \right)\left( {D^{2} - \alpha^{2} } \right)\phi - D^{2} u_{b} \,\phi \\ &\quad= \frac{1}{i\alpha R}\left( {D^{2} - \alpha^{2} } \right)^{2} \phi - \frac{1}{{i\alpha R\varLambda_{{}}^{2} }}\left( {D^{2} - \alpha^{2} } \right)^{3} \phi \\ & \quad + M^{2} \left[ {\frac{1}{{i\alpha R\,P_{m} }}D\left( {D^{2} - \alpha^{2} } \right)\psi + B_{b} \left( {D^{2} - \alpha^{2} } \right)\psi - D^{2} B_{b} \,\psi } \right] \\ \end{aligned} $$

(33)

$$ \left( {u_{b} - c} \right)\psi = \left( {\frac{1}{i\alpha R}D\phi + P_{m} B_{b} \phi } \right) + \frac{1}{{i\alpha R\,P_{m} }}\left( {D^{2} - \alpha^{2} } \right)\psi . $$

(34)

It is well known that P_m for the liquid sodium is of the order 10⁻⁵ and for mercury it is of the order 10⁻⁷ and hence terms in Eqs. (33) and (34) concerning B_b, and $\left( {u_{b} - c} \right)\psi$ in Eq. (34) can be neglected, provided that R is not too large. As a result, the above equations lead to a single stability equation

$$ \begin{aligned}& \left( {u_{b} - c} \right)\left( {D^{2} - \alpha^{2} } \right)\phi - \left( {D^{2} u_{b} } \right)\phi \\ &\quad= \frac{1}{i\alpha R}\left[ {\left( {D^{2} - \alpha^{2} } \right)^{2} \phi - \frac{1}{{\varLambda_{{}}^{2} }}\left( {D^{2} - \alpha^{2} } \right)^{3} \phi - M^{2} \,D^{2} \phi } \right]. \end{aligned} $$

(35)

Equation (35) agrees with Takashima [4] for the Newtonian case (Λ → ∞).

The boundary conditions on the magnetic field are no longer required now and the suitable boundary conditions are

$$ \phi = D\phi = D^{3} \phi = 0\quad {\text{at}}\quad z = \pm 1. $$

(36)

3 Numerical solution

The resulting stability equation is solved using the Chebyshev collocation method, which is an efficient and fast numerical solver for the investigation of the stability of fluid flow problems. We follow the procedure given in Shankar et al. [27] to discretize the stability equation, which yields

$$ \begin{aligned} & i\alpha R\left( {(u_{b} - c)\left( {\left( {1 - z_{j}^{2} } \right)^{2} \sum\limits_{m = 0}^{N} {B_{jm} \phi_{m} } - 8z_{j} \left( {1 - z_{j}^{2} } \right)\sum\limits_{m = 0}^{N} {A_{jm} \phi_{m} } + \left( {8z_{j}^{2} - 4\left( {1 - z_{j}^{2} } \right)} \right)\phi_{j} } \right) - \alpha^{2} (u_{b} - c)\phi_{j} - \frac{{d^{2} u_{b} }}{{dx^{2} }}\phi_{j} } \right) \\ & \quad = \left( {\left( {z_{j}^{2} - 1} \right)^{2} \sum\limits_{m = 0}^{N} {E_{jm} \phi_{m} } + 16z_{j} \left( {z_{j}^{2} - 1} \right)\sum\limits_{m = 0}^{N} {C_{jm} \phi_{m} } + 24\left( {3z_{j}^{2} - 1} \right)\sum\limits_{m = 0}^{N} {B_{jm} \phi_{m} } + 96z_{j} \sum\limits_{m = 0}^{N} {A_{jm} \phi_{m} } + 24\phi_{j} } \right) \\ & \quad \quad + \alpha^{4} \phi_{j} - 2\alpha^{2} \left( {\left( {1 - z_{j}^{2} } \right)^{2} \sum\limits_{m = 0}^{N} {B_{jm} \phi_{m} } - 8z_{j} \left( {1 - z_{j}^{2} } \right)\sum\limits_{k = 0}^{N} {A_{jm} \phi_{m} } + \left( {8z_{j}^{2} - 4\left( {1 - z_{j}^{2} } \right)} \right)\phi_{j} } \right) \\ & \quad \quad - \frac{1}{{\varLambda^{2} }}\left\{ \begin{aligned} & \left( {z_{j}^{2} - 1} \right)^{2} \sum\limits_{m = 0}^{N} {G_{jm} \phi_{m} } + 24z_{j} \left( {z_{j}^{2} - 1} \right)\sum\limits_{m = 0}^{N} {F_{jm} \phi_{m} } \\ & \quad + 60\left( {3z_{j}^{2} - 1} \right)\sum\limits_{m = 0}^{N} {E_{jm} \phi_{m} } + 480z_{j} \sum\limits_{m = 0}^{N} {C_{jm} \phi_{m} } + 360\sum\limits_{k = 0}^{N} {B_{jm} \phi_{m} } \\ & \quad - 3\alpha^{2} \left( \begin{aligned} \left( {z_{j}^{2} - 1} \right)^{2} \sum\limits_{m = 0}^{N} {E_{jm} \phi_{m} } + 16z_{j} \left( {z_{j}^{2} - 1} \right)\sum\limits_{m = 0}^{N} {C_{jm} \phi_{m} } + 24\left( {3z_{j}^{2} - 1} \right)\sum\limits_{m = 0}^{N} {B_{jm} \phi_{m} } \hfill \\ + 96z_{j} \sum\limits_{m = 0}^{N} {A_{jm} \phi_{m} } + 24\phi_{j} \hfill \\ \end{aligned} \right) \\ & \quad + 3\alpha^{4} \left( {\left( {1 - z_{j}^{2} } \right)^{2} \sum\limits_{m = 0}^{N} {B_{jm} \phi_{m} } - 8z_{j} \left( {1 - z_{j}^{2} } \right)\sum\limits_{m = 0}^{N} {A_{jm} \phi_{m} } + \left( {8z_{j}^{2} - 4\left( {1 - z_{j}^{2} } \right)} \right)\phi_{j} } \right) - \alpha^{6} \phi_{j} \\ \end{aligned} \right\}\backslash \\ & \quad \quad - M^{2} \left( {\left( {1 - z_{j}^{2} } \right)^{2} \sum\limits_{m = 0}^{N} {B_{jm} \phi_{m} } - 8z_{j} \left( {1 - z_{j}^{2} } \right)\sum\limits_{m = 0}^{N} {A_{jm} \phi_{m} } + \left( {8z_{j}^{2} - 4\left( {1 - z_{j}^{2} } \right)} \right)\phi_{j} } \right),\,j = 1\left( 1 \right)N - 1 \\ \end{aligned} $$

(37)

with the corresponding boundary conditions

$$ (1 - z_{j}^{2} )^{2} \sum\limits_{m = 0}^{N} {C_{jm} \phi_{m} } - 12z_{j} (1 - z_{j}^{2} )\sum\limits_{m = 0}^{N} {B_{jm} \phi_{m} } - 12(1 - 3z_{j}^{2} )\sum\limits_{m = 0}^{N} {A_{jm} \phi_{m} } + 24z_{j} \phi_{j} = 0, \, j{\text{ = 0}}\,\, \&\,\, N $$

(38)

where (Canuto et al. [40])

$$ A_{jk} = \left\{ {\begin{array}{*{20}l} {\frac{{c_{j} \left( { - 1} \right)^{m + j} }}{{c_{m} \left( {z_{j} - z_{m} } \right)}}} \hfill & {j \ne m} \hfill \\ {\frac{{z_{j} }}{{2\left( {1 - z_{j}^{2} } \right)}}} \hfill & {1 \le j = m \le N - 1} \hfill \\ {\frac{{2N^{2} + 1}}{6}} \hfill & {j = m = 0} \hfill \\ { - \frac{{2N^{2} + 1}}{6}} \hfill & {j = m = N} \hfill \\ \end{array} } \right. $$

(39)

$$ B_{jm} = A_{jk} \cdot A_{km} ,\quad C_{jm} = B_{jk} \cdot A_{km} ,\quad E_{jm} = C_{jk} \cdot A_{km} ,\quad F_{jm} = E_{jk} \cdot A_{km} ,\quad G_{jm} = F_{jk} \cdot A_{km} $$

(40)

with

$$ c_{j} = \left\{ {\begin{array}{*{20}l} 2 \hfill & {j = 0,N} \hfill \\ 1 \hfill & {1 \le j \le N - 1} \hfill \\ \end{array} } \right.. $$

The exceeding equations form the following system of linear algebraic equation

$$ \Delta_{1} X = c\Delta_{2} X $$

(41)

where c is the eigenvalue and X is the discrete representation of eigenfunctions; Δ₁ andΔ₂are matrices of order (N + 1). For fastened values of all parameters concerned within, the eigenvalue c which compose a definite non-trivial solution of Eq. (41) is reached. Once c is established, then the method and algorithm explained in Shankar et al. [41] are followed to find the critical parameters.

4 Energy analysis

To understand the physical mechanisms that contribute to instability, the two-dimensional kinetic energy balances are studied. The rate of change of kinetic energy in dimensionless form is given by

$$ \begin{aligned} & \frac{1}{2}\frac{\partial }{\partial t}\left\langle {u^{2} + v^{2} + w^{2} } \right\rangle = - \left\langle {uw\frac{{du_{b} }}{dz}} \right\rangle - \frac{1}{R}\left\langle {\left( {\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right) + \left( {\left( {\frac{\partial w}{\partial x}} \right)^{2} + \left( {\frac{\partial w}{\partial y}} \right)^{2} + \left( {\frac{\partial w}{\partial z}} \right)^{2} } \right)} \right\rangle \\ & \quad \quad - \frac{1}{{R\,\varLambda^{2} }}\left\langle {\left( \begin{aligned} u\left( {\frac{{\partial^{4} }}{{\partial x^{4} }} + \frac{{\partial^{4} }}{{\partial y^{4} }} + \frac{{\partial^{4} }}{{\partial z^{4} }} + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }} + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial z^{2} }} + 2\frac{{\partial^{4} }}{{\partial y^{2} \partial z^{2} }}} \right)u + \hfill \\ v\left( {\frac{{\partial^{4} }}{{\partial x^{4} }} + \frac{{\partial^{4} }}{{\partial y^{4} }} + \frac{{\partial^{4} }}{{\partial z^{4} }} + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }} + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial z^{2} }} + 2\frac{{\partial^{4} }}{{\partial y^{2} \partial z^{2} }}} \right)v + \hfill \\ w\left( {\frac{{\partial^{4} }}{{\partial x^{4} }} + \frac{{\partial^{4} }}{{\partial y^{4} }} + \frac{{\partial^{4} }}{{\partial z^{4} }} + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }} + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial z^{2} }} + 2\frac{{\partial^{4} }}{{\partial y^{2} \partial z^{2} }}} \right)w \hfill \\ \end{aligned} \right)} \right\rangle - \frac{{M^{2} }}{R}\left\langle {u^{2} } \right\rangle \\ & \quad = E_{s} + E_{d} + E_{c} + E_{M} . \\ \end{aligned} $$

(42)

Here, the brackets 〈 〉 represent the volumetric average over the volume of disturbance waves.

5 Results and discussion

The stability against small disturbances of the pressure-driven plane laminar motion of an electrically conducting couple stress fluid under a transverse magnetic field is investigated numerically using the Chebyshev collocation method. A necessary condition for the amplification of a disturbance in the basic flow field is found to be Λ > 2 M. We begin the presentation by demonstrating the basic velocity u_b and the basic magnetic induction B_b, which strongly modify the stability of the system. Figures 2a, b and 3a, b display the impact of Hartman number and couple stress parameter on u_b and B_b, respectively. Figure 2a, b, respectively exhibit that raise in the values of M and Λ is to boost the fluid flow. Figure 3a, b show that B_b is concealed with rising M (Fig. 3a) and Λ (Fig. 3b).

Fig. 2

Basic velocity profiles for different values of a Hartmann number and b couple stress parameter

Fig. 3

Basic magnetic field profiles for different values of a Hartmann number and b couple stress parameter

Figure 4 displays the neutral stability curves in the (R, α)—plane showing the division of the plane into stable and unstable zones. The neutral stability curve is obtained when M → 0 (hydrodynamic case) and $\varLambda \to \infty$(absence of couple stresses) (Fig. 4a) from the present code and it can be seen that R_c = 5772.22 andα_c = 1.020, which are the known standard results (Orszag [42]). The computed values of R_c for several values of M as Λ → ∞ are compared in Fig. 4b with those of Takashima [4] and the outcomes complement with one another. These cross checking of results inspire further assurance in the prophecy of our numerical procedure.

Fig. 4

Neutral stability curves

The neutral stability curves for various values of Hartman number and couple stress parameter are exhibited, respectively, in Fig. 4c, d. We observe that increasing M is to increase R_c, indicating that the Hartman number enhances the stability of the system (Fig. 4c), whereas a dual behavior is observed with increasing Λ (Fig. 4d). We locate that R_c move towards higher values of α with increasing M representing that the cell width diminishes. However, the cell width enlarges with increasing Λ.

Figure 5a illustrates the variation of R_c as a function of Λ for various values of M. When M = 0, the curve emanates from R_c = 45695.77 and experiences a steep fall as the value of Λ increases to 6. As the curve approaches to 20, the gradient of the curve changes from negative to positive. The curve progresses with a gradually increasing positive gradient thereafter. The curve of $M = \sqrt 2$ has a value of R_c = 11179.47 at Λ = 2.9. The curve faces a negative gradient initially and thereafter progresses with a gradually increasing positive gradient. The curves of M² = 5, 10, 20 and 25 follow a similar trend throughout the domain of Λ considered. The curve of M = 0 lies well below the curves of M ≠ 0 indicating the magnetic field is more effective in stabilizing the system. This is due to the Lorentz force seizes backing the flow and therefore higher Reynolds number is necessary to coerce the flow. It is further seen that R_c decrease with increasing value of Λ initially for each M due to decrease in the couple stress viscosity and thus it has a destabilizing effect on the flow. However, R_c increases at higher values of Λ as it turns to Newtonian case.

Fig. 5

Variation of a critical Reynolds number R_c, b critical wave number α_c and c critical wave speed c_c with couple stress parameter Λ for various values of Hartmann number M

Figure 5b establishes a relationship between α_c and Λ for different values ofM. The curve of M = 0 emanates from α_c= 1.604 when Λ = 1 and it progresses with a decreasing value of α_c for increasing value ofΛ. The curve of M² = 2 runs parallel to the curve of M = 0 but originates from (2.9, 1.538). The curve of M² = 5 emanates from (4.5, 1.480) and has a constant negative gradient throughout where the value of α_c decreases with increasing value ofΛ. The curves of M² = 10, 20 and 25 follow a similar trend with a positive gradient at the beginning followed by a gradual change to negative gradient, that is, the value of α_c increases initially and then gradually decreases as the curve progresses. The corresponding critical wave speeds are illustrated in Fig. 5c as a function of Λ for various values ofM. The curves of M² = 0, 2, 5, 10, 20 and 25 follow a similar trend where they experience a gradual fall in their value as they progress. The curves for higher values of M originate with a smaller value initially and the curves run almost parallel to each other. All the curves have their maximum value at their respective origin.

To obtain a clear understanding of the fluid flow stability characteristics for specific parameters, the secondary flow energy spectra are examined in detail. Theoretically at the critical points, ∂ E_kin/ ∂ t = 0. Of all the numerical results produced here for the energy analysis, this phenomenon can be observed at the critical points. It can be seen that for all the values of M considered here, E_s has a propensity to destabilize the flow whereas E_d, E_c and E_M stabilize it, throughout the domain of couple stress parameter. However, the contribution of E_M is negligible in the domain. One important finding of this study is that prior to the threshold value of couple stress parameter, the contribution of E_c to stabilize the flow is more than offered by E_d but beyond the threshold value this characteristic reverses. Threshold values of couple stress parameter from where this reversal observed is shown in Fig. 6a–d. Quantitatively, prior to the threshold value of couple stress parameter, contribution of E_c (E_d) in the stability of the fluid flow varies from 78 to 48% (19 to 48%). It is also noted that the contribution of E_d (E_c) is strictly increasing (decreasing) as a function of couple stress parameter.

Fig. 6

The rate of change of kinetic energy as a function of Λ when a M² = 5 b M² = 10 c M² = 20 d M² = 30

6 Conclusions

The stability of forced convective flow is investigated in a horizontal channel of electrically conducting couple stress fluid under the influence of a uniform vertical magnetic field. The complicated complex stability equation is obtained and solved computationally by using the Chebyshev collocation method after determining that two-dimensional motions are more unstable than three-dimensional motions via an analogue of Squire’s transformation. The existence of a point in the basic flow field, for which the couple stress parameter must be greater than twice the Hartman number, is a necessary condition to be noted in order to exacerbate a disturbance. The Hartman number significantly affects the flow and increase in its value results in the stabilization of the fluid flow while increase in the couple stress parameter shows a twofold behavior. Energy spectrum indicates that kinetic energy due to the shear term (E_s) has a propensity to destabilize the flow while kinetic energy due to surface drag (E_d) and couple stress viscosity (E_c) stabilizes it, throughout the domain of couple stress parameter. Nevertheless, the contribution of kinetic energy due to magnetic field (E_M) is found to be negligible. Contribution of E_c on the stability of flow is observed to be more (less) than E_d prior (beyond) the threshold value of couple stress parameter. Also noted that the contribution of E_d (E_c) is strictly increasing (decreasing) as a function of couple stress parameter. Finally, it is observed that the transverse magnetic field has a stabilizing effect on the Poiseuille flow even in the presence of couple stresses.