1 Introduction

1.1 Small-scale effect

The small-scale effect, which has been justified by various empirical observations of mechanical behavior in small-scale structures [1,2,3], plays a crucial role in optimal design of micro- and nanoelectromechanical systems (MEMS and NEMS) e.g. atomic force microscopes, chemical sensing device, actuators, and pumps. Owing to lack of the length scale parameters in its constitutive equations, the classical continuum theory cannot appropriately estimate the design parameters of micro- and nanostructures such as natural frequencies, maximum deflections and buckling loads. Consequently, several nonclassical continuum theories have been proposed to account for the small-scale effect on the mechanical behavior of small-scale structures and eliminate the differences between results determined by theoretical and experimental methods [3,4,5]. Concerning the submicron structures, the dispersion phenomenon which is the consequence of long-range intermolecular forces, was detected in propagations of waves with short wavelengths in elastic bodies [5,6,7]. To capture long-range effects, Eringen [6] considered that the nonlocal strain of points under translational motion is the same with that of the classical theory, but the stress at a point is relevant to the strain in a region near that point. In recent years, researchers’ attention has been devoted to survey static [8,9,10,11,12], vibration [13, 14], buckling and postbuckling [15,16,17], dynamic [18,19,20,21] and thermomechanical [22,23,24,25,26] behavior of micro-and nanostructures according to the nonclassical continuum theories such as the nonlocal, modified couples stress and modified strain gradient theories.

1.2 Carbon nanotubes reinforced composites

The initial idea of carbon nanotubes (CNTs), as a type of novel materials with excellent thermal, electrical and mechanical properties especially low density, extraordinary strength and corrosion resistance was proposed by Iijima [27]. By tradition, composites reinforced by carbon, glass, aramid or basalt fibers have a wide range of applications in structural systems in civil, mechanical, marine, aerospace engineering and many other modern industries. Recently, CNTs which can provide good interfacial bonds, have been utilized instead of traditional fibers for the reinforcement of matrix phases in composites. One of major applications of CNTs is to design nanosensors owing to their exceptional mechanical properties which leads to a reachable ultrahigh frequency range up to the terahertz order and a possible ultrahigh sensitivity. In order to analyze the mechanical behavior of CNT reinforced composites and simulate their effective material properties, various experiments and theoretical techniques have been presented namely, molecular dynamics (MD) simulation [28, 29], representative volume element (RVE) [30], rule of mixture [31,32,33], and experimentations [34,35,36]. In recent decade, many demands have been raised for production of multilayer MEMS and NEMS with variable properties which are used in thermal environment [37]. Consequently, manufacturing technologies were extended to make functionally graded (FG) layers in micron and submicron dimensions with the desired electrical and mechanical properties at their bottom and top sides. Therefore, many researchers have focused on the thermal [38,39,40] and mechanical [41,42,43,44] behavior of FG micro- and nanostructures. With the rapid advancement of manufacturing technology, CNTs are used as the favorite reinforcements for polymer nanolayers utilized in different engineering applications.

1.3 A literature review on CNTRC beams

Some studies accomplished on the bending, buckling and vibration behavior of CNTRC beams are reviewed here. By employing the Euler–Bernoulli beam theory and von Kármán geometric nonlinearity, Rafiee et al. [45] analyzed large-amplitude free vibrations of FG-CNTRC beams with surface-bonded piezoelectric layers in thermal environment and subjected to an input voltage. To solve the governing equations of the piezoelectric CNTRC beams, they applied the Galerkin method in conjunction with the multiple time scales method. Ke et al. [46] surveyed dynamic stability behavior of Timoshenko FG-CNTRC beams under axial loading. In their work, the material properties of FG-CNTRCs have been assumed to be determined corresponding to the rule of mixture. In order to solve three governing equations for assessment of the dynamic stability characteristics, they utilized the differential quadrature (DQ) method. In the work of Ansari et al. [47], by taking into account the von Kármán geometric nonlinearity, forced vibration behavior of Timoshenko CNTRC beams has been studied. They discretized the nonlinear governing equations and associated boundary conditions via the generalized differential quadrature (GDQ) method and then employed a Galerkin-based numerical technique to reduce the set of nonlinear partial differential equations into a time-varying set of Duffing-type ordinary ones. By implementing finite element method (FEM), dynamic analysis of Timoshenko and Euler–Bernoulli FG nanocomposite beams reinforced by randomly oriented carbon nanotubes under a moving load has been conducted by Yas and Heshmati [48]. They modelled the material properties via the Eshelby–Mori–Tanaka approach on the basis of an equivalent fiber. By defining the temperature-dependent material properties of fibers and polymeric matrix through a refined rule of mixture, Jam and Kiani [49] presented responses of Timoshenko FG-CNTRC beams subjected to the action of an impacting mass. To derive time history deflection, they used the conventional polynomial Ritz method together with the Runge–Kutta method. By applying the p-Ritz method to extract natural frequencies, Lin and Xiang [50] explored the linear free vibration of FG-CNTRC beams based on the first order and third order shear deformation theories. Shen and Xiang [51] carried out an investigation on the large amplitude vibration, nonlinear bending and thermal postbuckling behavior of CNTRC beams resting on an elastic foundation in thermal environments. They derived the motion equations of CNTRC beams by means of a higher order shear deformation beam theory and solved them by utilizing a two-step perturbation procedure. By accounting for the von Kármán geometric nonlinearity effect, Rafiee et al. [52] assessed thermal post-buckling behavior of Euler–Bernoulli CNTRC beams with surface-bonded piezoelectric layers. Based on the first-order shear deformation beam theory with von-Kármán geometric nonlinearity, Wu et al. [53] conducted an analysis on the thermal post-buckling behavior of FG-CNTRC beams subjected to in-plane temperature change incorporating the effect of imperfection sensitivity. In their study, generic imperfection function has been used to describe different possible imperfections such as sine type, global and localized imperfections. They solved the governing differential equations with the aid of DQ method in conjunction with modified Newton–Raphson technique. Yas and Samadi [54] carried out the free vibration and buckling analysis of Timoshenko CNTRC beams resting on an elastic foundation. In this work, to figure out natural frequencies and buckling loads, the governing equations have been solved through the GDQ method for beams with different boundary conditions.

1.4 Present study

From the abovementioned literature review, it is revealed that researches reported on the mechanical analysis of CNTRCs have been conducted on the basis of classical continuum theory, which is not able to account for small-scale effect. In addition, to solve governing equations presented in previous investigations, semi-analytical methods such as Ritz and Galerkin methods or numerical methods have been implemented. The main contribution of current study is to develop size-dependent exact solutions for bending, buckling and free vibration of FG-carbon nanotube-reinforced composite nanobeams in the framework of nonlocal elasticity theory. Material properties of FG-CNTRCs are assumed to be graded in the thickness direction and computed via extended rule of mixture. Based on the nonlocal elasticity theory and Timoshenko beam model, dynamic equilibrium equations of CNTRC nanobeams with arbitrary boundary conditions are derived. For bending and buckling analysis, the bending and stretching coupled equations of CNTRC nanobeams are reduced to a decoupled fifth-order ordinary differential equation with respect to rotation of cross-section which can be solved exactly. For free vibration analysis, the differential operator method is applied to obtain the decoupled sixth-order differential equations governing the in-plane displacement, transverse deflection and the rotation of cross-section. A system of homogenous algebraic equations is obtained for arbitrary boundary conditions and the frequency equation is derived by setting coefficients’ matrix to zero. Detailed numerical results are provided to discuss the effects of CNT distribution, nonlocal parameter, aspect ratio and boundary conditions on the deflection, buckling and natural frequency of FG-CNTRC nanobeams.

2 Theoretical formulation

2.1 Problem definition

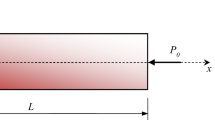
Consider a beam composed of CNTs and an isotropic matrix with length \(L\), width \(b\) and thickness \(h\), as shown in Fig. 1a. Also, the uniform distribution (UD) of CNTs and functionally graded (FG) CNTs, whose volume fraction is continuously varied through the thickness direction, are depicted in Fig. 1b. Moreover, a Cartesian coordinate system \(\left( {x,y, z} \right)\) is defined to indicate the components of displacement vector \((u_{1}\), \(u_{2}\), \(u_{3} )\) in these directions. According to Timoshenko beam model, the displacement components are given by:

$$u_{1} = u(x,t) + z\,\psi (x,t),\,\,\,\,\,u_{2} = 0,\,\,\,\,\,u_{3} = \,\,w(x,t)$$
(1)

where \(u\left( {x,t} \right)\) is the in-plane displacement component \(\left( {z = 0} \right)\) in the length direction and \(w\left( {x,t} \right)\) is the transverse displacement. Also, \(\psi \left( {x,t} \right)\) is the rotation of cross-section about the y-axis. Meanwhile, the variable t is time and z is the distance from mid-plane.

Fig. 1
figure 1

A carbon nanotube reinforced composite nanobeam

Full size image

2.1.1 Carbon nanotube-reinforced composites

Here, the effective material properties of Carbon nanotube-reinforced composites (CNTRCs) are estimated using the extended rule of mixture which considers the size-dependence of nanostructures. In the first step, the CNT volume fraction \(V_{cnt}\) for UD-CNTRC beams and two types of FG-CNTRC beams are as follows:

$${\text{UD}}:\,\,\,V_{cnt} = V_{cnt}^{*}$$
(2a)
$${\text{FGX}}:V_{cnt} = 4\frac{\left| z \right|}{h}V_{cnt}^{*} ,\quad {\text{FGO}}:V_{cnt} = \left( {2 - 4\frac{\left| z \right|}{h}} \right)V_{cnt}^{*}$$
(2b)

In the view of Eq. (2b), it can be readily concluded that the top and bottom surfaces of an FGX-CNTRC beam are CNT-rich while the mid-plane of an FGO-CNTRC beam is CNT-rich. The parameter \(V_{cnt}^{*}\) appearing in Eq. (2) is the total volume fraction of a CNTRC beam determined by the following:

$$V_{cnt}^{*} = \frac{{M_{cnt} }}{{\frac{{\rho_{cnt} }}{{\rho_{m} }} + M_{cnt} \left( {1 - \frac{{\rho_{cnt} }}{{\rho_{m} }}} \right)}}$$
(3)

where \(M_{cnt}\) is the mass fraction of CNTs. Also, and \(\rho_{m}\) denote the densities of CNT and matrix, respectively. Note that the total CNT volume fractions of UD- and FG-CNTRC beams given in Eq. (2) are exactly same. Taking into account the size-dependence of nanostructures, the extended rule of mixture is used to estimate the effective material properties of CNTRCs as follows:

$$\begin{aligned} &E_{11} = \eta_{1} V_{cnt} E_{11}^{cnt} + V_{m} E_{m} ,\quad \frac{{\eta_{2} }}{{E_{22} }} = \frac{{V_{cnt} }}{{E_{22}^{cnt} }} + \frac{{V_{m} }}{{E_{m} }},\quad \\&\frac{{\eta_{3} }}{{G_{12} }} = \frac{{V_{cnt} }}{{G_{12}^{cnt} }} + \frac{{V_{m} }}{{G_{m} }},\quad v_{12} = V_{cnt} v_{12}^{cnt} + V_{m} v_{m} , \end{aligned}$$
(4a)
$$\rho = V_{cnt} \rho_{cnt} + V_{m} \rho_{m}$$
(4b)

where \(E_{11}^{cnt}\), \(E_{22}^{cnt}\), \(E_{m}\), \(G_{12}^{cnt}\), \(G_{m}\), \(V_{12}^{cnt}\), and \(v_{m}\) are Young’s moduli, shear moduli and Poisson’s ratios. Also, superscript or subscript \(cnt\) and m stand for CNTs and the matrix, respectively. \(\rho_{cnt}\), \(\rho_{m}\), \(V_{cnt}\) and \(V_{m}\) are the densities and volume fractions of CNTs and the matrix. It is to be noticed that the volume fractions are related as \(V_{cnt} + V_{m} = 1\) with each other. Also, \(\eta_{i}\)’s (for \(i = 1,2,3)\) are the CNT efficiency parameters considering the size-dependent effects.

2.1.2 Nonlocal elasticity theory

According to the nonlocal elasticity theory [5,6,7], the stress tensor at a point x of an elastic body depends on the strain tensor at all other points of body. On the basis of atomic theory of lattice dynamics and experimental observations on phonon dispersion, the nonlocal stress tensor \({\varvec{\upsigma}}\) at point \({\text{x}}\) can be expressed as follows:

$${\varvec{\upsigma}}({\text{x}}) = \int_{V} {K(\left| {{\text{x}}^{\prime } - {\text{x}}} \right|} ,\tau ){\mathbf{t}}({\text{x}}^{\prime } ){\text{dx}}^{\prime }$$
(5)

In Eq. (5), the nonlocal modulus is denoted by the kernel function, \(K(|{\text{x}}^{\prime } - {\text{x}}|,\tau )\), in which \(\left| {{\text{x}}^{\prime } - {\text{x}}} \right|\) is the distance (in Euclidean norm) and \(\tau\) represents a material constant that depends on internal and external characteristic lengths. Also, \({\mathbf{t}}\left( {x^{\prime } } \right)\) is the classical, macroscopic stress tensor at point \(x^{\prime }\) given by the generalized Hooke’s law:

$${\mathbf{t}}({\text{x}}^{\prime } ) = {\mathbf{C}}({\text{x}}^{\prime } ):{\varvec{\upvarepsilon}}({\text{x}}^{\prime } )$$
(6)

where \({\mathbf{C}}\) and \({\varvec{\upvarepsilon}}\) are the fourth-order elasticity and strain tensor, respectively. The symbol: refers to the ‘double-dot product’. The nonlocal constitutive relation of a Hookean solid is defined using the constitutive relations given in Eqs. (5) and (6). Equation (5) denotes the weighted average of the strain field in the whole body related to the stress field at a point \({\text{x}}\). Since solving of the elasticity problems is effortful via integral constitutive relation in Eq. (5), an equivalent differential form of the integral constitutive relation is generally applied to model different problems. The differential form of nonlocal constitutive relations for an elastic body is written as below:

$$(1 - \mu \,\nabla^{2} ){\varvec{\upsigma}}({\text{x}}) = {\mathbf{C}}({\text{x}}):{\varvec{\upvarepsilon}}({\text{x}})$$
(7a)

where \(\mu\) is the nonlocal parameter given by:

$$\mu = (\tau l)^{2} \quad {\text{and}}\quad \tau = \frac{{e_{0} a}}{l}$$
(7b)

In Eq. (7b), \(e_{0}\) is a material constant, and \(a\) and \(l\) denote the internal and external characteristic lengths, respectively.

2.2 Motion equations

Here, motion equations of carbon nanotube-reinforced composite beams under axial and transverse loading are derived based on the nonlocal elasticity theory. To this purpose, the nonzero strain components of a Timoshenko beam are as follows:

$$\varepsilon_{xx} = \frac{\partial u}{\partial x} + z\,\frac{\partial \psi }{\partial x},\quad 2\varepsilon_{xz} = \frac{\partial w}{\partial x} + \psi$$
(8)

It is worth mentioning that the shear correction factor is required to compensate for the error of Timoshenko beam model which is due to the assumption of constant shear stress. Also, the shear correction factor is a multifunction of different variables such as the material, geometric parameters, the type of load and boundary conditions. Based on the continuum mechanics theory for a linear elastic body, the strain energy of the Timoshenko beam is given by [23, 24]:

$$\delta U = \int\limits_{0}^{L} {\left[ {N_{xx} \delta \left( {\frac{\partial u}{\partial x}} \right) + M_{xx} \delta \left( {\frac{\partial \psi }{\partial x}} \right) + Q_{x} \delta \left( {\frac{\partial w}{\partial x}} \right) + \psi )} \right]dx}$$
(9)

where \(N_{xx}\), \(M_{xx}\) and \(Q_{x}\) are, respectively the in-plane force, bending moment and transverse shear force resultants of a carbon nanotube-reinforced composite beam which are obtained using the nonlocal elasticity theory as follows:

$$\,N_{xx} - \mu \,\frac{{\partial^{2} N_{xx} }}{{\partial x^{2} }} = A_{11} \frac{\partial u}{\partial x} + B_{11} \frac{\partial \psi }{\partial x},$$
(10a)
$$\,M_{xx} - \mu \,\frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} = B_{11} \frac{\partial u}{\partial x} + D_{11} \frac{\partial \psi }{\partial x},$$
(10b)
$$\,Q_{x} - \mu \,\frac{{\partial^{2} Q_{x} }}{{\partial x^{2} }} = A_{55} \left( {\psi + \frac{\partial w}{\partial x}} \right)$$
(10c)

where, the stiffness coefficients appearing in (10) are defined by:

$$\,\left\{ {A_{11} ,B_{11} ,D_{11} } \right\} = b\mathop \smallint \limits_{ - h/2}^{h/2} \frac{{E_{11} (z)}}{{1 - v_{12} (z)v_{21} (z)}}\left\{ {1,z,z^{2} } \right\}dz$$
(11a)
$$A_{55} = bK_{S} \mathop \smallint \limits_{ - h/2}^{h/2} G_{12} (z)dz$$
(11b)

Here, \(K_{S}\) is the shear correction factor. Applying the integration by parts technique, the variation of strain energy in (9) can be rewritten as follows:

$$\begin{aligned} \delta U &= - \int\limits_{0}^{L} {\left[ {\frac{{\partial N_{xx} }}{\partial x}\,\,\delta u + \left( {\frac{{\partial M_{xx} }}{\partial x} - Q_{x} } \right)\delta \psi - \frac{{\partial Q_{x} }}{\partial x}\delta w} \right]} dx\\ &\quad + \left[ {N_{xx} \delta u + M_{xx} \delta \psi + Q_{x} \delta w} \right]_{x = 0}^{x = L} \end{aligned}$$
(12)

The variation of kinematic energy for a carbon nanotube-reinforced composite beam is expressed as follows:

$$\begin{aligned} T & = \frac{1}{2}\int\limits_{A} {\int\limits_{0}^{L} {\rho (z)\left[ {\left( {\frac{{\partial u_{1} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{2} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{3} }}{\partial t}} \right)^{2} } \right]dz\,dA} } \\ & \quad = \frac{1}{2}\int\limits_{0}^{L} {\left[ {I_{1} \left( {\frac{\partial u}{\partial t}} \right)^{2} + 2I_{2} \left( {\frac{\partial \psi }{\partial t}} \right)\left( {\frac{\partial u}{\partial t}} \right)}\right.}\\&\qquad{\left.{ +\, I_{3} \left( {\frac{\partial \psi }{\partial t}} \right)^{2} + I_{1} \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right]dz} \\ \end{aligned}$$
(13)

where \(\left\{ {I_{1} ,I_{2} ,I_{3} } \right\} = b\mathop \smallint \limits_{ - h/2}^{h/2} \rho \left( z \right)\left\{ {1,z,z^{2} } \right\}dz\). The variation of kinematic energy can be expressed as follows:

$$\delta T = \int\limits_{0}^{L} {\left\{ {\left[ {I_{1} \frac{\partial u}{\partial t} + I_{2} \frac{\partial \psi }{\partial t}} \right]\delta \left( {\frac{\partial u}{\partial t}} \right) + \left[ {I_{3} \frac{\partial \psi }{\partial t} + I_{2} \frac{\partial u}{\partial t}} \right]\delta \left( {\frac{\partial \psi }{\partial t}} \right) + I_{1} \frac{\partial w}{\partial t}\delta \left( {\frac{\partial w}{\partial t}} \right)} \right\}dz}$$
(14)

Using the integration by parts on time (\(t\)), the variation of kinematic energy is rewritten as follows:

$$\begin{aligned} \delta T & = \int\limits_{0}^{L} {\frac{\partial }{\partial t}\left\{ {\left[ {I_{1} \frac{\partial u}{\partial t} + I_{2} \frac{\partial \psi }{\partial t}} \right]\delta u }\right.}\\&\quad{\left.{+\, \left[ {I_{3} \frac{\partial \psi }{\partial t} + I_{2} \frac{\partial u}{\partial t}} \right]\delta \psi + I_{1} \frac{\partial w}{\partial t}\delta w} \right\}dz} \\ & \quad - \int\limits_{0}^{L} {\left\{ {\left[ {I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi }}{{\partial t^{2} }}} \right]\delta u }\right.}\\&\quad{\left.{+\, \left[ {I_{3} \frac{{\partial^{2} \psi }}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} u}}{{\partial t^{2} }}} \right]\delta \psi + I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }}\delta w} \right\}dz} \\ \end{aligned}$$
(15)

Finally, the variation of external work done by the transverse load per unit length with arbitrary distribution is given by:

$$\delta W = \int\limits_{0}^{L} {\left[ {q(x,t)\delta w + P\frac{\partial w}{\partial x}\delta \left( {\frac{\partial w}{\partial x}} \right)} \right]} dx$$
(16)

Applying the integration by parts, the variation of external work is rewritten as follows:

$$\delta W = \int\limits_{0}^{L} {\left[ {q(x,t) - P\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right]\delta w} \,dx + \left. {P\frac{\partial w}{\partial x}\delta w} \right|_{x = 0}^{x = L}$$
(17)

Substituting for the variations of strain energy, kinematic energy and external work from (12), (15) and (17) into the Hamilton principle \(\left( {\int {\int {\int {\left( {\delta U + \delta T - \delta W} \right)dV = 0} } } } \right)\) results in the motion equations of a carbon nanotube-reinforced composite beam subjected transverse load as follows:

$$\delta u:\,\,\frac{{\partial N_{xx} }}{\,\partial x} - I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \psi }}{{\partial t^{2} }} = 0,$$
(18a)
$$\delta \psi :\,\,\frac{{\partial M_{xx} }}{\,\partial x} - Q_{x} - I_{2} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{3} \frac{{\partial^{2} \psi }}{{\partial t^{2} }} = 0,$$
(18b)
$$\delta w:\,\,\frac{{\partial Q_{x} }}{\,\partial x} + q(x,t) - P\frac{{\partial^{2} w}}{{\partial x^{2} }} - I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} = 0,$$
(18c)

Using the fundamental lemma of calculus of variations, the boundary conditions involve specifying one element of each of the two pairs (\(N_{xx}\), \(\delta u\)), (\(M_{xx}\), \(\delta \psi\)) and (\(Q_{x} - P\partial w/\partial x\),\(\delta w\)).

In order to obtain the frequency responses of CNTRC beams, it is required to write the motion equations in the terms of kinematic variables and stiffness coefficients. To this end, substituting for \(\partial N_{xx} /\partial x\) from (18a) into Eq. (10a) results in:

$$\,N_{xx} = A_{11} \frac{\partial u}{\partial x} + B_{11} \frac{\partial \psi }{\partial x} + \mu \,\left[ {I_{1} \frac{{\partial^{3} u}}{{\partial t^{2} \partial x}} + I_{2} \frac{{\partial^{3} \psi }}{{\partial t^{2} \partial x}}} \right]\,$$
(19)

By eliminating \(Q_{x}\) between the governing equations given in (18b) and (18c), one can readily obtain

$$\,\frac{{\partial^{2} M_{xx} }}{{\,\partial x^{2} }} + q(x,t) - P\frac{{\partial^{2} w}}{{\partial x^{2} }} - I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{3} u}}{{\partial t^{2} \partial x}} - I_{3} \frac{{\partial^{3} \psi }}{{\partial t^{2} \partial x}} = 0$$
(20)

Substituting for \(\partial^{2} M_{xx} /\partial x^{2}\) from Eq. (20) into Eq. (10b) results in:

$$\begin{aligned} M_{xx} &= B_{11} \frac{\partial u}{\partial x} + D_{11} \frac{\partial \psi }{\partial x} + \mu \left[ { - q(x,t) + P\frac{{\partial^{2} w}}{{\partial x^{2} }} + I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }}\,\,\,\, }\right.\\&\quad\left.{+\, I_{2} \frac{{\partial^{3} u}}{{\partial t^{2} \partial x}} + I_{3} \frac{{\partial^{3} \psi }}{{\partial t^{2} \partial x}}} \right]\,\,\, \end{aligned}$$
(21)

By substitution of \(\partial Q_{x} /\partial x\) from Eq. (18c) into Eq. (10c), one can get:

$$Q_{x} = \,A_{55} \left( {\psi + \frac{\partial w}{\partial x}} \right) + \mu \left[ { - \frac{\partial q}{\partial x} + P\frac{{\partial^{3} w}}{{\partial x^{3} }} + I_{1} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}} \right].$$
(22)

2.3 Exact solutions

The optimal design of beams has an important role for development of MEMS and NEMS technology. The mechanical parameters including maximum deflection and stress, buckling load and frequency responses are selected as design variables in different applications. In this section, exact solutions for bending, buckling and vibration behavior of CNTRC beams with arbitrary boundary conditions are developed which can be used in the conceptual design.

2.3.1 Bending and buckling behavior

Here, the bending problem of CNTRC beams under arbitrary transverse loading \(q\left( x \right)\) and constant axial force \(P\) is investigated to find the displacement field variables \(u\left( x \right)\), \(\psi \left( x \right)\), and \(w\left( x \right)\). To this end, Eq. (18a) is integrated to yield (ignoring kinematic terms):

$$N_{xx} = P = {\text{constant}},$$
(23)

where \(P\) is a constant value of axial load. It is to be noticed that the kinematic terms appearing in the motion equations and the stress resultants are neglected for study of bending and buckling behavior. In the view of Eq. (23), term \(du/dx\) is obtained by solving of Eq. (19) as follows:

$$\frac{du}{dx}\, = \frac{1}{{A_{11} }}\left[ {P - B_{11} \frac{d\psi }{dx}} \right]\,$$
(24)

Upon substitution of Eq. (24) into Eq. (21), one can get

$$M_{xx} = \left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right)\frac{d\psi }{dx} + \frac{{B_{11} }}{{A_{11} }}P - \mu \left( {q - P\frac{{d^{2} w}}{{dx^{2} }}} \right)$$
(25)

By substituting of \(M_{xx}\) and \(Q_{x}\) from Eqs. (21) and (22) into (18b), ensuing equation may be solved for \(dw/dx\) to get

$$\frac{dw}{dx} = \frac{1}{{A_{55} }}\left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right)\frac{{d^{2} \psi }}{{dx^{2} }} - \psi$$
(26)

Upon substitution of Eq. (26) into Eq. (22), one can get

$$\begin{aligned} Q_{x} &= \left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right)\frac{{d^{2} \psi }}{{dx^{2} }} \\ &\quad+ \mu \left[ { - \frac{\partial q}{\partial x} + P\left\{ {\frac{1}{{A_{55} }}\left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right)\frac{{d^{4} \psi }}{{dx^{4} }} - \frac{{d^{2} \psi }}{{dx^{2} }}} \right\}} \right] \end{aligned}$$
(27)

By substitution of \(Q_{x}\) from Eq. (27) into Eq. (18c), the uncoupled fifth-order differential equation governing on \(\psi \left( x \right)\) is obtained as follows:

$$a_{1} P\frac{{d^{5} \psi }}{{dx^{5} }} + (a_{2} - a_{3} P)\frac{{d^{3} \psi }}{{dx^{3} }} + P\frac{d\psi }{dx} + \bar{q}(x) = 0$$
(28)

where

$$\begin{aligned} &a_{1} = \frac{\mu }{{A_{55} }}\left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right),\quad a_{2} = D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }},\quad\\& a_{3} = \mu + \frac{1}{{A_{55} }}\left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right) \end{aligned}$$
(29a)
$$\bar{q}(x) = \left[ {1 - \mu \frac{{d^{2} }}{{dx^{2} }}} \right]q(x)$$
(29b)

By integrating Eq. (26) results in

$$w = \frac{1}{{A_{55} }}\left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right)\frac{d\psi }{dx} - \int {\psi dx} + D_{0}$$
(30)

where \(D_{0}\) is an integration constant.

2.3.1.1 Bending problem

For bending problem (\(P = 0\)), the decoupled governing equation is simplified as follows:

$$\frac{{d^{3} \psi }}{{dx^{3} }} = - \frac{1}{{a_{2} }}\bar{q}(x)$$
(31)

Finally, the general solution of the fourth-order differential equation in (31) is obtained to be

$$\psi = C_{0} + C_{1} x + C_{2} x^{2} + \psi_{p} (x)$$
(32a)
$$\psi_{p} (x) = - \frac{1}{{a_{2} }}\iiint {\bar{q}(x)dxdxdx}$$
(32b)

where \(C_{i}\)’s are three integration constants which are determined by imposing the appropriate boundary conditions at \(x = 0\) and \(x = L\). Substituting for \(\psi\) from Eq. (32a) into Eq. (30) results in

$$\begin{aligned} w &= \frac{1}{{A_{55} }}\left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right)\left[ {C_{1} + 2C_{2} x} \right] \\ &\quad- \left[ {C_{0} x + C_{1} \frac{{x^{2} }}{2} + C_{2} \frac{{x^{3} }}{3}} \right] + D_{0} + w_{p} (x) \end{aligned}$$
(33a)
$$w_{p} (x) = \frac{1}{{A_{55} }}\left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right)\frac{{d\psi_{p} }}{dx} - \int {\psi_{p} dx}$$
(33b)

Here, three types of CNTRC beams with different boundary conditions are defined as follows

$${\text{Doubly clamped }}({\text{CC}}):\,\,w = \psi = 0\,\,\,\,\,\,at\,\,x = 0\,\,and\,\,L$$
(34a)
$$\begin{aligned} &{\text{Doubly simply supported (SS)}}:\,\,w = 0\,\,\,and\,\,\,\,\\&\frac{d\psi }{dx} = \frac{1}{{a_{2} }}\bar{\bar{q}}(x)\,\,\,\,\,at\,\,x = 0\,\,and\,\,L \end{aligned}$$
(34b)
$${\text{Cantilever}}\, ( {\text{CF)}}:\left\{ {\begin{array}{*{20}l} {w = 0} \hfill & {and} \hfill & {\psi = 0\quad at\quad x = 0} \hfill \\ {\psi + \frac{dw}{dx} = \frac{1}{{A_{55} }}\frac{{d\bar{\bar{q}}}}{dx}} \hfill & {and} \hfill & {\frac{d\psi }{dx} = \frac{1}{{a_{2} }}\bar{\bar{q}}\quad at\quad x = L} \hfill \\ \end{array} } \right.$$
(34c)

where

$$\overline{\overline{q}} (x) = \mu q(x).$$
(35)
2.3.1.2 Buckling problem

For buckling analysis (\(q = 0\)), the decoupled governing equation in (28) is simplified as follows:

$$a_{1} P\frac{{d^{5} \psi }}{{dx^{5} }} + (a_{2} - a_{3} P)\frac{{d^{3} \psi }}{{dx^{3} }} + P\frac{d\psi }{dx} = 0$$
(36)

The solution of Eigen-value differential equation in (36) is obtained to be:

$$\psi (x,P) = D_{1} + C_{1} e^{{\lambda_{1} x}} + C_{2} e^{{ - \lambda_{1} x}} + C_{3} e^{{\lambda_{2} x}} + C_{4} e^{{ - \lambda_{2} x}}$$
(37)

where,

$$\lambda_{1,2} = \sqrt {\frac{{ - a_{2} + a_{3} P \pm \sqrt \Delta }}{{2a_{1} P}}} \,\,\,\,\,\,{\text{in}}\,\,{\text{which}}\,\,\,\,\Delta = (a_{2} - a_{3} P)^{2} - 4a_{1} P^{2}$$
(38)

Substituting Eq. (37) into Eq. (30) yields

$$\begin{aligned} w & = \frac{{a_{2} }}{{A_{55} }}\left[ {\lambda_{1} \left( {C_{1} e^{{\lambda_{1} x}} - C_{2} e^{{ - \lambda_{1} x}} } \right) + \lambda_{2} \left( {C_{3} e^{{\lambda_{2} x}} - C_{4} e^{{ - \lambda_{2} x}} } \right)} \right] \\ & \quad - D_{1} x - \frac{1}{{\lambda_{1} }}\left( {C_{1} e^{{\lambda_{1} x}} - C_{2} e^{{ - \lambda_{1} x}} } \right) - \frac{1}{{\lambda_{2} }}\left( {C_{3} e^{{\lambda_{2} x}} - C_{4} e^{{ - \lambda_{2} x}} } \right) + D_{0} \\ \end{aligned}$$
(39)

It is to be noted that if the function of mode shapes is assumed to be harmonic, hence it is concluded that \(D_{0} = D_{1} = 0\). Furthermore, the buckling load \(P_{cr}\) can be calculated by vanishing the coefficients matrix in the system of homogenous algebraic equations which is formed by imposing the boundary conditions. Therefore, the buckling load of CNTCR beams with each type of boundary conditions can be computed as follows:

$$\left[ A \right]_{4 \times 4} \,\left\{ C \right\}_{4 \times 1} = 0$$
(40)

Here, two types of CNTRC beams with different boundary conditions are defined as follows

$$\begin{aligned} {\text{Doubly clamped }}({\text{CC}}):\,\,\,w = \psi = 0\,\,\,\,\,\,at\,\,x = 0\,\,and\,\, L\end{aligned}$$
(41a)
$$\begin{aligned} &{\text{Doubly simply supported (SS)}}:\,\,\,\,w = 0\,\,\,and\,\,\,\,\\& a_{2} \frac{d\psi }{dx} + \mu P\frac{{d^{2} w}}{{dx^{2} }} = - \frac{{B_{11}^{{}} }}{{A_{11} }}P\,\,\,\,\,at\,\,x = 0\,\,and\,\,L\end{aligned}$$
(41b)

2.3.2 Free vibration behavior

In this section, an exact solution for the free vibration behavior of CNTRC beams is developed. First, substituting for stress resultants from (19), (21) and (22) into (18) results in the nonlocal motion equations of CNTRC beams in terms of displacement components as follows:

$$\delta u:\,\,\,\,\,A_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + B_{11} \frac{{\partial^{2} \psi }}{{\partial x^{2} }}\, - \bar{\nabla }\left[ {I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi }}{{\partial t^{2} }}} \right] = 0,$$
(42a)
$$\begin{aligned} &\delta \psi :\,\,\,\,B_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + D_{11} \frac{{\partial^{2} \psi }}{{\partial x^{2} }} - A_{55} \left( {\psi + \frac{\partial w}{\partial x}} \right) \\ &\quad- \bar{\nabla }\left[ {I_{2} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{3} \frac{{\partial^{2} \psi }}{{\partial t^{2} }}} \right] = 0, \end{aligned}$$
(42b)
$$\delta w:\,\,\,A_{55} \left( {\frac{\partial \psi }{\partial x} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) - \bar{\nabla }\left[ { - q + I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right] = 0$$
(42c)

In Eq. (42), we have \(\bar{\nabla } = 1 - \mu d^{2} /dx^{2}\). To obtain the free vibration responses, the components of displacement vector can be proposed as follows:

$$\left\{ {u,\psi ,w} \right\} = \left\{ {\text{U} (x),\varPsi (x),\,\,\text{W} (x)} \right\}e^{i\omega t}$$
(43)

in which, \(\omega\) is the natural frequency. Next, substituting Eq. (43) into Eq. (42) results in:

$$\delta u:\,\,(A_{11} - \,\omega^{2} \,I_{1} \mu )\frac{{d^{2} \text{U} }}{{dx^{2} }} + (B_{11} - \,\,\omega^{2} \,I_{2} \mu )\frac{{d^{2} \varPsi }}{{dx^{2} }} + \,\omega^{2} (I_{1} \text{U} + I_{2} \varPsi ) = 0$$
(44a)
$$\begin{aligned} &\delta \psi :(B_{11} - \omega^{2} I_{2} \mu )\frac{{d^{2} \text{U} }}{{dx^{2} }} + (D_{11} - \omega^{2} I_{3} \mu )\frac{{d^{2} \varPsi }}{{dx^{2} }}\\ &\quad + A_{55} \left( {\varPsi + \frac{dW}{dx}} \right) + \omega^{2} (I_{2} \text{U} + I_{3} \varPsi ) = 0 \end{aligned}$$
(44b)
$$\delta w:A_{55} \frac{d\varPsi }{dx} + (A_{55} - I_{1} \omega^{2} \mu )\frac{{d^{2} W}}{{dx^{2} }} + I_{1} \omega^{2} W = 0$$
(44c)

Based on the operator differential method [55], a system of linear algebraic equations is obtained in the following form:

$$\left[ {\begin{array}{*{20}l} {(A_{{11}} - \,\omega ^{2} \,I_{1} \mu )D^{2} + \,\omega ^{2} I_{1} } \hfill &\quad {(B_{{11}} - \,\,\omega ^{2} \,I_{2} \mu )D^{2} + \,\omega ^{2} I_{2} } \hfill &\quad 0 \hfill \\ {} \hfill &\quad {(D_{{11}} - \,\,\omega ^{2} \,I_{3} \mu )D^{2} + \,\omega ^{2} I_{3} - A_{{55}} } \hfill &\quad { - A_{{55}} D} \hfill \\ {Syms} \hfill &\quad {} \hfill &\quad { - \,(A_{{55}} - I_{1} \,\omega ^{2} \mu )D^{2} - \,\omega ^{2} I_{1} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\text{U} (x)} \hfill \\ {\Psi (x)} \hfill \\ {\text{W} (x)} \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right\}$$
(45)

Solving the system of algebraic equations appearing in (45) using Cramer’s rule results in:

$$a_{1} \frac{{d^{6} \text{W} }}{{dx^{6} }} + a_{2} \frac{{d^{4} \text{W} }}{{dx^{4} }} + a_{3} \frac{{d^{2} \text{W} }}{{dx^{2} }} + a_{4} \text{W} = 0$$
(46a)
$$a_{1} \frac{{d^{6} \varPsi }}{{dx^{6} }} + a_{2} \frac{{d^{4} \varPsi }}{{dx^{4} }} + a_{3} \frac{{d^{2} \varPsi }}{{dx^{2} }} + a_{4} \varPsi = 0$$
(46b)
$$a_{1} \frac{{d^{6} U}}{{dx^{6} }} + a_{2} \frac{{d^{4} U}}{{dx^{4} }} + a_{3} \frac{{d^{2} U}}{{dx^{2} }} + a_{4} U = 0$$
(46c)

where, \(a_{i}\)’s are defined as follows:

$$\begin{aligned} a_{1} & = - \,(A_{55} - I_{1} \omega^{2} \mu )\left[ {(A_{11} - \,\omega^{2} \,I_{1} \mu )(D_{11} - \,\omega^{2} \,I_{3} \mu ) - (B_{11} - \,\omega^{2} \,I_{2} \mu )^{2} } \right] \\ B_{i} & = c_{i} C_{i} ,\,\,\,\,\,\,\,\bar{B}_{i} = - \,c_{i} \bar{C}_{i} \,,\,\,\,\,\,\,\,\,D_{i} = d_{i} B_{i} = d_{i} c_{i} C_{i} ,\,\,\,\,\,\,\,\,\,\,\,\,\bar{D}_{i} = d_{i} \bar{B}_{i} = - \,\bar{d}_{i} c_{i} C_{i} \,\text{W} (x) = \sum\limits_{i = 1}^{3} {\left( {C_{i} e^{{\lambda_{i} x}} + \bar{C}_{i} e^{{ - \lambda_{i} x}} } \right)} \\ a_{2} & = - \,(A_{11} - \,\omega^{2} \,I_{1} \mu )\left[ {(A_{55} - I_{1} \omega^{2} \mu )(\omega^{2} I_{3} - A_{55} ) + I_{1} \omega^{2} (D_{11} - \,\omega^{2} \,I_{3} \mu ) + A_{55}^{2} } \right] - (A_{55} - I_{1} \omega^{2} \mu )\left[ {I_{1} \omega^{2} (D_{11} - \,\omega^{2} \,I_{3} \mu ) - I_{2} \omega^{2} (B_{11} - \,\omega^{2} \,I_{2} \mu )} \right] + (B_{11} - \,\omega^{2} \,I_{2} \mu )\left[ {\,\omega^{2} \,I_{2} (A_{55} - I_{1} \omega^{2} \mu ) + I_{1} \omega^{2} (B_{11} - \,\omega^{2} \,I_{2} \mu )} \right] \\ a_{3} & = - \,\omega^{2} \,I_{1} \left[ {(A_{55} - I_{1} \omega^{2} \mu )(\omega^{2} I_{3} - A_{55} ) + I_{1} \omega^{2} (D_{11} - \,\omega^{2} \,I_{3} \mu ) + A_{55}^{2} } \right] - \omega^{2} \,I_{1} \left[ {(A_{11} - \,\omega^{2} \,I_{1} \mu )(\omega^{2} I_{3} - A_{55} ) - I_{2} \omega^{2} (B_{11} - \,\omega^{2} \,I_{2} \mu )} \right] + \omega^{2} \,I_{2} \left[ {\,\omega^{2} \,I_{2} (A_{55} - I_{1} \omega^{2} \mu ) + I_{1} \omega^{2} (B_{11} - \,\omega^{2} \,I_{2} \mu )} \right] \\ a_{4} & = - \,\omega^{2} \,I_{1} \left[ {(A_{11} - \,\omega^{2} \,I_{1} \mu )(\omega^{2} I_{3} - A_{55} ) - (I_{2} \omega^{2} )^{2} } \right] \\ \end{aligned}$$
(47)

The general solution of Eq. (46) is expressed as follows:

$${\text{W}}(x) = \sum\limits_{i = 1}^{3} {\left( {C_{i} e^{{\lambda_{i} x}} + \bar{C}_{i} e^{{ - \lambda_{i} x}} } \right)}$$
(48a)
$$\varPsi (x) = \sum\limits_{i = 1}^{3} {\left( {B_{i} e^{{\lambda_{i} x}} + \bar{B}_{i} e^{{ - \lambda_{i} x}} } \right)}$$
(48b)
$$U(x) = \sum\limits_{i = 1}^{3} {\left( {D_{i} e^{{\lambda_{i} x}} + \bar{D}_{i} e^{{ - \lambda_{i} x}} } \right)}$$
(48c)

where \(\lambda_{i}\)’s are the roots of characteristic equation \(\left( {a_{1} \lambda_{i}^{3} + a_{2} \lambda_{i}^{2} + a_{3} \lambda_{i} + a_{4} = 0} \right)\) and we have

$$B_{i} = c_{i} C_{i} ,\quad \bar{B}_{i} = - \,c_{i} \bar{C}_{i} ,\quad D_{i} = d_{i} B_{i} = d_{i} c_{i} C_{i} ,\quad \bar{D}_{i} = d_{i} \bar{B}_{i} = - \,\bar{d}_{i} c_{i} C_{i}$$
(49a)
$$\begin{aligned} c_{i} & = - \frac{1}{{A_{55} \lambda_{i} }}\left[ {(A_{55} - I_{1} \,\omega^{2} \mu )\lambda_{i}^{2} + I_{1} \,\omega^{2} } \right] \\ d_{i} & = - \frac{{(B_{11} - \,\,\omega^{2} \,I_{2} \mu )\lambda_{i}^{2} + \omega^{2} I_{2} }}{{\,(A_{11} - \,\omega^{2} \,I_{1} \mu )\lambda_{i}^{2} + I_{1} \,\omega^{2} }} \\ \end{aligned}$$
(49b)

Furthermore, the natural frequencies can be calculated by vanishing the coefficients matrix in the system of homogenous algebraic equations which is formed by imposing the boundary conditions. Therefore, the natural frequencies of CNTCR beams with each type of boundary conditions can be computed as follows:

$$\left[ A \right]_{6 \times 6} \,\left\{ C \right\}_{6 \times 1} = 0$$
(50)

Here, two types of CNTRC beams with different boundary conditions are defined as follows

$${\text{Doubly clamped (CC):}}\,\,\,\,u = w = \psi = 0\,\,\,\,\,\,at\,\,x = 0\,\,and\,\,L$$
(51a)
$$\begin{aligned} &{\text{Doubly simply supported (SS):}}\,\,\,\,u = w = 0\,\,\,and\,\,\,\,\\&\quad M_{xx} = 0\,\,\,\,\,\,at\,\,x = 0\,\,and\,\,L. \end{aligned}$$
(51b)

3 Numerical results and discussion

In Sect. 3.1, the parametric studies of bending behavior of SS, CC and CF-supported CNTRC beams subjected to transverse loads with uniform and sinusoidal distributions are presented. In Sects. 3.2 and 3.3, the effects of nonlocal parameter, CNT volume fraction and boundary conditions on the buckling values and natural frequencies of CNTRC beams are studied. To obtain the numerical results, the matrix of CNTRC material are assumed to be poly(methyl methacrylate) (PMMA) with material properties \(E_{m} = 2.5\,{\text{GPa}}\), \(\nu_{m} = 0.3\) and \(\rho_{m} = 1190 \,{\text{kg/m}}^{3}\). In addition, a \(\left( {10,10} \right)\) armchair SWCNT is selected as the reinforcement component with material properties \(E_{11}^{cnt} = 5646.6 \,{\text{GPa}}\), \(E_{22}^{cnt} = 7080\,{\text{GPa}}\), \(G_{12}^{cnt} = 1944.5 \,{\text{GPa}}\), \(\nu_{12}^{cnt} = 0.175\) and \(\rho_{cnt} = 2100\, {\text{kg/m}}^{3}\) [50]. Also, the CNT efficiency parameters for three values of volume fractions are given in Table 1. Moreover, the numerical value of the shear correction factor is taken to be 5/6. By letting the nonlocal parameter \(\mu\) equal to zero, the numerical results of CNTRC Timoshenko beams are obtained in the framework of the classical continuum theory. In order to present the numerical results, the dimensionless quantities of deflection, buckling load and natural frequency are defined as follows:

$$\bar{w} = w\frac{{384E_{m} I}}{{5q_{0} L^{4} }}$$
(52a)
$$\bar{P} = P\frac{{L^{2} }}{{\pi^{2} E_{m} I}}$$
(52b)
$$\bar{\omega } = \omega \frac{{L^{2} }}{{\pi^{2} }}\sqrt {\frac{{\rho_{m} A}}{{E_{m} I}}}$$
(52c)

where \(q = q_{0}\) for uniform load and \(q = q_{0} \sin \left( {\frac{\pi x}{L}} \right)\) for sinusoidal load.

Table 1 CNT efficiency parameters for different values of CNT volume fraction
Full size table

3.1 Bending behavior

Figure 2 depicts the effect of three types of CNT distributions on the bending behavior of an CNTRC beam with simply-supported (SS), clamped–clamped (CC) and cantilever (CF) boundary conditions which is subjected a uniform transverse load using the nonlocal theory \(\left( {\mu = 2\,{\text{nm}}^{2} } \right)\). The geometrical ratios of beam and CNT volume fraction are assumed to be \(L/h = 10\), \(b/h = 1\) and \(V_{cnt}^{*} = 0.12\). It is seen that among the CNTRC beams with any boundary conditions, FGO-CNTRCs and FGX-CNTRCs exhibit the maximum and minimum values of normalized deflection, respectively. The effect of CNT distribution on the bending behavior of CNTRC beams is more significant when the stiffness of supports decreases especially for cantilever beams.

Fig. 2
figure 2

The variations of transverse displacement of an CNTRC beam with different distribution forms of CNTs

Full size image

The variations of normalized deflection versus the normalized length for SS, CC and CF-supported FGX-CNTRC beams (\(h = b = 0.1\,\,L = 1\,{\text{nm}}\) and \(V_{cnt}^{*} = 0.12\)) under a uniform transverse load, predicted by the classical \(\left( {\mu = 0} \right)\) and nonlocal \(\left( {\mu = 2 {\text{and }}4\,{\text{nm}}^{2} } \right)\) theories, are compared in Fig. 3. It is observed that the small-scale effect on the mechanical behavior of nanobeams is strongly dependent on the boundary conditions at the beam ends. Contrary to bending behavior of SS-supported nanobeams, the normalized deflections of cantilever beams decrease by considering the nonlocality effect. For the case of only uniform transverse loading \((P = 0\) and \(q = q_{0} )\), the results predicted by classical and nonlocal theories are exactly same with each other, due to the terms including nonlocal parameter (\(\mu\)) in the governing equations [please see Eqs. (28)–(30)] are vanished and such terms do not exist in clamped–clamped boundary conditions given in (34a).

Fig. 3
figure 3

The variations of transverse displacement of an CNTRC beam for different values of \(\mu\)

Full size image

In Table 2, the effects of CNT volume fraction and boundary conditions on the maximum normalized deflections of FGX-CNTRC beams (\(L/h = 10\) and \(b/h = 1\)) subjected to two uniform (\(q = q_{0}\)) and sinusoidal (\(q = q_{0} \sin \left( {\frac{\pi x}{L}} \right)\)) distributions of transverse loads are studied using the nonlocal theory (\(\mu = 2\,{\text{nm}}^{2}\)). For various values of \(V_{cnt}^{ *}\) and each type of boundary conditions, the maximum normalized deflection of FGX-CNTRC beams subjected to the uniform transverse loading are larger than those caused by the sinusoidal distribution of transverse load. The differences between the results of uniform and sinusoidal distributions become larger as the stiffness of supports reduces especially for clamped-free boundary conditions.

Table 2 The maximum normalized deflections of SS, CC and CF-supported FGX-CNTRC beams under uniform and sinusoidal transverse loads for different values of \({\text{V}}_{\text{cnt}}^{ *}\) based on the nonlocal theory (\(\mu = 2\,{\text{nm}}^{2} )\)
Full size table

3.2 Buckling behavior

The normalized buckling loads of SS, and CC-supported CNTRC beams with \(L/h = 10\) and \(b/h = 1\) predicted by the classical \(\left( {\mu = 0} \right)\) and nonlocal \((\mu = 2\) and \(4 \,{\text{nm}}^{2} )\) theories are compared in Table 3, for various values of \(V_{cnt}^{ *}\) and CNT distribution. The highest increase in the normalized buckling loads of CNTRC beams is observed in the FGX distribution of CNT. Also, it is seen that the stiffness of FGO-CNTRC beams with any boundary conditions is the smallest for different values of \(V_{cnt}^{ *}\) and \(\mu\). From Table 3, it can be concluded that the boundary conditions, distribution form of CNT and nonlocal parameter, respectively have the most influence on the buckling values. Compared to the classical theory, the nonlocal theory predicts the smaller values for buckling loads of nanobeams with SS and CC supports, as expected from the results presented in the previous section.

Table 3 The normalized buckling loads of SS and CC-supported CNTRC beams for different values of \({\text{V}}_{\text{cnt}}^{ *}\)
Full size table

In Fig. 4, the variations with the aspect ratio (\(L/h\)) of normalized buckling loads of SS and CC supported CNTRC nanobeams \(\left( {b/h = 1} \right)\) are shown for three types of CNT distributions (UD, FGX and FGO) using the nonlocal theory \(\left( {\mu = 2\,{\text{nm}}^{2} } \right)\). For both SS and CC supports, it is seen that when \(L/h\) rises, values of normalized buckling load increase first and finally approach a constant value which is equal to the result predicted by Euler–Bernoulli beam theory. For SS support the values of \(L/h\), at which the results of Timoshenko and Euler–Bernoulli beam models are exactly same, are smaller than those of CC support.

Fig. 4
figure 4

The variations with aspect ratio of dimensionless buckling loads of an CNTRC beam (\(b/h = 1\)) with different distribution forms of CNTs

Full size image

In Fig. 5, the variations with aspect ratio of normalized buckling loads of the FGX-CNTRC nanobeams \((b/h = 1\) and \(V_{cnt}^{*} = 0.12)\) predicted by the classical \(\left( {\mu = 0} \right)\) and nonlocal \(\left( {\mu = 4\,{\text{nm}}^{2} } \right)\) theories are compared for both SS and CC supports. Comparing Fig. 5a, b, it is observed that the nonlocality effect on the normalized buckling loads is much smaller in comparison with that of boundary conditions. When the aspect ratio (\(L/h\)) decreases, the differences between the normalized buckling loads predicted by the classical continuum and nonlocal theories become more significant. However, the differences between results of SS and CC-supported nanobeams are decreased based on the classical and nonlocal theories.

Fig. 5
figure 5

The variations with aspect ratio of dimensionless buckling loads of an CNTRC beam (\(b/h = 1\)) with different distribution forms of CNTs

Full size image

3.3 Free vibration behavior

In Table 4, the normalized natural frequencies of SS and CC-supported CNTRC beams (\(L/h = 10\) and \(b/h = 1\)) predicted by the classical \(\left( {\mu = 0} \right)\) and nonlocal \((\mu = 2\) and \(4\,{\text{nm}}^{2} )\) theories are compared for different distributions and volume fractions of CNTs. From numerical results, it is readily concluded that the normalized natural frequencies of CNTRC nanobeams with FGX, UD and FGO distributions, respectively become larger for both supports. Also, it is seen that the normalized natural frequencies of SS and CC-supported nanobeams become smaller when the nonlocal parameter increases. Compared to results given in Tables 3 and 4, it is found that the variations with boundary conditions, \(V_{cnt}^{ *}\) and \(\mu\) of the normalized natural frequencies are smaller in the comparison with those of dimensionless buckling loads.

Table 4 The normalized natural frequencies of SS and CC-supported CNTRC beams for different values of \({\text{V}}_{\text{cnt}}^{ *}\)
Full size table

Figure 6 shows the variation of normalized natural frequency versus the aspect ratio for UD, FGX and FGO- nanobeams (b/h = 1 and \(V_{cnt}^{*} = 0.12)\) with SS and CC supports based on the nonlocal theory \(\left( {\mu = 2\,{\text{nm}}^{2} } \right)\). For both boundary conditions and various distributions of CNTs, it is seen that the ascending curves of normalized natural frequency converge to the values predicted by Euler–Bernoulli beam model. Similar to buckling behavior of CNTRC nanobeams, the maximum and minimum values of normalized natural frequency belong to FGX and FGO CNTRC beams, respectively.

Fig. 6
figure 6

The variations with aspect ratio of dimensionless natural frequencies of an CNTRC beam (\(b/h = 1\)) with different distribution forms of CNTs

Full size image

In Fig. 7, the variations with aspect ratio \(\left( {L/h} \right)\) of the normalized natural frequency predicted by the classical \(\left( {\mu = 0} \right)\) and nonlocal \(\left( {\mu = 4\,{\text{nm}}^{2} } \right)\) theories are compared for FGX-CNTRC nanobeams (b/h = 1 and \(V_{cnt}^{*} = 0.12)\) with SS and CC supports. It is observed that the difference of nonlocal and classical dimensionless natural frequencies diminishes with increase of \(L/h\) for both boundary conditions. From Figs. 5 and 7, it is concluded that the effect of supports on the values of normalized buckling loads is more significant in comparison with normalized natural frequencies.

Fig. 7
figure 7

The variations with aspect ratio of dimensionless natural frequency of SS and CC-supported FGX-CNTRC beam with \(b/h = 1\)

Full size image

4 Conclusion

In this study, exact solutions for bending, buckling and free vibration of CNTRC nanobeams with arbitrary boundary conditions considering the nonlocal parameter are developed. The material properties of FG- CNTRCs are assumed to be graded through the thickness direction according to several distributions namely UD, FGX and FGO. The solution presented in this study can be employed as a benchmark to evaluate the nonlocal effect on mechanical behavior of CNTRC nanostructures. Effects of boundary conditions, geometric ratios, distribution of CNT volume fraction and nonlocal parameter on transverse deflection, buckling load, and natural frequency of UD, FGX, and FGO-CNTRC nanobeams are studied. Findings are summarized as follows:

  • Among the considered CNT distributions, FGX distribution results in the stiffest behavior for nanobeam, while FGO distribution leads to the most flexible behavior.

  • For the cantilever beams, the influence of CNT distribution on bending CNTRC beams is more significant than simply supported and clamped beams.

  • Due to nonlocal effect, softening and hardening phenomenon take place for the simply supported and cantilever beams, respectively.

  • For bending analysis of CC-supported nanobeams under uniform transverse loading, the normalized deflections predicted by the classical and nonlocal elasticity theories are exactly the same.

  • Softening takes place as the nonlocal effect is considered in the buckling and free vibration analysis of nanobeams with SS and CC supports.

  • As \(L/h\) increases, the nonlocal and classical natural frequencies for SS and CC beams approach to each other.