Onset of Soret driven instability in a Darcy–Maxwell nanofluid

Abstract

This paper presents an analytical and numerical study of the salt particle drift driven by thermal gradient and the nanoparticle drift due to Brownian motion in a Darcy porous layer saturated by a Maxwellian nanofluid under passive management of nanoparticle flux at the boundaries influenced by the Stefan’s flow condition. Filtration law of Khuzhayorov et al. (Int J Eng Sci 38:487–504, 2000), for the Darcy–Maxwell fluid, has been used. It is shown that the steady state convection, under both linear and non-linear stability theory do not depend upon the relaxation parameter of the Maxwell fluid. Soret effect is responsible for delaying the stationary convection. It, however, enhances it in comparison to the convection in monodiffusive flow. Oscillatory convection exists, ceases and shifts to the stationary convection. In Soret effected steady convection, among heat, salt and nanoparticles, the transport of nanoparticles is most active while among monodiffusive, double diffusive and Soret governed convection, the heat transfer is most active in Soret induced convection. Streamlines, isotherms and isohalines are shown for steady as well as unsteady convection. Results are compared with some of the existing results.

1 Introduction

In 1879, the Swiss scientist Soret [2] performed an experiment with sodium chloride and potassium nitrate in a tube by maintaining the top and bottom ends of it at 800 °C and room temperature respectively. He noticed the non-uniformity in the concentration of salt and the migration of colloidal particles to the cold end and the hot end of the tube. He concluded that in isotropic fluid systems, in the absence of external forces, concentration gradient is induced by the driving force of applied temperature gradient until the system reaches into the steady state condition. During 1879 to 1884, Soret quantified the effect for many electrolyte solutions which were later summarized and discussed by Costesèque [3]. Although, Ludwig [4] observed and presented the phenomena several years before Soret in his brief lecture titled ‘On Haze and Dust’ in Royal Institute and later incorporated it in the book ‘Scientific Addresses’, but he was overlooked and the phenomenon was named as Soret effect. Later, it was also called Ludwig-Soret effect or thermodiffusion or thermal diffusion. The same phenomenon of suspended particles in carrier liquid or gas is called thermophoresis. Thus thermophoresis is the transport mechanism responsible for the formation of concentration currents. In 1962, De Groot and Mazur [5] appreciated this phenomenon and formulated it in the book ‘Non-Equilibrium Thermodynamics’. Considering the linear laws of irreversible thermodynamics, the mass flux J_i of the ith component in a multi-component mixtures (say p components), neglecting pressure gradient, is written as

$${\mathbf{J}}_{{\mathbf{i}}} = - \rho_{0} \sum\limits_{k = 1}^{p - 1} {D_{ik} } \nabla C_{i} - \rho_{0} D_{Ti} C_{i} (1 - C_{i} )\nabla T,$$

(1)

where $\rho_{0}$ is the specific mass or density, $D_{ik}$ is the isothermal molecular concentration diffusivity, $D_{Ti}$ is the thermodiffusion coefficient, $C_{i}$ is the concentration of the reference component, $\nabla C_{i}$ is the gradient of reference concentration induced by temperature gradient $\nabla T$.

Thus, the conservation equation for concentration field is written as

$$\left( {\frac{\partial }{\partial t} + q \cdot \nabla } \right)C_{i} = - \nabla \cdot {\mathbf{J}}_{{\mathbf{i}}} ,$$

(2)

where q represents the velocity field. Soret effect is characterized by Soret coefficient S_T, the ratio of the thermal diffusion coefficient to the molecular diffusion coefficient. It is proportional to the volume fraction generally having the magnitude in the range of 10⁻³–10⁻² K⁻¹ for gases or simple electrolytes [6] but can be of larger magnitudes for macromolecular and colloidal solutions. Soret coefficient may be positive or negative depending on the sense of migration of the reference components. Positive Soret coefficient means the denser colloids are forced to move towards lower temperature regions (regions of smaller agitation), while negative Soret coefficient means the accumulation of particles towards the regions of higher temperatures. In a simple fluid heated from below, viscous friction and thermal conductivity hamper the convection resulting in local density fluctuations, known as Rayleigh–Bènard convection while in mixtures, thermodiffusion, positive or negative (in case of fluid layer heated from below or above, see [7] for negative thermodiffusion), sets inverted concentration gradients that can only be relaxed by mass diffusion. Since it is far slower than heat transport, the convection threshold is substantially lowered. Both the situations are very commonly observed but no study has predicted the direction of thermodiffusion motion for a given solute. An overview on the basic physics of the Soret effect has been explained by Köhler and Wiegand [8]. The mechanism of thermophoresis works for nanoparticles as well. Thus, the Soret coefficient may be different for different matters of concentration. The mechanism of thermophoresis works for nanoparticles as well in such a way that the Soret coefficient may be different for different matters of concentration.

Since its discovery, large number of theoretical and experimental studies have established its importance as an agent of various convective phenomena like multiple steady oscillatory states, subcritical flows, standing–traveling waves, Hopf bifurcations and hysteresis effects (see [9,10,11,12] and references therein).

In a convective configuration, thermophoresis has a number of applications in many naturally occurring processes. Whether it is the operation of solar ponds [13] or the thermohaline convection in oceans [14] or the thermodiffusion in stars [15], convection is largely affected by thermophoresis. It is also helpful in the prediction of the concentrations of the different components of hydrocarbon mixtures of earth’s hydrocarbon reservoirs which is necessary for the optimum oil/gas recovery [16, 17]. Soret diffusion might also serve as an agent to fractionate isotopes of the elements like Mg, Ca, Fe, Si, O, Sr, Hf, and U found in high-temperature geochemical melts. Fractionation of isotopes is useful in a wide range of natural condensed systems, including the early solar system and the atmospheric water cycle. It is also helpful in mapping the temperature gradient in magma chambers, and in defining the initial isotopic composition of the earth from the solar nebula [18].

In biological systems, the mass transport across biological membranes of an organ or a tumor is induced by small thermal gradients and in some cases even the shape of the membrane may be manipulated by them [19, 20].

Thermophoresis helps in measuring bimolecular affinities in complex liquids and provides the basis for a size selective molecule trap. It has also been exploited as an industrial tool for aerosol collectors (thermal precipitators), gas cleaning, nuclear reactor safety, and the corrosion/fouling of heat exchangers. Paintings and other works of art may have a protection shield against airborne particles through thermophoresis [21]. Measurement of Soret coefficient is also important to conduct material science experiments and to measure their physical properties in a low-gravity environment, i.e. crystal growth from solution or vapor phase deposition on Skylab or space shuttle missions. For some of the useful experimental and theoretical studies predicting a noticeable Soret effect, the work of Hardin et al. [10] and references therein are worth mentioning. Recently many of the fields mentioned so far are concerned with nanofluids. Nanofluids are more stable suspensions having acceptable viscosity, better wetting capacity, and dispersion properties. In nanofluids the concentration flux of nanoparticles is also induced by thermal gradient resulting in a thermophoresis of nanoparticles. Recently Derakhshan et al. [22], Zangooee [23], Ghadikolaei et al. [24,25,26,27], Gholinia et al. [28], Hosseinzadeh et al. [29, 30] have studied convection in some important nanofluids considering the thermophoresis of nanoparticles. When a pure base fluid in a nanofluid is replaced by a binary fluid, the convection becomes more interesting. The simultaneous occurrence of two types of thermophoresis, the one induced by the thermal gradient affecting the flux of salt and the other the thermophoresis of nanoparticles, make binary nanofluids applicable in variety of natural fields.

There are a number of nanofluids exhibiting the exceptional behavior regarding viscosity and other properties of non-Newtonian medium but unfortunately, only a very few theoretical studies on Soret-driven thermosolutal instability in non-Newtonian nanofluids are reported in literature.

The main purpose of the present work is to explore the role of Soret effect on the thermal instability of a binary nanofluid when Bénard convection is governed by the Darcy Maxwell model, introduced by Alishayev [31]. Khuzhayorov et al. [1] interpreted the notion of macroscopic filtration law for describing transient linear viscoelastic fluid flows in porous media. The model has been used by Wang and Tan [32] to discuss the effect of Soret parameter on a regular Maxwell fluid. There are some other studies where the stability of single phase Maxwell fluid have been investigated using this model [33,34,35,36,37,38]. Recently, Jaimala et al. [39] used the model to investigate the classical Horton Rogers Lapwood problem for thermal diffusion in nanofluid. The important aspect to mention is that the present investigation deals with the Stefan’s flow condition which says that in natural situations the mass flux of fluid can only be controlled passively at the boundaries (see Baehr and Stephan [40]). Adopting the Stefan’s condition for the flux of nanoparticles at the boundaries, it is supposed that there is zero flux of nanoparticles. Nield and Kuznetsov [41] followed Stefan’s conditions to discuss the thermal stability of Newtonian nanofluid. Jaimala et al. [39] used this condition in discussing the thermal stability of Darcy–Maxwell nanofluid and showed that the nanoparticles are accountable for reduction in Horton–Rogers Rayleigh number notably. This paper reveals that the presence of nanoparticles in combination of weak concentration diffusivity and the pronounced solutal buoyancy force significantly alter the classical Horton–Rogers–Lapwood convection as compared to regular Maxwell fluid [42].

2 Formulation

The proposed model deals with the binary nanofluid suspension under the following assumptions:

• a. Binary nanofluid is a dilute mixture, i.e. $\phi$ ≪ 1. This assumption is consistent with almost every nanofluid studied so far.

• b. Nanoparticles and the binary fluid are in local-thermal-equilibrium (LTE). This situation is coherent with the size of nanoparticles such that the internal equilibration times are of the order of 1 ns, which is negligible as compared with the fluid-dynamics time scales.

• c. Chemical reactions are negligible.

• d. External forces except gravitational force, radiative heat transfer and viscous dissipation are negligible.

• e. The fluid layer is heated and soluted from below.

• f. The soluted nanofluid flow is subjected to thermophoresis of salt and thermophoresis of nanoparticles.

• g. Particle-related effects like particle inertia, Magnus effects etc. have not been considered.

• h. Darcy Maxwellian fluid model is designed by the filtration law proposed by Khuzhayorov et al. [1].

• i. Analogous to Stefan’s flow there is no nanoparticle flux at the boundaries.

The conservation equation for mass is taken as

$$\nabla^{*} \cdot {\mathbf{v}}_{D}^{*} = 0,$$

(3)

Following Khuzhayorov et al. [1], the momentum equation can be written as

$$\frac{\mu }{K}{\mathbf{v}}_{D}^{*} = \left( {1 + \lambda^{*} \frac{\partial }{{\partial t^{*} }}} \right)\left( { - \nabla^{*} p^{*} + \rho {\mathbf{g}}} \right).$$

(4)

Following Eastman et al. [43], the density of the salted nanofluid can be computed as the volume weighted average. Therefore, using the volume fractions $\phi$ as weights, density can be written as

$$\rho = \left[ {\phi^{*} \rho_{p} + (1 - \phi^{*} )\left\langle {\rho \left\{ {1 - \beta_{T} (T^{*} - T_{c}^{*} ) - \beta_{C} (C^{*} - C_{c}^{*} )} \right\}} \right\rangle } \right],$$

(5)

where $\rho \left\{ {1 - \beta_{T} (T^{*} - T_{c}^{*} ) - \beta_{C} (C^{*} - C_{c}^{*} )} \right\}$ is the density of the soluted base fluid.

Thus using (5), Eq. (4) becomes

$$\frac{\mu }{K}{\mathbf{v}}_{D}^{*} = \left( {1 + \lambda^{*} \frac{\partial }{{\partial t^{*} }}} \right)\left[ { - \nabla^{*} p^{*} + \left( {\phi^{*} \rho_{p} + (1 - \phi^{*} )\left\langle {\rho \left\{ {1 - \beta_{T} (T^{*} - T_{c}^{*} ) - \beta_{C} (C^{*} - C_{c}^{*} )} \right\}} \right\rangle } \right){\mathbf{g}}} \right],$$

(6)

Following Buongiorno [44] and Nield and Kuznetsov [45], equation of conservation of thermal energy is written as

$$\begin{aligned} & (\rho c)_{m} \frac{{\partial T^{*} }}{{\partial t^{*} }} + (\rho c)_{f} {\mathbf{v}}_{D}^{*} \cdot \nabla^{*} T^{*} \\ & \quad = \kappa_{m} \nabla^{*2} T^{*} + \varepsilon (\rho c)_{p} \left[ {D_{B} \nabla^{*} \phi^{*} \cdot \nabla^{*} T^{*} + (D_{T} /T_{c}^{*} )\nabla^{*} T^{*} \cdot \nabla^{*} T^{*} } \right]. \\ \end{aligned}$$

(7)

Following Hurle et al. [46], it is assumed that the value of mass fraction is very small (i.e. c₀ ≪ 1), therefore, for a fluid saturated in a porous medium, having two types of concentrations, salt and nanoparticles, Eqs. (2) using (1) can be written for the two species as

$$\frac{{\partial C^{*} }}{{\partial t^{*} }} + \frac{1}{\varepsilon }{\mathbf{v}}_{D}^{*} \cdot \nabla^{*} C^{*} = D_{S} \nabla^{*2} C^{*} + D_{CT} \nabla^{*2} T^{*} ,$$

(8)

$$\frac{{\partial \phi^{*} }}{{\partial t^{*} }} + \frac{1}{\varepsilon }{\mathbf{v}}_{D}^{*} \cdot \nabla^{*} \phi^{*} = D_{B} \nabla^{*2} \phi^{*} + (D_{T} /T_{c}^{*} )\nabla^{*2} T^{*} ,$$

(9)

where D_S is the diffusion coefficient of salt, $D_{CT}$ is the Soret coefficient of salt, D_B is the Brownian diffusion coefficient and D_T is the Soret coefficient of nanoparticles.

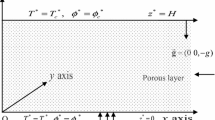
Let an infinite horizontal fluid layer of depth d be saturated in a porous layer lies between two stress free, rigid, perfectly conducting and impervious boundaries situated at $z = 0$ and $z = d$. The layer is heated and salted from below and the thermal and salinity gradients are constant (Fig. 1). At $z = 0$ and $z = d$, the thermal and salt concentrations are constant and the flux of nanoparticle concentration is zero there (Stefan’s flow) such that the associated boundary conditions are

Fig. 1

Physical configuration of the problem

$${\mathbf{v}}^{*}_{D} = 0,T^{*} = T_{h}^{*} ,C^{*} = C_{h}^{*} ,D_{B} \frac{{\partial \phi^{*} }}{{\partial z^{*} }} + \frac{{D_{T} }}{{T_{c}^{*} }}\frac{{\partial T^{*} }}{{\partial z^{*} }} = 0\;\;{\text{at}}\;z = 0,$$

(10)

$${\mathbf{v}}^{*}_{D} = 0,T^{*} = T_{c}^{*} ,C^{*} = C_{c}^{*} ,D_{B} \frac{{\partial \phi^{*} }}{{\partial z^{*} }} + \frac{{D_{T} }}{{T_{c}^{*} }}\frac{{\partial T^{*} }}{{\partial z^{*} }} = 0\;\;{\text{at}}\;z = d.$$

(11)

Choosing $d,$$\frac{{\sigma d^{2} }}{{\alpha_{m} }},$$\frac{{\alpha_{m} }}{d}$, $\frac{{\alpha_{m} }}{{d^{2} }}$ and $\frac{{\mu \alpha_{m} }}{K}$ as the units of length, time, velocity, relaxation time and pressure, where $\alpha_{m} = \frac{{\kappa_{m} }}{{(\rho c)_{f} }}$ and $\sigma = \left( {\frac{{(\rho c)_{m} }}{{(\rho c)_{f} }}} \right)$, and assuming

$$\phi = \frac{{\phi^{*} - \phi_{0}^{*} }}{{\phi_{0}^{*} }},\;\;T = \frac{{T^{*} - T_{c}^{*} }}{{T_{h}^{*} - T_{c}^{*} }},\;\;C = \frac{{C^{*} - C_{c}^{*} }}{{C_{h}^{*} - C_{c}^{*} }},$$

Equations (3), (6) to (9) and the boundary conditions (10) and (11) are rendered dimensionless and we obtain

$$\nabla \cdot {\mathbf{v}} = 0\;,$$

(12)

$${\mathbf{v}} = \left( {1 + \frac{\lambda }{\sigma }\frac{\partial }{\partial t}} \right)\left( { - \nabla p - Rm{\hat{\mathbf{e}}}_{{\mathbf{z}}} + RaT{\hat{\mathbf{e}}}_{{\mathbf{z}}} - Rn\phi {\hat{\mathbf{e}}}_{{\mathbf{z}}} + \frac{Rs}{Ln}C{\hat{\mathbf{e}}}_{{\mathbf{z}}} } \right),$$

(13)

$$\frac{\partial T}{\partial t} + {\mathbf{v}} \cdot \nabla T = \nabla^{2} T + \frac{{N_{B} }}{Le}\;\nabla \phi \cdot \nabla T + \frac{{N_{A} N_{B} }}{Le}\;\nabla T \cdot \nabla T,$$

(14)

$$\frac{1}{\sigma }\frac{\partial C}{\partial t} + \frac{1}{\varepsilon }{\mathbf{v}} \cdot \nabla C = \frac{1}{Ln}\nabla^{2} C + N_{CT} \nabla^{2} T,$$

(15)

$$\frac{1}{\sigma }\frac{\partial \phi }{\partial t} + \frac{1}{\varepsilon }{\mathbf{v}} \cdot \nabla \phi = \frac{1}{Le}\nabla^{2} \phi + \frac{{N_{A} }}{Le}\nabla^{2} T,$$

(16)

$${\mathbf{v}} = 0,T = 1,C = 1,\frac{\partial \phi }{\partial z} + N_{A} \frac{\partial T}{\partial z} = 0\;\;{\text{at}}\;z = 0,$$

(17)

$${\mathbf{v}} = 0,T = 0,C = 0,\frac{\partial \phi }{\partial z} + N_{A} \frac{\partial T}{\partial z} = 0\;\;{\text{at}}\;z = 1.$$

(18)

Where $\nabla^{2} \equiv \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }} + \frac{{\partial^{2} }}{{\partial z^{2} }}$,

• $Rm = \frac{{\left[ {\rho_{p} \phi_{0}^{*} + \rho (1 - \phi_{0}^{*} )} \right]gKd}}{{\mu \alpha_{m} }}$ is the “basic density Rayleigh–Darcy number”,

• $Ra = \frac{{\rho g\beta Kd(T_{h}^{*} - T_{c}^{*} )}}{{\mu \alpha_{m} }}$ is the “thermal Rayleigh–Darcy number”,

• $Rn = \frac{{(\rho_{p} - \rho )\phi_{0}^{*} gKd}}{{\mu \alpha_{m} }}$ is the “concentration Rayleigh–Darcy number”,

• $Rs = \frac{{\rho gKd\beta_{C} \left( {C_{h}^{*} - C_{c}^{*} } \right)}}{{\mu D_{S} }}$ is the “solutal Rayleigh–Darcy number”,

• $N_{A} = \frac{{D_{T} (T_{h}^{*} - T_{c}^{*} )}}{{D_{B} T_{c}^{*} \phi_{0}^{*} }}$ is the “modified diffusivity ratio”,

• $N_{B} = \frac{{\varepsilon \phi_{0}^{*} \left( {\rho c} \right)_{p} }}{{\left( {\rho c} \right)_{f} }}$ is the “modified particle-density increment”,

• $Le = \frac{{\alpha_{m} }}{{D_{B} }}$ is “thermo-nanofluid Lewis number”,

• $Ln = \frac{{\alpha_{m} }}{{D_{S} }}$ is the “thermo-solutal Lewis number”,

• $\;N_{CT} = \frac{{D_{CT} (T_{h}^{*} - T_{c}^{*} )}}{{(C_{h}^{*} - C_{c}^{*} )}}$ is the “Soret parameter”.

${\mathbf{v}}_{{\mathbf{D}}}$ is replaced by ${\mathbf{v}}$ for convenience.

We follow a time-independent stagnant solution of Eqs. (12)–(16) such that temperature, concentration and nanoparticle volume fraction vary in z-direction only. Thus, the basic state is described by:

$${\mathbf{v}} = 0,\;p = p_{b} (z),\;T = T_{b} (z),\;C = C_{b} (z),\;\phi = \phi_{b} (z),$$

(19)

$$\frac{{d^{2} T_{b} }}{{dz^{2} }} + \frac{{N_{B} }}{Le}\frac{{d\phi_{b} }}{dz}\frac{{dT_{b} }}{dz} + \frac{{N_{A} N_{B} }}{Le}\left( {\frac{{dT_{b} }}{dz}} \right)^{2} = 0,$$

(20)

$$\frac{{d^{2} C}}{{dz^{2} }} = 0,$$

(21)

$$\frac{{d^{2} \phi_{b} }}{{dz^{2} }} + N_{A} \frac{{d^{2} T_{b} }}{{dz^{2} }} = 0.$$

(22)

It provides the steady state solutions as

$$T_{b} = 1 - z,$$

(23)

$$C_{b} = 1 - z,$$

(24)

$$\phi_{b} = \phi_{0} + N_{A} z.$$

(25)

2.1 Linear stability analysis

Let the initial steady state be slightly perturbed. Following the classical lines of linear stability theory presented by Chandrasekhar [47], the perturbations are decomposed in terms of normal modes in the form

$$(w^{\prime } ,T^{\prime } ,C^{\prime } ,\phi^{\prime } ) = [W(z),\varTheta (z),\eta (z),\varPhi (z)]\exp (st + ilx + imy),$$

(26)

where l (in x-direction) and m (in y-direction) are dimensionless wave numbers respectively and $s$$\left( { = \omega_{r} + i\omega_{i} } \right)$ is a complex number predicting about the perturbations. So we arrive at the following boundary value problem:

$$(D^{2} - \alpha^{2} )W + \alpha^{2} \left( {1 + \frac{\lambda s}{\sigma }} \right)\left( {Ra\varTheta - Rn\varPhi + \frac{Rs}{Ln}\eta } \right) = 0,$$

(27)

$$W + \left( {D^{2} - \alpha^{2} - \frac{{N_{A} N_{B} }}{Le}D - s} \right)\varTheta - \frac{{N_{B} }}{Le}D\varPhi = 0,$$

(28)

$$\frac{W}{\varepsilon } + N_{CT} \left( {D^{2} - \alpha^{2} } \right)\varTheta + \left( {\frac{1}{Ln}(D^{2} - \alpha^{2} ) - \frac{s}{\sigma }} \right)\eta = 0,$$

(29)

$$N_{A} \frac{W}{\varepsilon } - \frac{{N_{A} }}{Le}\left( {D^{2} - \alpha^{2} } \right)\varTheta - \left( {\frac{1}{Le}(D^{2} - \alpha^{2} ) - \frac{s}{\sigma }} \right)\varPhi = 0,$$

(30)

$$W = 0,\varTheta = 0,\eta = 0,D\varPhi + N_{A} D\varTheta = 0\;\;{\text{at}}\;z = 0\;{\text{and}}\;z = 1,$$

(31)

where $D \equiv \frac{d}{dz}\;$${\text{and}}\;\alpha = (l^{2} + m^{2} )^{1/2}$ is a dimensionless horizontal wave number.

Here it is to be noted that the boundary value problem for Darcy–Maxwell nanofluid converts to Horton–Roger–Lapwood problem [42] for a double diffusive convection in a regular nanofluid as soon as the relaxation parameter $\lambda \to 0$.

To obtain an approximate solution for the system of Eqs. (27)–(31), we use the Galerkin-type-weighted residual method. Choosing trial functions (satisfying the boundary conditions)$W_{p}$, $\varTheta_{p}$, $\varPhi_{p}$ and $\eta_{p}$:$p = 1,2,3 \ldots N$ and writing

$$W = \sum\limits_{p = 1}^{N} {A_{p} W_{p} } ,\varTheta = \sum\limits_{p = 1}^{N} {B_{p} \varTheta_{p} } ,\varPhi = \sum\limits_{p = 1}^{N} {C_{p} \varPhi_{p} } ,\eta = \sum\limits_{p = 1}^{N} {D_{p} \eta_{p} } ,$$

(32)

we obtain a system of 4N linear algebraic equations in the 4N unknowns A_p, B_p, C_p and D_p. In view of the boundary conditions given by Eq. (31), the base functions mentioned in (32) may be assumed as

$$W_{p} = \varTheta_{p} = \eta_{p} = \sin p\pi z;\varPhi_{p} = - N_{A} \sin p\pi z.$$

(33)

Substituting Eqs. (33) in (32) and using the results in Eqs. (27)–(31), we get a system of equations of non-trivial solution for the first approximation i.e. at N = 1, under the necessary condition

$$\left| {\begin{array}{*{20}c} { - \delta^{2} } & {\alpha^{2} \left( {1 + \frac{s\lambda }{\sigma }} \right)Ra} & {\alpha^{2} \left( {1 + \frac{s\lambda }{\sigma }} \right)\frac{Rs}{Ln}} & {\alpha^{2} \left( {1 + \frac{s\lambda }{\sigma }} \right)RnN_{A} } \\ 1 & { - \left( {\delta^{2} + s} \right)} & 0 & 0 \\ {\frac{1}{\varepsilon }} & { - \delta^{2} N_{CT} } & { - \left( {\frac{{\delta^{2} }}{Ln} + \frac{s}{\sigma }} \right)} & 0 \\ {\frac{1}{\varepsilon }} & {\frac{{\delta^{2} }}{Le}} & 0 & { - \left( {\frac{{\delta^{2} }}{Le} + \frac{s}{\sigma }} \right)} \\ \end{array} } \right| = 0,$$

(34)

where $\delta^{2} = \pi^{2} + \alpha^{2}$.

2.1.1 Stationary convection

It follows from Eq. (34) that the stationary convection at the marginal state (s = 0) is governed by the Rayleigh number

$$Ra^{st} = \frac{{\delta^{4} }}{{\alpha^{2} }} - RnN_{A} \left( {1 + \frac{Le}{\varepsilon }} \right) - \frac{Rs}{\varepsilon }(1 - \varepsilon N_{CT} ),$$

(35)

Such that the critical Rayleigh number $Ra^{st}$ at the critical wave number $\alpha = \pi$ is obtained as

$$Ra^{st} = 4\pi^{2} - \left( {1 + \frac{Le}{\varepsilon }} \right)N_{A} Rn - \left( {1 - \varepsilon N_{CT} } \right)\frac{Rs}{\varepsilon },$$

(36)

In the absence of Soret parameter (N_CT = 0), Eq. (36) converts to

$$Ra^{st} = 4\pi^{2} - RnN_{A} \left( {1 + \frac{Le}{\varepsilon }} \right) - \frac{Rs}{\varepsilon },$$

(37)

which is obtained by Jaimala et al. [48].

Equation (37) in the absence of salt, converts to

$$Ra^{st} = 4\pi^{2} - RnN_{A} \left( {1 + \frac{Le}{\varepsilon }} \right).$$

(38)

This is the Rayleigh number obtained by Jaimala et al. [39].

2.1.2 Oscillatory convection

When $\left( {s = \omega_{i} + i\omega_{r} :\omega_{r} = 0} \right)$ at the marginal state, the Rayleigh number is obtained as:

$$Ra^{osc} = \frac{\sigma }{{\alpha^{2} \varepsilon }}\left[ {\frac{{\left( {X_{1} - X_{2} + X_{3} } \right)U + \omega^{2} \left( {Y_{1} - Y_{2} + Y_{3} } \right)V}}{{U^{2} + V^{2} }}} \right],$$

(39)

where

$$\begin{aligned} X_{1} & = \alpha^{2} RnN_{A} \left[ {\delta^{4} \sigma^{2} \left( {\varepsilon + Le} \right) - \lambda \delta^{2} \omega^{2} \left( {\sigma Le + \varepsilon Ln + LnLe} \right) - \omega^{2} \sigma LeLn} \right], \\ X_{2} & = \delta^{4} \left[ {\delta^{4} \sigma^{2} - \omega^{2} \left\{ {Ln\sigma + Le\sigma + LeLn} \right\}} \right], \\ X_{3} & = \alpha^{2} Rs\left[ {\delta^{4} \sigma^{2} \left( {1 - N_{CT} \varepsilon } \right) - \omega^{2} \left\{ {\delta^{2} \lambda \sigma + Le\left( {\sigma - \delta^{2} \lambda \varepsilon N_{CT} + \delta^{2} \lambda } \right)} \right\}} \right], \\ Y_{1} & = \alpha^{2} RnN_{A} \left[ {\sigma \delta^{2} \left\{ {\lambda \delta^{2} \left( {\varepsilon + Le} \right) + \left( {\sigma Le + \varepsilon Ln + LeLn} \right)} \right\} - \lambda \omega^{2} LeLn} \right], \\ Y_{2} & = \varepsilon \delta^{2} \left[ {\delta^{4} \sigma \left( {Le + \sigma + Ln} \right) - \omega^{2} LeLn} \right], \\ Y_{3} & = \alpha^{2} Rs\left\{ {\delta^{2} \sigma \left( {Le - \varepsilon N_{CT} Le + \sigma - \lambda \delta^{2} \varepsilon N_{CT} + \lambda \delta^{2} } \right) - \lambda \omega^{2} Le} \right\}, \\ U & = \left[ {\omega^{2} \sigma \left\{ {\lambda \delta^{2} \left( {Le + Ln} \right) + LeLn} \right\} - \delta^{4} \sigma^{3} } \right], \\ V & = \left[ {\lambda \omega^{2} LnLe - \delta^{2} \sigma^{2} \left( {\lambda \delta^{2} + Ln + Le} \right)} \right]. \\ \end{aligned}$$

We write $\omega$ in place of $\omega_{i}$ for convenience.

The frequency of oscillation is given by the following fourth order equation in $\omega$:

$$(P_{1} P_{2} + P_{3} P_{4} )\omega^{4} + (P_{1} P_{5} + P_{2} P_{6} + P_{3} P_{7} + P_{4} P_{8} )\omega^{2} + (P_{5} P_{6} + P_{7} P_{8} ) = 0,$$

(40)

where

$$\begin{aligned} P_{1} & = \delta^{4} \varepsilon \left( {\sigma Ln + \sigma Le + LeLn} \right) - \alpha^{2} RnN_{A} \left\{ {\sigma LeLn + \lambda \delta^{2} \left( {\sigma Le + \varepsilon Ln + LeLn} \right)} \right\} \\ & \quad - \,\alpha^{2} Rs\left\{ {\delta^{2} \lambda \left( {Le + \sigma - LeN_{CT} \varepsilon } \right) + \sigma Le} \right\}, \\ P_{2} & = - \lambda LeLn, \\ P_{3} & = Le\left( {\delta^{2} \varepsilon Ln - \alpha^{2} \lambda RnN_{A} Ln - \lambda \alpha^{2} Rs} \right), \\ P_{4} & = \sigma \left\{ {\delta^{2} \lambda \left( {Le + Ln} \right) + LeLn} \right\}, \\ P_{5} & = \delta^{2} \sigma^{2} \left( {\lambda \delta^{2} + Ln + Le} \right), \\ P_{6} & = \delta^{4} \sigma^{2} \left\{ {\alpha^{2} RnN_{A} \left( {\varepsilon + Le} \right) - \delta^{4} \varepsilon + \alpha^{2} Rs\left( {1 - N_{CT} \varepsilon } \right)} \right\}, \\ P_{7} & = - \delta^{4} \sigma^{3} , \\ P_{8} & = \delta^{2} \sigma \left[ \begin{aligned} & \alpha^{2} RnN_{A} \left\{ {\delta^{2} \lambda \left( {\varepsilon + Le} \right) + \sigma Le + \varepsilon Ln + LeLn} \right\} - \delta^{4} \varepsilon \left( {\sigma + Le + Ln} \right) \\ & \quad + \,\alpha^{2} Rs\left\{ {\left( {1 - N_{CT} \varepsilon } \right)\left( {Le + \delta^{2} \lambda } \right) + \sigma } \right\} \\ \end{aligned} \right]. \\ \end{aligned}$$

2.2 Nonlinear stability analysis

To get the information about the amplitude of motion and the behaviour of heat, salt and mass transfer, non-linear stability theory is used. After substituting T_b, C_b and $\phi_{b}$ given by Eqs. (23), (24) and (25) respectively in the two-dimensional perturbed state solution, after elimination of pressure and introduce the stream function in the resulting equation, we get

$$\nabla_{1}^{2} \psi = \left( {1 + \frac{\lambda }{\sigma }\frac{\partial }{\partial t}} \right)\left[ { - Ra\frac{\partial T}{\partial x} + Rn\frac{\partial \phi }{\partial x} - \frac{Rs}{Ln}\frac{\partial C}{\partial x}} \right],$$

(41)

$$\frac{\partial T}{\partial t} + \frac{\partial \psi }{\partial x} = \nabla_{1}^{2} T + \frac{\partial (\psi ,T)}{\partial (x,z)},$$

(42)

$$\frac{1}{\sigma }\frac{\partial C}{\partial t} + \frac{1}{\varepsilon }\left( {\frac{\partial \psi }{\partial x}} \right) = \frac{1}{Ln}\nabla_{1}^{2} C + \frac{1}{\varepsilon }\frac{\partial (\psi ,C)}{\partial (x,z)} + N_{CT} \nabla_{1}^{2} T,$$

(43)

$$\frac{1}{\sigma }\frac{\partial \phi }{\partial t} - \frac{{N_{A} }}{\varepsilon }\left( {\frac{\partial \psi }{\partial x}} \right) = \frac{1}{Le}\nabla_{1}^{2} \phi + \frac{{N_{A} }}{Le}\nabla_{1}^{2} T + \frac{1}{\varepsilon }\frac{\partial (\psi ,\phi )}{\partial (x,z)},$$

(44)

where $\nabla_{1}^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial z^{2} }}$.

Now Eq. (31) converts into

$$\psi = \frac{{\partial^{2} \psi }}{{\partial z^{2} }} = T = 0,C = 0,\frac{\partial \phi }{\partial z} + N_{A} \frac{\partial T}{\partial z} = 0\;\;{\text{at}}\;z = 0\;and\;z = 1.$$

(45)

We take Fourier expressions for $\psi ,\,T,\,\phi \,\;{\text{and}}\;\,C$ to perform nonlinear stability analysis as

$$\psi = A_{11} (t)\sin (\alpha x)\sin (\pi z),$$

(46)

$$T = B_{11} (t)\cos (\alpha x)\sin (\pi z) + B_{02} (t)\sin (2\pi z),$$

(47)

$$\phi = - N_{A} C_{11} (t)\cos (\alpha x)\sin (\pi z) - N_{A} C_{02} (t)\sin (2\pi z),$$

(48)

$$C = D_{11} (t)\cos (\alpha x)\sin (\pi z) + D_{02} (t)\sin (2\pi z),$$

(49)

where the coefficients $A_{11} (t),$$B_{11} (t),$$B_{02} (t),$$C_{11} (t)$, $\;C_{02} (t)$, $D_{11} (t)$ and $D_{02} (t)$ are time dependent amplitudes and are to be determined from the dynamics of the system. Substituting Eqs. (46)–(49) into the set of coupled non-linear partial differential equations given by (41)–(44) and applying the orthogonality condition in corresponding eigen-functions, we have

$$A_{11} = - \frac{\alpha }{{\delta^{2} }}\left\{ {RaB_{11} + RnN_{A} C_{11} + \frac{Rs}{Ln}D_{11} + \frac{\lambda }{\sigma }\left( {Ra\frac{{dB_{11} }}{dt} + RnN_{A} \frac{{dC_{11} }}{dt} + \frac{Rs}{Ln}\frac{{dD_{11} }}{dt}} \right)} \right\},$$

(50)

$$\frac{{dB_{11} }}{dt} = - \left( {\alpha A_{11} + \delta^{2} B_{11} + \pi \alpha A_{11} B_{02} } \right),$$

(51)

$$\frac{{dB_{02} }}{dt} = \frac{1}{2}\left( {\pi \alpha A_{11} B_{11} - 8\pi^{2} B_{02} } \right),$$

(52)

$$\frac{{dC_{11} }}{dt} = - \sigma \left\{ {\frac{\alpha }{\varepsilon }A_{11} - \frac{{\delta^{2} }}{Le}\left( {B_{11} - C_{11} } \right) + \frac{\pi \alpha }{\varepsilon }A_{11} C_{02} } \right\},$$

(53)

$$\frac{{dC_{02} }}{dt} = \frac{\sigma }{2}\left\{ {\frac{\pi \alpha }{\varepsilon }A_{11} C_{11} + \frac{{8\pi^{2} }}{Le}\left( {B_{02} - C_{02} } \right)} \right\},$$

(54)

$$\frac{{dD_{11} }}{dt} = - \sigma \left[ {\frac{\alpha }{\varepsilon }A_{11} + \delta^{2} N_{CT} B_{11} + \frac{{\delta^{2} }}{Ln}D_{11} + \frac{\pi \alpha }{\varepsilon }A_{11} D_{02} } \right],$$

(55)

$$\frac{{dD_{02} }}{dt} = \frac{\sigma }{2}\left[ {\frac{\pi \alpha }{\varepsilon }A_{11} D_{11} - 8\pi^{2} \left( {\frac{{D_{02} }}{Ln} + B_{02} N_{CT} } \right)} \right].$$

(56)

Equations (50)–(56) represent a non-linear autonomous system of simultaneous ordinary differential equations, which is not suitable to analytical analysis. Therefore, it is to be solved numerically using Runge–Kutta–Gill method. For steady state, setting the left-hand sides of Eqs. (51)–(56) equal to zero, the resulting equations are solved and the amplitudes are obtained in terms of A₁₁ as:

$$B_{11} = - \frac{{\alpha A_{11} }}{{\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)}},$$

(57)

$$B_{02} = - \frac{{\alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)}}{{\pi \left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}},$$

(58)

$$C_{11} = \frac{{\varepsilon^{2} \alpha LeA_{11} }}{{\varepsilon^{2} \delta^{2} + \alpha^{2} Le^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)}}\left[ {\frac{{\alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)}}{{\varepsilon \left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}} - \frac{{\delta^{2} }}{{Le\left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}} - \frac{1}{\varepsilon }} \right],$$

(59)

$$C_{02} = \frac{{\varepsilon \alpha^{2} Le^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)}}{{\pi \left\{ {\varepsilon^{2} \delta^{2} + \alpha^{2} Le^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right\}}}\left[ {\frac{{\alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)}}{{\varepsilon \left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}} - \frac{{\delta^{2} }}{{Le\left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}} - \frac{1}{\varepsilon }} \right] - \frac{{\alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)}}{{\pi \left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}},$$

(60)

$$D_{11} = \frac{{\varepsilon^{2} \alpha LnA_{11} }}{{\varepsilon^{2} \delta^{2} + \alpha^{2} Ln^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)}}\left[ {\frac{{\delta^{2} N_{CT} }}{{\left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}} - \frac{{\alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)LnN_{CT} }}{{\varepsilon \left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}} - \frac{1}{\varepsilon }} \right],$$

(61)

$$D_{02} = \frac{{\varepsilon \alpha^{2} Ln^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)}}{{\pi \left\{ {\varepsilon^{2} \delta^{2} + \alpha^{2} Ln^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right\}}}\left[ {\frac{{\delta^{2} N_{CT} }}{{\left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}} - \frac{{\alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)LnN_{CT} }}{{\varepsilon \left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}} - \frac{1}{\varepsilon }} \right] + \frac{{\alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)LnN_{CT} }}{{\pi \left( {\delta^{2} + \alpha^{2} \left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)} \right)}}.$$

(62)

The use of Eqs. (57)–(62) into (50) leads to

$$P\left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)^{3} + Q\left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right)^{2} + R\left( {{{A_{11}^{2} } \mathord{\left/ {\vphantom {{A_{11}^{2} } 8}} \right. \kern-0pt} 8}} \right) + S = 0,$$

(63)

where

$$\begin{aligned} P & = \delta^{2} \alpha^{6} Le^{2} Ln^{2} , \\ Q & = \delta^{4} \alpha^{4} Le^{2} Ln^{2} + \delta^{4} \alpha^{4} \varepsilon^{2} (Le^{2} + Ln^{2} ) \\ & \quad - \,\alpha^{6} Le^{2} Ln^{2} Ra - \varepsilon \alpha^{6} Le^{2} Rs(1 + LnN_{CT} ), \\ R & = \delta^{6} \alpha^{2} \varepsilon^{2} (Le^{2} + Ln^{2} + \varepsilon^{2} ) - \alpha^{4} \delta^{2} \varepsilon^{2} (Le^{2} + Ln^{2} )Ra \\ & \quad - \,RnN_{A} \varepsilon \delta^{2} \alpha^{4} Ln^{2} (Le + \varepsilon ) + \varepsilon \delta^{2} \alpha^{4} Le^{2} (N_{CT} \varepsilon - 1)Rs \\ & \quad - \,\varepsilon^{3} \delta^{2} \alpha^{4} (N_{CT} Ln + 1)Rs, \\ S & = \delta^{8} \varepsilon^{4} - \alpha^{2} \delta^{4} \varepsilon^{4} Ra - RnN_{A} \varepsilon^{3} \delta^{4} \alpha^{4} (Le + \varepsilon ) + \delta^{4} \alpha^{2} \varepsilon^{3} Rs(N_{CT} \varepsilon - 1). \\ \end{aligned}$$

2.2.1 Heat, salt and nanoparticle mass transport

The heat transport specified by the “thermal Nusselt number” is defined as

$$\begin{aligned} Nu(t) & = \frac{{{\text{Heat}}\;{\text{transport}}\;{\text{by}}\; ( {\text{conduction}}\,{ + }\,{\text{convection)}}}}{{{\text{Heat}}\;{\text{transport}}\;{\text{by}}\;{\text{conduction}}}} \\ & = 1 + \left[ {\frac{{\int\limits_{0}^{{2\pi /\alpha_{c} }} {\left( {\frac{\partial T}{\partial z}} \right)dx} }}{{\int\limits_{0}^{{2\pi /\alpha_{c} }} {\left( {\frac{{\partial T_{b} }}{\partial z}} \right)dx} }}} \right]_{z = 0} , \\ \end{aligned}$$

provides

$$Nu(t) = 1 - 2\pi B_{02} (t),$$

(64)

where $B_{02} (t)$ is given by Eq. (58).

Similarly, the solutal concentration Nusselt number $Nu_{C} (t)$ is found to be

$$Nu_{C} (t) = 1 - 2\pi D_{02} (t) + N_{CT} \left( {1 - 2\pi B_{02} (t)} \right),$$

(65)

where $D_{02} (t)$ is given by Eq. (62).

The nanoparticle concentration Nusselt number is defined as

$$Nu_{\phi } (t) = 1 + \left[ {\frac{{\int\limits_{0}^{{2\pi /\alpha_{c} }} {\left( {\frac{\partial \phi }{\partial z} + N_{A} \frac{\partial T}{\partial z}} \right)dx} }}{{\int\limits_{0}^{{2\pi /\alpha_{c} }} {\left( {\frac{{\partial \phi_{b} }}{\partial z}} \right)dx} }}} \right]_{z = 0} ,$$

gives

$$Nu_{\phi } (t) = 1 + 2\pi \left( {B_{02} (t) - C_{02} (t)} \right),$$

(66)

where $C_{02} (t)$ is given by Eq. (60).

Agrawal et al. [49] discussed the Rayleigh Bénard convection in a nanofluid with local thermal equilibrium (LTE) and showed that the mode of mass transfer was diffusion only, but Eqs. (64) to (66) show that heat, salt and nano concentration all are transferred through diffusion as well as convection. Clearly transfer of heat, salt and mass all are governed by Soret parameter.

3 Results and discussion

In the limiting case of monodiffusive convection in a Maxwell nanofluid, the problem discussed converts to the one investigated in detail recently by Jaimala et al. [39]. Similarly, for regular fluid (in the absence of nanoparticles), it represents the established Soret driven double diffusive convection studied by Wang and Tang [32]. The results reported here are also used for comparison with those obtained for double diffusive convection in a nanofluid.

3.1 Linear stability analysis

Linear stability theory provides the Rayleigh number for stationary and oscillatory convection. For stationary convection, we recover the Rayleigh number deduced for monodiffusive convection in the nanofluid [see Eq. (38)] and Bénard convection in Horton–Rogers problem for a regular fluid [42]. Comparing the Rayleigh number for nanofluid given by Eq. (38) with the classical Rayleigh number $Ra\, = \,4\pi^{2}$, it is clear that if the density of nanoparticles is greater than the density of base fluid the Rayleigh number is reduced substantially causing an early convection, which is further diminished in the presence of salt [see Eq. (37)] but the inclusion of Soret effect delays the convection in comparison to the convection in its absence.

Tables 1 and 2 present a comparison between the three Rayleigh numbers for a single phase nanofluid, binary nanofluid, and the Soret effect in a binary nanofluid for stationary and oscillatory convections respectively for fixed values of the concerned parameters. Table 1 shows that Ra_(thermal) ≥ Ra_{(Soret induced)} ≥ Ra_(salt) everywhere in the flow domain. The critical Rayleigh number Ra^cr for the three convections are 23.879 for thermal convection, 11.879 for Soret convection and 11.379 for thermosolutal convection. It confirms the analytical result that the presence of salt in Maxwell nanofluid enhances the convection and establishes the fact that though Soret effect delays the convection still it occurs earlier in comparison to the convection set in a single phase nanofluid. Readings of Table 1 are reflected through Fig. 2a. Table 2 shows that oscillatory thermal convection for single phase fluid, binary fluid and binary fluid with Soret effect diminishes approximately after α = 3.7396, 6.7636 and 7.066 respectively. Corresponding Fig. 2b predicts that the oscillatory convection sets up earliest in the single phase nanofluid and latest in binary fluid with Soret effect.

Table 1 Stationary convection: Ra for thermal convection, thermosolutal convection and Soret induced convection

Table 2 Oscillatory convection: Ra for thermal convection, thermo-solutal convection and Soret induced convection

Fig. 2

a Stationary convection for thermal, solutal and Soret induced convection. b Oscillatory convection for thermal, solutal and Soret induced convection

Behavior of Soret parameter with respect to Rayleigh number and wave number for stationary convection for $Rs = 5,\,Rn = 1,\;Le = 8,\,\varepsilon = 0.5,\;N_{A} = 1$ in Fig. 3. From figure we can show that on increasing the Soret parameter N_CT the critical Rayleigh number is increased and hence the Soret parameter is responsible for promoting the stability of the flow. The behavior of remaining parameters is the same as we have discussed in Jaimala et al. [48].

Fig. 3

Ra versus α for linear stationary convection for N_CT

Figure 4a–i show the variations of Rayleigh number for linear oscillatory modes at the marginal state in (Ra, α) plane for the parameters $Rs = 0.5,Rn = 0.4,\varepsilon = 0.4,N_{A} = 1,Le = 20,Ln = 5, \sigma = 1,\lambda = 0.1,N_{CT} = 0.1$, by varying one of the parameters and keeping others fixed. It is seen that in Soret induced convection, initially Ra decreases very sharply and after an initial fall it increases in a wave number range (2.42 < α<4.94), then again it decreases to diminish. It is also observed that on increasing any of the parameters Rn, $Ln$, $N_{A}$, σ and N_CT the peaks of oscillatory curves get higher (see Fig. 4b, e–g, i) and get further down when any of Rs, Le, ɛ or λ increases (see Fig. 4a, c, d, h). The results are in good agreement with double diffusive convection [39].

Fig. 4

Ra versus α for linear oscillatory curve for a Rs b Rn c Le d ε e Ln f N_A g σ h λ i N_CT

A comparison of stationary convection and oscillatory convection is shown in Fig. 5a–f for particular values of the parameters. It indicates that in all the cases the oscillatory convection occurs only for a particular range of wave number and there exist no wave number where the critical Rayleigh number exists. It occurs at the wave number beyond which the oscillatory convection ceases to exist.

Fig. 5

Comparison of stationary and oscillatory convection for a Rs b Rn c Le d ε e N_A f N_CT

3.2 Nonlinear stability analysis

3.2.1 Steady analysis

To detect the onset of convection in steady state, the effect of increasing Rayleigh number on heat, concentration and mass transport across the layer is important. It is noticed that the steady state flow depends upon the Soret parameters but is independent of σ and λ.

Figures 7 and 8 portray the effect of Ra on both the Nusselt numbers Nu_C and $Nu_{\phi }$ respectively for the values of the parameters Rs, Le, Rn, ε, Ln, N_A and N_CT by varying one of the parameters.

It is observed from Fig. 6 that, as Rayleigh number increases, thermal Nusselt number increases very sharply i.e. heat transfer increases at a sharp rate and as Rayleigh number is increased further, it attains a steady state. On increasing any of the values of the parameters Rs, Rn, ε, and N_A the heat transfer is increasing before attaining a steady state [48]. Also the parameters Le and Ln separately have reverse effect on heat transfer. It is decreased on increasing any of the parameters though it again becomes constant for large values of Rayleigh number [48]. It is interesting to note that Fig. 6 portrays a dual character of Soret parameter N_CT. Initially, on increasing N_CT, heat transfer is decreased then starts to increase for a fixed range of Rayleigh number (< Ra = 33.5 and at that point, value of Nu = 1.15) and finally reaches at a constant value for Ra > 300 (approximately). Figure 7 shows that, on increasing Ra, initially the salt is transferred in large amount but it becomes constant for large values of Rayleigh number (> 250 approximately). The parameters Rs, Rn, Ln, N_A and N_CT individually are responsible to increase the salt transfer. Figure 7c interprets that the Lewis number Le predicts very surprising behavior as for Le $\ge \,\,5.9$ salt transfer is decreased by a substantial amount. Further Fig. 7d depicts the behavior of porosity parameter ε. It shows that on increasing the medium porosity, the salt transfer is decreased. It is to be noted that on increasing the porosity, heat transfer is increased but the amount of salt transfer is decreased. The behavior of ε remains unaltered even in the presence of thermophoresis. It is observed from Fig. 7e, g that salt transfer is enhanced by a considerable amount for Ln $\ge 5$ and N_CT $\ge 0.5$.

Fig. 6

Thermal Nusselt number Nu versus Rayleigh number Ra for N_CT

Fig. 7

$Nu_{C}$ versus Ra for a Rs b Rn c Le d ɛ e Ln f N_A g N_CT

Figure 8a–g indicate that initially mass transfer is increased with the Rayleigh number but a sharp fall is noticed with increasing Ra which finally reaches to a steady state. In double diffusive convection, concentration Nusselt number is depending upon the parameters as Rs, Rn, Le, ɛ, Ln, N_A and N_CT. It is seen that the parameters Rs, Rn, ɛ and N_A have dual character (Fig. 8a, b, d, f). It is to be noticed that the parameters Rn, ɛ and N_A had the same nature in monodifusive convection in a nanofluid. On increasing Rs, Rn and N_A individually, the mass transfer is increased and after a certain Rayleigh number it starts to decrease. An increase in porosity initially results in a fall in mass transfer which is boosted for higher values of Rayleigh number. Surprisingly, Le changes its behavior and shows a dual nature. It is clear from Fig. 8c that initially mass transfer is increased by increasing Le but after a certain value of Ra it inhibits the transfer of mass. In thermal convection, it was noticed to increase the mass transfer. It is observed from Fig. 8e, g that thermosolutal Lewis number Ln, and Soret parameter N_CT follow the nature of porosity.

Fig. 8

$Nu_{\phi }$ versus Ra for a Rs b Rn c Le d ε e Ln f N_A g N_CT

A comparative study of the three Nusselt numbers Nu, Nu_C and Nu_Φ is shown in Fig. 9. It is observed that nanoparticles are transferred most actively. Though in the initial range of Ra (< 80) salt is transferred more rapidly than heat but for Ra > 80 it faces a fall and is decreased by a large amount in comparison to the transfer of heat.

Fig. 9

Comparison between Nu, Nu_C and $Nu_{\phi }$ for Soret-induced convection

In order to observe the intensity of heat, salt and mass transfer according to their existence in the three convections; thermal convection, double diffusive convection and Soret induced convection, the behavior of Nu, $Nu_{C}$ and $Nu_{\phi }$ verses Ra is shown separately in Fig. 10. Figure 10a, portraying Nu shows that heat is transferred most actively in Soret induced convection. It is also observed that in spite of a delay in heat transfer in terms of Rayleigh number in monodiffusive convection, it reaches to a steady state analogous to the double diffusive convection. Figure 10b, showing $Nu_{C}$ indicates that Soret effect decreases the transfer of salt and Fig. 10c shows that mass is transferred most actively in mono-diffusive convection and is least active in double diffusion convection but Soret effect helps it to enhance.

Fig. 10

a (Nu, Ra) curves for monodiffusive, double diffusive and Soret induced convection. b $(Nu_{C} ,Ra)$ curves for double diffusive and Soret induced convection. c (Nu_ɸ, Ra) curves for monodiffusive, double diffusive and Soret induced convection

Figure 11 shows the time independent evolution of the flow patterns in terms of stream lines, isotherms, isonanoconcentrations and isohalines for different values of Rayleigh number for the fixed values of the parameters Rs = 2, Rn = 0.5, Le = 2.5, ε = 0.4, Ln = 2, N_A= 2, N_CT= 0.1. It is clear from Figs. 11a, b that the magnitude of stream function increases with increasing Ra. The stream lines move alternately identical in the subsequent cells but move in the directions opposite to each other. It indicates the symmetrical formation of the convective cells. Isotherms shown in Fig. 11c, d predict that as Rayleigh number increases the convective mode of transfer of heat becomes weak and it starts to transfer through conduction. The patterns of isonanoconcentration show that the transfer of mass through diffusion also falls weak with increasing Ra (see Fig. 11e, f). Figure 11g, h portray that when the Rayleigh number is increased the transfer of salt concentration through both convection and diffusion persists but the amplitudes of the two gradually become weak.

Fig. 11

Streamlines, isotherms, isonanoconcentration, isohalines for Rs = 2, Rn = 0.5, Le =2.5, ε = 0.4, Ln =2, N _A= 2, N _CT= 0.1

3.2.2 Unsteady analysis

In the unsteady state of motion, the time history of all the three convection parameters Nu, Nu_C and $Nu_{\phi }$ are plotted in Figs. 12, 13 and 14 for the case $Rs = 5,Rn = 4,\,Le = 10,\,\varepsilon = 0.4,\,Ln = 10,$ $N_{A} = 2,\, \sigma = 0.8,\,\lambda = 0.5$ and $N_{CT} = 0.1$, when one of the parameters is varied and the others are kept constant. It is observed that initially for small values of time, the transfer of heat, salt concentration and nanoparticles increase sharply and then after an immediate sharp decline attain a steady state through a path of rigorous oscillations. Figure 12a, c, h show the unpredictable behavior of Rs, L_e and $\lambda$. At one instant of time these parameters increase the heat transfer, while at the other these are responsible to decrease it. Figure 12d, e shows that $\varepsilon$ and $Ln$ separately increase the amount of heat transfer as the time passes. From Fig. 12b, f it is observed that transfer of heat decreases with an increase in any of the two parameters $Rn$ and $N_{A}$. Further heat is transferred through oscillations only for lower values of the parameters. Figure 12g show that initially higher values of $\sigma$ lowers the transfer of mass then it is increased for a small range of time and after that it is again declined through oscillations. In case of Soret parameter higher values of it increases the transfer of heat through oscillations after a decline in it for a particular range of time (Fig. 12i). Figures 13 and 14 show that for all parameters salt and mass are transferred through strong unsteady oscillatory patterns.

Fig. 12

Nu versus t for a Rs b Rn c Le d ε e Ln f N_A g σ h λ i N_CT

Fig. 13

$Nu_{C}$ versus t for a Rs b Rn c Le d ε e Le f N_A g σ h $\lambda$ i $N_{CT}$

Fig. 14

$Nu_{\phi }$ versus t for a Rs b Rn c Le d ε e Ln f N_A g σ h λ i N_CT

Figure 15 shows the time dependent stream lines, isotherms, isonanoconcentration and isohalines for Rs = 2, Rn = 0.5, Le = 5.5, ε = 0.4, Ln = 5, N_A= 2, σ = 0.5, λ = 0.1, N_CT= 0.1. It is be noted from Fig. 15a, b that the magnitude of stream function decreases with time. The sense of motion of stream lines in the subsequent cells is alternately identical and opposite in direction. It again indicates the symmetrical formation of the convective cells. Figure 15c, d predict that as the time passes the convective mode of transfer of heat becomes weak and conduction starts near the walls. Figure 15e–h show that mass of nanoparticles and salt which were initially transferred through convection are also transferred through diffusion as the time passes.

Fig. 15

Streamlines, isotherms, isonanoconcentration, isohalines for Rs = 2, Rn = 0.5, Le = 10, ε = 0.4, Ln = 5, N_A= 2, σ = 0.5, λ = 0.1, N_CT= 0.1

4 Conclusion

Linear and non-linear analyses of Soret-driven convection in a horizontal porous layer saturated with a Darcy–Maxwell nanofluid with top heavy suspension is investigated theoretically as well as numerically. The problem is solved for destabilizing thermal and solutal gradients (i.e. when the layer is heated and soluted from below) with positive Soret coefficient. A modified Darcy–Maxwell model suggested by Khuzhayorov et al. [1] subjected to Stefan’s flow condition has been used. The results are compared with the existing relevant studies. The important results are summarized as follows:

4.1 Stability analysis (linear)

4.1.1 Non oscillatory or stationary convection

• The convection at the marginal state depends upon almost all-important parameters including Soret parameter. It is unaffected by the relaxation time of Maxwell fluid.

• The convection which was set up earlier due to the presence of salt in a nanoparticle suspended fluid is delayed by the Soret parameter but still earlier convection is noticed in Soret driven phenomena in comparison to the monodiffusive convection in a nanofluid.

• Concentration Rayleigh Number Rn, solutal Rayleigh Number Rs, thermosolutal Lewis number Ln and modified diffusivity ratio N_A are the parameters promoting the convection. On the other hand, the porosity parameter ε and the Soret parameter N_CT are responsible for postponing it.

4.1.2 Oscillatory convection

• The convection occurs only for a specific wave number range.

• Critical Rayleigh number exists for the wave number where oscillatory convection ceases and shifts to the stationary convection which occurs earlier to it.

• In the common wave number range of the three convections; thermal convection, thermosolutal convection and Soret-driven convection, the convection in a single-phase fluid which was last to set in stationary convection sets up earliest in oscillatory convection. It sets up latest in binary fluid with Soret effect. Thus, the thermal oscillatory convection is delayed by the presence of salt which is further postponed by the presence of thermophoresis.

4.2 Stability analysis (nonlinear)

4.2.1 Steady state

• The convection is independent of $\sigma$ (heat capacity ratio of the medium and the fluid) and the relaxation parameter $\lambda$.

• The three Nusselt numbers: thermal Nusselt number Nu, solutal Nusselt number Nu_C and nanoparticle concentration Nusselt number $Nu_{\phi }$ depend upon the Soret parameter.

• Heat and salt transfers are enhanced continuously with increasing Ra while after initial increment in mass transfer; a downfall is noticed in it. Finally, the heat, mass and salt transfers attain a steady state.

• R_S, Rn, ε and N_A are the parameters promoting the heat transfer while Le and Ln have the reverse effect. The Soret parameter N_CT has a dual character.

• R_S, Rn, Ln, N_A and N_CT are responsible for active salt transport but a substantial enhancement is noticed for Ln > 5 and N_CT> 0.5. Salt transfer is decreased due to ε and Le but again it has a sudden fall at large values of Le (> 5.9).

• In Soret governed convection, among heat, salt and mass, transport of nanoparticles is most active.

• Among monodiffusive, double diffusive and Soret governed convection, heat transfer is most active in Soret induced convection, salt transfer dominates in double diffusive convection and mass transfers most actively in mono-diffusive convection.

• Heat, mass and salt are transferred through diffusion and convection as well.

4.2.2 Unsteady analysis

• The parameters $\varepsilon$ and $Ln$ individually, increase the amount of heat transfer while Rn, $\sigma$ and $N_{A}$ are responsible to decrease it as the time passes.

• The salt and the mass transfer are through vigorous oscillatory patterns.

• The magnitude of stream function decreases with time and heat, mass and salt all are transferred through diffusion and convection both.