DQEM analysis of free transverse vibration of rotating non-uniform nanobeams in the presence of cracks based on the nonlocal Timoshenko beam theory

Abstract

This paper deals with the free transverse vibration characteristics of a rotating non-uniform nanocantilever with multiple open cracks. Employing Eringen’s nonlocal elasticity and the Timoshenko beam theory, the non-dimensional governing differential equations for the above-mentioned problem are derived. The cracked beam is divided into intact sub-beams between two subsequent cracks connected by linear and rotational springs. Differential quadrature element method is utilized to solve the established governing equations of motion of each segment, along with the corresponding boundary conditions and compatibility conditions at the cracked sections. The frequency parameters and vibration modes of the rotating cracked beam for different crack positions and severities under various nonlocal, geometric and dynamic conditions are studied, and the relevant graphs are plotted. Since rotating nanocantilevers are found mostly as blades of rotating nanodevices, the results can provide useful guidance for the study and design of the next generations of nanoturbines, nanogears etc.

1 Introduction

Since the invention of carbon nanotubes, first observed and identified by Iijima [1], nanomaterials have engrossed a great deal of attention of engineers and scientists. Nowadays, many nanostructures are being fabricated and used as the building blocks in the novel fields of nanotechnology. Numerous nanodevices such as nanomechanical resonators, electromechanical nanoactuators and nanogenerators incorporate different structural elements such as rods, beams and plates in nanolength scale [2, 3]. According to the fact that the dimensions of these structures are small and comparable to molecular distances, size effects are significant to analyze their mechanical behavior. The atomic and molecular modes require a great computational effort; therefore, simplified theories of continuum mechanics considering small length scales are useful tools to study such structures.

In other words, since the traditional continuum theories, which are scale-free, do not take account of the size influences, modified version of those have to be employed to study the mechanical behavior of structures at mico- and nanoscale levels accurately. The couple stress and strain gradient elasticity theories are often applied as the size-dependent models to analyze and estimate the mechanical behavior of microstructures such as microbeams [4,5,6,7,8,9,10,11,12,13,14] and microplates [15,16,17,18,19]. Among the size-dependent continuum theories, Eringen’s theory of nonlocal continuum mechanics [20,21,22] has been widely accepted and used to address various phenomena and subjects such as dynamics, wave propagation, dislocation and cracks for problems involving nanostructures [23,24,25]. In the nonlocal theory, the small-scale effects are captured by assuming that the stress at a point is a function of strains at all points in the domain. Indeed, this theory considers long-range interatomic interaction and therefore yields results comparable with those of discrete atomistic or molecular dynamics simulations [26].

Recently, some researchers shown that circularly polarized light can spin nanotubes [27, 28], and after that a great effort has been devoted to the study of carbon nanotubes (CNTs) and nanobeams under rotation. Pradhan and Murmu [29], used the nonlocal elasticity theory to investigate the flap wise bending vibration of a rotating uniform nanocantilever modeled by an Euler–Bernoulli beam. They utilized the differential quadrature method to solve the problem. Murmu and Adhikari [30], studied the vibration characteristics of the same problem subjected to an initial prestress. Narendar and Gopalakrishnan [31], investigated the wave dispersion behavior of a rotating uniform nanotube, using a nonlocal Euler–Bernoulli beam. They consider the maximum centrifugal force (at the root of the nanocantilever) as the axial force. Aranda-Ruiz et al. [32], analyzed the natural frequencies of the flap wise bending vibrations of a rotating non-uniform nanocantilever. They used a nonlocal Euler–Bernoulli beam to obtain the governing equations, and considered the true spatial variation of the axial force due to the rotation. More recently, Khanik [33], applied a modified differential quadrature method to solve and analyze the transverse vibration of a rotating nanobeam. He used the Euler–Bernoulli beam theory and Eringen’s nonlocal model to derive the equations of motion. Pouretemad et al. [34], applied Hamilton’s principle and the differential quadrature element method to investigate the effects of rotation and presence of multiple concentrated masses on the vibration behavior of nonlocal Timoshenko beams. They studied various geometric, dynamic and nonlocal conditions for this problem.

In the above-mentioned literature, it is assumed that the structures are intact, while the presence of defects may have profound effects on the mechanical behavior of structures. For instance, cracks, as a common defect, make structures more flexible and reduce their natural frequencies. Therefore, it is very important to detect the presence, size and position of cracks in a structure. Belytschko et al. [35], studied the fracture of carbon nanotubes by molecular mechanics simulations. Luque et al. [36], employed molecular dynamics techniques to investigate the tensile behavior of cylindrical copper wires of nanometric diameter, considering atomically sharp surface cracks. Loya et al. [37], studied flexural vibrations of cracked nanobeams modeled by nonlocal Euler–Bernoulli beams. Torabi and Dastgerdi [38], used an analytical method to address the same problem for the nonlocal Timoshenko beam model. Hasheminejad et al. [39], and Hosseini-Hashemi et al. [40], investigated the transverse vibration of cracked nanobeams in the presence of the surface effects. Also, Wang and Wang [41], studied the free vibration of a nanobeam based on the Timoshenko model with a single crack. They took account of the surface energy and shear deformation, and showed that the effect of shear deformation is significant on the vibration behavior of nanobeams, especially for higher modes.

Nanoelectromechanical system (NEMS) devices are emerging as the next generation technology which can change people’s lives significantly. Since rotating devices and rotary motors are particularly crucial for such advancing technology, in the present work, the vibration characteristics of nanobeams under rotation are studied. Also in order to have a more accurate study of the mechanical behavior of rotating parts, presence of cracks and variation of cross-section of these elements have to be considered. In the first place, the extended Hamilton’s principle is utilized to derive the equations of motion of a rotating cantilever Timoshenko beam, accounting for rotary inertia and shear deformation effects. The general constitutive equations of the nonlocal elasticity theory are introduced, and then the dynamic governing equations of a nonlocal Timoshenko beam undergoing rotation are obtained. Next, by dividing a cracked beam into intact segments between two subsequent cracks, and connecting them by massless linear and rotational springs, the cracked beam model is established. The differential quadrature element method (DQEM) is employed to solve the derived equations of motion with respect to the compatibility conditions of the cracked sections, and also the cantilever boundary conditions. The accuracy, convergence and versatility of the presented approach are confirmed in comparison with some relevant references using various solution methods. Finally, a parametric analysis is conducted in order to investigate the influences of the nonlocal, hub radius and rotational velocity parameters, as well as cracks positions and cracks severities on the final vibration characteristics of rotating non-uniform nanocantilever. It is shown that the application of this method makes It possible to efficiently solve the problem under different and arbitrary conditions of geometric, mechanical, dynamic properties while there are multiple cracks along the rotating beam, which is very time-consuming and even impossible for other present approaches in the literature. Therefore, the presented equations and solution of such a complex problem along with the results and various comparisons can be very helpful to design better and more accurate rotating devices on nano-scale in the future.

2 Rotating Timoshenko beam

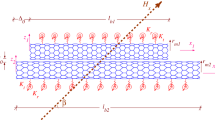
The present study focuses on rotating nanotubes based on the Timoshenko beam theory. Unlike the Euler–Bernoulli beam theory, the Timoshenko theory takes into account the rotational inertia of the cross-section and shear deformation. Therefore, this theory is more accurate for nanobeams, which are stubby and have high frequencies. The following governing equations are derived based on the assumptions that the beam is linear elastic and the steady state axial strain is small, also the material is homogenous and isotropic. Let a non-uniform beam of length L rotate about an axis parallel to the y-axis at a constant angular velocity Ω. The beam is clamped at point O (x = 0) to a rigid hub of radius R as shown in Fig. 1.

Fig. 1

Configuration of a rotating beam

Now, we will use the extended Hamilton’s principle to derive the equations of motion governing the free transverse vibration of a rotating Timoshenko beam. According to Meirovitch [42], the extended Hamilton’s principle for a dynamic system is expressed as:

$$\int_{{t_{1} }}^{{t_{2} }} {\left\{ {\delta T - \delta V + \delta W_{nc} } \right\}dt} = 0,$$

(1)

where T and V are the total kinetic and potential energy of the system, respectively, and $W_{nc}$ denotes the virtual work done by the nonconservative forces. The required equations of the energies and virtual work for a rotating Timoshenko beam are presented by Kaya [43]; therefore, introducing $v = v(x,t)$ and $\psi = \psi (x,t)$ to represent, respectively, the translational deflection along the coordinate y and rotation of the beam cross-section, the kinetic energy of the system is given by:

$$T = \frac{1}{2}\int_{0}^{L} {[\rho A(x)\left( {\frac{\partial v}{\partial t}} \right)^{2} + \rho I(x)\left( {\frac{\partial \psi }{\partial t}} \right)^{2} + \rho I(x)\psi^{2} \Omega^{2} ]dx} ,$$

(2)

where A(x) and I(x) are the beam cross-section area and moment of inertia, respectively, and ρ is the mass density. The total potential energy of the system is evaluated as:

$$V = \frac{1}{2}\int_{0}^{L} {[EI(x)\left( {\frac{\partial \psi }{\partial x}} \right)^{2} + k_{s} GA(x)\left( {\frac{\partial v}{\partial x} - \psi } \right)^{2} ]dx} ,$$

(3)

where k_s is a coefficient introduced to take into account the geometry-dependent distribution of the shear stress. Additionally, the virtual work is expressed as:

$$W_{nc} = - \frac{1}{2}\int_{0}^{L} {\left[ {N(x)\left( {\frac{\partial v}{\partial x}} \right)^{2} } \right]dx} ,$$

(4)

where N(x) is the centrifugal tension force due to the rotation of the beam and can be determined as follows:

$$N(x) = \int_{x}^{L} {[\rho A(x)\Omega^{2} (R + x)]dx} .$$

(5)

Substituting Eqs. (2)–(4) into Eq. (1) and using integration by parts, the equations of motion can be derived as:

$$\frac{\partial Q}{\partial x} + \frac{\partial }{\partial x}\left( {N(x)\frac{\partial v}{\partial x}} \right) = \rho A(x)\frac{{\partial^{2} v}}{{\partial t^{2} }},$$

(6)

$$\frac{\partial M}{\partial x} + Q + \rho I(x)\Omega^{2} \psi = \rho I(x)\frac{{\partial^{2} \psi }}{{\partial t^{2} }},$$

(7)

where the local moment M and the local shear force Q are defined as:

$$M = EI(x)\frac{\partial \psi }{\partial x},$$

(8)

$$Q = k_{s} GA(x)\left( {\frac{\partial v}{\partial x} - \psi } \right).$$

(9)

3 Nonlocal nanobeam model

Behavior of materials on the nanoscale is different from those of their bulk counterparts. In order to study micro- and nanoscale Timoshenko beams the small-size effects have to be included into the derived equations [44,45,46,47,48,49]. For analysis of nanoscale materials, Eringen proposed the nonlocal elasticity theory [21, 22]. This theory states that the stress at point x in a body depends not only on the strain at that point but also on those at all other points of the body. Thus, the nonlocal stress tensor σ at point x is defined as:

$$\sigma = \int_{\Theta } {\kappa (|x^{{\prime }} - x|,h)T_{c} (x^{{\prime }} )d\Theta (x^{{\prime }} )} ,$$

(10)

where $T_{c} (x^{{\prime }} )$ is the classic, microscopic stress tensor at point $x^{{\prime }}$, $\kappa (|x^{{\prime }} - x|,h)$ is the nonlocal modulus or attenuation function introducing into the constitutive equation the nonlocal effect at the reference point x produced by local strain at the source x′. $|x^{{\prime }} - x|$ is the Euclidean distance, and h = e₀a/l is defined as the scale coefficient that incorporates the small-scale factor, where e₀ is a material constant determined experimentally or approximated. Also, a and l are the internal and external characteristic lengths, respectively.

For a beam structure, the sizes in height and width are much smaller than the size in length. Therefore, for an elastic beam with transverse motion in the x − y plane, the nonlocal constitutive relations can be simplified to one-dimensional form as [23,24,25, 50]:

$$\sigma_{xx} - (e_{0} a)^{2} \frac{{d^{2} \sigma_{xx} }}{{dx^{2} }} = E\varepsilon_{xx} ,$$

(11)

$$\sigma_{xy} - (e_{0} a)^{2} \frac{{d^{2} \tau_{xy} }}{{dx^{2} }} = G\gamma_{xy} ,$$

(12)

where E and G are Young’s modulus and shear modulus, respectively, ɛ_xx is the axial strain, and γ_xy is the shear strain. Noting that the scale length e₀a takes into account the size effect on the response of nanostructures and when this parameter is equal to zero, one obtains the constitutive relations of the classical (local) theory.

4 Rotating nonlocal Timoshenko beam

In this section, the governing equations of motion of a rotating nanocantilever with non-uniform cross-section are derived by combining the resulted local equations with the nonlocal constitutive relations. Note that the expressions of the bending moment and shear force in the nonlocal beam theory are different from those in the classical beam theory.

Recall that the definitions of the bending moment, shear force and kinematic relations in a beam structure are given as:

$$\begin{array}{*{20}c} {{\text{M}} = - \int_{A} {\sigma_{xx} ydA} ,} & {Q = \int_{A} {\tau_{xy} ydA} } \\ \end{array} ,$$

(13)

$$\begin{array}{*{20}c} {\varepsilon_{xx} = - y\frac{\partial \psi }{\partial x},} & {\gamma_{xy} = } \\ \end{array} \frac{\partial v}{\partial x} - \psi .$$

(14)

Integrating Eqs. (11) and (12), multiplied by y, along the cross-section of the beam, and using Eqs. (13) and (14), the nonlocal constitutive relations can be expressed in terms of Mand Q. Now, combining the resulted expressions with Eqs. (6) and (7) leads to the nonlocal relations of the bending moment and shear force as follows:

$$\begin{aligned} M &= EI(x)\frac{\partial \psi }{\partial x} + (e_{0} a)^{2} \left[ {\frac{\partial }{\partial x}\left( {\rho I(x)\frac{{\partial^{2} \psi }}{{\partial t^{2} }}} \right) - \rho A(x)}\right.\\&\quad \left.\times\,{\frac{{\partial^{2} v}}{{\partial t^{2} }} + \frac{\partial }{\partial x}\left( {N(x)\frac{\partial v}{\partial x}} \right) - \frac{\partial }{\partial x}(\rho I(x)\Omega^{2} \psi )} \right], \end{aligned}$$

(15)

$$Q = k_{s} GA(x)\left( {\frac{\partial v}{\partial x} - \psi } \right) + (e_{0} a)^{2} \left[ {\frac{\partial }{\partial x}\left( {\rho A(x)\frac{{\partial^{2} v}}{{\partial t^{2} }}} \right) - \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {N(x)\frac{\partial v}{\partial x}} \right)} \right].$$

(16)

5 Rotating cracked nanocantilever

Consider now the rotating nanobeam subjected to n open cracks as depicted in Fig. 2. Indeed, the absence of one or more atoms in the structure of a nanobeam leads to increase in the strain energy, and is modeled as an edge crack. Here, the beam with n cracks is treated as n + 1 intact sub-beams connected by elastic linear and rotational springs. The stiffness of the springs depends on the crack severities determined from molecular dynamics models [35].

Fig. 2

Beam with edge cracks

Therefore, the equations of motion for each segment can be evaluated according to the analysis conducted for the rotating nonlocal Timoshenko beam in the previous sections. Substituting Eqs. (15) and (16) into Eqs. (6) and (7), the governing equations of the free vibration of a rotating uncracked nanoblade are derived, which can be solved by using the separation of variables method as:

$$\begin{array}{*{20}c} {v(x,t) = LV(x)e^{i\omega t} ,} & {\psi (x,t) = \Psi (x)e^{i\omega t} ,} \\ \end{array}$$

(17)

where ω is the natural frequency of vibration. Using the resulted equations and the non-dimensional variables and constants given by:

$$\begin{array}{*{20}c} {A^{*} (x) = \frac{A(x)}{{A_{0} }},} & {I^{*} (x) = \frac{I(x)}{{I_{0} }}} \\ \end{array} ,$$

(18)

$$\begin{aligned} & \zeta^{(i)} = \frac{{x^{(i)} }}{{L^{(i)} }},\quad l^{(i)} = \frac{{L^{(i)} }}{L},\quad i = 1, \ldots ,n + 1, \\ & \xi = \frac{x}{L},\quad \delta = \frac{R}{L},\quad h = \frac{{e_{0} a}}{L},\quad s^{2} = \frac{{EI_{0} }}{{k_{s} GA_{0} L^{2} }},\quad r^{2} = \frac{{I_{0} }}{{A_{0} L^{2} }},\quad \gamma^{4} = \frac{{\rho A_{0} L^{4} \Omega^{2} }}{{EI_{0} }},\quad \lambda^{4} = \frac{{\rho A_{0} L^{4} \omega^{2} }}{{EI_{0} }}, \\ \end{aligned}$$

(19)

in which A₀ and I₀ are the cross-section area and moment of inertia of the beam at the clamped edge, respectively. Finally, the governing equations for the ith segment are derived as:

$$\begin{aligned} & \frac{{ - \gamma^{4} s^{2} h^{2} }}{{A^{*} (\xi )}}\left( {\int_{\xi }^{1} {A^{*} (\xi )(\delta + \xi )} d\xi } \right)\left( {\frac{1}{{l^{(i)} }}} \right)^{4} \frac{{\partial^{4} V^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)^{4} }}\\&\quad + 3\gamma^{4} s^{2} h^{2} (\delta + \xi )\left( {\frac{1}{{l^{(i)} }}} \right)^{3} \frac{{\partial^{3} V^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)^{3} }} \\ & \quad + \left[ {\gamma^{4} s^{2} \left( {3h^{2} \left( {\frac{(\delta + \xi )}{{A^{*} (\xi )}}\frac{{\partial A^{*} (\xi )}}{\partial \xi } + 1} \right) + \frac{{\int_{\xi }^{1} {A^{*} (\xi )(\delta + \xi )} d\xi }}{{A^{*} (\xi )}}} \right) + 1} \right]\\&\quad\times\,\left( {\frac{1}{{l^{(i)} }}} \right)^{2} \frac{{\partial^{2} V^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)^{2} }} + \left[ {\gamma^{4} s^{2} \left( {\frac{{h^{2} }}{{A^{*} (\xi )}}\left( {(\delta + \xi )\frac{{\partial^{2} A^{*} (\xi )}}{{\partial \xi^{2} }}}\right.}\right.}\right.\\&\quad \left.{\left.{\left.{+ \frac{{\partial A^{*} (\xi )}}{\partial \xi }} \right) - (\delta + \xi )} \right) + \frac{1}{{A^{*} (\xi )}}\frac{{\partial A^{*} (\xi )}}{\partial \xi }} \right]\left( {\frac{1}{{l^{(i)} }}} \right)\frac{{\partial V^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)}} \\ & \quad - \left( {\frac{1}{{l^{(i)} }}} \right)\frac{{\partial \Psi^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)}} - \frac{1}{{A^{*} (\xi )}}\frac{{\partial A^{*} (\xi )}}{\partial \xi }\Psi^{(i)} \left( {\zeta^{(i)} } \right) \\ & \quad - \lambda^{4} s^{2} \left\{ {h^{2} \left( {\frac{1}{{l^{(i)} }}} \right)^{2} \frac{{\partial^{2} V^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)^{2} }} + \frac{{2h^{2} }}{{A^{*} (\xi )}}\frac{{\partial A^{*} (\xi )}}{\partial \xi }\left( {\frac{1}{{l^{(i)} }}} \right)}\right.\\&\left.{ \times\,\frac{{\partial V^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)}} + \left( {\frac{{h^{2} }}{{A^{*} (\xi )}}\frac{{\partial^{2} A^{*} (\xi )}}{{\partial \xi^{2} }} - 1} \right)V^{(i)} \left( {\zeta^{(i)} } \right)} \right\} = 0, \\ \end{aligned}$$

(20)

$$\begin{aligned} & s^{2} \left( { - \gamma^{4} r^{2} h^{2} + 1} \right)\left( {\frac{1}{{l^{(i)} }}} \right)^{2} \frac{{\partial^{2} \varPsi^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)^{2} }} + \frac{{s^{2} }}{{I^{*} (\xi )}}\frac{{\partial I^{*} (\xi )}}{\partial \xi }\left( { - 2\gamma^{4} r^{2} h^{2} + 1} \right)\left( {\frac{1}{{l^{(i)} }}} \right)\frac{{\partial \varPsi^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)}} \\ & \quad \left[ {\gamma^{4} s^{2} r^{2} \left( { - \frac{{h^{2} }}{{I^{*} (\xi )}}\frac{{\partial^{2} I^{*} (\xi )}}{{\partial \xi^{2} }} + 1} \right) - \frac{{A^{*} (\xi )}}{{I^{*} (\xi )}}} \right]\varPsi^{(i)} \left( {\zeta^{(i)} } \right) + \frac{{A^{*} (\xi )}}{{I^{*} (\xi )}}\left( {\frac{1}{{l^{(i)} }}} \right)\frac{{\partial V^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)}} \\ & \quad \quad - \lambda^{4} s^{2} r^{2} \left\{ {h^{2} \left( {\frac{1}{{l^{(i)} }}} \right)^{2} \frac{{\partial^{2} \varPsi^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)^{2} }} + \frac{{2h^{2} }}{{I^{*} (\xi )}}\frac{{\partial I^{*} (\xi )}}{\partial \xi }\left( {\frac{1}{{l^{(i)} }}} \right)\frac{{\partial \varPsi^{(i)} \left( {\zeta^{(i)} } \right)}}{{\partial \left( {\zeta^{(i)} } \right)}} + \left( {\frac{{h^{2} }}{{I^{*} (\xi )}}\frac{{\partial^{2} I^{*} (\xi )}}{{\partial \xi^{2} }} - 1} \right)\varPsi^{(i)} \left( {\zeta^{(i)} } \right)} \right\} = 0. \\ \end{aligned}$$

(21)

Note that the above 2i equations must be solved with the present boundary conditions of the beam, clamped-free, and the compatibility conditions in the vicinity of each crack.

Since the rotating beam is considered a cantilever beam, the deflection and derivative of the deflection are equal to zero at the hub, and also there is no bending moment and shearing force at the free end. Therefore, the following boundary conditions can be written:

$$\begin{array}{*{20}c} {\left. {V^{(1)} } \right|_{{\zeta^{(1)} = 0}} = 0,} & {\left. {\Psi^{(1)} } \right|_{{\zeta^{(1)} = 0}} = 0,} & {\left. {M^{(n + 1)} } \right|_{{\zeta^{(n + 1)} = 1}} = 0,} & {\left. {Q^{(n + 1)} } \right|_{{\zeta^{(n + 1)} = 1}} = 0.} \\ \end{array}$$

(22)

Also, in order to take into account the effects of the cracks, the successive segments of the beam are connected by linear and rotational elastic springs. Actually, the presence of the cracks increases the strain energy of the system, and this additional energy is considered by introducing one linear spring and one rotational spring for each crack. As a result, the compatibility conditions at the common node of two adjacent segments ($\xi = \xi_{crack}$) are calculated as follows [51]:

Continuity in the natural parameters:

$$\begin{array}{*{20}c} {M(\xi_{crack}^{ + } ) = M(\xi_{crack}^{ - } ),} & {Q(\xi_{crack}^{ + } ) = Q(\xi_{crack}^{ - } ).} \\ \end{array}$$

(23)

Discontinuity in the geometric parameters:

$$\begin{aligned} & V(\xi_{crack}^{(i + 1)} ) - V(\xi_{crack}^{(i)} ) = - \alpha_{q} \bar{Q}(\xi_{crack}^{(i + 1)} ),\quad \alpha_{q} = \frac{t}{L}\frac{{k_{s} }}{2(1 + \upsilon )}q\left( \varepsilon \right) = \frac{t}{L}\frac{{r^{2} }}{{s^{2} }}q\left( \varepsilon \right),\quad \bar{Q}(\xi ) = \frac{Q(\xi )}{{k_{s} GA}}, \\ & \Psi (\xi_{crack}^{(i + 1)} ) - \Psi (\xi_{crack}^{(i)} ) = \alpha_{m} \bar{M}(\xi_{crack}^{(i + 1)} ),\quad \alpha_{m} = \frac{t}{L}\Theta \left( \varepsilon \right),\quad \bar{M}(\xi ) = \frac{LM(\xi )}{EI}, \\ \end{aligned}$$

(24)

where α_q and α_m are the non-dimensional flexibility constants for linear and rotational springs, respectively. $\varepsilon = \tau /t$ is the ratio of the crack extension, τ, to the height of the beam, t (see Fig. 2), and υ is Poisson’s ratio. $q(\varepsilon )$ and $\Theta (\varepsilon )$ are configuration functions for the cracks and are dependent on ɛ and the cross-section geometry of the beam. For a beam with rectangular cross-section the following equations are evaluated based on fracture mechanics [52, 53]:

$$\begin{aligned} & \Theta (\varepsilon ) = 2\left( {\frac{\varepsilon }{1 - \varepsilon }} \right)^{2} (5.93 - 19.69\varepsilon + 37.14\varepsilon^{2} - 35.84\varepsilon^{3} + 13.12\varepsilon^{4} ), \\ & q(\varepsilon ) = \left( {\frac{\varepsilon }{1 - \varepsilon }} \right)^{2} ( - 0.22 + 3.82\varepsilon + 1.54\varepsilon^{2} - 14.64\varepsilon^{3} + 9.6\varepsilon^{4} ). \\ \end{aligned}$$

(25)

6 Differential quadrature element method (DQEM)

The differential quadrature method (DQM) is based on the idea that all derivatives of a function can be easily approximated by means of a weighted linear sum of the function values at N pre-selected grid of points as:

$$\left. {\frac{{d^{r} f}}{{dx^{r} }}} \right|_{{x = x_{i} }} \approx \sum\limits_{j = 1}^{N} {A_{ij}^{\left( r \right)} f_{j} } ,$$

(26)

where $A^{(r)}$ is the weighting coefficient associated with the rth order derivative and is given by Bert and Malik [54]:

$$\begin{array}{*{20}c} {A_{ij}^{{^{(1)} }} = \left\{ {\begin{array}{*{20}c} {\frac{{\prod\nolimits_{\begin{subarray}{l} m = 1 \\ m \ne i,j \end{subarray} }^{N} {\left( {x_{i} - x_{m} } \right)} }}{{\prod\nolimits_{\begin{subarray}{l} m = 1 \\ m \ne j \end{subarray} }^{N} {\left( {x_{j} - x_{m} } \right)} }}} & {i,j = 1,2,3, \ldots ,N;\,i \ne j} \\ {\sum\nolimits_{\begin{subarray}{l} m = 1 \\ m \ne i \end{subarray} }^{N} {\left( {x_{i} - x_{m} } \right)^{ - 1} } } & {i = j = 1,2,3, \ldots ,N} \\ \end{array} } \right.} \\ {\begin{array}{*{20}c} {A_{ij}^{{^{(r)} }} = A_{ij}^{{^{(1)} }} A_{ij}^{{^{(r - 1)} }} } & {2 \le r \le N - 1} \\ \end{array} } \\ \end{array} .$$

(27)

Distribution of the grid points is an important aspect in convergence of the solution. A well-accepted set of the grid points is the Gauss–Lobatto–Chebyshev points given for interval [0, 1] as:

$$\zeta_{i} = \frac{1}{2}\left\{ {1 - \cos \left[ {\frac{{\left( {i - 1} \right)\pi }}{{\left( {N - 1} \right)}}} \right]} \right\}.$$

(28)

The DQM may be employed as an efficient numerical tool for solving the domain problems having any kind of discontinuity in geometry, material, loading and boundary conditions in the form of small sub-domain elements to be called DQEM. In order to simplify the DQEM analogue of the equations, a modified form of the weighting coefficients of element i is defined as:

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {[A]^{(i)} = \frac{[A]}{{l^{(i)} }},} & {[B]^{(i)} = \frac{{[A]^{2} }}{{(l^{(i)} )^{2} }},} & {[C]^{(i)} = \frac{{[A]^{3} }}{{(l^{(i)} )^{3} }},} & {[D]^{(i)} = \frac{{[A]^{4} }}{{(l^{(i)} )^{4} }},} \\ \end{array} } & {} & {i = 1, \ldots ,n + 1.} \\ \end{array}$$

(29)

Applying the above-mentioned rules and rearranging, the DQ form of the governing set of Eqs. (20) and (21) becomes:

$$\left[ {K_{11} } \right]\left\{ V \right\} + \left[ {K_{12} } \right]\left\{ \Psi \right\} = \lambda^{4} \left[ {M_{1} } \right]\left\{ V \right\},$$

(30)

$$\left[ {K_{21} } \right]\left\{ v \right\} + \left[ {K_{22} } \right]\left\{ \Psi \right\} = \lambda^{4} \left[ {M_{2} } \right]\left\{ \Psi \right\},$$

(31)

where the following vectors are defined:

$$\begin{array}{*{20}c} {\left\{ V \right\}^{T} = \left\{ {\left\{ {V^{\left( 1 \right)} } \right\}^{T} ,\left\{ {V^{\left( 2 \right)} } \right\}^{T} , \ldots ,\left\{ {V^{{\left( {n + 1} \right)}} } \right\}^{T} } \right\},} & {\left\{ \Psi \right\}^{T} = \left\{ {\left\{ {\Psi^{\left( 1 \right)} } \right\}^{T} ,\left\{ {\Psi^{\left( 2 \right)} } \right\}^{T} , \ldots ,\left\{ {\Psi^{{\left( {n + 1} \right)}} } \right\}^{T} } \right\},} \\ \end{array}$$

(32)

also, the elements of the mentioned matrices, are expressed in “Appendix”.

Using the DQ rules in a similar manner, the compatibility conditions and boundary conditions, respectively, can be expressed in the following matrix forms:

$$\left[ P \right]\left\{ V \right\} + \left[ Q \right]\left\{ \Psi \right\} = \lambda^{4} \left( {\left[ R \right]\left\{ V \right\} + \left[ S \right]\left\{ \Psi \right\}} \right),$$

(33)

$$\left[ T \right]\left\{ V \right\} + \left[ X \right]\left\{ \Psi \right\} = \lambda^{4} \left( {\left[ Y \right]\left\{ V \right\} + \left[ Z \right]\left\{ \Psi \right\}} \right).$$

(34)

where the elements of the mentioned matrices, are presented in “Appendix”.

For the sake of ability to satisfy the compatibility equations and boundary conditions, the domain of the solution should be divided into three parts as follows [55]:

the boundary points:

$$\left\{ V \right\}_{b} = \left\{ {\begin{array}{*{20}l} {\left\{ {V_{1}^{{\left( 1 \right)}} } \right\}} \hfill \\ {\left\{ {V_{N}^{{\left( {n + 1} \right)}} } \right\}} \hfill \\ \end{array} } \right\},\quad \left\{ \Psi \right\}_{b} = \begin{array}{*{20}l} {\left\{ {\Psi _{1}^{{\left( 1 \right)}} } \right\}} \hfill \\ {\left\{ {\Psi _{N}^{{\left( {n + 1} \right)}} } \right\}} \hfill \\ \end{array},$$

(35)

the common nodes at adjacent elements:

$$\begin{aligned} \left\{ V \right\}_{c}^{T} & = \left\{ {\begin{array}{*{20}l} {\left\{ {V_{N}^{{\left( 1 \right)}} } \right\}} \hfill & {\left\{ {\begin{array}{*{20}l} {V_{1}^{{\left( 2 \right)}} } \hfill \\ {V_{N}^{{\left( 2 \right)}} } \hfill \\ \end{array} } \right\}^{T} } \hfill & \cdots \hfill & {\left\{ {\begin{array}{*{20}l} {V_{1}^{{\left( n \right)}} } \hfill \\ {V_{N}^{{\left( n \right)}} } \hfill \\ \end{array} } \right\}^{T} } \hfill & {\left\{ {V_{1}^{{\left( {n + 1} \right)}} } \right\}} \hfill \\ \end{array} } \right\} \\ \left\{ \Psi \right\}_{c}^{T} & = \left\{ {\begin{array}{*{20}l} {\left\{ {\Psi _{N}^{{\left( 1 \right)}} } \right\}} \hfill & {\left\{ {\begin{array}{*{20}l} {\Psi _{1}^{{\left( 2 \right)}} } \hfill \\ {\Psi _{N}^{{\left( 2 \right)}} } \hfill \\ \end{array} } \right\}^{T} } \hfill & \cdots \hfill & {\left\{ {\begin{array}{*{20}l} {\Psi _{1}^{{\left( n \right)}} } \hfill \\ {\Psi _{N}^{{\left( n \right)}} } \hfill \\ \end{array} } \right\}^{T} } \hfill & {\left\{ {\Psi _{1}^{{\left( {n + 1} \right)}} } \right\}} \hfill \\ \end{array} } \right\} \\ \end{aligned}$$

(36)

and the domain points:

$$\begin{array}{*{20}c} {\left\{ V \right\}_{d}^{T} = \left\{ {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {V_{2}^{\left( 1 \right)} } \\ \vdots \\ {V_{N - 1}^{\left( 1 \right)} } \\ \end{array} } \right\}^{T} } & {\left\{ {\begin{array}{*{20}c} {V_{2}^{\left( 2 \right)} } \\ \vdots \\ {V_{N - 1}^{\left( 2 \right)} } \\ \end{array} } \right\}^{T} } & {\begin{array}{*{20}c} \cdots & {\left\{ {\begin{array}{*{20}c} {V_{2}^{{\left( {n + 1} \right)}} } \\ \vdots \\ {V_{N - 1}^{{\left( {n + 1} \right)}} } \\ \end{array} } \right\}^{T} } \\ \end{array} } \\ \end{array} } \right\},} & {\left\{ \Psi \right\}_{d}^{T} = \left\{ {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\Psi_{2}^{\left( 1 \right)} } \\ \vdots \\ {\Psi_{N - 1}^{\left( 1 \right)} } \\ \end{array} } \right\}^{T} } & {\left\{ {\begin{array}{*{20}c} {\Psi_{2}^{\left( 2 \right)} } \\ \vdots \\ {\Psi_{N - 1}^{\left( 2 \right)} } \\ \end{array} } \right\}^{T} } & {\begin{array}{*{20}c} \cdots & {\left\{ {\begin{array}{*{20}c} {\Psi_{2}^{{\left( {n + 1} \right)}} } \\ \vdots \\ {\Psi_{N - 1}^{{\left( {n + 1} \right)}} } \\ \end{array} } \right\}^{T} } \\ \end{array} } \\ \end{array} } \right\}} \\ \end{array} .$$

(37)

where $V_{k}^{(i)}$ and $\Psi_{k}^{(i)}$, are $V^{(i)} (\xi_{k} )$ and $\Psi^{(i)} (\xi_{k} )$, respectively.

Therefore, by rearranging and partitioning Eqs. (30), (31), (33) and (34) into the boundary, adjacent and domain displacement and rotation components, one reaches the following eigenvalue problem:

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {\left[ {\bar{K}_{11} } \right]_{b} } & {\left[ {\bar{K}_{11} } \right]_{c} } & {\left[ {\bar{K}_{11} } \right]_{d} } & {\left[ {\bar{K}_{12} } \right]_{b} } & {\left[ {\bar{K}_{12} } \right]_{c} } & {\left[ {\bar{K}_{12} } \right]_{d} } \\ {\left[ {\bar{K}_{21} } \right]_{b} } & {\left[ {\bar{K}_{21} } \right]_{c} } & {\left[ {\bar{K}_{21} } \right]_{d} } & {\left[ {\bar{K}_{22} } \right]_{b} } & {\left[ {\bar{K}_{22} } \right]_{c} } & {\left[ {\bar{K}_{22} } \right]_{d} } \\ {\left[ P \right]_{b} } & {\left[ P \right]_{c} } & {\left[ P \right]_{d} } & {\left[ Q \right]_{b} } & {\left[ Q \right]_{c} } & {\left[ Q \right]_{d} } \\ {\left[ T \right]_{b} } & {\left[ T \right]_{c} } & {\left[ T \right]_{d} } & {\left[ X \right]_{b} } & {\left[ X \right]_{c} } & {\left[ X \right]_{d} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\left\{ V \right\}_{b} } \\ {\left\{ V \right\}_{c} } \\ {\left\{ V \right\}_{d} } \\ {\left\{ \Psi \right\}_{b} } \\ {\left\{ \Psi \right\}_{c} } \\ {\left\{ \Psi \right\}_{d} } \\ \end{array} } \right\} \\ \, & \quad = \lambda^{4} \left[ {\begin{array}{*{20}c} {\left[ {\bar{M}_{1} } \right]_{b} } & {\left[ {\bar{M}_{1} } \right]_{c} } & {\left[ {\bar{M}_{1} } \right]_{d} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {\left[ 0 \right]} \\ {\left[ 0 \right]} & {\left[ 0 \right]} & {\left[ 0 \right]} & {\left[ {\bar{M}_{2} } \right]_{b} } & {\left[ {\bar{M}_{2} } \right]_{c} } & {\left[ {\bar{M}_{2} } \right]_{d} } \\ {\left[ R \right]_{b} } & {\left[ R \right]_{c} } & {\left[ R \right]_{d} } & {\left[ S \right]_{b} } & {\left[ S \right]_{c} } & {\left[ S \right]_{d} } \\ {\left[ Y \right]_{b} } & {\left[ Y \right]_{c} } & {\left[ Y \right]_{d} } & {\left[ Z \right]_{b} } & {\left[ Z \right]_{c} } & {\left[ Z \right]_{d} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\left\{ V \right\}_{b} } \\ {\left\{ V \right\}_{c} } \\ {\left\{ V \right\}_{d} } \\ {\left\{ \Psi \right\}_{b} } \\ {\left\{ \Psi \right\}_{c} } \\ {\left\{ \Psi \right\}_{d} } \\ \end{array} } \right\}, \\ \end{aligned}$$

(38)

where $[0]$ is the zero matrix. The natural frequencies and corresponding modes will be obtained by solving this standard eigenvalue equation as long as one chooses the proper number of grid points satisfying the following relation for convergence of first m frequencies:

$$\begin{array}{*{20}c} {\left| {\frac{{\lambda_{l}^{\left( N \right)} - \lambda_{l}^{{\left( {N - 1} \right)}} }}{{\lambda_{l}^{{\left( {N - 1} \right)}} }}} \right| \le 0.01,} & {l = 1,2, \ldots ,m} \\ \end{array} .$$

(39)

7 Numerical applications and discussion

In this section, the computer package MATLAB is used to write code based on the DQE method to solved the obtained equations of motion, and analyze the problem of the rotating non-uniform Timoshenko nanocantilever beam with multiple cracks. The results are presented in non-dimensional forms, and the effects of the small-scale, angular velocity, hub radius parameters as well as cross-section and cracks conditions on the natural frequencies and mode shapes are investigated, and the related graphs are plotted.

First of all, in order to validate the reliability of the proposed solution, some illustrative examples are solved and the results are compared with the related ones presented in the literature. Table 1 reports the resulted data of the present study, Kaya [43] and Banerjee [56] for vibration analysis of a rotating Timoshenko beam. In this problem a local (h = 0) uniform beam without any cracks (ɛ = 0) are considered when $r = 1/30$, $E/k_{s} G = 3.059$ and $\delta = 0$. As depicted, the results of the present work are in agreement with those obtained by Kaya [43] and Banerjee [56] almost up to fourth digit.

Table 1 Variation of the fundamental frequency parameters of a rotating intact cantilever Timoshenko beam with the angular velocity parameters, when h = 0, ɛ = 0, δ = 0, $r = 1/30$, $E/k_{s} G = 3.059$ [43] and [56]

Also, the results given by Weaver et al. [57], for the problem of an uniform Timoshenko beam with a single crack in the middle of its length are compared to the data obtained by the presented approach. The local theory (h = 0) is used for a Timoshenko beam with the length, height and width of 100 mm, 25 mm and 12.5 mm. The other properties are: $E = 210\;{\text{Gpa}}$, $\upsilon = 0.3$, $\rho = 7860\;{\text{kg}}/{\text{m}}^{3}$ and $k_{s} = 5/6$. Table 2 shows the satisfactory agreement between the results of the proposed method and the exact solution for the values of the first four frequencies (Hz) for two different non-dimensional crack extensions, ɛ = 0.2 and ɛ = 0.35.

Table 2 Variation of the natural frequencies (Hz) of a nonrotating local cantilever Timoshenko beam with a crack in the middle of its length for two different crack depths, when L = 100 mm, b = 25 mm, t = 12.5 mm, E = 210 Gpa, υ = 0.3, ρ = 7860 kg/m³ and k_s = 5/6 [57]

The last comparison is made between our results and the data obtained by Wang et al. [58], for nonlocal cantilever beams. In this case, Wang considers vibration of (5,5) armchair single-walled carbon nanotubes (SWCNTs) with diameter $d = 0.678\;{\text{nm}}$, length $L = 10d$, thickness $t = 0.066\;{\text{nm}}$, and also the following mechanical parameters: $E = 5.5\;{\text{TPa}}$, $\upsilon = 0.19$, and $k_{s} = 0.563$. Table 3 confirms the accuracy (especially for lower frequencies) of the proposed approach in this study in comparison with the closed form vibration results given Wang, for the first four frequency parameters of cantilever Timoshenko beams with the aforementioned properties and three different nonlocal parameters ($h = 0,\,0.1$ and 0.3).

Table 3 First four frequency parameters of nanocantilever Timoshenko beams based on the closed form method [58] and the proposed approach for various nonlocal parameters h = 0, 0.3 and 0.5, when d = 0.678 nm, L = 10 d, t = 0.066 nm, E = 5.5 TPa, υ = 0.19, and k_s = 0.563(Wang et al. [58])

For the present study, we consider a tapered nanobeam with linearly varying height $t = t_{0} (1 + \beta \xi )$, where t₀ is the height (width) of the beam at the clamped section ($\xi = 0$), and β is a parameter representing the cross-section variation. From now on, a nanobeam of length $L = 20\;{\text{nm}}$ with $t_{0} = 4\;{\text{nm}}$ is used. Also, the adopted mechanical properties of the beam have the following values: $E = 1\,{\text{TPa}}$, $\upsilon = 0.25$, $k_{s} = 2/3$ and $\rho = 2300\,{\text{kg}}/{\text{m}}^{3}$ (Yoon et al. [59]). The nonlocal parameter, h, will be in the range of 0–0.3, the non-dimensional rotational velocity parameter $\gamma^{2}$ is assumed in the range of 0 to 5. Also, here we consider the non-dimensional hub radius $\delta$ from 0 up to 1.

Figure 3 depicts the variation of the first four non-dimensional modal frequency parameters of a rotating cracked non-uniform nanocantilever versus the non-dimensional angular velocity parameter for different values of the non-dimensional hub radius parameters. In this case, $h = 0.1$ and $\beta = - 0.2$, and the considered nanobeam has an open crack located in the middle of its length ($\xi = 0.5$) with non-dimensional extension parameter $\varepsilon = 0.1$. It is obvious that the frequency increases with the angular velocity, and this increase is intensified for the higher hub radii. This phenomenon is attributed to the stiffening effect of the centrifugal force, which is directly proportional to the rotational velocity, and hub radius.

Fig. 3

Variation of the first four non-dimensional modal frequency parameters with the non-dimensional angular velocity parameter of a non-uniform nanocantilever with a crack in the middle of its length, for different non-dimensional hub radius parameters

In order to show the effect of the number of grid points on the final results, a convergence study is presented in Table 4. The resulted values of the first fourth non-dimensional frequency parameters $\lambda$ are provided for a random case from the previous problem (Fig. 3). For this case, $\gamma^{2} = 1$ and $\delta = 0.1$, and the rest of conditions and properties are the exact same as those used in Fig. 3. It is seen that the results become closer to each other as the number of the grid points or N increase. For the grid points numbers of N = 7 and N = 8, all the resulted non-dimensional frequency parameters satisfy the condition stated in Eq. (39); therefore, for this example the final number will be N = 7.

Table 4 Convergence study for the first four non-dimensional frequency parameters $\lambda$ of a rotating nanocantilever Timoshenko beam with a crack in the middle of its length

The effects of the crack position and crack severity on the vibration behavior of a cracked nanoblade are considered in Fig. 4. In this case, the nonlocal and hub radius parameters are chosen as h = 0.1 and δ = 0.5, respectively, and the nanocantilever is non-uniform, β = − 0.2, and rotating with a constant angular velocity, γ² = 1. Figure 4 plots the variation of the first non-dimensional modal frequencies with the position of the single crack along the beam for the various non-dimensional crack depth parameters. As the figures reveal, whenever the crack is located at points which have higher values of curvature in the corresponding mode, the natural frequency is affected more. Therefore, there are some points depending on the mode under consideration, that the effects of the presence of a crack becomes almost disappear. The number of these spots that are located at the inflection points, is directly related to the number of the corresponding mode. Also, since the case of ɛ = 0 considers an intact beam, It is seen that the existence of damage decreases the magnitude of the natural frequency, and as the crack becomes more severe the final frequencies become even lower. In general, the presence of cracks makes a beam more flexible and, as a result, the magnitudes of obtained frequencies of a cracked beam are lower than those of an intact beam. This decrease can be even intensified as the number of the cracks or the severity of them increases.

Fig. 4

First four non-dimensional frequency parameters of an non-uniform cracked nanoblade under rotation versus the non-dimensional crack position, for different non-dimensional crack extension parameters

Consider an uniform (β = 0) nanoblade which is rotating at a constant angular velocity with multiple cracks. Figure 5 plots the variation of the first four non-dimensional modal frequency parameters versus the non-dimensional crack extension parameter. For this case, It is assumed that cracks are similar and equally spaced along the beam. The values of used non-dimensional parameter here are as follows: h = 0.1, δ = 0.5 and γ² = 1. As the plots show, generally speaking, as the number of the cracks is increasing, we have to expect lower natural frequencies for the blade. This expectation is correct unless some cracks are located near the inflation points at which the effects of cracks are almost vanished. For example, as it is obvious, the obtained natural frequencies of a beam with two equally spaced cracks are more than a beam with a single crack in the middle of its length for the fourth mode (see Fig. 5d). Another interesting point on this figure is the rate of change of the frequency parameters based on the number and severity of cracks.

Fig. 5

Variation of the first four non-dimensional modal frequency parameters of a cracked uniform nanoblade with the non-dimensional crack extension parameter, for various number of the cracks

Finally, Fig. 6 presents the 3-D plots of the variation of the first four normalized mode shapes of a non-uniform cracked nanoblade versus the nanlocal parameter. The nanoblade is not uniform β = − 0.2, and rotating at a constant angular velocity, γ² = 1 while δ = 0.5. There is a single open crack at ξ = 0.5 with ɛ = 0.1. Also, as the presented figures show, the assumed range for the nonlocal parameter is 0–0.3. As the plots show the results for the different nonlocal parameters h, size effects play an important role in the mechanical characteristics of nanosclae structures. Note that the mode shapes associated with h = 0 correspond to the mode shapes of a rotating local Timoshenko beam and have the smallest values for each mode number.

Fig. 6

First four normalized mode shapes versus the non-dimensional nonlocal parameter for a non-uniform cracked nanoblade under rotation

8 Conclusions

The vibration analysis of a rotating non-uniform nanocantilever Timoshenko beam with multiple cracks was presented in this study. The differential quadrature method was employed to solve the resulted equations and analyze the problem for different numbers, positions and severities of the cracks under various nonlocal, geometric and dynamic conditions.

It was observed that because of the centrifugal force effects, the non-dimensional frequencies grow with increasing the rotational angular velocity and hub radius for both the local and nonlocal elastic models. Also, the existence of the cracks makes the beam more flexible, therefore, as the number of cracks and severity of them increase the natural frequency values decrease more. It was seen that the position of the cracks may affect the vibration behavior of the beam too. Depending on the vibration mode, there are some spots along the beam at which that the presence of the cracks can have the maximum or minimum effects on the final frequencies. Finally, it was shown that the influences of the nonlocal parameter lead to increase the deflection of the beam for every mode of vibration, in comparison to the local beam modeling. The proposed procedure could help scholars and engineers who are working on rotation and damage detection in micro- or nanoelectromechanical devices, and provide them with a vibration solution that needs less computational effort and is more versatile.

Appendix

The appendix presents the elements of the matrices appeared in the DQ formulation. The components of $[K_{ab} ]$ and $[M_{ab} ]$, $a,b = 1,2$, in Eqs. (30) and (31) are evaluated as:

$$\begin{aligned}& \left[ {K_{11} } \right] = diag\left[ {[k_{11} ]^{(1)} \quad \left[ {k_{11} } \right]^{(2)} \quad \cdots \quad [k_{11} ]^{(n + 1)} } \right],\\& \left[ {K_{12} } \right] = diag\left[ {\left[ {k_{12} } \right]^{(1)} \quad \left[ {k_{12} } \right]^{(2)} \quad \cdots \left[ {k_{12} } \right]^{(n + 1)} } \right], \\& \left[ {K_{21} } \right] = diag\left[ {[k_{21} ]^{(1)} \quad \left[ {k_{21} } \right]^{(2)} \quad \cdots \quad [k_{21} ]^{(n + 1)} } \right],\\& \left[ {K_{22} } \right] = diag\left[ {\left[ {k_{22} } \right]^{(1)} \quad \left[ {k_{22} } \right]^{(2)} \quad \cdots \left[ {k_{22} } \right]^{(n + 1)} } \right], \\& \left[ {M_{1} } \right] = diag\left[ {[m_{1} ]^{(1)} \quad \left[ {m_{1} } \right]^{(2)} \quad \cdots \quad [m_{1} ]^{(n + 1)} } \right],\\& \left[ {M_{2} } \right] = diag\left[ {\left[ {m_{2} } \right]^{(1)} \quad \left[ {m_{2} } \right]^{(2)} \quad \cdots \left[ {m_{2} } \right]^{(n + 1)} } \right], \\ \end{aligned}$$

(40)

where “diag” operator is used to create the needed diagonal matrices. Also for the ith sub-beam the following relations are obtained:

$$\begin{aligned} &\begin{aligned} \left[ {k_{11} } \right]^{(i)}& = - \gamma^{4} s^{2} h^{2} \left[ a \right]^{\left( i \right)} \left[ D \right]^{\left( i \right)} + 3\gamma^{4} s^{2} h^{2} \left[ b \right]^{\left( i \right)} \left[ C \right]^{\left( i \right)}\\&\quad + \left\{ {\gamma^{4} s^{2} \left[ {3h^{2} \left( {\left[ b \right]^{\left( i \right)} \left[ d \right]^{\left( i \right)} + I} \right) + \left[ a \right]^{\left( i \right)} } \right] + I} \right\}\left[ B \right]^{\left( i \right)} \\ & \quad + \left\{ {\gamma^{4} s^{2} \left[ {h^{2} \left( {\left[ b \right]^{\left( i \right)} \left[ d \right]^{\left( i \right)} + \left[ c \right]^{\left( i \right)} } \right) - \left[ b \right]^{\left( i \right)} } \right] + \left[ c \right]^{\left( i \right)} } \right\}\left[ A \right]^{\left( i \right)} ,\end{aligned} \\ & \left[ {k_{12} } \right]^{(i)} = - \left[ A \right]^{\left( i \right)} - \left[ c \right]^{\left( i \right)} , \\ & \left[ {k_{21} } \right]^{(i)} = \left[ g \right]^{\left( i \right)} \left[ A \right]^{\left( i \right)} ,\\& \begin{aligned} \left[ {k_{22} } \right]^{(i)} &= s^{2} \left( {1 - \gamma^{4} r^{2} h^{2} } \right)\left[ B \right]^{\left( i \right)} + s^{2} \left( {1 - 2\gamma^{4} r^{2} h^{2} } \right)\left[ e \right]^{\left( i \right)} \left[ A \right]^{\left( i \right)}\\&\quad + \left[ {\gamma^{4} s^{2} r^{2} \left( {I - h^{2} \left[ f \right]^{\left( i \right)} } \right) - \left[ g \right]^{\left( i \right)} } \right], \\\end{aligned} \end{aligned}$$

(41)

$$\begin{aligned} \left[ {m_{1}^{{}} } \right]^{(i)} & = s^{2} \left\{ {h^{2} \left[ B \right]^{\left( i \right)} + 2h^{2} \left[ c \right]^{\left( i \right)} \left[ A \right]^{\left( i \right)} + \left( {h^{2} \left[ d \right]^{\left( i \right)} - I} \right)} \right\}, \\ \left[ {m_{2}^{{}} } \right]^{(i)} & = s^{2} r^{2} \left\{ {h^{2} \left[ B \right]^{\left( i \right)} + 2h^{2} \left[ e \right]^{\left( i \right)} \left[ A \right]^{\left( i \right)} + \left( {h^{2} \left[ f \right]^{\left( i \right)} - I} \right)} \right\}, \\ \end{aligned}$$

in which $[k_{ab} ]^{(i)}$ and $[m_{ab} ]^{(i)}$, $\begin{array}{*{20}c} {a,b = 1,2,} & {i = 1, \ldots ,n + 1} \\ \end{array}$ have the dimension of $N \times N$, and $I_{N \times N}$ is the identity matrix. Also, the diagonal matrices are defined as:

$$\begin{array}{*{20}c} {a_{jj}^{\left( i \right)} = \frac{{\int_{{\xi_{m} }}^{1} {A^{*} (\xi )\left( {\delta + \xi } \right)d\xi } }}{{A^{*} (\xi_{m} )}},} & {o_{jj}^{\left( i \right)} = \frac{{\int_{{\xi_{m} }}^{1} {A^{*} (\xi )\left( {\delta + \xi } \right)d\xi } }}{{I^{*} (\xi_{m} )}},} \\ {c_{jj}^{\left( i \right)} = \left. {\left( {\frac{1}{{A^{*} (\xi )}}\frac{{dA^{*} (\xi )}}{d\xi }} \right)} \right|_{{\xi = \xi_{m} }} ,} & {d_{jj}^{\left( i \right)} = \left. {\left( {\frac{1}{{A^{*} (\xi )}}\frac{{d^{2} A^{*} (\xi )}}{{d\xi^{2} }}} \right)} \right|_{{\xi = \xi_{m} }} ,} \\ {e_{jj}^{\left( i \right)} = \left. {\left( {\frac{1}{{I^{*} (\xi )}}\frac{{dI^{*} (\xi )}}{d\xi }} \right)} \right|_{{\xi = \xi_{m} }} ,} & {f_{jj}^{\left( i \right)} = \left. {\left( {\frac{1}{{I^{*} (\xi )}}\frac{{d^{2} I^{*} (\xi )}}{{d\xi^{2} }}} \right)} \right|_{{\xi = \xi_{m} }} ,} \\ {g_{jj}^{\left( i \right)} = \frac{{A^{*} (\xi_{m} )}}{{I^{*} (\xi_{m} )}},} & {b_{jj}^{\left( i \right)} = \delta + \xi_{m} ,} \\ \end{array} \begin{array}{*{20}c} {} & {for} & {\begin{array}{*{20}c} {i = 1,2, \ldots ,n + 1} \\ {j = 1,2, \ldots ,N} \\ {m = \left( {i - 1} \right)N + j = 1,2, \ldots ,\left( {n + 1} \right)N} \\ \end{array} } \\ \end{array} \,\,\,\,\,.$$

(42)

It is worth repeating that in the case of a beam with n cracks, we have to consider n + 1 sub-beams, in which there are N grid points.

Regarding the compatibility conditions equations, It is required to consider the relevant equations for each crack position, and then compose the obtained equations in order to reach an expression in matrix form as Eq. (35). Therefore the final matrices are comprised of smaller elements as:

$$\begin{aligned} P_{ab} & = \left\{ {\begin{array}{*{20}l} {[p]^{(i)} } & {4i - 3 \le a \le 4i} & {N(i - 1) + 1 \le b \le N(i + 1)} \\ {} & 0 & {else} \\ \end{array} } \right.\quad i = 1,2, \ldots ,n, \\ Q_{ab} & = \left\{ {\begin{array}{*{20}l} {[q]^{(i)} } & {4i - 3 \le a \le 4i} & {N(i - 1) + 1 \le b \le N(i + 1)} \\ {} & 0 & {else} \\ \end{array} } \right.\quad i = 1,2, \ldots ,n, \\ R_{ab} & = \left\{ {\begin{array}{*{20}l} {[r]^{(i)} } & {4i - 3 \le a \le 4i} & {N(i - 1) + 1 \le b \le N(i + 1)} \\ {} & 0 & {else} \\ \end{array} } \right.\quad i = 1,2, \ldots ,n, \\ S_{ab} & = \left\{ {\begin{array}{*{20}l} {[s]^{(i)} } & {4i - 3 \le a \le 4i} & {N(i - 1) + 1 \le b \le N(i + 1)} \\ {} & 0 & {else} \\ \end{array} } \right.\quad i = 1,2, \ldots ,n, \\ \end{aligned}$$

(43)

where the components for the mentioned matrices are obtained as:

$$\begin{aligned} p_{jk}^{\left( i \right)} & = \left\{ {\begin{array}{*{20}c} { - \delta_{Nk} } & {j = 1,\,1 \le k \le N} \\ {\delta_{{1\left( {k - N} \right)}} + \alpha_{Q} \left( {1 + \gamma^{4} s^{2} h^{2} \left( {c_{11}^{{\left( {i + 1} \right)}} b_{11}^{{\left( {i + 1} \right)}} + 1} \right)} \right)A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} + \alpha_{Q} \gamma^{4} s^{2} h^{2} \left( {2b_{11}^{{\left( {i + 1} \right)}} B_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} - a_{11}^{{\left( {i + 1} \right)}} C_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} } \right)} & {j = 1,\,N + 1 \le k \le 2N} \\ {\gamma^{4} h^{2} \left( {g_{NN}^{\left( i \right)} b_{NN}^{\left( i \right)} A_{{N\left( {k - N} \right)}}^{\left( i \right)} - o_{NN}^{\left( i \right)} B_{{N\left( {k - N} \right)}}^{\left( i \right)} } \right)} & {j = 2,\,1 \le k \le N} \\ { - \gamma^{4} h^{2} \left( {g_{11}^{{\left( {i + 1} \right)}} b_{11}^{{\left( {i + 1} \right)}} A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} - o_{11}^{{\left( {i + 1} \right)}} B_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} } \right)} & {j = 2,\,N + 1 \le k \le 2N} \\ { - \left[ {1 + \gamma^{4} s^{2} h^{2} \left( {c_{NN}^{\left( i \right)} b_{NN}^{\left( i \right)} + 1} \right)} \right]A_{Nk}^{\left( i \right)} - \gamma^{4} s^{2} h^{2} \left( {2b_{NN}^{\left( i \right)} B_{Nk}^{\left( i \right)} - a_{NN}^{\left( i \right)} C_{Nk}^{\left( i \right)} } \right)} & {j = 3,\,1 \le k \le N} \\ {\left[ {1 + \gamma^{4} s^{2} h^{2} \left( {c_{11}^{{\left( {i + 1} \right)}} b_{11}^{{\left( {i + 1} \right)}} + 1} \right)} \right]A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} + \gamma^{4} s^{2} h^{2} \left( {2b_{11}^{{\left( {i + 1} \right)}} B_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} - a_{11}^{{\left( {i + 1} \right)}} C_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} } \right)} & {j = 3,\,N + 1 \le k \le 2N} \\ 0 & {j = 4,\,1 \le k \le N} \\ {\gamma^{4} h^{2} \alpha_{M} \left( {g_{11}^{{\left( {i + 1} \right)}} b_{11}^{{\left( {i + 1} \right)}} A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} - o_{11}^{{\left( {i + 1} \right)}} B_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} } \right)} & {j = 4,\,N + 1 \le k \le 2N} \\ \end{array} } \right., \\ q_{jk}^{\left( i \right)} & = \left\{ {\begin{array}{*{20}c} 0 & {j = 1,\,1 \le k \le N} \\ { - \alpha_{Q} \delta_{{1\left( {k - N} \right)}} } & {j = 1,\,N + 1 \le k \le 2N} \\ { - \left( {1 - \gamma^{4} h^{2} r^{2} } \right)A_{Nk}^{\left( i \right)} + \gamma^{4} h^{2} r^{2} e_{NN}^{\left( i \right)} \delta_{Nk} } & {j = 2,\,1 \le k \le N} \\ {\left( {1 - \gamma^{4} h^{2} r^{2} } \right)A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} - \gamma^{4} h^{2} r^{2} e_{11}^{{\left( {i + 1} \right)}} \delta_{{1\left( {k - N} \right)}} } & {j = 2,\,N + 1 \le k \le 2N} \\ {\delta_{Nk} } & {j = 3,\,1 \le k \le N} \\ { - \delta_{{1\left( {k - N} \right)}} } & {j = 3,\,N + 1 \le k \le 2N} \\ { - \delta_{Nk} } & {j = 4,\,1 \le k \le N} \\ {\alpha_{M} \left( {\gamma^{4} h^{2} r^{2} - 1} \right)A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} + \left( {\gamma^{4} h^{2} r^{2} \alpha_{M} e_{11}^{{\left( {i + 1} \right)}} + 1} \right)\delta_{{1\left( {k - N} \right)}} } & {j = 4,\,N + 1 \le k \le 2N} \\ \end{array} } \right., \\ r_{jk}^{\left( i \right)} & = \left\{ {\begin{array}{*{20}c} {\alpha_{Q} s^{2} h^{2} \left[ {c_{11}^{{\left( {i + 1} \right)}} \delta_{{1\left( {k - N} \right)}} + A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} } \right]} & {j = 1,\,N + 1 \le k \le 2N} \\ {h^{2} g_{NN}^{\left( i \right)} \delta_{Nk} } & {j = 2,\,1 \le k \le N} \\ { - h^{2} g_{11}^{{\left( {i + 1} \right)}} \delta_{{1\left( {k - N} \right)}} } & {j = 2,\,N + 1 \le k \le 2N} \\ { - s^{2} h^{2} \left[ {c_{NN}^{\left( i \right)} \delta_{Nk} + A_{Nk}^{\left( i \right)} } \right]} & {j = 3,\,1 \le k \le N} \\ {s^{2} h^{2} \left[ {c_{11}^{{\left( {i + 1} \right)}} \delta_{{1\left( {k - N} \right)}} + A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} } \right]} & {j = 3,\,N + 1 \le k \le 2N} \\ {h^{2} \alpha_{M} g_{11}^{{\left( {i + 1} \right)}} \delta_{{1\left( {k - N} \right)}} } & {j = 4,\,N + 1 \le k \le 2N} \\ 0 & {else} \\ \end{array} } \right., \\ s_{jk}^{\left( i \right)} & = \left\{ {\begin{array}{*{20}c} { - h^{2} r^{2} \left( {e_{NN}^{\left( i \right)} \delta_{Nk} + A_{Nk}^{\left( i \right)} } \right)} & {j = 2,\,1 \le k \le N} \\ {h^{2} r^{2} \left( {e_{11}^{{\left( {i + 1} \right)}} \delta_{{1\left( {k - N} \right)}} + A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} } \right)} & {j = 2,\,N + 1 \le k \le 2N} \\ { - h^{2} r^{2} \alpha_{M} \left( {e_{11}^{{\left( {i + 1} \right)}} \delta_{{1\left( {k - N} \right)}} + A_{{1\left( {k - N} \right)}}^{{\left( {i + 1} \right)}} } \right)} & {j = 4,\,N + 1 \le k \le 2N} \\ 0 & {else} \\ \end{array} } \right.. \\ \end{aligned}$$

(44)

Also the elements of the used matrices in Eq. (34) are given as:

$$\begin{aligned} T_{jk} & = \left\{ {\begin{array}{*{20}c} {\delta_{1k} } & {j = 1,k = 1} \\ { - \gamma^{4} h^{2} \left( {g_{NN}^{{\left( {n + 1} \right)}} b_{NN}^{{\left( {n + 1} \right)}} A_{{N\left( {k - nN} \right)}}^{{\left( {n + 1} \right)}} - o_{NN}^{{\left( {n + 1} \right)}} B_{{N\left( {k - nN} \right)}}^{{\left( {n + 1} \right)}} } \right)} & {j = 3,nN + 1 \le k \le \left( {n + 1} \right)N} \\ {\left[ {1 + \gamma^{4} s^{2} h^{2} \left( {c_{NN}^{{\left( {n + 1} \right)}} b_{NN}^{{\left( {n + 1} \right)}} + 1} \right)} \right]\left[ A \right]_{Nk}^{{\left( {n + 1} \right)}} + \gamma^{4} s^{2} h^{2} \left( {2b_{NN}^{{\left( {n + 1} \right)}} B_{{N\left( {k - nN} \right)}}^{{\left( {n + 1} \right)}} - a_{NN}^{{\left( {n + 1} \right)}} C_{{N\left( {k - nN} \right)}}^{{\left( {n + 1} \right)}} } \right)} & {j = 4,nN + 1 \le k \le \left( {n + 1} \right)N} \\ 0 & {else} \\ \end{array} } \right., \\ X_{jk} & = \left\{ {\begin{array}{*{20}c} {\delta_{1k} } & {j = 2,k = 1} \\ {\left( {1 - \gamma^{4} h^{2} r^{2} } \right)A_{{N\left( {k - nN} \right)}}^{{\left( {n + 1} \right)}} - \gamma^{4} h^{2} r^{2} e_{NN}^{{\left( {n + 1} \right)}} \delta_{{N\left( {k - nN} \right)}} } & {j = 3,nN + 1 \le k \le \left( {n + 1} \right)N} \\ { - \delta_{{N\left( {k - nN} \right)}} } & {j = 4,nN + 1 \le k \le \left( {n + 1} \right)N} \\ 0 & {else} \\ \end{array} } \right., \\ Y_{jk} & = \left\{ {\begin{array}{*{20}c} { - h^{2} g_{NN}^{{\left( {n + 1} \right)}} \delta_{{N\left( {k - nN} \right)}} } & {j = 3,nN + 1 \le k \le \left( {n + 1} \right)N} \\ {s^{2} h^{2} \left[ {c_{NN}^{{\left( {n + 1} \right)}} \delta_{{N\left( {k - nN} \right)}} + A_{{N\left( {k - nN} \right)}}^{{\left( {n + 1} \right)}} } \right]} & {j = 4,nN + 1 \le k \le \left( {n + 1} \right)N} \\ 0 & {else} \\ \end{array} } \right., \\ Z_{jk} & = \left\{ {\begin{array}{*{20}c} {h^{2} r^{2} \left[ {e_{NN}^{{\left( {n + 1} \right)}} \delta_{{N\left( {k - nN} \right)}} + A_{{N\left( {k - nN} \right)}}^{{\left( {n + 1} \right)}} } \right]} & {j = 3,nN + 1 \le k \le \left( {n + 1} \right)N} \\ 0 & {else} \\ \end{array} } \right.. \\ \end{aligned}$$

(45)

Note that in the above equations, δ_ij is the Kronecker delta which is defined by

$$\delta_{ij} = \left\{ {\begin{array}{*{20}c} 1 & {i = j} \\ 0 & {i \ne j} \\ \end{array} } \right..$$

(46)