Abstract
Planar periodic surface lattice (PSL) structures based on thin, subwavelength substrates have been studied experimentally and numerically. Coupled eigenmode resonances composed of partial volume and surface modes are observed for PSLs with lattice periodicities of 1.50 mm and 1.62 mm etched onto thin copper-backed, substrates. We show that the copper backing is essential for mode-selection in a multi-moded structure and demonstrate good agreement between the experimental results and coupled dispersion plots calculated using CST Microwave Studio. For the first time, evidence of a coupled eigenmode in a metadielectric PSL is presented. It is shown that metadielectric PSLs can support coupled resonances over a narrow bandwidth and are relevant to the innovation of tunable filters, absorbers and sources. Concepts discussed in this work are valid across the frequency spectrum from optical to THz and mm-wave frequencies and are fundamental to the innovation of novel mm-wave–THz sources as well as highly efficient solar cells, diagnostic instruments and antennae.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Efficient, high power millimetre and terahertz radiation sources are highly sought after for their diverse and far-reaching applications in optics, imaging [1,2,3] and security [4], communications [4,5,6] medical technology, particle acceleration [7, 8] spectroscopy [9,10,11] and scientific research [12,13,14,15]. Traditionally, sources were scaled according to their output frequency, requiring smaller interaction regions and consequently diminished power capabilities, at shorter wavelengths. One method of overcoming this challenge is through the use of two-dimensional periodic surface lattice (PSL) structures, which have been successfully incorporated into high power microwave sources for a number of years [15,16,17,18,19] and enable mode rarefaction in a multi-moded structure. Higher output powers at mm-wave and THz frequencies, are achieved by coupling volume and surface modes to enable mode selection in an oversized cavity, providing single-mode excitation at high frequencies without compromising the power output [20, 21]. In the present work, PSLs of planar geometry (as opposed to cylindrical PSLs that are compatible with an electron beam) are discussed. The planar periodic, resonant surfaces mounted on metal-backed substrates accommodate both volume and surface fields and facilitate inductive field coupling. This work explores the fundamental volume and surface field coupling and determines the necessary criteria and optimum conditions for coupled eigenmode formation to better control the transverse modes and enable interaction with an electron beam in an oversized cylindrical interaction space. Mathematically, conversion between the cylindrical and planar systems can be achieved via conformal mapping.
One of the most desirable qualities of the PSL structures is their scalability and applicability over a broad frequency range from microwave to infrared. The concepts and mode-coupling principle described in this work are applicable to the development of mm-wave and THz radiation sources based on a range of different gain media such as vacuum electronic and condensed matter media. In addition to applications in sources, there are several potential applications in mm-wave and THz diagnostics [22], antennae [23], subwavelength absorbers [24, 25], filters [26,27,28] and solar cells [29]. Successful 3D printing of cylindrical mm-wave PSLs [30] and metamaterial microwave structures [31] have been reported by Phipps et al. and French and Shiffler respectively. Here, planar PSLs mounted on thin substrates have been fabricated via chemical etching. Laser etching has also been employed to produce a shorter period metamaterial PSL with a similar substrate.
In this paper we report the results of original experimental measurements and numerical simulations and demonstrate agreement between the experiments and the numerical simulations showing coupling of volume and surface fields. Interesting results have been obtained through extensive experimental measurements of a set of structures with different physical characteristics and mounted on thinner substrates than considered in [32, 33]. These novel PSL structures etched upon thin substrates have the capability to facilitate stronger coupling of volume and surface fields than structures studied in earlier work, and we show resonant coupled eigenmode formation at different frequencies to before. Additionally, we show that the fundamental mode coupling technique is relevant also to metadielectric periodic surface structures which have numerous potential applications and can also be ‘tailored for purpose’. In this metamaterial regime, the lattice period is small in comparison to the wavelength \( (d_{z} \ll \lambda ) \) unlike all the structures studied in [32, 33] where the lattice period and wavelength are comparable \( (d_{z} \sim\lambda ) \). The distinctive high –Q resonances observed in the metamaterial structure behave differently to those measured in other PSL structures and have possible applications in tunable mm-wave and THz sources and filters.
1.1 Resonant coupling in PSL structures
When the PSLs are irradiated by a suitable source, a surface current is induced around the copper edges and scattered into a surface field. Inductive coupling, involving mutual resonant scattering of the PSL’s surface and volume fields, can occur when the lattice is adequately synchronised and if the Bragg resonance conditions \( \left( {\bar{k}_{ \bot } } \right)^{2} = \left( {k_{ \bot }^{v} } \right)^{2} + \left( {k_{ \bot }^{s} } \right)^{2} \) (where \( \bar{k}_{ \bot ,z} = 2\pi /d_{ \bot ,z} \), \( d_{ \bot ,z} \) are the transverse and longitudinal lattice periods and \( k_{ \bot }^{v,s} \) are the transverse wavenumbers of the volume and surface fields) and \( \bar{k}_{z} = k_{z}^{s} - k_{z}^{v} \) (where \( k_{z}^{v,s} \) are the longitudinal wavenumbers of the volume and surface fields) are satisfied. The surface current synchronises adjoining cells, and excites a Fabry–Perot standing wave inside the substrate, due to the PSL and copper backing acting as reflectors, which provides overall lattice synchronisation. In cylindrical structures, an azimuthally symmetric and close to cut-off \( {\text{TM}}_{{0,{\text{N}}}} \) mode with a uniform field distribution is required for lattice synchronisation and coupling with a \( {\text{HE}}_{{{\bar{\text{m}}},1}} \) surface field where \( {\bar{\text{m}}} \) is the number of lattice azimuthal variations. However, for the planar PSLs, the individual volume and surface fields that constitute the cavity eigenmode depend on the specific lattice parameters and substrate thickness. For both geometries, the PSL structures behave as gain media only when coupled with a suitable source of energy, such as an energetic electron beam.
2 Experimental method
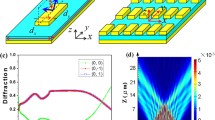
For convenience, and to demonstrate the fundamental ‘proof of principle’ coupling, a commercial epoxy fiberglass (FR-4) was used as the dielectric substrate. PSL structures were fabricated by etching copper-clad FR-4 circuit boards of thickness, t = 0.410 ± 0.005 mm. For some of the structures the copper cladding was entirely dissolved on one side, leaving only the PSL and dielectric, while in others the thin layer of copper foil was left as a metal backing behind the PSL and dielectric. For all the PSL structures the corrugation depth \( \Delta h \) is much smaller than the operating wavelength \( (\Delta h \ll \lambda \)) fulfilling the metamaterial criterion in the incident plane. A photograph of a copper PSL, with \( \Delta h = 35\,\upmu{\text{m}} \) and period \( d_{z} = 1.50\,{\text{mm}} \), etched onto a t = 0.41 mm thickness, copper-backed, FR–4 substrate is provided in Fig. 1. The relative permittivity \( \varepsilon_{r} \) of FR-4 varies depending on the samples’ exact composition. A value of \( \varepsilon_{r} = 5.69 \) (at 140–220 GHz) was established using a Vector Network Analyser to measure the phase difference between the substrates and free space. Taking into account the calculated \( \varepsilon_{r} \), total internal reflection is expected at incident angles \( \theta_{i} > \) 25°.
The PSL structures were studied through the use of an Anritsu ‘Vector Star’ Vector Network Analyser (VNA), calibrated to operate with a pair of mm-wave OML modules attached to 140–220 GHz standard gain antennae. The modules were fixed on rotating arms upon a large protractor with the PSL secured at the axis of rotation. The transmitting and receiving antennae were carefully aligned to maintain equal angles of incidence and reflection \( (\theta_{i} = \theta_{r} ) \) and positioned at an optimum distance within the far field, to irradiate as much of the PSL as possible whilst minimising diffractive edge effects. The parameter S21 is measured by the VNA, as a function of frequency from 140 to 220 GHz. In conventional VNA terminology S21 is the ‘insertion loss’ incurred in the signal transmission from the transmitting antenna (port1) to the receiving antenna (port 2). The transmission path between the two VNA heads depends crucially upon a reflection from the planar 2D PSL located between the transmitting antenna and the receiving antenna, as shown in Fig. 1. The insertion loss in this transmission path is therefore directly dependent upon the magnitude of the reflection from the planar 2D PSL. The parameter plotted on the vertical axis in Figs. 2, 3, and 5 is normalized and is labelled as the reflected power in dB that is reflected from the planar 2D PSL structures. The normalization sets the baseline for these reflected power graphs at zero for the non-resonant reflected power. The dips, or minima. in these curves then indicate resonances that are the subject of this paper.
Reflection measurements [34] for a dz = 1.50 mm, b dz = 1.62 mm, c dz = 1.74 mm, d dz = 1.94 mm PSLs etched upon t = 0.41 mm copper-backed substrates for varying \( \theta_{i} . \) The legend shows which traces correspond to each incident angle
3 Experimental results
3.1 PSL structures without metal backings
Reflection measurements for PSLs with periodicities of \( d_{z} = 1.50\,{\text{mm}} \), 1.64 mm and 1.94 mm, all etched upon thin, t = 0.41 mm substrates without copper backings, are presented in Fig. 2. Three distinct resonances are evident in each case. The highest frequency resonance (3) is the PSL’s surface mode as observed in equivalent ‘mesh’ PSLs [32]. The volume mode (resonance 1) is weakly defined without the copper backing, and prevalent at lower frequencies, while resonance 2 is suggestive of an eigenmode formed by the weak scattering of volume and surface modes due to field confinement and total internal reflection within the FR-4 dielectric. Despite the common substrate, all three resonances shift down the frequency band with increasing \( d_{z} \), demonstrating that the lattice periodicity influences both volume and surface modes.
3.2 PSL structures with metal backings
The mode coupling and single eigenmode excitation, central to the development of high power radiation sources at high frequencies, and relevant to antennae, diagnostic and also solar cell applications which rely on perfect absorption at optical frequencies, is observed only in structures with the copper backing. PSLs based on thin copper-backed substrates support sharp resonances at certain frequencies, as shown in Fig. 3. Resonances presented in Fig. 3a, b behave in a similar manner to the established, mode-locked eigenmodes described by MacLachlan et al. [32, 33]. However, the present structures (based on thinner substrates) facilitate stronger coupling between volume and surface modes than those studied previously due to smaller dielectric losses and based on the assumption that the magnitude of the coupling coefficient \( \alpha \) is related to the parameter \( \Delta h/t \). Although thinner substrates can accommodate higher frequency volume modes, this is somewhat offset by the significantly higher \( \varepsilon_{r} = 5.69 \), compared with typical values of εr= 4.45–4.71 measured in thicker samples at the same frequency [32, 33]. The strong coupling associated with the \( t = 0.41 \) mm substrates lowers the frequencies at which the coupled eigenmodes are formed. Numerical calculations were performed to rule out any potential involvement of a ‘quasi’ TEM mode which might exist due to the perforated PSL boundary and thin substrate. A TEM type mode was found to be possible only at lower frequencies, ceasing to exist beyond 93 GHz.
Under optimum conditions mode-locking (where the resonant frequency is fixed for all \( \theta_{i} \)) is observed. However, in practice some shifting up in frequency (rather than down) can occur even when the volume and surface modes are strongly coupled. Figure 3a shows coupled resonances that shift upwards with angle, measured in a dz= 1.50 mm PSL, while Fig. 3b illustrates ‘mode-locking’ at 140 GHz in a dz= 1.62 mm PSL. In both cases Fig. 3a, b demonstrates the potential for well-defined (~ 50 dB) cavity modes and single mode excitation in a multi-moded structure. Fabry–Perot resonances are evident towards the upper end of the frequency band for both the dz= 1.74 mm and dz= 1.94 mm PSL structures. The lower resonance of Fig. 3c—most prominent at small \( \theta_{i} \)—resembles a potential eigenmode. Similarly, the ~ 3 dB resonance observed for the dz= 1.94 mm PSL in Fig. 3d lies at a fixed frequency (~ 158 GHz) in close proximity to the frequency of the PSL’s surface field, and likely represents a weakly coupled eigenmode. In this instance, the dz= 1.94 mm PSL structure is adversely affected by losses.
4 Numerical dispersion study
Experimental measurements are compared to numerical dispersions calculated using the Eigenmode Solver of CST Microwave Studio (MWS). Specifically, the Advanced Krylov Subspace (AKS) Eigenmode Solver was chosen and configured to compute eigenmodes over the full phase range from − 2π to 2π using the parameter sweep function. To reduce computation time, just one lattice cell was modelled, with periodic boundaries in the x and z directions in place of the lattice corrugation. This method considers only allowed eigenmodes within the structure and does not calculate for a given incident angle. However, the simulation results still provide a useful comparison for the ‘mode-locked’ experimental results which show less angular dependence than in the cases of weak coupling where multiple resonances are present. The frequencies of the coupled dispersions’ maxima and minima indicate the positions of possible cavity eigenmodes. Dispersion plots for the set of PSLs mounted on the thin copper backed substrates are characterised by two branches, each formed by coupled volume and surface field dispersions, with flat profiles demonstrating the potential for mode-locking in a well synchronised PSL. As expected, the frequency positions of the upper (thin lines) and lower (bold lines) coupled dispersion branches vary depending on dz. The high-Q eigenmodes of Fig. 3a, b correlate to those predicted by the lower branches of the dz= 1.50 mm (bold red line) and dz= 1.62 mm (bold dashed green line) dispersions shown in Fig. 4, with some frequency deviation attributed to differences between the experiment and numerical modelling. The CST MWS solver does not consider losses or diffractive edge effects, and calculates for a structure irradiated at normal incidence. The resonance observed at 142.5 GHz at the lowest incident angle \( \theta_{i} = 25^\circ \)(closest to normal incidence) in Fig. 3c demonstrates excellent agreement with the lower dispersion branch for the dz= 1.74 mm PSL (bold dot-dash blue line) which shows potential eigenmode formation at 142.1 GHz. However, in the experimental study, Fabry–Perot effects were detrimental to strong mode-coupling. The dz= 1.94 mm PSL’s lower branch (bold dotted purple line) exists below the measured frequency range, accounting for the absence of low frequency resonances in the experiment. Here, the weak resonance at 159 GHz instead corresponds to the upper dispersion branch (thin dotted purple line). Interestingly, the dz= 1.94 mm PSL’s upper dispersion branch appears out of phase compared with those for the other periodicities, indicating that the surface mode might be dominating over the volume mode, due to the thin substrate and larger period. It has therefore been shown that the structure’s parameters must be carefully chosen to achieve effective mode-coupling and eigenmode formation.
Numerical dispersion diagrams for the dz = 1.50 mm (red, solid line), dz = 1.62 mm (green, dashed line) dz = 1.74 mm (blue, dot-dash line) and dz = 1.94 mm (purple, dotted line) PSLs with Δh = 35 µm mounted on t = 0.41 mm copper-backed, εr= 5.69 substrates and calculated using the Eigenmode Solver of CST MWS. Lower (thicker traces) and upper (thinner traces) coupled dispersion branches are observed for each structure with the maxima and minima of these branches corresponding to the frequencies of possible coupled eigenmodes
Experimental results, validated by numerical modelling, confirm that optimal coupling occurs when the thickness of the substrate t and lattice periodicity \( d_{z} \) are within an ideal range. Above a certain thickness t, the substrate may become over-moded and dielecric losses can impede the coupling of the volume and surface modes [32]. However, coupling is also less effective when the substrate is too thin in relation to \( d_{z} \). Experimental results suggest that strong coupling is observed when there is between half and one and a half optical wavelengths within the dielectric, where \( \lambda_{op} \cong d_{z} /n \) and n is the refractive index of the material, i.e. \( 0.5 \lambda_{op} \le t \le 1.5 \lambda_{op} \), however other factors including the dielectric loss should be taken into account.
5 Metamaterial periodic surface lattice
Up until this point in this work, the PSLs with shallow corrugations \( (\Delta h \ll \lambda_{s} ) \) have been likened to metamaterials in the plane of incidence only, with the relatively large \( \left( {d_{z} \sim\lambda } \right) \) transverse dimensions failing to satisfy the metamaterial criterion. Previously, a ~ 30 dB ‘mode-locked’ eigenmode was documented at 370 GHz for a dz= 0.64 mm PSL mounted on a t = 0.41 mm copper-backed substrate measured at 325–500 GHz [32]. In this present work, this same dz= 0.64 mm PSL is also studied at 140–220 GHz where \( d_{z} < \lambda \). The PSL, now closer to the true definition of a metamaterial, exhibits high-Q (~ 40 dB) resonances at approximately half the frequency and with significantly higher reflected powers than before [32]. Figure 5 illustrates an incremental rise in frequency with increasing \( \theta_{i} \); a tendency reported in certain cases of volume and surface mode coupling, but not observed at 325–500 GHz [32]. Although not strictly ‘mode-locked’, the coupled eigenmode resonances span a narrow (~ 178–187 GHz) bandwidth. This bandwidth without compromising the reflected power, may be exploited in certain applications including tunable THz sources and absorbers. It has been shown that the EM properties of the structure are subtly modified as \( d_{z} \) is decreased further towards the metamaterial regime, allowing the PSL structures discussed in this work to be individually ‘tailored for purpose’ by varying the lattice periodicity and dielectric thickness.
Reflected power for the dz= 0.64 mm metamaterial PSL etched onto a t = 0.41 mm copper-backed substrate and measured over a range of incident angles at 140–220 GHz. The resonances undergo a small increase in frequency with increasing angle, suggestive of volume and surface mode coupling. Reflected power changes of up to 40 dB at resonance are observed
6 Conclusions
In summary, we have shown the resonant coupling of volume and surface modes leading to the formation of well-defined coupled eigenmodes and demonstrating the principle of mode selection in multi-moded structures, with applications in novel radiation sources based on different gain media. It has been established that the structures’ parameters, in particular the lattice periodicity and dielectric thickness, must be carefully chosen to achieve optimum coupling. Mode coupling was found to be most effective in the dz= 1.50 mm and dz= 1.62 mm PSL structures, while lower signal to noise ratios and Fabry–Perot resonances were prevalent in PSLs with larger periodicities. It was shown that, despite the thin substrates with the capability to facilitate enhanced coupling, the copper backing was essential for single-mode excitation, and multiple resonances were observed for the structures based on PSLs and dielectric alone. The aim of this work was to demonstrate the fundamental ‘proof-of-principle’ coupling of volume and surface modes, but in practical applications a lower loss substrate designed for use at mm-wave and THz frequencies could increase the Q of the resonances. Experimental results have been validated by numerical dispersion calculations showing that the measured resonances correspond to the frequency locations of expected coupled eigenmodes. An important result of this paper, is the realization of a high-Q, coupled eigenmode observed in a metamaterial PSL structure. This metamaterial eigenmode verifies the scalability and broad interest of this work and is especially relevant to applications requiring tunable THz sources, filters, or absorbers due to the ability to tailor the frequency with angle. To conclude, the volume and surface mode-coupling demonstrated experimentally and numerically in this work is relevant to the generation of high power radiation at shorter wavelengths, and the development of highly efficient solar cells and mm-wave and THz antennae. Similar PSL structures with cylindrical geometry will be incorporated into future mm-wave source experiments at the University of Strathclyde.
References
Lu Z, Murakowski JA, Schuetz CA, Shi S, Schneider GJ, Prather DW (2005) Three-dimensional subwavelength imaging by a photonic-crystal flat lens using negative refraction at microwave frequencies. Phys Rev Lett 95(15):153901. https://doi.org/10.1103/PhysRevLett.95.153901
Abraham E, Younus A, El Fatimy A, Delagnes JC, Nguéma E, Mounaix P (2009) Broadband terahertz imaging of documents written with lead pencils. Opt Commun 282(15):3104–3107. https://doi.org/10.1016/j.optcom.2009.04.039
Seco-Martorell C, López-Domínguez V, Arauz-Garofalo G, Redo-Sanchez A, Palacios J, Tejada J (2013) Goya’s artwork imaging with terahertz waves. Opt Express 21(15):17800–17805. https://doi.org/10.1364/OE.21.017800
Kumar N, Singh U, Bera A, Sinha AK (2017) RF behavior of cylindrical cavity based 240 GHz, 1 MW gyrotron for future tokamak system. J Infrared Millim Terahertz Waves 38(11):1342–1356. https://doi.org/10.1007/s10762-017-0419-5
Lier E, Werner DH, Scarborough CP, Wu Q, Bossard JA (2011) An octave-bandwidth negligible-loss radiofrequency metamaterial. Nat Mater 10:216. https://doi.org/10.1038/nmat2950
Kleine-Ostmann T, Nagatsuma T (2011) A review on terahertz communications research. J Infrared Millim Terahertz Waves 32(2):143–171. https://doi.org/10.1007/s10762-010-9758-1
York AG, Milchberg HM, Palastro JP, Antonsen TM (2008) Direct acceleration of electrons in a corrugated plasma waveguide. Phys Rev Lett 100(19):195001. https://doi.org/10.1103/PhysRevLett.100.195001
Smirnova EI, Kesar AS, Mastovsky I, Shapiro MA, Temkin RJ (2005) Demonstration of a 17-GHz, high-gradient accelerator with a photonic-band-gap structure. Phys Rev Lett 95(7):074801. https://doi.org/10.1103/PhysRevLett.95.074801
Benabid F, Knight JC, Antonopoulos G, Russell PSJ (2002) Stimulated Raman scattering in hydrogen-filled hollow-core photonic crystal fiber. Science 298(5592):399–402. https://doi.org/10.1126/science.1076408
Grishin YA, Fuchs MR, Schnegg A, Dubinskii AA, Dumesh BS, Rusin FS, Bratman VL, Möbius K (2004) Pulsed orotron—a new microwave source for submillimeter pulse high-field electron paramagnetic resonance spectroscopy. Rev Sci Instrum 75(9):2926–2936. https://doi.org/10.1063/1.1778071
Carelli P, Chiarello F, Cibella S, Di Gaspare A, Leoni R, Ortolani M, Torrioli G (2012) A fast terahertz spectrometer based on frequency selective surface filters. J Infrared Millim Terahertz Waves 33(5):505–512. https://doi.org/10.1007/s10762-012-9884-z
Letizia R, Mineo M, Paoloni C (2016) Photonic crystal-coupler for sheet beam THz vacuum electron tubes. IEEE Electron Device Lett 37(9):1227–1230. https://doi.org/10.1109/LED.2016.2587903
Ginzburg NS, Malkin AM, Sergeev AS, Zaslavsky VY (2013) Oversized co-axial and cylindrical surface-wave oscillators with two-dimensional periodical grating (quasi-optical model). J Appl Phys 113(10):104504. https://doi.org/10.1063/1.4794008
Paoloni C, Gamzina D, Himes L, Popovic B, Barchfeld R, Yue L, Zheng Y, Tang X, Tang Y, Pan P, Li H, Letizia R, Mineo M, Feng J, Luhmann NC (2016) THz backward-wave oscillators for plasma diagnostic in nuclear fusion. IEEE Trans Plasma Sci 44(4):369–376. https://doi.org/10.1109/TPS.2016.2541119
Ginzburg NS, Ilyakov EV, Kulagin IS, Malkin AM, Peskov NY, Sergeev AS, Zaslavsky VY (2018) Theoretical and experimental studies of relativistic oversized Ka-band surface-wave oscillator based on 2D periodical corrugated structure. Phys Rev Accel Beams 21(8):080701. https://doi.org/10.1103/PhysRevAccelBeams.21.080701
Konoplev IV, Phelps ADR, Cross AW, Ronald K (2003) Experimental studies of the influence of distributed power losses on the transparency of two-dimensional surface photonic band-gap structures. Phys Rev E 68(6):066613. https://doi.org/10.1103/PhysRevE.68.066613
Konoplev IV, Fisher L, Cross AW, Phelps ADR, Ronald K, Robertson CW (2010) Surface wave Cherenkov maser based on a periodic lattice. Appl Phys Lett 96(26):261101. https://doi.org/10.1063/1.3456618
Konoplev IV, Fisher L, Cross AW, Phelps ADR, Ronald K, Thumm M (2010) Excitation of surface field cavity and coherence of electromagnetic field scattering on two-dimensional cylindrical lattice. Appl Phys Lett 97(26):261102. https://doi.org/10.1063/1.3529953
Konoplev IV, Fisher L, Ronald K, Cross AW, Phelps ADR, Robertson CW, Thumm M (2010) Surface-field cavity based on a two-dimensional cylindrical lattice. Appl Phys Lett 96(23):231111. https://doi.org/10.1063/1.3428776
Konoplev IV, MacLachlan AJ, Robertson CW, Cross AW, Phelps ADR (2011) Cylindrical periodic surface lattice as a metadielectric: concept of a surface-field Cherenkov source of coherent radiation. Phys Rev A 84(1):013826. https://doi.org/10.1103/PhysRevA.84.013826
Konoplev IV, MacLachlan AJ, Robertson CW, Cross AW, Phelps ADR (2012) Cylindrical, periodic surface lattice—theory, dispersion analysis, and experiment. Appl Phys Lett 101(12):121111. https://doi.org/10.1063/1.4754572
Doucas G, Blackmore V, Ottewell B, Perry C, Huggard PG, Castro-Camus E, Johnston MB, Hughes JL, Kimmitt MF, Redlich B, van der Meer A (2006) Longitudinal electron bunch profile diagnostics at 45 MeV using coherent Smith–Purcell radiation. Phys Rev Spec Top Accel Beams 9(9):092801. https://doi.org/10.1103/PhysRevSTAB.9.092801
Shoaib S, Shoaib N, Shoaib I, Chen X (2017) Design and performance analysis of pattern reconfigurable MIMO antennas for mobile smartphones. Microw Opt Technol Lett 59(1):148–156. https://doi.org/10.1002/mop.30256
Landy NI, Sajuyigbe S, Mock JJ, Smith DR, Padilla WJ (2008) Perfect metamaterial absorber. Phys Rev Lett 100(20):207402. https://doi.org/10.1103/PhysRevLett.100.207402
Kong H, Li G, Jin Z, Ma G, Zhang Z, Zhang C (2012) Polarization-independent metamaterial absorber for terahertz frequency. J Infrared Millim Terahertz Waves 33(6):649–656. https://doi.org/10.1007/s10762-012-9906-x
Ulrich R (1968) Interference filters for the far infrared. Appl Opt 7(10):1987–1996. https://doi.org/10.1364/ao.7.001987
Ulrich R (1967) Far-infrared properties of metallic mesh and its complementary structure. Infrared Phys 7(1):37–55. https://doi.org/10.1016/0020-0891(67)90028-0
Ri-Hui X, Jiu-Sheng L (2018) Double-layer frequency selective surface for terahertz bandpass filter. J Infrared Millim Terahertz Waves. https://doi.org/10.1007/s10762-018-0527-x
Mv L, Lenzmann F, Verschuuren MA, Polman A (2012) Mode coupling by plasmonic surface scatterers in thin-film silicon solar cells. Appl Phys Lett 101(22):221110. https://doi.org/10.1063/1.4767997
Phipps AR, MacLachlan AJ, Robertson CW, Zhang L, Konoplev IV, Cross AW, Phelps ADR (2017) Electron beam excitation of coherent sub-terahertz radiation in periodic structures manufactured by 3D printing. Nucl Instrum Methods Phys Res Sect B 402:202–205. https://doi.org/10.1016/j.nimb.2017.03.093
French DM, Shiffler D (2016) High power microwave source with a three dimensional printed metamaterial slow-wave structure. Rev Sci Instrum 87(5):053308. https://doi.org/10.1063/1.4950904
MacLachlan AJ, Robertson CW, Cross AW, Phelps ADR (2018) Volume and surface mode coupling experiments in periodic surface structures for use in mm-THz high power radiation sources. AIP Adv 8(10):105115. https://doi.org/10.1063/1.5020542
MacLachlan AJ, Robertson CW, Konoplev IV, Cross AW, Phelps ADR, Ronald K (2019) Resonant excitation of volume and surface fields on complex electrodynamic surfaces. Phys Rev Appl 3(11):034034. https://doi.org/10.1103/PhysRevApplied.11.034034
MacLachlan AJ et al. Data underpinning this publication are available from the University of Strathclyde KnowledgeBase at http://doi.org/10.15129/a7717713-5369-4e8b-ae3f-776f36e3013e
Acknowledgements
Useful discussions with Dr. Ivan Konoplev of the John Adams Institute, Department of Physics, University of Oxford, UK are gratefully acknowledged. The authors would like to thank Mr David Barclay for his help making experimental components. This research has received support from AFOSR under Awards FA8655-13-1-2132 and FA9550-17-1-0095.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
MacLachlan, A.J., Robertson, C.W., Ronald, K. et al. Mode coupling in periodic surface lattice and metamaterial structures for mm-wave and THz applications. SN Appl. Sci. 1, 613 (2019). https://doi.org/10.1007/s42452-019-0596-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-019-0596-z