Network real-time kinematic data screening by means of multivariate statistical analysis

Abstract

We introduce a novel approach to the computation of network real-time kinematic (NRTK) data integrity, which can be used to improve the position accuracy for a rover receiver in the field. Our approach is based on multivariate statistical analysis and stochastic generalized linear model (SGLM). The new approach has an important objective of alarming GNSS network RTK carrier-phase users in case of an error by introducing a multi-layered approach. The network average error corrections and the corresponding variance fields are computed from the data, while the squared Mahalanobis distance (SMD) and Mahalanobis depth (MD) are used as test statistics to detect and remove data from satellites that supply inaccurate data. The variance-covariance matrices are also inspected and monitored to avoid the Heywood effect, i.e. negative variance generated by the processing filters. The quality checks were carried out at both the system and user levels in order to reduce the impact of extreme events on the rover position estimates. The SGLM is used to predict the user carrier-phase and code error statistics. Finally, we present analyses of real-world data sets to establish the practical viability of the proposed methods.

1 Introduction

An integrity service is a set of procedures used to check the correctness of the information provided by a system. Such services are already implemented in safety of life navigation augmentation systems such as WAAS, EGNOS, GAGAN and others.

There are also other types of integrity algorithms, for instance GNSS receiver-based integrity monitoring known as receiver autonomous integrity monitoring (RAIM) and fault detection and exclusion (FDE) algorithms [1, 2]. These algorithms identify satellites with bad observations using a least-squares method, and then exclude them from the solution. However, RAIM and FDE were developed as pseudo-range residual data analysis algorithms for GNSS safety-critical applications, such as e.g. the approach phase of flight. For high-accuracy applications, an extension of pseudo-range RAIM (PRAIM) known as carrier-phase based RAIM (CRAIM) was proposed by [3].

Data quality checks and integrity monitoring techniques have been a research topic for many years in geodesy, surveying and navigation. For instance, Baarda [4] developed a test procedure for use in geodetic networks, which has been used to check data against outlying observations in many different applications, for instance the analysis of the deformation problem in geodesy [5]. An elegant method for data quality check for deformation monitoring can be found in [6, 7]. The DIA procedure [8] can be applied to any set of GNSS observation equations, such as GPS quality control [9], geodetic networks [10] or integrated navigation system [10]. Another approach to error modeling is to perform a reliability and quality control procedure [11], using statistical methods for the analysis [12], multi-state reliability analysis with application to NRTK [13].

Our aim is to provide the user in the field with continuously high quality corrections with the ability to identify the periods for which the reliability of the network RTK performance is reduced in terms of accuracy and availability. Therefore, solution quality indicators describing the reliability of the network RTK are needed to transfer the status of the network to the user in the field. Intensive research has been conducted recently in this field to derive such quality indicators, and can be classified into two main classes: (1) spatially correlated (ionosphere, troposphere and orbital) error indicators; (2) residuals errors indicators. Most network RTK used quality indicators are; residual integrity monitoring (RIM) and irregularity parameters (IP) quality indices [14], residual interpolation uncertainty (RIU) [15], geometry-based quality indicator (GBI) [15], and the ionospheric index I95 [16].

In recent years, mobile phones have also emerged as a new market for GNSS applications. Quality control for handset-based users is already in demand. For instance, Trimble introduced the CenterPoint RTX system, which offers real-time position estimation and coordinates integrity via a mobile app (Trimble pivot), including an analysis of the ionosphere activity and network status [17, 18].

The users of high accuracy GNSS NRTK positioning systems have requested the development of data integrity for a long time. In this article, we consider how such a service can be designed and implemented, which can be of interest to both the NRTK service providers and their users.

The NRTK processing chain can be summarized as follows. The first step is to collect raw measurements from the network of reference stations, solve for the ambiguities within the reference network, and generate error estimates. Then an interpolation/smoothing scheme is applied to generate the NRTK corrections for the user location. For information on how to avoid loss of information under interpolation of NRTK data, the interested reader is referred to [19]. The NRTK corrections are then transmitted to users who can perform real-time positioning with an accuracy at the cm-level [20]. Several NRTK techniques exist, and the most common used ones are the master auxiliary concept (MAC) [21, 22], the virtual reference station (VRS) concept [23], and the FKP techniques [24]. However, we limit the discussion in this paper to the network adjustment (NetAdjust) method developed by [25]. Figure 1 shows the structure of the NRTK processing chain. The new data integrity segment (red box) is the main focus of this article. At the system level, the integrity service is driven by a three-step process, where the average correction field and associated variances are generated by constructing time series with a sliding window. The size of the sliding window is set to the correlation length, i.e. the time span for which the observations can be considered completely decorrelated.

As described in Sect. 5, we use two Mahalanobis metrics (SMD and MD) to detect extremal events, and use the t-distribution as a local identification test rather than Gaussian distribution. The t-distribution is used as an alternative to the normal distribution when sample sizes are small. The interested reader is referred to [26] for more details. For adaptation, we can either send the satellite identities to the rover, or just ignore them and abstain from sending the corrections.

The reason for using this type of metrics is that when using the SMD approach, the explanatory observations are those that lie far from the bulk of the data. The computed metric values may then be compared with quantiles of the $\chi ^2$-distribution with $p -1$ degrees of freedom, where p is the number of common satellites used by the filters. Another important characteristic of the metric is that there exists a unique mapping to the diagonal of the prediction matrix shown in Eq. (14)  [27, p. 224]. For more information about the properties and benefits of SMD-based approaches, please consult [27,28,29]. MD-based approaches are similarly described by [30,31,32].

At the user level, the raw phase observations can be inspected to ensure that only high-quality observations are included in the analysis, and this can be accomplished using the Danish method [33]. The main reason for choosing the Danish method is that ordinary least-squares methods are sensitive to outliers. Unfortunately, most estimators that are robust to outliers are only applicable to uncorrelated data sets, while e.g. double-difference carrier phase observables and network baseline vectors are examples of the abundant correlated observables in GNSS systems [12]. However, a straight-forward solution to this problem is to decorrelate the original data set using e.g. a Mahalanobis transformation, and then apply well-known robust estimation methods for uncorrelated data to the results. Various such schemes exist that provide a certain resistance against outlying observations and reduce their influences on the estimation process. Additional benefits are that the method guarantees convergence, and can automatically locate and eliminate errors. For more information, see for instance [12].

Finally, as described in Sect. 7, the residuals of the baseline and corresponding variances are used to predict the position error. The focus is directed to the double-difference error covariance matrix, which will be used to construct the relevant prediction function. The covariance matrices at both the system and user levels are continuously inspected for Heywood cases [34], i.e. anomalous generation of negative variance. The validation procedure is carried out by excluding all suspicious satellites from the position computation.

In order to evaluate our proposed integrity method, we use a data sample from the Norwegian GNSS network, which is described in detail in Sect. 2. The NetAdjust method is briefly discussed in Sect. 3. The architecture of the proposed integrity solution is then presented in Sect. 4. After that, the network correction integrity is discussed in Sect. 5, rover observation integrity in Sect. 6, and relative positioning integrity in Sect. 7. Finally, the implementation and analysis are presented in Sect. 8, and the discussion and conclusion in Sect. 9.

Fig. 1

Extension of network real-time kinematics segments with a new service known as the NRTK data integrity segment (red rectangle)

2 Test data

The data sample used to evaluate our proposed method was provided by the Norwegian RTK network known as CPOS, which is operated by the Norwegian Mapping Authority (NMA). The test area is from the Rogaland region in the south west of Norway. Reference receivers are equipped with Trimble NetR9 receivers, tracking GPS and GLONASS satellite signals. Baselines vary between 35 to 112 km and the height difference between the sites is about 225 m. Tables 1, 2 and 3 give a description of the sub-network while Fig. 2 shows the location of reference receivers.

The NRTK software modules are executed at the same rate, of one second interval. Once every ten seconds, the network modules generate the user corrections. The updating rate was chosen intentionally and corresponds to the optimal update rate of the network corrections, dispersive and non-dispersive, respectively. The module can be interpreted as a discrete event model. The user position is computed once every second.

Many tests have been carried out in this research. For the manuscript, we have used data from DOY 152, 2013 to illustrate the NRTK concept. For Network results shown in this paper, approximately five and a half hours data is used and for baseline processing and rover position computations, approximately two hours of data is used.

Table 1 Sub-network reference receivers characteristics

Table 2 Distances in sub-network [km]

Table 3 Reference receiver coordinates— ETRF89 XYZ coordinates in meter

Fig. 2

Test area used in this investigation, from Rogaland region in Norway. Composed of six reference receivers. Baseline distances are in km

3 Network adjustment method

As mentioned in Sect. 1, several NRTK techniques exist as described in for instance [21,22,23,24]. The integrity monitoring algorithms developed and described in the remainder of this paper works independent of the method used for generation of the NRTK corrections.

Our proposed NRTK data integrity concept is built on top of existing NRTK services. However, the computation of the correction field depends strongly on the method employed. For instance, it is essential whether the data itself is un-, single-, or double-differenced. The output from these filters are the dispersive and geometric biases, which can be provided either as one component or as separate components. For further analysis, the correction field has to be explicitly constructed, and their covariance matrices have to be examined closely. In addition, the filters variance-covariance matrices has to be inspected for Heywood cases. However, our method is independent of the approach and linear combinations used to generate these biases, and whether they are decomposed or not.

For derivation and development of the integrity and quality control algorithms we need a test case and we have based our work on the conceptual approach as given by the NetAdjust method [25, 35]. Most of the NRTK techniques mentioned above are developed commercially and details about these are not readily available. But the NetAdjust method is well-described in literature, it is therefore suitable as a starting point for our work, and we provide a review of the method in the following.

The network adjustment method known as NetAdjust uses least-squares collocation techniques [36, Chap. 10] to compute the user network corrections. The Danish geodesist Torben Krarup [37] was the first to build the theoretical foundation for this new concept, namely the collocation methods. Since then, the method has been considered by geodesists as an algorithm for performing geodetic computations. For statisticians, this method is also known as kriging, a spatial linear interpolation algorithm named after the South African mining engineer D. G. Krige [38, p. 216]. In this paper, we will refer to such collocation methods as kriging.

The NetAdjust method is based on carrier-phase double-difference techniques. Taking the difference between the original observation signals allows us to eliminate or reduce the effect of uncanceled differential biases. In addition, the technique has the advantage of a reduction in both the measurement and parameter count. One need not to include the entire set of double-difference measurements because it contains redundant information. In the case of double-difference observations, receiver and satellite clock errors are eliminated, i.e. the results become independent of the receiver and satellite clock biases. In this work, the effect of residual double-differenced code and phase hardware delays is assumed to be negligible.

The overarching philosophy behind the NetAdjust design can be summarized as follows [25]:

• 1. Main equation:

  $$\begin{aligned} \varDelta \nabla \ell = \underbrace{\varDelta \nabla \delta \ell }_\text {first-term} + \underbrace{\varDelta \nabla N}_\text {second-term} \end{aligned}$$

  (1)

  Note that $\varDelta \nabla$ is the double-difference operator and $\varDelta \nabla \ell$ is the double-difference carrier-phase measurements, after subtracting range observables and the troposphere delay. This equation states that after correcting for double-difference ambiguity $\varDelta \nabla N$, this is equivalent to the double-difference error $\varDelta \nabla \delta \ell$, which is composed of residual atmospheric effects (ionosphere and troposphere), residual effects of the satellite position errors, as well as residual effects of multipath, receiver noise, antenna phase center variation, etc.

• 2. NetAdjust signature: Regardless of what ambiguity resolution algorithm one uses, the resolution is improved when the GNSS errors are minimized. This can be accomplished by reducing the uncertainties in the first term of Eq. (1), which facilitates the estimation of the second term, yielding improved ambiguity resolution.

• 3. Error characteristics: The NetAdjust method describes the error as a function of the position.

• 4. Optimization: Given the network measurements minus range observables and troposphere delay, one can estimate the differential measurement error $\delta l$ that minimizes the total variance (TV). The optimal estimator is determined using a Bayesian method, i.e. selecting a suitable loss function $L(\,\cdot \,)$ and thus an appropriate Bayes risk function $B(\,\cdot \,) = {\mathbf{E}}[L(\,\cdot \,)]$, where ${\mathbf{E}}$ is the expectation operator. For more details, e.g. [39] offers an elegant explanation of decision theory and Bayesian analysis.

• 5. Prediction: Least-squares collocation is a statistical estimation method that combines least-squares adjustment and prediction methods. The NetAdjust method uses the least-squares covariance analysis for accuracy prediction, i.e. to predict the carrier-phase error statistics for a given network configuration. For more details of this technique, the reader is referred to e.g. [40].

We will now provide a brief discussion of the mathematical details of the method. We assume that the relationship between the parameter vector ${\mathbf{x}}$ and observation vector ${\mathbf{Y}}$ is a simple linear model ${\mathbf{Y}} = {\mathbf{A}} {\mathbf{x}} + {\mathbf{e}}$, where ${\mathbf{e}}$ is an error vector. The Bayesian optimal estimator ${\hat{\mathbf{x}}}_\text {opt}$ with quadratic loss function is then obtained by minimizing the Bayes risk $B({\mathbf{x}}) = {\mathbf{E}}\big [\! \left\| {\mathbf{x}} - {\hat{\mathbf{x}}} \right\| ^2\!\big ]$, thus yielding

$$\begin{aligned} {\hat{\mathbf{x}}}_{\text {opt}} = {\mathbf{C}}_{{\mathbf{x}}{\mathbf{Y}}} {\mathbf{C}}_{{\mathbf{Y}}}^{-1} {\mathbf{Y}} , \end{aligned}$$

(2)

where ${\mathbf{C}}_{\mathbf{Y}}$ is the covariance matrix between sample locations, and ${\mathbf{C}}_{{\mathbf{x}}{\mathbf{Y}}}$ the covariance matrix between sample and prediction locations. This is also known as the kriging equation, and is used to compute the weights ${\mathbf{W}} = {\mathbf{C}}_{{\mathbf{x}}{\mathbf{Y}}} {\mathbf{C}}^{-1}_{\mathbf{Y}}$. To be more specific:

• 1. The elements of the covariance matrix ${\mathbf{C}}_{{\mathbf{Y}}}$ for the locations ${\mathbf{Y}}$ in the sample are defined as:

  $$\begin{aligned} \forall i,j: \quad \big [{\mathbf{C}}_{{\mathbf{Y}}}\big ]_{ij} = \text {Cov}(Y_i, Y_j) \,. \end{aligned}$$

  (3)

• 2. The elements of the covariance matrix ${\mathbf{C}}_{\mathbf{xY}}$ between the prediction points ${\mathbf{x}}$ and the sample locations ${\mathbf{Y}}$ are:

  $$\begin{aligned} \forall i,j: \quad \big [{\mathbf{C}}_{\mathbf{xY}}\big ]_{ij} = \text {Cov}(x_i, Y_j) \,. \end{aligned}$$

  (4)

• 3. The NetAdjust estimator ${\hat{\mathbf{x}}}_\text {opt}$ is the optimal minimum variance error estimator. Note that Eq. (2) can also be written in the simple form ${\hat{\mathbf{x}}}_{\text {opt}} = \mathbf{W Y}$, which is a linear function of the observation vector ${\mathbf{Y}}$, and takes into consideration the covariance structure of the problem when estimating the weight matrix ${\mathbf{W}}$.

  Computationally, the bottleneck when calculating the weight matrix ${\mathbf{W}}$ is the matrix inversion ${\mathbf{C}}_{\mathbf{Y}}^{-1}$. If the covariance matrix is large, the matrix inversion can become very time consuming. Moreover, if the matrix is ill-conditioned, there is also a risk of negative variance generation [34].

NetAdjust uses the kriging equation [Eq. (2)] to compute the network corrections. The corrections are then transmitted to the user, and the position computation process is then carried out in the user’s rover receiver. For more details, the reader is referred to [25].

4 NRTK integrity design

In this section, we first briefly introduce the classical RTK data processing schemes. We then follow up with a discussion of the advantages of NRTK systems, which extend the classical schemes through a network of reference receivers. We then discuss a further extension of NRTK systems with a novel and currently unavailable layer, namely the NRTK Quality Control or data integrity layer, referred to as the network RTK integrity segment in Fig. 1.

Figure 3 shows the high-level functional decomposition of the NRTK data integrity, where the quality control is performed at both the system and user levels. Different processing schemes can be used to generate the user corrections: un-, single-, or double-differenced  [41,42,43]. The user corrections may optionally be further decomposed into dispersive and geometric contributions based on their frequency-dependence. Our aim is to identify the exact locations in the NRTK data processing chain where data quality ought to be inspected and diagnosed. The result of this analysis should be a list of suspicious satellites that generate anomalous data.

At the network level, a check barrier is implemented to check the quality of the user corrections and the uncertainty provided by the covariance matrices. This check guarantees high quality for a simulated reference receiver, known as a virtual reference receiver (VRS) or computation point (CP). This check is referred to as network data integrity. The curved line of the left panel in Fig. 3 indicates the output for this computation point. The next check barrier is at the baseline level, where the local data integrity is handled. The raw rover observation data is inspected by the variance weighting algorithm (i.e. the Danish method). The covariance matrix can then be analyzed at the double-difference level to check for stability. The relative positioning between the computation and rover points is handled at this level, as shown in the middle panel of Fig. 3. Finally, the last check barrier is the inspection of the rover position accuracy and the construction of the error ellipse.

Other NRTK methods typically use two filters to compute the user corrections. The first filter uses an ionosphere-free linear combination to compute the geometric corrections, i.e. corrections for distortions caused by the troposphere, satellite position errors, and clocks. The advantage of this method is that the ionosphere path delay is practically eliminated. The second filter uses geometry-free linear combinations to estimate the ionospheric corrections. The advantage of this method is that it is independent of receiver clocks and geometry, and contains the ionospheric path delay and initial phase ambiguity. Regardless of the method, an average error level must be determined, and the statistical procedure and test statistics are similar for both approaches.

Fig. 3

Check barriers of the network RTK data integrity. The left panel shows a network with five reference receivers $S_i$ and a rover R. The middle panel shows the baseline quality check. The right panel shows the rover position error

4.1 Network corrections quality check

Network real-time data processing is a pure spatio-temporal process, since data is continuously recorded at different stations, and the analysis has to account for both spatial and temporal correlations in the observation data. First of all, the observations at each station have intrinsic correlations when they are in geographical proximity. Additional correlations are introduced by both differencing schemes [44] and network processing [12]. All of these effects have to be considered in a rigorous spatio-temporal analysis.

One way to treat the spatial part of the correlations, is to perform a Cressie decomposition [45, Chap. 3]:

$$\begin{aligned} R({\mathbf{s}},t) = M({\mathbf{s}},t) + V({\mathbf{s}},t); \end{aligned}$$

(5)

where ${R}({\mathbf{s}},t)$ is the real signal, ${M}({\mathbf{s}},t)$ is the mean function known as the trend (large-scale variation), ${V}({\mathbf{s}},t)$ is the variance function (small scale variation) and $({\mathbf{s}},t)$ are the spatial and temporal variables.

The mean function ${M}({\mathbf{s}},t)$ is calculated using standard GNSS processing techniques, including the detection and mitigation of GNSS error sources. These errors include models for the signal path delays caused by e.g. tropospheric or ionospheric activity. Challenges in estimating this mean function include mapping out the covariance structure of the network, handling non-stationarity, handling non-Gaussian processes, and constructing models that are computationally efficient for large-scale data processing.

The variance function ${V}({\mathbf{s}},t)$ is actually just the uncertainty of the network correction field. Although it seemingly plays a lesser role compared to the mean function $M({\mathbf{s}},t)$, the importance of the variance function $V({\mathbf{s}},t)$ cannot be overemphasized. This is because it can be used as a feedback control component when estimating $M({\mathbf{s}},t)$, where one monitors undetected anomalies in $V({\mathbf{s}},t)$ and attempt to compensate for its weaknesses. Thus, the variance function can be used to inform users in the field when the network corrections cannot be trusted, which is what we refer to as a data integrity. The main objective is to allow only satellites with high-quality data to be involved in the generation of the correction of the computation points, as discussed in more detail in Sect. 5.

4.2 Integrity of raw carrier-phase data

Figure 3 illustrates the importance of local data integrity. The NetAdjust system constructs high quality computation point(s) using data from the reference receivers. If the rover raw carrier phase observations have not been inspected for signal diffraction, multipath interference, and possibly also scintillation, the result of the double-difference baseline processing will be biased. Robust estimation techniques reduce the influence of outliers on the result. The distorted signals of the cases mentioned above, are not really outliers but biased observations.

Outliers are usually not just biased observations, but observations that deviate from the distribution of regular observations, and this makes them straight-forward to eliminate. For identification and classification of outlier types, the reader is referred to [27].

In contrast, data distortion caused by multipath [33], scintillation, etc. result in biased observations that still resemble regular data, and these data points are much more challenging to detect in real-time.

Nevertheless, in cases where the bias itself is not explicitly modeled, one must take care to assign lower weights to these biased observations to prevent them from skewing the results. The combination of carrier-phase signal-to-noise ratios and the double-difference phase residuals is discussed in Sect. 6.

4.3 Baseline data integrity

The output from the baseline computations are the widelane double-difference carrier-phase residuals and the corresponding error covariance matrix. These parameters are combined in an appropriate way to predict the carrier-phase and code error statistics. This topic is the subject of the Sect. 7. The methods used in this subsection are summarized in [33].

5 Integrity for network corrections

The NetAdjust method as well as other NRTK methods can use widelane double-difference observations to generate the user corrections. In this paper, we aim to construct the corrections and corresponding variance fields on a satellite-by-satellite basis. This includes both test statistics and a determination of the temporal correlation length of observation combinations, which has to be computed from the observed data. For this purpose, we employ powerful methods from multivariate statistical data analysis for detection, identification and adaptation procedures, which produces a list of satellites that generate anomalous data.

Global tests are needed to assess whether a set of observations includes errors or not, while local tests are needed to identify the main reasons behind the failure of the global test. We have two candidates for global test statistics, and t distribution for local test statistics. For adaptation, the corrections from high residual values and variances are flagged for exclusion, and are thus not involved in the solution computation.

Using the theory of excursion probability [46, Chap. 4], one can construct an optimal alarm condition for NRTK systems:

$$\begin{aligned} P_{\text {exc}} = \mathbb{P} \left\{ \underset{{\mathbf{s}} \in {S},\,{t} \in {T}}{\mathrm {sup}} \int G({\mathbf{s}},t) \,\text {d}{\mathbf{s}}\, \text {d}t \ge \text {Th} \right\} \,, \end{aligned}$$

(6)

where sup stands for supremum (least upper bound), S and T are the spatial and the temporal spaces, while $G({\mathbf{s}},t)$ is an empirical Green function that is constructed from the data. Our main concern is directed to those extremal events of the correction field that exceed some chosen threshold $\text {Th}$. When solving an optimization problem, one tries to solve the inherent conflict between accuracy and some heuristic cost function in the best possible way. These level-crossing events can bias the position solution of the rover. The next sections will be focused on constructing the components of $G({\mathbf{s}},t)$.

5.1 Network average error levels

This section is devoted to construction of the average error level for each satellite observed at each configured reference receiver in network. Multivariate statistical analysis is used for this purpose.

5.1.1 Time series

Let $Y = \{ Y_{ijk} \}$ be observations, where $i=1,\ldots ,n_\text {rec}$ are the reference receivers, $j=1,\ldots ,n_\text {sat}$ are the satellites observed at each site i, and k is size of the moving window. The size of the moving window is equal to the correlation length of the observations used. According to [47], this correlation length is in the range of 300–600 seconds in the widelane case. Odolinski [48] presented two methods to estimate the correlation length, and found $\sim \!\! 17$ min for the horizontal component, and $\sim \!\! 37$ min for the vertical one. In any case, the larger the moving window, the lower the correlation separation time.

The correlation time can also vary depending on the baseline length. For example, for short baselines of only a few kilometers, we expect only multipath errors and internal receiver effects to be relevant, and that these two factors will determine the correlation time. However, for longer baselines, larger correlation times can be expected if any residual atmospheric delays still remain.

We can describe Y as a matrix-valued sequence of length k, describing the dynamics of the network correction field $G({\mathbf{s}},t)$. Figure 4 shows the constructed average error level for ionospheric corrections in a network of six receivers. The geometry-free linear combination $L_4 = L_1 - L_2$ is used to generate the data presented in Fig. 4. This observation cancels out all the geometry information leaving only the ionosphere effects and initial phase ambiguities. It is commonly used for the estimation of the ionosphere path delay [49]. In the plot the variation of different receivers is shown. Three sites contribute with an equal average error level (top curves), the next two contribute almost equally too (middle), but the final one is distinct from all the other (bottom).

Fig. 4

Computed ionospheric average error level for a configured network. Year 2013, DOY 155

5.1.2 Missing observations

In order to compute the mean, median, and corresponding covariance matrices of $Y_i$ on satellite-by-satellite basis, the constructed time series need to have the same length. In practice, this will of course be nearly impossible, so we need to perform a procedure known as data imputation. For this, one can apply an expectation-maximization data augmentation algorithm, such as the one proposed by [50].

5.2 Global and local test statistics

The empirical stochastic correction field $G({\mathbf{z}})$ can be regarded as a function of ${\mathbf{Y}}_i$, where ${\mathbf{z}} = ({\mathbf{s}},t)$ is a 4-dimensional vector in space ${\mathbf{s}}$ and time t. We will assume that it is a Gaussian field with a p-dimensional probability density function $f({\mathbf{z}})$, which is parametrized by a mean vector ${\varvec{\mu }}$ and covariance matrix ${\varvec{\varSigma }}$:

$$\begin{aligned} \begin{aligned} f({\mathbf{z}})&= |2\pi |^{-p/2} |{\varvec{\varSigma }}|^{-1/2} \exp \left\{ -\frac{1}{2} ({\mathbf{z}}-{\varvec{\mu }})^\text {T} {\varvec{\varSigma }}^{-1} ({\mathbf{z}}-{\varvec{\mu }}) \right\} \\&= T_A({\mathbf{z}}) \,\exp \left\{ -\frac{1}{2} T_B({\mathbf{z}}) \right\} \end{aligned} \end{aligned}$$

(7)

where the notation $|\cdot |$ refers to the matrix determinant, and the functions $T_A$ and $T_B$ are defined respectively by the expressions $|2\pi |^{-p/2} |{\varvec{\varSigma }}|^{-1/2}$ and $({\mathbf{z}}-{\varvec{\mu }})^\text {T} {\varvec{\varSigma }}^{-1} ({\mathbf{z}}-{\varvec{\mu }})$. $T_A$ and $T_B$ are elementary building blocks of the test statistics used in this article.

Our check algorithm is a three-step process, composed of Detection, Identification, and Adaptation. Extremal crossing events can be detected using the global test statistic given by Eqs. (11) and (12). Let our current correction vector for reference receiver i be denoted ${\mathbf{x}}_i$. If we are interested in measuring how far the observation ${\mathbf{x}}_i$ is from the mean ${\varvec{\mu }}_i$, then a Euclidean metric, given by Eq. (8) performs well mathematically, but is sensitive to the specific units of measurements.

$$\begin{aligned} E_i = ({\mathbf{x}}_i - {{\varvec{\mu }}}_i)^\text {T} ({\mathbf{x}}_i - {{\varvec{\mu }}}_i) \end{aligned}$$

(8)

One may therefore wonder if there is a more informative way, particularly in a statistical sense, to measure if the distance ${\mathbf{x}}_i$ is far from the mean ${\varvec{\mu }}_i$. One such metric is given by the squared Mahalanobis distance (SMD) defined in Eq. (9), which accounts for the correlations between the observations and measures the distance in units of standard deviations.

$$\begin{aligned} M_i = ({\mathbf{x}}_i - {\varvec{\mu }}_i)^\text {T}_{\phantom {T}}\, {\varvec{\varSigma }}^{-1}_{\phantom {T}} ({\mathbf{x}}_i - {\varvec{\mu }}_i) \end{aligned}$$

(9)

An alternative metric is the Mahalanobis depth (MD):

$$\begin{aligned} m_i = \frac{1}{1 + M_i} \end{aligned}$$

(10)

This time, we measure how far the observations ${\mathbf{x}}_i$ are from the median, and we note that large values of $m_i$ correspond to values of $x_i$ that are deep inside the distribution.

5.2.1 Definition of global test statistics

In order to detect when extremal events occur, we need some kind of global statistical tests. For this purpose, we have chosen two test statistics:

$$\begin{aligned} T_1({\mathbf{z}}_i)&= ({\mathbf{z}}_i - {\varvec{\mu }}_i)^T {\varvec{\varSigma }}^{-1} ({\mathbf{z}}_i - {\varvec{\mu }}_i) \end{aligned}$$

(11)

$$\begin{aligned} T_2({\mathbf{z}}_i)&= \frac{1}{1+T_1({\mathbf{z}}_i)} \end{aligned}$$

(12)

where ${\mathbf{z}}_i$ is the correction vector observed at reference receiver i at time epoch t. Note that $T_1$ and $T_2$ follow the multivariate $\chi ^2$-distribution and its inverse.

Figures 5 and 6 show how global tests can detect the extremal events caused by network corrections. The plots are provided as functions on time. We see that both the tests are capable of detecting the same events – but while the SMD detects the maxima that exceed the threshold value $T_h$, the MD detects the minima in the data set. Note that this approach is based on the median vector, and not the less robust mean vector.

For SMD, the threshold $T_h$ and level of significance $\alpha$ was set to 15 and $90 \%$, respectability in this test, and correspond to $\chi _{9}^2(.10) \approx 15$. The subscript 9 corresponds to degree of freedom (i.e. average of observed satellites). In contrast to the MD case, the threshold $T_h$ was set to 1 / 16 in this test.

The resolution is set to 10 seconds intentionally and corresponds to the update rate of the network corrections.

Fig. 5

Sample of SMD based on 2500 epochs with a resolution of 10 s. Red horizontal line shows the rejection region of the test

Fig. 6

Sample of MD based on 2500 epochs with a resolution of 10 s. Red horizontal line shows the rejection region of the test

With one sample from a univariate normal distribution, the variability of the sample variance $S^2$ is governed by the chi-squared distribution $\chi ^2$. This distribution also holds an important role in multivariate statistics [51, Chap. 4]. To see this, let us first define ${\mathbf{X}} \sim N_p({\varvec{\mu }}, {\varvec{\varSigma }})$, i.e. ${\mathbf{X}}$ is a normally distributed random variable with a mean vector ${\varvec{\mu }}$ and a positive-definite covariance matrix ${\varvec{\varSigma }}$. We denote the SMD of this variable as $M({\mathbf{X}}) = ({\mathbf{X}} - {\varvec{\mu }})^\text {T} {\varvec{\varSigma }}^{-1} ({\mathbf{X}} - {\varvec{\mu }})$. It can then be shown that:

• 1. $M({\mathbf{X}}) \sim \chi ^2_p$, meaning that the SMD follows a chi-squared distribution with p degrees of freedom.

• 2. There is a probability $(1 - \alpha )$ for an observation to be within the ellipsoid defined by $M({\mathbf{X}}) \le \chi ^2_p(\alpha )$. We therefore use the index $\chi ^2_p(\alpha )$ as the appropriate threshold value.

  Here, $\chi _{p}^2(\alpha )$ refers to the quantiles of the chi-squared distribution with p degrees of freedom, where $(p+1)$ is the number of satellites used in the computation. The argument $\alpha$ is the level of significance (e.g. $99 \%$), and defines the rejection level of the crossing events. Note that this is different from the false alarm rate, which instead refers to error type I [52, p. 346].

If we combine the MD [Eq. (10)] with the median ${\varvec{\mu }}_\text {med}$, we can interpret $G({\mathbf{z}})$ as the median correction field. On the other hand, combining the SMD [Eq. (9)] with the mean ${\varvec{\mu }}$, the correct interpretation of $G({\mathbf{z}})$ is the mean correction field. The accuracy of this method is measured by the expected variance with respect to a certain distribution. This means that the standard deviation field $F({\mathbf{z}})$ has to be determined. Note that the standard deviation of the widelane observation combinations depends on the standard deviations of the original $L_1$ and $L_2$ observations, which again vary with e.g. the receiver type and antennas used for the observations. For a summary of the most common linear combinations of carrier phases and the corresponding variances, see e.g. [53, Tab. 7.7]. These procedures are similar to the ones used for the corrections field itself; at each reference receiver, the standard deviation of each observed satellite has to be investigated with respect to $F({\mathbf{z}})$.

5.2.2 Interpretation of the global tests

The SMD $M({\mathbf{z}})$ is a statistical metric that measures the squared distance between some point ${\mathbf{z}}$ and the population mean ${\varvec{\mu }}$. One way to understand this metric $M({\mathbf{z}}) = ({\mathbf{z}} - {\varvec{\mu }})^\text {T} {\varvec{\varSigma }}^{-1} ({\mathbf{z}} - {\varvec{\mu }})$, is that it is similar to the Euclidean metric $E({\mathbf{z}}) = ({\mathbf{z}} - {\varvec{\mu }})^\text {T} ({\mathbf{z}} - {\varvec{\mu }})$, but deformed by the covariance structure ${\varvec{\varSigma }}^{-1}$ of the data. This has two important consequences which render $M({\mathbf{z}})$ more useful than $E({\mathbf{z}})$ for our purposes:

• 1. Even though some components of ${\mathbf{z}}$ have a larger variance than others, they can contribute equally to the SMD;

• 2. Two highly correlated random variables will contribute to the SMD more than two uncorrelated randoms variables.

In order to use the inverse of the covariance matrix ${\varvec{\varSigma }}^{-1}$ properly, these steps are recommended in practical implementations:

• 1. Standardize all the variables, that is, transform the random variable ${\varvec{Z}}$ into p independent standard normal random variables ${\varvec{X}}$.

• 2. One can eliminate the correlation effects by performing a variable transformation ${\mathbf{x}} = {\varvec{\varSigma }}^{-1/2} ({\mathbf{z}} - {\varvec{\mu }})$, since this results in ${\mathbf{x}} \sim N_p({\mathbf{0}}, {\mathbf{I}}_p)$ having a trivial normal distribution with zero mean and a diagonal covariance structure. The SMD can then be calculated as if ${\mathbf{z}}$ is transformed into p independent random variables (i.e. the elements of ${\mathbf{x}}$), where each variable follows a standard normal distribution.

5.2.3 Definition of local test statistics

The next step in the investigation process is the identification of influential residuals, and the assessment of their effects on various aspects of the analysis.

Considering the general linear model ${\mathbf{y}} = {\mathbf{X}} {\varvec{\beta }} + {\varvec{\epsilon }}$, where ${\mathbf{y}}$ is a vector of response variable, ${\mathbf{X}}$ is the design matrix, ${\varvec{\beta }}$ is a vector of unknown coefficients to be estimated, and ${\varvec{\epsilon }}$ is a vector of random disturbances. Applying a least-squares parameter estimation, we find:

$$\begin{aligned} \hat{{\varvec{\beta }}}&= ({\mathbf{X}}^\text {T}{\mathbf{X}})^{-1}{\mathbf{X}}^\text {T} {\mathbf{y}} \end{aligned}$$

(13)

$$\begin{aligned} \hat{{\mathbf{y}}}&= {\mathbf{X}}\hat{{\varvec{\beta }}} = {\mathbf{X}}({\mathbf{X}}^\text {T}{\mathbf{X}})^{-1}{\mathbf{X}}^\text {T} {\mathbf{y}} = {\mathbf{P}} {\mathbf{y}} \end{aligned}$$

(14)

$$\begin{aligned} {\mathbf{e}}&= {\mathbf{y}} - \hat{{\mathbf{y}}} = ({\mathbf{I}} - {\mathbf{P}}) {\varvec{\epsilon }} \end{aligned}$$

(15)

The error vector ${\mathbf{e}}$ can then be considered as a reasonable substitute of ${\varvec{\epsilon }}$. Note the error vector ${\mathbf{e}}$ depends strongly on the prediction matrix ${\mathbf{P}}$. It is also required that the design matrix ${\mathbf{X}}$ is homogeneous, meaning that the diagonal elements of ${\mathbf{P}}$ are equal, while the off-diagonal elements are reasonably small. For these reasons, it is preferable to use a transformation of the ordinary residuals for diagnostic purposes. That is, instead of using the error vectors ${\mathbf{e}}_i$, one may use the reduced error vectors ${\mathbf{T}}_i$, where $\sigma _i$ is the standard deviation of the $i'$th residual.

$$\begin{aligned} {\mathbf{T}}_i = \frac{{\mathbf{e}}_i}{\sigma _i}. \end{aligned}$$

(16)

In this research, we restrict the local test statistics to the normal distribution and t-distribution. Both tests are used interchangeably, and we find that they produce nearly identical results. Interested readers are referred to [54, Chap. 4] for a discussion of other tests that can be constructed for this purpose.

5.2.4 Variance monitoring

It is critical to monitor the variance of each satellite when performing GNSS NRTK calculations. For an example of how the variance changes for reference receivers, see Fig. 7.

Fig. 7

Standard deviations for the reference receivers in the network. This plot shows that the variance at each site behaves in the same way

5.2.4.1 Generalized variance

According to the large sample theory, it is clear that the correction field should be well-described by a multivariate normal distribution known as a Gaussian field. This means that the distribution should converge to this regardless of the parent population we sample from.

If we take a close look at the probability density function given by Eq. (7), it contains the prefactor $|{\varvec{\varSigma }}|$, which is also known as the generalized variance (GV) and provides a way of writing the information on all variances and covariances as a single judging number. The drawback is that the GV does not contain any information on the orientation of the pattern.

The covariance matrix contains a lot of information: the diagonal describes the variance of each observed satellite, while the off-diagonal corresponds to the covariance between them. When the generalized variance is computed, all directional information contained in the structure of the matrix is discarded. In other words, the covariance matrix is distilled down to a single number, which we can heuristically treat as the “generalized variance” of the system. In this paper, our goal is to monitor the variation of the generalized variance itself. We therefore form a time-series from the generalized variance of the sample covariance matrix ${\mathbf{S}}$, and study its variations on an epoch-by-epoch basis.

We will define a new stochastic variable $y_i = |{\mathbf{S}}_i|$, where ${\mathbf{S}}$ is the sample covariance matrix. We can then construct a time-series for these $y_i$, and thus monitor the variations over time.

Fig. 8

Computed squared total variance for baseline of 41 km between reference receivers HFSS and SAND. Year = 2013, DOY=152

5.2.4.2 Total variance

Given the sample covariance matrix ${\mathbf{S}}$, we may define the total variance as $z = {\text {tr}}\left( {\mathbf{S}}\right)$. This definition can be intuitively understood, since variance is an additive quantity, and the diagonal of the covariance matrix contains the variance of each component of the random variable. If we then construct a time-series for the observable quantity z, we can directly monitor how the total variance changes on an epoch-by-epoch basis. The total variance is attractive to investigate for instance due to the following facts:

• For any estimator e(Y) of type Linear Unbiased Minimum Variance (LUMV). The following expression [25, p. 54] holds.

  $$\begin{aligned} \mathbf{E } ( {\mathbf{x}} - e(Y) )^2&= {\mathbf{E}} [ ( {\mathbf{x}} - e(Y) )^T ( {\mathbf{x}} - e(Y) ) ]\nonumber \\&= {{\,\mathrm{Tr}\,}}\left\{ {\mathbf{E}} [ ( {\mathbf{x}} - e(Y) ) ( {\mathbf{x}} - e(Y) )^T ] \right\} \end{aligned}$$

  (17)

  The left expression of the Eq. (17) is the Bayesian risk with quadratic loss function, while the right side is the total variance given by covariance of the estimator e(Y).

• The optimization of a Kalman filter [55, pp. 216–217] is the minimization of the trace of the error covariance matrix of the state vector ${\mathbf{x}}$.

5.2.5 Link function definition

Construction of the prediction function of the rover position error is directly linked to the total variance of the error covariance matrix ${\varvec{C}}_\mathbf{err }$.

Our proposed model is the stochastic generalized linear model (SGLM). The GLM model was proposed by [56], and is an extension of the classical linear model (LM) with additional component known as a linear predictor $\varPsi = g(.)$. Note that the function g(.) is the link function.

Let Eq. (18) be the double-difference (DD) observation model of the baseline between the rover receiver and the computation point.

$$\begin{aligned} {\mathbf{y}} = {\mathbf{X}} {\varvec{\beta }} + {\mathbf{A}} {\varvec{a}} + {\varvec{\epsilon }} \end{aligned}$$

(18)

The random component ${\mathbf{y}}$ of the SGLM may come from any exponential family distribution rather than a Gaussian distribution as in case of a LM. ${\mathbf{y}}$ is a vector of Observed Minus Computed (OMC) values; ${\varvec{\beta }}$ is a vector of all parameters except the DD ambiguities; ${\varvec{a}}$ is a vector of unknown DD ambiguity parameters, ${\mathbf{X}}$ and ${\mathbf{A}}$ are design matrices.

The systematic component in GLM is computed by the covariates of ${\mathbf{X}}$, that is $\varPsi = {\mathbf{X}} {\varvec{\beta }}$. In our case, this component is linked to the uncertainty of the model.

$$\begin{aligned} \varPsi = g( \mathbf trace ({\varvec{C}}_\mathbf{err } )) = \left\{ \frac{1}{p} \sum \limits _{1}^{p} c_{ii} \right\} ^{1/q} \end{aligned}$$

(19)

where p i the number of satellites, $c_{ii}$ are diagonal elements of the covariance matrix $C_\mathbf{err }$, and $q\in \{1, \cdots ,p\}$ is a parameter. For $q=2$, $\varPsi (.)$ function is the Root Mean Square (RMS) of the diagonal elements of $C_\mathbf{err }$.

The link function $\varPsi (.)$ is stochastic due to the facts that it is a function of uncertainties of the model. A realistic definition of $\varPsi (.)$ can be any monotonic differentiable function. Since $\varPsi$ relates the linear predictor to the expected average variance, various forms of $\varPsi (.)$ are given in [56, p. 31].

Figure 8 shows the computed generalized variance for a baseline of 41 km, while Fig. 11 shows the predicted square root of the average variance. In this case $q=2$ and is the predicted RMS.

6 RTK user level phase observable integrity

One common problem with GNSS systems is that some satellite signals arrives at the user receivers with damaged data due to factors such as low signal quality, low elevation angle, multipath interference, diffraction, or scintillation. It is therefore important to inspect the raw observation data, so that signals suffering from such problems can be discarded from the processing chain at an early stage. It is especially critical that this inspection is performed before the widelane double-difference processing of the baseline.

Since GNSS users often find themselves in places with limited quality satellite signals, the optimal approach is to help these users discard the low-quality satellite data in the field, without requiring further assistance from NRTK systems that may also suffer from limited signal quality. Therefore, the raw phase observations at the users location have to be investigated for the error sources discussed above, before one proceeds with any processing of the data. In practice, this always results in some kind of trade-off between satellite geometry and accuracy. This is because if data from satellites with low elevation are included in the processing, this generally increases noise and systematic errors due to the long signal path through the ionosphere and troposphere.

Several weighting schemes based on the measured carrier-to-noise power density ratio r can be used to model this random error and the relevant distortions. [57] showed that the standard deviation of phase observations in the phase-locked loop (PLL) of a GPS receiver is a function of carrier-to-noise ratio r, bandwidth $B_w$, and carrier frequency $f_c$. Moreover, according to the SIGMA-$\epsilon$ weight model [33], the ratio r can be linked to the variance of the phase measurements using some empirical coefficients $\beta _i$. The model reads:

$$\begin{aligned} \sigma _{\phi ,i}^2 = \alpha _i + \beta _i \times 10^{-r/10} \end{aligned}$$

(20)

where $\sigma _{\phi ,i}$ is the standard deviation of the undifferenced carrier-phase observation, $\alpha _i$ and $\beta _i$ are the model parameters, and i is an index that determines the receiver type, antenna type, and frequency. Note, however, that Eq. (20) has a well-known drawback: the detection process is delayed.

This is because observations become biased when subjected to local disturbances such as multipath interference, diffraction, or scintillation. The detection of level changes caused by increasing variance, takes a time to be detected by applying the function given by Eq. (20), and the Danish method is very sensitive to small level changes.

The ameliorations are therefore carried out by the Danish method [33] in this work, because this is a robust estimator based on iterative least squares reweighting algorithm.

7 Baseline integrity

The last step in the NRTK integrity scheme is a three-step baseline computation. At the first step, we require that the double-difference ambiguity between the computation point and rover receiver is correctly resolved. For short baselines $< 20$ km, this can be done using for instance an algorithm developed by [58]. Figure 9 shows the convergence of the ambiguity and the estimated double differenced ionospheric delay as function of time.

Fig. 9

Short baseline ambiguity resolution, year = 2014, DOY=85, and baseline length $\sim 1$ km between HFSS and mobile receiver MHFS. a Upper panel shows the convergence of the double-difference widelane ambiguity resolution. b Lower panel shows the corresponding ionospheric path delay

The weighting scheme proposed by [33] combines the information inherent in the ratio r, and the double-difference residuals are then used for the local data integrity calculations. With local, we here mean scintillation [59], multipath interference, or any other environmental disturbances that affect the rover receiver. The results show that the proposed scheme significantly improves the precision of the positioning service.

In Sect. 5, a computation point is constructed corresponding to the average error level of the sub-network of reference receivers, while in Sect. 6, the carrier-phase observables are checked against outliers. After these calculations, it is appropriate to combine both quality control in the form of model residual minimization, ambiguity in the form of time-to-fix, and finally the user accuracy.

Fig. 10

Sample of global test statistics for a baseline based on 3200 epochs with a resolution of 1 s. Dashed red horizontal line determines the rejection region of the test. Year = 2013, DOY = 152

The next step is the analysis of the double-difference residuals and the corresponding error covariance matrix. Test statistics similar to the ones introduced for network data integrity, Eqs. (11) and (12) are also suitable for baseline processing. Figure 10 shows the results of the global tests used in the detection process. The shadowed rectangle is caused by the occurrence of negative variance in the covariance processing matrix, known as Heywood case [34].

The upper and lower panels of the Fig. 10 show the SMD and MD test results. The thresholds used in the detection process are 6.5 and .133, respectively. These values correspond to the critical quantile of the Chi-squared distribution ($\chi _p^2$), where $p=12$ and correspond to the number of observed satellites used in the computation at $\alpha =90 \%$ significance level.

In addition, a prediction function is obtained by using the SGLM to predict the user carrier-phase error and code statistics.

The last and final step is the computation of the user position standard deviation, and a comparison of the results obtained before and after the improvement, while conserving the geometry of the setup.

8 Implementation and analysis

In order to carry out the performance analysis of NRTK methods, and predict the carrier-phase and code statistics, an averaging variance level of the baseline processing is constructed. Figure 11 shows the predicted RMS from the double-difference error covariance matrix as a function of time. The discontinuities are caused by the reference satellite changes when resolving the ambiguities.

Fig. 11

Predicted RMS computed from the double-difference error covariance matrix. Data used in this investigation are from a baseline of $\sim 41\,\hbox {km}$. Year = 2013, DOY=152

8.1 Validation of NRTK integrity

Validation is a complex and challenging process to implement correctly, and careful planning is required in order to define appropriate validation procedures. In order to validate the implemented algorithms at both the system and the user levels, a side-by-side comparison of the candidates has to be conducted. According to [1], the accuracy of a GPS position is proportional to the product of a geometry factor and a pseudorange error factor. The geometric error factor can be described by the Dilution of Precision (DOP) parameter, while the pseudorange error factor is the User Equivalent Range Error (UERE), so one can say that the position error is proportional to $\text {DOP}\times \text {UERE}$. Thus, high values of either the DOP or UERE will result in a poor positioning accuracy.

The first step of such a validation procedure, is to compute the quality of the rover position errors $\varvec{\varDelta }_\mathbf{enu }=(\varDelta e, \varDelta n, \varDelta u)$ relative to the standard deviations $\sigma _{\varvec{\varDelta }_\mathbf{enu }}$, and to calculate the DOP without enabling the mechanisms of NRTK data integrity. The next step is to enable the network data integrity quality check and produce a list of all detected satellites on an epoch-by-epoch basis. This list is read by a software program within observations from RINEX files, excluding all data from satellites mentioned in the list, and produce new RINEX files. After that, the first step is repeated again. The geometry expressed by DOP and standard deviation of the rover position error are then re-computed, and the results may then be compared. For an illustration of results of this processing, see Figs. 12 and 13.

Fig. 12

Rover position error as function of time without enabling the quality check procedures

Fig. 13

Rover position error as function of time after removing satellites with bad data on an epoch basis. The quality check procedures are enabled at network level

8.2 Rover position error

The final product is to plot the rover position error in the horizontal plane on the receiver display. The user may then choose to either accept or reject the measurement results for the present epoch based on user requirements to acceptable error ellipse or standard deviation of total position error as illustrated in Figs. 14 and 15. Ideally, there should be no need for re-evaluating the quality of the measurements, potentially saving time for the end-user.

Fig. 14

Error ellipse displaying the rover position error in the horizontal plane. The center of the ellipse is displayed by the red point and the actual user location is given by the intersection between the horizontal and vertical blue lines. Each ellipse corresponds to the probability of acceptance of the null hypothesis $H_0$

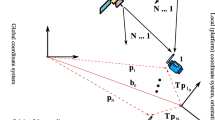
The position error vector is usually defined in a Cartesian coordinate system, i.e. $\varvec{\varDelta }_1 = (X, Y, Z)$. However, in practice, it is much more convenient to analyze the covariance matrices in a local topocentric coordinate system, i.e. $\varvec{\varDelta }_2 = (E, N, U)$ where the coordinates are given as east, north, and height (up). The transformation between these coordinate systems [60, p. 48] is then given by the orthogonal matrix T.

$$\begin{aligned} {\varvec{T}} = \begin{bmatrix} \sin (N)&\quad \cos (N)&\quad 0 \\ \sin (E) \cos (N)&\quad \sin (E) \sin (N)&\quad \cos (E) \\ \cos (E) \cos (N)&\quad \cos (E) \sin (N)&\quad \sin (E) \end{bmatrix} \end{aligned}$$

(21)

In addition, the covariance matrix ${\varvec{C}}_{\text {XYZ}}$ is expressed in $\varvec{\varDelta }_1$ coordinates and our aim is to construct the user error ellipse in a topocentric coordinate system $\varvec{\varDelta }_2$. Applying the covariance propagation law reads

$$\begin{aligned} {\varvec{C}}_{\text {ENU}} = {\varvec{T}} \ {\varvec{C}}_{\text {XYZ}} \ {\varvec{T}}^{'} \end{aligned}$$

(22)

The constructed error ellipse in the horizontal plane in a topocentric coordinate system is illustrated by the Fig. 14.

The number of observations displayed in the figure, corresponds to the correlation length of the observation combinations used to compute the rover positions. In this test it is set to 300 seconds.

Figure 15 shows the error radius given by the expression $D= \sqrt{ \left( (\delta e)^2 + (\delta n)^2 +(\delta u)^2 \right) }$ with threshold value $T_h = 4.5$ cm.

The value of $T_h = \chi _{p}^2(.05) = 4.5$ corresponds to degrees of freedom $p=11$ at $\alpha =0.95 \%$ significance level. On average, the number of observed satellites between the rover and the base receivers in this test is eleven satellites.

Fig. 15

Standard deviation of the rover total position error as function of time. The horizontal line signals the crossing of the extremal events and separates the acceptance and the rejection regions

9 Conclusion and discussions

An improvement of the rover position estimation can be achieved by applying procedures for integrity monitoring at the system and user levels in network RTK. In this paper we have presented a multi-layered approach based on multivariate statistics, where the network average error corrections and the corresponding variance fields are computed from the raw data, while the squared Mahalanobis distance (SMD) and Mahalanobis depth (MD) are used as test statistics to detect and remove inaccurate data. Quality checks are carried out at both the network system level and at the rover user level in order to reduce the impact of extreme events on the rover position estimates. The stochastic generalized linear model (SGLM) is proposed and used to predict the rover carrier-phase and code error statistics.

The methods tested makes it possible to identify satellites with bad data so these can be eliminated or down weighted in the positioning process leading to an improvement in the rover position from epoch to epoch. Tests carried out as described in the paper show that there is indeed an indication of improvement in the rover position after applying the new method.

It is expected that the suggested approach will reduce the number of wrong or inaccurate rover positions encountered by NRTK users in the field, which subsequently will lead to a more efficient work flow for NRTK users.

All test results shown in this paper are based on GPS data only, but the algorithms will work just as well with data from e.g. GLONASS or Galileo satellites.

More tests will be carried out in the future by including other constellations for instance GLONASS and Galileo.

10 Discussion and considerations on implementation

• 1. Benefit from NRTK data integrity

  Network RTK data integrity helps the user in the field. To benefit from the NRTK data integrity, use of the new RTCM 3.x [61] message types is recommended. From network data integrity, an anomaly list is produced and the list of suspicious satellites is sent to the rover. In addition, the network quality indicators shall be transmitted to the user in the field and must be displayed on the rover’s display. The quality indicators give a snapshot of the network status, that is, the quality of ionosphere and geometrical corrections for each satellite involved in the computation.

  The rover software must also be upgraded to be able to decode and use the data properly. This task requires a new software module to be implemented in the rover. Figure 16 illustrates the concept.

• 2. NRTK data integrity block diagram

  Figure 16 shows the NRTK data integrity block diagram exemplified in a case where both GPS and GLONASS are used. The anomaly list is produced, packed and transmitted in RTCM 3.x format to the user rover. The software in the rover decodes the messages and excludes data from the given satellite(s) in the solution computation. The double difference error covariance matrix is used to estimate the user position, and an error ellipse (Fig. 14) can be constructed and e.g. displayed to the user.

• 3. Data exclusion and processing

  When testing the concept for this paper, we have excluded approximately $0.1 \%$ of bad data from the computation and we have processed only the GPS data. This exclusion caused the change in both the location (mean) and the shape (variance) of the target distribution (see the Figs.  12 and  13). We have computed the standard deviation of the rover position while keeping the mean value computed before enabling the quality check procedures. The result shows that the standard deviations of $(\delta e, \delta n, \delta u)$ drop from = (6.859, 8.776, 10.872) to (6.857, 8.774, 10.870) mm. This shows that there is indeed an indication of improvement in the rover position accuracy.

  In addition, we have excluded only one satellite in the detection step. If there is more than one suspicious satellite, say two or three satellites with bad data, only one satellite with high value is removed.

• 4. Performance analysis

  The performance analysis of our NRTK data integrity is measured in terms of carrier-phase and code error statistics at the user location (position domain). The SGLM is used for this purpose.

• 5. Ambiguity resolution:

  Key for precise positioning is correct determination and validation of the carrier phase ambiguity resolution. Often, this task is carried out by a Kalman filter [55, Figure 5.8]. Kalman gain $K_k$ is involved in the computation of state vector update ${\hat{x}}^{+}_k = {\hat{x}}^{-}_k + K_k (z_k -H_k {\hat{x}}^{-}_k)$ and the corresponding error covariance matrix ${\hat{P}}^{+}_k=(I - K_kH_k) {\hat{P}}^{-}_k$. Therefore, ${\hat{P}}^{+}_k$ must be inspected for Heywood case and $K_k$ must be monitored correctly to avoid the filter instability.

Fig. 16

Design blocks of the network RTK data integrity. a The right panel shows the network integrity monitoring (NIM) quality of service (QoS) parameters generation. b The left panel shows data processing at the rover receiver

Appendix

1.1 Software development tool

Various computer programs have been developed to process the GNSS data and generate the figures in this paper. Software modules are classified into three categories, namely the network, baseline and rover receiver respectively.

• 1. Network data processing

  • NMA network SW This module is used to generate the NRTK corrections on a satellite-by-satellite basis. Data used in this test is from Rogaland region, year 2013, day of year 152 and classified as a day with high ionosphere activity.

  • Parsing the generated corrections A new C++ module is developed to parse and generate corrections, and it produces a suitable matrix format that is easy to process with Matlab, Python, or R.

    The corrections are ionospheric and geometrical (troposphere, clocks and orbit errors), obtained by forming respectively geometry-free and ionosphere-free linear combinations of the observables.

  • Satellite data exclusion A C++ program is developed to exclude satellite(s) data on an epoch basis.

  • Plots generation Various R scripts are developed and used to generate the Figs. 3, 4, 5, 6 and 16.

• 2. Baseline data processing

  • RTKLIB Open source program package for GNSS positioning developed by Takasu is used for experimentation [62].

  • Baseline processing A C program based on RTKLIB developed and used to process baseline of different length. The output are the residuals and the variance-covariance matrix.

  • Matlab script Ambiguity resolution for baseline $\le 20$ km, developed to produce the Fig. 8.

  • R scripts Scripts are developed to generate the Figs. 2 and 9, 10. Data used for this investigation are from a baseline of $\sim \,41$ km between HFSS and SAND, year=2014, and day-of-year= 85.

• 3. Rover data processing: R scripts are developed and used to generate the Figs. 12, 13 and 14.