The Complete Set of Thermo-mechanical-Radiation Methods, Simulations and Results for a Swarm of Nanorovers Deployed on the Moon’s Surface (Lunar Zebro Mission)

Abstract

Lunar Zebro’s mission is heading the race for deploying the world’s smallest and lightest swarm of nanorovers on the surface of Moon. The concept validation of a single nanorover is of crucial importance, as it will be the launching pad for deploying a swarm of those nanorovers thereafter. Then, they will get connected in a network, acting as a single device and performing scientific missions analyzing data from remote points on the Moon’s surface. In the current study, the complete set of thermo-mechanical-radiation analyses for Lunar Zebro nanorovers are carried out. These range from the Ground Segment to the Moon environment, taking also into account the extreme mechanical and thermal environment at launch-transit conditions when the nanorover is attached to the lander. An innovative ray tracing method to evaluate the effect of the thermal environment on the Lunar Zebro nanorovers is explained in this paper. Material choices, structural design, and mechanical/thermal strategies for the nanorover to overcome the launch, space and Moon’s conditions are shown. The different analyses methods used, expected loads and results obtained should serve as a baseline for evaluating the behaviour of other small devices attached to a lander when aiming for any space mission. More specifically, for those aiming to go to the Moon, the environmental and mechanical expectations here can also be implemented. The ultimate outcome of the paper is the environmental survivability assurance from an analytical perspective of these nanorovers when being sent to the Moon. The validation of the survivability of a single nanorover will be a breakthrough in the space swarm robotics’ field, resulting in the successful performance of the lightest swarm of nanorovers ever deployed on the Moon’s surface.

1 Introduction

Robotic exploration has become a hot topic for both research and industry, and an extensive work to innovate in space exploration is being carried out during the last decades [1]. Specially, the miniaturization of their different subsystems reaching performance level of bigger rovers already developed (such as Curiosity, Spirit, Opportunity, Marsokhod or Perseverance rovers) is of particular interest. For that purpose, several projects have been developed (such as Wilcox JPL Nano Rover and others [2,3,4,5,6], and extensive research is being carried out to bring space exploration a step closer to reality.

The Lunar Zebro project, presented at the 70th International Astronautical Congress 2019 in Washington (US) [7], has continued its evolution during 2019–2022 to achieve its ultimate goal: to design, build and launch the world’s smallest and lightest rover ever deployed on the Moon’s surface.

This extremely miniaturized nanorover ($270\times 330\times 100$ mm, weighting less than 2 kg with a 1.5 mm chassis thickness) is developed to showcase the viability of this design and its potential for future radio astronomy missions using a swarm network configuration. By doing that, OLFAR¹ and its newest mission [10], together with their roadmap associated projects, such as LUFAR and LOFAR [11], could become a reality and make enormous breakthroughs in science. For example, by exploring the universe’s so-called dark ages, map the interstellar medium, and discover planetary and solar bursts in other solar systems [10].

Bearing this in mind, Lunar Zebro targets to be the first student team to “walk” on the Moon by building the world’s smallest and lightest rover ever. However, the accomplishment of this goal is not straightforward. Spacecraft are subjected to extreme conditions in all of its many mission segments, which should each be carefully evaluated. Specially, the inhospitable environment provided by the Moon, imposes the most severe thermal, structural, radiation² requirements on any device when trying to remain fully functional in any type of long term mission there. Lunar Zebro nanorovers’ structure, specially its 1.5 mm-thick chassis, will be challenged to sustain launch and Moon’s conditions, as it will be shown on the results obtained.

To start with, material and methods are explained (Sect. 2). This section starts by overviewing the different simplified models and material properties chosen. Afterwards, a deep overview of the different simulation tools used for the thermo-mechanical-radiation studies is addressed: MATLAB in-house software for thermal analyses, ANSYS for thermal and mechanical analyses and SPENVIS for radiation analyses. Particularly, the in-house software developed for the thermal analysis ($R^2TM$) is explained step by step, following previous works presented [7]. This section concludes with an overview of the thermo-mechanical-radiation loads and challenges that any device for a lunar mission might face (specially, miniaturized devices such as these nanorovers). These range from Ground, Launch-Transit and Moon’s environment, giving the whole overview of the different challenges expected in space. Generally, they can be used as a formal guideline for designing devices for any space mission, specially for nanodevices and swarm robotics exploration vehicles.

Fig. 1

Different model simplifications of Lunar Zebro nanorovers for structural and thermal analysis (Real Model $\xrightarrow {}$ ANSYS Model $\xrightarrow {}$ MATLAB Model) [7]

Table 1 Lunar Zebro Nodes definition: mechanical and thermal properties. [7]

These inputs and methods are used for obtaining the results addressed in the subsequent Sect. 3. The thermal results from Ground, Launch-Transit and Moon phases are shown first (Sect. 3.1), both using ANSYS and the in-house developed software $R^{2}TM$. The results obtained suggested the most suitable spot for the nanorovers to be deployed on. Then, the mechanical results from Launch-Transit and Moon (Sect. 3.2) segments are commented. Finally, the radiation results (Sect. 3.3) are shown. All together, they give the whole environmental behaviour of Lunar Zebro nanorovers, ensuring their survivability on the Moon’s surface.

Finally, a summary of the thermo-mechanical-radiation conclusions from the work obtained is shown in Sect. 4.

2 Materials and Methods

This section gives an extensive overview of the different material and methods used throughout the paper. Results will be supported by the described methodologies and assumptions explained here. In the first place, material selection and simplified CAD models for the simulations are overviewed. Secondly, the simulation tools used for obtaining the results are introduced. These range from in-house software to commercial tools, such ANSYS or SPENVIS. Thirdly, all the different inputs (in terms of expected temperatures and/or loads) in all different segments of the mission (Ground, Launch-Transit and Moon segment) are shown. All in all, they provide a complete baseline for results replicability in other space missions.

2.1 Simplified Model and Material Selection

Figure 1 shows two different simplified CAD models of the complete nanorover’s assembly, compared to the real Lunar Zebro nanorover model. The simplified models are used to perform Finite Element Analyses (FEA) with the different software used (Sect. 2.2). A more detailed CAD model is used in ANSYS software whereas a simplified version is selected when using the in-house developed software.

Table 2 Material properties used for the simulations at Lunar Zebro

Table 1 shows the main node division to evaluate results on the nanorover. This table is the final result of multiple iterations performed on these nanorovers. Notice that each single node is divided into several ones, up to a total of more than 40,000 nodes in ANSYS software. Small nodes (like the ones needed for connecting two elements, like pins or screws) are not shown in Table 1. Duplicate components (like the different motor drive electronics or legs) are just displayed once. Multi-layer insulation’s (MLI) effective emittance ($\epsilon = 0.01$) was taken considering approximately 14 layers of MLI [12]. The bottom part of the chassis is made of Ceramic Matrix Composite (CMC), coated with a black surface to eject the heat out. The Solar Panel plate, made of CMC material as well, incorporates a thin copper layer on top, to better conduct heat throughout the solar panels’ plate. Finally, the bottom side of the Solar Panel plate is coated black as well, to evacuate the received heat.

The material properties’ data, which can be seen in Table 2, are taken from different literature references [13,14,15,16]. Some other properties are taken from CES Edupack [17]. Notice that some material properties are dependent on the temperature. The expected range of temperatures experienced by the nanorover during its mission range from $-180$ to $130\,^{\circ }\text {C}$ [18], and because of this huge $\Delta T$, it is necessary to consider the evolution of material properties with respect to the ambient temperature. For visualization purposes, Table 2 shows just the average of the material properties. For anisotropic materials (like Ceramic Matrix Composite), the properties along the fiber direction are shown first, and then the transverse and out of plane ones.

It is worth mentioning that a spacecraft passive thermal control system (PTCS) strategy has been sought during the whole thermal analyses, as being one of the requirements for the mission. Some of those strategies can be seen in Table 1. By doing that, not only the simplicity of the lunar vehicle increases, but also lowers the probability of failure and the overall cost; a remarkable requirement in any space mission composed of multiple devices. Most of the strategies follow the guidelines of ’Thermal Control of Spacecrafts’, by Peter Fortescue [13]. In general, the PTCS strategies applied can be summarized as:

• 1. Optimized design and positioning of the internal parts, to avoid unnecessary heat concentrations/cold areas or ineffective heat paths.

• 2. Appropriate control of emissivity/absorptance properties of the different color surfaces and protecting layers to evacuate/take in heat better, or to protect the spacecraft from adverse environment conditions.

• 3. Enhance/decrease of the thermal conductance for the different parts that are joint together, by means of insulators or heat pipes.

2.2 Simulation Tools

Three different software tools have been used to get the complete overall behaviour of the nanorover and analyze the whole mission: MATLAB (thermal analyses). ANSYS (both thermal and structural Analyses) and SPENVIS (radiation analyses).

2.2.1 MATLAB: Thermal Simulation Tool

Thermal analyses are performed by implementing an in-house thermal mathematical model (TMM) in MATLAB (denoted as “Thermal Approach 1”) and ANSYS (denoted as “Thermal Approach 2”). For approach 1, a New Ray Tracing Method called $R^{2}TM$ is explained, as being one of the core parts of the TMM and introducing new techniques from already implemented software methods’. Thermal approach 2 simulations have been carried out to verify the results obtained, assess the sources of discrepancy in both approaches and enhance the scope of knowledge of the nanorover behaviour. These are overviewed in Sect. 2.2.2.

Approach 1 is based on a set of isothermal nodes, (Table 1). These interact with each other and with the environment, by means of radiation and conduction. Atmospheric convection terms are negligible due to the low atmospheric density present on the Moon’s surface, and therefore are not included.

Radiation heat exchange, although being less effective than other heat exchange methods such as conduction (see Eq. 1), is of equal importance to properly assess a realistic behaviour of any device in the space environment [13], and therefore a major effort has been devoted to accurately calculate them.

As several thermal models have been already implemented for commercial and scientific purposes, some of them being specific for space applications [19,20,21], this subsection is mainly focused on the novelties that this TMM offers compared to those thermal models, together with the strategies used to simulate a rover’s (instead of a satellite’s) thermal behaviour and study its performance in different scenarios. Notice that any other type of computing software can be used instead of MATLAB to configure this model, and a step-by-step guide is included to do so.

${R^{2}TM}$ (Ray Tracing Method) Implementation

Complex algorithms have been implemented to solve surface to surface radiation problems. Some of them using Monte Carlo tracing [22, 23], and/or complex algorithms for an accurate representation [24]. However, computational efficiency and straightforward implementation are the main motivation factors for using this Ray Tracing Method instead, getting results within an acceptable tolerance range for any kind of thermal simulation. An unique parameter (known as PRM: Precision Ray Method) is set up to balance precision and simulation time, allowing the user to perform a trade-off analysis depending on the simulation requirements. A detailed guide of how it can be implemented is described in the following steps. Figure 2 shows a sequence flow diagram which summarizes these steps.

Fig. 2

Implementation algorithm sequence diagram of $R^{2}TM$

Table 3 $R^{2}TM$ (Ray Tracing Method) inputs and recommended values

Fig. 3

$R^{2}TM$ Ray Tracing Visualization (a) 2D Representation of $R^{2}TM$ dealing with opacity and different nodes, using the implementation explained in section (b): general 3D Ray Tracing in sphere directions. Each node throws rays in a sphere shape centered in its CG to compute VF with respect to other nodes. Points within the nanorover represents the CG of each corresponding node

• 1. $R^{2}TM$ Inputs implementation(Table 3): where NPoints refers to the discretization of each node as a set of points. NCurves are the number of curves (i.e. rays) that will be generated in each node for computing the View Factors, Lmax is the ray length (a security factor of 1.5 times MD—Maximum Distance: the length between the two farthest situated points in the model—is recommended to ensure that every ray is capable of reaching the furthest node), VFERR is the distance between the ray and node in which it is considered they have touched each other (i.e. the error in distance allowed for considering contact) and RLPoints are the set of points which compose the discretization of the ray that is traced.

  For this model, parallelepipeds (straight or tilted), cylinders and spheres are used. When doing the discretization, it is recommended to keep and preserve the distance between points in all nodes. Therefore, bigger nodes are meshed with more points. Errors when computing conductivity between different nodes are avoided by doing so.

• 2. Far Away Distance (FAD) calculation: for each node (called ‘reference node’ when used), the distance with respect to the other nodes is computed, based on the position of their Center of Gravity (CG). This distance determines which node should be considered first when getting the View Factors with respect to the reference node, saving computational time and enhancing the precision of the method.

• 3. Rays Vector’s Direction (RVec) calculation: the direction of the ray is calculated, and discretized as a set of points. Several approaches can be used here. For example, random ray’s directions can be generated using Monte Carlo ray tracing simulations [22, 23]. In this analysis, the rays are generated from the CG of each node following the shape of a sphere, to make sure that all 3D space locations are considered (similar strategy as the one used in other literature studies [24]). Figure 3 shows graphically the ray tracing strategy used for that purpose. Regardless of whatever method is used, the number of direction is recommended to be $\mathcal {O}(PRM)$. Notice that this parameter can be higher if more accuracy is needed (see Sect. 3.1.4).

• 4. Rays tracing: for each node at its CG, for each ray generated and starting from the first point of the ray, the distance between any point of the discretization of the first considered node (order given by FAD) and the position of the ray length is calculated (CG-R distance). That distance is compared with VFERR, to consider or not contact between them:

  • (a) Case 1 (CG-R < VFERR): the ray has reached a node, which means that the View Factor between those two nodes in that direction exists. The value (n+1) is then stored in a matrix using a consistent formula that should depend on the parameter already defined NCurves:

    $$\begin{aligned} VF_{i,j} (n+1) = VF_{i,j} (n) + \frac{1}{NCurves} \end{aligned}$$

    (1)

    The simulation for that vector direction is completed and the next direction is considered.

  • (b) Case 2 (CG-R > VFERR): in that case, it is considered that the ray has not reached the node. As a result, the next closest node is chosen and the distance is compared. If “Case 1” is not achieved for any of the other nodes, the consequent point of the ray discretization is considered and compared. If it is unsuccessful once more, this ray has not reached any node and no VF coefficient is added. The next direction is considered and the process starts again.

Now that all steps are explained, the scheme working method is summarized in the following lines (take Fig. 2 as a reference): after having prepared the set-up for the model (Step 1), FAD shorts out the nodes surrounding the reference node according to its relative distance (Step 2). Then, the ray directions are generated as a set of points following user’ defined directions (Step 3). Subsequently, a ray is traced from CG of reference node, in RVec direction. In each ray discretized point, CG-R < VFERR condition is checked, starting on FAD order and taking $N^{*}=N-1$ nodes (i.e. all nodes expect the reference one). If that condition is reached, a VF is associated for the combination of ij nodes using Eq. 1. The next ray is then traced and the process repeated. If not, the next point of the discretization of the ray is used, until it reaches either CG-R < VFERR condition or Lmax. If Lmax is then reached without CG-R < VFERR condition, (situation of Figure 3 in the lower ray), then Eq. 1 is not used and the next ray starts. This process is repeated for all nodes of the model.

Conductivity Areas An estimation of the conductivity area between nodes is also implemented. The following method introduced is simply a variant of the already explained $R^{2}TM$ method, and shows powerful parallel applications of that novel strategy:

Table 4 Conductivity inputs and recommended values

• 1. Inputs to implement Conductivity touching areas (Table 4): where the only new parameter introduced is CERR: the distance between the point of Node i and the point of Node j from which those points are considered to be joint together (and, therefore, they transfer heat by conduction). The initial value recommended is 0.1 times the minimum distance between two discretization points (Dmin).

• 2. ‘Far Away Distance’ (FAD) calculation: same approach as in Sect. 2.2.1, saving computational time and enhancing method precision.

• 3. ‘Distance Comparison’: for each node, starting from the first point of its discretization, the distance between this point and the ones from the closest node (given by FAD), is compared. If it is lower than CERR, these points are considered to be touching each other. The amount of points having contact with the other nodes is stored (Touching Points: TPoints), and then the Conductivity Area (Acond) is computed as follows:

  $$\begin{aligned} Acond = \frac{AreaT \cdot TPoints}{NAreaPoints}, \end{aligned}$$

  (2)

  where AreaT is the sum of the areas of the 3D node. This area is scaled by the ratio between the number of points that are considered to be in contact (TPoints) and the number of points that the total node area is composed of (NAreaPoints). Notice that the inner points do not count for area calculation, and, as a result, it is necessary to just consider NAreaPoints and not NPoints.

Additional ${R^{2}TM}$ applications

Apart from computing the VF between nodes by radiation and conductivity areas, other interesting applications can be found by implementing small changes into the already defined set-up. In this case, this method has also been used to assess the different areas receiving heat from the Sun or the Moon. To do so, a ’Visual Heat Factor (VHF)’ coefficient is computed, which scales the node’s area to get the proper one subjected to this external heat source. The Sun and Moon’s surfaces are defined as other nodes which throw rays into the nanorover position. Depending on the number of rays that reach a certain node, this coefficient is calculated. Figure 4 shows the directions defined for computing heat areas from the Sun (rays are traced from the expected Sun position to the surface area behind the nanorover). The same approach is used for computing Moon’s albedo and Moon’s planetary radiation. In this case, rays are traced from the Moon’s surface area behind the nanorover to a virtual ceiling covering the nanorover at a certain altitude.

Fig. 4

Solar VHF calculation: rays traced from the Sun towards the surface area behind Lunar Zebro nanorover

2.2.2 ANSYS: Thermal and Structural Analyses

On one hand, ANSYS (Approach 2) has been selected, to crosscheck MATLAB results from Sect. 2.2.1 and to further explore the thermal overview of the Lunar Zebro nanorovers; making use of its powerful thermal analysis and meshing capacity (Thermal Approach 2). On the other hand, ANSYS is used for structural simulations, using general guidelines and standards [25].

In fact, a rover (or nanorover) is a very special spacecraft which does not either rotate around any celestial object nor travels through space. Consequently, ANSYS (although it is not meant to be a software for space applications) comes out as a suitable tool which can accurately model a rover behaviour if the correct set-up and boundary conditions are applied.

As structural analyses do not differ too much from space-earth applications using ANSYS software, an overview of how actually ANSYS can simulate the space thermal environment is highlighted. For structural simulations, it is recommended to follow the guidelines explained in [25], using Structural, Explicit Dynamic, Vibration and Harmonic Responses ANSYS modulus.

In contrast to MATLAB, each node is not considered isothermal but it is meshed into a mixed triangular/squared grid, to refine the results and get an overview of the heat distribution within each node. As remarked before, the mean values of the heat distribution within each node are taken into account when comparing with Sect. 2.2.1.

Different algorithms can be incorporated to enhance ANSYS capabilities and make it suitable for the research purpose. In this case, a Radiosity Solver for the WB Simulations has been incorporated, following the guidelines given at [26]. This new solver is capable of including the radiation exchange between surfaces, making results more accurate and comparable with Approach 1. Within this solver, Hemicube method is used the compute VF coefficients in 3D [25].

Once the geometry is defined and the thermal parameters introduced, transient thermal simulations are carried over. The correct selection of boundary conditions is essential to simulate a realistic environment taking into account all possible heat sources. Notice that the conduction between nodes is already defined when assigning the contacts in the geometry.

Thermal Boundary Conditions The different boundary conditions applied are the following:

• 1. Internal volumetric heat: nodes that dissipate heat are considered to do it uniformly around its surface. Notice that only when the operative range is reached, these devices are switched on and this internal heat is considered. These values are found in Table 1.

• 2. Radiation between surface–environment: surfaces of external nodes (the ones that are in direct contact with the environment) exchange heat with the environment by radiation.

• 3. Radiation between surfaces: this type of radiation needs to be defined either by a single set of surfaces or within a surface package (several surfaces subjected to the same time of radiation defined by an equivalent cross emissivity factor). Considering the increment in simulation time when more radiation boundary conditions are included (which are nonlinear), only the most relevant radiation heat exchanges (the ones expected to have a greater VF between them) are implemented.

• 4. Heat flux applied to surface: when defining the heat coming from the Sun or the Moon, an external heat flux applied to a certain surface is simulated. Notice that this value should be scaled by the material’s absorptance (which is defined by the node’s surface color), and the Cosine Losses coming from the relative position between Sun/Moon and rover, already addressed in Approach 1. To assess the Cosine Losses from the relative position between Sun-Rover, it is considered that, at a latitude of $0^{\circ }$ in the peak hour (Fig. 5), there are no losses. Then, for any other temperature of the Moon surface that is lower, a linear scaling cosine loss factor is calculated taking into account this temperature difference with respect to the one in the peak hour: $109\,^{\circ }$C.

• 5. Surface at a certain temperature: some nodes need to be set at a certain temperature, like the Moon’s surface (data taken from [18]), to simulate the heat conduction and the radiation heat exchange between legs and Moon.

Fig. 5

Moon’s temperature evolution for several latitudes (data taken from Diviner Lunar Radiometer experiment, [18]) in a full Moon’s rotation period

2.2.3 SPENVIS: Radiation Analysis

Although Lunar Zebro is aimed to go on a 14 days mission and therefore the expected radiation dose (i.e., exposition to high energy particles coming from outer space) is not significant enough for this mission’s duration, its effects are also analyzed. Indeed, as one of the possible payloads of the rover is a dosimeter, how much radiation can get to the inside of the rover (through its 1.5 mm aluminium chassis shield) is analyzed. If the results show that the chassis will block most of the expected radiation, then this payload will have to be placed outside the rover, (which will impact the mechanical and thermal behaviour of the nanorover).

For that purpose, radiation is studied using SPENVIS software. SPENVIS (SPace ENVironment Information System) is a software from ESA which is accessible online and that allows to model the space environment and its effects. These include cosmic rays, natural radiation belts, solar energetic particles, among others. The different recommended practices from the ECSS Standards [27,28,29] were followed while working with the software.

2.3 Thermal Environment

Now that the software tools have been explained, the environment of the nanorover throughout all the mission phases is shown, starting from the thermal phase. These inputs will be used to obtain the results shown in Sect. 3.1.

2.3.1 Ground Segment

The Ground Segment begins at the moment of manufacturing, until the moment the nanorover is integrated into the lander. Within this period, the nanorover may be stored for a couple of months at a long-term storage facility, at a different storage temperature range. The main goal here is to address the final temperatures of the nanorover, considering different scenarios. This information is needed because this set up will be replicated in a thermal vacuum chamber in a later stage of the project, to assess the differences between the two numerical models and the experiment. For that purpose, it is necessary to collect data from the software simulators over a large range of $\Delta T$ that can be experimentally tested afterwards to compare the results obtained. Tables 5 and 6 shows the several thermal scenarios defined in this segment.

Table 5 Ground segment, scenario 1: lower to upper electronics operative temperature

Table 6 Ground segment, scenario 2: upper to lower electronics operative temperature

Table 7 Launch-transit segment scenario

In this scenario, the nanorover is supposed to be surrounded by a virtual box, which represents its environment (e.g. the clean room where it is being assembled). It is modelled as a node with an infinite³ thermal capacity and initiated at a specific temperature. Due to this thermal capacity, the walls do not change the temperature, and they communicate their heat by radiation to the nanorover, being completely isolated from the outside and getting the required environment for the simulation.

2.3.2 Launch-Transit Segment

Launch-Transit Segment starts once the nanorover is dispatched to space within the rocket and ends when the nanorover is about to be deployed on the Moon’s surface. The main goal here is to address the time needed for the nanorover to cool down to such surrounding temperature. That time will be critical to assess the temperature stresses being present in the nanorover, being one of the sources of thermo-mechanical stresses (Sect. 2.5). Furthermore, in the worst scenario, the nanorover is assumed to be stored outside the lander, being subjected to free space and to a quick temperature reduction. In quantitative words, the nanorovers are supposed to be exposed to an uniform overall temperature condition of $-180\,^{\circ }$C, starting at the temperature of $20\,^{\circ }$C (as this is the environmental temperature in the launcher at the start of the lift-off). The electronic devices will be switched off during this segment to prevent any damage.

The same approach as in Sect. 3.1.1 is used to simulate the nanorover environment. The scenario simulation set up and results are displayed in Tables 7 and 10. Data obtained in the results from those scenarios will be compared with the experimental results (Sect. 4.4).

Fig. 6

Expected loads for Lunar Zebro nanorovers when placed into the lander. Qualification vibration loads are 1.25 times the flight loads. a Normal Sinusoidal vibration loads. b Parallel Sinusoidal vibration loads. c Shock vibration loads. d Normal Random vibration loads. e Parallel Random vibration loads. f Acoustic loads

2.3.3 Moon Segment

Because of the landing spot constraint, it is necessary to evaluate the thermal behaviour of the nanorover at several Moon’s latitudes. The main goal here is to achieve the greatest operational time of the nanorover depending on the final latitude spot. This is not straightforward, as the Sun heat flux reaching the Moon is also hourly dependent, varying the environment temperature over time accordingly. Figure 5 shows the different temperature ranges in a full Moon’s rotation period (27.3 Earth days), for the different latitudes in which the nanorover is considered to be possibly deployed by the lander. Data extracted from the Diviner Lunar Radiometer experiment [18].

Once the nanorover is released from the lander, it is expected to be heated to a temperature range in which the electronic devices are capable of operating normally. Then, the nanorover will start moving until the temperature is close to their upper operability thermal limit. When it is the case, the nanorover will return to the Moon’s shadow area to cool down or it will wait until the environment temperature is low enough for the nanorover to operate.

On the Moon’s segment, the whole thermal simulation model comes into play (making use of the already defined VF, VHF, conductivity areas and all boundary conditions selected). Nodes are set to start exchanging heat between them and the environment at a certain initial temperature. In Approach 1, to simulate the heat exchange between nanorover and Moon’s surface, the latest one is modelled as another node with an infinite⁴) thermal capacity that starts at a specific temperature corresponding to the Moon’s surface.

The operative time of the nanorover is evaluated taking into account all these variable factors over time for three different latitudes ($0^{\circ }$, $40^{\circ }$ and $80^{\circ }$), for a starting temperature of $-180\,^{\circ }$C and considering that it is deployed at Moon’s midnight time (so it is subjected to the heating phase of the Moon, where it can be operative as soon as the lowest temperature limit of the electronics is achieved: $-25\,^{\circ }$C ). By analyzing the results obtained, it will be decided which latitude is more appropriate for deploying the launcher, judged by which latitude can give the largest operating time.

Section 3.1.3 shows the results obtained and the most convenient latitude for the nanorover’s deployment.

2.4 Structural Environment

Now, the different mechanical loads that the nanorover is expected to be subjected to throughout the mission are overviewed. The results obtained using these conditions are shown in Sect. 3.2. Notice that the Ground segment does not impose any load on the nanorover, and therefore it is not considered here.

2.4.1 Launch-Transit Segment

From a structural point of view, the Launch-Transit Segment is the most severe one for any payload mounted to a lander. Vibration loads are coming from different sources, together with a progressive pressure decrement throughout the ascending procedure. The nanorover will be attached to the lander by a Frangibolt found at its top.

It is especially important to simulate the nanorover with these loads before going to any real prototyping phase, to ensure their suitability for the lander and the viability of the design to be part of a space mission. Figures 6 and 7 show the input loads applied to the nanorover during launch. An approximate duration of 2 min of load per axis is expected. Shock Loads are coming from different events during launch, such as lander separation, landing, or fairing release. Lunar Zebro nanorovers are evaluated in all that range to ensure their survivability during launch.

Loads during the launch period are based on the expected thermo-mechanical conditions when Lunar Zebro nanorovers are located in the lander. Although small differences can be found from lander to lander, these loads can be used as a baseline of any device willing to be part of a space mission in a lander. Notice that these loads already take into account the mechanical interface between the rover and the lander, so they are the actual loads expected.

From a thermo-mechanical perspective, it is also important to take into account the different stresses coming from the thermal expansion of the different materials. The nanorover will cool down progressively from environmental conditions to $-180\,^{\circ }$C (as it was explained at Sect. 2.3.2), and it is expected to be heavily stressed because of that. ANSYS software has been selected to simulate the nanorover in this extreme environment, using their different submodules (static/dynamic structural and thermo-mechanical coupling loads).

Using this setup, the maximum stress and strain in the different parts of the nanorover has been post-processed and the results can be seen in Sect. 3.2.1.

Fig. 7

Longitudinal and Lateral acceleration loads expected for Lunar Zebro nanorovers in the lander, coming from the different flight events. The minus sign with longitudinal loads indicates compression. Lateral loads might act in any direction simultaneously with longitudinal loads

Table 8 Results from ground segment scenario 1: heating (PRM = 30)

Table 9 Results from ground segment scenario 2: cooling (PRM = 30)

2.5 Moon Segment

On the Moon’s segment, the nanorover will experience significant stresses in two possible scenarios.

The first one is the deployment from the lander. It is expected that the nanorover will have to experience a 1.5 m deployment fall from the lander. Using that information, the nanorover has been simulated against that fall using ANSYS Explicit Dynamic’s analyses. Moreover, the nanorover has been tested for higher altitude falls (4 m), in case it is trapped in an unforeseen event throughout its Moon’s journey.

The second one is the thermal stresses coming from the extreme temperature of the nanorover on the Moon (Fig. 5). The results from these loads can be found in Sect. 3.2.2.

2.6 Radiation Environment

Lunar Zebro nanorovers will be protected while it is within the selected lander, but it is not guaranteed that it will be when it is attached to the outside of the lander. As an example, Blue Origin’s landers have their payloads placed outside, in direct contact with the free space. In that case, radiation damage may occur not only when the nanorover is already on the Moon’s surface, but also on its way to the Moon. This analysis is considering this worst case situation in which the nanorover will be affected by any kind of radiation starting at launch-transit segment. As a result, the starting point for receiving radiation will be from the Launch-Transit segment to the end of the mission on the Moon’s surface.

CREME-96 model is used to analyze Solar Particle peak fluxes and ISO 15390 GCR model for evaluating Galactic Cosmic Ray (GCR) fluxes. The results obtained can be seen in Sect. 3.3.

3 Results

3.1 Thermal Analysis Results

Results from all mission segments are introduced here, taking into account the assumptions and environmental conditions explained in Sect. 2.3.

3.1.1 Ground Segment

Tables 8 and 9 show the results obtained. Temp_SS references to the temperature when it reaches steady-state, Time_SS is the time it takes to be in that situation and r.error is the relative error between the two approaches. The temperature range between $-25/40\,^{\circ }$C ($Range_{Temp} = 65\,^{\circ }$C ) has been used to estimate the relative error in temperature:

$$\begin{aligned} r.error_{Temp} = \frac{| MATLAB_{Temp} - ANSYS_{Temp} |}{Range_{Temp}} \end{aligned}$$

3.1.2 Launch-Transit Segment

Table 10 shows the obtained results from a thermal point of view in the Launch-Transit segment. As it can be seen, a great correlation between the two methods is again obtained, validating the implemented Approach 1.

3.1.3 Moon Segment

Figure 8 shows the results obtained by making use of the strategies explained in Sect. 2.3. For clarity purposes, just Approach 2 results are displayed, which are the ones considered as the reference. The electronics’ temperatures are displayed, as they are the ones restricted the most in terms of operating temperature (range from $-25$ to $40\,^{\circ }$C ). Approach 1 manages to follow this trend within 10% of error in time and temperature.

Table 10 Results from Launch-Transit segment: time needed to reach steady-state temperature with the environment (PRM = 30)

Fig. 8

Lunar Zebro nanorovers’ thermal results. a nanorover’s electronics average temperature at different latitudes of Moon’s surface, for an electronics’ temperature operating range from $-25$ to $40\,^{\circ }$C in a full Moon’s rotation period, b: temperature of the different components of the nanorover at the preferable latitude of $80^{\circ }$ in a full Moon’s rotation period

Table 11 shows the total time (in hours) that the nanorover can be operative on the Moon’s surface, (as it remains within the operative temperature range for the electronics during that period) for the three different latitudes evaluated, using results from Fig. 8.

Therefore, the preferable landing spot is $80^{\circ }$, as it can presumably remain operative 39.21% of the time. Other latitudes will offer a shorter operative time, roughly 50% less. It is clear that the landing spot makes a significant difference in terms of the operating time and influences the overall mission. Taking into account the solar panel’s recharge time and the number of hours Lunar Zebro nanorovers will be exposed at $80^{\circ }$ latitude, deploying at the latitude will be successful for the mission. Experimental analyses will be carried out as part as the future work to validate the assumptions taken (Sect. 4.4).

Figure 8b shows the evolution of the different temperature components for this preferable latitude of $80^{\circ }$. A significant thermal inertia can be appreciated during the cold phase, as the nanorover does not follow exactly the temperature drop of the environment it is surrounded by.

Table 11 Lunar Zebro total operating time and its percentage value with respect to the total time, in a full Moon’s rotation period of 27.3 Earth days (655.2 Earth hours), for an operative range from $-25$ to $40\,^{\circ }$C

3.1.4 Computational Time

From a computational point of view, Approach 1 converges at an average time of less than 30 min (for a PRM value equal to 30). This time depends on the mission segment, being 30 minutes maximum on the Moon segment and less than 10 min on Launch-Transit and Ground segments. On the other hand, Approach 2 needs around 8 hours to reach the same state. This result is compared using the same computer device, running at the maximum number of cores possible in both cases. That means: MATLAB TMM (Approach 1) is at least 16 times more computationally efficient than ANSYS (Approach 2). It is thought that the Approach 1 results could be refined even more, reducing this error discrepancy. However, the computational time is heavily affected, using approximately the same computational time as in Approach 2.

Fig. 9

Stress vs strain of the different parts of the Lunar Zebro nanorover coming from: a Sinusoidal vibration loads (normal and parallel), b shock vibration loads, c Random vibration loads (normal and parallel) d acoustic loads, e lateral and longitudinal accelerations, f thermal expansion loads

3.2 Mechanical Analysis Results

The results from a mechanical point of view are also divided into the different segments of the mission. However, Ground segment loads are not considered so the nanorover starts being simulated when it is already prepared in the lander to take off (Launch-Transit segment). These are the outcome of multiple iterations from a mechanical design, using different materials, multiple dimensions’ values, and diverse location of the components. Ultimately, they prove the suitability of the nanorover for launch conditions when being attached to the lander and on the Moon’s surface.

Fig. 10

Stress vs strain of the different parts of the Lunar Zebro nanorover because of the free-fall at the lander’s deployment phase on the Lunar surface: a 1.5 m fall, b 4 m fall

3.2.1 Launch-Transit Segment

Launch-Transit segment results are obtained using the methods explained in Sect. 2.4.1, from the expected loads in Figs. 6 and 7. The results are shown in Fig. 9. Log-log “Max Stress VS Max Strain” plots are displayed, indicating the three possible zones in which these values can be. Notice that, ideally, these results should follow the individual material Stress vs Strain plots. The different regions (green, yellow and red) have been identified only for visualization purposes. The red zone limits are delimited taking into account the ultimate stress of the most conservative and relevant material in Lunar Zebro (Table 2), and their correspondent strains. The yellow zones’ limits are identified using a safety factor margin from the red zone:

• 1. Green zone: the loads do not suppose any challenge neither in Stress or Strain. The nanorovers’ node is capable of sustaining those loads without any problem.

• 2. Yellow zone: the loads suppose a challenge either in terms of stress or strain. However, the nanorovers’ node should be still capable of sustaining them, proven they do not increase in value.

• 3. Red zone: the loads are a challenge for the nanorovers’ node. When possible, it should be avoided to have the nanorover under these conditions. A long exposure of those loads can lead to its mechanical collapse. Experimental tests are needed to verify their behaviour under these conditions.

As a different temperature range is expected at launch conditions (between 0 and 27 $^{\circ }$C), the nanorover is simulated for these loads over that range of temperatures. The maximum values over that range are displayed.

The results show that under sinusoidal loads the nanorover normally behaves in low stress conditions, except for the antenna. Although it should be capable of sustaining these loads, experimental tests will confirm its final behaviour.

Random vibration loads, although higher than the ones found in the previous sinusoidal vibration loads, are still in the green and yellow areas, which means that the current design will be capable of sustaining those loads. Under shock conditions, the nanorover will experience the highest stresses and strains in all components. To assess the suitability of the design, the nanorover will be tested experimentally, as part of the future work of the project. The results obtained will determinate how well the nanorover can actually sustain these loads. The expected performance, according to these results obtained, is that the nanorovers of Lunar Zebro mission will be capable of surviving with the current design (as the loads do not reach the red area). Neither lateral and longitudinal accelerations nor acoustic loads suppose a challenge for the rover. For the thermal expansion loads (Fig. 9f), the worst case scenario is taken, which corresponds to the deployment of the nanorover on the Moon’s surface. This is further investigated in the next section.

3.2.2 Moon Segment

The results from the loads expected on the Moon’s segment (as explained in Sect. 2.5), can be found in Fig. 10 (deployment loads). These loads should be combined with the thermal expansion loads of the rover (Fig. 9f) as, initially, both might be coupled together. As in Sect. 3.2.1, Log-log plots of “Max Stress vs Max Strain” are shown.

On one hand, it can be seen in Fig. 10 that the nanorover will experience significant stresses for a vertical deployment at 1.5 m height. Although most of the nanorover’s nodes are in the yellow area (acceptable load level), the electronics will be significantly stressed during that period. Because of the simplified model used for the simulations, which trades off computational time and accuracy, the electronics are not fully designed and incorporated in the model (i.e., the different clips, heat sinks, capacitors, and so on). As a result, it is necessary to perform experimental tests to check how well the electronics can sustain that hit.

In Fig. 10, it can be seen that, for any deployment at a greater altitude, the electronics will not withstand the loads that are caused by it. The electronics will be stressed at the most, and the overall mechanical behaviour of the nanorover will be at maximum acceptance stress. On the other hands, Fig. 9f shows that the nanorover will experience high stresses because of the thermal expansion and the extreme temperatures in the Moon’s surface. Specifically, the maximum stresses will be found at $-180\,^{\circ }$C.

Increasing the chassis thickness and other mechanical strategies changing the design do not contribute significantly to reduce those stresses. Although they are still in the yellow area, the problem relays on those thermal stresses (Fig. 9f) combined with the deployment hit (Fig. 10). For that purpose, it has been concluded it is necessary to wait in the lander until the temperature in the nanorover goes closer to Earth standard conditions (around 22 $^{\circ }$C)⁵ By doing that, thermal stresses will be released from the nanorover before the deployment phase, ensuring the survivability of the nanorover in that challenging condition.

3.3 Radiation Results

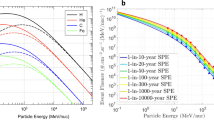
Figure 11 shows the radiation dose in the nanorover as a function of its chassis aluminium thickness.

On one hand, it can be seen that the radiation dose of the nanorover decreases around one order of magnitude from no shield to 1.5 mm chassis thickness’s shield. The reason is that protons are blocked out in that thickness and therefore not captured by the sensor if placed inside. Afterwards, it remains practically constant over the first 10 mm aluminum thickness of the nanorover’s chassis.

On the other hand, it is seen that an aluminum chassis with a thickness of around 19 mm mitigates most of the radiation. Only Bremsstrahlung (or braking) radiation, remains unavoidable regardless of the aluminum protection layer’s thickness. Notice that this radiation is the one coming from the deceleration of charged particles (which includes synchrotron radiation, cyclotron radiation and beta decay [28]). However, as explained throughout the paper, Lunar Zebro is planned to go to a 14 days’ mission and using a radiation shield of 19mm is not considered as it will heavily impact the cost and mass budget of the mission.

Fig. 11

Lunar Zebro Radiation Dose for the total mission time as a function of its aluminium chassis shielding thickness. Data extracted from SPENVIS software

4 Conclusions and Future Work

The main conclusions are depicted from a thermal, mechanical and radiation point of view:

4.1 Thermal Conclusions

• 1. Implementation of $R^{2}TM$ in-house software thermal mathematical model (Approach 1) for all thermal segments (Ground, Launch-Transit and Moon), capable of reproducing results within %10 of accuracy in all segments and at least 6 times faster than ANSYS (Approach 2).

• 2. Validation of $R^{2}TM$ in-house software using ANSYS software (discrepancy less than 10% in all scenarios, Tables 8, 9, 10 and Fig. 3.1). Therefore, it can be used for future missions and refined analyses.

• 3. Solar Panel plate needs a high conductivity, and a copper layer is added to the CMC material. By doing that, the temperature is homogeneous throughout the solar panel plate, getting uniform efficiency of the Solar Cells (Sect. 2.1).

• 4. The bottom part of the Solar Panel plate needs to be coated black to radiate the heat out from the Sun’s heat flux (Table 1).

• 5. White MLI is covering the chassis of the nanorovers with an effective emittance of $\epsilon = 0.01$, except for the bottom part of the nanorovers, which is a black surface to eject the heat out (Sect. 2.1).

• 6. Final material’s coating for the different parts of the nanorovers (Table 1) is obtained.

• 7. Evolution of the nanorovers’ temperature in all different scenarios (Ground Segment: Sect. 3.1.1, Launch: Sect. 3.1.2 and in the Moon’s surface: Sect. 3.1.3), for different scenarios and latitudes (when applicable): Tables 8, 9, 10 and Fig. 3.1.

• 8. Ideal deployment latitude for Lunar Zebro nanorovers (80$^\circ$), to remain operative approximately 40% of the lunar daytime (Table 11).

• 9. Thermal results to compare with experimental tests: Tables 8, 9.

4.2 Mechanical Conclusions

• 1. Mechanical environment of the nanorovers at launch conditions (Figs. 6, 7).

• 2. Final material selection of the different parts of the nanorovers (Table 1), including their material properties (Table 2).

• 3. Final position of the elements in the nanorovers (Fig. 1).

• 4. Behaviour of the nanorover for all expected loads at launch conditions, including the thermo-mechanical behaviour of the nanorovers in terms of the component’s thermal expansion (Fig. 9).

• 5. Behaviour of the nanorover when being deployed in the Moon’s surface: deployment load of 1.5 and 4 m height, (Fig. 10).

• 6. Lunar Zebro nanorovers should not undergo falls greater than 1.5 m height, to preserve its operability and structural integrity.

• 7. Lunar Zebro nanorovers should wait in the lander until its temperature reaches Earth standard conditions, to relieve the stresses coming from the thermal expansion. By doing that, a coupling between stresses coming from thermal expansion and drop impact will be avoided.

• 8. Mechanical and environmental survivability assurance of the nanorovers during all conditions of the space mission.

4.3 Radiation Conclusions

• 1. Radiation does not suppose a limiting factor for the nanorovers, as the electronics are meant to hold the expected radiation dose in a 14 days’ Moon mission.

• 2. Dependency of the aluminum chassis thickness over the radiation dose in the nanorovers (Fig. 11) identifying all possible radiation sources from Launch-Transit segment to Moon’s segment.

• 3. The radiation sensor, considered a potential payload for the mission, can still be placed inside the nanorovers, getting the core values about the environmental radiation in the Moon environment, blocking radiation and getting results in one order of magnitude lower.

• 4. The radiation sensor will be located next to the nanorovers’ lenses (Fig. 1) in an approximately 45$^{\circ }$ angle with respect to the ground. Using that placement, Solar Panels will not interfere blocking radiation, and the angular placement will optimize the possibilities of receiving radiation from outer space.

4.4 Future Work

The next steps on Lunar Zebro mission are divided into the ones related to the New Ray Tracing Method and the whole Thermal Mathematical Model (TMM and $R^{2}TM$), and the experimental tests to be carried out on those nanorovers to give the final green light before launch.