Skip to main content
SpringerLink
Log in

Nonlinear Dynamics of Two-Directional Functionally Graded Beam Under a Moving Load with Influence of Homogenization Scheme

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

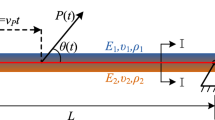
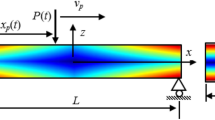
A third-order shear deformation beam model for nonlinear dynamic analysis of a two-directional functionally graded (2D-FG) beam under a moving load is presented. Distinct from the existing higher-order beam models, the present model employs the transverse shear rotation rather than the cross-sectional rotation as an independent variable. The material properties are continuously varied in both the axial and thickness directions by power distribution laws, and they are estimated by four homogenization schemes, namely the schemes due to Voigt, Mori–Tanaka, Hashin–Shtrikman and Reuss. A beam element is derived and used to transfer the nonlinear differential equation to a discretized form. Nonlinear dynamic response of the beam is predicted by the Newmark method in conjunction with Newton–Raphson iterative procedure. Numerical results reveal that the derived beam element which ensures a quadratic variation of the moment in axial direction is capable of furnishing accurate nonlinear dynamic characteristics with a smaller number of elements as compared to the one based on the conventional cross-sectional rotation. It is shown that the difference in the nonlinear dynamic responses predicted by different homogenization schemes decreases by increasing the power-law indices, and the variation of the material properties along the beam length in the 2D-FG beam mitigates this difference. The effects of the material gradation, the moving load velocity and the homogenization scheme on the nonlinear dynamic behaviour are studied in detail. The difference in dynamic responses obtained from linear and nonlinear dynamic analyses is also examined and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data availability

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

References

  1. Frýba L (1999) Vibration of solids and structures under moving loads. Thomas Telford, London

    Book  Google Scholar 

  2. Koizumi M (1997) FGM activities in Japan. Compos Part B Eng 28:1–4. https://doi.org/10.1016/S1359-8368(96)00016-9

    Article  Google Scholar 

  3. Şimşek M, Kocatürk T (2009) Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load. Compos Struct 90:465–473. https://doi.org/10.1016/j.compstruct.2009.04.024

    Article  Google Scholar 

  4. Şimşek M (2010) Vibration analysis of a functionally graded beam under a moving mass by using different beam theories. Compos Struct 92:904–917. https://doi.org/10.1016/j.compstruct.2009.09.030

    Article  Google Scholar 

  5. Khalili SMR, Jafari AA, Eftekhari SA (2010) A mixed Ritz-DQ method for forced vibration of functionally graded beams carrying moving loads. Compos Struct 92:2497–2511. https://doi.org/10.1016/j.compstruct.2010.02.012

    Article  Google Scholar 

  6. Esen I (2019) Dynamic response of a functionally graded Timoshenko beam on two-parameter elastic foundations due to a variable velocity moving mass. Int J Mech Sci 153:21–35. https://doi.org/10.1016/j.ijmecsci.2019.01.033

    Article  Google Scholar 

  7. Esen I, Akif KM, Yusuf C (2018) Finite element formulation and analysis of a functionally graded Timoshenko beam subjected to an accelerating mass including inertial effects of the mass. Lat Am J Solids Struct. https://doi.org/10.1590/1679-78255102

    Article  Google Scholar 

  8. Esen I (2019) Dynamic response of functional graded Timoshenko beams in a thermal environment subjected to an accelerating load. Eur J Mech A Solid 78:103841. https://doi.org/10.1016/j.euromechsol.2019.103841

    Article  MathSciNet  Google Scholar 

  9. Şimşek M, Kocatürk T, Akbaş ŞD (2012) Dynamic behavior of an axially functionally graded beam under action of a moving harmonic load. Compos Struct 94:2358–2364. https://doi.org/10.1016/j.compstruct.2012.03.020

    Article  Google Scholar 

  10. Gan BS, Trinh TH, Le TH, Nguyen DK (2015) Dynamic response of non-uniform Timoshenko beams made of axially FGM subjected to multiple moving point loads. Struct Eng Mech 53:981–995. https://doi.org/10.12989/sem.2015.53.5.981

    Article  Google Scholar 

  11. Wang Y, Wu D (2016) Thermal effect on the dynamic response of axially functionally graded beam subjected to a moving harmonic load. Acta Astronaut 127:171–181. https://doi.org/10.1016/j.actaastro.2016.05.030

    Article  Google Scholar 

  12. Ghatage PS, Kar VR, Sudhagar PE (2020) On the numerical modelling and analysis of multi-directional functionally graded composite structures: a review. Compos Struct 236:111837. https://doi.org/10.1016/j.compstruct.2019.111837

    Article  Google Scholar 

  13. Lezgy-Nazargah M (2015) Fully coupled thermo-mechanical analysis of bi-directional fgm beams using nurbs isogeometric finite element approach. Aerosp Sci Technol 45:154–164. https://doi.org/10.1016/j.ast.2015.05.006

    Article  Google Scholar 

  14. Şimşek M (2015) Bi-directional functionally graded materials (bdfgms) for free and forced vibration of Timoshenko beams with various boundary conditions. Compos Struct 133:968–978. https://doi.org/10.1016/j.compstruct.2015.08.021

    Article  Google Scholar 

  15. Nguyen DK, Nguyen QH, Tran TT, Bui VT (2017) Vibration of bidimensional functionally graded Timoshenko beams excited by a moving load. Acta Mech 228:141–155. https://doi.org/10.1007/s00707-016-1705-3

    Article  MathSciNet  Google Scholar 

  16. Nguyen DK, Vu ANT, Pham VN, Truong TT (2022) Vibration of a three-phase bidirectional functionally graded sandwich beam carrying a moving mass using an enriched beam element. Eng Comput 38:4629–4650. https://doi.org/10.1007/s00366-021-01496-3

    Article  Google Scholar 

  17. Nguyen DK, Tran TT, Pham VN, Le NAT (2021) Dynamic analysis of an inclined sandwich beam with bidirectional functionally graded face sheets under a moving mass. Eur J Mech A Solid 88:104276. https://doi.org/10.1016/j.euromechsol.2021.104276

    Article  MathSciNet  Google Scholar 

  18. Rajasekaran S, Khaniki HB (2019) Size-dependent forced vibration of non-uniform bi-directional functionally graded beams embedded in variable elastic environment carrying a moving harmonic mass. Appl Math Model 72:129–154. https://doi.org/10.1016/j.apm.2019.03.021

    Article  MathSciNet  Google Scholar 

  19. Zhang Q, Liu H (2020) On the dynamic response of porous functionally graded microbeam under moving load. Int J Eng Sci 153:103317. https://doi.org/10.1016/j.ijengsci.2020.103317

    Article  MathSciNet  Google Scholar 

  20. Liu H, Zhang Q, Ma J (2021) Thermo-mechanical dynamics of two-dimensional FG microbeam subjected to a moving harmonic load. Acta Astronaut 178:681–692. https://doi.org/10.1016/j.actaastro.2020.09.045

    Article  Google Scholar 

  21. Mei C, Decha-Umphai K (1985) A finite element method for non-linear forced vibrations of beams. J Sound Vib 102:369–380. https://doi.org/10.1016/S0022-460X(85)80148-6

    Article  Google Scholar 

  22. Ribeiro P, Petyt M (1999) Non-linear vibration of beams with internal resonance by the hierarchical finite-element method. J Sound Vib 224:591–624. https://doi.org/10.1006/jsvi.1999.2193

    Article  Google Scholar 

  23. Ribeiro P (2001) Hierarchical finite element analyses of geometrically non-linear vibration of beams and plane frames. J Sound Vib 246:225–244. https://doi.org/10.1006/jsvi.2001.3634

    Article  Google Scholar 

  24. Shooshtari A, Rafiee M (2011) Nonlinear forced vibration analysis of clamped functionally graded beams. Acta Mech 221:23–38. https://doi.org/10.1007/s00707-011-0491-1

    Article  Google Scholar 

  25. Hosseini SM, Mareishi S, Kalhori H, Rafiee M (2014) Large amplitude free and forced oscillations of functionally graded beams. Mech Adv Mater Struct 21:255–262. https://doi.org/10.1080/15376494.2012.680670

    Article  Google Scholar 

  26. Kanani AS, Niknam H, Ohadi AR, Aghdam MM (2014) Effect of nonlinear elastic foundation on large amplitude free and forced vibration of functionally graded beam. Compos Struct 115:60–68. https://doi.org/10.1016/j.compstruct.2014.04.003

    Article  Google Scholar 

  27. Ansari R, Shojaei MF, Mohammadi V, Gholami R, Sadeghi F (2014) Nonlinear forced vibration analysis of functionally graded carbon nanotube-reinforced composite Timoshenko beams. Compos Struct 113:316–327. https://doi.org/10.1016/j.compstruct.2014.03.015

    Article  Google Scholar 

  28. Paul A, Das D (2018) Non-linear forced vibration analysis of higher-order shear-deformable functionally graded material beam in thermal environment subjected to harmonic excitation and resting on non-linear elastic foundation. J Strain Anal Eng Des 53:446–462. https://doi.org/10.1177/0309324718782230

    Article  Google Scholar 

  29. Ghayesh MH (2018) Nonlinear vibration analysis of axially functionally graded shear-deformable tapered beams. Appl Math Model 59:583–596. https://doi.org/10.1016/j.apm.2018.02.017

    Article  MathSciNet  Google Scholar 

  30. Sheng GG, Wang X (2019) Nonlinear forced vibration of size-dependent functionally graded microbeams with damping effects. Appl Math Model 71:421–437. https://doi.org/10.1016/j.apm.2019.02.027

    Article  MathSciNet  Google Scholar 

  31. Hino J, Yoshimura T, Ananthanarayana N (1985) Vibration analysis of non-linear beams subjected to a moving load using the finite element method. J Sound Vib 100:477–491. https://doi.org/10.1016/S0022-460X(85)80002-X

    Article  Google Scholar 

  32. Yoshimura T, Hino J, Kamata T, Ananthanarayana N (1988) Random vibration of a non-linear beam subjected to a moving load: a finite element method analysis. J Sound Vib 122:317–329. https://doi.org/10.1016/S0022-460X(88)80357-2

    Article  Google Scholar 

  33. Mamandi A, Kargarnovin MH, Younesian D (2010) Nonlinear dynamics of an inclined beam subjected to a moving load. Nonlinear Dyn 60:277–293. https://doi.org/10.1007/s11071-009-9595-8

    Article  Google Scholar 

  34. Mamandi A, Kargarnovin MH (2011) Dynamic analysis of an inclined Timoshenko beam traveled by successive moving masses/forces with inclusion of geometric nonlinearities. Acta Mech 218:9–29. https://doi.org/10.1007/s00707-010-0400-z

    Article  Google Scholar 

  35. Sheng GG, Wang X (2017) The geometrically nonlinear dynamic responses of simply supported beams under moving loads. Appl Math Model 48:183–195. https://doi.org/10.1016/j.apm.2017.03.064

    Article  MathSciNet  Google Scholar 

  36. Şimşek M (2010) Non-linear vibration analysis of a functionally graded Timoshenko beam under action of a moving harmonic load. Compos Struct 92:2532–2546. https://doi.org/10.1016/j.compstruct.2010.02.008

    Article  Google Scholar 

  37. Chen Y, Fu Y, Zhong J, Li Y (2017) Nonlinear dynamic responses of functionally graded tubes subjected to moving load based on a refined beam model. Nonlinear Dyn 88:1441–1452. https://doi.org/10.1007/s11071-016-3321-0

    Article  Google Scholar 

  38. Xie K, Wang Y, Fu T (2020) Nonlinear vibration analysis of third-order shear deformable functionally graded beams by a new method based on direct numerical integration technique. Int J Mech Mater Des 16:839–855. https://doi.org/10.1007/s10999-020-09493-y

    Article  Google Scholar 

  39. Zuiker JR (1995) Functionally graded materials: choice of micromechanics model and limitations in property variation. Compos Eng 5:807–819. https://doi.org/10.1016/0961-9526(95)00031-H

    Article  Google Scholar 

  40. Loja MAR, Barbosa JI, Soares CMM (2012) A study on the modeling of sandwich functionally graded particulate composites. Compos Struct 94:2209–2217. https://doi.org/10.1016/j.compstruct.2012.02.015

    Article  Google Scholar 

  41. Karami B, Shahsavari D, Janghorban M, Li L (2019) Influence of homogenization schemes on vibration of functionally graded curved microbeams. Compos Struct 216:67–79. https://doi.org/10.1016/j.compstruct.2019.02.089

    Article  Google Scholar 

  42. Sahmani S, Safaei B (2020) Influence of homogenization models on size-dependent nonlinear bending and postbuckling of bi-directional functionally graded micro/nano-beams. Appl Math Model 82:336–358. https://doi.org/10.1016/j.apm.2020.01.051

    Article  MathSciNet  Google Scholar 

  43. Nguyen DK, Bui TTH, Tran TTH, Alexandrov S (2022) Large deflections of functionally graded sandwich beams with influence of homogenization schemes. Arch Appl Mech 92:1757–1775. https://doi.org/10.1007/s00419-022-02140-2

    Article  Google Scholar 

  44. Lei J, He Y, Li Z, Guo S, Liu D (2019) Postbuckling analysis of bi-directional functionally graded imperfect beams based on a novel third-order shear deformation theory. Compos Struct 209:811–829. https://doi.org/10.1016/j.compstruct.2018.10.106

    Article  Google Scholar 

  45. Voigt W (1889) Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann Phys 274:573–587. https://doi.org/10.1002/andp.18892741206

    Article  Google Scholar 

  46. Reuss A (1929) Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM J Appl Math Mech 9:49–58. https://doi.org/10.1002/zamm.19290090104

    Article  Google Scholar 

  47. Mori T, Tanaka K (1973) Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall Mater 21:571–574. https://doi.org/10.1016/0001-6160(73)90064-3

    Article  Google Scholar 

  48. Hashin Z, Shtrikman S (1963) A variational approach to the theory of the elastic behaviour of multiphase materials. J Mech Phys Solids 11:127–140. https://doi.org/10.1016/0022-5096(63)90060-7

    Article  MathSciNet  Google Scholar 

  49. Reddy JN (1984) A simple higher-order theory for laminated composite plates. J Appl Mech 51:745–752. https://doi.org/10.1115/1.3167719

    Article  Google Scholar 

  50. Shi G, Lam KY, Tay TE (1998) On efficient finite element modeling of composite beams and plates using higher-order theories and an accurate composite beam element. Compos Struct 41:159–165. https://doi.org/10.1016/S0263-8223(98)00050-6

    Article  Google Scholar 

  51. Krenk S (2009) Non-linear modeling and analysis of solids and structures. Cambridge University Press, Cambridge

    Book  Google Scholar 

Download references

Acknowledgements

This article was supported by National Foundation for Science and Technology Development (NAFOSTED) of Vietnam, the Grant 107.02.2021.11.

Author information

Author notes

  1. An Ninh Thi Vu and Dinh Kien Nguyen have contributed equally to this work.

Authors and Affiliations

  1. Faculty of Basic Sciences, University of Transport and Communications, 3 Cau Giay, Dong Da, Hanoi, Vietnam

    An Ninh Thi Vu

  2. Institute of Mechanics, VAST, 18 Hoang Quoc Viet, Hanoi, Vietnam

    Dinh Kien Nguyen

  3. VNU University of Engineering and Technology, 144 Xuan Thuy, Cau Giay, Hanoi, Vietnam

    Dinh Kien Nguyen

Authors
  1. An Ninh Thi Vu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dinh Kien Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dinh Kien Nguyen.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vu, A.N.T., Nguyen, D.K. Nonlinear Dynamics of Two-Directional Functionally Graded Beam Under a Moving Load with Influence of Homogenization Scheme. J. Vib. Eng. Technol. (2024). https://doi.org/10.1007/s42417-024-01409-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42417-024-01409-w

Keywords

Search

Navigation