Introduction

Vibration reduction in lightweight slender structures is a persistent challenge in many applications, including automotive, aerospace, and civil engineering. The origin of this problem is the contradictory requirements for a lightweight and low-vibration structural design. Besides, the lower the frequency the more difficult to attenuate corresponding waves, since the dimensions of an attenuating structure should, for most solutions, be comparable with a (large) wavelength scale [1].

Recent developments in vibration mitigation in lightweight structures rely on the concept of acoustic black holes (ABHs) proposed by Krylov [2]. The ABH phenomenon implies trapping flexural waves by locally reducing the structural thickness (according to a decreasing power-law function) which results in slowing down the phase velocity of waves and accumulating vibrational energy in the thinnest parts. The ABH thus performs effective broadband wave focalization, as shown theoretically [3, 4] and experimentally [5, 6] for different one-dimensional (1D) and two-dimensional (2D) ABH designs. Such functionality, combined with the simplicity of implementation and the reduction of structural weight, makes ABHs appealing for practical applications [7, 8].

Traditional ABH designs are however inefficient at low-frequencies, since their vibration suppression features emerge near or above a so-called ABH characteristic frequency [9, 10], which is estimated by equating the wavelength of a corresponding flexural wave in regions with uniform thickness to the diameter of an ABH. Nevertheless, multi-ABH clusters exhibit strong local-resonance modes below the ABH characteristic frequency, opening a way to improve the wave attenuation performance with multiple ABHs below this characteristic frequency [4, 11]. It was, for instance, proposed to couple ABHs with Bragg scattering or locally resonance mechanisms in periodic designs to obtain multiple bandgaps [12,13,14,15]. In such scenarios, they analyzed the influence of a profile shape or the effects of added stiffeners in the ABH indentation or folded structures with ABHs to enhance the Bragg scattering and thus to widen bandgaps below the characteristic frequency [13, 16, 17]. These approaches have shown improved wave attenuation and indeed allow extending attenuation ranges, though often at the cost of an increased structural mass or larger dimensions. The periodic design strategy is limited in terms of the vibration attenuation bandwidth with the constrain on light weight. Furthermore, the attenuation splitting phenomenon prevents achieving broadband attenuation bands in finite-size ABH lattices [18]. Other design strategies are thus required for truly broadband vibration mitigation in structures with ABHs at these frequencies.

In the quest for such strategies, we were inspired by acoustic metamaterials that exploit disorder or graded designs [19,20,21,22,23] to broaden inherently limited local-resonance bandgaps [24, 25]. It is found that the disorder or graded designs usually achieve broadband attenuation at the cost of reduced attenuation intensity within bandgaps [19,20,21, 23]. In essence, disorder arrangements of resonators enable eliminating transmission peaks caused by wave amplification at anti-resonances that occur in periodic local resonators [1, 22]. The graded designs can trap and spatially segregate the frequencies of local resonators allowing for broadband wave control [26]. As ABHs can also act as multi-frequency resonators [27], their graded or aperiodic arrangements might be beneficial to broaden attenuation frequency ranges. Recent studies support this hypothesis by analyzing graded double-leaf ABHs and experimentally proving their broadband attenuation functionality [28]. Also, gradient metabeams with graded 1D ABHs were shown to achieve broadband attenuation bands [29]. Disordered arrangements or heterogeneous profiles of “classic” two-dimensional (2D) ABHs have not been analyzed yet for the enhancement of both attenuation bandwidth and intensity, and are thus, the focus of this study.

This work aims to achieve broadband wave attenuation in a strip with spatially disordered and/or heterogeneous 2D ABHs below the ABH characteristic frequency, when warranting the comparable attenuation intensity to periodic configurations. After analyzing the influence of the characteristic parameters of ABHs on attenuation bands in a periodic design, propose design strategies for aperiodic ABH strips to obtain heterogenous periodic and identical non-periodic ABHs. The obtained aperiodic designs are analyzed by tracing the evolution of the wave transmission and structural vibration modes and comparing their wave attenuation functionality with that of periodic counterparts. The effectiveness of these designs in broadening wave attenuation band is also proven experimentally.

Transmissibility of Strip with Periodic ABHs

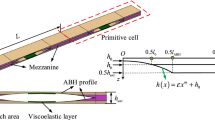
We consider out-of-plane elastic waves in an aluminum strip of dimensions L × W × h1 = 800 mm × 120 mm × 5.18 mm (Young’s modulus 71 GPa, Poisson’s ratio 0.33, mass density 2820 kg/m3) decorated, initially, with five identical ABHs arranged periodically at center-to-center distance a = 160 mm (Fig. 1a). The ABH profile is described by function \({\text{h}}\left({\text{r}}\right)\) (Fig. 1b), where ri and hm are the radius and the height of a central plateau [30]. External diameter D = 100 mm is identical for all the ABH indentations and kept constant throughout this study. We assume that the lateral faces of the plate are stress-free, and flexural waves are induced by a harmonic point-like excitation applied in the middle of the input side.

Fig. 1
figure 1

a Schematics of flexural waves propagating in a finite-size ABH-patterned strip. b The ABH unit and its profile function. c, d The condensed transmission diagrams indicating the transmission levels below − 10 dB for periodic arrangements of ABHs with different profile parameter r0 or different position parameter a. The colorful insets are mode shapes.

Full size image

We used the finite-element method implemented in the Solid Mechanics Module of COMSOL Multiphysics 5.5 to estimate wave transmission in the strip with ABHs. The geometric model of the strip is meshed by quadratic Lagrange elements with at least ten finite elements per the wavelength of the highest analyzed frequency that results in a mesh containing 32,484 elements. The simulation time for a single-frequency transmission problem is around 5 s by using 24 cores of Inter Xeon E5 2680 v3 (2.4 GHz) processor and operational memory of 48 GB.

Note that in the simulations we assume no damping for the material of the strip as aluminum has negligible intrinsic losses at the target frequencies [31, 32]. Therefore, the wave attenuation in the strip is solely governed by wave scattering from the ABHs. To demonstrate different attenuation scenarios, we vary ri by keeping a = 160 mm, m = 2 and hm = 0.5 mm fixed. The condensed transmission diagrams for five values of r0 (ri = r0 is identical for all the ABHs) are shown in Fig. 1c, where the intensity of the black color indicates the wave attenuation from 10 to 50 dB. The insets with the mode shapes of periodic ABHs indicate strong Bragg scattering and local resonances that can be recognized by periodic patterns and strong motion localization in the thinnest parts of the ABH profiles, respectively [18]. The two modes at 3053 Hz and 4109 Hz for r0 = 10 mm (Fig. 1c) are known as the multi-frequency local resonances [18, 27]. As r0 increases from 10 to 13 mm, the frequency of the lowest of these modes decreases and its displacement distribution also changes though preserving the localized character; the other mode is, in contrast, insensitive to the value of r0 that further confirms the different wave control mechanisms inherent to these modes. Hence, the lower bound of the wave attenuation band extends to lower frequencies as r0 increases, and its upper bound remains around 4 kHz. Only larger values of r0 show a reduced bandwidth after a certain threshold (cf. the diagrams for r0 = 13 mm and r0 = 21 mm in Fig. 1c) resulting in significant change in modes above 3 kHz and thus are not considered here.

To examine the influence of the spatial arrangement of the ABHs on wave transmission and the local resonances in ABHs, we vary position parameter a by keeping m = 2, r0 = 10 mm, and hm = 0.5 mm fixed. The condensed transmission diagrams for three values of a are shown in Fig. 1d. As can be seen, the change of a by 20 mm alters the bandwidth influencing the higher frequency mode above 3.8 kHz, while not affecting the mode around 3.1 kHz. This behavior is expected for the Bragg-scattering and local-resonance modes.

The obtained results reflect the sensitivity of waves propagating in the ABH-patterned strip to the profile and spatial arrangement of ABHs thus opening a way to explore the potential of aperiodic ABHs in increasing the attenuation bandwidth below the ABH characteristic frequency defined as \(f_{{\text{c}}} = {{2\pi h_{1} } \mathord{\left/ {\vphantom {{2\pi h_{1} } {D^{2} }}} \right. \kern-0pt} {D^{2} }}\sqrt {{E \mathord{\left/ {\vphantom {E {12\rho (1 - \nu^{2} )}}} \right. \kern-0pt} {12\rho (1 - \nu^{2} )}}}\), which is 4990 Hz for the considered ABH size and material. Specifically, we focused on the range 3–4.5 kHz indicated by the red dashed lines in Fig. 1c, d.

To quantify the wave attenuation, we define an attenuation bandwidth level in terms of the design variable sets \({{\varvec{X}}}^{{\text{p}}}\) and \({{\varvec{X}}}^{{\text{c}}}\):

\(\mathop J\limits_{{[f_{\min } ,f_{\max } ]}} \left( {{\mathbf{X}}^{p} ,{\mathbf{X}}^{c} } \right) = \frac{1}{{N_{f} }}\sum\limits_{i = 1}^{{N_{f} }} {J_{i} \left( {{\mathbf{X}}^{p} ,{\mathbf{X}}^{c} } \right)} ,\;J_{i} \left( {{\mathbf{X}}^{p} ,{\mathbf{X}}^{c} } \right) = \left\{ {\begin{array}{*{20}c} 1 & {T_{i} \le - 10\;{\text{dB}}} \\ 0 & {T_{i} > - 10\;{\text{dB}}} \\ \end{array} } \right.\) (1)

Here, transmission Ti at the ith frequency is defined as \(T_{i} = 20\log \left( {{{\overline{w}_{{{\text{out}}}} } \mathord{\left/ {\vphantom {{\overline{w}_{{{\text{out}}}} } {\overline{w}_{{{\text{in}}}} }}} \right. \kern-0pt} {\overline{w}_{{{\text{in}}}} }}} \right)\), where \(\overline{w}_{in}\) is the averaged amplitude of flexural displacements on the excited side of the plate strip (called driving side) and \(\overline{w}_{out}\) is its counterpart on the receiving side [32]. The set of variables \({{\varvec{X}}}^{{\text{p}}}=\left({{l}_{0},l}_{1},{l}_{2},\cdots ,{l}_{N-1}\right)\) describes the positions of the ABHs with \({l}_{0}\) indicating the distance between the center of the 1st ABH to the input side and sub-set \({{\widetilde{{\varvec{X}}}}^{{\text{p}}}=(l}_{1},{l}_{2},\cdots ,{l}_{N-1})\) indicating the distances between adjacent ABHs. For the fixed \(m\) and\({h}_{m}\), the ABH profiles are fully described by the set of ri in\({\boldsymbol{ }{\varvec{X}}}^{{\text{c}}}=\left({r}_{1},{r}_{2},\cdots ,{r}_{N}\right)\). Here and further the scalars in the sets are given in millimeters.

The bandwidth J depends on frequency spacing, \(\Delta f={f}_{i+1}-{f}_{i}\left(i=\mathrm{1,2},\cdots ,{N}_{f}-1\right)\). For the periodic case with r0 = 10 mm (Fig. 1c), we found slight variations in the J values for different \(\Delta f\), namely: \({J}_{\Delta f=0.5 {\text{Hz}}}=0.6135, {J}_{\Delta f=1 {\text{Hz}}}=0.6136, {J}_{\Delta f=2 {\text{Hz}}}=0.6138, {J}_{\Delta f=4 {\text{Hz}}}=0.6117\). Since the largest variation does not exceed 0.3%, we use \(\Delta f=4{\text{Hz}}\) in the simulations to reduce computational costs.

Design Strategies of Aperiodic ABHs and Results

For aperiodic arrangements of the ABHs, we aim to increase the value of J defined by Eq. (1) in [fmin = 3 kHz, fmax = 4.5 kHz]. Aperiodic designs can be recognized by non-identical entries of \({\widetilde{{\varvec{X}}}}^{{\text{p}}}\) or/and \({{\varvec{X}}}^{{\text{c}}}\). To distinguish them, we call the designs with non-identical entries in \({{\varvec{X}}}^{{\text{c}}}\) as heterogeneous since they describe sets of ABHs with different profiles, and the designs with non-identical entries in \({\widetilde{{\varvec{X}}}}^{{\text{p}}}\) as disordered since they describe spatially disordered positions of identical ABHs. Finally, the designs with non-identical entries in both sets are called disordered heterogeneous.

Periodic Arrangement of Heterogeneous ABHs

The first strategy to design heterogeneous ABHs relies on modifying the profiles of the five ABHs (N = 5) in the periodic setting, one-by-one, by keeping their periodic arrangement. It implies finding geometric parameters \({r}_{i}\) for the ith ABH profile described by \(h\left(r\right)={\varepsilon \left(r-{r}_{i}\right)}^{2}+0.5 {\text{mm}}, { r}_{i}<r<50 {\text{mm}}\) to increase J.

We start from a periodic arrangement of identical ABHs with \({{\varvec{X}}}^{{\text{c}}}=\left(\mathrm{10,10,10,10},10\right)\), \({\widetilde{{\varvec{X}}}}^{{\text{p}}}=\left(\mathrm{150,150,150,150}\right)\), and \({l}_{0}=100 {\text{mm}}\) that has the widest attenuation bandwidth (J = 0.85) among the periodic designs described in Sect. “Transmissibility of strip with periodic ABHs”. We vary the radius \({r}_{i}\) between 5 and 25 mm with a step of 1 mm for each ABH sequentially. The indicated limits enable preserving the center plateau and the smoothness of an ABH profile[33]. The design steps are described below (schematically shown in Supplementary Material Fig. A1):

  • Step 1: the \({r}_{1}\) of ABH1 is subsequently assigned all admissible values, while the ABH2-ABH5 are unchanged. The \({r}_{1}\) maximizing J is stored in \({{\varvec{X}}}^{{\text{c}}}=\left({r}_{1},{r}_{20},\cdots ,{r}_{N0}\right)\) and used in the following steps.

  • Step i (i = 2,…,N): Identical to Step 1 when \({r}_{i0}\) is replaced by the \({r}_{i}\). The procedure stops when J = 1 or once the Nth profile is identified.

The updated profile set \({{\varvec{X}}}^{{\text{c}}}\) describes the heterogeneous ABH design.

Figure 2 reveals that J increases at each step of the described procedure. Figure 3 illustrates the obtained heterogeneous ABH plate design corresponding to the maximum value J = 0.98 together with the transmission curves for this design and the periodic counterpart. As can be seen, the transmission peaks for the heterogeneous design are about 10 dB lower proving that the heterogeneous ABHs enable effectively extending the attenuation bandwidth almost in the whole target frequency range.

Fig. 2
figure 2

The step-wise values of J for the heterogeneous ABH design

Full size image
Fig. 3
figure 3

The wave transmission curves for the Al plates with heterogeneous \({{\varvec{X}}}^{{\text{c}}}=\left(21,12,11,\mathrm{13,11}\right)\) and periodic (\({{\varvec{X}}}^{{\text{c}}}=\left(10,10,10,\mathrm{10,10}\right)\) ABHs

Full size image

To elucidate the mechanisms behind the extension of the attenuation bandwidth in the heterogeneous case, we consider the evolution of the transmission curves corresponding to the maximum value of J (as marked by the arrows in Fig. 2) at every step, as indicated in Fig. 4. One can see that the attenuation bandwidth progressively extends, and the magnitudes of most transmission peaks gradually decrease.

Fig. 4
figure 4

Evolution of the wave transmission at subsequent steps of the procedure to design heterogeneous ABHs with maximum J at every step. Grey regions highlight the frequency ranges with T below − 10 dB in steps 1–4. Triangle, square and circular markers indicate partial structural modes for periodic, intermediate, and final heterogeneous designs, respectively

Full size image

To explain this behavior, we track the changes in the structural modes at selected frequencies (indicated by dots in Fig. 4) at each step (Fig. 5). From Step 1, the increase of r1 introduces fundamental changes in the displacement distribution governed by the Bragg scattering and local resonances in the initially periodic identical ABHs (the first row in Fig. 5). First, the periodic patterns disappear at all the considered frequencies. Second, there occurs substantial redistribution of the localized motions. Similar modal localization (and vibrational energy redistribution) was observed previously in other quasi-periodic and disorder systems [34, 35]. It occurs in our design because the large internal plateau of the ABH1 enables the focalization of vibrational energy within the ABH1 thus reducing the amount of energy reaching the other ABHs, i.e., a signature of strong local resonances. Thus, the local resonances in the ABH2–ABH5 are largely suppressed that results in confining vibrations in the region close to the excitation point. This localization phenomenon is observed at 3180 Hz, 3797 Hz and 4415 Hz (Step 1 in Fig. 5), at which mode localization in ABH1 is activated. The detuning of a single ABH profile thus enables broadband energy localization attributed to the multi-frequency local resonances in ABHs, and the ABH with the larger plateau allows extending this feature to lower frequency. The ABH2 with a different profile from ABH1 acts similarly enabling mode localization at 4024 Hz in Step 1.

Fig. 5
figure 5

Evolution of the structural modes at each step of the design procedure for heterogeneous ABHs. The mode shapes correspond to frequencies marked by triangle, square, and circle markers in Fig. 4. The frequencies indicated in bold correspond to the localized modes that dominate in the attenuation band of the final design

Full size image

Variations of the ABH2–5 profiles in the subsequent steps result in the local changes of the wave fields in ABH2 and ABH3 (cf. 4415 Hz in Step 1 and 4405 Hz in Step 5, Fig. 5) that improves the attenuation above 4000 Hz and lowers the frequencies of several transmission peaks (cf. the peaks at 3035 Hz in Step 2 and 2995 Hz in Step 3) thus extending the attenuation to lower frequency. Note that the modes with the vibrations localized near the excitation point (e.g., at 3171 Hz, 3774 Hz, 3996 Hz and 4405 Hz in Step 5) dominate within the attenuation bands of the final design.

To summarize, with nearly unchanged mass, the heterogeneous ABHs enable activating multiple local resonances at low frequencies that can be used to widen the attenuation bandwidth and increase the attenuation intensity for a fixed number of ABHs, as compared to a periodic arrangement. Yet, truly broadband attenuation can be out of reach as certain transmission peaks remain insensitive to variations of the ABH profile. Specifically, two modes with close frequencies and similar displacement distributions on the opposite sides of the plates (4016 Hz and 4024 Hz in step 1 in Fig. 5) result in a transmission peak that cannot be eliminated by changing r1 in Step 1 (Fig. 6). This pair of modes is not sensitive to subsequently modifying the profiles of ABH2–5 (Fig. 4b–d).

Fig. 6
figure 6

The condensed transmission diagram for different ABH1 profiles considered at Step 1

Full size image

Disordered Arrangement of Identical ABHs

To uncover possible advantages of spatial aperiodicity, we propose a strategy that implies a sequential adding of ABHs to an initially homogeneous plate. This approach is illustrated for identical ABHs with fixed entries of \({{\varvec{X}}}^{{\text{c}}}=\left(10,10,10,\mathrm{10,10}\right)\). Note that we allow possible overlapping of adjacent ABHs that was out of consideration previously[4]. The position of an ABH is varied with the step of 10 mm. The procedure can be described as follows (schematically shown in Supplementary Material Fig. A2).

  • Step 1: \({l}_{0}\) is subsequently assigned all admissible values from \({l}_{0}^{{\text{min}}}=3D/5\) to \({l}_{0}^{{\text{max}}}=L-3D/5\). The \({l}_{0}\) maximizing J is stored in \({{\varvec{X}}}^{{\text{p}}}=\left({l}_{0}\right)\) and used in the following steps.

  • Step i (i = 2,…, N): Identical to Step 1 assuming the fixed designs for the ABH(i−1), ABH(i − 2), … obtained at Step i − 1. The admissible range for \({l}_{i-1}\) spans from \({l}_{i-1}^{{\text{min}}}=10 {\text{mm}} {\text{to}} {l}_{i-1}^{{\text{max}}}=L-\sum_{k=0}^{i-1}{l}_{k}-3D/5.\) The found \({l}_{i-1}\) maximizing J is stored in \({{\varvec{X}}}^{{\text{p}}}\) and used in the subsequent steps.

The procedure stops if the \({l}_{i-1}\) maximizing J equals to \({l}_{i-1}^{{\text{max}}}\) in the ith step, or J = 1, or once the position of the Nth ABH is identified.

We considered two initial configurations. In the first case, the position of the ABH1 is identified from the condition of \(\underset{[3\mathrm{ kHz}, 4.5\mathrm{ kHz}]}{{\text{max}}}J\left({l}_{0}\right)\) for the strip with a single ABH resulting in \(J\left({l}_{0}=240\right)=0.52\). In the second case, the ABH1 is placed randomly, skipping Step 1. In particular, ABH1 nears the excited end of the strip that resulted in much smaller \(J\left({l}_{0}=110\right)=0.04\) as compared to the first case. Considering the plate and ABHs dimensions, the number of possible ABHs is limited to five.

For the two initial configurations, we found the disordered designs with \({{\varvec{X}}}^{{\text{p}}}=\left(240,280,130,90\right)\) for four ABHs (1st case) and \({{\varvec{X}}}^{{\text{p}}}=\left(110,130,160,160,160\right)\) for five ABHs (2nd case). The corresponding J values at each step are given in Fig. 7. As can be seen, a larger number of ABHs allows more broadband wave attenuation, despite the skipped Step 1 maximizing J in the 1st case (cf. the max J being 0.81 for I4 in Fig. 7a and J = 0.87 in Fig. 7b). Note that overlapping of adjacent ABHs provides no relevant improvement for the attenuation bandwidth in the considered cases.

Fig. 7
figure 7

The step-wise values of J for disordered ABHs designs: a with the 1st ABH maximizing J; b with the 1st ABH corresponding to a small J

Full size image

Figure 8 shows the transmission curves for the disordered design with five ABHs (J = 0.88, 2nd case) and the periodic one with \({\widetilde{{\varvec{X}}}}^{{\text{p}}}=\left(\mathrm{150,150,150,150}\right)\) and \({l}_{0}=110 {\text{mm}}\), which delivers the widest bandwidth for the identical ABHs with \({{\varvec{X}}}^{{\text{c}}}=\left(10,10,10,10\right)\). The comparison of the two curves reveals that the disordered arrangement increases the attenuation bandwidth and intensity above 3.17 kHz, while the transmission below 3.17 kHz is almost unchanged.

Fig. 8
figure 8

(top) The disordered design with five ABHs and (bottom) the transmission curves for the disordered and periodic designs

Full size image

The evolution of the transmission curves, which correspond to the maximum values of J at every step (indicated by the arrows in Fig. 7b), shows that every added ABHs contributes to extending the attenuation bandwidth and increasing the attenuation intensity (Fig. 8). To identify the mechanisms causing this behavior, we examine vibration modes at selected frequencies indicated by symbols in Fig. 9. As can be seen in Fig. 10, the single ABH added at Step 1 only activates strong vibration localization around 3.8 kHz. Hence, ABH1 results in a narrow-band attenuation of a comparatively low intensity (Fig. 9a). By subsequently adding the other ABHs, the vibration localization above 3.2 kHz is further enhanced, and the wave field in ABH1 is altered (cf. the mode at 3848 Hz in Step 1 and the modes around 3.8 kHz in Steps 3–5). Interestingly, ABH2-5 in the disordered configuration (Fig. 8, top) are actually arranged periodically with\({{\varvec{X}}}^{{\text{p}}}=\left(\mathrm{80,160,160,160,160}\right)\), which corresponds to case r0 = 10 mm in Fig. 1c. That is, the shift of only ABH1 from its periodic position (by decreasing space between ABH1 and ABH2) enables greatly widening the attenuation above 3.2 kHz, while hardly affecting the lower band edge. One can also see that the local characteristics of ABHs are sensitive to the spatial arrangement of every ABH, despite the identical profiles.

Fig. 9
figure 9

Evolution of transmission curves for the disordered ABHs. The grey strips mark the ranges with T < − 10 dB in steps 1–4. The triangle, square and circular markers indicate partial structural modes for the initial, intermediate, and final heterogeneous designs, respectively

Full size image
Fig. 10
figure 10

The evolution of the structural modes for at each step of the disordered ABHs design procedure. The shown modes correspond to frequencies marked by triangle, square, and circle markers in Fig. 9

Full size image

Finally, the analysis of the structural modes in Step 5 (Fig. 10) suggests that ABH1 and ABH3 mainly contribute to the vibration localization around 3.8 kHz, 3.84 kHz, and 4.3 kHz. Specially, different vibrational pattern of ABH1 in these modes is attributed to the multi-frequency local resonance of the ABH cell. The observed multi-frequency local resonances in the ABH and their sensitivity to the spatial arrangement of ABHs promises broadband vibration localization, thus clarifying the extended attenuation bandwidth in the final disordered design (Fig. 9d). Note that each ABH affects the wave field at both sides of its position that partially explains the independence of the final design configuration from the choice of the position of ABH1.

Disordered Arrangement of Non-identical ABHs

To explore possible benefits from the combination of spatial disorder and heterogeneous ABHs in terms of the increased attenuation bandwidth and attenuation intensity, we developed two other design strategies described in Supplementary Material Section 2. In a nutshell, these strategies imply gradually varying the positions of non-identical ABHs, one-by-one, at a step of 10 mm, starting from ABH1. The remaining ABHs are either moved altogether, as a group, by preserving mutual distances (P-group method) or remaining fixed (P-fixed method). The overlapping of adjacent ABH profiles is allowed.

We first applied these procedures to the heterogeneous design obtained in Fig. 3 to further increase the attenuation bandwidth and surprisingly found out that none of possible disordered arrangements provides a wider bandwidth or an enhanced attenuation level (details in Supplementary Material Section 2). This can be explained by the sensitivity of vibration localization in the ABHs to the changes in the wave propagation path introduced by both the ABH profiles [36] and their position. The heterogenous profiles for broadband attenuation were identified under the assumption on periodic arrangement. Based on the above analysis, the disordered arrangement apparently destroys the tuned broadband attenuation (details in Supplementary Material Fig. A4). Therefore, combining spatial disorder and heterogeneous ABHs in the finite-size scenarios should be approached carefully.

Next, we applied the P-group and P-fixed procedures to the graded ABH profiles. Specifically, we analyzed an initially periodic arrangement, \({{\varvec{X}}}^{{\text{p}}}=\left(\mathrm{120,140,140,140,140}\right)\), of five ABHs with gradually increasing ri, i.e., \({{\varvec{X}}}^{{\text{c}}}=\left(\mathrm{5,7},\mathrm{9,11,13}\right)\), which has a wider attenuation bandwidth (J = 0.88) compared to other periodic designs in Figs. 3 and 8. As a result, we obtained two disordered graded configurations (J = 0.95 for both) with \({{\varvec{X}}}^{{\text{p}}}\)= (120,200,140,140,140) and \({X}^{{\text{p}}}= \left(\mathrm{90,170,160,120,140}\right)\).

The obtained aperiodic designs (periodic heterogeneous, disordered homogeneous, and disordered graded) can be compared in terms of the attenuation performance by considering their condensed transmission diagrams shown in Fig. 11. As can be seen, the heterogeneous design provides more uniform and broadband attenuation in comparison with the disordered graded designs. The disordered graded arrangements deliver several narrow attenuation bands separated by high transmission peaks that cannot be reduced below − 10 dB by changing the spatial positions of the ABHs (details in Supplementary Material Section 2.2). In terms of the attenuation level, the disordered homogeneous designs are preferential but have comparatively narrow bandwidths. Note also that a larger number of ABHs provides better wave attenuation as follows from the comparison of the four- and five-ABHs designs, in terms of both the attenuation bandwidth and attenuation intensity. This is remarkable since a more lightweight structure can successfully attenuate low-frequency waves in a broad range.

Fig. 11
figure 11

Condensed transmission diagrams for the obtained aperiodic designs. The highlighted regions in gray indicate the attenuation intensity below than − 10 dB

Full size image

We thus conclude that, in general, the variation of the spatial arrangement of identical or heterogeneous ABHs enables effectively extending the wave attenuation bandwidth and ensures a larger attenuation intensity as compared to corresponding periodic designs. The proposed aperiodic ABH configurations and design strategies are also suitable for the flexible choice of the strip size (containing larger or smaller ABHs) and the base materials as wave attenuation is governed by the structural design.

Aperiodic ABHs vs. Phononic Strips

To further highlight the advantages of the aperiodic ABH patterns, we compare their wave attenuation performance with that of elastic metamaterials with Spiral and Hub-Spoke patterns, which have low-frequency bandgaps due to local resonances and Bragg scattering, respectively [24, 37]. For a fair comparison, we keep the overall mass identical for the three structures and use the same number and identical locations of the unit cells.

Specifically, we consider the heterogeneous ABH design shown in Fig. 3 and introduce the Spiral and Hub-spoke patterns by removing the same amount of material at the same locations within a plate as for the ABH indentation. The relevant geometric parameters are listed in Table 1 together with the bandwidth attenuation J.

Table 1 Geometric parameters of the heterogeneous ABH, Spiral and Hub-spoke designs and the wave attenuation levels for the corresponding five-unit-cell structures. R and REx are equal to 50 mm
Full size table

The heterogeneous Spirals design reveals several narrow attenuation bands separated by high peaks in the transmission curves as shown in Fig. 12a. For the heterogeneous Hub-spokes design, there are nearly no significant attenuation bands (Fig. 12b) that can be attributed to two factors: the lack of periodicity, which is crucial for wave attenuation in the Bragg-scattering-driven structures, and the mismatch between the target frequencies and bandgap frequencies. The locally-resonance Spiral design is independent of periodicity, yet, its attenuation bandwidth is intrinsically narrow requiring careful tuning of its geometric parameters to target frequencies. We also compare the heterogeneous Spiral and Hub-Spoke designs with their periodic counterparts and estimate the difference in the attenuation level by calculating \(\Delta J = (J_{{{\text{Heterogeneous}}}} - J_{{{\text{Periodic}}}} )/J_{{{\text{Periodic}}}} \times 100\%\). As can be expected, the periodic Hub-Spoke configuration performs either better (case 1 in Table 2) in terms of wave attenuation as compared to the aperiodic design or no improvement can be seen due to the mismatch between the bandgap and the target frequency range (case 2 in Table 2). Small differences in the attenuation performance for the Spiral design can be explained by couplings between closely located unit cells[38].

Fig.12
figure 12

Transmission curves for the heterogeneous ABHs strip compared to a heterogeneous Spiral and b heterogeneous Hub-spokes strips of identical structural mass

Full size image
Table 2 Attenuation bandwidth comparison for the heterogeneous and periodic designs
Full size table

For the specified restriction on the structural mass and the choice of the base material, it is impossible to tune the Spiral or Hub-spoke design to achieve sufficient attenuation at the target frequencies (see Refs. [24, 37] for details). More material should be removed to lower the attenuation frequency range that can only be done at the cost of decreased structural stiffness. For the ABHs, the small disturbance of the periodicity not linked to the change of the structural mass shows a satisfactory improvement considering the limited number of the unit cells.

Experimental Validation

The strips with periodic arrangements of identical and heterogeneous ABHs were fabricated and tested in the transmission experiments to valid the advantage of aperiodic ABH design. To reduce manufacturing costs, we replaced aluminum as a base material by resin with Young’s modulus 2 GPa, Poisson’s ratio 0.4, mass density 1177 kg/m3 and produced the samples by Stereolithography 3D printing. The heterogeneous ABHs in the resin strip are designed using the proposed strategy for the targeted frequencies from 1 to 2 kHz. For the strip of external dimensions L × W × h1 = 550 mm × 100 mm × 5 mm (limited by the sizes of the print bed), we considered ABHs with the profiles described by hm = 0.4 mm, D = 80 mm and a set of ri listed in Table 3. The target frequency range is below the ABH characteristic frequency here, which is 2015 Hz for the 3D printed design.

Table 3 Geometric parameters for periodic ABHs of 80-mm diameter with identical and heterogeneous profiles
Full size table

The transmission tests were performed on three strips with periodic ABHs, heterogeneous ABHs, and a homogeneous plate (reference) without ABHs (Fig. 13a). To ensure free boundary conditions, the strips were suspended by four elastic strings. The test set-up (Fig. 13b) includes an electromagnetic shaker (B&K 4809), which generates a periodic chirp signal between 10 Hz and 4 kHz, and is driven by a power amplifier (B&K 2718). A flexible slim rod connects the shaker to a free end of a strip through a force transducer (PCB 208C02) that measures the excitation force. A Polytec Laser Scanning Vibrometer (PSV 500) was employed to scan the vibrational response of the strip.

Fig. 13
figure 13

a 3D-printed resin strips studied experimentally; b test set-up for transmission measurements; c measured transmission curves with the highlighted regions in gray indicating the improved bandwidth by the heterogenous ABHs

Full size image

The measured transmission for the reference strip reveals decreased values with the increase of frequency (Fig. 13c) indicating intrinsic losses of the resin material. We estimated the loss factor to be around 0.04 (see details in Supplementary Material Section 3) at room temperature in the analyzed frequency range by means of the half-power bandwidth method [39]. The resin strip with periodic ABHs shows transmission reduction at higher frequencies and comparatively large transmission values below 1.3 kHz, while the strip with heterogeneous ABHs shows the lowest transmission in the target frequency range, from 1 to 2 kHz, as predicted by design. Additionally, the heterogeneous ABHs reduce two transmission peaks below 1 kHz, thus, further improve the low-frequency attenuation. Therefore, these data prove the superiority of the optimized aperiodic design and confirm the efficiency of the proposed design strategy in finding a proper combination of ABH profiles to achieve target broadband attenuation. Note that this strategy also remains valid when the base material has intrinsic losses as in our experiments.

Conclusions

This work has uncovered the potential of spatially disordered and heterogeneous 2D ABH designs to widen attenuation bandwidth in lightweight mono-material strips. We showed that the overall attenuation intensity in the extended attenuation bandwidth is the same or better than that for periodic counterparts.

To explore the role of heterogeneous ABHs and their disordered arrangements in broadband wave attenuation and to implement the aperiodic ABHs in the practical setting, we proposed several design strategies, which can easily be adapted for any number of ABHs and different target frequencies. These strategies could especially be useful under severe limitations on structural dimensions (that restrict the number of possible ABHs) and strong demand in broadband attenuation. The numerical analyses and the presented experimental validation demonstrated the efficiency of the strategies to find appropriate aperiodic ABH arrangements in a small design subset.

The identified heterogeneous ABHs configuration reveals the widest attenuation bandwidth and the comparable attenuation intensity to that of periodic counterparts. The disordered arrangements of identical or graded ABHs show enhanced attenuation levels. The heterogeneous and disordered ABH designs enable thus different attenuation scenarios that can be realized based on specific application requirements, especially under severe limitations on structural dimensions that restrict the number of possible ABH s. We attributed the broadening of the attenuation bandwidth and enhanced attenuation intensity in the aperiodic ABHs to the activation of strong localized modes at broadband frequencies. These abundant modes are linked to multi-frequency local resonances in ABHs that are sensitive to both the ABH profile and their spatial arrangement.

Therefore, the aperiodic ABH designs are promising to overcome the narrow-band performance of traditional local resonators [21, 24, 25] by preserving structural stiffness that is of relevance in many applications. We believe that the proposed design procedures and the reported advantages of the aperiodic ABHs will give an impetus to further exploit spatial disorder and heterogeneous ABH profiles for effective vibration attenuation in different structures and will boost the use of the ABH concepts in a wider range of applications.