Introduction

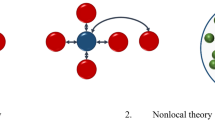
The concept of the particle damping technique can be traced back to the work of Paget [1]. He introduced the concept of an impact damper to reduce the vibration amplitude of turbine blades. In an impact damper, a box containing a single particle or mass is attached to a vibrating structure. The collision of the single particle with the container walls leads to momentum transfer from the primary structure to the impact mass, which results in reducing the vibration amplitude of the main structure. A schematic representation of an impact damper mounted on the tip of a cantilever beam can be seen in Fig. 1 (upper). The impact damper has been successfully implemented in turbine blades [1], boring tools or drills [2], and cable-stayed bridges [3]. However, high noise levels, high impact forces, and sensitivity toward excitation amplitude restrict its applications [4]. Furthermore, an impact damper can also cause excessive wear to the contact surfaces. Hence, to overcome these disadvantages, the particle damping technique can be used in which the single particle in the impact damper has been replaced by multiple small auxiliary masses. Therefore, particle dampers can be seen as extended or generalized versions of impact dampers or single-particle dampers. Like impact dampers, particle dampers can also be mounted to the vibrating structure, see Fig. 1 (lower).

Fig. 1
figure 1

Schematic representation of an impact damper (upper) and a particle damper (lower) mounted on the tip of a cantilever beam under dynamic load

Full size image

Different design approaches for particle dampers have been suggested depending on the field of application. For instance, Panossian [5] has proposed a non-obstructive particle damper design in which small cavities are created in the vibrating structure, which can be partially filled with granular materials. In our previous work, the honeycomb damping plate concept [6] and the existing cavity concept [7] have been introduced for particle dampers to reduce the vibration amplitude of a wind turbine generator. Furthermore, our previous work has also carried out a comparative study for these two concepts [7]. Because of the particle dampers simplicity, cost-effectiveness, and broadband damping capabilities, they have been successfully implemented in several industries, like wind turbine generators and blades [6, 8], automotive [9], aerospace [10], machine tools [11], and civil structures [12]. Particle dampers also have many advantages over other passive damping techniques. For instance, particle dampers can sustain low and high-temperature environments depending on the granular materials. On the other hand, similar to particle dampers, friction dampers can also bear high temperatures and harsh environmental conditions. However, the dependency of the frictional and thermal forces of a frictional damper on the surface condition can limit its usage [13]. Furthermore, particle dampers provide damping across a wide frequency range, while tuned mass dampers, another passive technique for vibration attenuation, are effective only within a narrow range centered around their resonance frequency [14]. Ma et al. [15] have shown that the performance of the suspended particle damper is significantly higher in comparison to a tuned mass damper. Generally, the passive damping technique is more effective in the high-frequency range [16]. But, in our previous work, it has been shown that passive dampers, like particle dampers, can also be used to reduce the low-frequency vibration amplitude from wind turbine components [6, 8].

A particle damper consists of multiple auxiliary masses, which are either mounted on a vibrating structure or placed inside an existing cavity of the structure. When the primary structure experiences vibration, the kinetic energy of the vibrating structure is transferred to the particle damper, which causes a collision between the particles as well as between the particle and cavity walls. As a result, the vibration amplitude of the primary structure is reduced. A schematic representation of the particle damping mechanism concept can be seen in Fig. 2. The energy dissipation mechanism of a particle damper depends on several factors. For instance, the type of granular material used to design a particle damper shows a strong influence on vibration attenuation [6,7,8,9, 17, 18]. Furthermore, filling ratios, the number of particles, shape, and size of particles, and the intensity of excitation show significant influence on reducing the vibration amplitude of a structure [19]. Although the particle damping technique is conceptually simple, the analytical models [20, 21] of particle dampers are very limited due to their highly nonlinear behavior. Therefore, an analytical approach to design a particle damper for real-world application is not possible. Apart from this most of the proposed analytical methods require a numerical approach to get the solution [22]. In contrast to the analytical methods, numerical approaches like the discrete element method (DEM) and finite element method (FEM) provide a promising outcome [23,24,25,26,27,28]. However, at a large industrial scale, the DEM or FEM–DEM coupling approach is not suitable due to a large number of particles available in a particle damper. Additionally, the calibration process to identify the contact material parameter in DEM is also a tedious and time-consuming task. Besides this, the irregular shapes of real particles are highly idealized in the numerical approach. Therefore, the experimental approach to designing a particle damper is still very prominent.

Fig. 2
figure 2

Schematic representation of particle damper concept [17]. µp represent the friction coefficient among particles, while µw denotes the friction coefficient between particles and the wall

Full size image

As mentioned above, the dependency of the damping performance of a particle damper on numerous parameters makes their design process for real-world applications significantly challenging. Hence, in this contribution, an extensive series of experimental studies has been conducted to offer valuable insights into the design of particle dampers, particularly for vibration attenuation of a large hollow structure. The findings drawn from the laboratory experiments are then also put to the test on a real-scale wind turbine generator.

The paper is structured into seven sections, each addressing specific aspects of the particle damping technique. “A Brief Review of Particle Damper Designs” section provides a comprehensive discussion on the application and design approaches of particle damping. In “Test Specimen and Design Strategies” section, the design of the test specimen and all the configurations examined in the experiments are presented. The experimental setup is outlined in “Experimental Setup” section. In “Results and Discussion” section, the obtained results are discussed in detail. The implementation of the design variants at an industrial scale can be seen in “Industrialization” section. Finally, “Summary and Outlook” section contains the summary and outlook of the work.

A Brief Review of Particle Damper Designs

Sun et al. [29] have used statistical energy analysis to model sand as a fluid to predict the vibration attenuation of a structure, which is filled with sand. They have shown that by increasing the sand layer thickness the vibration reduction increases. The increment in the sand thickness after a certain limit shows a negative effect on damping efficiency, i.e., instead of vibration amplitude reduction, a slight increase in amplitude has been observed. The dependency of the damping properties of the sand upon the static pressure can be seen in the theoretical and experimental investigation by Schmidt [30]. He also urged that the maximum vibration attenuation in the structure occurs because of the resonance in the sand. Panossian [5] has proposed a non-obstructive particle damping technique in which small cavities are created in the vibrating structure, which can be partially filled with granular materials. He has effectively implemented four different kinds of granular materials to reduce the vibration response of a space shuttle main engine liquid oxygen inlet tee. He has drilled four holes of 1 mm diameter in the liquid oxygen inlet tee splitter and filled them partially with steel balls of three different sizes (0.18 mm, 0.28 mm, and 0.58 mm), zirconium oxide ceramic balls (0.25 mm), nickel powder, and tungsten powder. It was found that the vibration attenuation due to tungsten powder is significantly higher in comparison to other materials. The damping performance of materials is not straightforward and shows slightly different damping capabilities for different mode shapes. For instance, steel balls of 0.18 mm diameter vibration attenuation capabilities at 3807 Hz and 4309 Hz are significantly higher in comparison to other materials. Furthermore, nickel powder damping performance is better at 4257 HZ. Therefore, the author has concluded that the vibration attenuation by particle dampers is a complex function of material and their damping capabilities can be influenced by several parameters, which need further investigation. Cempel et al. [31] investigated the influence of different shot packing configurations to reduce the vibration amplitude of an aluminum cylinder. Overall, they have studied eight different shot-filling configurations. It has been found that stable and maximum vibration reduction can be achieved when shots are either randomly distributed in the container or tightly packed in a plastic bag. Papalou et al. [32] have demonstrated the strong influence of particle size on vibration attenuation using steel balls. The particle damper for their experimental study has been designed with four aluminum edge brackets. They fixed one of the brackets on the vibrating plate and the rest three brackets were movable to modify the particle damper size. The authors have also shown that the relationship between the mass ratio and the vibration response of the system is nonlinear. Furthermore, the dependency of particle damper efficiency on the excitation level has been observed. Moreover, the vibration response of the system becomes independent of the intensity of excitation when it is high enough to overcome the friction forces between the particles. However, the direction of excitation shows no effect on particle damping performance. Holkamp et al. [33] have used a cantilever beam with drilled holes to study several parameters that can influence the damping properties of a particle damper. They investigated the damping efficiency of tungsten carbide, cobalt, aluminum, titanium, stainless steel, and glass beads. It has been found that the damping performance of steel, tungsten, and titanium are almost similar. On the other hand, vibration attenuation capability of glass beads is significantly higher than that of aluminum. The authors have also concluded that the shape of particles has a negligible effect on vibration attenuation. Furthermore, it has been observed that increasing the mass of the granular material after a certain amount shows no effect on damping. A similar observation can be also seen in our previous study [9]. Tomlinson et al. [34] have used the particle damper consisting of steel balls of a diameter of 0.8 mm to reduce the vibration response of a mild steel plate. For their experimental studies, they used a hollow steel cylinder with different aspect ratios to design the particle damper. The investigation has indicated that the particle dampers geometry plays an important role in vibration attenuation. Yang et al. [35] have successfully implemented 200 brass balls to reduce the vibration amplitude of an aluminum beam, which is clamped at both ends. Their studies have revealed that the gap size can influence the efficiency of particle dampers. Gap size has been defined as the ratio of particles height and threaded securing ring that is used to adjust particle enclosure. They have illustrated that the damping efficiency increases and reaches its maximum as the gap size increases. Hence, an increment in the gap size after an optimum value will make the particle damper inefficient. Nayfeh et al. [36] have filled a rectangular box beam with 3 M glass microbubbles (average particle size 65 microns) to show that the low-density granular material filling can achieve higher vibration attenuation. Furthermore, they have suggested that the wave propagation properties of granular material play a significant role in the energy dissipation mechanism. Particle damper application in reducing the vibration amplitude of a bank note machine can be seen in the work of Xu et al. [37]. To implement the particle damping technique on the bank note machine, the authors have drilled 10 holes of 3 mm diameter on the machine shaft and filled it fully with tungsten particles of 0.5 mm diameter. Furthermore, on the plate element of the machine, several holes of 4 mm diameter were generated to enclose the tungsten particles. According to their experimental investigation, it has been found that the particle damper is highly effective in the frequency range of 4000–6000 Hz and can reduce the vibration amplitude of the primary structure up to 40 dB. However, for the frequency range of 0–2000 Hz, the tungsten particles show moderate damping capabilities. Furthermore, 6 dB (A) noise reduction has been also achieved. A particle damper consisting of small steel particles (0.18–0.24 mm) is successfully implemented to avoid chatter in a milling workpiece [38]. Rongong et al. [39] have studied various design parameters of a particle damper.

The authors have shown that particle interface friction plays a major role in the damping capabilities of a particle damper. To demonstrate this, they mixed light and heavy oil with the particles and compared it with the damping efficiency of dry particles. It has been found that the dry particles can reduce the vibration amplitude significantly higher in comparison to the particles mixed with light and heavy oil. Furthermore, an electromagnet was used to create magnetic flux, which can modify the contact forces in the particle damper. The application of a magnetic field has improved damping efficiency slightly. Moreover, several methods, like inserting a cellular honeycomb structure in a disk-shaped particle damper and applying a magnetic field, have been discussed to modify the static pressure distribution to improve the damping efficiency of a particle damper. Sand particles with an average particle size of 0.3 mm have been successfully implemented to reduce the vibration of an automotive engine. It has been found that increasing the thickness of sand layers also increases the vibration attenuation of the engine and after a certain amount of the sand thickness no significant damping has been observed. Furthermore, the study also concludes that the reduction in vibration amplitude of the oil pan is mainly because of the damping mechanism of particle dampers and not merely because of the additional mass of the sand [9]. Koch et al. [40] have expanded the idea of Duvigneau et al. [9] and have investigated the influence of particle sizes on vibration attenuation of an oil pan. For this, sand particles of three different sizes have been used. Moreover, the original oil pan bottom was replaced by a honeycomb plate to make the primary structure light as well as to study the effect of granular material distribution on vibration attenuation. The experimental investigation indicates that the larger sand particles with rough textures are more damping efficient. Such particles often show a large angle of repose, which can be used as an indicator for the damping capability of a material. The authors also propose the optimal position of the granular material filling, i.e., granular material should be placed at the location where the vibration amplitude is high. Furthermore, they have demonstrated the effectiveness of this concept on a running engine test bench. The damping performance of eight different granular materials has been investigated by Koch et al. [18]. For the experimental investigation, they chose rubber granulate, sand, corundum, glass balls, silicon, gelatin gel, polystyrene, and glass with two different grain sizes. They have concluded that rubber granulate can reduce the vibration amplitude of the primary structure significantly higher in comparison to other materials. An et al. [41] experimentally investigated three different materials to reduce the vibration amplitude of a tensegrity prism. They have used steel spheres (7 mm), 3D-printed spheres (7 mm), and glass spheres with four different diameters. namely: 5 mm, 6 mm, 7 mm, and 8 mm. The glass sphere with four different sizes is used to study the effect of particle size on vibration attenuation and it has been found that the smaller the particles, the higher the vibration attenuation rate. They find out that the vibration attenuation rate of glass spheres is significantly higher in comparison to other materials at higher excitation magnitude. The damping capability of the 3D-printed sphere is lower than the glass sphere but is higher than the steel spheres damping capabilities. Michon et al. [42] have used soft hollow particles instead of classical hard particles to keep the additional mass of the granular materials low. The overall damping performance of the hollow particles is significantly higher. However, it should be noted that in their experimental investigation the honeycomb cantilever beam, which is partially filled with hollow particles shows no damping for the first vibration mode. Simonian [43] has applied the particle damping technique to the aerospace industry. He has shown that particle damper containing lead shot shows tremendous damping capability under random vibration conditions. He also suggested that particle dampers are more efficient for vibration attenuation in comparison to other conventional passive dampers techniques, like viscoelastic materials or viscous fluids. Another application of particle damper for the aerospace industry can be seen in the work of Veeramuthuvel et al. [10]. Veeramuthuvel et al. [10] have attached a particle damper capsule of a square shape on a printed circuit board (PCB), which is used in a spacecraft. Authors have used tungsten carbide, stainless steel, and aluminum alloy as granular materials. In their investigation, it has been observed that materials with higher densities are more efficient for vibration attenuation. Authors have found the packing ratio of 60% is effective for vibration suppression for all the materials they have investigated. Furthermore, they have observed that irrespective of granular materials, the packing ratio of 100% is not effective for reducing the vibration amplitude. Elastomer particle damper has been implemented to reduce the vibration amplitude of a wind turbine tower by Stauber et al. [44]. They suggested that the particle with rough and textured surfaces is useful for energy dissipation. The experimental investigation has shown that particle dampers containing elastomer particles can show a significant reduction in vibration amplitude for the frequency ranges of 100–600 Hz. Jehring [45] has studied different parameters, like particle size, mass ratio, and cavity size, that can affect the damping efficiency of a particle damper. Jehring et al. [46] have also shown that metal hollow spheres filled with ceramic powder are effective for reducing structure-borne sound emission. Göhler et al. [47] have used the particle damper concept for reducing the vibration amplitude of a milling slide. To demonstrate this they have replaced the conventional steel plate of the milling slide with particle-filled hollow sphere sandwiches. Zhou et al. [48] has also studied the damping efficiency of the particle-filled hollow sphere to reduce the vibration amplitude of machine tool components. Kumar et al. [49] have used copper and lead particles to attenuate the vibration amplitude in a boring bar. They have shown that the damping performance of copper particles is higher than that of lead particles. They have also observed that the particles with a larger size are more effective for damping the structure. Lu et al. [50] have successfully used buffered material to design a particle damper for a multi-degree-of-freedom system to reduce the impact forces. A particle damper has also been successfully implemented in a wind turbine blade [51]. In their work, the authors have attached the particle dampers at three different locations on the blade. Furthermore, they have also investigated the influence of rotating speed on the particle damper. It has been found that mounting the particle damper near the blade root is effective. Moreover, the study shows that particle damper can reduce the vibration amplitude more effectively at a lower speed (60 rpm). In our previous experimental investigations, we also examined the damping efficiency of a particle damper on a scaled wind turbine blade in rotation [52]. To this end, a particle damper containing 1 g of rubber granulate was mounted to a 15 cm model wind turbine blade. The utilization of rubber granulate is favorable owing to its lightweight characteristic, a critical design parameter for wind turbine blades, as well as lightning protection requirements. Our findings reveal that the particle damper is more effective at a rotational speed of 180 rpm as opposed to rotational speeds of 120 rpm, 660 rpm, and 1080 rpm.

The above review reveals that most research on particle dampers has focused on plate-like or beam-like structures. The review also highlights that the predominant approach in particle damper design involves attaching a partially filled cavity to the main structure or enclosing granular materials by creating small holes within the structure. However, there has been limited discussion regarding utilizing available space within a large hollow structure for particle damper design. Therefore, this present contribution experimentally investigates various design strategies to design a particle damper for a large hollow structure. It is important to highlight that keeping the additional mass of the granular material as low as possible was also one of the primary focuses of the proposed design. Furthermore, extensive research has been devoted to the use of conventional materials like steel balls, tungsten, aluminum, and titanium in the design of particle dampers, resulting in a significant increase in the total mass of the primary structure. Hence, in this study, rubber granulate material manufactured by recycling the waste of automotive tires is used to design the particle damper. The use of rubber granulate to design a particle damper not only leads to a significant reduction in the additional mass of the particle damper but also demonstrates promising vibration attenuation capabilities. To the best of the author’s knowledge, there is no existing literature reporting the use of rubber granulate in the design of a particle damper to mitigate vibration amplitudes in large-scale structures. Generally, the movement of granular material within a particle damper results from the vibrations of the primary structure. Nevertheless, some authors have introduced electromagnets to induce additional motion in the granular materials, aiming to increase damping efficiency. While this approach demonstrates substantial enhancements in the damping performance of a particle damper, its effectiveness is limited to specific materials. Thus, in this present study, several passive design variations are introduced that aim to increase the relative motion of granular materials, thereby enhancing the efficiency of the particle damper. The ultimate objective of this research is to extrapolate the laboratory-scale findings to an industrial-scale structure. Thus, the design variants investigated at the laboratory scale are also subjected to testing on a real-sized wind turbine generator.

Test Specimen and Design Strategies

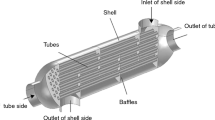
Mechanical structures made of steel hollow sections are used in several industries because of their excellent resistance to bending, torsion, and buckling. For instance, hollow steel structures are widely used in wind turbine components, agricultural equipment, piping systems, and support structures for offshore construction. For this reason, i.e., to cover a wide range of application areas, the current contribution chose an L-shaped hollow steel structure to study the design specification of particle dampers. Furthermore, the inner space of the hollow test specimen gives possibilities to design a particle damper without modifying the primary structure. The dimensions and designs of the test specimen are given in Fig. 3. The dimensions of the test specimen draw inspiration from a stator arm found in the direct-drive wind turbine generator. The dimensions shown in Fig. 3 represent a scaled-down version of the original stator arm of a wind turbine generator, measuring half its size. In the design of a direct-drive wind turbine generator, the stator is comprised of a large circular component known as the stator ring. Additionally, multiple L-shaped hollow sections are attached to the ring to offer structural support to the entire assembly, which is referred to as stator arms [6].

Fig. 3
figure 3

Design and dimension of the L-shaped test specimen. All dimensions are given in mm

Full size image

Furthermore, the total mass of the test specimen without particle damper is 100 kg. The decision for the design and dimension of the test specimen is taken collectively with the project partners, especially the Fraunhofer Institute for Manufacturing Technology and Advanced Materials Dresden (IFAM). In the first design strategy, i.e., in the thin-walled cavity (TWC) design variant, thin plates of rectangular shapes are used to design particle damper cavities inside the test specimen. The size of the particle damper cavity depends on the mounting positions of the thin plates. The possible mounting locations of the thin plates are given in Fig. 4. The thin plates are attached inside the hollow section of the test specimen using identical bolts and nuts, see Fig. 5. Moreover, a minimum of two thin plates are required to design a particle damper with a single cavity inside the test specimen. The idea of using thin plates is to provide extra motion to the particles. The wall thickness of the plates is much smaller in comparison to the test specimen wall thickness. Because of this, the thin plates can vibrate with a higher amplitude that can provide additional motion to the particles of the granular material. Altogether 44 identical holes of 6.5 mm diameter have been drilled at eleven different locations in the test specimen, see Fig. 4. Furthermore, the position of the two adjacent holes is kept at 60 mm, see Fig. 3. Moreover, with the help of these holes, TWCs of three different heights can be designed, namely: 60 mm, 120 mm, and 180 mm. Additionally, there is a possibility to design a TWC of size 180 × 180 × 240 mm by attaching the thin plates at locations four and five, respectively, see Fig. 4. However, this will increase the additional mass of the granular material significantly. Therefore, the TWC of dimension 180 × 180 × 240 mm is not considered in this study. It should be noted that due to the fixed dimension of the test specimen, the length and width of the TWC are constant throughout this design study. But, the height of the TWC can be varied, which depends on the location of the thin plates. With the given number of holes in the test specimen, it is possible to design eight different TWCs at three different locations, namely: the top part (Fig. 5a–c), the middle part (Fig. 5d, e), and the bottom part (Fig. 5f–h) of the L-shaped test specimen. The positions of the TWCs in the test specimen are decided in such a way that it should be possible to reach those positions manually, which makes the granular material filling and emptying process more convenient.

Fig. 4
figure 4

Location numbering for mounting the thin sheet to design a cavity inside the test specimen

Full size image
Fig. 5
figure 5

Locations and dimensions of the TWCs: a TWC 1, b TWC 2, c TWC 3, d TWC 4, e TWC 5, f TWC 6, g TWC 7, h TWC 8, i multi-unit TWC, j mix TWC

Full size image

Designing a TWC at the top and middle positions of the test specimen is done in three steps. To begin with, a thin plate is attached to the bottom of the cavity. Afterward, the granular material is filled inside that cavity. Finally, the cavity is closed with another thin plate, which is identical to the one used for the bottom part. For instance, to design TWC 1, see Fig. 5a, a thin plate is first attached at location 2, see Fig. 4. In the next step, the cavity is filled with granular materials followed by mounting a thin plate at location 1. However, designing a TWC at the bottom part of the test specimen is slightly different in comparison to the designing process of the TWCs at the upper and middle parts of the test specimen. For this, three holes of 30 mm in diameter have been drilled on the surface of the bottom part of the test specimen. Through these holes, the granular materials can be filled inside the TWCs (TWC 6, TWC 7, and TWC 8), which have been designed by attaching the two thin plates at different locations, see Fig. 5f–h. Apart from eight single-unit (SU) TWCs, a multi-unit (MU) TWC has also been designed at the top part of the test specimen using four identical plates see, Fig. 5i. The MU TWC consists of two SU TWCs having an identical dimension of 180 × 180 × 60 mm. The idea behind this study is to compare the damping efficiency of a SU TWC and a MU TWC in terms of vibration attenuation.

In addition, two SU TWCs of similar dimensions have been designed at the top and bottom parts of the test specimen, see Fig. 5j. Furthermore, it is important to mention that the smallest possible height of a cavity can be 60 mm and the largest available cavity height can be 180 mm at a given position, see Fig. 6. The reason behind this choice is to design a particle damper volume in such a way that the additional mass of the granular material can be kept as low as possible. Moreover, it is also important to ensure a sufficient number of particles in the cavity to show a significant reduction in vibration amplitude.

Fig. 6
figure 6

Schematic representation of the smallest TWC variant (left) and the largest TWC variant (right) filled with granular materials created using two thin plates

Full size image

The choice of a granular material is one of the primary factors in designing a particle damper. In our previous study, the effect of twenty different granular materials in reducing the vibration amplitude of a vibrating system has been investigated [17]. The experimental study has shown that the rubber granulate “RG 4.6 mm”, which is manufactured by the waste of automotive tires, is one of the best-suited materials for designing a particle damper. Therefore, in the current contribution, the rubber granulate “RG 4.6 mm” is used to design the particle damper. As mentioned above, the thin plates are used for the TWCs design in this contribution and the vibration behavior of the thin plates depends on several factors, among which the wall thickness can have a major influence on the damping efficiency of TWCs. Therefore, to better understand the influence of the wall thickness of the TWCs design on the dynamic response of the system, plates of three different wall thicknesses, namely: 2.0 mm, 1.0 mm, and 0.5 mm have been selected, see Fig. 7. These plates are rectangular in shape and are rounded in the corner, which makes the insertion of these plates inside the test specimen easier. All these plates contain four identical holes which are used for fixing these thin plates inside the hollow structure.

Fig. 7
figure 7

Thin plates of different wall thickness t to design TWCs

Full size image

Furthermore, in this contribution, the concept of a thin-walled cavity with additional sheets (TWC-AS) is introduced to improve the efficiency of TWCs strategy in reducing the vibration amplitude of a mechanical structure, see Fig. 8. The idea behind attaching a suspended sheet to the TWC variant is to provide an additional source of motion to the particles. The supplementary motion provided to the particles of the granular material through the suspended sheet can increase the probability of collision between particles, which may be useful in reducing the vibration amplitude of the structure significantly higher in comparison to the TWC variant without these suspended sheets. The vibration behavior of the suspended sheets depends on their shape, size, number of suspended sheets, and thickness. Furthermore, different widths and heights of the suspended sheet can provide an extra contact surface between granular material particles and the sheet surfaces, which can contribute to vibration attenuation. Moreover, the different shapes and sizes of the suspended sheet can have different contact surfaces between granular material particles and the sheet, which can have an effect on the overall dynamic response of the system. For this reason, the influence of the suspended sheet design on the system response has been experimentally investigated, see Fig. 8. The suspended sheet is manufactured by welding thin sheets of different shapes, sizes, and thicknesses to a base plate of 1.0 mm thickness, see Fig. 8. Nevertheless, the effect of the number of suspended sheets on vibration attenuation has been also briefly investigated. The dimensions of the suspended sheets are given in Table 1.

Fig. 8
figure 8

TWC-AS of different shapes, sizes, and thicknesses

Full size image
Table 1 Dimension, wall thickness, and number of hanging sheets. All dimensions are in mm
Full size table

The additional mass of a particle damper due to the granular materials is one of the major obstacles to utilizing the concept of particle damping technique in lightweight industries. In our previous work, it has been shown how the choice of granular materials can influence the mass of a particle damper significantly [17]. However, once the selection of the granular materials has been made, it becomes challenging to reduce the additional mass of the particle damper further. Therefore, in the current contribution, the ring cavity (RC) design variant is presented. In the RC variant, the granular material can be distributed in such a way that the additional mass of the granular material can be kept low in comparison to the conventional particle damper design. Furthermore, the design of the RC increases the contact surface between the wall and granular material particles. Moreover, the vibration of the ring and its base plate can also increase the probability of particle–particle collision. The design of the RC used for the current experimental investigation can be seen in Fig. 9.

Fig. 9
figure 9

Geometry of RC: a large RC, b small RC

Full size image

There are three different possibilities to distribute the rubber granulate “RG 4.6 mm” inside the RC, namely: configuration 1, configuration 2, and configuration 3, see Fig. 10. In configuration 1, the rubber granulate “RG 4.6 mm” is distributed along the outside wall of the ring, see Fig. 10a. In this manner, both the test specimen and the RC vibration induce kinetic energy within the rubber granulate. This may reduce the test specimen vibration amplitude by decreasing the granular materials’ additional mass. Besides this, the rubber granulate “RG 4.6 mm” can only be partially filled inside the ring of RC (configuration 2), which can reduce the granular material mass further, see Fig. 10b. However, in this scenario, the rubber particles can solely engage with each other and with the thin walls of the ring, meaning that the motion within the granular materials is solely induced by the RC. Furthermore, the distribution of the rubber granulate “RG 4.6 mm” in configuration 3 occurs both inside and outside the ring, see Fig. 10c. Nonetheless, this adaptation will increase the mass of the rubber granulate “RG 4.6 mm” in comparison to the first two variants. But, this can also increase the vibration reduction of the test specimen in comparison to the first two variants. Altogether, rings of two different heights have been experimentally investigated, see Fig. 9. The dimension of the RC is given in Table 2.

Fig. 10
figure 10

Distribution pattern of the rubber granulate “RG 4.6 mm” for the RC design variant: a configuration 1: along the outside wall of the ring, b configuration 2: inside the ring, c configuration 3: both inside and outside the ring

Full size image
Table 2 RC dimension in mm
Full size table

Experimental Setup

The experimental setup to study the design variable for a particle damping technique is given in Fig. 11.

Fig. 11
figure 11

Experimental setup to study design approaches of particle dampers for large-scale application

Full size image

To measure the dynamic response of the system, a Polytec laser scanning vibrometer (model PSV-400) device has been used, which is based on the Doppler effect and is a contactless measuring technique. Using a laser scanning vibrometer, the out-of-plane and in-plane surface velocity of a system under dynamic load can be measured. Furthermore, the bottom part of the test specimen is fixed on the measuring table using two identical beam-like structures of 10 mm thickness. The reason behind fixing the test specimen on the measuring table for the entire experiment duration is to reduce the uncertainties in the experiment. Moreover, attaching the steel beam will also decouple the test specimen from the measuring table. To fix the L-form test specimen with two steel beams attached, four similar bolts and sliding blocks are used. In our previous studies, it has been found that the vibration behavior of a system can be affected by the bolt-tightening procedure [6, 9]. Therefore, it is necessary to maintain a similar pre-load on each bolt. To achieve this, a torque wrench is utilized during the bolt assembly process, applying 5 Nm of torque to each individual bolt. Furthermore, an adhesive reflective foil is attached to the measuring area of the specimen to improve the quality of the reflected laser light. To excite the test specimen, an electrodynamic shaker from TIRA has been used, which is mounted on the measuring table with the help of two identical bolts. Furthermore, an impulse input signal represented by the Dirac function has been selected as the excitation signal due to its ability to excite all resonances of the test specimen across the desired frequency range. Additionally, a force transducer from the PCB Piezotronics of model 208C02 is fixed between the shaker and impact hammer head to record the applied load on the test specimen. It is essential to highlight that the impact hammer head is composed of hard plastic material, enabling signal acquisition within a frequency range spanning from 1 to 1000 Hz. An amplifier (Type 2693) from Bruel Kjær and a power amplifier (Type 50009) from TIRA have been used for the force sensor and the shaker, respectively. The excitation point is chosen in such a way that it is possible to excite as many as possible eigenfrequencies below 1000 Hz. In the current investigation, the location of the excitation point is on the bottom side of the test specimen. Moreover, to avoid the double strokes near the test specimen, the distance between the hammer head and the test specimen is kept at approximately 2 mm. The test specimen and shaker are kept fixed for the entire duration of the experiment to maintain the location of the excitation point identical for each experiment. Additionally, this experimental setup was kept fixed for the duration of the entire study to obtain a comparable frequency response. The scanning head of the laser scanning vibrometer has been placed horizontally to the test specimen to measure the out-of-plane surface velocity of the test specimen. A fine grid of rectangular shape that consists of 302 measuring points is defined on the measuring area, see Fig. 12. The decision on the number of scanning points is based on an empirical study, which shows that the above-mentioned number of scan points is sufficient to maintain the measurement accuracy by keeping the measurement time as low as possible. The location of the scan point is defined on the long arm of the test specimen and is kept fixed for each experiment, see Fig. 12.

Fig. 12
figure 12

Rectangular shape grid consisting of 302 scan points

Full size image

Furthermore, a parameter study has been carried out on the reference test specimen to find a correlation between several parameters to carry out all the experimental investigations. In this context, the reference test specimen means the test specimen without a particle damper. To minimize the uncertainty and signal-to-noise ratio for the actuation signal and response signal, the frequency response is computed by taking six complex averaging per measuring point. Furthermore, the Hann-window function has been implemented to avoid spectral leakage. The values of all the parameters used for each experiment can be seen in Table 3.

Table 3 List of parameters for data acquisition
Full size table

Ensuring the reproducibility of an experiment is one of the major steps in maintaining the quality of an experimental investigation and making the respective studies more reliable. Furthermore, repeatable experiments can minimize the margin of error. To assure reproducibility and repeatability of the experimental studies in this contribution, several tests have been carried out, in which all the experimental conditions, like the location of scan points, the distance between hammer head and test specimen, position of the laser scanning vibrometer, etc., are kept the same. To confirm the repeatability of the experiment, the reference test specimen is measured twice, once at the beginning of the design study and a second time at the end of the design study. Furthermore, to check the robustness of the experimental reproducibility, the vibration behavior of the reference test specimen has been controlled every time after carrying out a certain number of measurements for design variables. Afterward, the frequency response of the reference test specimen is analyzed after completing the entire study. The obtained results confirm the robustness of the experimental setup in terms of reproducing the system response, see Fig. 13.

Fig. 13
figure 13

Repeatability of the experimental results

Full size image

Results and Discussion

The frequency response function (FRF) of the test specimen with and without granular materials is plotted in a narrow frequency band spectrum and also in a one-third octave band. The narrow-banded frequency spectrum is used to extract the information about the number of resonance peaks or frequencies occurring in the frequency range of our interest, i.e., from 20 to 1000 Hz. Hence, the appendix contains plots of all the narrow-banded frequency spectra for reference purposes. The range of frequencies under consideration can be categorized into low-frequency and high-frequency segments. The lower limit of the low-frequency range is typically set at 20 Hz, though the upper limit is subject to occasional adjustments. Moller et al. [53] have set the frequency range between 20 and 200 Hz to study the noise emission from a large wind turbine. Moreover, Zhou et al. [54] have defined the low-frequency range spanning from 20 to 300 Hz. In this contribution, the low-frequency range is considered to encompass frequencies from 20 to 300 Hz. Additionally, a one-third octave band plot has been used throughout the analysis of the results for a further in-depth outlook on the system response. Furthermore, to examine the exact amount of reduction in the vibration amplitude of the test specimen due to particle dampers, a difference in the one-third octave band is plotted. In this plot, the difference is computed by subtracting the level of the reference test specimen from the level of the test specimen with granular materials. The horizontal red line in the difference plot represents 0 dB. The region above the red line shows an increase in the vibration amplitude and the region below represent a reduction in the vibration amplitude. In this contribution, only one-third of octave bands around the most prominent resonance peaks are of special interest. A narrow-band spectrum of the reference test specimen with eigenfrequencies and their respective eigenmodes can be seen in Fig. 14.

Fig. 14
figure 14

Frequency response function and eigenmodes of the reference test specimen centered around the normal direction of measurement

Full size image

Influence of Plate Thickness on the Damping Performance of TWC

In the first design strategy, i.e., in the TWC design variant, the thin plates of three different wall thicknesses (2 mm, 1 mm, and 0.5 mm) are mounted at the topmost position of the test specimen, i.e., at location 1, see Fig. 4. Fixing the thin plates at this location can create a TWC of dimension 180 × 180 × 60 mm, which is partially filled with the rubber granulate “RG 4.6 mm”. The total mass of the rubber granulate “RG 4.6 mm” in this TWC is 700 g. It should be noted that the rubber granulate “RG 4.6 mm” in this particular case increases the additional mass of the entire system by 0.7%, which is significantly less in comparison to the particle damper designed using conventional materials like steel balls and tungsten. The aim of these experimental investigations is to study the effect of the wall thickness of the thin plates on the damping performance of the TWC design variant. The experiment is first carried out on the reference test specimen, i.e., the test specimen without TWC. Thereafter, the frequency response of the system is measured for the test specimen with an empty TWC consisting of thin plates of different wall thicknesses at location 1, i.e., the frequency response of the system containing a particle damper without granular material filling. Subsequently, the test specimen containing TWC enclosed with the rubber granulate “RG 4.6 mm” has been measured. The results obtained for the TWC strategy are plotted in Figs. 15 and 16.

Fig. 15
figure 15

One-third octave band plot of empty and partially filled TWC with varying wall thicknesses (t). The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image
Fig. 16
figure 16

Difference in the one-third octave band of partially filled TWC with varying wall thicknesses (t). The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

From the narrow-band spectrum in Fig. 33, it can be seen that the empty TWC can change the vibration behavior of the primary structure, especially for the torsion modes in the frequency range of 410–536 HZ. Furthermore, the bending modes of the primary structure in the frequency range of 632–718 HZ also get affected due to the thin plates, which are mounted at location 1. The changes in the FRF because of the empty TWC occur either in terms of frequency shift or reduction in amplitude. However, below 410 Hz, the influence of the empty TWC on the vibration behavior of the primary structure is significantly lower, see Fig. 33.

It has been observed that all the configuration of TWC irrespective of the thin plate thickness shows a significant reduction in the vibration amplitude, see Fig. 15. However, a decrease in the vibration amplitude has also been noticed because of an empty TWC, see Fig. 15. For instance, the empty TWC consisting of a 0.5 mm thin plate (blue dash-dotted line) and 1.0 mm thin plate (green dash-dotted line) reduced the vibration amplitude around the central frequency of 400 Hz, Fig. 15. Nevertheless, around the same frequency, the TWC with a 2.0 mm thin plate (purple dash-dotted line) increases the vibration amplitude of the main structure. Nonetheless, for the rest of the frequency ranges, vibration reduction has been observed because of an empty TWC irrespective of its wall thickness. Therefore, the exact amount of vibration attenuation due to a partially filled TWC is computed by subtracting the level of the empty TWC from the level of the reference test specimen, see Fig. 16.

In the amplitude reduction plot, a significant vibration reduction has been observed due to each plate irrespective of their thickness. Furthermore, it can be seen that the TWC with a thin plate of 1.0 mm (light green dashed line) can reduce the vibration amplitude up to 4.7 dB and 6.5 dB, around the resonance frequencies of 400 Hz and 800 Hz, respectively. However, above 450 Hz, the TWC consisting of a 0.5 mm thin plate (sky blue dashed line) is not much effective for damping the structure. The maximum vibration attenuation achieved by the TWC consists of a 2.0 mm thin plate (orange dashed line) is 5.5 dB around the resonance frequency of 800 HZ, see Fig. 16. Based on the preceding analysis, it is apparent that using a 1.0 mm thin plate to construct the TWC results in a substantial reduction in vibration amplitude of the test specimen, in comparison to the TWCs designed with 0.5 mm and 2.0 mm thick plates. This observation can also be justified by comparing the sum level (SL) value of the surface velocity for 1.0 mm plate thickness (178.10 dB), which is significantly less than the rest of the TWCs. In “Test Specimen and Design Strategies” section, it was explained that TWC aims to create a particle damper with a much thinner wall compared to the test specimen. Since thin plates tend to be sensitive to vibrations, they can transfer more kinetic energy to the granular materials. Hence, it is reasonable to expect that the TWC with a 0.5 mm thin plate would provide significantly higher vibration damping compared to other plates due to its higher vibration characteristic. However, it has been observed that TWC consisting of a plate with a 1.0 mm wall thickness exhibits significantly higher damping performance than the others. Thus, it is conceivable that the vibration behavior of the thinnest plate (0.5 mm) is altered by the rubber granulate mass. Therefore, the kinetic energy induced in the rubber granulate “RG 4.6 mm” by the test specimen and TWC featuring a 0.5 mm wall thickness falls short of delivering notable vibration dampening, particularly in the high-frequency spectrum. Hence, it is recommended to uphold a specific wall thickness for the TWC design to minimize the impact of granular material mass on the vibration characteristics of the TWC. However, the specific thickness of the TWC wall is determined by factors such as the hollow space available within the test specimen, the wall thickness of the test specimen, and the mass of the granular materials.

Influence of Location and Dimension of the TWCs Variant

Previous studies indicate that the positioning of particle dampers and the arrangement of granular materials within them can impact the damping effectiveness of a particle damper [6, 18]. For a beam or plate-like structure, it is convenient to approximate the location where displacement is more pronounced. For instance, placing a particle damper at the tip of a cantilever beam can be highly effective as the free end of the beam undergoes substantial motion [8, 55]. Nonetheless, for complex geometries, it becomes challenging to estimate the precise location of a particle damper without conducting a prior investigation. Furthermore, in our earlier studies, it has been also observed that the vibration response of the system remains unchanged beyond a specific increase in the amount of granular material within a particle damper [9, 17]. Moreover, in order to enhance the efficiency of TWCs design, while keeping the additional mass of the granular material to a minimum, it is crucial to investigate the influence of the location and size of TWCs on the vibration response of the test specimen. Hence, this section investigates the damping effectiveness of the TWCs at various locations on the test specimen and explores how the sizes of TWCs affect the vibration response of the L-shaped test specimen. Furthermore, the experimental studies for the TWCs in “Influence of Plate Thickness on the Damping Performance of TWC” section has shown that the thin plate of 1.0 mm thickness is optimal for designing a particle damper for the hollow test specimen. Therefore, to study the influence of TWCs position on the test specimen and the effect of the TWCs dimensions on vibration attenuation, thin plates of 1.0 mm are used to design the TWC. It is essential to highlight that to investigate the impact of cavity sizes on vibration attenuation, the filling ratio within each cavity is maintained at a constant level. In our previous studies [8, 17], it has been observed that an 80% filling ratio is most effective in reducing the vibration amplitude of the main structure significantly while maintaining the additional mass of the granular material as low as possible. Earlier studies [9, 10] have also indicated that a filling volume of 100% is not efficient for reducing the vibration amplitude as it hinders the relative motion of the granular materials within the cavity. Thus, to investigate how cavity sizes influence the damping performance of TWCs while maintaining a consistent filling volume, each cavity is filled with 80% rubber granulate “RG 4.6 mm”. In the current section, three different particle damper locations have been investigated, namely: the top, middle, and bottom parts of the test specimen, see Fig. 5. The location of the TWCs is chosen in such a way that the granular material filling and emptying process can be done manually.

Top Position of TWC

The present section investigates how the vibration reduction of the structure is influenced by the dimensions of TWCs, which are mounted on the top part of the specimen. For this, three different TWCs are designed at the top position of the L-shaped hollow structure, namely: TWC 1, TWC 2, and TWC 3, see Fig. 5a–c. The dimensions of the TWC 1, TWC 2, and TWC 3 are 180 × 180 × 60 mm, 180 × 180 × 120 mm, and 180 × 180 × 180 mm, respectively. Additionally, TWC 1, TWC 2, and TWC 3 are comprised of 800 g, 1600 g, and 2400 g of rubber granulate, respectively, which corresponds 80% of the filling volume for every individual TWC. It has been found that the empty TWC irrespective of their dimensions changes the vibration behavior of the primary structure, especially for the torsion modes in the frequency range of 410–535 Hz, see Fig. 34. Furthermore, the bending mode of the test specimen around the resonance frequency of 668 HZ also gets affected by the empty TWC. Moreover, as it has been observed in “Influence of Plate Thickness on the Damping Performance of TWC” section, here also the empty TWC has almost a negligible effect on the dynamic response of the test specimen below 400 HZ. Besides this, a significant vibration reduction has been observed around the central frequencies of 400 Hz and 500 Hz due to the empty TWC, see Fig. 17. However, vibration attenuation of the primary structure because of the empty TWC mounted at the top position of the test specimen is significantly lower for the bending modes. Hence, for determining the exact amount of vibration reduction of the test specimen due to the TWC at the top position of the test specimen, an amplitude reduction plot is created using the same method as discussed in “Influence of Plate Thickness on the Damping Performance of TWC” section. This means the reduction plot is computed by subtracting the empty TWC level from the partially filled TWC level, see Fig. 18. Figures 17 and 18 show that all three TWCs, i.e., TWC 1, TWC 2, and TWC 3, at the top position of the test specimen are capable of reducing the vibration amplitude. However, for the frequency range 354–562 Hz, TWC 2 (golden rod dashed line) of dimension 180 × 180 × 120 mm can reduce the vibration amplitude of the test specimen significantly higher in comparison to TWC 1 (light coral dashed line) and TWC 3 (saddle brown dashed line). Around the resonance frequency of 500 Hz, TWC 2 can achieve vibration attenuation up to 15 dB. Moreover, around the resonance frequency of 35 Hz and 400 Hz, TWC 2 is capable of reducing the vibration amplitude of the primary structure up to 14 dB and 13 dB, respectively. It should be noted that TWC 1 contains 800 g of rubber granulate “RG 4.6 mm”, which is 50% less than the mass of rubber granulates enclosed in TWC 2. Hence, the presence of a larger number of rubber particles in TWC 2 increases the number of contact and collision points along with the friction coefficient of the bulk material, which is one of the dominating factors for the energy dissipation mechanism in particle dampers. Hence, the damping efficiency of TWC 2 is significantly higher in comparison to TWC 1. Although, TWC 3 contains a higher number of rubber granulate “RG 4.6 mm” particles, the damping efficiency of TWC 3 is still significantly less than that of TWC 2. The reason behind this can be the higher mass of the granular materials, which can restrict the relative motion of the lower layer of the rubber granulate particles. Therefore, there is a possibility that a certain amount of rubber particles in TWC 3 does not contribute to the particle damping mechanism and behave like a rigid mass. Hence, it can be said that the primary reason for the vibration attenuation in the test specimen is attributed to the particle damping mechanism, rather than solely due to the increase in mass. A very similar effect has been also observed in our previous works [8, 9, 17].

Fig. 17
figure 17

One-third octave band of empty and partially filled TWCs with varying dimensions and the same filling ratio (80%) at the top of the test specimen. The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image
Fig. 18
figure 18

Difference in the One-third octave band of partially filled TWCs with varying dimensions and the same filling ratio (80%) at the top of the test specimen. The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

Mid Position of TWC

With the given number of holes in the middle position of the test specimen, it is possible to design two TWCs, namely: TWC 4 and TWC 5, see Fig. 5d, e. The dimensions of TWC 4 and TWC 5 are 180 × 180 × 60 mm and 180 × 180 × 120 mm, respectively. Similar to the cavities at the upper position of the test specimen, the filling volume in both cavities intended for the middle position of the test specimen remains consistent, i.e., TWC 1 and TWC 2 are 80% filled with rubber granulate “RG 4.6 mm”. Similar to the effect seen in “Top Position of TWC” section, the empty TWC at mid position of the test specimen also alters the vibration characteristic of the test specimen, see Fig. 35. The trends observed for the TWC configuration at the mid position of the test specimen around the central frequencies of 400 Hz and 500 Hz are similar to the TWC design at the top position of the specimen. However, the reduction in vibration amplitude caused by empty TWC at the top and mid positions varies in magnitude. As expected, vibration reduction has been also observed because of the empty TWC located at the middle position of the test specimen, see Fig. 19. Therefore, the amplitude reduction plot for this configuration is also estimated in a similar fashion as discussed in “Influence of Plate Thickness on the Damping Performance of TWC” and “Top Position of TWC” sections.

Fig. 19
figure 19

One-third octave band of empty and partially filled TWCs with various dimensions and the same filling ratio (80%) at the mid position of the test specimen. The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

It can be observed from Fig. 20 that the vibration response of the system is lower for TWC of dimension 180 × 180 × 120 mm (TWC 5) for the entire range of frequency. However, the vibration response of TWC of dimension 180 × 180 × 60 mm (TWC 4) is not effective below 700 Hz. Very similar damping behavior is also observed for the particle damper of the same sizes mounted at the top position of the test specimen, see Fig. 18. Nonetheless, it is important to note that despite having the same dimensions and identical mass, the damping efficiency of TWC 1 is significantly higher compared to TWC 4. Furthermore, TWC 2 can reduce the vibration amplitude around the resonance frequencies of 35 Hz, 400 Hz, and 500 Hz up to 13 dB, 12 dB, and 15 dB, respectively. On the other hand particle damper of the same size (TWC 5) on the middle position of the test specimen can reduce the vibration amplitude around the resonance frequencies of 35 Hz, 400 Hz, and 500 Hz up to 11 dB, 8 dB, and 10 dB, respectively. It should be noted that both TWCs contain a similar amount of rubber granulate “RG 4.6 mm”. However, around the resonance frequency of 800 Hz, TWC 5 can lower the vibration response of the system by 7.2 dB. In contrast, TWC 3 shows no significant vibration attenuation around 800 Hz although the dimension and filling material mass are identical to TWC 5. The reason for this difference in damping efficiency can be the region of the bending mode shape with the largest displacement at the middle position of the test specimen, see Fig. 14.

Fig. 20
figure 20

Difference in the one-third octave band of partially filled TWCs with various dimensions and the same filling ratio (80%) at the mid position of the test specimen. The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

For the resonance frequency of 800 Hz, the maximum bending displacement around the middle region of the test specimen increases the relative motion of the rubber granulate particles enclosed in TWC 5. Hence, the probability of particle–particle and particle–wall collision increases, which increases the damping effect.

Bottom Position of TWC

The third possible position of TWC is at the bottom part of the L-shaped hollow test specimen. From the above discussion, it is known that the empty TWC can change the vibration behavior of the primary structure. Similar to the previous outcomes, in this case also the empty TWC 6, TWC 7, and TWC 8 at the bottom part of the test specimen change the vibration characteristics of the main structure. However, in this case, the empty TWC changes the vibration behavior of the test specimen below 400 HZ, especially at the torsion mode around the resonance frequency of 200 Hz, which is not the case for the empty TWC mounted at the top and middle position of the test specimen, see Fig. 21.

Fig. 21
figure 21

One-third octave representation of the FRF of empty and partially filled TWCs with various dimensions and the same filling ratio (80%) at the bottom position of the test specimen. The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

Nevertheless, in the frequency range of 410–535 Hz, there is no significant shift in the frequency because of the empty TWC as it was seen in the previous cases. Furthermore, frequency shift and reduction in vibration amplitude were also observed above 500 Hz because of empty TWC. The amplitude reduction plot for this configuration, see Fig. 22, is also computed by subtracting the level of empty TWC with partially filled TWC. As seen from Fig. 22, a significant vibration attenuation can be achieved by each cavity mounted at the bottom part of the test specimen. The maximum reduction in the vibration amplitude because of these cavities is achieved around 100 Hz, 500 Hz, 650 Hz, and 900 Hz. It is important to note that below 550 Hz, the damping performance of TWC 8 is higher than that of TWC 7. However, above 550 Hz, the damping efficiency of TWC 7 is better than that of TWC 8. Furthermore, as expected TWC 6 can reduce the vibration amplitude of the test specimen significantly less in comparison to TWC 7 and TWC 8. The discussion beforehand suggests that positioning the TWC at the top of the test specimen can lead to a substantially more pronounced decrease in vibration amplitude in comparison to other locations of the TWC. Furthermore, the damping performance of the TWC mounted at the bottom position of the specimen is lower than the TWC mounted at the top and middle positions. The poor performance of the TWC at the bottom position can be because of the boundary condition. As explained in “Experimental Setup” section, the bottom part of the test specimen is completely fixed on the measuring table with the help of two identical steel beams to reduce the uncertainties in the experiments and also to maintain the reproducibility of the experimental investigation. Because of this boundary condition, the movement of rubber granulate particles in the TWC at the bottom part of the test specimen gets restricted. Therefore, the damping capability of this TWC configuration is significantly lower in comparison to other configurations.

Fig. 22
figure 22

Difference in the one-third octave band to of partially filled TWCs with various dimensions and the same filling ratio (80%) at the bottom position of the test specimen. The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

From the above discussion, it can be concluded that the location of TWCs plays a crucial role in reducing the vibration amplitude of the test specimen. Furthermore, the investigation of the various locations of the TWCs has also shown that mounting the TWCs around the region of the mode shape with a larger displacement or surface velocity value can be more effective for vibration attenuation. A similar outcome has also been observed in our previous studies in which a particle damper is employed to reduce vibration amplitude in both a wind turbine generator and an automotive oil pan [6, 18]. Moreover, it has been also observed that cavity size with a fixed filling ratio can also influence the vibration attenuation capability of the TWCs. The studies involving TWCs of varying sizes positioned at different locations on the test specimen has demonstrated that increasing the mass of granular materials does not necessarily lead to an increase in the damping effectiveness of a particle damper.

Multi-unit and Single-Unit TWC

It is known that configurations like single-unit (SU) particle dampers and multi-unit (MU) particle dampers are additional parameters that can influence the vibration response of a system [6, 56]. Hence, this section presents the results of a brief experimental investigation aimed at assessing the impact of SU and MU particle dampers on the damping performance of the TWCs design concept. Furthermore, based on the discussion presented above, it can be concluded that the top position of the test specimen with a higher displacement value is the best location for the TWC. Additionally, the mounting, demounting, filling, and refilling process of TWC at this location is significantly easier in comparison to other locations. Therefore, the top position of the test specimen is chosen to conduct a comparative study between the SU and MU TWC damping efficiency. To design a MU TWC, two thin plates of 1.0 mm thickness have been mounted at locations 2 and 3, see Figs. 4 and 5i. Furthermore, the TWC 3 positioned at the top of the test specimen is categorized as an SU TWC. The SU and MU TWC contain the same amount of granular materials, i.e., 2400 g of rubber granulate. Moreover, it is important to note that in the MU TWC, each cavity contains 800 g of rubber granulate. However, in SU TWC, a single cavity contains 2400 g of rubber granulate “RG 4.6 mm”.

The narrow-band FRF of these configurations can be seen in Fig. 37. As expected and discussed above, empty MU TWC also changes the dynamic response of the system above 300 Hz, see Fig. 37. In Figs. 23 and 24, it can be seen that the resonance frequencies around, 40 Hz, 125 Hz, and 400 Hz, the SU TWC damping performance is significantly higher in comparison to the MU TWC.

Fig. 23
figure 23

One-third octave representation of the FRF of empty and partially filled SU and MU TWCs. The sum level value of the surface velocity (SL) is given in dB and the mass of the granular filling materials is given in g

Full size image
Fig. 24
figure 24

Difference in the one-third octave band to the empty and partially filled SU and MU TWCs. The sum level value of the surface velocity (SL) is given in dB and the mass of the granular filling materials is given in g

Full size image

However, above 450 Hz, the damping performance of MU TWC increases significantly. Nevertheless, the overall damping performance of MU TWC is significantly higher than the SU TWC. This observation can be justified by comparing the SL values of both configurations in Fig. 24. The increased number of thin plates in the MU TWC can be considered the underlying factor responsible for inducing greater vibration into the rubber granulate, as compared to the two thin plates utilized in the SU TWC. Furthermore, it can be concluded that a higher amount of mass in a single cavity can restrict the relative motion among granular material particles, resulting in a reduction in the damping efficiency of the SU TWC. Our previous work has also shown that the MU particle damper is significantly more efficient in comparison to a SU particle damper. However, in our previous studies, the MU particle damper was designed by combining two honeycomb damping plates together [6].

Composition of TWC

The previous findings indicate that the placement of TWC at the topmost position of the test specimen results in a significant reduction in vibration amplitude compared to other locations. In contrast, mounting TWC at the bottom part of the test specimen was found to be less effective. Therefore, this section presents a concise experimental study conducted to assess the impact of combining the most and least efficient TWC positions on vibration reduction. For this, two TWCs with dimensions 180 × 180 × 180 mm have been concurrently designed at the top and bottom positions of the test specimen, as illustrated in Fig. 5j. Furthermore, these TWCs were partially filled with 2400 g of rubber granulate “RG 4.6 mm”, and the results of this configuration are presented in Figs. 25 and 26.

Fig. 25
figure 25

One-third octave representation of the empty and partially filled SU and mix TWCs. The sum level value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image
Fig. 26
figure 26

Difference in the one-third octave of the partially filled SU and mix TWCs. The sum level value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

For comparison purposes, the FRF spectrum of the TWC 3 and TWC 8 has also been plotted. Notably, the TWC 3 is situated at the topmost position of the test specimen, while the TWC 8 is located at the bottom. Furthermore, the dimensions of TWC 3 and TWC 8 are identical. In Fig. 26 it can be seen that the combination of TWCs can reduce the vibration amplitude of the test specimen significantly higher in comparison to the TWC 3 and TWC 8. One of the reasons for this can be the increased number of rubber granular particles inside the cavities. Furthermore, it is observed that around 500 Hz TWC 8 demonstrates a significantly higher reduction in the vibration amplitude of the test specimen compared to TWC 3. A comparable effect has also been noted around 650 Hz and 950 Hz. Therefore, it is reasonable to assume that around these eigenfrequencies, the bottom part of the test specimen exhibits higher displacement in bending or torsion mode shapes as compared to the upper part. Thus, the overall reduction in vibration of the test specimen experiences a substantial increase when two TWCs are integrated. Nonetheless, additional experimental or numerical investigations can be conducted to measure or compute the eigenmode shapes of the lower section of the test specimen.

Thin-Walled Cavity with Additional Sheets (TWC-AS)

In the thin-walled cavity with additional sheets (TWC-AS), the thickness of the suspended sheet is much smaller in comparison to the wall thickness of the original structure. Hence, the suspended sheet can vibrate easily, which can introduce more vibrating energy into the particles. Thus, the kinetic energy of the vibrating structure and the suspended sheet can increase the collision between the particles themselves as well as between particles and walls. Therefore, it is assumed that the TWC-AS can be more damping efficient in comparison to the TWCs. The TWC-AS is composed of two components, namely: a thin plate of 1.0 mm thickness (base plate) and thin hanging sheets of different sizes. The design and different configurations of the TWC-AS can be seen in Fig. 8. Based on the preceding discussion, it is evident that the top position of the test specimen is the best-suited location to mount a particle damper. For this reason, the TWC-AS is designed at the top position of the test specimen to study its influence on the vibration response of the system. To create TWC-AS inside the hollow test specimen, a thin plate of 1.0 mm thickness is mounted at location 4. Afterward, 2700 g of rubber granulate “RG 4.6 mm” is filled inside the cavity. Subsequently, the TWC-AS is fixed at location 1 of the test specimen, allowing the insertion of suspended thin sheets into the rubber granulate. Furthermore, utilizing this configuration permits the maximum surface of the hanging sheet to be in contact with the rubber granulate particles. Additionally, fixing the TWC-AS at location 1 can considerably simplify the experimental process compared to its installation at location 4. The amount of rubber granulate “RG 4.6 mm” is chosen in such a way that the additional mass of the particle damper does not exceed more than 3%. The dimension of the TWC-AS is similar to the TWC 3. It is known that the empty TWC designed using two thin plates of 1.0 mm thickness modifies the primary vibration characteristic of the test specimen. Moreover, the TWC-AS is similarly comprised of a 1.0 mm thick base plate, and the overall design of the TWC-AS also integrates a 1.0 mm thin plate. Thus, the empty TWC 3 is considered as a reference measurement (black solid line) for evaluating the vibration attenuation due to the TWC-AS, see Fig. 39. To facilitate comparative analysis, the FRF of the partially filled TWC 3 is presented in both a narrow-band spectrum and a one-third octave-band spectrum (magenta color solid line), see Figs. 27 and 39.

Fig. 27
figure 27

One-third octave representation of the test specimen with TWC-AS. The sum level value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

Figures 27 and 28 illustrate that all TWC-AS regardless of their shape, size, or thickness are capable of reducing the vibration amplitude of the test specimen remarkably. Furthermore, it was observed that the damping performance of the majority of TWC-AS is significantly higher in comparison to TWC 3. Around the resonance frequencies of 125 Hz, 400 Hz, and 800 Hz, the TWC-AS with a suspended sheet thickness of 1.0 mm (orange–red dashed line) exhibits significantly higher vibration attenuation compared to the TWC-AS with a suspended sheet thickness of 0.5 mm (saddle brown dashed line). It should be noted that both TWC-AS contain two suspended sheets of identical width and height. However, comparing TWC-AS with a sheet width of 170 mm and height of 45 mm (smaller TWC-AS), the overall damping performance of smaller TWC-AS with a suspended sheet thickness of 0.5 mm (SL value 178.77 dB) is higher than that of the smaller TWC-AS with a 1.0 mm sheet thickness (SL value 179.60 dB). Furthermore, it was noticed that the TWC-AS consisting of four sheets of dimensions 80 mm × 45 mm (compact TWC-AS) is more effective in reducing the vibration amplitude of the test specimen for the low-frequency range (20–300 Hz) in comparison to the compact TWC-AS with two suspended sheets of identical dimensions. For the low-frequency range, the compact TWC-AS with four suspended sheets (dark slate gray dotted line) can achieve vibration attenuation up to 1.2 dB, 7.1 dB, and 6.6 dB around the resonance frequencies of 40 Hz, 125 Hz, and 200 Hz. In contrast, the compact TWC-AS consisting of two suspended sheets (cyan dotted line) is significantly effective for the higher frequency range. Around the resonance frequency of 400 Hz, 630 Hz, and 800 Hz, the compact TWC-AS with two suspended sheets can reduce the vibration amplitude of the primary structure up to 10.1 dB, 7.4 dB, and 7.8 dB, respectively. Additionally, to design the particle damper using compact TWC-AS inverted, the thin plate of 1.0 mm wall thickness is mounted on location 1 of the test specimen and the compact TWC-AS inverted is mounted on location 4. The experimental investigation of this TWC-AS design has shown that it is significantly less effective in comparison to the other TWC-AS. However, around the resonance frequency of 40 Hz, the compact TWC-AS inverted (rosy brown dotted line) is significantly more efficient for vibration attenuation in comparison to the rest of the TWC-AS and can achieve a vibration reduction of up to 16.1 dB.

Fig. 28
figure 28

Difference in the one-third octave band to the partially filled test specimen with TWC-AS. The sum level value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

From the above discussion, it can be concluded that the implementation of TWC-AS can reduce the vibration amplitude of the test specimen remarkably higher in comparison to the best damping-performing of TWC. Consequently, it can be said that the presence of a suspended sheet within the granular materials can introduce more vibration energy into the particles. Hence, the probability of particle–particle and particle–wall collision can increase significantly and this reduces the vibration response of the structure further. In general, the vibration sensitivity of the thin plate is much higher in comparison to the thick plate with identical shapes and sizes. However, the mass of the granular materials can change the vibration characteristic of the plates. In contrast, if the thickness of the plate is too large, then the vibration sensitivity of the plate is not enough to bring the particles of the granular materials into motion. Hence, a certain amount of sheet thickness and stiffness is required to provide motion to filling materials, which is a prominent factor for particle damper design, i.e., the plate should be not too thin or too thick. Nevertheless, just like the design of TWCs, the specific wall thickness of the TWC-AS is subject to the mass of the granular materials. It has been observed that the thin plate of 1.0 mm thickness is more efficient for vibration attenuation than the thin plates having a wall thickness of 0.5 mm and 2.0 mm. For this reason, the TWC-AS with long suspended sheets (extended TWC-AS) of 1.0 mm wall thickness is significantly more effective in comparison to extended TWC-AS with 0.5 mm thickness. Moreover, the size of the suspended sheet has a significant influence on the damping characteristic of the TWC-AS. Longer sheets are more effective in reducing the vibration amplitude of the test specimen. Longer sheets of the TWC-AS have larger contact areas, which increases the probability of particle–wall collision. Thus, it has been observed that the TWC-AS of dimension 170 mm × 105 mm × 1.0 mm (extended TWC-AS) can reduce the vibration amplitude of the test specimen significantly higher in comparison to the TWC-AS of dimension 170 mm × 45 mm × 1.0 mm (smaller TWC-AS). However, it should be noted that the length of the suspended sheet depends on the height of the cavity. Consequently, the length of the suspended sheet can be long enough to induce vibration in the granular materials, but it should be slightly shorter than the cavity height to ensure unrestricted vibration. As it has been observed in the case of TWC, the location of TWC-AS also affects vibration attenuation. Consequently, mounting the TWC-AS at location 1 can achieve significantly higher vibration attenuation in comparison to the TWC-AS mounted at location 4.

To carry out a comparative study, the best-performing TWCs are compared with the highest-performing TWC-AS, see Fig. 29. As mentioned above, it can be also observed here that the TWC 2 (golden rod dashed line) can reduce the vibration amplitude of the structure significantly higher in comparison to the TWC 5 (cadet blue dashed line) and TWC 8 (magenta dashed line). Therefore, it can be concluded that the position exhibiting the maximum displacement is the ideal location for installing a particle damper.

Fig. 29
figure 29

Comparison between the TWC and TWC-AS design variant: Difference in the one-third octave band of partially filled TWC and TWC-AS with various dimensions at the top position of the test specimen. The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

Moreover, it is evident that TWC 8 exhibits a considerably lower ability to reduce the vibration amplitude when compared with other high-performing TWCs. Interestingly, TWC 8 contains an additional 800 g more rubber granulate “RG 4.6 mm”. From the previous discussion, it is apparent that the MU TWC exhibits notably superior damping performance in comparison to the SU TWC. However, despite possessing a higher mass of granular material, the damping performance of MU TWC is significantly lower than that of TWC 2. Thus, it is reasonable to assume that the mass of the granular material does not necessarily enhance the efficiency of a particle damper. Additionally, the overall damping efficiency of the highest-performing TWC-AS (extended TWC-AS) is significantly superior to that of both the best-performing TWCs and MU TWC. However, at the resonance frequency of 400 Hz, extended TWC-AS and TWC 2 yield comparable vibration attenuation. Nonetheless, near 500 Hz TWC-AS performs significantly lower in comparison to TWC 2, TWC 5, and TWC 8. Therefore, it is plausible to hypothesize that the existence of a suspended sheet in TWC-AS could potentially transmit additional vibration energy to the granular particles. Consequently, the effectiveness of TWC-AS is notably superior to that of TWCs.

Ring Cavity Design Variant

To study the influence of the ring cavity (RC) on vibration attenuation, two different ring sizes have been chosen, namely: large RC and small RC, see Fig. 9.

The RCs are mounted at location 4 inside the hollow space of the test specimen. The aim of the RC concept is to decrease the additional weight of the particle damper while preserving or enhancing its vibration-damping effectiveness. Therefore, to experimentally investigate this concept, the rubber granulate “RG 4.6 mm” inside the RC is distributed in three different patterns, namely: outside the ring (configuration 1), inside the ring (configuration 2), and both inside and outside the ring (configuration 3), see Fig. 10. The results obtained for the RC experimental studies have been plotted in Figs. 30 and 31. To facilitate comparison, the frequency spectrum of TWC consisting of a single thin plate of 1.0 mm thickness, which is also mounted at location 4 of the test specimen, is plotted. As evident from the preceding discussion, empty TWC and TWC-AS alter the vibration characteristics of the primary structure. Likewise, empty RC irrespective of their ring height also modifies the vibration characteristic of the test specimen, see Fig. 40. Thus, to compute the actual amount of vibration reduction due to RC and TWC, the level of partially filled particle dampers is subtracted from their corresponding empty variant. In Fig. 31, it can be seen that around the resonance frequencies of 40 Hz, 315 Hz, and 500 Hz, the damping efficiency of TWC with a single thin plate is higher in comparison to the large RC and small RC. For large RC it has been observed that the vibration attenuation achieved by configuration 1 (yellow–orange dashed line) is nearly equivalent to the vibration reduction obtained by configuration 3 (lawn green dashed line), see Fig. 31. Around the central frequency of 200 Hz, 500 Hz, and 630 Hz, both configurations, i.e., configuration 1 and configuration 3 can reduce the vibration amplitude of the test specimen up to 5.4 dB, 20 dB, and 4.6 dB, respectively. However, for the central frequencies 125 Hz, 800 Hz, and 1000 Hz, distributing the rubber granulate only on the outside of the large RC ring can be more effective for damping the structure. In contrast, the damping performance of RC increases around the resonance frequencies of 40 Hz, 315 Hz, ad 400 Hz, by allocating the rubber granulate both inside and outside of the large RC ring. Nevertheless, the difference in vibration attenuation achieved by configurations 1 and 3 is marginally less. Furthermore, configuration 2, in which the rubber granulate is only filled inside the ring, can also reduce the vibration amplitude of the test specimen significantly. Nonetheless, the overall damping performance of configuration 2 is significantly less in comparison to the other two configurations. One of the reasons for this can be that are no particles in contact with the vibrating primary structure (which is of interest and measured). Furthermore, particles of the granular material inside the ring can either collide within themselves or with ring walls. However, in configuration 1 and configuration 3, particles of the rubber granulate can collide within themselves, with the ring walls as well as with the primary structure walls. Therefore, the probability of particle–particle and particle–wall collision is higher for configuration 1 and configuration 3. A very similar damping trend was also observed for all the rubber granulate distribution patterns inside the small RC. Furthermore, comparative studies between the large and small RC containing a similar amount of rubber granulate “RG 4.6 mm” have been carried out. For this purpose, configuration 3 has been chosen and 2700 g of rubber granulate “RG 4.6 mm” is filled inside the large and small RC. It has been observed that around the resonance frequencies 200 HZ, 400 Hz, and 500 Hz, the large RC, which is partially filled with 2700 g of rubber granulate, can reduce the vibration amplitude of the test specimen up to 5.5 dB, 13 dB, and 20 dB, respectively, which is significantly higher in comparison to the small RC, which is also partially filled with 2700 g of rubber granulate. However, the small RC is more effective at reducing the vibration amplitude of the structure than the large RC within the frequency range of 600 − 1000 Hz. However, the overall damping efficiency of the larger (and consequently softer) RC is significantly better than the small RC.

Fig. 30
figure 30

One-third octave representation of the RC design variant. The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image
Fig. 31
figure 31

Difference in the One-third octave band representation of the ring cavity design variant. The sum level (SL) value of the surface velocity is given in dB and the mass of the granular filling materials is given in g

Full size image

Based on Figs. 30 and 31, it is evident that implementing RC results in significantly higher vibration attenuation compared to the TWC with a single thin plate. Moreover, it was observed that the granular material distribution pattern can reduce the additional mass of the granular material significantly. For instance, the granular material mass in the configuration in which the rubber granulate is distributed only outside the ring is 18% less than the setup in which the rubber granulate is distributed both inside and outside the ring. Furthermore, it has been also observed that granular material distribution plays a major role in vibration attenuation. From the above discussion, it can be assumed that the thin ring of rectangular shape in direct contact with the primary structure as well as granular materials can induce vibration energy into the particles because of their vibration-sensitive nature. Thus, the chances for particle–particle and particle–wall collision increase, which lowers the system response. Nevertheless, a ring shape optimization can improve the vibration attenuation further.

Industrialization

Laboratory-scale experimental studies have demonstrated that all the design variations presented in this paper can effectively reduce the vibration amplitude of the test specimen. To evaluate these approaches on an industrial scale, a commercial wind turbine generator has been selected for testing, see Fig. 32a. The vibration and sound emissions from a wind turbine result from the relative movement of its mechanical elements and the dynamic responses occurring within these components. The generator is a prominent source of sound emission. Within the generator, vibrations are generated by electromagnetic interactions between the rotating rotor poles and the stator. These vibrations are subsequently transmitted to other sections of the turbine, leading to the emission of sound into the surrounding environment. To apply the particle damper concept to the wind turbine generator, the stator of the generator has been chosen to neglect the impact of centrifugal force on the particle damper efficiency. All the concepts investigated on a laboratory scale have been integrated, revealing that the design strategies initially developed in the lab can also significantly reduce the vibration amplitude of a real-scale wind turbine generator, see Fig. 32. A reduction of 4 dB at the most prominent tonal component was achieved. However, detailed experimental configurations and approaches cannot be presented in this paper due to confidential reasons.

Fig. 32
figure 32

a Particle dampers at different positions on a real-scale wind turbine generator. b Exemplary result of the acceleration for an arbitrarily selected sensor position with and without particle damper

Full size image

Summary and Outlook

The purpose of this paper is to present various strategies for the design of particle dampers, with a particular focus on their appropriateness for application in large-scale hollow structures. In the current contribution, thin-walled cavity (TWC), thin-walled cavity with the additional sheet (TWC-AS), and ring cavity (RC) design variants have been introduced. The proposed technique of the TWC variant involves the use of thin plates with varying wall thicknesses to generate a defined cavity within the hollow section of the specimen. It should be noted that the wall thickness of the thin plates is significantly smaller than that of the primary structure. Due to their reduced thickness, the plates can vibrate easily and consequently introduce more vibration energy into the particles. Hence, the damping efficiency of the system can be considerably enhanced. It was observed that the wall thickness of the plates can influence the damping performance of a TWC. It is interesting to note that the TWC design variant consisting of a 1.0 mm plate thickness is overall significantly more efficient in comparison to the TWC consisting of plates of thickness 0.5 mm and 2.0 mm. Therefore, it is advisable to maintain a particular wall thickness for the TWC design in order to minimize the influence of the mass of the granular materials on the vibration characteristics of the TWC. Nevertheless, determining the specific wall thickness of the TWC depends on factors such as the available hollow space within the test specimen, the test specimen wall thickness, and the mass of the granular materials. Furthermore, the location and size of the particle dampers also play a crucial role in vibration attenuation. Thus, three different positions and dimensions of the TWC variant were investigated. The results show that mounting the damper around the region of the mode shape with a larger displacement or surface velocity can be more effective for vibration attenuation. The studies on the influence of TWC dimensions with a fixed filling volume on vibration attenuation have shown that TWC 2 of dimension 180 × 180 × 120 mm is more effective than TWC 1 (180 × 180 × 60 mm) and TWC 3 (180 × 180 × 180 mm). Hence, it can be suggested that the mass of the granular material is not the sole reason for vibration reduction, and a higher mass can even restrict the relative motion of particles at the lower layer. Thus, it is possible that a certain amount of rubber particles in the thin plate particle damper with a bigger cavity size does not contribute to the particle damping mechanism and behaves almost like a rigid mass. It is known that the configurations like single-unit and multi-unit particle dampers are other particle dampers parameters that can influence the system response. In the current contribution, the studies demonstrate that a single-unit TWC is more efficient in reducing the low-frequency vibration amplitude of the system. Conversely, a multi-unit TWC is more effective in reducing high-frequency vibration amplitudes. However, the overall damping performance of the multi-unit TWC is significantly higher in comparison to the single-unit TWC. The reason behind this can be the availability of a higher number of thin plates inside the multi-unit TWC design, which can induce more vibration energy into the granular materials. Hence, the damping performance of a multi-unit TWC increases hugely. Moreover, the particle dampers are mounted at the most and the least performing location on the test specimen simultaneously. The outcome of this configuration has shown a tremendous damping performance, meaning the combination was in the whole frequency range better than the single combined configurations (while causing much more additional mass).

Furthermore, to make the TWC design variant even more efficient for vibration attenuation, the TWC-AS has been developed. This variant consists of two or more hanging sheets, which are attached to a base plate of 1.0 mm wall thickness. The primary concept underlying this design is to bring an extra vibration-sensitive structure into the overall system, which can be in direct contact with granular materials. The ultimate goal is to increase the amount of vibration energy transferred to the particles of granular materials. The damping performance of the TWC-AS is influenced by various factors, such as their shape, size, and thickness, as well as the number of hanging sheets. Therefore, an experimental investigation was conducted to study the impact of these multiple parameters on the vibration attenuation capabilities of the TWC-AS. The outcome of the studies shows that the implementation of the TWC-AS can reduce the vibration amplitude of the test specimen remarkably in comparison to the best-performing TWC variant. Hence, it can be concluded that the extra thin suspended sheet can induce more vibration energy in the particles of the granular material, which can increase the probability of particle–particle and particle–wall collision. Like the TWC design concept, in the case of TWC-AS, the thickness of the suspended sheet is influenced by the mass of granular materials. Additionally, it has been noted that a longer sheet can enhance vibration attenuation, with its length contingent upon the height of the cavity.

The mass of the granular material is another factor, which can restrict the real-world application of particle damper. Therefore, to address this challenge, the current contribution has proposed an RC design variant. It has been observed that the RC can reduce the vibration amplitude of the test specimen significantly in comparison to the TWC variant containing the same amount of rubber granulate “RG 4.6 mm”. Furthermore, several distribution patterns of the granular material inside the RC have been studied. It has been shown that the additional mass of the granular material can be reduced by 18% either by maintaining the same value of vibration reduction or by increasing the vibration reduction of the test specimen around several resonance frequencies. However, further design optimization is required for the ring shape to make the ring cavity design variant more efficient. In general, it seems to be the case that a large area contact with the primary structure of interest is beneficial.

Furthermore, incorporating all the concepts studied on a laboratory scale, it has become evident that the design strategies initially conceived in the laboratory can also effectively reduce the vibration amplitude of a real-scale wind turbine generator.

This paper has presented various design variants for reducing the vibration amplitude of a hollow-structured test specimen. Depending on the specific application criteria, one can opt for either a TWC, TWC-AS, or RC design variation. Moreover, it’s possible to create a particle damper by integrating all three proposed variations into a single system, thus harnessing the benefits of each design variant. This integrated approach has been successfully tested on a real-scale wind turbine generator. The results obtained can be applied to design a particle damper for other real-world large hollow structures beyond wind turbines.