Turbine Inlet Valve’s Self-Excited Vibrations Risk the Safe Operation of Hydropower Plants

Abstract

Purpose

The main function of the turbine inlet valve (TIV) in a hydroelectric power plant is to prevent flow of water to the turbine whenever the turbine is not operating. Usually, the valve responsible for this operation is spherical with annular seals to perform the sealing function. Occasionally, when the valve is set into a closed orientation, the annular seal may not execute its sealing function properly though develop periodic oscillations accompanied by periodic leakage flows. These seal vibrations cause pressure fluctuations in the penstock pipeline, which risks the plant’s reliable and safe operation. Therefore, the primary goal of this research is to present a simplified theoretical model, able to clarify the excitation mechanism of the periodic seal vibration and simulate the plant’s transient behavior. Afterwards, develop some recommendations to enhance the stable operation of the (TIV).

Methods

The system governing equations comprises the water hammer equations to model the water flow through the various pipelines, the vibrating seal equation of motion, and the system boundary conditions.

Results

The dynamic instability of the (TIV) vibrations is more likely to arise at higher input reservoir energy levels and at the first harmonic of the seal oscillation. In addition, modifying the (TIV) by increasing pilot pipeline head losses and reducing its diameter can eliminate the (TIV) vibrations and warrant the plant’s safe operation.

Conclusion

Results revealed that fluid compressibility and acoustic transmission have a decisive effect on the fluid-dynamic forces acting on the seal and the (TIV) stability. In addition, the origin of the (TIV) vibrations is the valve leakage flow through the service seal.

Introduction

Hydropower generates almost one-sixth of the global power generation, trailing only natural gas and coal [1]. The industry’s contribution to power production is almost 55% more than nuclear technologies and greater than all other renewable energy resources combined, including solar PV, wind, geothermal, and bioenergy [2]. Thus, performing transient flow analysis on the hydropower plants is essential to maintain the safe and reliable operation of the power plants.

A hydroelectric power plant consists of a reservoir, penstocks, a turbine inlet valve (TIV), a turbine-generator mechanism for producing electricity, and a draft tube to discharge the water flow out of the turbine, such as the Salime power plant. The Salime plant is a reservoir power plant located in the southwestern area of Asturias, Spain [3]. The plant has a nominal head of 105 m and 160 MW rated output power, divided into four power units with a 170 m³/s joint flow rate. Each unit consists of a Francis turbine coupled to an electric generator on a vertical shaft. Furthermore, each unit has its own 80 m long penstock, as well as its own valves and control elements, allowing each unit to operate independently, as shown in Fig. 1.

Fig. 1

Layout of the main hydraulic elements for each unit of the Salime power plant

The turbine inlet valve (TIV) at the Salime plant is a spherical (ball) valve that prevents water flow to the turbine when it is not operating or is undergoing maintenance. The (TIV) at the Salime power plant comprises two annular metal seals and a ball with a bore in the midst, as in Fig. 2a, b. The upstream seal is the fixed maintenance seal that provides additional water tightness (i.e., under manual operation) when the service seal malfunctions. On the other hand, the sliding service seal is responsible for blocking any leakage flow between the valve casing and the ball.

Fig. 2

Description of the (TIV) at the Salime power plant. a Spherical valves at the Salime power house, before (left) and after (right) installation. b Spherical valve in closed position with pilot pipeline to transmit penstock pressure. c The Sliding seal operation

When the ball valve is closed, in normal situations, the penstock water pressure flows thru the pilot pipe and presses the seal against its seat on the ball’s surface, as shown in Fig. 2b, c. As a result, the seal seats on the ball surface, blocking any leakage flow. In practice, however, when the turbine is not working and the valve is oriented into a close position, the service seal starts to vibrate instead of staying fixed to the ball surface. These periodic vibrations were observed as violent internal hits coupled with significant pressure fluctuations, which can surpass the penstock’s pressure security limit of 13.5 Bar in case no security actions are applied, as shown in Fig. 3.

Fig. 3

Penstock pressure signal recorded at the (TIV) upstream side at a vibratory episode of the valve of unit number 3 [4]

Unfortunately, during this vibration incident, the Salime plant’s acquisition system can only register one data per second, so the signal quality has been insufficient for appropriate dynamic analysis. Although according to the subjective perception of the plant technicians, the tapping frequency would be of the order of 1–3 Hz. In addition, the likeliness of the vibratory events might increase when the reservoir’s water level falls below the maximum value; but no clear trend was established by the technicians.

This phenomenon ceased once an alarm sensor installed near the (TIV) revealed a pressure value surpassing the penstock pipeline’s pressure security limit. The alarm sensor caused the butterfly valve at the penstock’s entrance, as in Fig. 1, to close, eliminating the pressure oscillations and the seal vibrations, as in Fig. 3. Although the butterfly valve closure solved the problem, this solution was not favorable for managers of the power plant due to the subsequent reasons: first, the subsequent operation following this event is more complex and takes a longer time compared to usual conditions. Second, there was high water leakage flow passing through the valve, and lastly, there were not extra security measures if another unexpected event happens.

Therefore, in the meantime, another solution is applied at the power plant to overcome these drawbacks according to the following hypothesis. Since no external force was applied to the seal to cause the periodic seal oscillations, the seal vibrations are expected to be self-excited [5] as a result of an unsteady leakage flow passing through a gap that may exist between the ball surface and the service seal. This gap may be a result of the subsequent causes: (1) deficiency of water pressure forces applied to the seal after the valve closure, (2) seal manufacturing defect, or (3) inaccurate seal assembly. Consequently, an additional compressed air system is installed at the pilot pipeline of the (TIV), which aims to ensure the seal’s full closure by augmenting the pressure forces applied to the seal. Indeed, this solution effectively eliminated the periodic seal’s vibration and solved the first solution’s drawbacks, although it was noticed on several occasions that the (TIV) vibrations still appear if the compressor does not operate or if there is a delay in the operation of the compressor air system.

In fact, the trouble of (TIV) self-excited vibrations has long been recognized in various power plants, though cases mentioned in the literature are pretty scarce. Abbott et al. in 1963 [6] and Wylie and Streeter in 1965 [7] studied the penstock’s self-excited vibrations and pressure fluctuations due to the leakage of the penstock valve at the Bersimis No. 2 power station (Canada). System analysis revealed that the valve leakage caused by the deficiency of pressure forces applied to the inflatable seal was the source of the penstock's pressure fluctuations. Gummer in 1995 [8] reported on significant pressure fluctuations in the penstock pipeline throughout priming as well as load rejection at the Maraetai 1 hydro station (New Zealand). In a similar way, head gate seal leakage caused by insufficient oil pressure application was the cause of these pressure oscillations. More recently, Caney and Zulovic [9] in 2004 and Kube et al. [10] in 2010 investigated the penstock pressure oscillations at the Gordon power plant (South-West Tasmania) utilizing a computer code-named (Hytran solutions). Likewise, the developed pressure fluctuations were caused by the leakage of the (TIV), which was a spherical valve as in the case of the Salime plant. The computer code exhibited the ability to compute the frequency of pressure oscillations. However, it could not calculate the correct pressure oscillation values due to neglecting the dynamic characteristics of the seal. Finally, Chaudry in 2014 [11] used a leakage flow velocity graph to compare the stability conditions of a normal valve and a leaking valve. It is observed that for a stable normal valve, a system disruption triggered by altering the velocity of the leakage flow diminishes over a period of time until it reaches steady-state conditions. On the other hand, a system disturbance increases over time for a leaking valve.

In accordance with the mentioned studies, (TIV) vibration is a significant issue that can jeopardize the power plant's safe and reliable operation. In fact, the authors have previously studied the problem of the (TIV) vibration in the Salime plant as in [12, 13]. In these studies, the developed theoretical models can explain the cause of the (TIV) vibrations as well as compute the maximum value of the pressure oscillations. However, they could not calculate the frequency of both the (TIV) vibration and the pressure oscillations, which is in the range of 1 to 3 Hz as proclaimed by the technicians in the power plant. According to Chaudry [11], if the pipeline flow oscillation speed L_j ω is minimal compared to the pipeline wave speed a_j (i.e., $\frac{{L}_{j}\omega }{{a}_{j}} \ll 1$), the system can be modeled as a lumped system where fluid compressibility effects can be neglected. But for the case of the Salime power plant, by considering the proclaimed frequency range, the 80 m penstock length, and the pipeline wave speed of 1275 m/s, the $\frac{{L}_{j}\omega }{{a}_{j}}$ is not much smaller than one. Thus, it is believed that the previous established models could not predict the frequency of the (TIV) oscillations because fluid compressibility and pipeline wall elasticity effects were neglected.

Therefore, the first goal of this research is to create a simplified theoretical model capable of explaining and computing the self-excited vibrations of the (TIV) while considering fluid compressibility and pipeline wall elasticity effects, seal dynamic characteristics, and power plant relevant data. The second aim is to establish the conditions of the stable and unstable operation of the (TIV), in which an evaluation stage for these stability conditions will be carried out under various system configurations to deliver some suggestions on how to improve the (TIV) dynamic performance related to the seal’s vibrations. Finally, this research makes a contribution to the sustainable development goals (SDGs) number 7 and 9, since the outcomes of this work can enhance the reliable and safe operation of the power plant (target 7.1) and improve the manufacturing of the (TIV) (target 9.5).

Theoretical Model

Preliminary Assessment of the (TIV) Dynamic Behavior Leading to the Model Construction

As stated in the introduction, the (TIV) dynamic behavior is believed to be a result of the seal’s vibration due to the unsteady leakage flow passing through the gap between the ball surface and the service seal. This kind of vibration is correlated to a category named movement-induced excitation flow-induced vibrations, as the vibrations of the seal are self-excited [5]. Regarding the case at hand, if the seal is disturbed, the flow rate on both sides of the seal varies due to the clearance of the seal. Hence, the pressure force applied to the service seal varies where the seal begins to vibrate because of the elasticity of the seal’s structure. In this case, as the fluid system and the seal start to oscillate, they couple in a way that the energy source for the seal’s oscillatory motion is the fluid system. In case that the energy provided by the fluid system surpasses the system’s dissipation energy, the system becomes dynamically unstable. In this circumstance, the pressure fluctuations and the seal oscillations amplitudes augment until they reach the limit cycle oscillations, where the energy provided by the fluid system is equal to the system’s dissipation energy.

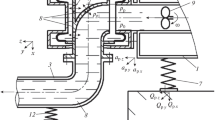
In order to keep the theoretical model as simple as possible while containing the real plant relevant data, it was decided to take into account the (TIV) scheme of Fig. 4a in addition to the hydro-mechanical model describing every group of the Salime power plant as in Fig. 4b. The presented system’s relative dimensions and positions are specified such as in Table 1.

Fig. 4

a Simplified diagram of the closed valve with relevant positions. b Simplified hydro-mechanical diagram for each group of Salime hydroelectric power plant with seal physical features, notations and vibration coordinate

Table 1 Relative positions and dimensions of the Salime power plant hydro-mechanical model

The (TIV) dynamic behavior is computed in two steps as it is assumed that the (TIV) vibrations are self-excited because of the presence of unsteady leakage flow. The first step is calculating the dynamic fluid force applied to the seal due to the existence of the unsteady leakage flow, while the following step is solving the equation of motion of the seal to determine the dynamic behavior of the valve.

Calculation of the Dynamic Fluid Force Applied to the Seal

According to Fig. 4a, b, three types of equations are considered to calculate the dynamic fluid force applied to the service seal. First, the water hammer equations are applied for the pipelines to compute the unsteady pressure and flow rate taking into consideration fluid compressibility and pipeline wall elasticity effects [11]. In addition, for the system boundary conditions, presented in the system different junctions and the fluid flow through the service seal clearance, the continuity and the energy equations are applied [14]. Therefore, the fluid system governing equations constructing the theoretical model for the Salime power plant are as follows:

1. Pipeline j water hammer equations:

Continuity equation:

$$\frac{{g A_{j} }}{{a_{j}^{2} }} \frac{\partial H}{{\partial t}} + \frac{\partial Q}{{\partial x}} = 0.$$

(1)

Momentum equation:

$$\frac{\partial H}{{\partial x}} + \frac{1}{{g A_{j} }}\frac{\partial Q}{{\partial t}} + \frac{{f_{j} Q_{j}^{n} }}{{2gd_{j} A_{j}^{n} }} = 0.$$

(2)

2. System boundary conditions:

Branching junction at point 2:

$$H_{2}^{L} = H_{2}^{r} = H_{3}^{L}$$

(3)

$$Q_{2}^{L} = Q_{2}^{r} + Q_{3}^{L} .$$

(4)

Service seal inlet boundary at point 4:

$$H_{4}^{L} + \frac{{Q_{4}^{{L^{2} }} }}{{2gA_{b3}^{2} }} = H_{4}^{r} + \frac{{Q_{4}^{{r^{2} }} }}{{2gA_{g}^{2} }}$$

(5)

$$Q_{4}^{L} = Q_{4}^{r} .$$

(6)

Oscillating service seal boundary at point 45:

$$H_{4}^{r} + \frac{{Q_{4}^{{r^{2} }} }}{{2gA_{g}^{2} }} = H_{5}^{L} + \frac{{Q_{5}^{{L^{2} }} }}{{2gA_{g}^{2} }}$$

(7)

$$Q_{5}^{L} = Q_{4}^{r} + i\omega A_{ss} y.$$

(8)

Service seal exit boundary at point 5:

$$H_{5}^{L} + \frac{{Q_{5}^{{L^{2} }} }}{{2gA_{g}^{2} }} = H_{5}^{r} + \frac{{Q_{5}^{{r^{2} }} }}{{2gA_{d}^{2} }} + \frac{{Q_{5}^{{r^{2} }} }}{2g}\left( {\frac{1}{{A_{g} }} - \frac{1}{{A_{d} }}} \right)^{2}$$

(9)

$$Q_{5}^{L} = Q_{5}^{r} .$$

(10)

Oscillating dead-end boundary at section 3r_r :

$$Q_{3}^{r} = i\omega A_{os} y.$$

(11)

The fluid system governing equations can be solved in the time domain using the method of characteristics (MOC) or in the frequency domain using the transfer matrix or the impedance method. The water hammer equations and the system boundary conditions are solved in the frequency domain using the transfer matrix method due to its simplicity and low computational time compared to the (MOC). In addition, applying the transfer matrix method to compute the mentioned equations is appropriate since the developed model considers decayed or diverged sinusoidal pressure and flow rate oscillations (i.e., according to the stability of the periodic seal’s oscillations), linear friction terms, and linear boundary conditions.

Transfer Matrix Method

By applying the transfer matrix method, the instantaneous pressure head H and discharge Q are split into mean components and time-dependent components superimposed over them (i.e., Q = Q_o + q and H = H_o + h), where the oscillated pressure head h and discharge q are complex variables function of time t and distance x along the pipeline as follows:

$$h = {\text{Re}}\left( {h\left( x \right)e^{i\omega t} } \right)$$

(12)

$$q = {\text{Re}}\left( {q\left( x \right)e^{i\omega t} } \right).$$

(13)

The transfer matrix method calculates the fluid system transient behavior by computing the following three transfer matrices. The first transfer matrix is the field transfer matrix F_j, which relates the upstream state variables (pressure and flow rate oscillations) to the downstream state variables of pipeline j. The second transfer matrix is the point transfer matrix P_j that relates the state variables just to the right and to the left of a boundary condition j. Finally, the third transfer matrix is the overall transfer matrix U, which relates the downstream state variables of a system to the upstream state variables.

For the case of interest, the seal oscillations are of diverging or decaying amplitude (i.e., depending on system stability) as the seal vibrations are self-excited. Therefore, the system components transfer matrices (i.e., field and point transfer matrices) are written for the free-damped oscillation as the related pressure and flow rate oscillations are expected to be as well of decayed or diverged amplitudes. Thus, to represent the free-damped oscillations, the estimated transfer matrices are written by replacing iω with the complex frequency iω + δ [11].

Pipeline Field Transfer Matrix (F _j)

For free-damped oscillations, the field transfer matrix relating the downstream and upstream state variables of a pipeline j can be computed as follows [11]:

$$Z_{j + 1}^{L} = F_{j} Z_{j}^{R} ,$$

(14)

where ${Z}_{j+1}^{L}$ and ${Z}_{j}^{R}$ represent the state vectors that comprises the state variables ($h \, \mathrm{and} \, q$) at both ends of a pipeline j, as in Fig. 5, while ${F}_{j}$ resembles the pipeline j field transfer matrix.

Fig. 5

Boundaries of pipeline j

In matrix notation, Eq. (14) becomes

$$\left[ {\begin{array}{*{20}c} q \\ h \\ \end{array} } \right]_{j + 1}^{L} = \left[ {\begin{array}{*{20}c} {\cosh \left( {\mu_{j} L_{j} } \right)} & { - \sinh \left( {\mu_{j} L_{j} } \right)\frac{1}{{Z_{j} }}} \\ { - \sinh \left( {\mu_{j} L_{j} } \right)Z_{j} } & {\cosh \left( {\mu_{j} L_{j} } \right)} \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} q \\ h \\ \end{array} } \right]_{j}^{r} ,$$

where $\mu_{j} = \sqrt {\left( {\frac{i\omega + \delta }{{a_{j} }}} \right)^{2} + \frac{{g\left( {i\omega + \sigma } \right)R_{j} A_{j} }}{{a_{j}^{2} }}}$ and $Z_{j} = \frac{{\mu_{j} a_{j}^{2} }}{{g\left( {i\omega + \delta } \right)A_{j} }}$where Z_j represents pipeline j characteristic impedance, R_j resembles pipeline j friction losses, a_j is pipeline j wave speed, and iω + δ is the complex frequency for free-damped oscillations.

Point Transfer Matrix (P _j)

For the case under consideration, there are two boundary conditions the branch with an oscillating dead end, as in Fig. 4b section 3r, and the valve service seal. The following sections present the computation of the point transfer matrices related to these boundary conditions.

Branching Junction with an Oscillating Dead End (Point matrix P₂)

To estimate the mainline $\overline{12\dots 6 }$ overall transfer matrix, the branching junction point transfer matrix P₂, as in Fig. 4b, must be calculated first. To compute P₂, the boundary condition at section 3_r must be specified [11]. Therefore, as there is no other forces boundaries at the branch, and by considering ${Q}_{3}^{r}=\left(i\omega +\delta \right){A}_{os}y$ and neglecting the head losses at point 2, the branch junction with oscillating dead-end point transfer matrix P₂ can be computed as follows:

$$Z_{2}^{r} = P_{2} Z_{2}^{L} .$$

(15)

In matrix notation, Eq. (15) becomes

$$\left[ {\begin{array}{*{20}c} q \\ h \\ Y \\ \end{array} } \right]_{2}^{r} = \left[ {\begin{array}{*{20}c} 1 & {\frac{{ - \sinh \left( {\mu_{d} L_{d} } \right)}}{{Z_{c} \cosh \left( {\mu_{d} L_{d} } \right)}}} & {\frac{{ - A_{os} \left( {i\omega + \delta } \right)}}{{\cosh \left( {\mu_{d} L_{d} } \right)}}} \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} q \\ h \\ Y \\ \end{array} } \right]_{2}^{L} .$$

Valve Service Seal Transfer Matrix (P _v)

In the presented hydro-mechanical model, the valve service seal point transfer matrix P_v is divided into three-point transfer matrices. The first point P₄ represents the seal inlet point transfer matrix at point 4. The second point P₄₅ presents the oscillating service seal point transfer matrix at point 45 between sections 4r_r and 5_L. Finally, the third point P₅ resembles the seal exit point transfer matrix at point 5, as in Fig. 4b.

The point transfer matrix at points 4 and 5 can be computed by relating the energy head and the flow rate at both sides of points 4 and 5. Using the energy and continuity Eqs. (5, 6, 9, and 10), linearizing the nonlinear equations, and converting the developed linearized equations into the frequency domain using Eqs. (12 and 13) for free-damped oscillations, ${P}_{4}$ and ${P}_{5}$ can be computed as follows:

$$\left[ {\begin{array}{*{20}c} q \\ h \\ Y \\ \end{array} } \right]_{4}^{r} = \underbrace {{\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ {\frac{{Q_{{o_{b} }} }}{g}\left( {\frac{1}{{A_{b3}^{2} }} - \frac{1}{{A_{{o_{g} }}^{2} }}} \right)} & 1 & { - \frac{{Q_{{o_{b} }}^{2} L_{o} }}{{gA_{{o_{g} }}^{3} }}} \\ 0 & 0 & 1 \\ \end{array} } \right]}}_{{P_{4} }}\left[ {\begin{array}{*{20}c} q \\ h \\ Y \\ \end{array} } \right]_{4}^{L}$$

(16)

$$\left[ {\begin{array}{*{20}c} q \\ h \\ Y \\ \end{array} } \right]_{5}^{r} = \underbrace {{\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ {\frac{{2Q_{{o_{g} }} }}{{gA_{c}^{2} }}\left( {\frac{{A_{c} }}{{A_{{o_{g} }} }} - 1} \right)} & 1 & {\frac{{Q_{{o_{g} }}^{2} L_{o} }}{{gA_{d} A_{{o_{g} }}^{2} }}} \\ 0 & 0 & 1 \\ \end{array} } \right]}}_{{P_{5} }}\left[ {\begin{array}{*{20}c} q \\ h \\ Y \\ \end{array} } \right]_{5}^{L} .$$

(17)

The point transfer matrix P₄₅ can be calculated in the same manner as in P₄ and P₅ while neglecting the head losses between section 4_r and 5_L, and applying the continuity and energy Eqs. (7 and 8). Accordingly, P₄₅ can be calculated as follows:

$$\left[ {\begin{array}{*{20}c} q \\ h \\ Y \\ \end{array} } \right]_{5}^{L} = \underbrace {{\left[ {\begin{array}{*{20}c} 1 & 0 & {\left( {i\omega + \delta } \right)A_{ss} } \\ 0 & 1 & { - \frac{{Q_{{o_{g} }} \left( {i\omega + \delta } \right)A_{ss} }}{{g A_{{o_{g} }}^{2} }}} \\ 0 & 0 & 1 \\ \end{array} } \right]}}_{{P_{45} }} \left[ {\begin{array}{*{20}c} q \\ h \\ Y \\ \end{array} } \right]_{5}^{L} .$$

(18)

Overall Transfer Matrix U

After computing system components transfer matrices, a general block diagram of the hydro-mechanical model is drawn as in Fig. 6. The inner blocks represent system component’s transfer matrices. The overall transfer matrix U is computed by multiplying the field and point transfer matrices in order from the right side to the left side to relate upstream and downstream state variables as follows:

$$\begin{gathered} Z_{6}^{L} = UZ_{1}^{r} \hfill \\ U = F_{c} P_{5} P_{45} P_{4} F_{b1} P_{2} F_{a} . \hfill \\ \end{gathered}$$

(19)

Fig. 6

Transfer matrix block diagram of the hydro-mechanical model

The field transfer matrices of pipelines a, b, c and d can be computed by utilizing Eq. (14). However, since R_j alters due to pipeline minor losses and type of flow, each pipeline friction losses presented in Fig. 4b are calculated as follows:

$$R_{a} = \frac{{f_{a} Q_{{o_{a} }} }}{{gd_{a} A_{a}^{2} }},\;R_{b} = \frac{{f_{b1} Q_{{o_{b} }} }}{{gd_{b} A_{b1}^{2} }} + \frac{{Q_{{o_{b} }} \left( {\frac{1}{{A_{b2} }} - \frac{1}{{A_{b3} }}} \right)^{2} }}{{2gL_{b1} }},\;R_{c} = \frac{{f_{c} Q_{{o_{c} }} }}{{gd_{c} A_{c}^{2} }}\;{\text{and}}\;R_{d} = \frac{32 \nu }{{gd_{d} A_{d}^{2} }} + K_{Ld} .$$

Service Seal’s Equation of Motion

As stated in the introduction, the clearance between the ball surface and the service seal is believed to be the cause of the periodic seal vibrations and the related penstock pressure fluctuations. According to the structure of the seal, it is anticipated that one part of the seal adheres to the ball surface while the other part deflects away from it, as shown in Fig. 7.

Fig. 7

(TIV) service seal specifications. a Service seal section view. b Side view of the un-deformed service seal with dimensions in mm. c Deformed service seal side view with maximum clearance position

In order to compute the (TIV) vibrations related to the seal’s oscillations, the seal structure mass, stiffness, and damping coefficients corresponding to the clearance circumference length ${L}_{o}$ are calculated first. Thus, the seal structure coefficients are computed in the same way as in [12], where an average seal vibration displacement and mean seal clearance thickness are taken into consideration:

$$m_{sg} = m_{s} \left( {\frac{{{\uptheta }_{{\text{g}}} }}{2\pi }} \right)$$

(20)

$$k_{sg} = \frac{720 E I}{{L_{o}^{3} }}.$$

(21)

where $L_{o} = L_{s} \left( {\frac{{{\uptheta }_{{\text{g}}} }}{2\pi }} \right)$, $L_{s} = \pi \emptyset$, and ${\uptheta }_{{\text{g}}}$ is the gap angle corresponding to the clearance circumference length $L_{o}$

$$c_{sg} = 2\xi \sqrt {m_{sg} k_{sg} } .$$

(22)

Once the dynamic fluid force applied to the seal is determined, the periodic seal’s oscillations can be calculated employing the equation of motion of the seal [15] as follows:

$$m_{sg} \ddot{y} + c_{sg} \dot{y} + k_{sg} y = F\left( t \right)$$

(23a)

System Stability Conditions

For the case under consideration, the hydrodynamic force exerted on the seal depends only on the seal vibration motion since the vibration of the seal is self-excited [5]. Therefore, the hydrodynamic force applied to the seal can be presented as parameters function of the seal vibration components $y$, $\dot{y}$ and $\ddot{y}$ [5]. In consequence, the vibrating seal equation of motion can be presented as in Eq. (23b) where ${m}_{w}$, ${c}_{w}$ and ${k}_{w}$ are the added water mass, damping and stiffness coefficients representing the fluid dynamic force as follows:

$$\begin{gathered} m_{sg} \ddot{y} + c_{sg} \dot{y} + k_{sg} y = F\left( t \right) \hfill \\ \underbrace {{\left( {m_{sg} + m_{w} } \right)}}_{{m_{eq} }}\ddot{y} + \underbrace {{\left( {c_{sg} + c_{w} } \right)}}_{{c_{eq} }}\dot{y} + \underbrace {{\left( {k_{sg} + k_{w} } \right)}}_{{k_{eq} }}y = 0. \hfill \\ \end{gathered}$$

(23b)

The developed seal equation of motion Eq. (23b) presents the behavior of a free vibration damped system where the characteristic root of Eq. (23b) designates the seal vibration behavior. The characteristic root of the seal equation of motion is considered to be the same as the time-dependent pressure and flow rate complex frequency $i\omega +\delta$ as the developed model considers free-damped oscillations and the hydrodynamic force depends only on the seal motion. Therefore, the seal response and the equation of motion characteristic root can be computed as follows [15]:

$$y = Ye^{{\left( {i\omega + \delta } \right)t}}$$

(24)

$$\omega = \omega_{n} \sqrt {1 - \xi^{2} } = \sqrt {\frac{{k_{eq} }}{{m_{eq} }}} \sqrt {1 - \left( {\frac{{c_{eq} }}{{2\sqrt {m_{eq} k_{eq} } }}} \right)^{2} }$$

(25)

$$\delta = - \omega_{n} \xi = - \sqrt {\frac{{k_{eq} }}{{m_{eq} }}} \frac{{c_{eq} }}{{2\sqrt {m_{eq} k_{eq} } }}$$

(26)

In addition, the added water mass, damping, and stiffness coefficients representing the fluid dynamic force can be computed as in Eqs. (27–29) with the aid of both the seal equation of motion Eq. (23b), and the seal response Eq. (24):

$$m_{w} = 0$$

(27)

$$c_{w} = - \frac{{F_{{\text{I}}} }}{Y\omega }$$

(28)

$$k_{w} = - \frac{{F_{{\text{R}}} }}{Y} + \frac{{F_{I} \sigma }}{Y\omega }.$$

(29)

F_R and F_I represent the seal’s hydrodynamic force real and imaginary components, while Y is the seal vibration displacement amplitude and is considered to be a real number since there is no other forcing function in the system [11].

For such a system, the dynamic stability is recognized by the seal equivalent damping coefficient ${c}_{eq}$ and $\delta$ values. If $\delta >0$, the system is dynamically unstable as the seal response will grow exponentially (i.e., see Eq. (24)). In contrast, if $\delta <0$, the system is dynamically stable since the seal response will damps over time reaching its equilibrium position y_og. In addition to the dynamic stability limit ($\delta \le 0$), there is also a static limit because the thickness of the clearance depends on the hydro-pressure force applied to the seal. Therefore, if the average seal clearance y_og under static load is equal to zero, thus no leakage flow is developed and the seal could not undertake vibrations.

Theoretical Model Computation Procedure

The computation of the pressure and flow rate oscillations in the frequency domain is established through several steps as follows. First, the steady-state variables such as steady-state flow rate, pressure head, and seal gap cross-section area are calculated. Once the steady-state variables are computed an expression for the overall transfer matrix U, function of ω and δ, can be calculated through Eq. (19). Afterwards, by employing the free end conditions (i.e. ${h}_{1}^{r}=0$ and ${h}_{6}^{L}=0$) to the overall transfer matrix $U$, the fluctuated flow rate at the intake reservoir ${q}_{1}^{r}$ and at the discharge chamber ${q}_{6}^{L}$ can be determined as a function of ω and $\delta$. Next, the equivalent hydrodynamic force applied to the seal can be solved in the frequency domain as a function of ω and $\delta$ by applying ${q}_{1}^{r}$, and ${q}_{6}^{L}$ into the other transfer matrices Eqs. (14–18). Finally, By converting the equivalent hydrodynamic force acting on the seal into added water mass, damping, and stiffness coefficients such as in Eqs. (27, 28, and 29), and by substituting the seal response Eq. (24) into the seal’s equation of motion Eq. (23b), the complex version of the seal’s equation of motion Eq. (23b) could be adopted to solve ω and $\delta$.

Discussion and Results

The turbine inlet valve (TIV) self-excited vibrations is a significant problem, which can raise the penstock pressure beyond its security limit of 13.5 Bar, as in Fig. 3. Consequently, if no security actions are applied, these pressure fluctuations can cause devastating accidents such as penstock burst and powerhouse submerging, risking the safe operation of the hydropower plant. Therefore, the discussion and result section is divided into two sections. The first section tackles the next questions: How both the unstable (TIV) vibrations and the related pressure fluctuations are developed?, what are the operating parameters that may influence the (TIV) vibration problem?, and finally, is the presented compressible flow model capable of simulating the practical problem of both the (TIV) vibrations and the related penstock pressure oscillation at the Salime plant?.

Next, the second section presents an evaluation phase that aims to yield some recommendations to enhance the penstock pressure fluctuations as well as the (TIV) vibrations. The evaluation phase is based on assessing the influence of different system configurations on the (TIV) vibrations. The methodology applied to alter the system configuration is based on the parameters that can be practically modified.

Finally, since this study considers fluid compressibility, the fluid of the piping system can be represented by an infinite number of springs and masses connected in series where springs represent fluid compressibility. As a result, the hydro-mechanical model, presented in Fig. 4b, is modeled as a distributed system with infinite degrees of freedom or modes of oscillations with infinite oscillation periods, in which, the first period is named fundamental, while the others are named higher harmonics [11]. However, in this study, the first 10 harmonics are only computed as they are of practical importance [11].

(TIV) Self-Excited Vibrations

Basically, power plant managers may shut down a turbine due to load requirements or maintenance procedures by closing the turbine inlet valve at various input reservoir energy levels. Therefore, Fig. 8 shows the effect of the input reservoir energy level H₁ on the (TIV) dynamic behavior. The results are computed at a fixed gap angle θ_g = 60º and pipeline wave speed a = 1270 m/s. The (TIV) dynamic behavior is identified by two parameters δ as in Eq. (26) and the seal’s oscillation frequency $f=\frac{\omega }{2\pi }$ as in Eq. (25). According to Eq. (26), the sign of δ, which characterizes the dynamic behavior of the (TIV), depends on the seal’s equivalent damping coefficient c_eq. In addition, the seal equivalent damping coefficient depends mainly on the added water damping c_w, which describes the action of the dynamic fluid force on the seal’s motion, since the seal’s structure damping c_sg is constant for a fixed gap angle. If ${c}_{w} <0$, in this situation, the fluid force excites the seal vibrations rather than damping it. As a result, the (TIV) may have three different dynamic behaviors. First, if ${c}_{eq}>0$ (i.e., $\left|{c}_{sg}\right| > \left|{c}_{w}\right|$ and δ < 0), the dynamic system is said to be a dynamically stable system as the displacement of seal’s vibration y and the related penstock pressure fluctuations P₂ damp over time until reaching their steady-state values, such as in the case of point A, see Fig. 8a and 8c. Second, If ${c}_{eq}=0$ (i.e., $\left|{c}_{sg}\right| = \left|{c}_{w}\right|$ and δ = 0), the dynamic system is said to be critically stable. In this case, both the seal vibrations and the related penstock pressure fluctuations oscillate but with constant amplitude, as in the case of point B, see Fig. 8a, d. Finally, if ${c}_{eq}<0$ (i.e., $\left|{c}_{sg}\right|< \left|{c}_{w}\right|$ and δ > 0), the hydro-mechanical system is identified as an unstable dynamic system. In this situation, the (TIV) vibrations correlated to the seal vibrations and the penstock pressure fluctuations diverge over time, as in the case of point C, see Fig. 8a, e.

On the other side, since the damping factor values $\xi$ are minimal, and the seal’s equivalent mass is constant for a fixed gap angle hence the seal’s vibration frequency f is influenced mainly by the seal’s equivalent stiffness coefficient k_eq according to Eqs. (25 and 27). As a result, at a fixed gap angle, the seal’s oscillation frequency is predominantly affected by the added water stiffness k_w because the seal structure stiffness is constant. If ${k}_{w}<0$, in this case, the fluid dynamic force is in phase with the seal displacement. In this situation, the dynamic fluid force reduces the seal’s equivalent stiffness leading to lower oscillation frequency for the seal’s vibration as well as the related penstock pressure fluctuations. Although, if ${k}_{w}>0$, the fluid dynamic force is out of phase of the seal vibration displacement. Therefore, the dynamic fluid force tends to augment the seal’s equivalent stiffness leading to higher frequency values.

Therefore, according to the previous explanations, Fig. 8 can interpret the effect of H₁ on the dynamic behavior of the (TIV) through the following points. First, for the mentioned gap angle and pipeline wave speed, increasing H₁ excites more the seal’s oscillation since δ increases for all harmonics except for the second harmonic. Second, at θ_g = 60º and a = 1270 m/s, the (TIV) dynamic behavior is only unstable at the first harmonic when H₁ > 62.5 m as the δ values are > 0, as in Fig. 8a. Third, at a specific harmonic, varying H₁ has a trivial effect on the seal’s equivalent stiffness. As a result, at a particular harmonic, the oscillation frequency for the (TIV) vibrations and the penstock pressure fluctuation is independent of H₁ as in Fig. 8b. Finally, since the damping factor values at all harmonics are minimal, the seal’s vibration frequency is approximately the same as the seal's natural frequency (i.e., $\omega \approx {\omega }_{n}$ as in Eq. (25)).

Fig. 8

Influence of H₁ on the (TIV) dynamic behavior at θ_g = 60º and a = 1270 m/s. a Relation between H₁, δ, and c_eq for the first ten harmonics. b Relation between H₁, and f for the first ten harmonics. c–e Relation between seal vibration displacement y and penstock pressure P₂ for the three points A, B, and C

Practically, if the valve is set into a closed position and there is a deficiency of the pressure forces applied to the service seal, a gap is developed between the seal and the ball surface, which is usually unknown. Therefore, Fig. 9 evaluates the effect of the seal gap angle and the input reservoir energy level on the dynamic seal behavior.

Fig. 9

Influence of θ_g and H₁ on δ and f at 30º ≤ θ_g ≤ 80º, 50 m ≤ H₁ ≤ 150 m, and a = 1270 m/s

Figure 9 demonstrates that at low gap angles (i.e., θ_g < 60º), both the periodic seal’s vibrations and the related penstock pressure fluctuations are dynamically stable since the δ values, for all values of H₁, are below zero. However, increasing the gap angle (i.e., θ_g ≥ 60º) increases the dynamic fluid force excitation to the seal oscillation. As a result, the seal oscillations increase over time (i.e., δ > 0), leading to dynamically unstable penstock pressure oscillations, which risks the reliable and safe operation of the power plant. In addition, Fig. 9 exhibit that at θ_g > 60º, the seal oscillations as well as the penstock pressure oscillations are only unstable at the first harmonic since δ > 0 and increases by increasing H₁. Finally, Fig. 9f evaluates the system dynamic stability only for H₁ ≤ 100 m because for H₁ > 100 m, there was no clearance between the service seal and the ball of the (TIV). In this situation, no leakage flow originates to initiate the periodic seal’s vibrations.

Figure 10 exhibits the penstock pressure P₂ at the first harmonic to validate the ability of the developed model to appropriately simulate the practical problem of the penstock pressure oscillations at the Salime power plant. The penstock pressure P₂ is computed at H₁ = 90 m, pipeline wave speed of 1270 m/s and various seal gap angles from 40° to 80°.

Fig. 10

Penstock pressure oscillation P₂ over time at H₁ = 90 m and a = 1270 m/s. a 40º ≤ θ_g ≤ 55º. b 60º ≤ θ_g ≤ 80º

By observing the dynamic behavior of the penstock pressure oscillations P₂ over time, the following observations are concluded. First, for all gap angles, the theoretical model can calculate the value of the penstock steady-state pressure (i.e., ${P}_{{o}_{2}}=9 \mathrm{Bar}$) for both the dynamically stable and unstable pressure oscillations, which agrees with the experimental data, see Figs. 3 and 10. Second, for the dynamically unstable systems (i.e., θ_g ≥ 60º), the pressure fluctuations can surpass the penstock pressure security limit (13.5 Bar) in case no security actions are applied, which agrees also with the experimental data as in Figs. 3 and 10b. Finally, the theoretical model confirmed that the frequency of the penstock pressure fluctuations lies in the same proclaimed frequency range from 1 to 3 Hz, as in Fig. 10. In which, the computed results proved that at large gap angles θ_g ≥ 70º, the seal’s equivalent stiffness k_eq decreases significantly because the seal’s structure stiffness reduces at a significant rate, see Eq. (21). As a result, the seal’s vibration frequency reduces at higher gap angles, such as in Fig. 10b. Therefore, according to the available experimental data, the technician’s observations and the mentioned results, the developed theoretical model can develop the (TIV) vibrations as well as the penstock pressure fluctuations. In addition, it confirms that the origin of the (TIV) vibrations and the related penstock pressure oscillations is the service seal leakage.

Parametric Study

The parametric study aims to yield some recommendations to enhance the stability of (TIV) vibrations, which consequently warrants the reliable and safe operation of the hydropower plant. Therefore, the (TIV) vibrations are assessed under various system configurations. The methodology applied to change the system configuration is based on the parameters that can be practically modulated, such as the pilot pipeline’s geometry and hydraulic losses, and the seal’s physical and geometrical parameters. Finally, all the upcoming evaluations are based on the case of H₁ = 150 m and θ_g = 70º, representing the worst seal dynamic behavior (i.e., maximum δ) as in Fig. 9e, to exhibit the efficiency of these system configuration modifications on improving the stability of the (TIV) vibrations.

Figure 11 shows the effect of the pilot pipeline geometry on the stability of the (TIV) vibrations. The pilot pipeline geometry is changed by varying the pilot pipeline length from 10 to 20 m and the pipeline diameter from 5 to 70 mm. The results mentioned in Fig. 11 are only for the first four harmonics since the δ values for all other harmonics are below zero. By observing the variation of δ over d_d and L_d, results showed that modifying the pilot pipeline diameter to be in the range of 5 ≤ d_d ≤ 15 improves the stability of the (TIV) vibrations as δ < 0 for all harmonics and pilot pipeline lengths. As a result, the (TIV) vibrations damp over time (i.e., δ < 0), eliminating the penstock pressure divergence and enhancing the power plant safe operation.

Fig. 11

Influence of pilot pipeline geometry L_d and d_d on δ at H₁ = 150 m, θ_g = 70º, a = 1270 m/s, and for the first four harmonics

To assess the effect of the pilot pipeline hydraulic losses on the (TIV) vibrations while maintaining the dimensions of the pilot pipeline; the head losses are varied by changing the pipeline minor losses coefficient K_Ld as in Fig. 12. By augmenting the pilot pipeline hydraulic losses (i.e., by augmenting K_Ld), the energy dissipated by the fluid system surpasses the energy transferred to the seal structure, particularly at the first two harmonics. As a result, the negative added water damping decreases, decreasing the δ values, and damping the periodic seal’s vibrations over time (i.e., δ < 0), such as in Fig. 12.

Fig. 12

Influence of pilot pipeline minor loss coefficient K_Ld on δ at H₁ = 150 m, θ_g = 70º, a = 1270 m/s, and for the first ten harmonics

Figure 13 evaluates the seal geometry influence on the dynamic stability of the (TIV) vibrations. The seal geometry is varied by changing both the seal’s surface area facing the gap flow A_ss and the seal’s external surface area A_os facing the flow pressure passing thru the pilot pipeline. Figure 13a demonstrates that decreasing A_os while increasing A_ss could improve the dynamic stability of the (TIV) vibrations for the first harmonic since the values of δ decreases, although this modification has the opposite effect for the second harmonic as it significantly increases the seal dynamic instability as both the negative added water damping and the values of δ increase, as in Fig. 13b. Therefore, modifying the seal geometry cannot guarantee to enhance the (TIV) dynamic stability across all seal vibrations harmonics.

Fig. 13

A_ss and A_os influence on δ at H₁ = 150 m, θ_g = 70º, a = 1270 m/s, and for the first four harmonics

Figure 14 evaluates the effect of the seal material on the vibrations of the (TIV), at: H₁ = 150 m, different gap angles, fixed pilot pipeline geometry L_d = 15 m, and d_d = 30 mm, and for four different materials [16]. The service seal’s materials properties are identified as in Table 2.

Fig. 14

Seal material effect on δ and f at H₁ = 150 m, a = 1270 m/s, and for the first ten harmonics

Table 2 Seal’s different materials’ properties

For the first harmonic and all θ_g, increasing the seal structure stiffness by choosing a material of higher modulus of elasticity E, such as Carbon-Ultra modulus, decreases the negative added water damping. Thus, the seal’s vibration damps over time, leading to a stable dynamic system (i.e., δ < 0), as in Fig. 14. Although, for the second harmonic, increasing the seal structure stiffness excites more the seal vibrations (i.e., δ > 0). Therefore, from the dynamic stability point of view, choosing a material of higher modulus of elasticity may help enhance the (TIV) vibrations at higher gap angles as in Fig. 14c. However, at lower gap angles, it may increase the (TIV) vibrations over time, particularly at the second harmonic such as in Fig. 14a.

Besides the dynamic stability limit (i.e., $\delta \le 0$), there is also a static stability limit since the origin of seal’s oscillation is the clearance between the valve’s ball surface and service seal. Therefore, Fig. 15 examines the effect of the seal's material and geometry on achieving the static stability condition. The static stability condition is achieved when there is no clearance between the ball surface and the service seal of the valve (i.e., y_og = 0). In this case, no leakage is developed and the seal could not vibrate. As shown in Fig. 14, varying the material of the seal could not maintain the valve vibrations stability since it also depends on the gap angle of the seal θ_g and the harmonic of the seal’s vibration. However, the material of the seal has a significant effect on the thickness of the seal clearance y_og. Choosing a material of low modulus of elasticity E, such as Monel 400 as in Table 2, decreases the structure stiffness of the seal. Consequently, the seal clearance thickness y_og decreases under the same H₁ as in Fig. 15a. As a result, choosing a material with a lower modulus of elasticity is preferable because the full closure of the seal clearance (i.e., y_og = 0) can be achieved at a lower input reservoir energy level, as shown in Fig. 15a.

Fig. 15

a Effect of seal material on y_og and Q_og at θ_g = 70º. b Effect of seal geometry on y_og and Q_og at θ_g = 70º and for steel seal’s material

Similarly, although the seal’s geometry cannot guarantee the stability of the (TIV) vibrations at all harmonics, such as in Fig. 13, it influences significantly the clearance of the seal creating the leakage flow. Figure 15b displays how the seal’s surface areas affect the gap flow rate and the seal clearance employing the parameter γ that defines the ratio between the surface areas of the seal $\gamma =\frac{{A}_{\mathrm{ss}}}{{A}_{\mathrm{os}}}$. It can be seen that augmenting the surface area of the seal facing the pilot pipe A_os (decreasing γ) decreases the input reservoir energy level H₁ needed to fully close the seal’s clearance (i.e., y_og = 0 and Q_og = 0) since the steady-state pressure forces applied to the seal increases. Hence, augmenting A_os while selecting a seal material with a lower modulus of elasticity can enhance the vibration problem of the (TIV) as the static stability condition can be achieved at lower H₁.

Conclusions

The proposed study confirmed the importance of analyzing the turbine inlet valve (TIV) vibration because it may provoke pressure fluctuations in the pipelines surpassing the designated safety limit, causing disastrous accidents such as penstock bursts. The theoretical model developed showed the capability to explain the mechanism behind the periodic (TIV) vibrations. Moreover, it can estimate the transient hydraulic behavior of the plant depending on the relevant physical and geometrical characteristics. The developed study using the constructed model has confirmed that the case of interest belongs to the type of flow-induced vibrations denoted as movement-induced excitation since the periodic (TIV) vibrations result from the unstable coupling between the valve’s service seal oscillatory motion and the fluid system due to the service seal leakage. Therefore, even when the seal is in equilibrium, a slight disturbance can cause decaying (stable system) or increasing (unstable system) pressure and flow oscillations, depending on the dynamic fluid force excitation to the seal oscillation.

The developed theoretical model succeeded to establish the conditions for stable and unstable (TIV) vibrations. After evaluating these conditions, the following points are concluded.

• 1. Theoretical model analysis shows that (TIV) vibration instability occurs when the fluid system and the valve’s service seal motion interact in a way where the coupled flow-structure system possesses a negative equivalent damping coefficient. In addition, the unstable behavior of the periodic seal’s vibrations and the related penstock pressure fluctuations are less likely to occur at lower input reservoir energy levels and tight seal's gap angle. Moreover, the seal vibration instability is more often to be established at the first harmonic of the periodic seal vibrations where the dynamic fluid force tends to excite more the seal oscillations rather than damping them.

• 2. Augmenting pilot pipeline friction losses can improve the dynamic stability of the (TIV) vibrations. As a result, installing a valve at the pilot pipeline that can be closed to a particular degree can improve the plant’s stable operation. In addition, decreasing the diameter of the pilot pipeline can improve the dynamic stability of the (TIV) vibrations as it decreases the dynamic fluid force excitation to the service seal oscillations, particularly at the first harmonic.

• 3. From the dynamic stability point of view, varying the seal’s geometry or material cannot guarantee stable operation across all harmonics of the (TIV) vibrations. However, the steady-state analysis showed that enlarging the surface area of the seal confronting the pilot pipeline and choosing a seal material with a low modulus of elasticity can establish the seal’s full closure at a lower input reservoir energy head, eliminating the reason behind the (TIV) vibrations.

• 4. To appropriately simulate the (TIV) self-excited vibrations and the related penstock pressure oscillations at the Salime power plant, the dynamic seal characteristics, fluid compressibility, and pipeline wall elasticity effects must be considered.

Finally, this study can help in interpreting the vibrations of other types of valves (check valves, and pressure relief valves) [17,18,19,20,21] that operate at small openings since they share a common feature regarding the development of the destabilizing force. A common feature for the developing of the valve’s vibration instability is that when the fluid system and the valve obstructing element are in oscillatory motion, they interact in a way that the fluid force reinforces the oscillatory motion of the valve’s obstructing element. In this situation, the fluid system provides an ongoing supply of energy to the vibrating element, causing the unstable vibration (i.e. vibrations of increasing amplitude) of the valve’s obstructing element.