Introduction

Maglev train travel is an efficient modern mode of railway transportation. Unlike conventional wheel-on-rail systems, maglev trains often travel along a guideway by making use of the magnetic levitation technology. Such an unconventional mode of train travel offers a number of advantages over its wheeled counterparts. This includes the ability of achieving higher speeds owing to the elimination of physical wheel–rail contact and friction, much reduced wear and tear and thus lower levels of maintenance needs and cost, capability of climbing steeper grades and turning on smaller radii of curvature, emitting less noise, and being more environmentally friendly [1].

Owing to the advantages, maglev trains attracted great attention by researchers and engineers. Several testing and demonstration projects, including the Transrapid and SCMaglev developments, were successfully carried out after the technical concepts of the magnetic levitation and propulsion technologies were patented in the 1940s, following which commercial operations of maglev trains were realised. To date, there exists six commercially operating maglev lines in the world [2].

In railway transportation, travel comfort and safety are factors that are paramount to passengers. Even though the maglev technology enables safer and more comfort train travels, the dynamic response of a maglev train traversing its sustaining guideway needs to be carefully examined to ensure that the vibrational levels are within the tolerable limits. In a maglev line, the guideway plays an important role in the dynamic responses of a passing train. A study of the Changsha maglev line examined the effect of the guideway weight and flexural rigidity [3, 4]. The study revealed that significantly higher levels of vibrational responses for both the electromagnets and the track when both the aforementioned parameters were reduced to two-thirds or one-third of their original values, while heavier and stiffer guideways tend to be superior in the suppression of vibrational responses of the train. Besides, guideway irregularities arising from uneven surfaces on the guideway and the joints are an important source of dynamic excitations and thus ride discomfort. It was found that the vertical acceleration of a maglev train could be two times higher than the case without guideway irregularities [5]. Resonant response could also occur when the irregularity wavelength is one or two times of the length of the electromagnet [6]. Clearly, a careful design and maintenance of the guideway can help mitigate the dynamic response levels and thus improve the ride comfort of maglev train travel.

In the analysis and design of guideway bridge systems under moving train loads, it is crucial to employ a computationally efficient and accurate analysis model. The coupled maglev train-guideway dynamics is essentially a moving load on beam problem, which has been extensively studied [7], especially for the conventional wheel-on-rail systems. Simplified studies often treat the trains as moving concentrated loads traversing the sustaining track/bridge structures [8, 9]. Although these models are computationally efficient and able to give some physical insights into the dynamics of the system, they fail to account for the inertia of vehicles which becomes important when the train mass-to-bridge mass ratio is not small and the track irregularity is not smooth [10]. To capture this important parameter, different vehicle models have been employed in coupled train-bridge systems. The commonly used train models include the moving mass [11] and the moving sprung mass [12] models. In most studies, the train is modelled by applying multi-body theory in which the car body, bogies, and wheelsets are treated as rigid bodies and the suspension systems are represented by spring–dashpot units. There also exist studies employing detailed vehicle modelling using the finite-element method which can predict both global and local dynamic responses of the train in detail but at the cost of high computational efforts [13].

On the other hand, bridge structures are often modelled by employing the Euler–Bernoulli beam theory owing to their slenderness [14,15,16]. Although such models have been proven to be accurate enough for applications involving slender structures and low-frequency vibration problems, they tend to overestimate the natural frequencies of deep beams and their higher vibrational modes [17]. The Rayleigh beam theory improves the Euler–Bernoulli by taking into account the effect of rotation of the cross-section. Results show that although the Rayleigh model partially corrects the overestimation of natural frequencies suffered by the Euler–Bernoulli models, its improvement is found to be limited [18]. The Timoshenko beam theory [19,20,21], which takes into account both the shear deformation and rotary inertia of the cross-section, is found to significantly improve the analysis accuracy, particularly for non-slender beams undergoing high-frequency vibrations. Besides beam models, plate [22], grillage [23], and sophisticated solid spatial element [24] bridge models have also been developed and employed to account for the spatial behaviour of bridge structures.

When it comes to the solutions to the coupled train-bridge systems, analytical approaches such as the Fourier transform method [25] and mode superposition method [9] for the conventional wheel-on-rail systems are applicable. Semi-analytical solutions also found their applications in more sophisticated moving load problems considering, e.g., the critical velocity and instability of two moving proximate masses [26] and the nonlinearity of the track structure [27]. Besides, numerical solutions such as the finite-element method (FEM) are often employed [28, 29] owing to their versatility and superiority than analytical solutions when dealing with complex train-track dynamics. It should be highlighted; however, the conventional FEM utilising a land-fixed coordinate system encounters two main complications in the treatment of moving load problems. The first complication is associated with the artificial boundary effects when adopting a truncated domain to represent a nearly infinitely long guideway for the sake of computational efficiency. Furthermore, the train will soon move out of the truncated domain, especially at high speeds. When the domain size is enlarged to mitigate the aforementioned complication, the second complication of increased computational cost arises. An accurate and computationally efficient method for the dynamic response analysis of the coupled maglev train-guideway system is thus highly desirable. In this regard, the moving element method (MEM) which employs a convected moving coordinate system attached to the moving source may be superior. Such a method overcomes the aforementioned two complications faced by the conventional FEM and has been successfully applied to various train-track problems [30,31,32,33,34,35]. In the treatment of an “infinitely” long guideway considering mechanical connections between neighbouring girders under a moving maglev train; however, the applicability and accuracy of the MEM need examination. Besides, structure-preserving numerical methods for accurate simulation of dynamical systems [36,37,38,39,40,41,42,43,44,45] may be considered and employed.

This paper is concerned with the response analysis of a maglev train traversing a multiple-span guideway bridge. Each guideway span is modelled as simply supported beam with rotational springs connecting to the adjacent spans. The maglev vehicle is modelled by employing the multi-body system. The vehicle and the guideway are coupled via the electromagnetic force. In the numerical analysis, a computational scheme in conjunction with the MEM is proposed. The accuracy of the proposed numerical model is examined by comparison with results obtained using the equivalent finite-element model. Parametric studies are carried out to investigate the effect of various factors on the dynamic response of the coupled system. These include the speed of the train, stiffness of vehicle suspension systems, guideway support stiffness, coupling connection stiffness, and guideway irregularities.

The remainder of the paper is organised as follows: The section “Numerical models and methodology” presents the problem definition and describes the mathematical models for the coupled maglev train-guideway bridge system. The accuracy of the proposed numerical model is verified in the section “Numerical verification”. The section “Response of coupled maglev-multiple-span guideway system” investigates the effects of various parameters on the dynamic response of the coupled train-track system. Finally, the section “Conclusions” concludes the findings of the study.

Numerical Models and Methodology

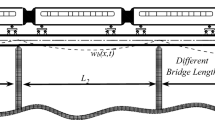
This study investigates the dynamic response of a maglev train traversing a multiple-span guideway bridge. Figure 1 shows a schematic view of the coupled maglev-guideway system. This section presents the mathematical models for each component of the coupled system together with the numerical solution for the time-domain analysis.

Fig. 1
figure 1

Coupled maglev-multiple-span guideway system

Full size image

Train Model

The train model employed in this study is based on the Shanghai Transrapid 08 model. A maglev vehicle is idealised as a multi-body system comprising a car body of mass mc and pitch moment of inertia Jc, four levitation bogies of mass mb and pitch moment of inertia Jb each, and eight magnets of mass mm each, as shown in Fig. 2. The magnets are spaced apart uniformly at an interval of 3.1 m. Each bogie is connected to two magnets by the primary suspensions with stiffness kp and damping cp. The car body is resting on four bogies by the secondary suspension with stiffness ks and damping cs. The car body and levitation bogies have vertical and rotational degrees of freedom (DOFs), while the magnets have only a vertical degree of freedom. In total, there are 18 DOFs. According to Newton’s second law of motion, the governing equations of motion can be written in a compact matrix form as

$${\mathbf{M}}_{t} \ddot{y}_{t} \, + \,{\mathbf{C}}_{{\text{t}}} {\dot{\text{y}}}_{{\text{t}}} \,{ + }\,{\mathbf{K}}_{{\text{t}}} {\text{y}}_{{\text{t}}} \,{ = }\,{\mathbf{F}}_{{\text{t}}} ,$$
(1)

where Mt, Ct, Kt, and Ft denote the mass, damping and stiffness matrices, and external force vector of the train model, respectively. ÿt, ẏt, and yt denote the acceleration, velocity, and displacement vector of the train, respectively. Note that the external force vector contains both the gravitational forces and the electromagnet forces acting between the train and the guideway. Table 1 lists the parameters of the maglev train [46].

Fig. 2
figure 2

Maglev train model

Full size image
Table 1 Train parameters
Full size table

Guideway Model

The guideway used in the Shanghai Transrapid line consists of I-shaped concrete girders with rails mounted on the two ends of the top flange. Figure 3 schematically illustrates a two-span guideway bridge model for sake of simplicity. Note that, in this study, a multi-span bridge representing an infinitely long guideway is considered. In view of the relatively large span-to-width ratio of the guideway, it is justifiable to model it according to the Euler–Bernoulli beam theory. The guideway girders with mass per unit length ρA, length L, and flexural rigidity EI rest on bearing supports with stiffness kb at their two ends. The adjacent spans are connected through coupling connections with rotational stiffness kc. Table 2 lists the guideway parameters [46].

Fig. 3
figure 3

Guideway model

Full size image
Table 2 Guideway parameters
Full size table

Let u be the displacement of the guideway girder at distance X along the longitudinal direction of the guideway and time T. The governing equations of motion of a guideway considering Rayleigh damping are given by

$$EI\frac{{\partial^{4} u}}{{\partial X^{4} }} + \alpha_{1} EI\frac{{\partial^{5} u}}{{\partial X^{4} \partial T}} + \alpha_{0} \rho A\frac{\partial u}{{\partial T}} + \rho A\frac{{\partial^{2} u}}{{\partial T^{2} }} = \sum\nolimits_{n = 1}^{{n_{m} }} {F_{en} \delta \left( {X - X_{n} } \right)} ,$$
(2)

where α0 is the mass proportional Rayleigh damping coefficient, α1 is the stiffness proportional Rayleigh damping coefficient, Fen is the electromagnet force between the nth magnet and the guideway, Xn is the location of the nth magnet, δ is the Dirac delta function, and nm is the total number of magnets on the incident guideway girder. Based on the modal parameters obtained from the field tests [29], the first two modal circular frequencies of the guideway are 9.3 Hz and 12.5 Hz, respectively. The corresponding modal damping ratios are 2.67% and 3.51%, respectively. Based on this, the Rayleigh damping coefficients can be calculated.

Electromagnetic Force Model

For the Shanghai Transrapid line, the train (Eq. (1)) and the guideway (Eq. (2)) are coupled via the electromagnet forces. Figure 4 schematically illustrates a magnet suspended beneath the guideway during operation. The electromagnet force Fen between the nth magnet and the guideway is a nonlinear function of the electric current I and the air gap hn, which is given by

$$F_{en} = \frac{{\mu_{0} N^{2} A}}{4}\left( {\frac{i}{{h_{n} }}} \right)^{2} = K_{0} \left( {\frac{i}{{h_{n} }}} \right)^{2} ,$$
(3)

where μ0 = 4π × 10–7 H/m is the magnetic permeability of vacuum, N is the number of turns of the coil, A is the magnetic pole area, and K0 = (μ0N2A)/4 is the coupling factor.

Fig. 4
figure 4

Electromagnet model

Full size image

Considering i0 = 25 A and h0 = 0.01 m as the nominal current and air gap, respectively [46], the electromagnetic force at static equilibrium state Fe0 is

$$F_{e0} = K_{0} \left( {\frac{{i_{0} }}{{h_{0} }}} \right)^{2} = \frac{1}{8}\left( {m_{c} + 4m_{b} + 8m_{m} } \right)g.$$
(4)

A reasonable simplification can be made by linearizing the electromagnetic force about the nominal static equilibrium state. Then, the electromagnetic force Fen can be rewritten as

$$F_{en} = F_{e0} + C_{i} \Delta i - C_{h} \Delta h_{n} ,$$
(5)

where Ci = 2K0i0/(h0)2, Ch = 2K0i02/(h0)3, Δi = in – i0, and Δhn = hn – h0. According to the current control law [47], Δi = khΔhn + kvẏmn + kaÿmn, where kh = 6500, kv = 40, and ka = 0.2 are the feedback gains corresponding to the air gap change, velocity, and acceleration of the magnet, respectively [46].

Moving Element Method

The moving element method (MEM) is a computationally efficient numerical method for solving moving load-related problems such as train-track dynamics. Contrary to the conventional finite-element method (FEM) that employs a land-fixed coordinate system (X, T), the MEM formulates the governing equations of motion for the guideway bridge using a moving coordinate (x, t) whose origin is attached to the moving train travelling at speed V. The relationship between the two coordinates is defined by the Galilean transformation as

$$x = X - VT,$$
(6)
$$t = T.$$
(7)

By employing the moving coordinate system, the MEM overcomes the complication faced by a conventional FEM model that a large domain size is needed to allow for a high-speed train to travel a sufficient amount of time needed for realistic analysis. Besides, the train loads are stationary in the moving coordinate x, and thus, they are always located at the same nodal points regardless of the train speed, thereby avoiding the necessity of tracking the position of the train loads at each time speed as needed in a conventional FEM analysis.

A segment of the guideway in the moving coordinate is next truncated and discretised into a series of finite elements. Such a mesh and the train appear to be stationary, while the guideway material and supports flow in the opposite direction of the heading of the train. With the moving coordinate system, the governing equations of motion expressed in Eq. (2) are now rewritten as

$$\begin{gathered} EI\frac{{\partial^{4} u}}{{\partial x^{4} }} + \alpha_{1} EI\left( { - V\frac{{\partial^{5} u}}{{\partial x^{5} }} + \frac{{\partial^{5} u}}{{\partial x^{4} \partial t}}} \right) + \alpha_{0} \rho A\left( { - V\frac{\partial u}{{\partial x}} + \frac{\partial u}{{\partial t}}} \right) \hfill \\ + \rho A\left( {V^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} - 2V\frac{{\partial^{2} u}}{\partial x\partial t} + \frac{{\partial^{2} u}}{{\partial t^{2} }}} \right) = \sum\nolimits_{n = 1}^{{n_{m} }} {F_{en} \delta \left( {x_{n} } \right)} . \hfill \\ \end{gathered}$$
(8)

Next, Galerkin’s approach is adopted to derive the weak form of the equation. In this study, the Hermitian cubic polynomials are employed as the shape and weighting functions, following which the element matrices and load vectors for the guideway can be derived. In addition, the guideway bridge supports idealised by springs move in the opposite direction of the maglev train, whose effects need to be taken into account. This study employs the numerical scheme proposed by the first author that takes advantage of the periodic nature of the guideway supports [32, 33]. Figure 5 schematically illustrates a truncated multi-span guideway model under a train load. The domain size is assumed to be sufficient, such that the artificial boundary effects are negligible such that fixed boundary conditions are employed. In this study, the guideway has uniform spans. Therefore, the motion of the guideway supports is completely periodic. Under such a circumstance, the dynamic guideway element matrices for the duration when the train travels across one span can be stored and retrieved conveniently for the computation for subsequent periods.

Fig. 5
figure 5

Motion of discrete supports in moving coordinate

Full size image

After assembling the element matrices and load vectors for the guideway model in the moving coordinate system, the maglev train model, and the electromagnetic force model, the global equations of motion for the coupled maglev-guideway system can be written in the following matrix form as:

$${\mathbf{M\ddot{y}}} + {\mathbf{C\dot{y}}} + {\mathbf{Ky}} = {\mathbf{F}},$$
(9)

where M, C, K, and F denote the global mass, damping and stiffness matrices, and external force vector of the coupled system, respectively, and ÿ, ẏ, and y denote the acceleration, velocity, and displacement vectors, respectively.

For the numerical analysis of the coupled maglev-guideway system in the time-domain, the Newmark’s constant acceleration method which is unconditionally stable is employed.

Numerical Verification

In an attempt to examine the accuracy of the proposed model, the case of a single train travelling across a single span guideway on the test line at a speed of 25 km/h at Tongji University [29] was considered. In this case, a simplified 10-DOF train model was employed, as shown in Fig. 6, where the levitation bogies are neglected, but their mass are evenly distributed to the magnets underneath. Table 3 lists the parameters for the test line guideway. According to the study by Zhang and Huang [29], the first two modal frequencies were obtained from the measured responses, which are found to be 18.92 Hz and 74.61 Hz, respectively. The corresponding modal damping ratios are 3.43% and 0.29%. Based on this, the Rayleigh damping coefficients presented in the section “Guideway model” can be derived.

Fig. 6
figure 6

Simplified maglev-guideway model

Full size image
Table 3 Test line guideway parameters
Full size table

Figure 7 shows the vertical displacement time history of the guideway at its mid-span by the passage of a maglev train at a speed of 25 km/h obtained using the proposed MEM model. In the employed MEM model, each guideway girder is discretised into 50 elements of 0.247 m each and a time step size of 0.036 s is adopted. Also shown in the figure are the results reported in [29] using a detailed FEM model made of 3D solid elements. Note that the FEM model properties were updated according to the field measurement results on the test line. It is clear that both results agree with each other quite well, despite some minor discrepancies due to the differences in the numerical models. This shows that the proposed MEM model of idealised guideway is able to generate reasonably good results even with an idealised model when compared with a sophisticated FEM model.

Fig. 7
figure 7

Simplified maglev-guideway model

Full size image

Response of Coupled Maglev-Multiple-Span Guideway System

The coupled maglev-multiple-span guideway model presented in the section “Numerical models and methodology” is next employed to investigate the effect of various parameters on the dynamic response of the system. These include the maglev train speed, stiffness of train suspension system, stiffness of guideway coupling connections, and guideway irregularities. As the passengers’ comfort is of great significance, this study will focus on the vehicle acceleration responses under the influence of various parameters.

Train Speed

Maglev trains have the advantage of being able to travel at high speeds thanks to the magnetic levitation that removes physical contact and friction between the train and the track. However, resonant responses of the vehicle body can still occur when the frequency of excitation coincides with the natural frequency of the train. The nth natural angular frequencies of the train ωtn can be evaluated according to the equation below

$$\det \left( {{\mathbf{K}}_{t} - \omega_{tn}^{2} {\mathbf{M}}_{t} } \right) = 0,$$
(10)

where det() denotes the determinant of a matrix.

By solving Eq. (1), one gets a series of natural frequencies where the fundamental natural frequency is found to be ωt1 = 8.84 rad/s. This mode corresponds to a pitching rotation of the train body about its centre of gravity.

As the train travels along the guideway, the vertical motion of the guideway gives an excitation to the train at a circular frequency of V/L. Consequently, the first critical train speed Vc1 that leads to resonant responses is given by

$$V_{c1} = \frac{{\omega_{t1} }}{2\pi }L.$$
(11)

Figure 8 shows the effect of train speed on the maximum vertical acceleration of the train over a practical operational speed range between 100 and 600 km/h. Clearly, the proposed MEM model is able to capture the resonant response of the train when the train is operating at the critical speed Vc1. After this critical speed, a minimum vertical acceleration is observed when the train speed is increased to 250 km/h, after which a generally increasing train acceleration with the increase in the train speed is observed. As can be seen in Fig. 8, the optimal operational speed for Transrapid Shanghai line is between 200 and 400 km/h. In any case, the maximum vertical acceleration of the train when operated outside the critical speed is found to be below the limit of 0.6 m/s2 according to the German maglev design guide [48], which indicates that the commercial maglev train fulfils the designed comfort level for its practical operational speed range.

Fig. 8
figure 8

Effect of train speed on maximum train vertical acceleration

Full size image

Stiffness of Train Suspension System

The suspension system of a train plays an important role in mitigating the amount of vibration that propagates to the car body. As such, it is worth examining the effect that the suspension system has on the acceleration of the train body.

In this sub-section, the effect of the stiffness of the primary suspension system kp varied from 1 × 102 to 1 × 108 N/m is examined. The maximum vertical acceleration of the train body at various values of kp is shown in the plot in Fig. 9(a). Similarly, the effect of the stiffness of the secondary suspension system ks varied from 1 × 102 to 1 × 108 N/m on the maximum train vertical acceleration is shown in Fig. 9(b). For both cases, the train is assumed to travel at a constant speed of 300 km/h.

Fig. 9
figure 9

Effect of suspension stiffness on maximum train vertical acceleration: a primary suspension and b secondary suspension

Full size image

For both the primary and secondary suspension systems, the relationship between the stiffness and train acceleration takes the form of an “S”-shaped curve graphically. At lower stiffnesses (kp < 1 × 104 N/m or ks < 1 × 105 N/m), the maximum acceleration of the train body is approximately constant at 0.01 m/s2. At higher stiffnesses, there is also little variation in the maximum vertical acceleration of the train body. When kp > 1 × 106 N/m, the maximum vertical acceleration of the train body just exceeds 0.03 m/s2. When ks > 1 × 108 N/m, the maximum vertical acceleration of the train car body is around 0.15 m/s2. This shows that the secondary suspension system exerts a greater influence on the motion of the train body, which is expected as it is directly connected to the car body of the train. At intermediate levels of the suspension stiffnesses, the vertical acceleration of the train body is more sensitive to small changes in the stiffnesses of the suspension system.

At present, the stiffness of the primary suspension of the Shanghai Transrapid is kp = 4 × 107 N/m. As evident from Fig. 9(a), this corresponds to high stiffness and may lead to higher acceleration levels of the car body. It is thus recommended to replace this suspension with those that have a lower stiffness if a reduction in the vertical acceleration of the train body is desired. The current stiffness of the secondary suspension of the Shanghai Transrapid is ks = 4 × 105 N/m. Since the value of this stiffness is towards the lower end, the secondary suspension is considered to be effective in reducing the acceleration of the car body.

Stiffness of Guideway Coupling Connection

In addition to the train suspension stiffness, it is also worthwhile to examine the effect of guideway parameters on the dynamic responses of the coupled system. This parametric study involves the stiffness of the coupling connection. By varying the stiffness of the coupling connection kc from 1 × 104 to 1 × 1014 N m/rad, the corresponding maximum vertical acceleration of the train body and the maximum mid-span displacement of the guideway can be evaluated. The results corresponding to a train speed of 300 km/h are presented in Figs. 10(a) and (b), respectively.

Fig. 10
figure 10

Effect of coupling connection stiffness on: a maximum train vertical acceleration and b maximum mid-span guideway displacement

Full size image

Similar to the effect of the train suspension stiffness on the dynamic responses, an “S”-shaped curved is again exhibited for the guideway coupling connection stiffness. However, a key difference is that the maximum vertical acceleration of the train body and the maximum mid-span displacement of the guideway are found to be lowered when the stiffness of the coupling connection is increased. Apparently, higher stiffness of the coupling connection enhances the ability of the guideway to mitigate the vibrational level of the train system.

For coupling connection stiffness kc < 1 × 108 N m/rad, the coupling connection may be considered as a hinged connection, whereas when kc > 1 × 1011 N m/rad, the coupling connection may be considered as a fixed connection. In between these two values, the coupling connection appears to be semi-rigid. The stiffness of the coupling connection in the Shanghai Transrapid is presently kc = 1 × 107 N m/rad, which implies that it is closer to a hinged connection. A stiffer coupling connection in the rigid zone will enhance the travel performance, and thus, the passenger comfort level of the maglev train travel as the parametric study shows that the maximum vertical acceleration of the train body and the maximum mid-span vertical displacement of the guideway can be reduced by almost 30% and 50%, respectively.

Guideway Irregularities

Thus far, the analysis of the maglev train system had been limited to the idealistic case of a perfectly smooth guideway. However, irregularities of the guideway can amplify the acceleration of the train car body, thereby affecting ride comfort. It is suggested that irregularities of wavelengths of less than one span length (25 m) are caused by misalignment of the stator and functional components, while those of longer wavelengths that are integer multiples of the span length may be attributed to subsidence of the foundation [49].

For simplicity, it shall be assumed that the guideway irregularity follows a sinusoidal profile with amplitude Az and wavelength λz. Hence, the height of the irregularity z at position X along the guideway in fixed coordinates can be expressed as

$$z = A_{z} \sin \left( {\frac{2\pi X}{{\lambda_{z} }}} \right).$$
(12)

Resonant response occurs when the frequency of excitation is an integer multiple of the natural frequency of the train [20]. Therefore, the resonant train speed Vres for a given irregularity of wavelength λz can be determined by

$$V_{res} = n\frac{{\omega_{t1} }}{2\pi }\lambda_{z} ,$$
(13)

where n is integer. Accordingly, resonant train speeds of 200 km/h, 300 km/h, and 400 km/h correspond to irregularities of wavelength 39.5 m, 59.2 m, and 78.9 m, respectively.

The maximum vertical acceleration of the train car body for irregularities of wavelength λz in the range of 10–100 m with a constant amplitude Az = 0.1 mm is shown in Fig. 11. Peaks in the maximum vertical acceleration of the train body around the above-mentioned resonant wavelengths are observed for the three train speeds V = 200 km/h, 300 km/h, and 400 km/h. In all cases, the maximum acceleration of the train car body at the resonant wavelength is found to be approximately doubled as compared to that of the case of a smooth guideway without irregularities.

Fig. 11
figure 11

Effect of irregularity wavelength on maximum train vertical acceleration: a V = 200 km/h, b V = 300 km/h, and c V = 400 km/h

Full size image

Next, the effect of the amplitude of irregularity on the maximum vertical acceleration of the car body when the train is travelling at a speed of 300 km/h is investigated. The results corresponding to the irregularities of four different wavelengths (λz = 1 m, 5 m, 25 m, and 50 m) are shown in Fig. 12. As can be seen, the maximum vertical acceleration of the train body is linearly proportionally related to the amplitude of guideway irregularity. Of the four wavelengths investigated, the highest acceleration stems from λz = 50 m, which is close to the resonant velocity Vres = 59.2 m/s. Under such a condition, it is recommended that the amplitude of irregularity be limited to Az < 2 mm to prevent the acceleration of the train car body from exceeding the limit of 0.6 m/s2 [48].

Fig. 12
figure 12

Effect of irregularity amplitude on maximum train vertical acceleration

Full size image

Conclusions

This paper is concerned with a numerical study of the dynamic response of a coupled maglev train-multiple-span guideway bridge system. The maglev train is idealised as an 18-degree-of-freedom model by employing the multi-body system, while the guideway is modelled as Euler–Bernoulli beams that are interconnected via coupling connections. The train and the guideway are coupled via the electromagnetic forces. For the numerical analysis in the time-domain, a computational scheme in conjunction with the moving element method is proposed. The accuracy of the proposed computational model is validated by comparison with available data for a maglev test line in the literature. Next, the proposed numerical maglev-guideway model is put forward to examine the effect of various factors on the dynamic response of a Shanghai Transrapid train. The main findings from this study are summarised as follows:

  1. 1.

    The resonant response of the train in the gravitational direction is observed at a train speed of 127 km/h. When the train is operated away from the critical speed, the vertical accelerations are within the design limits. The optimal operational speed range is between 200 and 400 km/h.

  2. 2.

    A lower stiffness of the train suspension system helps reduce the vertical acceleration of the car body, with the optimal range being kp < 1 × 104 N/m for the primary suspension and ks < 1 × 105 N/m for the secondary suspension.

  3. 3.

    A stiffer guideway coupling connection helps reduce the vertical acceleration of the car body and the vertical displacement of the guideway, with the optimal range being kc > 1 × 1011 N m/rad.

  4. 4.

    The presence of guideway irregularities can induce resonant responses in the train for certain combinations of the train speed and the wavelength of irregularity. Additionally, the maximum vertical acceleration of the car body is found to increase linearly with the amplitude of guideway irregularity.

The computational model presented in this study in conjunction with the moving element method has the advantage of computationally efficient analysis and accurate prediction of the dynamic responses of a maglev train traversing an “infinitely” long multi-span guideway bridge over the conventional finite-element method, especially when the train is travelling at high speeds. The numerical verification study also showed that the employment of the Euler–Bernoulli beam theory to model the guideway girders is sufficient for the parameters considered in the case study. For other types of guideway bridges with shorter and deeper spans and/or scenarios where high-frequency vibrations need to be accurately captured, it may be necessary to employ the Timoshenko beam theory or more sophisticated bridge models with e.g., solid elements. Furthermore, 3-D train models are needed when studying the dynamic responses of a train negotiating horizontally curved guideway or under horizontal excitations due to crosswind or seismic attack. The consideration of flexural modes of the vehicle body is also important when investigating the travel comfort of passengers during the journey. The methodology and models presented in this study may be further extended with appropriate modifications to consider more complex and practical cases such as the above-mentioned examples.