Introduction

During the last few decades, smart structures were developed to be effective components for numerous modern structural systems. Nowadays, their applications are not limited to high-tech systems, such as aviation or space ships; they have spread to take part in many activities of our daily life, such as vehicles, infrastructure, building management systems (BMS), etc.

Many definitions have pinpointed the characteristics, functionality, and components of smart structures. One of the most classic definitions classified them as structure components with sensors and actuators embedded in or attached to them, and these actuators/sensors are functioning through a coordinated control system. Thus, the structural component is capable of responding remotely and simultaneously to any external stimuli, giving the desired designated react for such stimuli [1].

The previous definition is obviously declaring the main characteristic of smart structures, which is an organized interaction between mechanical and electronic components to produce elasto-mechanical structural properties. Also, the main target functions of smart structures can be summarized as follows:

  • Structural health monitoring (SHM)

  • Active vibration control

  • Active shape control

  • Active noise control

All these functions need mainly specific components to act properly, which are: structure, sensors, actuators, and control system [2, 3].

Implementation of smart materials for the sake of smart structures functionality opened a new horizon for such systems, which is referred to as their unique coupled abilities that improved smart structure systems to be lighter and more operational.

Piezoelectric material family is one of the most familiar smart material families, whose development has been so impressive lately. One of these smart material various forms for instance, is Lead Zirconium Titanate ceramics (PZT) and Polyvinylidene Fluoride polymers (PVDF). This kind of material introduces an adequate option to permanently place a very small and cheap piece of material in a structure that lasts for its whole working life, providing sustainable stimulation for the substrate structure [1]. Piezoelectric wafer active sensor (PWAS) capabilities gained attention due to their electro-mechanical coupling, which qualifies them as be simultaneous energy transducers from mechanical to electrical energy and vice versa. Hence, it can act as both a sensor and an actuator.

As stated earlier, structural health monitoring (SHM) is one of the smart structures’ main target functions, for which innumerable aspects were placed to guarantee the accepted integrity of the substrate structure [4, 5]. Incorporating PWAS in such a process showed promising capabilities through combining its electromechanical coupling properties with the structure vibration characteristics to detect any possible flaws [6, 7]. So far, plenty of research efforts concerning these field have been made. For instance, Na and Baek [8] have reviewed the most recent topics about electromechanical impedance application in SHM. Jiao et al. [9] summarized the main concepts of PZT use for SHM purposes. Wang et al. [10] designed an effective array system of PZT to reduce flaw detection time. Amin and Salem [7] introduced an integrated SHM system to detect, quantify, and localize presumed different cases of damage using an attached array of PWAS for a thin plate of carbon fiber-epoxy, in which PWASs are used to excite the substrate structure over a designated frequency interval.

On the other hand, vibration control is not a less important issue, especially for the structures subjected to a working environment of noticeable ambient vibrations, which may cause remarkable troubles starting from simple malfunction or inappropriate performance of the structural systems, and up to catastrophic failure disasters [11]. Many researchers have implied vibration control systems in which integrated actuators excite all structural modes of interest at which the structure tends to exhibit destructive behaviour even under low amplitudes of cyclic load [12]. Of course, piezoelectric ceramic was one of the most popular smart materials to be used in such fields, as well as SHM, due to its tremendous advantages [13]. PWASs were used to control the vibrations of cantilevered structures [14,15,16,17], frame structures [18], and plate structures [19, 20].

Hence, the integration of SHM and vibration control systems using the same actuating set simultaneously for thin-walled structures will be compatible with the use of PWASs’ actuators. And so, placing actuators is important deal to achieve an acceptable compromise between the two systems. Besides, several practical limitations may be implied to avoid incompetence in the structural systems, such as weight, space, cost…, etc.

Many aspects have been placed and met success in fulfiling the desired criteria for which PZT actuators were employed [21]. Hać and Liu [22], based on controllability and observability, proposed the application of a system performance index (SPI) for actuators placement. Quek et al. [23] performed discrete direct pattern search optimization based on a controllability model for PZT actuators’ location. He overcame the problem of local maxima by selecting starting points near maxima of integrated normal strains, so that the maximum virtual work of the actuator is obtained. Yang and Zhang [24] discussed the maximization of certain plate model deflection based on PZT actuator location. Mehrabin and Koma [25] developed an optimal actuator positioning method by applying an optimization algorithm to the frequency response function (FRF) of the target system, where FRF is considered an objective function. Zoric et al. [12] presented optimal actuators’ sizes and locations over the first 5 modes of a smart cantilever beam by implementing fuzzy to transform controllability-based multi-objective function and constraints to pseudo-goal function, and hence, applied particle swarm optimization package to achieve the desired goal. Huang et al. [26] established an experimental platform of an aircraft framework to verify the proposed method of actuators and sensors distribution. The comparison between different optimization algorithms showed that  the genetic algorithm is more favorable than the particle swarm algorithm for the proposed system’s vibration suppression rate . Tarhini et al. [27] introduced a mixed integer nonlinear approach as an optimization tool to maximize the coverage of presumed control points by allocating PZT wafers at optimal positions. The precision  of such an approach was then experimentally validated through some different locations damage scenarios. Liu et al. [28] took advantage of topology optimization technique and assigned SPI as an objective function that has to be maximized to reveal the transformed energy from actuator to structure. The process was fulfilled by topology optimization of the PZT layer for different cases of boundary conditions and natural modes of the smart plates. Based on the analytical Euler–Bernoulli model, Muthalif et al. [29] employed ant colony optimization (ACO) verified with GA and the enumerative method (EM) to estimate proportional integral derivative (PID) controller gains, as well as the location of a single actuator under the influence of a single fixed excitation point for simply supported thin plate over low-frequency range. Optimization is based on minimizing frequency average energy. The optimal values of PZT sensor–actuator position and PID controller gains are verified experimentally.

The present work investigates the optimal placement of PZT actuators on a thin plate to serve both target functions of SHM and vibration control. Since the primary function of actuators in any vibration-based SHM system is to achieve the full excitation of the monitored structure at desired modes [30], the goal function of locating the PZT actuators is to maximize the exerted work done by the actuator. This criterion shall also fulfil the main target of the vibration control which is to overcome any undesired vibration especially at natural frequencies of interest [12, 23, 25] by placing PZT actuators where they can offer maximum work. Quek et al. [23] introduced the exerted work done by PZT actuator/s in order to select the starting point of optimization nearby the maximum strain location. However, they based their discrete optimization objective function on controllability model. In this paper, genetic algorithm (GA) is utilized to perform a continuous optimization problem directly based on the exerted work identified by Wang et al. and Quek et al. [23, 31] rather than to perform a discrete optimization based on controllability principle. In addition to the location of PZT actuator/s, the current research considers the PZT applied voltage as an optimization parameter.

Piezoelectric Constitutive Equations

Due to electro-mechanical coupling exhibited by piezoelectric materials, the conventional mechanical stress–strain relationship of such materials was modified to integrate electrical properties as well and connectivity between them. From Ikeda [32, 33], one of the main forms of 3D piezoelectric constitutive equations showing such coupling is stress–charge form:

$$\left[ {\begin{array}{*{20}c} {\left\{ \sigma \right\}} \\ {\left\{ D \right\}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {c^{E} } \right]} & { - \left[ e \right]^{T} } \\ {\left[ e \right]} & {\left[ { \in^{S} } \right]} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left\{ \varepsilon \right\}} \\ {\left\{ E \right\}} \\ \end{array} } \right]$$
(1)

The Eq. (1) can be expanded to Eqs. (2) and (3):

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ \end{array} } \\ {\sigma_{33} } \\ {\sigma_{23} } \\ \end{array} } \\ {\sigma_{13} } \\ {\sigma_{12} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {c_{11}^{E} } & {c_{12}^{E} } & {c_{13}^{E} } \\ {c_{12}^{E} } & {c_{11}^{E} } & {c_{23}^{E} } \\ {c_{13}^{E} } & {c_{23}^{E} } & {c_{33}^{E} } \\ \end{array} \begin{array}{*{20}c} {0_{{}}^{{}} } & {0_{{}}^{{}} } & {0_{{}}^{{}} } \\ {0_{{}}^{{}} } & {0_{{}}^{{}} } & {0_{{}}^{{}} } \\ { 0_{{}}^{{}} } & { 0_{{}}^{{}} } & {0_{{}}^{{}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {0_{{}}^{{}} } & { 0_{{}}^{{}} } & {0_{{}}^{{}} } \\ {0_{{}}^{{}} } & {0_{{}}^{{}} } & {0_{{}}^{{}} } \\ {0_{{}}^{{}} } & {0_{{}}^{{}} } & {0_{{}}^{{}} } \\ \end{array} \begin{array}{*{20}c} {c_{44}^{E} } & {0_{{}}^{{}} } & {0_{{}}^{{}} } \\ {0_{{}}^{{}} } & {c_{44}^{E} } & {0_{{}}^{{}} } \\ {0_{{}}^{{}} } & {0_{{}}^{{}} } & {c_{66}^{E} } \\ \end{array} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ \end{array} } \\ {\varepsilon_{33} } \\ {\varepsilon_{23} } \\ \end{array} } \\ {\varepsilon_{13} } \\ {\varepsilon_{12} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0_{{}} } & {0_{{}} } & {e_{31} } \\ {0_{{}} } & {0_{{}} } & {e_{31} } \\ {0_{{}} } & {0_{{}} } & {e_{33} } \\ \end{array} } \\ {\begin{array}{*{20}c} {0_{{}} } & {e_{15} } & {0_{{}} } \\ {e_{15} } & {0_{{}} } & {0_{{}} } \\ {0_{{}} } & {0_{{}} } & {0_{{}} } \\ \end{array} } \\ \end{array} } \right]\left\{ E \right\}$$
(2)
$$\left\{ {\begin{array}{*{20}c} {D_{1} } \\ {D_{2} } \\ {D_{3} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {e_{31} } & {e_{31} } & {e_{33} } \\ \end{array} \begin{array}{*{20}c} 0 & {e_{15} } & 0 \\ {e_{15} } & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ \end{array} } \\ {\varepsilon_{33} } \\ {\varepsilon_{23} } \\ \end{array} } \\ {\varepsilon_{13} } \\ {\varepsilon_{12} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} { \in_{11}^{S} } & 0 & 0 \\ 0 & { \in_{11}^{S} } & 0 \\ 0 & 0 & { \in_{33}^{S} } \\ \end{array} } \right]\left\{ E \right\}$$
(3)

For thin plate’s configuration, the normal stress in the thickness direction of the piezoceramic and the related transverse shear stress components are insignificant due to two-dimensional strain variations. [34] i.e \({\sigma }_{23}= {\upsigma }_{13}= {\upsigma }_{33}=0\).

Hence, Eqs. (2) and (3) are reduced to (4) and (5):

$$\left\{ {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\sigma_{12} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & {0_{{}} } \\ {Q_{12} } & {Q_{22} } & {0_{{}} } \\ {0_{{}} } & {0_{{}} } & {Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{12} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} 0 & 0 & {e^{\prime}_{31} } \\ 0 & 0 & {e^{\prime}_{31} } \\ 0 & 0 & 0 \\ \end{array} } \right]\left\{ E \right\}$$
(4)
$$\left\{ {\begin{array}{*{20}c} {D_{1} } \\ {D_{2} } \\ {D_{3} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {e^{\prime}_{31} } & {e^{\prime}_{31} } & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{12} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} { \in^{{s^{\prime}}}_{11} } & {0_{{}}^{{}} } & {0_{{}}^{{}} } \\ {0_{{}}^{{}} } & { \in^{{s^{\prime}}}_{22} } & {0_{{}}^{{}} } \\ {0_{{}}^{{}} } & {0_{{}}^{{}} } & { \in^{{s^{\prime}}}_{33} } \\ \end{array} } \right]\left\{ E \right\}$$
(5)

where

$$e^{\prime}_{31} = \frac{{d_{31} }}{{S_{11}^{E} + S_{12}^{E} }}$$
(6)
$$\in^{\prime s}_{11} = \int_{11}^{T} ; \; \in^{\prime s}_{22} = \int_{22}^{T} ; \; \in^{\prime s}_{33} = \; \in_{33}^{T} - \frac{{2d_{31} }}{{S_{11}^{E} + S_{12}^{E} }}$$
(7)

Analytical Model

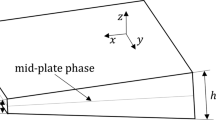
Kirchoff's classical laminate plate theory (CLPT) would be appropriate to simulate deflections and strains for the research object, since the goal study substrate structure is a thin plate (Fig. 1).

Fig. 1
figure 1

Deformation of a transverse normal plane according to classical laminate plate theory [35]

Full size image

Therefore, the displacement vector \(\left\{ U \right\}\) will be:

$$\left\{ U \right\} = \left\{ {U^{o} } \right\} + z\left\{ {U^{\prime}} \right\}$$
(8)

Displacements in the main axis directions x, y, and z (u, v, and w respectively) will be:

$$u\left( {x,y,z} \right) = u_{0} \left( {x,y,t} \right) - z\frac{{\partial w_{o} \left( {x,y} \right)}}{\partial x}$$
(9)
$$v\left( {x,y,z} \right) = v_{0} \left( {x,y,t} \right) - z\frac{{\partial w_{o} \left( {x,y} \right)}}{\partial y}$$
(10)
$$w\left( {x,y,z} \right) = w_{0} \left( {x,y,t} \right)$$
(11)

Hence, according to CLPT, strain–displacement relationships are:

$$\varepsilon_{xx} = \frac{\partial u}{{\partial x}} = \frac{{\partial u_{o} }}{ \partial x} - z \frac{{\partial^{2} w_{o} }}{{ \partial x^{2} }}$$
(12)
$$\varepsilon_{yy} = \frac{\partial v}{{\partial y}} = \frac{{\partial v_{o} }}{ \partial y} - z \frac{{\partial^{2} w_{o} }}{{ \partial y^{2} }}$$
(13)
$$\varepsilon_{zz} = \frac{\partial w}{{\partial z}} = 0$$
(14)
$$\varepsilon_{xy} = \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} = \frac{{\partial u_{o} }}{ \partial y} + \frac{{\partial v_{o} }}{ \partial x} - 2 z\frac{{\partial^{2} w_{o} }}{ \partial x\partial y}$$
(15)
$$\varepsilon_{yz} = \frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}} = - \frac{{\partial w_{o} }}{ \partial y} + \frac{{\partial w_{o} }}{ \partial y} = 0$$
(16)
$$\varepsilon_{xz} = \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}} = - \frac{{\partial w_{o} }}{ \partial x} + \frac{{\partial w_{o} }}{ \partial x} = 0$$
(17)

And finally can be summarized in:

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{o} }}{ \partial x}} \\ {\frac{{\partial v_{o} }}{ \partial y}} \\ {\frac{{\partial u_{o} }}{ \partial y} + \frac{{\partial v_{o} }}{ \partial x}} \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} { - \frac{{\partial^{2} w_{o} }}{{ \partial x^{2} }}} \\ { - \frac{{\partial^{2} w_{o} }}{{ \partial y^{2} }}} \\ { - 2\frac{{\partial^{2} w_{o} }}{ \partial x\partial y}} \\ \end{array} } \right\}$$
(18)

Or simply can be written:

$$\left\{ \varepsilon \right\} = \left\{ {\varepsilon^{o} } \right\} + z\left\{ {\varepsilon^{\prime}} \right\}$$
(19)

For a 2D isotropic thin plate, the stress–strain relationship will be reduced to:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\sigma_{12} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & {0_{{}} } \\ {Q_{12} } & {Q_{22} } & {0_{{}} } \\ {0_{{}} } & {0_{{}} } & {Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{12} } \\ \end{array} } \right\}$$
(20)

where

$$Q_{11} = \frac{{E_{1} }}{{1 - \nu_{12} \nu_{21} }},\;\;Q_{12} = Q_{21} = \frac{{\nu_{21} E_{1} }}{{1 - \nu_{12} \nu_{21} }} = \frac{{\nu_{12} E_{2} }}{{1 - \nu_{12} \nu_{21} }},\;Q_{66} = G_{12}$$
(21)

Based on Quek et al. [23], virtual work done by surface attached PZT actuator is defined as:

$$W = - \varphi \left[ {\left( {\overline{m}^{2} e_{31} + \overline{n}^{2} e_{32} } \right)\mathop \int \limits_{{\overline{\psi }}}^{{}} \varepsilon_{x} {\text{d}}\psi + \left( {\overline{m}^{2} e_{32} + \overline{n}^{2} e_{31} } \right)\mathop \int \limits_{{\overline{\psi }}}^{{}} \varepsilon_{y} {\text{d}}\psi } \right]$$
(22)

However, PZT is orthotropic material

$$x \equiv 1 , y \equiv 2 \;{\text{and}} z \equiv 3$$
(23)

And:

$$e_{31} = e_{32}$$
(24)

Substituting Eqs. (6), (21), (23), and (24) in Eq. (22), we can obtain the virtual work done by (n) actuators oriented to principle axes of the substrate:

$$W = \sum\limits_{i = 1}^{n} - \varphi^{i} \times e^{\prime}31^{i} \left[ {\int\limits_{{x_{1}^{i} }}^{{x_{2}^{i} }} {\int\limits_{{y_{1}^{i} }}^{{y_{2}^{i} }} {\varepsilon_{xx} } } {\text{d}}y {\text{d}}x + \int\limits_{{x_{1}^{i} }}^{{x_{2}^{i} }} {\int\limits_{{y_{1}^{i} }}^{{y_{2}^{i} }} {\varepsilon_{yy} } } {\text{d}}y {\text{d}}x} \right]$$
(25)

Ritz Solution Technique

The unknown displacements \({u}_{0}, {v}_{0},\mathrm{ and }{w}_{0}\) are approximated in the Ritz method by x–y-dependent approximation functions or interpolation functions that satisfy the geometric boundary conditions [36].

Therefore, displacements \({u}_{0}, {v}_{0},\mathrm{ and }{w}_{0}\) can be approximated using:

$$u_{o} \left( {x,y} \right) = \mathop \sum \limits_{i = 1}^{{N_{u} }} q_{1} \left( i \right) x^{mu\left( i \right)} y^{nv\left( i \right)} = \left\{ {a_{1} \left( {x,y} \right)} \right\}^{T} \left\{ {q_{1} } \right\}$$
(26)
$$v_{o} \left( {x,y} \right) = \mathop \sum \limits_{i = 1}^{{N_{v} }} q_{2} \left( i \right) x^{mv\left( i \right)} y^{nv\left( i \right)} = \left\{ {a_{2} \left( {x,y} \right)} \right\}^{T} \left\{ {q_{2} } \right\}$$
(27)
$$w_{o} \left( {x,y} \right) = \mathop \sum \limits_{i = 1}^{{N_{w} }} q_{3} \left( i \right) x^{mw\left( i \right)} y^{nw\left( i \right)} = \left\{ {a_{3} \left( {x,y} \right)} \right\}^{T} \left\{ {q_{3} } \right\}$$
(28)

Polynomial type interpolation functions are most widely used, which is handled by assuming adequate polynomial functions Eqs. (26, 27, and 28) for the simulated structure. Applying Ritz solution to CLPT assumptions of displacements (8–11):

$$\left\{ {U^{o} } \right\} = \left[ {\begin{array}{*{20}c} {\left\{ {a_{1} } \right\}^{T} } & 0 & 0 \\ 0 & {\left\{ {a_{2} } \right\}^{T} } & 0 \\ 0 & 0 & {\left\{ {a_{3} } \right\}^{T} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {q_{1} } \\ {q_{2} } \\ {q_{3} } \\ \end{array} } \right\} = \left[ {\overline{U}^{o} } \right]\left\{ q \right\}$$
(29)
$$\left\{ {U^{\prime}} \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{\partial \left\{ {a_{3} } \right\}^{T} }}{\partial x}} \\ 0 & 0 & { - \frac{{\partial \left\{ {a_{3} } \right\}^{T} }}{\partial y}} \\ 0 & 0 & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {q_{1} } \\ {q_{2} } \\ {q_{3} } \\ \end{array} } \right\} = \left[ {\overline{U}^{^{\prime}} } \right]\left\{ q \right\}$$
(30)

Performing the same process to the strains to (12–19):

$$\left\{ {\varepsilon^{o} } \right\} = \left[ {\begin{array}{*{20}c} {\frac{{\partial a_{1}^{T} }}{\partial x}} & 0 & 0 \\ 0 & {\frac{{\partial a_{2}^{T} }}{\partial y}} & 0 \\ {\frac{{\partial a_{1}^{T} }}{\partial y}} & {\frac{{\partial a_{2}^{T} }}{\partial x}} & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {q_{1} } \\ {q_{2} } \\ {q_{3} } \\ \end{array} } \right\} = \left[ {\overline{\varepsilon }^{o} } \right]\left\{ q \right\}$$
(31)
$$\left\{ {\varepsilon^{\prime}} \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{\partial^{2} a_{3}^{T} }}{{\partial x^{2} }}} \\ 0 & 0 & { - \frac{{\partial^{2} a_{3}^{T} }}{{\partial y^{2} }}} \\ 0 & 0 & { - 2\frac{{\partial^{2} a_{3}^{T} }}{\partial x\partial y}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {q_{1} } \\ {q_{2} } \\ {q_{3} } \\ \end{array} } \right\} = \left[ {\overline{\varepsilon }^{^{\prime}} } \right]\left\{ q \right\}$$
(32)

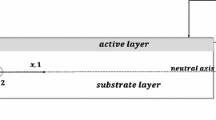
The variational formulas of strain and kinetic energies for the mechanical system composed of the substrate plate of thickness (ts) and (n) actuators of the same thickness (tz) attached to the plate surface Fig. 2, can be expressed as follows:

$$\delta V = \delta \left( {\frac{1}{2}\mathop \int \limits_{A}^{{}} \left\{ {\mathop \int \limits_{{z_{o} }}^{{z_{1} }} \left\{ \varepsilon \right\}^{T} \left[ Q \right]\left\{ \varepsilon \right\} {\text{d}}z} \right\}{\text{d}}A} \right)_{s} + \mathop \sum \limits_{i = 1}^{n} \delta \left( {\frac{1}{2}\mathop \int \limits_{{\overline{\psi }^{i} }}^{{}} \left\{ {\mathop \int \limits_{{z_{1} }}^{{z_{2} }} \left\{ \varepsilon \right\}^{T} \left[ Q \right]^{i} \left\{ \varepsilon \right\} {\text{d}}z} \right\}{\text{d}}\psi } \right)_{z}$$
(33)
$$\delta T = \delta \left( {\mathop \int \limits_{A}^{{}} \left\{ {\mathop \int \limits_{{z_{o} }}^{{z_{1} }} \rho_{s} \left[ {\left\{ {\dot{U}} \right\}^{T} \left\{ {\dot{U}} \right\}} \right] {\text{d}}z} \right\}{\text{d}}A} \right)_{s} + \mathop \sum \limits_{i = 1}^{n} \delta \left( {\mathop \int \limits_{{\overline{\psi }^{i} }}^{{}} \left\{ {\mathop \int \limits_{{z_{1} }}^{{z_{2} }} \rho_{z} \left[ {\left\{ {\dot{U}} \right\}^{T} \left\{ {\dot{U}} \right\}} \right] {\text{d}}z} \right\}{\text{d}}\psi } \right)_{z}$$
(34)
Fig. 2
figure 2

Configuration of attached PZT actuator to substrate plate

Full size image

By expanding variational formulas of Eqs. (33) and (34), stiffness and mass will be [37]:

$$K={\left({\int }_{A}{\int }_{{z}_{o}}^{{z}_{1}}({\left[{\overline{\varepsilon }}^{o}\right]}^{T} {\left[Q\right]}_{s} \left[{\overline{\varepsilon }}^{o}\right]+z\times {\left[{\overline{\varepsilon }}^{o}\right]}^{T}{\left[Q\right]}_{s}\left[{\overline{\varepsilon }}^{^{\prime}}\right]+z\times {\left[{\overline{\varepsilon }}^{^{\prime}}\right]}^{T}{\left[Q\right]}_{s}\left[{\overline{\varepsilon }}^{o}\right]+{z}^{2}\times {\left[{\overline{\varepsilon }}^{^{\prime}}\right]}^{T}{\left[Q\right]}_{s}\left[{\overline{\varepsilon }}^{^{\prime}}\right])\mathrm{d}z \mathrm{d}A\right)}_{s}+\sum_{i=1}^{n}{\left({\int }_{{\overline{\psi }}^{i}}{\int }_{{z}_{1}}^{{z}_{2}}({\left[{\overline{\varepsilon }}^{o}\right]}^{T}{\left[Q\right]}_{z}^{i}\left[{\overline{\varepsilon }}^{o}\right]+z\times {\left[{\overline{\varepsilon }}^{o}\right]}^{T}{\left[Q\right]}_{z}^{i}\left[{\overline{\varepsilon }}^{^{\prime}}\right]+z\times {\left[{\overline{\varepsilon }}^{^{\prime}}\right]}^{T}{\left[Q\right]}_{z}^{i}\left[{\overline{\varepsilon }}^{o}\right]+{z}^{2}\times {\left[{\overline{\varepsilon }}^{^{\prime}}\right]}^{T}{\left[Q\right]}_{z}^{i}\left[{\overline{\varepsilon }}^{^{\prime}}\right])\mathrm{d}z \mathrm{d}\psi \right)}_{z}$$
(35)
$${M=\rho }_{s}{\left({\int }_{A}{\int }_{{z}_{o}}^{{z}_{1}}({\left[{\overline{U} }^{o}\right]}^{T}\left[{\overline{U} }^{o}\right]+z\times {\left[{\overline{U} }^{o}\right]}^{T}\left[{\overline{U} }^{^{\prime}}\right]+z\times {\left[{\overline{U} }^{^{\prime}}\right]}^{T}\left[{\overline{U} }^{o}\right]+{z}^{2}\times {\left[{\overline{U} }^{^{\prime}}\right]}^{T}\left[{\overline{U} }^{^{\prime}}\right])\mathrm{d}z \mathrm{d}A\right)}_{s}+\sum_{i=1}^{n}{\rho }_{z}^{i}{\left({{\int }_{{\overline{\psi }}^{i}}{\int }_{{z}_{1}}^{{z}_{2}}({\left[{\overline{U} }^{o}\right]}^{T}\left[{\overline{U} }^{o}\right]+z\times {\left[{\overline{U} }^{o}\right]}^{T}\left[{\overline{U} }^{^{\prime}}\right]+z\times {\left[{\overline{U} }^{^{\prime}}\right]}^{T}\left[{\overline{U} }^{o}\right]+{z}^{2}\times {\left[{\overline{U} }^{^{\prime}}\right]}^{T}\left[{\overline{U} }^{^{\prime}}\right])\mathrm{d}z \mathrm{d}\psi }\right)}_{z}$$
(36)

Solving the Eigen value problem for the mechanical system described by Eqs. (35) and (36) yields to the natural frequencies as well as the corresponding modal shape matrices, which can be decomposed into the vector \(\left\{ {q_{i} } \right\}\) used to solve each mode of the extracted modes separately.

Iterative Optimization Process

To position the PZT actuator/s at the location where the virtual work done by them is maximized, initial approach is proceeded by maximizing the work Eq. (25). The function is based on the mechanical system strains (\(\varepsilon_{xx} \;{\text{and}}\;\varepsilon_{yy}\)) obtained initially by neglecting the mass and stiffness of actuators, when the location is initially assigned, actuator location is incorporated in the mechanical system Eqs. (35 and 36). Subsequently, process of maximization is repeated with the strains (\(\varepsilon_{xx} \;{\text{and}}\;\varepsilon_{yy}\)) of PZT mass and stiffness involved in the mechanical system in order to enhance localization tuning of actuators. This optimization process is iterated until convergence of PZT actuator is achieved.

To formulate optimization problem, GA optimization package offered by MATLAB software is performed for the unknown variables \(\left( {Xi,Yi,\varphi i} \right)\), and fitness function (W) obtained from Eq. (25). Population size is set to be 400, generation number is set to be 600, both mutation and crossover functions are set to be constraint-dependent, and both function tolerance and constraint tolerance are set to be zero.

The optimization problem formulation Fig. 3 can be expressed as:

$$\begin{gathered} {\text{Maximize}}\;\;W\left( {Xi,Yi,\varphi i} \right)\;\;\;i = 1,2,3, \ldots ..n \hfill \\ {\text{Subjected to}} 0 \le Xi \le A \hfill \\ 0 \le Yi \le B \hfill \\ - 1 \le \varphi i \le 1 \hfill \\ g_{{\left( {j,k} \right)}} \left( {Xi,Yi,\varphi i} \right) \ge 0\;\;\;\;j = n,n - 1,n - 2, \ldots ..,2\;\;k = 1,2, \ldots ..,\left( {j - 1} \right) \hfill \\ \end{gathered}$$
(37)

where \(g_{{\left( {j,k} \right)}} \left( {Xi, Yi, \varphi i} \right)\) are \(\left( m \right)\) constraints that avoid overlap between any actuators. However, their numbers are—

$$m = n^{2} - \mathop \sum \limits_{i = 1}^{n} i$$
(38)
$$g_{{\left( {j,k} \right)}} = \left| {\left( {X\left( j \right) - X\left( {j - k} \right)} \right) + \left( {Y\left( j \right) - Y\left( {j - k} \right)} \right)} \right| + \left| {\left( {X\left( j \right) - X\left( {j - k} \right)} \right) - \left( {Y\left( j \right) - Y\left( {j - k} \right)} \right)} \right| - 2l$$
(39)

where \(Xi\) and \(Yi\) are the coordinates of the ith actuator lower left corner.

Fig. 3
figure 3

Optimization problem configuration

Full size image

Numerical Examples

To examine the proposed methodology, an aluminum plate of dimensions 30 \(\times\) 50 cm and thickness of 1 cm is assumed to the test sample. The plate has a Young’s modulus (E) of 69 Gpa, density (\(\rho_{s}\)) of 2700 kg/m3 Poisson ratio (\(\nu\)) of 0.33. The specimen is equipped with APC850 4 \(\times\) 4 cm PZT actuator of thickness 1 mm with the properties shown in Table 1.

Table 1 Properties of APC850 material [38]
Full size table

Three cases of boundary conditions are assumed with single, double, and triple actuators per each boundary condition case, where several mode shapes are studied.

Cantilever Plate

The Ritz polynomials for such case were proposed by Abbas et al. [36] Eqs. (40–42):

$$\left\{ {a_{1} \left( {x,y} \right)} \right\}^{T} = \left[ {x xy x^{2} x^{2} y } \right]_{1 \times 4}$$
(40)
$$\left\{ {a_{2} \left( {x,y} \right)} \right\}^{T} = \left[ {x^{2} x^{2} y x^{3} x^{3} y } \right]_{1 \times 4}$$
(41)
$$\left\{ {a_{3} \left( {x,y} \right)} \right\}^{T} = \left[ {x^{2} x^{2} y x^{3} x^{2} y^{2} x^{3} y x^{4} x^{3} y^{2} x^{4} y x^{4} y^{2} } \right]_{1 \times 9}$$
(42)

The chosen polynomials verify the boundary conditions along the side where x = 0 (\(u_{o} ,v_{o} ,w_{o} ,\frac{{\partial w_{o} }}{\partial x}{\text{and}} \frac{{\partial v_{o} }}{\partial x}\) are equal to zero), Fig. 4a. Also the Eigen problem \(\left( {K,M} \right)\) of the proposed analytical model is solved, and the first four mode shapes as well as their corresponding frequencies are extracted, which are compared to those extracted from a numerical model established by ANSYS 22R1 software. The results shown in Table 2 show good agreement between the proposed model and the numerical one.

Fig. 4
figure 4

Configuration of Ritz problem for: a cantilever plate. b SSSF plate. C SSFF plate

Full size image
Table 2 Comparison between analytical and numerical simulation of cantilever plate shape modes
Full size table

Simple Simple Simple Free (SSSF) Plate

Al-Shugaa et al. [39] studied large deflection of orthotropic thin plates for mixed boundary conditions cases, among them (SSSF) shown in Fig. 4b. Ritz polynomial functions were introduced and verified to simulate the deflection of the aforementioned plate using Eqs. (43–45).

$$\left\{ {a_{1} \left( {x,y} \right)} \right\}^{T} = \mathop \sum \limits_{h = 0}^{2} \mathop \sum \limits_{i = 0}^{4} \left( {a^{2} - x^{2} } \right)x^{2i + 1} y^{h + 1}$$
(43)
$$\left\{ {a_{2} \left( {x,y} \right)} \right\}^{T} = \mathop \sum \limits_{h = 0}^{2} \mathop \sum \limits_{i = 0}^{4} \left( {a^{2} - x^{2} } \right)x^{2i} y^{h + 1}$$
(44)
$$\left\{ {a_{3} \left( {x,y} \right)} \right\}^{T} = \mathop \sum \limits_{h = 0}^{2} \mathop \sum \limits_{i = 0}^{6} \left( {a^{2} - x^{2} } \right)x^{2i} y^{h + 1}$$
(45)

Mode shapes of interest as well as their corresponding frequencies are obtained by solving Eigen problem \(\left( {K,M} \right)\), and then compared with numerical model developed with Ansys 22R1 where acceptable agreement was established. Table 3 presents the desired shape modes for both analytical and numerical models as well as their corresponding frequencies.

Table 3 Comparison between analytical and numerical simulation of (SSSF) plate shape modes
Full size table

Simple Simple Free Free (SSFF) Plate

This special case shown in Fig. 4c was introduced by many researchers, in order to present more diverse conditional boundary cases for deflection and vibration analysis of thin plates, such as Lopatin and Morozov [40], Pouladkhan et al. [41], etc. The trial polynomial required to satisfy the boundary conditions of such case along the side where x = 0 (\(\;v_{o} ,w_{o} \;{\text{and}}\;\frac{{\partial w_{o} }}{\partial y} { }\) are equal to zero), and along the side where y = 0 (\(u_{o} ,w_{o} {\text{and}}\frac{{\partial w_{o} }}{\partial x}\) are equal to zero), is found to be

$$\left\{ {a_{1} \left( {x,y} \right)} \right\}^{T} = \left[ {aby - ay^{2} - 2bxy - 2xy^{2} } \right]_{1 \times 4}$$
(45)
$$\left\{ {a_{2} \left( {x,y} \right)} \right\}^{T} = \left[ {abx - bx^{2} - 2axy - 2x^{2} y } \right]_{1 \times 4}$$
(46)
$$\left\{ {a_{3} \left( {x,y} \right)} \right\}^{T} = \left[ {xy \frac{{ - 2x^{3} y}}{{a^{2} }} \frac{{ - 2xy^{3} }}{{b^{2} }} \frac{{4x^{3} y^{3} }}{{a^{2} b^{2} }} \frac{{x^{4} y}}{{a^{3} }} \frac{{ xy^{4} }}{{b^{3} }} \frac{{ - 2x^{4} y^{3} }}{{a^{3} b^{2} }} \frac{{ - 2x^{3} y^{4} }}{{a^{2} b^{3} }} \frac{{x^{4} y^{4} }}{{a^{3} b^{3} }} } \right]_{1 \times 9}$$
(47)

Modal analysis is used to extract the first three mode shapes of proposed analytical model and their corresponding natural frequencies as well. The results are compared to numerical model established in ANSYS 22R1 software. The comparison shows good between the two models. Table 4 presents the comparison between analytical and numerical shape modes of such boundary condition case and their natural frequencies as well.

Table 4 Comparison between analytical and numerical simulation of (SSFF) plate shape modes
Full size table

Results and Discussion

The results of iterative GA-based optimization are summarized in the Tables 5, 6, and 7 in which the coordinates \(\left( {X_{i} ,Y_{i} } \right)\) of each actuator as shown in Fig. 3 are obtained in addition to the normalized volt acting on each actuator where the + ve sign denotes the voltage in same direction of the actuator polarity and the –ve sign denotes the voltage of opposite direction. Also, the actuators optimum locations are graphically dropped on the distribution diagram for the summation of strains in the x and y directions to show the relation between the strain and optimum location of actuators. The voltage load of the same polarity as the actuator poling voltage is assigned with black color border, while the voltage load of the opposite polarity is assigned with white border, Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14

Table 5 Optimum location coordinates for single actuator
Full size table
Table 6 Optimum location coordinates for double actuators
Full size table
Table 7 Optimum location coordinates for triple actuators
Full size table
Fig. 5
figure 5

Strains distribution of cantilever plate at 1st mode: a single actuator b double actuators c triple actuators

Full size image
Fig. 6
figure 6

Strains distribution of cantilever plate at 2nd mode: a single actuator b double actuators c triple actuators

Full size image
Fig. 7
figure 7

Strains distribution of cantilever plate at 3rd mode: a single actuator b double actuators c triple actuators

Full size image
Fig. 8
figure 8

Strains distribution of cantilever plate at 4th mode: a single actuator b double actuators c triple actuators

Full size image
Fig. 9
figure 9

Strains distribution of SSSF plate at 1st mode: a single actuator b double actuators c triple actuators

Full size image
Fig. 10
figure 10

Strains distribution of SSSF plate at 2nd mode: a single actuator b double actuators c triple actuators

Full size image
Fig. 11
figure 11

Strains distribution of SSSF plate at 3rd mode: a single actuator b double actuators c triple actuators

Full size image
Fig. 12
figure 12

Strains distribution of (SSFF) plate at 1st mode: a single actuator b double actuators c triple actuators

Full size image
Fig. 13
figure 13

Strains distribution of (SSFF) plate at 2nd mode: a single actuator b double actuators c triple actuators

Full size image
Fig. 14
figure 14

Strains distribution of (SSFF) plate at 3rd mode: a single actuator b double actuators c triple actuators

Full size image

It is worth telling that in the case of using odd number of actuators (single and triple actuators) for cantilever plate at 3rd mode, the optimum location kept altering between the two corners adjacent to the clamping side which is referred to symmetric concentration of the maximum strains at the both corners. So, locating of the actuator at any of them will give the same result. While, the axisymmetric distribution of strains led to equal amount of exerted work at the end corners, but with different sign when single and double actuators are used for the 2nd and 4th modes. Meanwhile, when three actuators are used at the 4th mode, the third actuator location doesn’t alter between the end corners; it is optimally placed at the shown strain peak that is arisen due to the configuration of the mode shape.

A very little variation in the distribution of normal strains as well as their values is noticed when the number of actuators is changed for some cases which is referred to the actuators mass and stiffness incorporated in the mechanical system. Another remarkable notice in Fig. 8b, where the actuators are optimally located in the vicinity of maximum strain points (not directly above them), happened because the integration of the normal strains with respect to the actuator area is the main effective component of the virtual work (i.e. the change of the size of actuator can lightly change its location).

Conclusion

Ritz polynomial functions solution is involved in CPLT to define the normal strains for a thin plate equipped with square PZT actuator/s with mixed boundary conditions. Hence, the virtual work done by the PZT actuator/s is expressed as a function of location and applied voltage. GA-based iterative optimization is used to achieve convergence of the optimum actuator/s location, as well as the value of the normalized voltage via simple and rapid steps. To precisely incorporate the effect of the mass and stiffness of PZT actuator/s and their location on the observed natural mode frequencies, an iterative optimization approach has been introduced. The results are compatible with those obtained by Quek et al. [23] optimization of controllability model for PZT actuators’ location. By implying real-value voltage in the operating limits of PZT with respect to optimum normalized voltage, the value of exerted virtual work can be increased. This process is valid for any mixed boundary conditions thin plate with any number of square actuators with a minimum computational effort.