Introduction

Mathematical modeling of a single-degree-of-freedom oscillator system with a mechanical spring and a motion limiter, as well as a periodically forced one, is a fairly common topic of consideration in scientific publications. Commonly used mathematical models of impact treated as soft and based on Hertzian contact stiffness and various damping models [1,2,3,4,5,6,7,8] do not allow for a precise description of the real impact. The precursors of works on this type of systems are articles by Shaw and Holmes [9, 10]. For example, in the work [1], an oscillator with one degree of freedom with periodic excitation and perfectly plastic impacts was analyzed. Discontinuous mappings that undergo period doubling bifurcations and other complex transitions resulting from discontinuities were used for modeling and analysis. Peterka and Vacik proposed in the work [2] an explanation of the rules of transition to chaotic motion and an illustration of both periodic and chaotic motion. In turn, Foale and Bishop [3] presented evidence that discontinuous bifurcations occurring in oscillators with shocks can be interpreted as the limits of classical bifurcations occurring in smooth dynamical systems. In works [11,12,13], some modifications of the soft impact models known from the literature were proposed, assuming a simple model of resistance in a linear bearing consisting of a constant component, dependent on the direction of movement, and a component proportional to the velocity. In the literature devoted to the study of mechanical systems with impacts, one can encounter rigid, usually based on the coefficient of restitution [1,2,3,4,5,6, 9, 10, 14,15,16,17] and soft models of impacts. Soft models assume local compliance (of obstacle or bumper) at the collision place, usually modeled based on Hertz theory or in the form of spring and damper configurations. In the work [18], the full form of the Hunt–Crossley model [19, 20] in the form of \(F=kh^{(n_1)}+\lambda h^{(n_2)} h^{(n_3)}\) was used to describe the impacts occurring in typical engineering devices, assuming the parameters k,\(n_1\), \(n_2\), \(n_3\) and \(\lambda\) as constants and with the aim of developing a computational tool to predict system dynamics. Moreover, in the work [21], an attempt was made to build discontinuous equivalents of the previously tested models of continuous impacts over time (so-called soft impacts) assuming the compliance of the obstacle. These models assume a step change in velocity based on the coefficient of restitution. Special algebraic functions were proposed to describe the dependence of the restitution coefficient on the velocity before the impact, as well as taking into account the duration of the impact, also described by special functions.

In addition, due to the widespread use of permanent neodymium magnets, the experimental magneto-mechanical system built as part of this work turns out to be a very good tool for testing, among others, magnetic vibration damper [22], magnetic springs as elements absorbing vibration energy [22, 23] or generating non-linear elasticity [24,25,26], etc. In the work [26], an oscillator with one degree of freedom and stiffness similar to that of Duffing oscillators. A pair of neodymium magnets set perpendicularly to the direction of motion in a position corresponding to the static equilibrium position of the oscillator with mechanical springs generated a system with two potential minima. Original stiffness functions were proposed, the parameters were identified and the obtained models were validated for five different versions of stiffness models.

In the present paper, it has been shown that the proposed continuous and discontinuous impact models [18, 21] and the adopted model of non-linear elasticity [26] can be used to study the bifurcation dynamics of an oscillator with a stiffness generating a double potential minimum and a one-sided motion limiter. The main purpose of the work was to compare the results obtained from the experiment and numerical calculations, proving that the mathematical model, which combines a new discontinuous impact model and a special odd form of the rational function describing the magnetic force, is a good tool for analyzing the dynamic behavior of the proposed oscillator configuration.

The work is divided into seven sections, where “Experimental Rig” is entirely devoted to the description of the construction and operation of the proposed experimental setup, and “Physical and Mathematical Model” presents mathematical modeling with particular emphasis on the proposed model of the magnetic interaction force and the comparison of the continuous and discontinuous model of the impact. In “Model Versions and Their Parameters”, different versions of the proposed models are described along with identification methods and their parameters are given. “Experimental and Numerical Investigations” presents results of validation of the proposed mathematical models made by numerical and experimental analysis of bifurcation dynamics of the investigated system. The last section presents concluding remarks and indicates the prospects for further applications of the adopted models.

Experimental Rig

Fig. 1
figure 1

Experimental stand of the investigated oscillator

Full size image

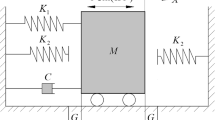
The experimental stand designed and constructed for the purposes of the research is shown in Fig. 1. It is a one-degree-of-freedom oscillator with an unilateral limiter (bumper) of motion (10) and inertial excitation generated by unbalanced mass \(m_0\) (1), moving at a constant radius of \(e=60\,\text{mm}\), placed on the disk (12) rotating in the axis of the servo motor (13). The main part of the oscillator is the cart (6) integrated with the Hall sensor (7), moving along the profile rail (8), at the top of which a magnetic tape (9) is glued in a specially made groove. The repeatability of angular position of the unbalanced mass (1) is achieved by using a slot optocoupler (14). The special non-linear stiffness is realized by the simultaneous action of mechanical springs (2) fixed in holders (11) placed on the trolley (3) and supports (15) and a pair of repulsive neodymium magnets (4) placed transversely to the movement of the cart, one of which is mounted on the cart and the other on the fixed plate (5).

Physical and Mathematical Model

Figure 2 shows the physical model of the real system (Fig. 1) investigated in this work. It is a combination of models of a one-degree-of-freedom oscillator with magnetic elasticity generating stiffness similar to Duffing type stiffness [26] and an oscillator with a one-sided motion limiter [21] The position of the cart of mass m is described by the x coordinate. It is assumed that in the initial position \(x=0\) (zero position) the forces of the springs with stiffness described as k/2 are balanced, and the axes of perpendicular neodymium magnets intersect the assumed position of static equilibrium. In addition to the force generated by the magnetic field between the magnets, the cart is subjected to a resistance force of linear bearings consisting of a viscous component \(c \dot{x}\) and a non-linear smoothed version of the rolling resistance with a model equivalent to the model of dry friction \(T \frac{\dot{x}}{\sqrt{{\dot{x}}^2+\epsilon ^2}}\), where T denotes a constant value of the resistance force and \(\epsilon\) is a regularization parameter of a function which is the equivalent of the signum function.

Fig. 2
figure 2

The physical model of the investigated oscillator

Full size image

The inertial excitation force \(f_0 \dot{\phi }^2 \sin \phi\) (where: \(f_0=m_0 e\)) is realized by rotation of the unbalanced mass \(m_0\) on the radius e with the angular frequency \(\dot{\phi }\). In the presented configuration, the adjustable distance in the equilibrium position \(x=0\) between the right-side stops is \(x_I\), and between the faces of the magnets is z.

Mathematical Model of the System with Hunt–Crossley Model of Collisions

Based on our previous works [18, 21, 26], we start the mathematical description of the physical concept presented in Fig. 2 with assumption of compliant impacts against the obstacle

$$\begin{aligned} m \ddot{x} + F_{R} (\dot{x}) + F_{SAi} (x) + F_I (x,\dot{x})=m_0 e {\dot{\phi }}^2 \sin \phi , \end{aligned}$$
(1)

where the total resistance force \(F_R\) is given by the formula

$$\begin{aligned} F_{R} (\dot{x})=c \dot{x} +T \frac{\dot{x}}{\sqrt{{\dot{x}}^2+\epsilon ^2}} , \end{aligned}$$
(2)

and \(F_{SAi}\) is the total elastic force coming from mechanical and magnetic springs, where \(Ai (i=1,3,5,\ldots ,n)\) according to [26] is a special nth degree model of elasticity

$$\begin{aligned} F_{SAn} (x)=kx+\frac{a_1 x+a_3 x^3+\cdots +a_n x^n}{1+b_2 x^2+b_4 x^4\cdots +b_{n+1} x^{n+1}}, \end{aligned}$$
(3)

where \(a_i\) and \(b_i\) are some constant parameters.

The impact force is modelled based on the following function (generalized Hunt–Crossley model) [21]

$$\begin{aligned} F_I=\left\{ \begin{array}{ll} k_I (h^{n_1}+h^{n_2} b |\dot{h}|^{n_3} \text{sign} \dot{h})\\ \quad \text{for}\ h^{n_1}+h^{n_2} b \dot{h} |\dot{h}|^{n_3-1} \ge 0\\ 0 \\ \quad \text{for}\ h^{n_1}+h^{n_2} b \dot{h} |\dot{h} |^{n_3-1} < 0, \end{array}\right. \end{aligned}$$
(4)
$$\begin{aligned} h= \left\{ \begin{array}{ll} x-x_I &{}\quad \text{for}\ x \ge x_I \\ 0 &{}\quad \text{for}\ x<x_I, \end{array}\right. \end{aligned}$$
(5)

where \(k_I\) and b are the coefficients of stiffness and damping, h is the obstacle penetration, while \(n_1\), \(n_2\) and \(n_3\) are other parameters of the contact with obstacle.

Mathematical Model of the System with Discontinuous Model of Collisions

In this section, we present, based on work [21], a discontinuous equivalent of the Hunt–Crossley impact model described in “Mathematical Model of the System with Hunt–Crossley Model of Collisions”. It is proposed operation of this model in the following three regimes:

  1. I.

    Free motion of the oscillator, where the following governing equations of motion is valid:

    $$\begin{aligned} &m \ddot{x} + F_{R} (\dot{x})+F_{SAi} (x)=m_{0e} \dot{\phi }^{2} \sin \phi \\ &\quad \text{for}\ x<x_{I}. \end{aligned}$$
    (6)
  2. II.

    Temporary sticking of the oscillator and obstacle during a collision in which the following equation is satisfied

    $$\begin{aligned} x(t)=x_I \quad \text{for}\ t<t^+ . \end{aligned}$$
    (7)
  3. III.

    Permanent contact of the cart and obstacle, when the following relations holds

    $$\begin{aligned} x(t)=x_I \quad {\texttt{for}}\ m_0 e \phi ^2 \sin \phi -F_{SAi} (x)>0 . \end{aligned}$$
    (8)

In addition, the models in Eqs. 6, 7, and 8 are supplemented by the following dependencies

$$\begin{aligned} t^+=t^-+T_{\textrm{imp}}, \end{aligned}$$
(9)
$$\begin{aligned} v^+=-\kappa \cdot v^-, \end{aligned}$$
(10)
$$\begin{aligned}{} T_{\textrm{imp}} (v^- )=(T_{i0}-T_{i1} ) \exp (-\alpha _{Ti} |v^- |)+T_{i1}, \end{aligned}$$
(11)
$$\begin{aligned} \kappa (v^- )=(\kappa _0-\kappa _1 ) \exp (-\alpha _\kappa |v^- |)+\kappa _1, \end{aligned}$$
(12)

where \(T_{\textrm{imp}}\) is the impact duration; \(\kappa -\) the restitution coefficient; \(t^-\), \(v^- (t^+,v^+)\)—time and velocity at the end of mode I (model II). \(T_{i0}\), \(_0\), \(T_{i1}\), \(\kappa _1\), \(\alpha _{Ti}\), \(\alpha _{\kappa }\) are the system parameters. At the end of mode I, when an obstacle is detected \((x= x_I),\) there is always a transition to mode II. At the end of mode II, for \(t=t^+\), there is checked the condition: \(|v^+|<\epsilon _v\) and \(m_0 e \dot{\phi }^2 \sin \phi -F_{SAi} (x)>0\), where \(\epsilon _v\) the threshold value of the post-impact velocity (it was assumed to be equal to \(10^{-4}\,\text{m}/\text{s}\)). If this condition is true, the system goes to mode 3, otherwise, returns to mode 1 with the initial speed \(v^+\). At the end of mode 3, when the normal force \(m_0 e\dot{\phi }^2 \sin \phi -F_{SAi} (x)\) crosses zero, the system goes back to mode 1 with zero initial velocity. For more details see the work [21].

Model Versions and Their Parameters

The experimental stand examined in the current work was created on the basis of a system with Duffing stiffness, which was the object of research in the work [26], by adding to it the same buffer as used in the works [18, 21]. For this reason, in the current work, certain types of models with all their parameters (concerning the excitation amplitude, resistance in bearings and total stiffness) were used on the basis of work [26] and relevant fragments of models from works [18, 21] concerning only impacts of the oscillator against the bumper were added to them, with the parameter \(x_I=0\). No additional parameter identification was performed here. Thus, based on the work [26], the total mass of the oscillator \(m=6.73766\,\text{kg}\) (determined on the basis of direct measurements) and the regularization coefficient of the model \(\epsilon = 10^{-6}\,\text{m}/\text{s}\) are assumed here. Other parameters adopted here were identified in that work on the basis of selected periodic orbits, for selected versions of the model of elastic forces, which are presented in Table 1. The models A1 and A3 denote different degrees of model of elasticity (3). The parameters of the impact models are taken from works [18, 21], where they were identified on the basis of vanishing free vibrations with impacts. The selected versions of these models used in the current work with the corresponding parameters are presented in Tables 2 and 3. The versions of Hunt–Crossley models are denoted by the symbols C and C1, where the exponents \(n_1=n_2= 1.5\) are not identified. In the case of model C, the obstacle stiffness \(k_I\) belongs to the set of estimated parameters. In model C1, it is assumed to be high \((k_I=10^{12}\,\text{N}/\text{m}^{3/2}),\) thus the impacts can be regarded as infinitely short events. Discontinuous models of impacts are denoted by symbol G and H. In the case of model H all the parameters are estimated, i.e. it is assumed variable impact duration and restitution coefficient. In model G some of the parameters are predefined and not identified, so that the model G is characterized by a variable coefficient of restitution but the impact duration time is equal to zero. In the current work, the combined model will be validated, which has been marked as XY, where \(X = A1\), A3 means the type of stiffness model, and \(Y=C, C1, G, H\) means the impact model.

Table 1 Model versions with parameter values for the system without obstacle [26]
Full size table
Table 2 Hunt–Crossley model versions of impact with the corresponding parameter values [18, 21]
Full size table
Table 3 Discontinuous model versions of impact with the corresponding parameter values [21]
Full size table

Experimental and Numerical Investigations

In the current section, we present the results of experimental validation of mathematical models presented in “Physical and Mathematical Model” and “Experimental and Numerical Investigations”. The first panel of Fig. 3 (EF) exhibits experimental forcing, i.e. time history of angular velocity \(\dot{\phi }(t)=\omega (t)\) applied in the experiment. It increases slowly and linearly until it reaches 25.1 rad/s after time 2800 s, after which it quickly drops to zero. The chart also shows a window showing the time and frequency ranges, for which the other bifurcation plots presented in this figure were made. They are only made for increasing frequency \(\omega (t)\). The next panel (Experiment-EF) shows the experimental bifurcation diagram, in which the position of the real system was sampled at moments of time meeting the condition \(\phi =2\pi i\) \((i\in Z),\) where \(\phi\) is the angular position of the unbalance mass, for slowly increasing frequency of experimental forcing according to the plot situated above. The next plot (Model A1C-EF) shows the same kind of bifurcation diagram obtained numerically for the model A1C and for the same forcing time history as used in the experiment (EF). In the next panel (Model A1C-CF), there is a numerical bifurcation diagram for the same model (A1C), but for a differently constructed time history of forcing frequency changes, called here “classical changes” (CF). It means that the bifurcation diagram consists of 300 Poincaré sections computed for 300 constant values of the forcing frequency \(\omega\) uniformly spanned over the interval (0, 25) rad/s. Each Poincaré map consists of 70 points corresponding to the steady state motion after ignoring the 20 points of the transient motion starting from the final state of the previous Poincaré map. This diagram was made in order to compare it with the diagram obtained for the continuous change of excitation frequency and check whether the speed of this continuous change is not too high. Comparing the two diagrams (Model A1C-EF and Model A1C-CF), it can be concluded that there are no significant differences between them and that the continuous change of excitation frequency used in the experiment is appropriate. Therefore, the remaining four panels of Fig. 3 exhibit bifurcation diagrams of the same type (for “classical changes” of bifurcation parameter) and for other versions of the model (Model A1C1-CF, Model A3C-CF, Model A1G-CF, Model A1H-CF). The observation of the bifurcation diagram in Fig. 3 allows us to conclude that certain phenomena occur in the real system and in all versions of the models shown here and they are as follows. For small excitation frequencies, the oscillator is in a position close to \(x=0\), it does not oscillate or the oscillations are so small that they are invisible. With an increase in the excitation frequency, for its certain value, there is observed a sudden jump to a periodic orbit with a period equal to the period of forcing. Subsequently, this periodic attractor undergoes period doubling bifurcation and then goes into a chaotic regime. Only in the case of models A1C1 and A1G, this regime is interrupted by a very wide periodic window, and in the case of other models and in the real system, this window does not occur. However, for each mathematical model and during the experiment, this chaotic region ends in an inverted period doubling cascade and returns to a period-1 orbit. In general, there is a very good agreement between the bifurcation dynamics of particular mathematical models and the dynamics observed during the experiment. Only the models A1C1 and A1G show slightly different dynamics and less agreement with the experiment. It is worth noting that both of these models are characterized by an infinitely or negligibly short duration of the impact. So the duration of the impact turns out to be important in modeling the dynamics of the system. Both of the applied models of elastic forces (A1 and A3) work well in modeling the tested system.

Fig. 3
figure 3

Time history of angular velocity \(\dot{\phi }(t)=\omega (t)\) applied in the experiment-(EF); experimental bifurcation diagram (Experiment-EF); numerical bifurcation diagram for the A1C model obtained for the experimental forcing (Model A1C-EF); five numerical bifurcation diagrams obtained for the“classic”change in forcing frequency (Model A1C, A1C1, A3C, A1G, A1H-CF)

Full size image

Concluding Remarks

In this work we validated previously developed models of non-linear elasticity containing an odd form of a rational function and impact models, continuous—based on the generalized Hunt–Crossley model and discontinuous—based on a special algorithm switching between different regimes and functions describing the restitution coefficient and impact duration.

The main and original achievements of the work include:

  1. 1.

    Construction of an original experimental system with non-linear stiffness and a one-sided motion limiter, which is a combination of systems previously studied by the authors.

  2. 2.

    Development of a mathematical model of the tested system by combining previously used model.

  3. 3.

    Successful validation of the mathematical model, paying attention to its different versions and elements.

  4. 4.

    Demonstrating that the impact duration is an important element of impact modeling in the tested system.

  5. 5.

    Particularly noteworthy is the positive validation of the discontinuous model, presented for the first time in [21], for the next configuration of the experimental setup.

From pt. 4 it results that the application of the classical discontinuous impact model based on the restitution coefficient and infinitely short duration of the impact cannot lead to satisfactory results when simulating real systems with collisions. A certain solution may be to use here a model with a compliant obstacle of the Hunt–Crossley type, but it involves a greater computational effort. An alternative is the discontinuous model with finite duration of the collision tested in this work, which, as shown, allows to obtain results as good as the Hunt–Crossley model.